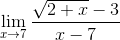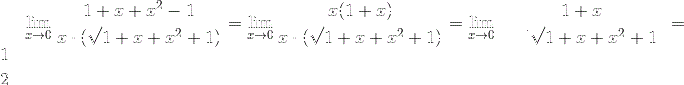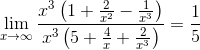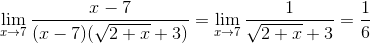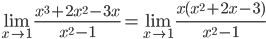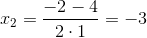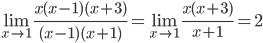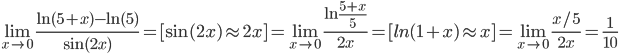Решение пределов
Число A называется пределом функции y=f(x) в точке x0, если для любой последовательности точек из области определения функции, отличных от x0, сходящейся к точке x0(lim xn = x0), последовательность соответствующих значений функции сходится к числу A.
- Решение онлайн
- Видеоинструкция
- Оформление Word
- Также решают
Если выбрать вид предела, то подробное решение по шагам будет доступно в MS Word:
1. Не знаю
2. Пределы вида 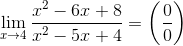
3. Вычислить предел, используя правило Лопиталя.
4. Пределы простейших иррациональности вида
5. Нахождение пределов, используя свойства первого замечательного предела ,
6. Нахождение пределов, используя свойства второго замечательного предела ,
,
Для нахождения предела слева
используйте знак -, справа
: +. Например, 0-, 1+
Примечание: число «пи» (π) записывается как pi, знак ∞ как infinity
Некоторые виды записи пределов
Например, найти предел 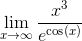
см. также нахождение пределов, используя свойства первого замечательного предела и второго замечательного предела.
Примеры.
Вычислить указанные пределы:
1. 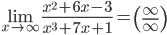
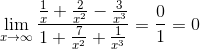
2. 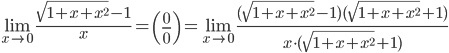
3. 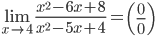
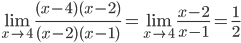
4. 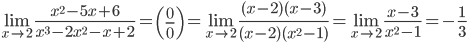
5. 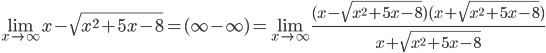
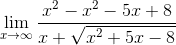
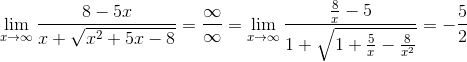
6. 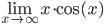
7. 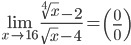
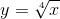
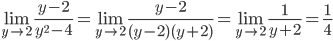
8. 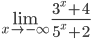
9. 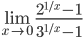
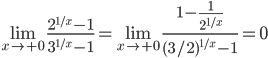
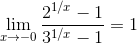
Следовательно, 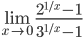
Найти пределы функции, не применяя правило Лопиталя.
а)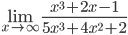
Ответ: 1/5
б) 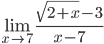
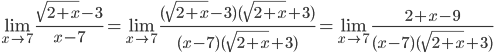
Ответ: 1/6
в) 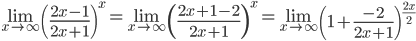
e-2/2 = e-1
Ответ: 1/e
г)
Так как числитель и знаменатель обратились в нуль при x=1, то 1 – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет (x-1).
Найдем корни первого многочлена: x2+2x-3=0
D=22-4•1•(-3)=16
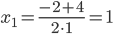
Найдем корни второго многочлена: x2-1=(x-1)(x+1)
Получаем:
Ответ: 2
д) 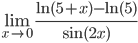
Ответ: 1/10
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Подборка онлайн калькуляторов для полного исследования функции и построение графика.
Найти Область определения функции
Вычислить Четность функции
Периодичность функции
Вычисление точек пересечения графика с осью (нули функции)
Промежутки знакопостоянства
Асимптоты функции
Найти экстремумы функции
Точки перегиба, интервалы выпуклости и вогнутости
Построить график функции
even – четная функция;
odd – нечетная функция;
neither even nor odd – функция общего вида;
Для нахождения интервалов на которых функция положительна используйте знак «>»
для интервалов на которых функция отрицательна используйте знак «<«.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки
Примеры
-
y=frac{x^2+x+1}{x}
-
f(x)=x^3
-
f(x)=ln (x-5)
-
f(x)=frac{1}{x^2}
-
y=frac{x}{x^2-6x+8}
-
f(x)=sqrt{x+3}
-
f(x)=cos(2x+5)
-
f(x)=sin(3x)
- Показать больше
Описание
Изучите функции шаг за шагом
functions-calculator
ru
Блог-сообщения, имеющие отношение к Symbolab
Functions
A function basically relates an input to an output, there’s an input, a relationship and an output. For every input…
Read More
Введите Задачу
Сохранить в блокнот!
Войти

Ограниченность функции
Функция у = f(x) называется ограниченной, если ее область значений ограничена, т. е. если все ее значения лежат на каком-нибудь конечном промежутке. В противном случае функцию называют неограниченной.
Примеры функций, ограниченных на всей области определения:
Замечание 1. Можно дать следующее определение ограниченности функции: функция у = f(x) называется ограниченной на всей области определения D(f), если существует такое число С>0, что |f(x)|≤C для каждой точки x∈D(f).
Замечание 2. Функция y = f(x) называется ограниченной на множестве X⊂D(f), если существует такое число С>0, что |f(x)|≤C для каждого х є X.
Функция, ограниченная на некотором множестве X⊂D(f), может быть неограниченной на всей области определения. Например, функция у = 1/х ограничена при х є [1/10;10], но на всей области определения она является неограниченной.
Монотонность функции
Функция у = f(x) называется возрастающей на данном числовом промежутке X, если большему значению аргумента хєX соответствует большее значение функции f(x), т. е. для любых x1,х2ЄX из x2>x1 => f(x2)>f(x1).
Функция у = f(x) называется убывающей на данном числовом промежутке X, если большему значению аргумента хєX соответствует меньшее значение функции f(x), т. е. для любых x1,х2ЄX из x2>x1 => f(x2)<f(x1).
Функция, только возрастающая или только убывающая на данном числовом промежутке, называется монотонной на этом промежутке.
Примеры монотонных функций на всей области определения:
Функция у =x² не является монотонной на всей области определения, однако при хє(—∞;0) она является убывающей, а при хє(0;+∞) у = х² является возрастающей. Функция y=sinx не является монотонной на всей области определения, однако внутри каждого из интервалов
она является возрастающей, а внутри каждого из интервалов
— убывающей.
Предел по-шагам

Примеры пределов
- Пределы от рациональных дробей на бесконечности
-
(x - 1)/(x + 1)
-
(x^3 + 2*x - 1)/(-7*x^3 - 4*x^2)
- Пределы от рациональных дробей в конечной точке
-
(x - 1)/(sqrt(x) - 1)
- Пределы от дроби в нуле
-
log(x)/x
- Первый замечательный предел
-
sin(7*x)/x
-
(1 - cos(x)^2)/x^2
- Второй замечательный предел
-
(1 - 7/x)^x
-
(1 + x/2)^((5*x + 3)/x)
- Пределы с квадратными корнями
-
sqrt(x + 5) - sqrt(x + 2)
-
x - sqrt(x^2 - 7)
- Правило Лопиталя
-
(e^(x) - x^e)/(x - e)
-
log(1+2*x^2)/x
Что умеет калькулятор пределов?
- Детальное решение для указанных методов:
- Правило Лопиталя
- Теорема о двух милиционерах
- Второй замечательный предел
- Разложение функции на множители
- Использование замены
- Первый замечательный предел
- Типы пределов:
- От одной переменной
- На бесконечности
- Односторонние пределы
- Строит график функции и её предела
- Предлагает другие пределы
Подробнее про Предел функции
.
Указанные выше примеры содержат также:
- модуль или абсолютное значение: absolute(x) или |x|
-
квадратные корни sqrt(x),
кубические корни cbrt(x) -
тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - показательные функции и экспоненты exp(x)
-
обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x),
арккотангенс acot(x) -
натуральные логарифмы ln(x),
десятичные логарифмы log(x) -
гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x),
гиперболический тангенс и котангенс tanh(x), ctanh(x) -
обратные гиперболические функции:
гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x),
гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x) -
другие тригонометрические и гиперболические функции:
секанс sec(x), косеканс csc(x), арксеканс asec(x),
арккосеканс acsc(x), гиперболический секанс sech(x),
гиперболический косеканс csch(x), гиперболический арксеканс asech(x),
гиперболический арккосеканс acsch(x) -
функции округления:
в меньшую сторону floor(x), в большую сторону ceiling(x) -
знак числа:
sign(x) -
для теории вероятности:
функция ошибок erf(x) (интеграл вероятности),
функция Лапласа laplace(x) -
Факториал от x:
x! или factorial(x) - Гамма-функция gamma(x)
- Функция Ламберта LambertW(x)
-
Тригонометрические интегралы: Si(x),
Ci(x),
Shi(x),
Chi(x)
Правила ввода
Можно делать следующие операции
- 2*x
- — умножение
- 3/x
- — деление
- x^2
- — возведение в квадрат
- x^3
- — возведение в куб
- x^5
- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- Действительные числа
- вводить в виде 7.5, не 7,5
Постоянные
- pi
- — число Пи
- e
- — основание натурального логарифма
- i
- — комплексное число
- oo
- — символ бесконечности