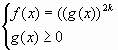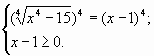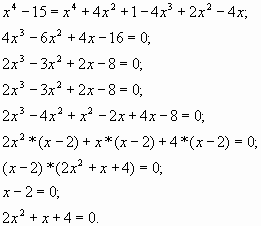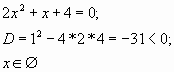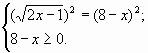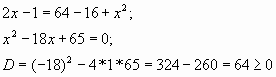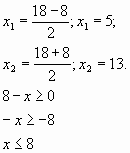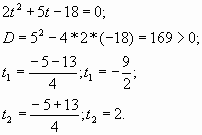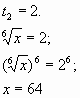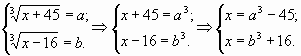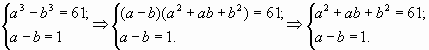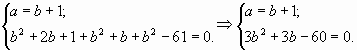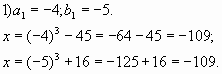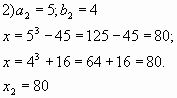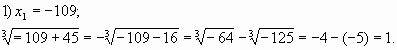Как найти одз иррационального уравнения

Иррациональные уравнения. Можно ли писать ОДЗ?

Анна Малкова

Иррациональными называются уравнения, содержащие знак корня – квадратного, кубического или n-ной степени.

Мы помним из школьной программы: как только в уравнении или неравенстве встретились корни, дроби или логарифмы – пора вспомнить про область допустимых значений (ОДЗ) уравнения или неравенства.

По определению, ОДЗ уравнения (или неравенства) – это пересечение областей определения всех функций, входящих в уравнение или неравенство.

Например, в уравнении присутствует арифметический квадратный корень . Он определен
при .

В 2018-2019 году среди учителей появилось такое мнение, что писать слова «область допустимых значений» уже не модно. И что за это даже могут снизить оценку на экзамене.

Нет, оценку не снизят. И основных понятий школьной математики никто не отменял. Однако есть еще лучший способ оформления решения – в виде цепочки равносильных переходов. Смотрите, как решать и оформлять иррациональные уравнения:

1. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Выражение под корнем должно быть неотрицательно. И сам корень – величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе:

Повторим, что решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов. Если вы не очень хорошо понимаете, что такое система уравнений и совокупность уравнений, — повторите эту тему.

или

В ответ запишем меньший из корней: — 9.

Теперь уравнение, в котором есть ловушка.

2. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Что получилось у вас? Правильный ответ: . Если у вас получилось – это был посторонний корень. Запишите решение в виде цепочки равносильных переходов, как в задаче 1, и вы поймете, что
не может быть корнем этого уравнения.

3. Решите уравнение:

Запишем решение как цепочку равносильных преобразований. Учитесь читать такую запись и применять ее.

Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю, а другие при этом не теряют смысла.

4. Решите уравнение:

Ответ: или .

А теперь сложное уравнение. Как это часто бывает, нас выручит замена переменной.

Причем новая переменная будет не одна, а целых две.

5. Решите уравнение

Найдем ОДЗ:
.

Мы можем, как в задаче 10, возвести обе части уравнения в квадрат. Но после этого придется еще раз возводить в квадрат, а это долгий способ.

Есть короткий путь!

Сделаем замену: , .

Выразим через и :

и . Это выражения можно приравнять друг к другу.

Получим систему

Решим одно из уравнений. Все равно, какое, — ведь нам надо найти .

Ответ: . Заметим, что является также и корнем уравнения

Что такое иррациональные уравнения?

Не секрет же, что большинство чисел можно представить в виде обыкновенной дроби с натуральными числами в числителе и знаменателе?

Например, число 7 – это (frac{21}{3})

Иррациональные числа не такие. Их невозможно представить в виде дроби. Они странные.

Гиппас создал античным математикам множество проблем: их теории о том, что все в мире соизмеримо целым числам, рушились одна за другой. И они боялись.

Но мы будем смелыми 🙂

Сначала разберемся, что такое рациональные уравнения, а потом научимся находить решение иррациональных уравнений.

Итак, что из себя представляют рациональные уравнения, а что – иррациональные:

• ( 3cdot (x+1)=x) – как думаешь, какое это? Тут сложение, умножение, нет корней, и степеней никаких – рациональное!
• ( 3cdot (x+1)=sqrt{x}) – вот тебе и корень из переменной, значит уравнение НЕ рациональное (или иррациональное);
• ( 3cdot (x+1)=frac{1}{x}) – а это – рациональное;
• ( 3cdot (x+1)={{x}^{2}}) – тут вот степень, но она с целым показателем степени (( 2)– целое число) – значит, это тоже рациональное уравнение;
• ( 3cdot (x+1)={{x}^{-1}}) – даже уравнение с отрицательным показателем степени тоже является рациональным, ведь, по сути, ( {{x}^{-1}}) – это ( frac{1}{x});
• ( 3cdot (x+1)={{x}^{0}}) – тоже рациональное, т.к. ( {{x}^{0}}=1);
• ( 3cdot (x+1)={{x}^{frac{1}{2}}}) – а с ним поосторожнее, степень-то дробная, а по свойству корней ( {{x}^{frac{1}{2}}}=sqrt{x}), как ты помнишь, корня в рациональных уравнениях не бывает.

Надеюсь, теперь ты сможешь различить, к какому виду относится то или иное уравнение.

Дадим oпределение:

Иррациональными уравнениями называются уравнения, в которых переменная содержится под знаком корня или знаком возведения в дробную степень. 

А вот как это выглядит: ( sqrt{x}); ( {{x}^{frac{1}{3}}}).

Но только отличать рациональное от иррационального недостаточно, тебе же решать их надо! Вся сложность в корнях, так?

Так избавься от них, вот и все дела!

Если еще не догадался, как, то я подскажу: просто возведи в нужную степень обе части уравнения, а потом решай его как простое рациональное уравнение.

Но проверяй все корни! Позже ты поймешь, почему делать это необходимо.

Как рациональные уравнения решать помнишь? Если забыл, то советую почитать «Рациональные уравнения».

Если читать лень, напомню вкратце. Для верного решения рациональных уравнений, ты должен придерживаться следующего алгоритма:

Пример №3

( sqrt{12-x}=x)

После возведения обеих частей в квадрат имеем:

( 12-x={{x}^{2}}), упрощаем и решаем квадратное уравнение по теореме Виета

( {{x}^{2}}+{x}-12=0)

( left[ begin{array}{l}{{x}_{1}}=3\{{x}_{2}}=-4end{array} right.)

У нас два корня, пробуем их подставить в исходное для проверки.

Подставляем ( 3), ( sqrt{9}=3), ( 3=3) – подходит.

Подставим ( -4), получим ( sqrt{16}=-4)…

Но ведь ( 4ne -4)! Что же получается, ( -4) – посторонний корень.

Заговор какой-то!

Думаю, интрига затянулась, настало время объяснить, почему получаются какие-то посторонние корни.

Опять объяснять буду на примере:

( -2ne 2), но если мы возведем в квадрат обе части, ( {{(-2)}^{2}}={{(2)}^{2}}), ( 4=4).

Ну как тебе фокус? 🙂

То же самое получается и в нашем примере с иррациональным уравнением, в результате преобразования мы можем найти все корни, но могут примешаться и посторонние.

Их надо отфильтровать проверкой, проверив, будет ли соблюдаться равенство исходного уравнения при их подстановке.

А если взять не вторую, а третью степень:

( {{(-2)}^{3}}ne {{(2)}^{3}})

( -8ne

Пример №4 (метод уединения радикала)

( sqrt{2x+1}+sqrt{x}=1)

В этом примере есть два подкоренных выражения и число ( 1).

Чтобы избавиться от корня, нужно обе части возвести в квадрат, но, прежде чем сделать это, перенесем ( sqrt{x}) в правую часть. 

( sqrt{2x+1}=1-sqrt{x})

«Зачем?» –  спросишь ты.

Дело в том, что, если возводить в квадрат в таком виде, упрощать придется дольше, не веришь – попробуй сам, а я, пожалуй, избавлю себя от расписывания этого 🙂

Теперь возводим в квадрат обе части и упрощаем.

Этот метод решения математики называют «метод уединения радикала».

Радикал (выражение с корнем) надо уединить в одной стороне уравнения. Но уединять и возводить в степень придется не один раз.

Чтобы избавиться от корней и получить нормальное (рациональное 🙂 ) уравнение, придется выполнять множество замысловатых махинаций, которые заключаются в уединении и возведении в степень.

С другой стороны, можно заметить, что на определенной стадии решения становится без дальнейших упрощений понятно, что в уравнении, например, нет решений.

Например…

Корни степени больше 2

Ты спросишь: а что всё про квадратные корни? Как же быть с остальными степенями?

Спрошу в ответ: а чем они отличаются?

Отличие, на самом деле, есть. Но важна не конкретная степень корня, а четность этой степени.

Корни четной степени

Корни ( displaystyle 2), ( displaystyle 4), ( displaystyle 6), и т.д. степеней очень похожи друг на друга, и принцип решения уравнений с ними абсолютно одинаковый. Дело в том, что корень четной степени можно всегда привести к квадратному (вспоминаем тему «Корень и его свойства»!):

( displaystyle sqrt[4]{x}=sqrt{sqrt{x}};text{ }sqrt[6]{x}=sqrt{sqrt[3]{x}};text{ }sqrt[2k]{x}=sqrt{sqrt[k]{x}})

Например:

( displaystyle sqrt[4]{A}=Btext{ }Leftrightarrow text{ }left{ begin{array}{l}A={{B}^{4}}\Bge 0end{array} right.)

Корни нечетной степени

С нечетными степенями (( displaystyle 3), ( displaystyle 5), …) все намного проще!

Дело в том, что корень нечетной степени можно извлекать из любого числа! (И снова, если ты этого не знал, вспомни тему «Корень и его свойства»!)

Что это значит?

Теперь никаких дополнительных условий, никаких ограничений – просто возводим все в нужную степень и решаем:

( displaystyle begin{array}{l}sqrt[3]{A}=Btext{ }Leftrightarrow text{ }A={{B}^{3}}\sqrt[5]{A}=Btext{ }Leftrightarrow text{ }A={{B}^{5}}end{array})

Примеры:

• ( displaystyle sqrt[5]{2-x}=-2)
• ( displaystyle sqrt[4]{3+2{x}-{{x}^{2}}+{{x}^{4}}}=x)
• ( displaystyle sqrt[3]{{{x}^{3}}+3x+5}=x)
• ( displaystyle sqrt[3]{6+{{x}^{2}}-{{x}^{3}}}=1-x)

Ответы:

Решение иррациональных уравнений через ОДЗ

Очень часто частью процесса решения уравнений является нахождение области допустимых значений (ОДЗ). Причины, заставляющие искать ОДЗ, могут быть разными: требуется провести преобразования уравнения, а они, как известно, проводятся на ОДЗ, выбранный метод решения подразумевает нахождение ОДЗ, осуществление проверки по ОДЗ и т.д. А в определенных случаях ОДЗ выступает не только как вспомогательный или контрольный инструмент, но и позволяет получить решение уравнения. В связи с этим, существует метод решения уравнений через ОДЗ. В этой статье мы на примерах подробно разберем, в каких случаях и каким образом этот метод применяется при решении иррациональных уравнений.

В каких случаях применяется метод решения через ОДЗ?

К методу решения уравнений через ОДЗ обращаются в двух случаях:

• когда ОДЗ есть пустое множество и
• когда ОДЗ есть конечный набор чисел.

Значит, чтобы понять, решается ли заданное иррациональное уравнение через ОДЗ, надо сначала найти область допустимых значений и посмотреть, каким множеством она является. По записи уравнения практически невозможно сказать, решается это уравнение через ОДЗ или нет.

Как проводится решение?

Понятно, что если ОДЗ для иррационального уравнения есть пустое множество, то уравнение не имеет решений.

Если ОДЗ представляет собой конечный набор чисел, то несложно выяснить, какие из этих чисел являются корнями, а какие не являются, через проверку подстановкой. Те числа, которые удовлетворяют решаемому уравнения, являются корнями. Остальные — не являются корнями уравнения. Других корней быть не может, так как все остальные числа находятся за пределами ОДЗ.

Решение примеров

Рассмотрим решения двух примеров, которыми мы закроем обе ситуации: ОДЗ есть пустое множество, и ОДЗ есть конечный набор чисел.

Начнем с решения иррационального уравнения, ОДЗ для которого, есть пустое множество. Это уравнение не имеет решений.

Решить уравнение

Осталось рассмотреть случай, когда ОДЗ для иррационального уравнения представляет собой конечный набор чисел. Для примера возьмем иррациональное уравнение, ОДЗ для которого состоит из двух чисел, а подстановка показывает, что только одно из них является корнем уравнения, откуда и делается вывод, что этот корень есть единственное решение уравнения.

Решите иррациональное уравнение

Можно считать, что мы разобрались с решением иррациональных уравнений через ОДЗ. Давайте продолжим изучение методов решения иррациональных уравнений материалом «Решение иррациональных уравнений «дробь равна нулю»».

Область допустимых значений (ОДЗ): теория, примеры, решения

Любое выражение с переменной имеет свою область допустимых значений, где оно существует. ОДЗ необходимо всегда учитывать при решении. При его отсутствии можно получить неверный результат.

В данной статье будет показано, как правильно находить ОДЗ, использовать на примерах. Также будет рассмотрена важность указания ОДЗ при решении.

Допустимые и недопустимые значения переменных

Данное определение связано с допустимыми значениями переменной. При введении определения посмотрим, к какому результату приведет.

Начиная с 7 класса, мы начинаем работать с числами и числовыми выражениями. Начальные определения с переменными переходят к значению выражений с выбранными переменными.

Когда имеются выражения с выбранными переменными, то некоторые из них могут не удовлетворять. Например, выражение вида 1 : а , если а = 0 , тогда оно не имеет смысла, так как делить на ноль нельзя. То есть выражение должно иметь такие значения, которые подойдут в любом случае и дадут ответ. Иначе говоря, имеют смысл с имеющимися переменными.

Если имеется выражение с переменными, то оно имеет смысл только тогда, когда при их подстановке значение может быть вычислено.

Если имеется выражение с переменными, то оно не имеет смысл, когда при их подстановке значение не может быть вычислено.

То есть отсюда следует полное определение

Существующими допустимыми переменными называют такие значения, при которых выражение имеет смысл. А если смысла не имеет, значит они считаются недопустимыми.

Для уточнения вышесказанного: если переменных более одной, тогда может быть и пара подходящих значений.

Для примера рассмотрим выражение вида 1 x — y + z , где имеются три переменные. Иначе можно записать, как x = 0 , y = 1 , z = 2 , другая же запись имеет вид ( 0 , 1 , 2 ) . Данные значения называют допустимыми, значит, можно найти значение выражения. Получим, что 1 0 — 1 + 2 = 1 1 = 1 . Отсюда видим, что ( 1 , 1 , 2 ) недопустимы. Подстановка дает в результате деление на ноль, то есть 1 1 — 2 + 1 = 1 0 .

Что такое ОДЗ?

Область допустимых значений – важный элемент при вычислении алгебраических выражений. Поэтому стоит обратить на это внимание при расчетах.

Область ОДЗ – это множество значений, допустимых для данного выражения.

Рассмотрим на примере выражения.

Если имеем выражение вида 5 z — 3 , тогда ОДЗ имеет вид ( − ∞ , 3 ) ∪ ( 3 , + ∞ ) . Эта область допустимых значений, удовлетворяющая переменной z для заданного выражения.

Если имеется выражения вида z x — y , тогда видно, что x ≠ y , z принимает любое значение. Это и называют ОДЗ выражения. Его необходимо учитывать, чтобы не получить при подстановке деление на ноль.

Область допустимых значений и область определения имеет один и тот же смысл. Только второй из них используется для выражений, а первый – для уравнений или неравенств. При помощи ОДЗ выражение или неравенство имеет смысл. Область определения функции совпадает с областью допустимых значений переменной х к выражению f ( x ) .

Как найти ОДЗ? Примеры, решения

Найти ОДЗ означает найти все допустимые значения, подходящие для заданной функции или неравенства. При невыполнении этих условий можно получить неверный результат. Для нахождения ОДЗ зачастую необходимо пройти через преобразования в заданном выражении.

Существуют выражения, где их вычисление невозможно:

• если имеется деление на ноль;
• извлечение корня из отрицательного числа;
• наличие отрицательного целого показателя – только для положительных чисел;
• вычисление логарифма отрицательного числа;
• область определения тангенса π 2 + π · k , k ∈ Z и котангенса π · k , k ∈ Z ;
• нахождение значения арксинуса и арккосинуса числа при значении, не принадлежащем [ — 1 ; 1 ] .

Все это говорит о том, как важно наличие ОДЗ.

Найти ОДЗ выражения x 3 + 2 · x · y − 4 .

Решение

В куб можно возводить любое число. Данное выражение не имеет дроби, поэтому значения x и у могут быть любыми. То есть ОДЗ – это любое число.

Ответ: x и y – любые значения.

Найти ОДЗ выражения 1 3 — x + 1 0 .

Решение

Видно, что имеется одна дробь, где в знаменателе ноль. Это говорит о том, что при любом значении х мы получим деление на ноль. Значит, можно сделать вывод о том, что это выражение считается неопределенным, то есть не имеет ОДЗ.

Ответ: ∅ .

Найти ОДЗ заданного выражения x + 2 · y + 3 — 5 · x .

Решение

Наличие квадратного корня говорит о том, что это выражение обязательно должно быть больше или равно нулю. При отрицательном значении оно не имеет смысла. Значит, необходимо записать неравенство вида x + 2 · y + 3 ≥ 0 . То есть это и есть искомая область допустимых значений.

Ответ: множество x и y , где x + 2 · y + 3 ≥ 0 .

Определить ОДЗ выражения вида 1 x + 1 — 1 + log x + 8 ( x 2 + 3 ) .

Решение

По условию имеем дробь, поэтому ее знаменатель не должен равняться нулю. Получаем, что x + 1 — 1 ≠ 0 . Подкоренное выражение всегда имеет смысл, когда больше или равно нулю, то есть x + 1 ≥ 0 . Так как имеет логарифм, то его выражение должно быть строго положительным, то есть x 2 + 3 > 0 . Основание логарифма также должно иметь положительное значение и отличное от 1 , тогда добавляем еще условия x + 8 > 0 и x + 8 ≠ 1 . Отсюда следует, что искомое ОДЗ примет вид:

x + 1 — 1 ≠ 0 , x + 1 ≥ 0 , x 2 + 3 > 0 , x + 8 > 0 , x + 8 ≠ 1

Иначе говоря, называют системой неравенств с одной переменной. Решение приведет к такой записи ОДЗ [ − 1 , 0 ) ∪ ( 0 , + ∞ ) .

Ответ: [ − 1 , 0 ) ∪ ( 0 , + ∞ )

Почему важно учитывать ОДЗ при проведении преобразований?

При тождественных преобразованиях важно находить ОДЗ. Бывают случаи, когда существование ОДЗ не имеет место. Чтобы понять, имеет ли решение заданное выражение, нужно сравнить ОДЗ переменных исходного выражения и ОДЗ полученного.

• могут не влиять на ОДЗ;
• могут привести в расширению или дополнению ОДЗ;
• могут сузить ОДЗ.

Рассмотрим на примере.

Если имеем выражение вида x 2 + x + 3 · x , тогда его ОДЗ определено на всей области определения. Даже при приведении подобных слагаемых и упрощении выражения ОДЗ не меняется.

Если взять пример выражения x + 3 x − 3 x , то дела обстоят иначе. У нас имеется дробное выражение. А мы знаем, что деление на ноль недопустимо. Тогда ОДЗ имеет вид ( − ∞ , 0 ) ∪ ( 0 , + ∞ ) . Видно, что ноль не является решением, поэтому добавляем его с круглой скобкой.

Рассмотрим пример с наличием подкоренного выражения.

Если имеется x — 1 · x — 3 , тогда следует обратить внимание на ОДЗ, так как его необходимо записать в виде неравенства ( x − 1 ) · ( x − 3 ) ≥ 0 . Возможно решение методом интервалов, тогда получаем, что ОДЗ примет вид ( − ∞ , 1 ] ∪ [ 3 , + ∞ ) . После преобразования x — 1 · x — 3 и применения свойства корней имеем, что ОДЗ можно дополнить и записать все в виде системы неравенства вида x — 1 ≥ 0 , x — 3 ≥ 0 . При ее решении получаем, что [ 3 , + ∞ ) . Значит, ОДЗ полностью записывается так: ( − ∞ , 1 ] ∪ [ 3 , + ∞ ) .

Нужно избегать преобразований, которые сужают ОДЗ.

Рассмотрим пример выражения x — 1 · x — 3 , когда х = — 1 . При подстановке получим, что — 1 — 1 · — 1 — 3 = 8 = 2 2 . Если это выражение преобразовать и привести к виду x — 1 · x — 3 , тогда при вычислении получим, что 2 — 1 · 2 — 3 выражение смысла не имеет, так как подкоренное выражение не должно быть отрицательным.

Следует придерживаться тождественных преобразований, которые ОДЗ не изменят.

Если имеются примеры, которые его расширяют, тогда его нужно добавлять в ОДЗ.

Рассмотрим на примере дроби вида x x 3 + x . Если сократить на x , тогда получаем, что 1 x 2 + 1 . Тогда ОДЗ расширяется и становится ( − ∞ 0 ) ∪ ( 0 , + ∞ ) . Причем при вычислении уже работаем со второй упрощенной дробью.

При наличии логарифмов дело обстоит немного иначе.

Если имеется выражение вида ln x + ln ( x + 3 ) , его заменяют на ln ( x · ( x + 3 ) ) , опираясь на свойство логарифма. Отсюда видно, что ОДЗ с ( 0 , + ∞ ) до ( − ∞ , − 3 ) ∪ ( 0 , + ∞ ) . Поэтому для определения ОДЗ ln ( x · ( x + 3 ) ) необходимо производить вычисления на ОДЗ, то есть ( 0 , + ∞ ) множества.

При решении всегда необходимо обращать внимание на структуру и вид данного по условию выражения. При правильном нахождении области определения результат будет положительным.

Методы решения иррациональных уравнений

Разделы: Математика

Основные понятия

Опеределение 1. Уравнение f(x) = g(x) называется иррациональным, если функции f(x) и g(x) – алгебраические и по крайней мере одна из них иррациональна относительно x (т.е. содержит переменную x в подкоренном выражении).

Основным техническим приемом, который используется при решении иррациональных уравнений, является возведение обеих частей уравнения в одну и туже степень. Если рассматривать уравнения над полем действительных чисел, то это преобразование регулируется следующими теоремами.

Теорема 1. Уравнение.

Теорема 2. Уравнение.

Эквивалентно смешанной системе:

Пример 1. Решить уравнение

Возведем обе части уравнения в четвертую степень:

Корень x=2 удовлетворяет этому неравенству.

Иррациональные уравнения, если неизвестное находится в подкоренном выражении корня четной степени, имеют, как правило, ограниченную область допустимых значений (ОДЗ). ОДЗ иррационального уравнения определяется условием: Подкоренное выражение корня четной степени должно быть неотрицательным.

Метод уединения радикала

Суть этого метода состоит в следующем. Радикал (корень) оставляют в одной части уравнения, а остальные члены уравнения переносят в другую часть. После этого обе части уравнения возводят в степень, показатель которой равен показателю уединенного радикала. Если уравнение содержит несколько радикалов, то процедура уединения производится над одним из них, после чего повторяется вплоть до полного избавления уравнения от корней.

Пример 2. Решить уравнение

, ,

,

Очевидно, что оба корня входят в ОДЗ, но x=13 не удовлетворяет неравенству x 4.07.2013

Что, если в правой части иррационального уравнения будет стоять не число, а выражение, зависящее от (x). В общем виде такие уравнения выглядят так: (sqrt{f(x)}=g(x)).
Разберем подробно, как такое решать на примере:

Пример 4
$$sqrt{12-x}=x;$$
Практически любое иррациональное уравнение с квадратным корнем решается путем возведения в квадрат всего уравнения. Давайте сделаем это:
$$(sqrt{12-x})^2=x^2;$$
И решим получившееся уравнение:
$$12-x=x^2;$$
$$x^2+x-12=0;$$
$$D=1+4*12=49;$$
$$x_1=frac{-1+sqrt{49}}{1*2}=frac{-1+7}{2}=3;$$
$$x_2=frac{-1-sqrt{49}}{1*2}=frac{-1-7}{2}=-4;$$

Мы получили два корня, попробуем подставить каждый из них в исходное уравнение, чтобы проверить, действительно ли они являются корнями:
$$sqrt{12-x}=x;$$
$$Downarrow$$
$$sqrt{12-3}=3;$$
$$Downarrow$$
$$sqrt{9}=3;$$
Получилось верное равенство: корень из (9) действительно равен (3).
Проверим теперь второй корень (x_2=-4):
$$sqrt{12-x}=x;$$
$$Downarrow$$
$$sqrt{12-(-4)}=-4;$$
$$Downarrow$$
$$sqrt{16}=-4;$$
А вот тут нас ждет разочарование: корень из (16) не равен (-4). Поэтому (x_2=-4) вычеркиваем.
Ответ: (x=3.)

Теперь давайте разбираться, как же так произошло, что один корень подходит, а другой нет. Мы же все делали правильно, откуда взялся посторонний корень? Теперь всегда надо в иррациональных уравнениях делать проверку? А ведь корней может быть много, да и само уравнение может быть сложным, чтобы в него все подставлять. В простых иррациональных уравнениях, как в примере №4, можно и подставить, ничего страшного — такие задания обычно встречаются в первой части ЕГЭ по профильной математике.

А в более сложных уравнениях неплохо было бы понимать, откуда берутся посторонние корни.

Еще раз посмотрите на исходное уравнение: (sqrt{12-x}=x).
Квадратный корень не может быть равен отрицательному числу, поэтому, если правая часть уравнения меньше нуля, то корней не будет. В правую часть вместо (x) можно подставлять абсолютно любые значения, значит мы не знаем, отрицательная у нас правая часть или нет. Поэтому для того, чтобы были корни, необходимо, чтобы правая часть уравнения была неотрицательной (больше или равна нуля):
$$x geq 0;$$
Действительно, наш второй корень (x_2=-4) не удовлетворяет этому условию, и его можно было сразу отбросить.

Посторонний корень (x_2=-4) появился в тот момент, когда мы возвели в квадрат левую и правую части уравнения. Ведь пропадает информация о том, что правая часть не может быть отрицательной. Из нового уравнения (12-x=x^2) никак не следует, что (x geq 0). Поэтому это условие мы должны тащить за собой при решении, чтобы не появились лишние корни.

Грамотное решение должно было выглядеть в виде системы так:

$$sqrt{12-x}=x;$$
$$Downarrow$$
$$begin{cases}
12-x =x^2, \
x geq 0.
end{cases}$$
Решив квадратное уравнение, получим корни (x_1=3) и (x_2=-4), но второй корень не удовлетворяет второму условию в системе (x geq 0), поэтому его отбрасываем.

Возведение уравнения в квадрат — это неравносильная операция, в результате которой могут появиться посторонние корни, поэтому необходимо накладывать дополнительные условия. Будьте внимательны.

Рассмотрим еще одно иррациональное уравнение:

Пример 5
$$sqrt{2x^2+21x+4}=2+11x;$$
Возводим обе части уравнения в квадрат, чтобы избавиться от иррациональности, при этом не забываем наложить условие на правую часть:
$$begin{cases}
(sqrt{2x^2+21x+4})^2=(2+11x)^2, \
2+11x geq 0;
end{cases}
$$
$$
begin{cases}
2x^2+21x+4=4+44x+121x^2, \
11x geq -2;
end{cases}
$$
$$begin{cases}
2x^2+21x+4-4-44x-121x^2=0, \
x geq -frac{2}{11};
end{cases}
$$
$$
begin{cases}
-119x^2-23x=0, \
x geq -frac{2}{11};
end{cases}
$$
$$
begin{cases}
-x(119x-23)=0, \
x geq -frac{2}{11};
end{cases}
$$
$$
begin{cases}
begin{gathered}
x=0, \
119x-23=0;
end{gathered} \
x geq -frac{2}{11};
end{cases}
$$

$$
begin{cases}
begin{gathered}
x_1=0, \
x_2=frac{23}{119};
end{gathered} \
x geq -frac{2}{11};
end{cases}
$$
Оба корня больше (-frac{2}{11}), значит записываем их в ответ:
Ответ: (x_1=0) и (x_2=frac{23}{119}.)

У внимательных студентов может возникнуть вопрос: а почему мы не накладывали условие на выражение, стоящее под квадратным корнем, оно тоже должно быть больше либо равно нуля. Все помнят, что нельзя извлекать квадратный корень из отрицательных чисел.
$$sqrt{f(x)}=g(x) Rightarrow f(x) geq 0 ???$$
Дело в том, что в рассмотренных примерах это условие будет излишним, ведь после возведения в квадрат, уравнение сводится к виду (f(x)=g^2(x)), то есть мы ищем такие корни, при которых (f(x)) равняется квадрату (g^2(x) geq 0), а значит (f(x)) не может быть меньше нуля.

Уединение квадратного корня

Иррациональные уравнения вида (sqrt{f(x)}+q(x)=g(x))

Рассмотрим уравнения, в которых помимо квадратного корня в левой части есть еще другие слагаемые. Общий вид такого уравнения:
$$sqrt{f(x)}+q(x)=g(x);$$
Тут уже так просто левую часть уравнения в квадрат не возведешь:
$$left(sqrt{f(x)}+q(x)right)^2=$$
$$=left(sqrt{f(x)}right)^2+2*sqrt{f(x)}*q(x)+q^2(x)=$$
$$=f(x)+2*sqrt{f(x)}*q(x)+q^2(x);$$
Как видите, от корня мы не избавились, смысла возводить в квадрат нет.

Но проблема легко решается переносом всех лишних слагаемых в исходном уравнении из левой части в правую так, чтобы в левой части остался только корень и больше ничего:
$$sqrt{f(x)}=g(x)-q(x);$$
Теперь можно возводить в квадрат и решать аналогично примерам №4,5:
$$begin{cases}
left(sqrt{f(x)}right)^2=(g(x)-q(x))^2, \
g(x)-q(x) geq 0;
end{cases}
$$
$$Downarrow$$
$$
begin{cases}
f(x)=(g(x)-q(x))^2, \
g(x)-q(x) geq 0;
end{cases} $$

Рассмотрим на примере:

Пример 6
$$sqrt{x+7}+x+1=0;$$
В левой части уравнения кроме корня (sqrt{x+7}) есть еще слагаемое ((x+1)). Перекинем лишнее слагаемое в правую часть:
$$sqrt{x+7}=-x-1;$$
Уравнение стало аналогичным примерам №4 и №5. Теперь можно возводить уравнение в квадрат, и не забываем накладывать дополнительное условие на правую часть, чтобы исключить появление посторонних корней:
$$begin{cases}
(sqrt{x+7})^2=(-x-1)^2, \
-x-1 geq 0;
end{cases}
$$
$$Downarrow$$
$$
begin{cases}
x+7=x^2+2x+1, \
x le -1;
end{cases}
$$
$$Downarrow$$
$$
begin{cases}
x^2+x-6=0, \
x le -1;
end{cases}
$$
$$Downarrow$$
$$
begin{cases}
left[
begin{gathered}
x_1=-3, \
x_2=2;
end{gathered}
right. \
x le -1;
end{cases}
$$
Корень (x_2=2) не удовлетворяет условию (x le -1), поэтому вычеркиваем его.
Ответ: (x=-3.)

Решение иррациональных уравнений вида (g(x)*sqrt{f(x)}=0)

Чтобы решить уравнение (g(x)*sqrt{f(x)}=0), его не нужно возводить в квадрат, как другие иррациональные уравнения. Достаточно заметить, что левая часть уравнения представляет собой произведение двух множителей: (g(x)) и (sqrt{f(x)}). А произведение равно нулю только в том случае, когда хотя бы один из множителей равен нулю:
$$g(x)=0 qquad или qquad sqrt{f(x)}=0;$$
Кроме того, не забываем про то, что выражение под корнем не может быть отрицательным, поэтому необходимо учесть ОДЗ: (f(x) ge 0.)
Запишем получившееся уравнения грамотно — в виде системы и совокупности:
$$
begin{cases}
left[
begin{gathered}
g(x) = 0, \
sqrt{f(x)} = 0;
end{gathered}
right. \
f(x) ge 0;
end{cases}
$$
Квадратный корень равен нулю, если подкоренное выражение равно нулю:
$$
begin{cases}
left[
begin{gathered}
g(x) = 0, \
f(x) = 0;
end{gathered}
right. \
f(x) ge 0;
end{cases}
$$
Решаем оба уравнения в совокупности, учитываем ОДЗ и все. Рассмотрим пример:

Пример 8
$$(x^2-16)*sqrt{x+3}=0;$$
Сразу выпишем ОДЗ:
$$x+3 ge 0;$$
И приступаем к решению:
$$
begin{cases}
left[
begin{gathered}
x^2-16 = 0, \
sqrt{x+3} = 0;
end{gathered}
right. \
x+3 ge 0;
end{cases}
$$
$$Downarrow$$
$$
begin{cases}
left[
begin{gathered}
x^2 = 16, \
x+3 = 0;
end{gathered}
right. \
x ge -3;
end{cases}
$$
$$Downarrow$$
$$
begin{cases}
left[
begin{gathered}
x_{1,2} = pm 4, \
x_3 = -3;
end{gathered}
right. \
x ge -3;
end{cases}
$$
Корень (x_2=-4) нужно отбросить, так как он не удовлетворяет ОДЗ.
Ответ: (x_{1}= 4) и (x_3=-3.)

Рассмотрим наши рассуждения на примере:

Пример 9
$$sqrt{3-2x}=sqrt{x-3};$$
Возводим левую и правую части уравнения в квадрат и накладываем ограничения:
$$begin{cases}
3-2x=x-3, \
x-3 ge 0;
end{cases}$$

Обратите внимание, так как подкоренное выражение не должно быть отрицательным, то мы накладываем условие (x-3 ge 0). Условие (3-2x ge 0) будет выполняться автоматически в силу равенства (3-2x=x-3): мы ищем такие (x), при которых левая и правая части уравнения равны, а значит если одна часть больше либо равна нуля, то другая тоже будет неотрицательна. Можно было наложить условие (3-2x ge 0) вместо (x-3 ge 0), разницы совершенно никакой. Но неравенство (x-3 ge 0) немного легче.
Осталось только решить систему:
$$begin{cases}
-3x=-6, \
x ge 3;
end{cases}
$$
$$Downarrow$$
$$
begin{cases}
x=2, \
x ge 3.
end{cases}
$$
Учитывая, что (x ge 3), корней нет.
Ответ: Корней нет.

Пример 10
$$sqrt{x^4+8x^3+2x^2-1}=sqrt{x^4+2x^2};$$
Для выполнения данного равенства необходимо, чтобы подкоренные выражения были равны и неотрицательны:
$$
begin{cases}
x^4+8x^3+2x^2-1=x^4+2x^2, \
x^4+2x^2 ge 0;
end{cases}
$$
$$Downarrow$$
$$
begin{cases}
8x^3-1=0, \
x^2(x^2+2) ge 0;
end{cases}
$$
Второе неравенство будет верно при любых значениях (x), так как множители (x^2) и скобка ((x^2+2)) всегда больше либо равны нулю. А произведение двух положительных множителей всегда положительно.

Система сводится к решению простого кубического уравнения:
$$8x^3-1=0;$$
$$x^3=frac{1}{8};$$
$$x=frac{1}{2};$$
Ответ: (x=frac{1}{2}.)

Иррациональные уравнения вида (sqrt{f(x)}=sqrt{g(x)}+q(x).)

Уравнения, в которых несколько квадратных корней и, кроме того, есть дополнительные слагаемые и множители, считаются уравнениями повышенной сложности. Как правило, для решения требуется несколько раз возводить уравнение в квадрат и при этом внимательно следить, чтобы не нарушалась равносильность преобразований.
Единого алгоритма решения тут нет, каждое уравнение обычно имеет свои особенности.

Главное правило в таких уравнениях: записывать ОДЗ.

Так как квадратный корень от отрицательного числа не существует, то нужно внимательно следить, чтобы подкоренные выражения не были отрицательными — это и будет ОДЗ:
$$sqrt{f(x)}=sqrt{g(x)}+q(x);$$
ОДЗ:
$$
begin{cases}
f(x) ge 0, \
g(x) ge 0;
end{cases}
$$

Рассмотрим несколько примеров:

Пример 11
$$sqrt{4+x}-sqrt{5-x}=3;$$
Запишем ОДЗ:
$$
begin{cases}
4+x ge 0, \
5-x ge 0;
end{cases}
$$
$$Downarrow$$
$$
begin{cases}
x ge -4, \
x le 5;
end{cases}
$$

Теперь приступаем к решению самого уравнения. Уравнение в исходном виде лучше не возводить в квадрат, тогда придется накладывать ограничение ((sqrt{4+x}-sqrt{5-x} ge 0)). А решать такое неравенство с двумя корнями не самое приятное занятие. Подробнее про то, как решать иррациональные неравенства можно посмотреть тут.

Чтобы избежать этого, перекинем отрицательный корень в правую часть уравнения:
$$sqrt{4+x}=3+sqrt{5-x};$$
В таком виде уравнение смело можно возводить в квадрат, так как обе части уравнения точно неотрицательны: слева стоит квадратный корень (всегда больше либо равен нулю), а справа сумма положительного числа и неотрицательного корня (тоже точно положительный). Поэтому при возведении в квадрат не нужно накладывать условия, все само собой выполняется:
$$left(sqrt{4+x}right)^2=left(3+sqrt{5-x}right)^2;$$
$$4+x=9+2*3*sqrt{5-x}+left(sqrt{5-x}right)^2;$$
$$4+x=9+2*3*sqrt{5-x}+5-x;$$
Уравнение свелось к виду, рассмотренному выше. Уединяем квадратный корень, перекидывая все лишние слагаемые в левую часть:
$$4+x-9-5+x=6*sqrt{5-x};$$
$$-10+2*x=6*sqrt{5-x};$$
И еще раз возводим в квадрат, тут уже без ограничений на левую часть не обойтись:
$$
begin{cases}
(-10+2*x)^2=left(6*sqrt{5-x}right)^2, \
-10+2x ge 0;
end{cases}
$$
$$Downarrow$$
$$
begin{cases}
100-40x+4x^2=36(5-x), \
2x ge 10;
end{cases}
$$
$$Downarrow$$
$$
begin{cases}
4x^2-4x-80=0, \
x ge 5;
end{cases}
$$
$$Downarrow$$
$$
begin{cases}
left[
begin{gathered}
x_{1} = 5, \
x_{2} = -4;
end{gathered}
right. \
x ge 5;
end{cases}
$$
Условию (x ge 5) удовлетворяет только корень (x_1=5). Проверяем, чтобы этот корень удовлетворял ОДЗ: (x in [-4;5]) — все хорошо. Записываем ответ:
Ответ: (x=5.)

Пример 12
$$sqrt{3x^2-5x+8}-sqrt{3x^2-5x+1}=1;$$
Найдем ОДЗ:
$$
begin{cases}
3x^2-5x+8 ge 0, \
3x^2-5x+1 ge 0;
end{cases}
$$
Вспомнить, как решаются квадратные неравенства, можно тут. Решим каждое по-отдельности:
$$3x^2-5x+8 ge 0;$$
$$D=(-5)^2-4*3*8=25-96=-71;$$
Дискриминант получился отрицательным, так как ветки параболы направлены вверх, то это неравенство справедливо при любых (x).
Решим второе неравенство:
$$3x^2-5x+1 ge 0;$$
Раскладываем через дискриминант квадратный многочлен на множители:
$$3(x-frac{5+sqrt{13}}{6})(x-frac{5-sqrt{13}}{6}) ge 0;$$
$$x in left[- infty; frac{5+sqrt{13}}{6}right] cup left[- infty; frac{5+sqrt{13}}{6}right].$$
Мы решаем систему неравенств, значит нужно найти пересечение этих решений. Так как первое неравенство справедливо при любых (x), то пересечением будет просто решение второго:
$$x in left[- infty; frac{5-sqrt{13}}{6}right] cup left[frac{5+sqrt{13}}{6}; +inftyright].$$
ОДЗ нашли. Отмечу, что решать неравенства было здесь необязательно. Можно найти корни уравнения и потом просто подставить их либо в исходное уравнение, либо подставить в неравенства из ОДЗ.

Теперь можно приступать к решению исходного уравнения. Перекинем второй квадратный корень в правую часть, чтобы обе части уравнения были положительны:
$$sqrt{3x^2-5x+8}=1+sqrt{3x^2-5x+1};$$
Возводим в квадрат:
$$left(sqrt{3x^2-5x+8}right)^2=left(1+sqrt{3x^2-5x+1}right)^2;$$
$$3x^2-5x+8=1+2*1*sqrt{3x^2-5x+1}+left(sqrt{3x^2-5x+1}right)^2;$$
$$3x^2-5x+8=1+2*sqrt{3x^2-5x+1}+3x^2-5x+1;$$
Уединяем корень, для этого перекидываем все слагаемые, кроме арифметического корня, в левую часть уравнения:
$$3x^2-5x+8-1-3x^2+5x-1=2*sqrt{3x^2-5x+1};$$
$$6=2*sqrt{3x^2-5x+1};$$
Разделим уравнение на (2):
$$3=sqrt{3x^2-5x+1};$$
И еще раз возводим в квадрат. Здесь не нужно накладывать никаких ограничений, так как в результате возведения в квадрат подкоренное выражение будет равно положительному числу, то есть автоматически будет положительно:
$$9=3x^2-5x+1;$$
$$3x^2-5x-8=0;$$
$$D=25-4*3*(-8)=25+96=121;$$
$$x_1=frac{-(-5)+sqrt{121}}{2*3}=frac{5+11}{6}=frac{16}{6}=frac{8}{3};$$
$$x_2=frac{-(-5)-sqrt{121}}{2*3}=frac{5-11}{6}=frac{-6}{6}=-1;$$
Оба корня удовлетворяют ОДЗ, записываем ответ:
Ответ: (x_{1}= frac{8}{3}) и (x_{2}=-1.)

Иррациональные уравнения с корнями (n-й) степени

Если в уравнении корень не квадратный, а большей степени, то решение таких уравнений зависит от того, четная или нечетная степень у корня.

Уравнения с корнем четной степени

Такие уравнения ничем не отличаются от уравнений с квадратными корнями. Все рассуждения, которые мы проводили для арифметических квадратных корней, справедливы и для корней четной степени. Единственное логичное отличие в решении: мы будем возводить уравнение не в квадрат, а в ту степень, в какой корень.

Пример 14
$$sqrt[4]{x+2}=3;$$
Возводим левую и правую части уравнения в четвертую степень:
$$(sqrt[4]{x+2})^4=3^4;$$
$$x+2=81;$$
$$x=79;$$
Ответ: (x=79.)

Уравнения с корнем нечетной степени

Иррациональные уравнения с нечетными корнями, как правило, гораздо проще уравнений с четными. Дело в том, что корень нечетной степени существует и от отрицательных, и от положительных значений, а это означает, что при избавлении от корня нечетной степени в иррациональном уравнении не нужно бояться, что появятся посторонние корни. Можно возводить уравнение в нечетную степень, чтобы избавиться от иррациональности, без каких либо условий.

Пример 15
$$sqrt[3]{3-x}-sqrt[3]{10-x}=-1;$$
Поменяем местами слагаемые:
$$sqrt[3]{10-x}=1+sqrt[3]{3-x};$$
И возведем уравнение в куб. Тут понадобится знание формулы куба суммы: ((a+b)^3=a^3+3a^2b+3ab^2+b^3.)
$$(sqrt[3]{10-x})^3=(1+sqrt[3]{3-x})^3;$$
$$10-x=1^3+3*1^2*sqrt[3]{3-x}+3*1*(sqrt[3]{3-x})^2+(sqrt[3]{3-x})^3;$$
$$10-x=1+3*sqrt[3]{3-x}+3*(sqrt[3]{3-x})^2+3-x;$$
Приведем подобные слагаемые:
$$3*(sqrt[3]{3-x})^2+3*sqrt[3]{3-x}-6=0;$$
Пусть (t=sqrt[3]{3-x}):
$$3t^2+3t-6=0;$$
$$
begin{gathered}
t_{1} = 1, \
t_{2} = -2;
end{gathered}
$$
Обратная замена:
$$
begin{gathered}
sqrt[3]{3-x} = 1, \
sqrt[3]{3-x} = -2;
end{gathered}
$$
Получилось, что кубический корень равен отрицательному числу, но это нормально: корни нечетной степени могут быть равны отрицательным числам.

Чтобы решить получившиеся уравнения, необходимо возвести их в третью степень:
$$
begin{gathered}
3-x = 1, \
3-x = -8;
end{gathered}
Rightarrow
begin{gathered}
x_1 = 2, \
x_2 = 11;
end{gathered}
$$
Ответ: (x_1=2) и (x_2=11.)

Как видите, никаких условий при решении уравнения с кубическим корнем, мы не накладывали, просто избавлялись от корня, возводя все уравнение в куб. С нечетными степенями в этом плане никаких проблем, как правило, нет.

Основные понятия

Опеределение 1. Уравнение f(x) = g(x) называется
иррациональным, если функции f(x) и g(x) –
алгебраические и по крайней мере одна из них
иррациональна относительно x (т.е. содержит
переменную x в подкоренном выражении).

Основным техническим приемом, который
используется при решении иррациональных
уравнений, является возведение обеих частей
уравнения в одну и туже степень. Если
рассматривать уравнения над полем
действительных чисел, то это преобразование
регулируется следующими теоремами.

Эквивалентно уравнению

Теорема 2. Уравнение.

Эквивалентно смешанной системе:

Пример 1. Решить уравнение

Возведем обе части уравнения в четвертую
степень:

Корень x=2 удовлетворяет этому неравенству.

Проверка:

Ответ: 2.

Иррациональные уравнения, если неизвестное
находится в подкоренном выражении корня четной
степени, имеют, как правило, ограниченную область
допустимых значений (ОДЗ). ОДЗ иррационального
уравнения определяется условием: Подкоренное
выражение корня четной степени должно быть
неотрицательным.

Метод уединения радикала

Суть этого метода состоит в следующем. Радикал
(корень) оставляют в одной части уравнения, а
остальные члены уравнения переносят в другую
часть. После этого обе части уравнения возводят в
степень, показатель которой равен показателю
уединенного радикала. Если уравнение содержит
несколько радикалов, то процедура уединения
производится над одним из них, после чего
повторяется вплоть до полного избавления
уравнения от корней.

Пример 2. Решить уравнение

Найдем ОДЗ.

, ,

Решим уравнение.

,

Очевидно, что оба корня входят в ОДЗ, но x=13 не
удовлетворяет неравенству x < 8, а следовательно,
этот корень посторонний.

Проверка:

Ответ: 5.

Метод замены переменной

Суть метода замены переменной (метод этот
универсален и применяется отнюдь не только к
иррациональным уравнениям) состоит в том, что
некоторое выражение заменяется новой
переменной, в результате чего получаем более
простое уравнение. Решим это уравнение,
выполняем обратную замену и получаем уравнение
либо объединение уравнений (в зависимости от
количества корней уравнения с новой переменной).

1) Уравнение вида

При решении уравнений этого типа напрашивается
замена:

Пример 3. Решить уравнение.

Так как

Уравнение примет вид:

Сделаем замену:

Получим:

Очевидно, что так как:

Противоречит смыслу замены уравнение:

Не может иметь решений, подставим:

Проверка:

Ответ: 64.

Метод приведения иррационального
уравнения к системе уравнений

Суть этого метода состоит в том, что два
иррациональных выражения обозначаются двумя
различными переменными, в результате чего мы
получаем систему двух уравнений с двумя
неизвестными (в принципе, возможна и замена,
приводящая к системе с большим количеством
неизвестных).

Сделаем замену:

Поскольку левые части обоих равенств
одинаковы, мы вправе приравнять их правые части:

Второе уравнение системы получим, выполнив
замену в уравнении:

Решим систему:

Решим уравнение:

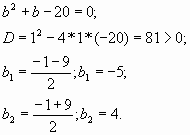
Система имеет два решения:

Выполним обратную замену:

Таким образом,

Решение для a и b должны были получиться
одинаковыми.

Сделаем проверку, хотя ОДЗ уравнения –
множество всех действительных чисел, а в
процессе решения мы не прибегали к
преобразованиям, которые могли бы привести к
появлению посторонних корней.

Ответ:

1. Бесчетнов В.М. Математика: Курс лекций для
   учащихся 7-11 классов: в 2-х т.: Т.1. – М.: Демиург, 1994.
   – 288 с.
2. Гайшут О.Г., Литвиненко Г.М. Алгебра. Решение
   задач и упражнений. – Киев: “Магистра – S№”, 1997.
   – 256 с.
3. Мерзляк А.Г., Полонский В.Б., Якир М.С.
   Алгебраический тренажер: Пособие для школьников
   и абитуриентов. – М.: Илекса, Хариков: Гимназия,
   1998. – 320 с.
4. Олехник С.Н., Потапов М.К., Пасиченко П.И.
   Уравнения и неравенства. Нестандартные методы
   решения. – М.: Издательство Фактория, 1997. – 217 с.
5. Черкасов О.Ю., Якушев А.Г. Математика:
   интенсивный курс подготовки к экзамену. – М.:
   Рольф, 1997. – 384 с.