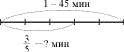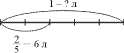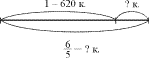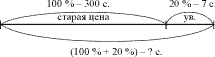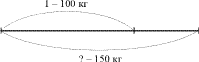Как найти третью часть отрезка?
На этой странице сайта размещен вопрос Как найти третью часть отрезка? из категории
Математика с правильным ответом на него. Уровень сложности вопроса
соответствует знаниям учеников 1 — 4 классов. Здесь же находятся ответы по
заданному поиску, которые вы найдете с помощью автоматической системы.
Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по
заданной теме. На этой странице можно обсудить все варианты ответов с другими
пользователями сайта и получить от них наиболее полную подсказку.
Ольга ТАРАКАНОВА
Решение задач на дроби
Статья посвящена решению задач с дробями.
Примеры иллюстрируются задачами из учебника:
Петерсон Л.Г. «Математика», 3 класс (1-3), часть
2,3, что соответствует 4 классу (1–4). Основное
внимание уделяется поиску решения задачи,
который проводится либо в виде диалога учителя с
учениками, либо в виде самостоятельного
рассуждения ученика. Большое внимание уделяется
грамотному оформлению решения задачи.
I. Этап мотивации изучения дробей
Первые задачи, которые рассматривает
учитель при введении темы, – это исторические
задачи, цель которых – заинтересовать учеников
изучением нового материала. Полезно рассмотреть
две или три задачи, а потом вернуться к ним, когда
материал о дробях будет уже как следует изучен.
Задача 1
В произведении знаменитого римского
поэта I в. до н.э. Горация так описана беседа
учителя с учеником в одной из римских школ этой
эпохи.
Учитель: Пусть скажет сын Альбина,
сколько останется, если от 5 унций отнять одну
унцию?
Ученик: Одна треть.
Учитель: Правильно. Ты
сумеешь беречь свое имущество.
Пользуясь схемой, докажи, что ученик
был прав. (Ч. 1, № 1, с. 64)*.
Поиск решения. Моделируем ситуацию
с помощью отрезков. Давайте одну унцию обозначим
отрезком. Тогда 5 унций – отрезок, состоящий из 5
данных отрезков. Отнимем одну унцию, сколько
унций останется? [4 унции.] А что ответил ученик на
вопрос: «Сколько останется, если от 5 унций
отнять одну?» [Одна треть.] Если одну треть
составляет 4 унции, сколько унций составляет все
имущество? [В 3 раза больше, чем 4 унции, – значит, 12
унций.]
Схема.
Решение. 1) 5 – 1 = 4 (унц.) – осталось.
2) 4 х 3 = 12 (унц.) – все имущество.
Ответ: 12 унций.
Задача 2
Задача из «Арифметики» известного
среднеазиатского математика IX в. Мухаммеда
ибн-Мусы ал-Хорезми. «Найди число, зная, что
если отнять от него одну треть и одну четверть, то
получится 10». (Ч. 2, № 2, с. 64).
Поиск решения. Обозначим число
отрезком, длина которого делится на 3 и на 4, это
может быть 12, или 24, или 36 и т.д. Возьмем наименьшее
из них – 12, нарисуем 12 равных отрезков или мерок.
Найдем одну треть отрезка. [12 : 3 = 4 (ч.).] Найдем одну
четверть отрезка. [12 : 4 = 3 (ч.).] Сколько частей
вычли? [4 + 3 = 7 (ч.).] Сколько частей осталось? [12 – 7 = 5
(ч.).] 10 приходится на сколько частей? [На 5.] Сколько
приходится на одну часть? [10 : 5 = 2.] Число 2
приходится на одну часть, а сколько всего частей?
[12.] Как найти число? [2 х 12 = 24.]
Решение.
1) 12 : 3 = 4 (ч.) – треть числа.
2)12 : 4 = 3 (ч.) – четверть числа.
3) 3 + 4 = 7 (ч.) – вычли.
4)12 – 7 = 5 (ч.) – осталось.
5) 10 : 5 = 2 – приходится на одну часть.
6) 2 х 12 = 24 – число.
Ответ: Это число 24.
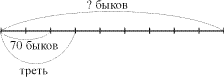
Задача 3
Задача из «Папируса Ахмеса»
(Египет, 1850 г. до н.э.).
«Приходит пастух с 70 быками. Его
спрашивают:
– Сколько приводишь ты своего
многочисленного стада?
Пастух отвечает:
– Я привожу две трети от трети скота.
Сочти!»
Используя схему, найди, сколько быков
было во всем стаде? (Ч. 2, № 3, с. 64)
Поиск решения.
Обозначим отрезком все стадо. Какой
должна быть длина отрезка, чтобы легко делилась
на части? [Длина должна быть кратна 9.] Обозначим
число быков отрезком, состоящим из 9 частей. Как
найти треть от 9? [9 разделить на 3, получится 3
части.] Покажем это на отрезке. Найдем две трети
от 3. Нужно 3 разделить на 3, получится 1 часть, и
взять две таких части. Сколько быков приходится
на 2 части? [70 быков.] Сколько быков приходится на
одну часть? [70 разделить на 2, получится 35 быков.]
Если 35 быков в одной части, сколько быков в 9
частях? [35 х 9 = 315.] Сколько быков в стаде? [315 быков.]
Схема.
Решение.
1) 9 : 3 = 3 (ч.) – треть стада.
2) 3 : 3 х 2 = 2 (ч.) – две трети от трети.
3) 70 : 2 = 35 (б.) – в I части.
4) 35 х 9 = 315 (б.) – в стаде.
Ответ: 315 быков.
Задача 4
Староиндийская задача (XI в.).
Есть кадамба цветок,
На один лепесток
Пчелок пятая часть опустилась.
Рядом тут же росла
Вся в цвету сименгда,
И на ней третья часть поместилась.
Разность их ты найди,
Ее трижды сложи
И тех пчел на кутай посади.
Только две не нашли
Себе места нигде,
Все летали то взад, то вперед и везде
Ароматом цветов наслаждались.
Назови теперь мне,
Подсчитавши в уме,
Сколько пчелок всего здесь собралось?
(Ч. 2, № 4, с. 64).
Поиск решения.
Обозначим число пчел отрезком. Сколько
мерок полезно взять в отрезке? [Число мерок
должно делиться на 5, на 3, т.е. на 15. Отрезок будет
состоять из 15 мерок.] Сколько мерок отрезка
составляет пятая часть? [15 разделим на 5,
получится 3 мерки.] Сколько мерок составляет
третья часть отрезка? [15 разделить на 3 получится 5
мерок.] Чему равна разность между третьей и пятой
частями? [Из 5 мерок вычтем 3 мерки, получится 2
мерки.] Три раза отложим по 2 мерки, сколько мерок
мы отложили? [2 умножим на 3, получится 6 мерок.]
Сколько мерок останется? [15 – 3 – 5 – 6 = 1, одна
мерка.] Сколько пчел приходится на одну мерку?
[Две.] Как найти все количество пчел? [2 умножить на
15, получится 30. Всего собралось 30 пчел.]
Схема.
Решение.
1) 15 : 5 = 3 (м.) – пятая часть.
2) 15 : 3 = 5 (м.) – третья часть.
3) 5 – 3 = 2 (м.) – разность.
4) 2 х 3 = 6 (м.) – кутай.
5) 15 – 3 – 5 – 6 = 1 (м.) – осталось.
6) 2 х 15 = 30 (пч.) – собралось.
Ответ: 30 пчел.
II. Этап решения задач на доли
Рассмотрим поиск решения, оформление
решения простых задач на доли. При составлении
схем к первым задачам полезно дроби писать над
выделенной частью (схема, 1). В дальнейшем
схема будет меняться. Изменения показаны на
схеме (3). Сначала меняется место записи дроби
и выделяется целая часть в виде единицы (схема, 2).
Сами части на отрезке сначала выделяются, затем
нет (схема, 3). Если ребенку трудно решить
задачу без деления отрезка на части, он может
продолжать их выделять.
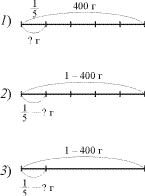
Задача на нахождение части числа
Яблоко весит 400 г. Сколько весит часть
этого яблока. (Ч. 2, № 10, с. 68.).
Схема.
Рассуждение ученика. Обозначим
массу яблока отрезком, в котором 5 мерок. Чтобы
найти массу одной пятой части, нужно 400 разделить
на 5, получится 80. 80 граммов весит часть яблока.
Решение. 400 : 5 = 80 (г).
Ответ: 80 граммов.
Задача на нахождение числа по его
части
Сколько стоит книга, если часть ее цены составляет 30
рублей? (Ч. 2, № 2, с. 75).
Схема.
Рассуждения ученика. Известно, что часть цены книги
составляет 30 рублей. Чтобы найти цену книги, надо
30 умножить на 6, получится 180. 180 рублей цена книги.
Решение. 30 х 6 = 180 (р.).
Ответ: 180 рублей.
Составная задача с долями
Сделав 16 деталей, рабочий выполнил часть задания.
Сколько деталей ему осталось сделать? (Ч. 2, № 5, с.
75).
Схема.
Рассуждения ученика. Одна
четвертая часть задания составляет 16 деталей.
Чтобы найти объем всего задания, нужно 16 умножить
на 4, получится 64. 64 детали составляет все задание.
16 деталей сделано. Чтобы найти, сколько деталей
осталось сделать, нужно из 64 вычесть 16, получится
48. 48 деталей осталось сделать.
Решение.
По действиям с пояснениями:
1) 16 х 4 = 64 (д.) – все задание.
2) 64 – 16 = 48 (д.) – осталось сделать.
Или выражением:
16 х 4 – 16 = 48 (д.).
Ответ: 48 деталей.
Задачи на проценты
Задачи на проценты являются частным
случаем задач на доли.
Задача на нахождение части числа
Папа получил премию 8000 рублей. 1% премии
он потратил на покупку торта. Сколько стоил торт?
(Ч. 2, № 8, с. 73).
Схема.
Рассуждения ученика. 1% – это одна
сотая часть числа. Чтобы найти одну сотую часть
от числа 8000, надо 8000 разделить на 100, получится 80. 80
рублей потратил папа на торт.
Решение. 8000 : 100 = 80 (р.).
Ответ: 80 рублей.
Задача на нахождение числа по его
части
Сколько человек было в кинотеатре,
если 1% всех зрителей составляет 7 человек? (Ч.2, № 3,
с.75).
Схема.
Рассуждения ученика. Целое
составляет 100%, его нужно найти. 1% – это одна сотая
часть от целого. Одну сотую часть составляет 7
человек, значит, чтобы найти целое, нужно 7
умножить на 100, получится 700. 700 человек было в
кинотеатре.
Решение. 7 х 100 = 700 (чел.).
Ответ: 700 человек.
III. Этап решения задач на правильные
дроби
Задача на нахождение части числа
Урок длится 45 минут. части урока ученики писали
самостоятельную работу. Сколько времени она
длилась?
Схема.
Рассуждение ученика.
Найдем сначала часть от 45, для этого 45 разделим на
5, получится 9. Дальше найдем части, для этого 9
умножим на 3, получим 27. 27 минут ученики писали
самостоятельную работу.
Решение.
По действиям с пояснениями:
1) 45 : 5 = 9 (мин) – приходится на .
2) 9 х 3 = 27 (мин) – приходится на .
Или выражением: 45 : 5 х 3 = 27 (мин).
Ответ: 27 минут.
Задача на нахождение части числа,
выраженной в процентах
На строительство доставили 24 000
кирпичей. Бой составляет 3% всех кирпичей. Сколько
кирпичей разбилось по дороге? (Ч. 2, № 5, с. 85).
Схема.
Рассуждения ученика.
24 000 кирпича составляет 100%, 3% – это . Чтобы найти
части от числа 24 000,
нужно 24 разделить на 100 и умножить на 3, получится
720. 720 кирпичей разбилось.
Решение.
По действиям с пояснениями:
1) 24000 : 100 = 240 (к.) – приходится на 1%.
2) 240 х 3 = 720 (к.) – приходится на 3%.
Или выражением:
24000 : 100 х 3=720 (к.).
Ответ: 720 кирпичей.
Задача на нахождение числа по его
части
В аквариум налили 6 л воды, заполнив части его объема.
Сколько литров воды вмещает аквариум? (Ч.2, № 5, с.
90).
Схема.
Рассуждения ученика.
Известно, что части объема аквариума составляет 6 л,
следовательно, часть
составляет в 2 раза меньше, т.е. 6, деленное на 2.
Таким образом, часть
составляет 3 л. А объем аквариума в 5 раз больше,
т.е. 3, умноженное на 5. 15 л вмещает аквариум.
Решение.
По действиям с пояснениями:
1) 6 : 2 = 3 (л) – пятая часть.
2) 3 х 5 = 15 (л) – аквариум.
Или выражением:
6 : 2 х 5 = 15 (л).
Ответ: 15 литров.
Задача на нахождение числа по его
части, выраженной в процентах
Бурый медведь весит 320 кг, что
составляет 40% массы белого медведя. Какова масса
белого медведя? (Ч.2, № 5, с. 88).
Схема.
Рассуждения ученика.
Вариант 1. 320 кг составляют 40%. Чтобы
узнать, сколько килограммов приходится на 1%,
нужно 320 разделить на 40, получится 8. Чтобы узнать,
сколько килограммов приходится на 100%, нужно 8
умножить на 100, получится 800. 800 кг – масса белого
медведя.
Вариант 2. Чтобы найти число по его
части, выраженной дробью, надо разделить эту
часть на числитель и умножить на знаменатель. 40%
– это ,
значит, нужно 320 разделить на 40 и умножить на 100,
получится 800. 800 кг – масса белого медведя.
Решение.
По действиям с пояснениями:
1) 320 : 40 = 8 (кг) – приходится на 1%.
2) 8 х 100 = 800 (кг) – приходится на 100%.
Или выражением:
320 : 40 х 100 = 800 (кг).
Ответ: 800 кг.
Задача на нахождение части, которую
одно число составляет от другого
От доски длиной 9 м отпилили 4 м. Какую
часть доски отпилили? (Ч.3, № 1, с.4).
Схема.
Рассуждения ученика.
Чтобы выразить дробью часть, которую
одно число составляет от другого, надо первое
число разделить на второе. Аналогично, чтобы
выразить, какую часть отпилили от доски, нужно 4
разделить на 9, так как 4 – часть, которую
отпилили, а 9 – это целое.
Решение. 4 : 9 = (ч.).
Ответ: части.
IV. Этап решения задач на неправильные
дроби
Задачи на нахождение части числа
1. На стройке Дома дружбы Чебурашка
должен был за день положить 620 кирпичей, но ему
удалось положить части этого числа. На сколько Чебурашка
перевыполнил задание?
Схема.
Рассуждения ученика.
Вариант 1. 620 кирпичей приходится на
5 равных частей. Чтобы узнать, сколько кирпичей
приходится на 1 часть, нужно 620 разделить на 5,
получится 124. Чтобы узнать, сколько кирпичей
приходится на 6 таких частей, нужно 124 умножить на
6, получится 744. 744 кирпича приходится на . Чтобы
узнать, на сколько Чебурашка перевыполнил план,
нужно из 744 вычесть 620, получится 124. На 124 кирпича
Чебурашка перевыполнил задание.
Вариант 2. Чтобы найти от 620, нужно 620
разделить на 5 и умножить на 6, получится 744. Чтобы
найти, на сколько Чебурашка перевыполнил план,
нужно из 744 вычесть 620, получится 124. На 124 кирпича
Чебурашка перевыполнил задание.
Решение.
По действиям с пояснениями:
1) 620 : 5 = 124 (к.) – приходится на одну
часть.
2) 124 х 6= 744 (к.) – выполнил.
3) 744 – 620 = 124 (к.) – перевыполнил.
Или выражением:
620 : 5 х 6 – 620 = 124 (к.).
Ответ: на 124 кирпича.
2. Буратино решил купить для папы Карло
новый дом за 300 сольдо. Но пока он копил деньги,
цена дома увеличилась на 20%. Сколько теперь
должен заплатить Буратино за этот дом? Сколько
денег надо ему дополнительно заработать? (Ч.3, № 3,
с. 20).
Схема.
Рассуждения ученика.
Вариант 1. 300 сольдо приходится на
100%, значит, на 1% приходится 300, деленное на 100, т.е. 3.
Новая цена дома от старой составляет 120% – это 100 +
20. Чтобы узнать, сколько сольдо приходится на 120%,
нужно 3 умножить на 120, получится 360. 360 сольдо
стоит дом. Чтобы узнать, сколько дополнительно
заработать, нужно из 360 вычесть 300, получится 60. 60
сольдо нужно Буратино дополнительно заработать.
Вариант 2. Чтобы найти 20% от 300, нужно
300 разделить на 100 и умножить на 20, получится 60. 60
сольдо нужно дополнительно заработать Буратино.
Теперь дом будет стоить 300 плюс 60, т.е. 360 сольдо.
Решение.
Способ 1.
1) 300 : 100 = 3 (с.) – приходится на 1%.
2) 100 + 120 = 120 % – стоит дом от старой цены.
3) 3 х 120 = 360 (с.) – новая цена дома.
4) 360 – 300 = 60 (с.) – нужно заработать.
Способ 2.
1) 300 : 100 х 20 = 60 (с.) – надо заработать.
2) 300 + 60 = 360 (с.) – новая цена дома.
Ответ: 60 сольдо.
Задача на нахождение числа по его
части.
Почтальону Печкину пришло на почту в
марте 48 писем. Это составило части писем,
пришедших на почту в феврале. Сколько писем
пришло в феврале? Сколько писем пришло за эти 2
месяца? (Ч.3, №4, с. 20).
Схема.
Рассуждения ученика.
Вариант 1. 48 писем приходится на ,
т.е на 8 равных частей. Сначала узнаем, сколько
писем приходится на одну часть, для этого 48
разделим на 8, получится 6. Дальше найдем, сколько
писем приходится на 7 таких же частей. Для этого 6
умножим на 7, получится 42. Чтобы найти количество
писем за 2 месяца, нужно сложить 48 и 42, получится 90.
90 писем пришло за 2 месяца.
Вариант 2. Чтобы найти число по его
части, выраженной дробью, надо эту часть
разделить на числитель дроби и умножить на
знаменатель. Чтобы найти число, зная, что на
приходится 48, нужно 48 разделить на 8 и умножить на
7, получится 42. Чтобы найти, сколько писем пришло
за 2 месяца, надо сложить 48 и 42, получится 90. 90
писем пришло за 2 месяца.
Решение.
По действиям с пояснениями:
Способ 1.
1) 48 : 8 = 6 (п.) – приходится на 1 часть.
2) 6 х 7 = 42 (п.) – пришло в феврале.
3) 48 + 42 = 90 (п.) – пришло за 2 месяца.
Способ 2.
1) 48 : 8 х 7 = 42 (п.) – пришло в феврале.
2) 48 + 42 = 90 (п.) – пришло за 2 месяца.
Ответ: 42 письма и 90 писем.
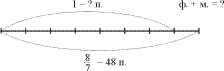
Задача на нахождение части, которую
одно число составляет от другого
Мачеха, уходя с дочерьми на бал, велела
Золушке перебрать 100 кг крупы. Золушка, чтобы
угодить мачехе, перебрала 150 кг. Какую часть
своего задания выполнила Золушка? Вырази эту
часть в процентах. На сколько процентов Золушка
перевыполнила задание? (Ч. 3, № 7, с. 21).
Схема.
Рассуждения ученика.
Чтобы найти, какую часть задания
Золушка выполнила, нужно ту часть, которую она
выполнила, т.е. 150, разделить на само задание, т.е.
на 100, получится ,
или 150%. Так как все задание составля-ет 100%, то она
перевыполнила его на 150 – 100 = 50. На 50% Золушка
перевыполнила задание.
Решение.
1) 150 : 100 = (ч.) – выполнила.
2) =150%, 150 – 100 = 50%
– перевыполнила.
Ответ: части, 150%, 50%.
Надеемся, что рассмотренный материал
окажется полезным не только учителям, работающим
по авторской методике Л.Г. Петерсон, но и всем, кто
интересуется вопросами преподавания математики
в начальной школе.
* Здесь и далее по тексту ссылка на учебник
Петерсон Л.Г. «Математика», 3 класс.
Ну если они пересекаются и пр пересечении они похожи на букву Т
Итак, мы имеем вектор a{3;-2} и вектор b{1;-2}.
Умножение вектора на число: p*a=(pXa;pYa;), где p — любое число.
В нашем случае имеем: вектор 5а{15;-10} и вектор 9b{9;-18}.
Разность векторов : a-b=(Xa-Xb;Ya-Yb).
В нашем случае имеем: вектор c=5а-9b={15-9;-10-(-18)}={6;8}.
Итак, мы имеем вектор с{6;8}.
Модуль или длина вектора: |c|=√(Xc²+Yc²) или |с|=√(36+64)=10.
Координаты вектора ab равны разности соответствующих координат точек его конца и начала ab{x2-x1;y2-y1).
В нашем случае координаты вектора с известны: Xc=6 и Yc=8. Известны и координаты его конца: Xm=3 и Ym=2.Пусть точка N — начало вектора с. Зная, что Xc=Xm-Xn и Yc=Ym-Yn, находим координаты начала вектора с (точки N). Эти координаты будут: Xn=Xm-Xc или Xn=3-6=-3 и Yn=Ym-Yc или Yn=2-8=-6.
Остается только на координатной плоскости отметить две точки: N(-3;-6) и M(3;2).
Соединив эти две точки, получим искомый вектор С.
Пусть дан параллелепипед ABCD, BK- высота
Теорема Пифагора
a^2+b^2=c^2
a=6
b=корень из 13
36+13=c^2
c^2=49
c=7
Ответ:7
|
без линейки. Дан отрезок АВ найти точки С и D которые точно делят отрезок АВ на три равные части Ответ должен в виде точки которая получается пересечением отрезка с дугой либо касанием дуги этого отрезка. Циркуль нельзя ломать, бумагу не сгибать. бонус за лучший ответ (выдан): 5 кредитов Сечас попробую объяснить все на пальцах, как получится. Если следовать пошаговой моей инструкции, и делать все на бумаге, то получается следующее. У нас есть отрезок. Мы должны его поделить на три равные части с помощью циркуля. Диаметр циркуля должен быть больше половниы данного отрезка, но меньше длины этого отрезка. С двух концов отрезка (точка А,В) проводим окружность,они пересекаются в двух точках над отрезком (точка С, D). Строим лучи АС И DВ, они получаются паралельными. С помощью того же циркуля с произвольным диаметром отмеряем 4 одинаковых отрезка по линиям АС и ВD. На линии АС получаем точки А1,А2,А3. На линии ВD — В1,В2,В3. Соединяем между собой А1 ти В3 и т.д. И ссответственно на отрезке АВ получаем три равніе части. Как то так. Если бы можно было лично с вами пообщаться, я бы все разложил досконально на бумаге. система выбрала этот ответ лучшим Текстовое описание решения: 1) строим удвоенный и утроенный отрезок, 2) из концов исходного отрезка проводим две дуги утроенной длины, чтобы они пересеклись между собой, 3) из концов исходного отрезка проводим две дуги удвоенной длины, примерно на условной линии соединяющей концы отрезка и точку пересечения из шага 2, 4) из точки пересечения из шага 2 проводим дугу радиусом в размер отрезка эта дуга каснется двух дуг из шага 3. 5) расстояние между точками из шага четыре есть 1/3 от исходного отрезка, берем его и на исходном отрезке делаем зачеки. Задача решена. Я пока привел решение без доказательств, промежуточных выкладок и построений, если будет что непонятно пишите распишу подробно. PS данным методом можно делить отрезок одним циркулем на любое количество частей. Так как я не смог найти в инете предложенное мной решение, то хочу без лишней скромности закрепить за собой авторство такого способа. 29.03.2014 18:55 МСК PavelR 9 лет назад Кроме циркуля нам понадобятся линейка без делений для проведения прямых линий и ручка для того, чтобы чертить эти линии. Отмечаем на бумаге 2 точки А и В и проводим через эти точки прямую линию. На этой прямой линии имеем отрезок длиной АВ. С помощью циркуля чертим окружность радиусом равным АВ с центром в точке А. То есть окружность проходит через точку В. Затем чертим вторую такую же окружность радиусом АВ, но с центром в точке В. Эта окружность проходит через точку А. Эти наши окружности пересекаются в двух точках С и Д. Проводим прямую линию СД. Эта линия пересекает отрезок АВ в точке Е. Линия СД перпендикулярна АВ и делит наш отрезок АВ пополам. То есть АЕ = ЕВ. Так можно с помощью циркуля разделить любой отрезок пополам. Но нам надо на 3 части. Возьмем линию СЕ. На середину этого отрезка ставим точку Ф. (Как делить отрезок пополам, мы уже знаем). Через точку Ф проводим окружность с центром в точке А. И еще такую же окружность через точку Ф, но с центром в точке В. Точки пересечения этих окружностей с нашим отрезком АВ делят отрезок АВ на 3 равные части. А как обойтись без линейки и ручки, я пока не знаю. bezdelnik 9 лет назад В вопросе не оговаривается точность деления, значит допускается приближенное деление. Такое деление без всяких построений можно выполнить методом последовательных приближений. Но автор предполагает геометрическое построение. Я предлагаю следующее построение. 1)чертим первую окружность с центром в точке А или В радиусом равным длине отрезка АВ, например с центром в точке В ; 2) чертим дугу второй окружности с центром в точке А тем же радиусом АВ до пересечения с первой окружностью и получаем точку Т и Т1; 3) чертим дугу третьей окружности с центром Т касательную к АВ и получаем точку касания Е, которая разделит АВ надвое (АЕ=1/2АВ); 4)аналогичным образом делим АЕ надвое и получаем точку К (АК=1/4АВ); 5) чертим дугу окружности с центром в точке В радиусом ВК до пересечения с первой окружностью и получаем точку М; 6)чертим дугу окружности с центром в точке М касательную к АВ и получаем точку касания С, АС будет приблизительно равен 1/3 АВ и откладываем СD равный АС. Проповедник 9 лет назад Делим отрезок AB на 4 части *. Далее рисуем отрезок AC равный 3/4 от первоначального отрезка так, чтобы он начинался из точки первоначального A и чтобы он лежал не на одной прямой с ним. Далее отмечаем на втором отрезке AC две точки D и E, которые поделят его на 3 части *. Конец второго отрезка соединяем с концом первого отрезком BC. Далее проводим через точки D и E две прямые, параллельные отрезку BC *. Они поделят отрезок AB на 3 равных отрезка в соответствии с теоремой Фалеса. Звездочкой * отмечены тривиальные задачи, которые слишком долго объяснять, но додуматься до которых можно быстро и самому. Что же касается черчения прямых, то у меня рука твердая, прочертить могу и без линейки. Ну или с помощью бесконечного циркуля, что тоже является тривиальной задачей. Если дан отрезок, то циркулем с концов отрезка проведите засечки, радиусом равным длине отрезка и полученную точку соедините с концами отрезков — у Вас получится равнобедренный треугольник со стороной, равной длине отрезка. С конца двух вершин данного трегольника проведите медианы к сторонам треугольника (с помощью циркуля это легко сделать, ведь медианы перпендикулярны будут сторонам). Медина делится в пропорции 1:2 — то, что надо. Из точки перекрещения медиан проведите прямую, параллельную стороне созданного треугольника, она пропорционально разделит сторону отрезка на одну треть, что нам и необходимо. Galina7v7 7 лет назад Заинтересовалась задачей.только про решение задачи без линейки и слушать не хочу.Понравилось решение по простоте у Katar .проще и быть не может.Пусть данный отрезое ВМ.Восстановим к нему перп-ляр к т.М .известным методом.и от него по разные стороны отложим циркулем МА=МС.получим тр-ник АВС.Проведем медианы АМ1 и СМ2.Т.О пересчения всех медиан делит отрезок ВМ на ОМ=13 ВМ и ОВ=23 ВМ.Отложим циркулем ОО1=МО и О1В=О1О=ОМ-3 равных отрезка.Есто еще один способ тоже простой-но с линейкой! Водяной 9 лет назад Такую операцию можно проделать методом последовательных приближений, с бесконечной точностью при бесконечном количестве действий. Алгоритм: Первоначальный раствор циркуля берем меньше длины отрезка и пробуем уложить данный раствор три раза в длину отрезка, с последующей коррекцией в плюс или минус величины раствора циркуля. Знаете ответ? |
Раздел:
Домашние задания
В блог
Подписаться на Дзен!
Отвечать в конференциях и заводить новые темы может любой участник, независимо от наличия регистрации на сайте 7я.ру.
Как решить задачу с дробями?
Найти число, зная, что если отнять от него 1/3 и 1/4, то получится 10. Приведение к общему знаменателю не проходили. И как?
*** Тема перенесена из конференции «СП: посиделки»
02.11.2015 15:51:13,
9 комментариев
Получится 120
10.11.2017 12:47:25, Полина Новикова
я думаю, если речь о последовательных действиях, от оставшегося, то я б рассуждала
число сначала умнжили на 2/3 ( отняли треть), а потом уможили на 3/4 ( отняли четверть), тройки сократиилсь, осталась 2/4, т.е. половинка от числа это и есть 10.
а какой это класс???
вот всегда самый вопрос в методологии, только что решала 6 классную задачку, так над каждым действием думала, могут они так или нет….
02.11.2015 16:08:11, Челюсть На Оленях
4 класс, второй урок по дробям
02.11.2015 16:12:07, arrdana
Вам нужна первая часть. Где сказано «так мы решили бы задачу в начальной школе». Там три части всего. Найдите все, разберитесь сами, потом ребенку объясните на его уровне.
03.11.2015 15:08:28, Красно Солнышко
а 1-4 отнимать от оставшегося или от первоначального?
02.11.2015 16:04:52, Челюсть На Оленях
Яндекс спросить проще
Задача из «Арифметики» известного среднеазиатского математика IX в. Мухаммеда ибн-Мусы ал-Хорезми. «Найди число, зная, что если отнять от него одну треть и одну четверть, то получится 10». (Ч. 2, № 2, с. 64).
Поиск решения. Обозначим число отрезком, длина которого делится на 3 и на 4, это может быть 12, или 24, или 36 и т.д. Возьмем наименьшее из них – 12, нарисуем 12 равных отрезков или мерок. Найдем одну треть отрезка. [12 : 3 = 4 (ч.).] Найдем одну четверть отрезка. [12 : 4 = 3 (ч.).] Сколько частей вычли? [4 + 3 = 7 (ч.).] Сколько частей осталось? [12 – 7 = 5 (ч.).] 10 приходится на сколько частей? [На 5.] Сколько приходится на одну часть? [10 : 5 = 2.] Число 2 приходится на одну часть, а сколько всего частей? [12.] Как найти число? [2 х 12 = 24.]
Решение.
1) 12 : 3 = 4 (ч.) – треть числа.
2)12 : 4 = 3 (ч.) – четверть числа.
3) 3 + 4 = 7 (ч.) – вычли.
4)12 – 7 = 5 (ч.) – осталось.
5) 10 : 5 = 2 – приходится на одну часть.
6) 2 х 12 = 24 – число.
Ответ: Это число 24.
02.11.2015 15:54:36, КалиНа*
Спасибо! А я уравнение забивала 
02.11.2015 15:55:43, arrdana
© 2000-2023, 7я.ру
Материалы сайта носят информационный характер и предназначены для образовательных целей. Мнение редакции может не совпадать с мнениями авторов. Перепечатка материалов сайта запрещена без письменного согласия компании SIA «ALP-Media» и авторов. Права авторов и издателя защищены.
7я.ру — информационный проект по семейным вопросам: беременность и роды, воспитание детей, образование и карьера, домоводство, отдых, красота и здоровье, семейные отношения. На сайте работают тематические конференции, ведутся рейтинги детских садов и школ, ежедневно публикуются статьи и проводятся конкурсы.
18+
Если вы обнаружили на странице ошибки, неполадки, неточности, пожалуйста, сообщите нам об этом. Спасибо!