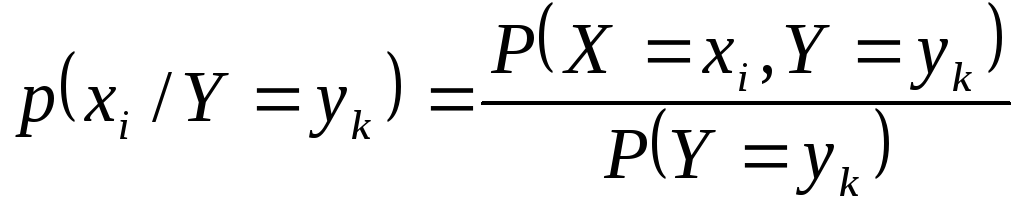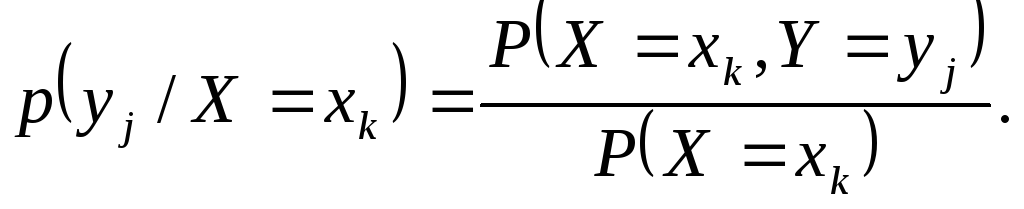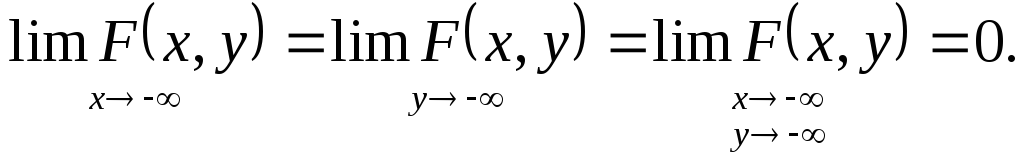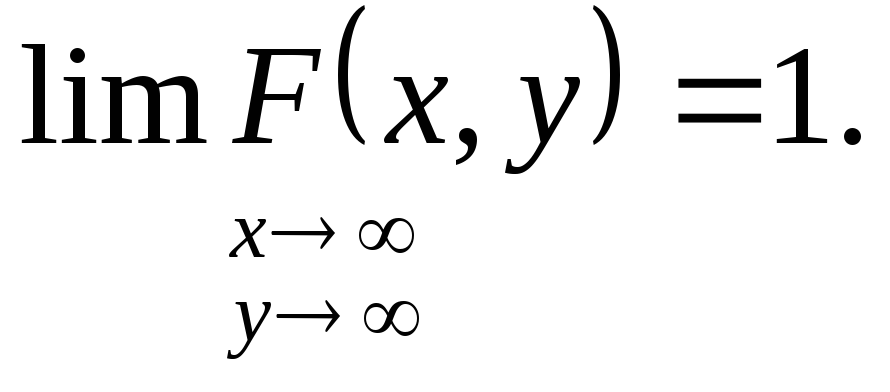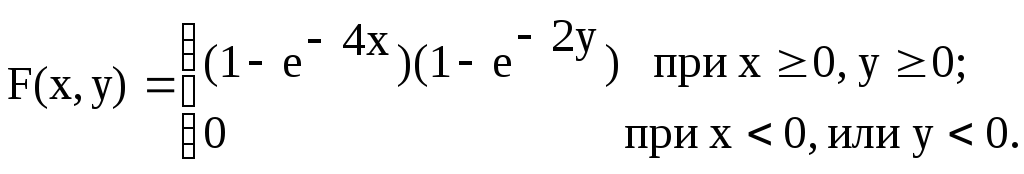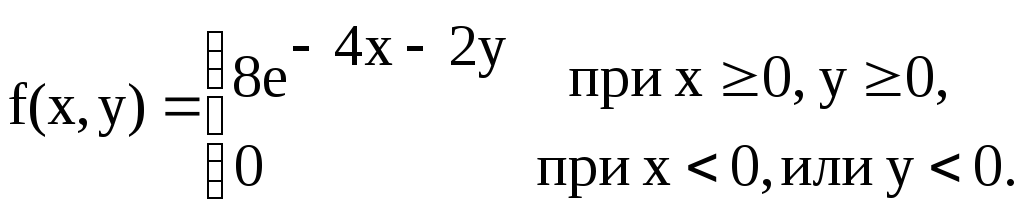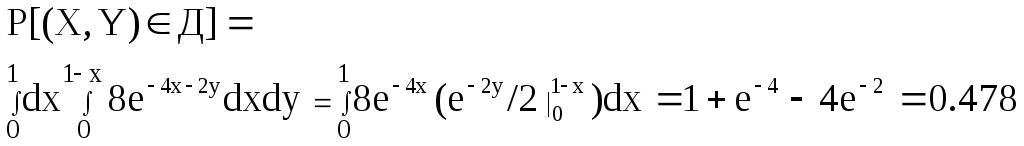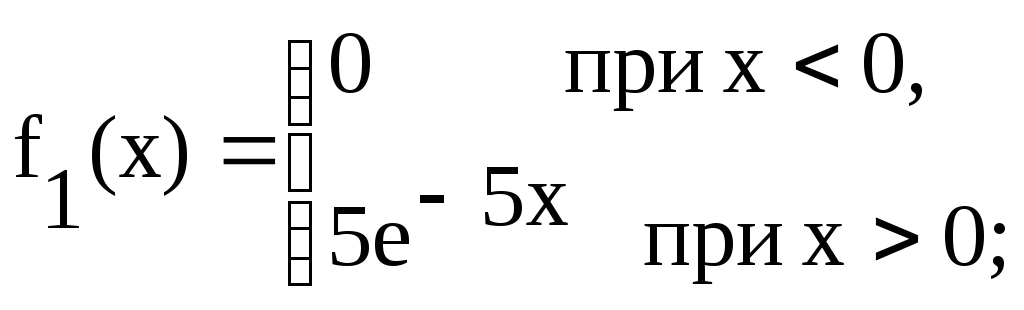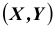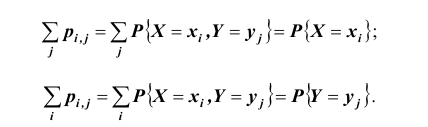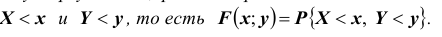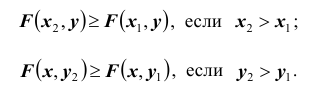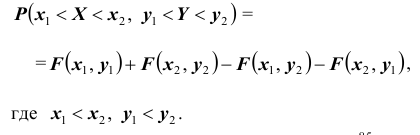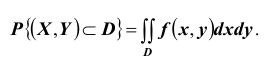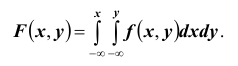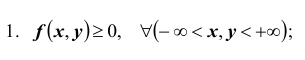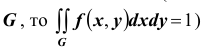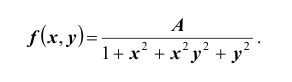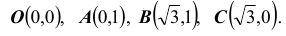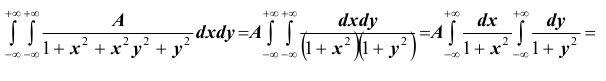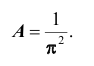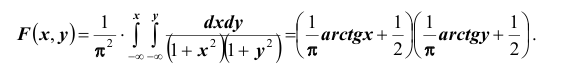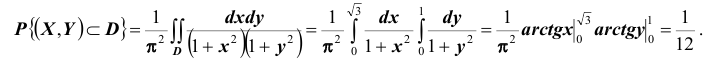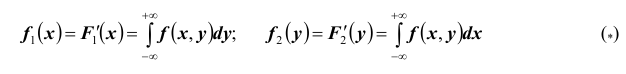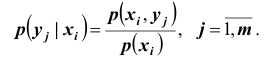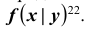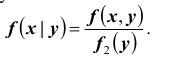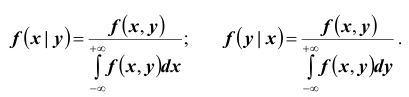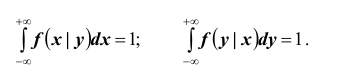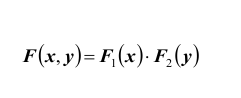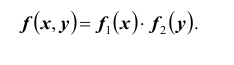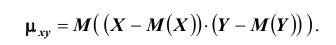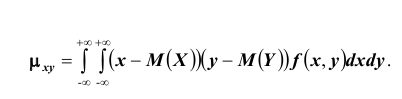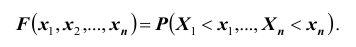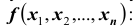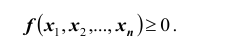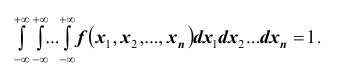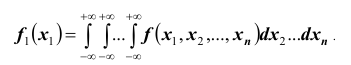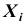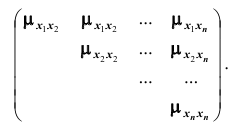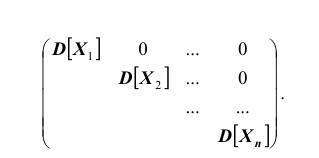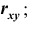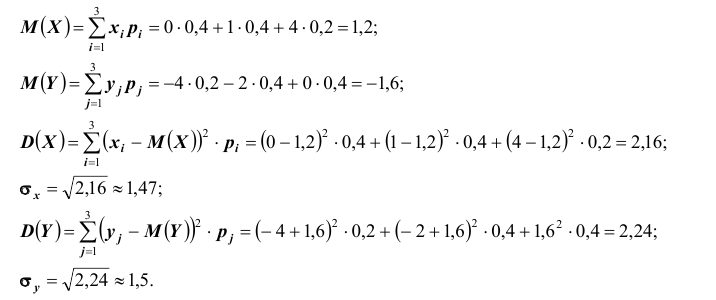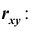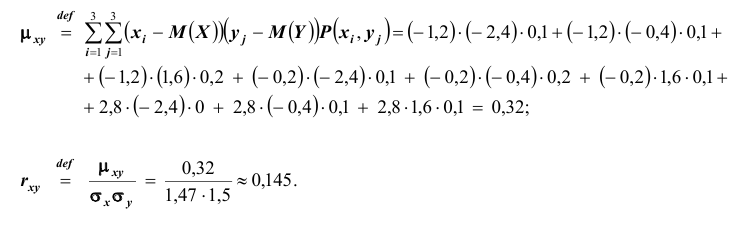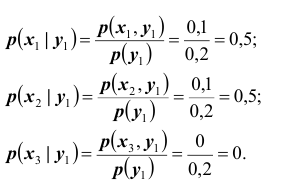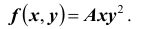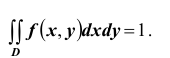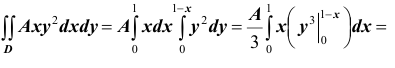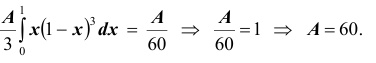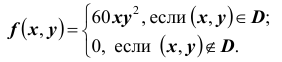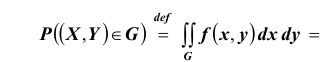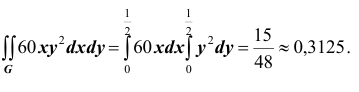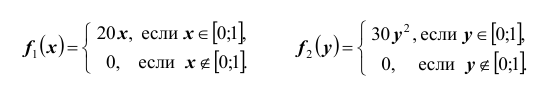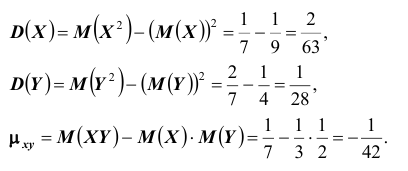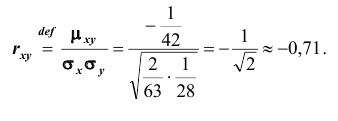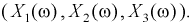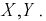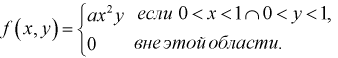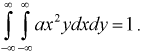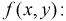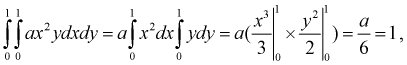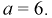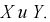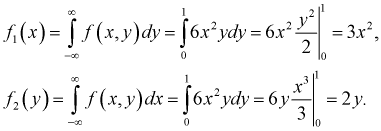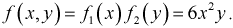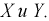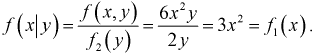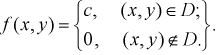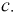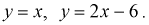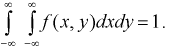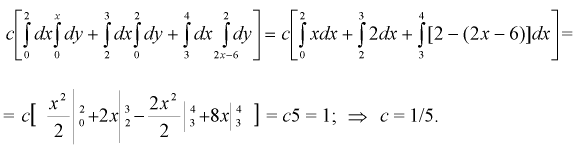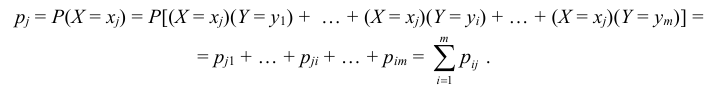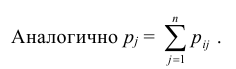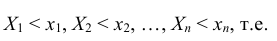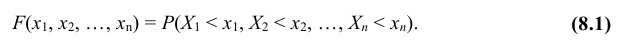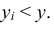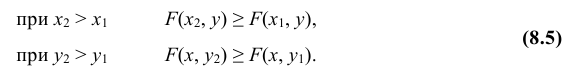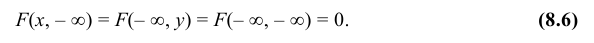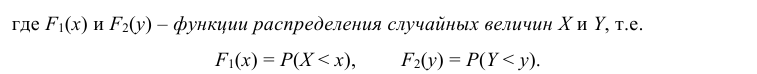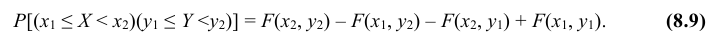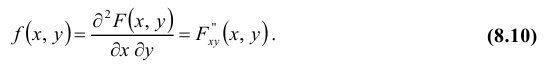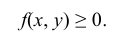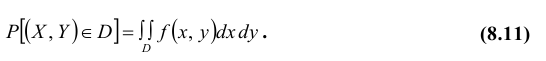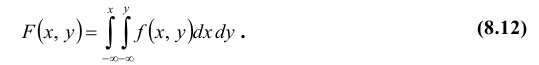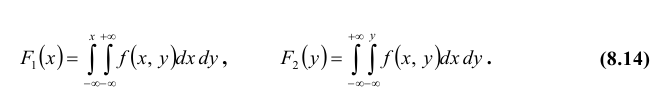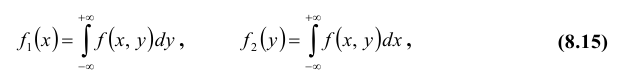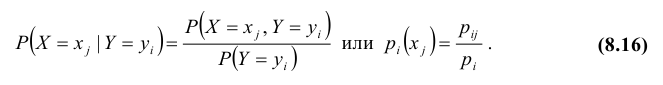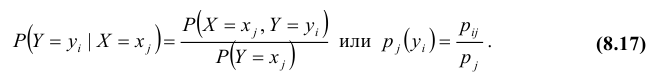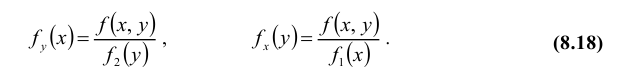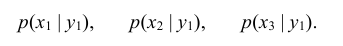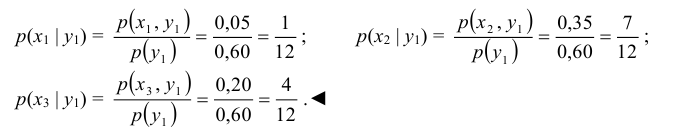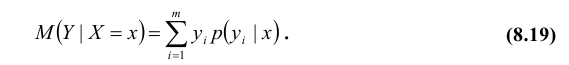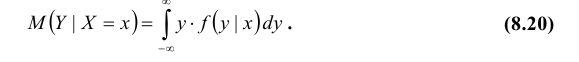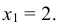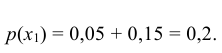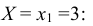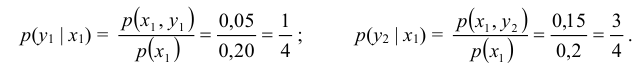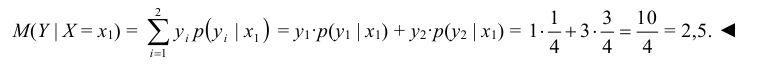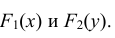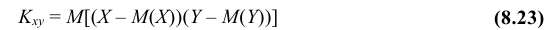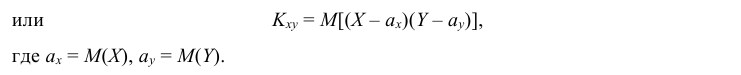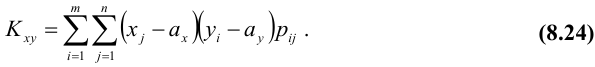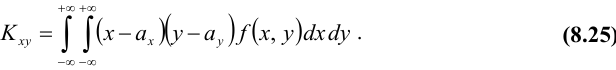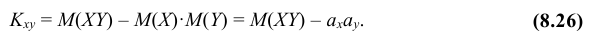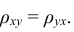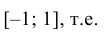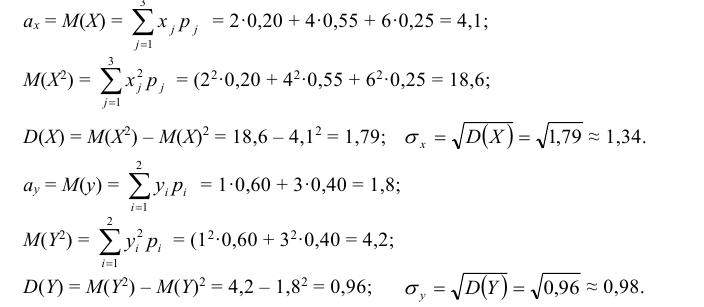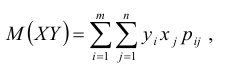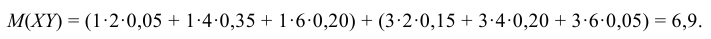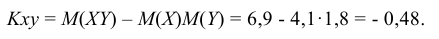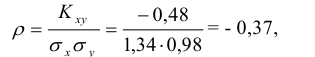Как найти одномерные распределения составляющих

Двумернойназывают случайную величину (X,Y), возможные значения
которой есть пары чисел (x,y). СоставляющиеXиYобразуют систему двух
случайных величин.

Геометрически
двумерную величину можно истолковать
как случайный вектор.

Дискретнойназывают двумерную величину, составляющие
которой дискретны.

Непрерывнойназывают величину, составляющие которой
непрерывны.

Закон распределения
дискретной двумерной величины может
быть задан в виде таблицы с двойным
входом, в которой указан перечень
возможных значений (x_i,y_j) и
соответствующих вероятностей

удовлетворяющих
условию

.

Одномерные
законы распределения составляющих
можно получить, вычисляя вероятности
их появления по формулам

,
,
т.е. проводя суммирование по столбцам
или строкам таблицы.

Условным
законом распределениясоставляющейXпри условии, чтоY=y_kназывают совокупность возможных значенийx_iи
соответствующих этим значениям условных
вероятностей, определяемых равенством:

_.

Аналогично
можно задать условное распределение
составляющей Y, причем:

Функцией
распределениявероятностей двумерной
случайной величины интегральной функции
называют функциюF(x,y),
определяемую соотношением:

Она
является неубывающей функцией и обладает
следующими свойствами:

1. при
   

2. 

3. 

4. где
   F_X(x)
   – функция распределения составляющей
   X,
   а F_Y(y)
   – составляющей Y.

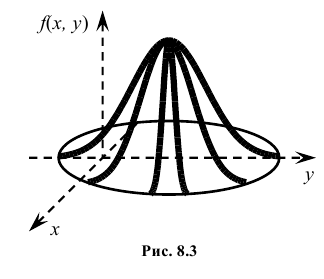
5. Вероятность
   попадания случайной точки в прямоугольник
   вычисляется по формуле:

_.

Плотностью
совместного распределениявероятностей
случайного вектора (X,Y)
называют вторую смешанную производную
от функции распределения:

_.

Свойства
совместной двумерной плотность
распределения аналогичны свойствам
плотности распределения вероятностей
одной случайной величины:

Условной плотностью
распределения, составляющейXпри заданном значенииY=yназывается функция

Аналогично:

Если
условые плотности распределения
случайных величин Х,Yравны их безусловным плотностям, то
такие величины называют независимыми.

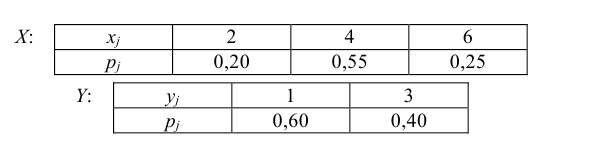
Пример
10.Задан закон распределения вероятностей
двумерной случайной величины (X,Y).

Найти: а) законы
распределения составляющих; б) условный
закон распределения Xпри
условии, чтоY=-2; в) условный
закон распределенияY,
при условии, чтоX=2.

Решение.а) Для
отыскания вероятностей появления
возможных значений х_iпроведем
суммирование вероятностей по существующим
столбцам, а для y_k– по строкам.
Результаты вычислений занесем в таблицу.
Тогда первая и четвертая строки будут
определять закон распределения для X,
а первый и пятый столбцы – для Y.

б)
Для отыскания условных вероятностей
значений X поделим вероятность совместного
появления X=x_i, Y=-2, на p(y_k=-2)=0,45
и результат запишем в последней строке:
0,1/0,45=2/9; 0,2/0,45=4/9; 0,15/0,45=1/3.

в)
Аналогично найдем условные вероятности
для Y: 0,15/0,4=3/8; 0,25/0,4=5/8.

Тогда
первая и пятая строки будут определять
условный закон распределения для X, а
первый и шестой столбцы – для Y.

Пример 11.Задана
функция распределения двумерной
случайной величины

Найти:
а) двумерную плотность распределения
систему (X,Y); б) плотность распределения
составляющих; в) условные плотности
распределения составляющих; г) вероятность
попадания случайной точки (X,Y) в треугольник
с вершинами О(0,0); А(0,1); В(1,0).

Решение.а)
Двумерную плотность вероятности системы
найдем по формуле:Следовательно

б)
Найдем плотность распределения
составляющей X:

Для
составляющей Y:

в)
Условные плотности распределения равны:

Заметим,
что условные плотности распределения
совпали с безусловными, следовательно
X и Y независимы.

г)
Вероятность попадания случайной точки
в область Д вычисляется по формуле:

Область
Д – треугольник ОАВ, уравнения сторон
которого имеют вид: x=0; y=0; x+y=1. Тогда

12. Задана двумерная
плотность вероятности системы двух
случайных величин: f (х, у) = (1/2)sin(х+у) в
квадрате
,; вне квадрата f(x,y)= 0. Найти функцию
распределения системы (X, Y).

13. Задана двумерная
плотность вероятности системы случайных
величин (X, Y)

.

Найти
функцию распределения системы.

Указание:
использовать формулу

14. Задана двумерная
плотность вероятности
системы (X, Y) двух случайных величин.
Найти постоянную С.

15. Задана дискретная
двумерная случайная величина (Х, Y):

Найти:
а) условный закон распределения X при
условии, что Y = 10; б) условный закон
распределения У при условии, что Х = 6.

16. Непрерывная
двумерная случайная величина (X, Y)
распределена равномерно внутри
прямоугольника с центром симметрии в
начале координат и сторонами 2a и 2b,
параллельными координатным осям. Найти:
а) двумерную плотность вероятности
системы; б) плотности распределения
составляющих.

17. Заданы плотности
распределения независимых составляющих
непрерывной двумерной случайной величины
(X, Y):

Найти:
а) плотность совместного распределения
системы; б) функцию распределения
системы.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

1.
Понятие двумерной (n-мерной) случайной
величины. Примеры.

Одномерные
распределения ее составляющих. Условные
распределения.

Зачастую результат
опыта описывается несколькими случайными
величинами:

.
Например, погоду в данном месте в
определенное время суток можно
охарактеризовать следующими случайными
величинами: Х₁
– температура,
Х₂
– давление,
Х₃
– влажность воздуха, Х₄
– скорость ветра. Рассмотрим двумерную
случайную величину

,
возможные значения которой есть пары
чисел

.
Геометрически двумерную случайную
величину можно истолковать как случайную
точку на плоскости

.

Пример
1.
Найти законы распределения составляющих
Х
и Y,
если задано
распределение двумерной случайной
величины в виде таблицы

Решение. Так как

_{,
то проводя суммирование по строкам
таблицы 6.1.2 получим распределение Х:}

Аналогично суммируя
по столбцам, получим распределение Y:

Если зафиксировать
значение одного из аргументов, например

,
то полученное распределение величины
Х
называется условным распределением.
Аналогично определяется условное
распределение Y.

Пример
2.
По распределению двумерной случайной
величины, заданной табл., найти: а)
условный закон распределения составляющей
Х
при условии

;
б) условный закон распределения Y
при условии, что

.

Решение. Условные
вероятности составляющих Х
и Y
вычисляются
по формулам

,

.

Тогда

а)

,

,

.

Условный закон
распределения Х
при условии

имеет вид

Контроль:

.

б) Аналогично находим
условный закон Y
при условии

.

Контроль:

.

2. Функция
распределения и плотность вероятности
2-мерной случайной величины, их свойства,
примеры.

Двумерной случайной
величиной называется функция вероятного
события, наступившего в результате
принятия величинами х и y
случайных значений.

где

X
и Y
случайные величины, которые могут быть
как дискретными, так и непрерывными.

Для дискретной
случайной величины функция распределения
имеет следующий вид:

где вероятность
суммируется для всех xi
< x
и yi
< y.

Свойства функции
распределения двумерной случайной
величины.

1.Функция 0 ≤ F(x,y)
≤ 1, т.е. величина неотрицательная меньше
1.

2.Функция F(x,y)
есть возрастающая функция по каждому
из аргументов.

3.Функция распределения
F(x,y)
= 0, если хотя бы один из аргументов x
или y
стремится к минус бесконечности.

4.Функция F(x,y)
равна функции от одного аргумента F(x)
(F(y)),
если y
(x)
стремится к бесконечности.

5. Функция F(x,y)
равна 1, если оба аргумента стремятся к
плюс бесконечности.

3.Числовые
характеристики 2-мерной случайной
величины и свойства этих характеристик.
Примеры.

Рассмотрим
числовые характеристики двумерных
случайных величин и их свойства.

1. Математическое
   ожидание

Пусть
(x , h ) — двумерная случайная
величина, тогда M(x , h )=(M(x ), M(h )),
т.е. математическое ожидание случайного
вектора — это вектор из математических
ожиданий компонент вектора.

Если
(x , h ) — дискретный случайный
вектор с распределением

то
математические ожидания компонент
вычисляются по формулам:

, 
.

Эти
формулы можно записать в сокращенном
виде.

Обозначим 
 и 
,
тогда 
 и 
.

Если p(x , h )(x, y)-
совместная плотность распределения
непрерывной двумерной случайной величины
(x , h ), то

 и 
.

Поскольку 
 -плотность
распределения случайной величины x ,
то 
и,
аналогично, 
.

1. Дисперсия

Приведем
формулы для вычисления дисперсии
компонент двумерного случайного вектора.

Если
(x , h ) — двумерная случайная
величина, то

Dx = M(x — Mx )2 = Mx 2 — M(x )2, Dh = M(h — Mh )2 = Mh 2 — M(h )2.

Входящие
в эту формулу математические ожидания
вычисляются по приведенным выше формулам.

1. Условное
   математическое ожидание

Между
случайными величинами может существовать
функциональная зависимость. Например,
если x — случайная величина и h =x 2,
то h — тоже случайная величина,
связанная с x функциональной
зависимостью. В то же время между
случайными величинами может существовать
зависимость другого рода,
называемая стохастической.

Математическое
ожидание, вычисленное по условному
распределению, называется условным
математическим ожиданием.

Для
двумерного дискретного случайного
вектора (x , h ) с распределением

условное
математическое ожидание случайной
величины x при условии, что случайная
величина hпринимает значение yj,
вычисляется по формуле 
.

Аналогично,
условное математическое ожидание
случайной величины h при условии,
что случайная величина x принимает
значение xi, равно 
.

Видно,
что условное математическое ожидание
случайной величины x является
функцией значений случайной величины h ,
т.е. M(x /h = y) = f1(y) и, совершенно
аналогично, M(h /x = x) = f2(x).

Функцию f1(y)
называют регрессией случайной
величины x на случайную
величину h , а f2(x) — регрессией
случайной величины h на случайную
величину x .

Если p(x ,h )(x, y)
совместная плотность вероятностей
двумерной случайной величины (x ,h ),
то

 и 
.

1. Ковариация

Если
между случайными величинами x и h существует
стохастическая связь, то одним из
параметров, характеризующих меру этой
связи является ковариация cov(x , h ).
Ковариацию вычисляют по формулам
cov(x , h )=M[(x — Mx )(h — Mh )] = M(x h)
— Mx Mh .

Если
случайные величины x и h независимы,
то cov(x ,h )=0.

Свойства
ковариации:

cov(x , x )
= Dx ;

;

;

,

где C1 и C2 —
произвольные константы.

Ковариационной
матрицей случайного вектора (x ,h ) называется
матрица вида

.

Эта
матрица симметрична и положительно
определена. Ее определитель
называется обобщенной дисперсией и
может служить мерой рассеяния системы
случайных величин (x ,h ).

Как
уже отмечалось ранее, дисперсия
суммы независимых случайных
величин равна сумме их дисперсий: 
.
Если же случайные величины зависимы, то 
.

1. Корреляция

Понятно,
что значение ковариации зависит не
только от “тесноты” связи случайных
величин, но и от самих значений этих
величин, например, от единиц измерения
этих значений. Для исключения этой
зависимости вместо ковариации используется
безразмерный коэффициент корреляции 
.

Этот
коэффициент обладает следующими
свойствами:

—
он безразмерен;

—
его модуль не превосходит единицы,
т.е. 
;

если x и h независимы,
то k(x ,h )=0 (обратное неверно!);

если 
,
то случайные величины x и h связаны функциональной
зависимостью вида h = ax +b,
где a и b- некоторые числовые
коэффициенты;

;

Корреляционной
матрицей случайного вектора называется
матрица

.

Если 
 и 
,
то ковариационная и корреляционная
матрицы случайного вектора (x ,h )
связаны соотношением 
,
где 
.

4.
Зависимые и независимые случайные
величины. Ковариация и коэффициент
корреляции случайных величин. Связь
между некоррелированностью и независимостью
случайных величин.

Случайные
величины называются независимыми, если
закон распределения одной из них не
зависит от того какое значение принимает
другая случайная величина.

Условные
распределения независимых случайных
величин равны их безусловным распределениям.

Теорема. Для
того, чтобы случайные величины Х и Y были
независимы, необходимо и достаточно,
чтобы функция распределения системы
(X, Y) была равна произведению функций
распределения составляющих.

Аналогичную
теорему можно сформулировать и для
плотности распределения:

Теорема. Для
того, чтобы случайные величины Х и Y были
независимы, необходимо и достаточно,
чтобы плотность совместного распределения
системы (X, Y) была равна произведению
плотностей распределения составляющих.

Пусть
имеется двумерная СВ (Х,Y), распределение
которой известно, т.е. известна табл.
5.1 или совместная плотность вероятности .
Тогда можно найти математические
ожидания М(Х) = а_х,
М(Y) = а_у и
дисперсии и
одномерных
составляющих Х иY. Однако математические
ожидания и дисперсии случайных величин
Х и Y недостаточно полно характеризуют
двумерную случайную величину (Х,Y), т.к.
не выражают степени зависимости ее
составляющих Х и Y эту роль
выполняют ковариация и коэффициент
корреляции.

Определение. Ковариацией (или корреляционным
моментом) К_ху случайных
величин Х и Y называется математическое
ожидание произведения отклонений этих
величин от своих математических ожиданий,
т.е.

,
Или ,

Где ,
.

Из
определения следует, что .
Кроме того,
.

т.е.
ковариация СВ с самой собой есть ее
дисперсия.

Для
дискретных случайных величин:

 .

Для
непрерывных случайных величин:

 .

Ковариация
двух случайных величин характеризует
как степень
зависимости случайных
величин, так и их рассеяние
вокруг точки .
Об этом, в частности, свидетельствуютсвойства
ковариации случайных величин.

1. Ковариация
   двух независимых случайных величин
   равна нулю.

2. Ковариация
   двух случайных величин равна
   математическому ожиданию их произведения
   минус произведение математических
   ожиданий, т.е. ,
   или
   .

3. Ковариация
   двух случайных величин по абсолютной
   величине не превосходит произведения
   их средних квадратических отклонений,
   т.е.
   .

Ковариация,
как уже отмечено, характеризует не
только степень зависимости двух случайных
величин, но и их разброс, рассеяние.
Кроме того, она — величина размерная, ее
размерность определяется произведением
размерностей случайных величин. Это
затрудняет использование ковариации
для оценки степени зависимости для
различных случайных величин. Этих
недостатков лишен коэффициент корреляции.

Определение. Коэффициентом
корреляции двух
случайных величин называется отношение
их ковариации к произведению средних
квадратических отклонений этих величин:

.

Из
определения следует, что .
Очевидно также, что коэффициент корреляции
естьбезразмерная
величина.

Свойства
коэффициента корреляции:

1. Коэффициент
   корреляции принимает значения на
   отрезке [-1;1], т.е. .

2. Если
   случайные величины независимы, то их
   коэффициент корреляции равен нулю,
   т.е. .

Случайные
величины называются некоррелированными,
если их коэффициент корреляции равен
нулю. Т.о., из независимости случайных
величин следует их некоррелированность.
Обратное утверждение, вообще говоря,
неверно: из некоррелированности двух
случайных величин еще не следует их
независимость.

1. Если
   коэффициент корреляции двух случайных
   величин равен (по абсолютной величине)
   единице, то между этими случайными
   величинами существует линейная
   функциональная зависимость.

Закон
распределения дискретной с.в.задан
таблицей

Найти
коэффициент корреляции 

Решение. Находим
законы распределения составляющих
и
:

Теперь
вычислим м.о. составляющих:

.

Этих
величин можно было находить на основании
таблицы распределения с.в. 

из
равенства (1) пункта 12.1. Например,

.

Аналогично, 
находите
самостоятельно.

Вычислим
дисперсии составляющих при это будем
пользоваться вычислительной формулой:

Следовательно,
Далее,
на основании первой формулы

(6) имеем:

Составим
закон распределения 
,
а затем найдём
:

При
составлении таблицы закона распределения
следует выполнять действия:

1) оставить
лишь различные значения всевозможных
произведений 
.

2) для
определения вероятности данного
значения 
,
нужно

складывать
все соответствующие вероятности,
находящиеся на пересечении основной
таблицы, благоприятствующие наступлению
данного значения.

В нашем
примере с.в.
принимает
всего три различных значения
.
Здесь первое значение (
)
соответствует произведению
из
второй строки и
из
первого столбца, поэтому на их пересечении
находится вероятностное число
аналогично

,

которое
получено из суммы вероятностей,
находящихся на пересечениях соответственно
первой строки и первого столбца (0,15 ;
0,40; 0,05) и одно значение 
,
которое находится на пересечении второй
строки и второго столбца, и наконец,
,
которое находится на пересечении второй
строки и третьего столбца.

Из нашей
таблицы находим:

Находим
корреляционный момент, используя формулу
(38):

Находим
коэффициент корреляции по формуле (41)

Таким
образом, отрицательная корреляция.

5.
Вариационный ряд, его разновидности.
Средняя арифметическая и дисперсия
ряда. Эмпирическая функция распределения.
Полигон и гистограмма.

Вариационным
рядом называется
ранжированный в порядке возрастания
(или убывания) ряд вариантов с
соответствующими им весами (частотами
или частостями).

При
изучении вариационных рядов наряду с
понятием частоты используется
понятие накопленной
частоты (обозначаем 
).
Накопленная частота показывает, ск-ко
наблюдалось вариантов со значением
признака, меньшим х. Отношение на
копленной частоты к общему числу
наблюдений n назовемнакопленной
частостью 
.

Накопленные
частоты (частости) для каждого интервала
находятся последовательным суммированием
частот (частостей) всех предшествующих
интервалов, включая данный.

Для
задания вариационного ряда достаточно
указать варианты и соответствующие им
частоты (частости) или накопленные
частоты (частости).

Вариационный
ряд называется дискретным,
если любые его варианты отличаются на
постоянную величину, и
— непрерывным (интервальными),
если варианты могут отличаться один от
другого на сколь угодно малую величину.

Для
графического изображения вариационных
рядов наиболее часто используются
полигон, гистограмма, кумулятивная
кривая:

Полигон,
как правило, служит для изображения
дискретного вариационного ряда и
представляет собой ломаную, в которой
концы отрезков прямой имеют координаты
(
),
i = 1, 2,…, m.

Гистограмма служит
только для изображения интервальных
вариационных рядов и представляет собой
ступенчатую фигуру из прямоугольников
с основаниями, равными интервалам
значений признака 
,
i = 1, 2, …,m, и высотами, равными частотам
(частостям) 
(
)
интервалов. Если соединить середины
верхних оснований прямоугольников
отрезками прямой, то можно получить
полигон того же распределения.

Кумулятивная
кривая (кумулята) —
кривая накопленных частот (частостей).
Для дискретного ряда кумулята представляет
ломаную, соединяющую точки (
,
)
или (
,
),
i = 1, 2, …, m. Для интервального вариационного
ряда ломаная начинается с точки, абсцисса
к-ой равна началу первого интервала, а
ордината — накопленной частоте (частости),
равной нулю. Другие точки этой ломаной
соответствуют концам интервалов.

Содержание:

Многомерные случайные величины:

До сих пор рассматривались случайные величины, возможные значения которых определялись одним числом. Такие величины называют одномерными. Например, число очков, которое может выпасть при бросании игральной кости – дискретная одномерная величина; расстояние от орудия до места падения снаряда – непрерывная одномерная случайная величина. Однако, при изучении случайных явлений в зависимости от их сложности иногда приходится использовать две, три и более случайных величин. Например, точка попадания снаряда определяется не одной, а двумя случайными величинами – абсциссой и ординатой. При различных измерениях очень часто имеем дело с двумя или тремя случайными величинами. Совместное рассмотрение двух или нескольких случайных величин приводит к понятию системы случайных величин. Условимся систему нескольких случайных величин X ,Y , . . . , W обозначать (X ,Y , . . . , W) Такая система называется также многомерной случайной величиной. При изучении системы случайных величин недостаточно изучить отдельно случайные величины, составляющие систему, а необходимо учитывать связи или зависимости между этими величинами.

При рассмотрении системы случайных величин удобно пользоваться геометрической интерпретацией системы. Например, систему двух случайных величин

В дальнейшем, при изучении системы случайных величин ограничимся подробным рассмотрением системы двух случайных величин.

Закон распределения вероятностей системы случайных величин

Законом распределения вероятностей системы случайных величин называется соответствие, устанавливающее связь между областями возможных значений данной системы случайных величин и вероятностями появления системы в этих областях.

Так же, как и для одной случайной величины, закон распределения системы случайных величин может быть задан в различных формах. Рассмотрим таблицу распределения вероятностей системы двух дискретных случайных величин. Пусть

Одномерную случайную величину иногда называют скалярной случайной величиной.

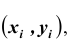
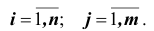
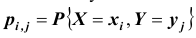
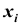
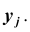
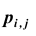
X и Y – дискретные случайные величины, возможные значения которых  где Тогда распределение системы таких случайных величин может быть охарактеризовано указанием вероятностей y того, что случайная величина X примет значение и одновременно с этим случайная величина Y примет значение . Вероятности фиксируются в таблице

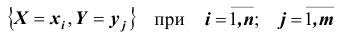
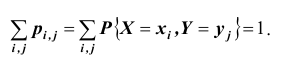
Такая таблица называется таблицей распределения вероятностей системы двух дискретных случайных величин с конечным числом возможных значений. Все возможные события составляют полную группу несовместных событий, поэтомупри этом 

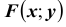
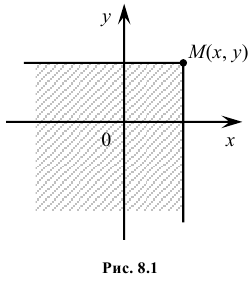
Функцией распределения вероятностей системы двух случайных величин называется функция двух аргументов, равная вероятности совместного выполнения двух неравенств 

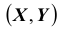
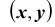
Геометрически функцию распределения системы двух случайных величин можно интерпретировать как вероятность попадания случайной точки в левый нижний бесконечный квадрант с вершиной в точке плоскости XOY (см. рис.).

5. Функция распределения является неубывающей функцией по каждому из своих аргументов, то есть:

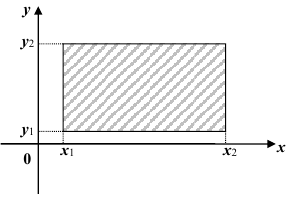
6. Вероятность попадания случайной точки (X,Y ) в произвольный прямоугольник со сторонами, параллельными координатным осям (см. рис.) вычисляется по формуле:

Плотность распределения вероятностей системы двух случайных величин

Предположим, что функция распределения F(x, y) всюду непрерывна и дважды дифференцируема21 (за исключением, быть может, конечного числа кривых). Тогда, смешанная частная производная функции F(x, y)

Функция называется плотностью распределения (или, дифференциальной функцией распределения) системы непрерывных случайных величин .
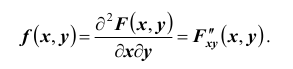
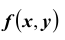
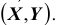
Геометрически эту функцию можно истолковать как поверхность, которую называют поверхностью распределения.
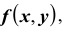
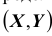
Зная плотность распределения можно определить вероятность попадания случайной точки в произвольную область D:

Используя последнюю формулу, выразим интегральную функцию F(x, y) распределения вероятностей системы двух непрерывных случайных величин через плотность распределения f (x, y):

Рассмотрим некоторые свойства плотности распределения системы двух непрерывных случайных величин:

Предполагается, что интегральная функция распределения вероятностей имеет непрерывную
смешанную частную производную второго порядка

если случайная величина (X,Y ) распределена на всей координатной плоскости (если же (X,Y ) распределена в некоторой плоской области 

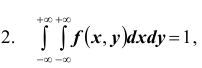
Пример №1

Пусть плотность распределения системы двух случайных величин (X,Y ) задана выражением:

Найти параметр А. Определить функцию распределения F(x, y) и вероятность попадания случайной точки (X,Y ) в прямоугольник D с вершинами:

Решение. Использовав свойство 2 плотности распределения, найдём постоянную величину А:

Следовательно 

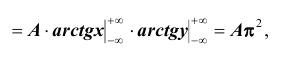
Определим теперь интегральную функцию распределения:

Таким образом, нетрудно теперь найти вероятность попадания случайной точки (X,Y ) в заданный прямоугольник D:

Условные законы распределения

Пусть известна плотность распределения системы двух случайных величин. Используя свойства функций распределения, можно вывести формулы для нахождения плотности распределения одной величины, входящей в систему:

Перейдём теперь к решению обратной задачи: по известным законам распределения отдельных случайных величин, входящих в систему, найти закон распределения системы. Легко увидеть, что в общем случае эта задача неразрешима. Действительно, с одной стороны, законы распределения отдельных случайных величин, входящих в систему, характеризуют каждую из случайных величин в отдельности, но ничего не говорят о том, как они взаимосвязаны. С другой стороны, искомый закон распределения системы должен содержать все сведения о случайных величинах системы, в том числе и о характере связей между ними. Таким образом, если случайные величины X ,Y взаимозависимы, то закон распределения системы не может быть выражен через законы распределения отдельных случайных величин, входящих в систему. Это приводит к необходимости введения условных законов распределения. Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина, входящая в систему, приняла определённое значение, называется условным законом распределения.

Для дискретных случайных величин условным распределением составляющей
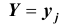
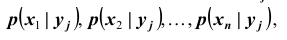
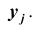
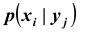
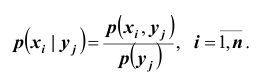
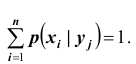
X при условии, чтоназывается совокупность условных вероятностей вычисленных в предположен, что случайная величина Y уже приняла значение Для нахождения пользуются формулой Заметим что Аналогично находим 

Условный закон распределения можно задавать как функцией распределения, так и плотностью распределения. Условная функция распределения обозначается F(x | y); условная плотность распределения обозначается 

Плотностью распределения для случайной величины X при условии, что случайная величина Y приняла определённое значение (условной плотностью распределения), назовём величину 

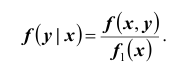
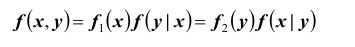
Аналогично, плотностью распределения для случайной величины Y при условии, что случайная величина X приняла определённое значение, назовём величинуОтсюда получаем или, с учётом формул (*)

Условная плотность распределения обладает всеми свойствами безусловной плотности распределения. В частности,

Числовые характеристики условных законов распределения

Для описания условных законов распределения можно использовать различные характеристики подобно тому, как для одномерных распределений. Наиболее важной характеристикой является условное математическое ожидание. Условным математическим ожиданием дискретной случайной величины X при Y = y ( y – определённое возможное значение случайной величины Y )

Мы записали условные законы распределения случайной величины X при условии, что другая случайная величина Y приняла определённое значение.

называется сумма произведений возможных значений X на их условные вероятности:

Для непрерывных случайных величин:где f x | y – условная плотность распределения случайной величины X приY = y . Аналогично, условным математическим ожиданием дискретной случайной величины Y при X = x ( x – определённое возможное значение случайной величины X ) называется сумма произведений возможных значений Y на их условные вероятности:Для непрерывных случайных величин:где – условная плотность распределения случайной величины Y при X = x. Аналогично вводятся условные дисперсии и условные моменты более высоких порядков (предлагаем это сделать самостоятельно).

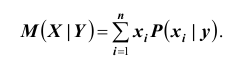
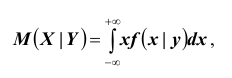
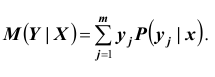
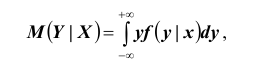
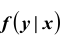
Числовые характеристики системы двух случайных величин

Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. Из этого определения следует, что условные распределения независимых случайных величин равны их безусловным распределениям. Укажем необходимые и достаточные условия независимости случайных величин.

ТЕОРЕМА 1: Для того чтобы случайные величины X и Y были независимыми, необходимо и достаточно, чтобы функция распределения
системы (X ,Y ) была равна произведению функций распределения составляющих: 

ТЕОРЕМА 2: Для того чтобы случайные величины X и Y были независимыми, необходимо и достаточно, чтобы плотность вероятности
системы (X ,Y ) была равна произведению плотностей вероятностей составляющих:

Для описания системы двух случайных величин кроме математических ожиданий и дисперсий составляющих используют и другие характеристики, к которым относятся корреляционный момент и коэффициент корреляции. Корреляционным моментом 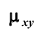случайных величин X и Y называют математическое ожидание произведения отклонений этих величин:

Для вычисления корреляционного момента дискретных величин используют формулу: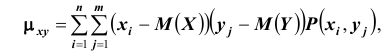а для непрерывных величин:

Корреляционный момент служит для характеристики связи между величинами X и Y .
 

ТЕОРЕМА 3: Корреляционный момент двух независимых случайных величин X и Y равен нулю.
 

Замечание: из теоремы 3 следует, что если корреляционный момент двух случайных величин X и Y не равен нулю, то X и Y – зависимые случайные величины.
 

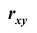
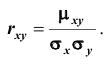
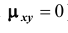
Коэффициентом корреляции случайных величин X и Y называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин:Очевидно, коэффициент корреляции двух независимых случайных величин равен нулю (так как ).

Коррелированность и зависимость случайных величин

Две случайные величины X и Y называются коррелированными, если их корреляционный момент (или коэффициент корреляции) отличен от нуля; X и Y называют некоррелированными величинами, если их корреляционный момент равен нулю. Две коррелированные величины также и зависимы. Обратное утверждение не всегда имеет место, то есть если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными. Другими словами, корреляционный момент двух зависимых величин может быть не равным нулю, но может и равняться нулю.

Заметим, что для нормально распределённых составляющих двумерной случайной величины понятия независимости и некоррелированности равносильны.

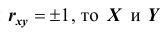
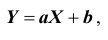
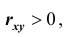
Если связаны линейной зависимостью Если , то говорят о положительной (или прямой) корреляции между
X и Y , то есть с возрастанием одной случайной величины другая случайная величина также возрастает.
Если 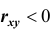, то говорят об отрицательной корреляции между X и Y , то есть с возрастанием одной случайной величины другая случайная величина убывает.
 

Функция и плотность распределения системы случайных величин

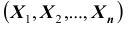
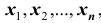
На практике очень часто приходится рассматривать системы более чем двух случайных величин. Функция распределения системы нескольких (более двух) случайных величин вводится как обобщение функции распределения системы двух случайных величин. Так, функцией распределения системы n случайных величин  называется функция n аргументов , равная вероятности
совместного выполнения n неравенств 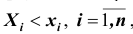, то есть:

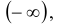
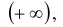
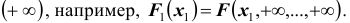
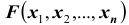
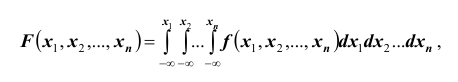
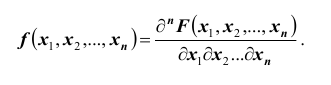
Эта функция является неубывающей функцией каждой переменной при фиксированных значениях других переменных. Если хотя бы одна из переменных стремится к , то функция распределения стремится к нулю. Если все переменные стремятся к, то функция распределения стремится к единице. Функция распределения каждой из величин, входящих в систему, получится, если в функции распределения системы все остальные аргументы положить равнымиАналогично одномерному случаю можно вывести формулу, связывающую функцию распределенияи плотность вероятности 

или что тоже самое Плотность распределения системы не может быть отрицательной:

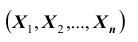
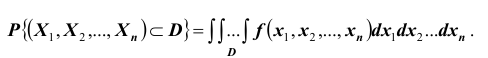
Вероятность попадания случайной точки с координатамив n – мерную область Dвыражается интегралом Используя свойства функции распределения, получаем 

Плотность распределения каждой из величин, входящих в систему, получится, если плотность распределения системы проинтегрировать в бесконечных пределах по всем остальным аргументам. Например,

Числовые характеристики произвольного числа случайных величин

Основными числовыми характеристиками, с помощью которых может быть охарактеризована система n случайных величин 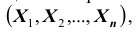являются следующие:

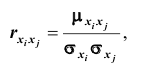
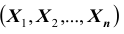
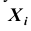
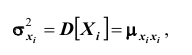
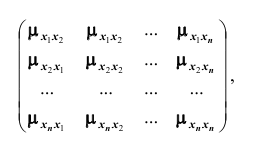
Зная корреляционные моменты, можно найти коэффициенты корреляции которые характеризуют степень связи между каждой парой случайных величин. Так как дисперсия каждой из случайных величин системы есть не что иное, как частный случай корреляционного момента, а именно: корреляционный момент величины и той же величины 

то все корреляционные моменты и дисперсии располагают в виде прямоугольной таблицы (матрицы)

которая называется корреляционной матрицей системы n случайных величин.

Из определения корреляционного момента следует, что 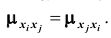 . Это означает, что элементы корреляционной матрицы, расположенные симметрично по отношению к главной диагонали, равны. В этой связи часто для простоты в корреляционной матрице заполняют только её половину (правый верхний треугольник):

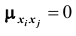
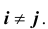
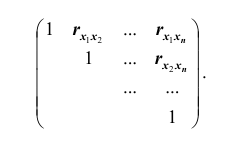
Если случайные величины системы некоррелированы, имеемпри Следовательно, корреляционная матрица системы некоррелированных случайных величин имеет вид:

Такая матрица, как вам известно, называется диагональной. Вместо
корреляционной матрицы часто используют нормированную корреляционную матрицу. Матрица, элементами которой являются коэффициенты корреляции, называется нормированной корреляционной матрицей. Все элементы главной диагонали нормированной корреляционной матрицы равны единице. Нормированная корреляционная матрица имеет вид:

Задача 1.

Закон распределения двумерной дискретной случайной величины (X ,Y ) задан таблицей 

Найти:
— собственные законы распределения случайных величин X и Y ;
— математические ожидания M(X) M(Y );
— дисперсии D(X), D(Y );
— корреляционный момент ;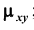
— коэффициент корреляции
— закон распределения случайной величины X при условии, что случайная
величина Y принимает своё наименьшее значение.

Решение. Складывая вероятности по строкам, получим закон распределения случайной величины X в виде ряда распределения

Складывая вероятности по столбцам, получим закон распределения случайной величины Y в виде ряда распределения

Найдём математические ожидания и дисперсии составляющих:

Найдём корреляционный момент 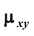и коэффициент корреляции

Найдём закон распределения случайной величины X при условии, что случайная величина Y принимает своё наименьшее значение, то есть при условии, что 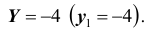   Искомый закон распределения, как ранее отмечалось,
определяется совокупностью условных вероятностей 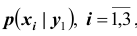    где 

Следовательно, искомый закон распределения имеет вид:

Задача 2.

Вне области 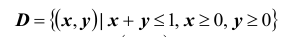плотность распределения двумерной случайной величины (X ,Y ) равна 0; в области D
плотность распределения 

Найти:

Решение. Для нахождения параметра А воспользуемся формулой 

тогда 

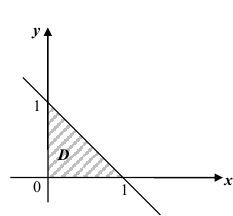
Получим 

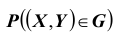
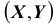
Найдём теперь вероятность попадания двумерной случайной величины в плоскую область G:

Далее, найдём одномерные плотности распределения:

Итак 

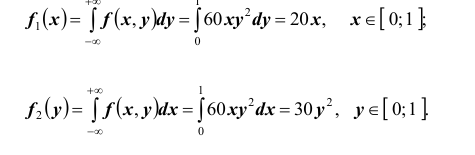
Найдём математические ожидания и дисперсии составляющих 

далее тогда 

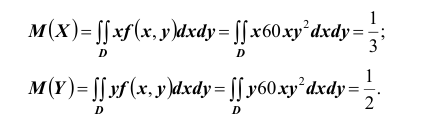
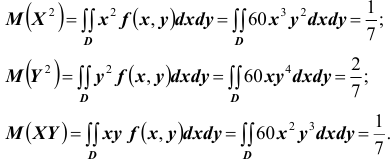
Так как 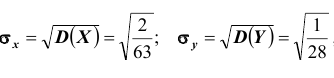, то нетрудно вычислить 

Что такое многомерные случайные величины

Ранее мы рассматривали случайные величины, возможные значения которой определялись одним числом. Такие величины называют одномерными. Однако часто результат испытания характеризуется не одной случайной величиной, а некоторой системой случайных величин, которую называют многомерной случайной величиной или случайным вектором.

Понятие многомерной случайной величины

Многомерная случайная величина, случайный вектор, система случайных величин – это все различные интерпретации одного и того же математического объекта. В зависимости от удобства изложения мы будем пользоваться той или иной интерпретацией.

Так же, как и в случае одномерных случайных величин, случайные величины входящие в систему, могут быть как дискретными, так и непрерывными. Например, успеваемость студентов вуза, которая характеризуется системой n случайных величин 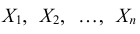– оценками по различным дисциплинам, проставленными в зачетной книжке – является дискретной многомерной величиной. А размер деталей, который характеризуются длиной (X), шириной (Y) и высотой (Z) – является непрерывной трехмерной величиной.

Геометрически двумерную (X, Y) и трехмерную (X, Y, Z) случайные величины можно изобразить случайной точкой плоскости Oxy или трехмерного пространства Oxyz. При этом случайные величины X, Y или X, Y, Z являются составляющими этих векторов. В случае n-мерного пространства (n > 3) также говорят о случайной точке этого пространства, хотя геометрическая интерпретация в этом случае теряет свою наглядность.

Пример №2

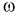
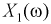
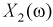
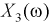
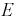
Пусть вероятностный эксперимент состоит в рождении ребенка. Тогда каждому элементарному событию  (каждому новорожденному) можно поставить в соответствие следующие числа:  — рост,  — вес,  — пол (0 или 1). Таким образом , эксперимент  описывается трехмерной случайной величиной, или системой трех случайных величин, или трехмерным вектором 

Пример №3

Пусть эксперимент состоит в измерении коэффициента усиления транзистора  на высокой частоте. Тогда элементарное событие  — это  одного транзистора и ему можно поставить в соответствие следующие случайные величины:  — коэффициент передачи тока на высокой частоте,  — обратный ток коллекторного перехода,  — входная проводимость,  — емкость эмиттерного перехода,  — емкость коллекторного перехода,  — выходная проводимость. 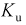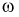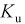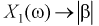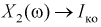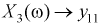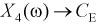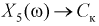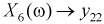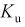Все перечисленные параметры для каждого транзистора при массовом производстве полупроводниковых приборов имеют отклонения от некоторого среднего значения (ввиду сложности поддержания технологического процесса стабильным для каждого кристалла при напылении, диффузии, травлении и т. д.). Поэтому их можно считать случайными величинами, и от значения каждого из них зависит коэффициент усиления транзистора  на высокой частоте. Тогда в данном случае эксперимент описывается шестимерной случайной величиной, или шестимерным вектором, или системой шести случайных величин.

При изучении многомерных случайных величин удобно пользоваться следующей геометрической интерпретацией. Например (рис. 3.1), систему двух случайных величин  можно рассматривать как случайную точку на плоскости с координатами  или как случайный вектор на плоскости со случайными составляющими 

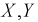
Пример №4

Пусть двумерная случайная величина 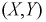 задана плотностью распределения.

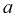
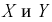
 Найти коэффициент  и показать, что случайные величины  независимые.

Решение.

Для определения коэффициента 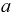 используем условие нормировки

Учтем область определения 

откуда 

1-й способ проверки независимости 

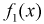
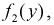
Найдем плотности распределений отдельных составляющих  и применяя (3.4):

Подставим эти выражения в условие (3.13):

Значит случайные величины 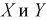 независимы.

2-й способ проверки независимости 

Найдем условную плотность распределения:

Видим, что выполняется условие (3.12), значит случайные величины 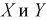независимы.

3-й способ проверки независимости 

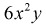
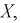
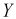
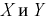
Все предыдущие вычисления можно не делать, а сослаться на следствие к доказанной выше теореме. Видим, что двумерная плотность  представима в виде произведения двух сомножителей, один из которых содержит только  а другой только  составляющие. Тогда на основании следствия из доказанной выше теоремы случайные величины  независимы.

Пример №5

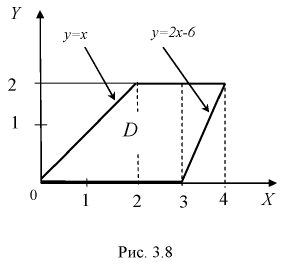
Двумерная случайная величина равномерно распределена внутри области 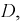 выделенной на рис. 3.8 жирными прямыми:

Найти константу

Решение.

Запишем уравнения прямых (см. рис. 3.7): 

Используем условие нормировки 

Этот интеграл вычислим в виде суммы трех интегралов, разбивая область 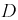 на три части (пунктирные прямые на рис. 3.8):

Закон распределения вероятностей двумерной дискретной случайной величины

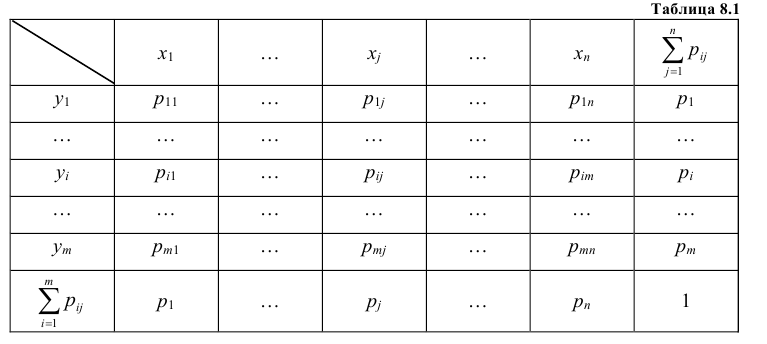
Так же как и для одномерной случайной величины наиболее полным, исчерпывающим описанием многомерной случайной величины является закон ее распределения. При конечном множестве возможных значений многомерной случайной величины такой закон может быть задан в виде таблицы (матрицы), содержащей все возможные сочетания значений каждой из одномерных величин, входящих в систему, и соответствующие им вероятности. Так, если рассматривается двумерная дискретная случайная величина (X, Y), то ее двумерное распределение можно представить в виде таблицы распределения (табл. 8.1), в каждой клетке (i, j) которой располагаются вероятности произведения событий

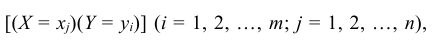
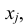
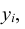
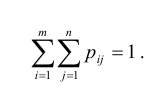
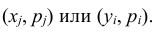
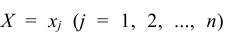
Так как события состоящие в том, что случайная величина Х примет значение , а случайная величина Y – значение , несовместны и единственно возможны, то сумма их вероятностей равна единице, т.е. Итоговые столбцы или строки таблицы распределения (X, Y) представляют соответственно распределение одномерных составляющих Действительно, распределение одномерной случайной величины Х можно получить, вычислив вероятность события как сумму вероятностей несовместных событий

Таким образом, чтобы по таблице распределения (табл. 8.1) найти вероятность того, что одномерная случайная величина примет определенное значение, надо просуммировать вероятности pij из соответствующего этому значению строки (столбца) данной таблицы.

Пример №6

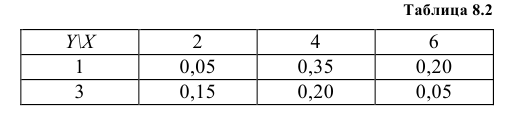
Закон распределения дискретной двумерной случайной величины (X, Y) задан в табл. 8.2. Найти законы распределения одномерных случайных величин X и Y.

Решение:

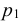
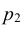
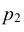
Случайная величина Х может принять значения: Х = 2 с вероятностью = 0,05 + 0,15 = 0,20; Х = 4 с вероятностью = 0,35 + 0,20 = 0,55; Х = 6 с вероятностью = 0,20 + 0,05 = 0,25. т.е. ее закон распределения

Аналогично закон распределения Y

Функция распределения многомерной случайной величины

При изучении одномерных случайных величин уже говорилось, что самой универсальной характеристикой случайной величины является функция распределения. Она существует для всех случайных величин: как дискретных, так и непрерывных. Точно также функция распределения полностью характеризует и многомерную случайную величину.

Определение: Функцией распределения n-мерной случайной величины 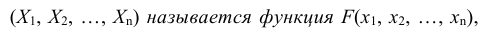выражающая вероятность

совместного выполнения n неравенств

В случае двумерной случайной величины XY функция распределения определяется неравенством

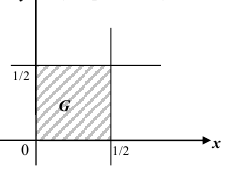
Геометрически функция распределения F(x, y) означает вероятность попадания случайной точки (X, Y) в заштрихованную область – бесконечный квадрант, лежащий левее и ниже точки M(x, y). Правая и верхняя границы области в квадрант не включаются – это означает, что функция непрерывна с л е в а по каждому аргументу. В случае двумерной дискретной случайной величины ее функция распределения определяется по формуле: где суммирование вероятностей распространяется на все j, для которых и все i, для которых

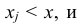
Отметим свойства функции распределения двумерной случайной величины.

1. Функция распределения есть неотрицательная функция, заключенная между нулем и единицей, т.е.

2. Функция распределения есть неубывающая функция по каждому из аргументов, т.е.

3. Если хотя бы один из аргументов обращается в – ∞, то функция распределения равна нулю, т.е.

4. Если один из аргументов обращается в + ∞, то функция распределения становится равной функции распределения случайной величины, соответствующей другому аргументу, т.е.

5. Если оба аргумента равны + ∞, то функция распределения равна единице:

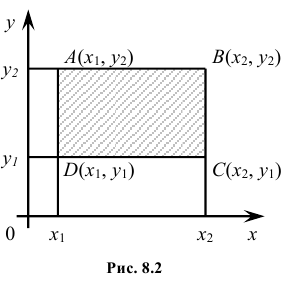
Геометрически функция распределения есть некоторая поверхность, обладающая перечисленными свойствами. Для дискретной двумерной случайной величины (X, Y) ее функция распределения представляет собой некоторую ступенчатую поверхность, ступени которой соответствуют скачкам функции F(x, y). Зная функцию распределения F(x, y) можно найти вероятность попадания случайной точки (X, Y) в пределы прямоугольника ABCD (рис. 8.2). 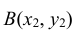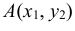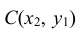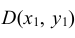Эта вероятность равна вероятности попадания в бесконечный квадрант с вершиной минус вероятность попадания в квадранты с вершинами в точкахиплюс вероятность попадания в квадрант с вершиной в точке (так как эта вероятность вычиталась дважды), т.е.

Плотность вероятности двумерной случайной величины

Для непрерывной двумерной случайной величины, так же как и для одномерной, существует понятие плотности вероятности.

Определение: Плотностью вероятности (или совместной плотностью) непрерывной двумерной случайной величины XY называется вторая смешанная частная производная ее функции распределения, т.е.

Геометрически плотность вероятности двумерной случайной величины XY представляет собой поверхность распределения в пространстве Oxyz.

Отметим свойства плотности вероятности двумерной случайной величины.

1. Плотность вероятности двумерной случайной величины есть неотрицательная функция, т.е.

2. Вероятность попадания непрерывной случайной величины XY в область D равна

3. Функция распределения непрерывной случайной величины может быть выражена через ее плотность вероятности по формуле:

4. Двойной несобственный интеграл в бесконечных пределах от плотности вероятности двумерной случайной величины равен единице: Зная плотность вероятности двумерной случайной величины (X, Y) можно найти функции распределения и плотность вероятностей ее одномерных составляющих X и Y.

Так как в соответствии с (8.7) 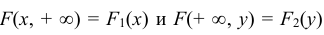то взяв в формуле (8.12) соответственно x = + ∞ и y = + ∞, получим функции распределения одномерных случайных величин X и Y:

Дифференцируя функции распределения 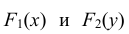соответственно по аргументам x и y, получим плотности вероятности одномерных случайных величин X и Y:

т.е. несобственный интеграл в бесконечных пределах от совместной плотности двумерной случайной величины по аргументу x дает плотность вероятности , а по аргументу y – плотность вероятности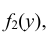

Условные законы распределения двумерной случайной величины

Итак, мы выяснили, как по известному закону распределения системы двух случайных величин определить законы распределения одномерных величин, входящих в систему.

Естественно возникает вопрос: нельзя ли по законам распределения одномерных величин, входящих в систему, найти закон распределения системы в целом? Оказывается, в общем случае этого сделать нельзя. Для того, чтобы полностью описать систему случайных величин, недостаточно знать распределение каждой из ее составляющих. Нужно еще знать зависимость между величинами, входящими в систему. Эта зависимость характеризуется с помощью условных законов распределения.

Определение: Условным законом распределения одной из одномерных составляющих двумерной случайной величины XY называется ее закон распределения, вычисленный при условии, что другая составляющая приняла определенное значение (или попала в определенный интервал).

Для дискретных случайных величин условные вероятности находятся по формулам:

В случае непрерывных случайных величин необходимо определить плотность вероятности условных распределений. Заменяя в формулах для дискретных величин вероятности событий «элементами вероятностей», получим:

т.е. условная плотность вероятности одной из одномерных составляющих двумерной случайной величины равно отношению ее совместной плотности к плотности вероятности другой составляющей.

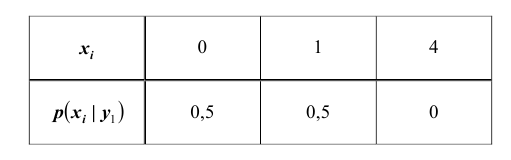
Пример №7

По данным примера 8.1 найти условный закон распределения составляющей Х при условии, сто составляющая Y приняла значение y1 =1.

Решение:

Искомый закон определяется следующей совокупностью условных вероятностей

Воспользовавшись формулой (8.16) и учитывая, что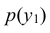= 0,6 (пример 8.1), получаем:

Важной характеристикой условного распределения вероятностей является условное математическое ожидание. Условным математическим ожиданием дискретной случайной величины Y при Х = х (х – определенное возможное значение Х) называют произведение возможных значений Y на их условные вероятности:

Для непрерывных величин

Аналогично определяется условное математическое ожидание случайной величины Х.

Пример №8

Найти условное математическое ожидание составляющей Y при условии, что составляющая Х примет значение

Решение:

Найдем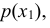, для чего сложим вероятности, помещенные в первом столбце табл. 8.2

Найдем условное распределение вероятностей величины Y при при

Найдем условное математическое ожидание по формуле (8.19):

Условное математическое ожидание случайной величины Y при Х = х, т.е. Mx(Y), есть функция от х, называемая функцией регрессии или просто регрессией Y по Х. Аналогично My(X) называется функцией регрессии или регрессией X по Y. Графики этих функций называются соответственно линиями регрессии (или кривыми регрессии) Y по Х и Х по Y.

Зависимые и независимые случайные величины

Ранее мы назвали две случайные величины независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. Теперь можно дать общее определение независимости случайных величин, основанное на независимости событий X < x и Y < y, т.е. функций распределения

Определение: Случайные величины X и Y называются независимыми, если их совместная функция распределения F(x, y) представляется в виде произведения функций 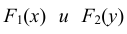этих случайных величин, т.е.

При невыполнении этого равенства случайные величины называются зависимыми. Дифференцируя дважды равенство (8.19) по аргументам x и y, получим

т.е. для независимых непрерывных случайных величин их совместная плотность равна произведению плотностей вероятностей этих случайных величин.

Другими словами, независимость двух случайных величин, что условные вероятности каждой из них совпадают с соответствующими безусловными плотностями вероятностей.

Числовые характеристики двумерной случайной величины

Для описания системы двух случайных величин, кроме математических ожиданий и дисперсий составляющих, используются и другие характеристики, к числу которых относятся ковариация и коэффициент корреляции.

Определение: Ковариацией (или корреляционным моментом) случайных величин X и Y называется математическое ожидание произведения отклонений этих величин от своих математических ожиданий, т.е.

Из определения следует, что Kxy = Kyx.

Для дискретных случайных величин

Для непрерывных случайных величин

Ковариация двух случайных величин характеризует как степень зависимости случайных величин, так и их рассеяние вокруг точки (ax, ay).

Отметим свойства ковариации:

1. Ковариация двух независимых случайных величин равна нулю.

2. Ковариация двух случайных величин равна математическому ожиданию их произведения минус произведение математических ожиданий, т.е.

3. Ковариация двух случайных величин по абсолютной величине не превосходит произведения их средних квадратических отклонений, т.е.

Не трудно заметить, что ковариация имеет размерность, равную произведению размерностей величин X и Y. Другими словами, величина ковариации зависит от единиц измерения случайных величин. Такая особенность затрудняет сравнение ковариаций различных систем случайных величин. Для устранения этого недостатка вводится безразмерная характеристика – коэффициент корреляции.

Определение: Коэффициентом корреляции двух случайных величин называется отношение их ковариации к произведению средних квадратических отношений этих величин, т.е.

Из определения следует, что

Отметим свойства коэффициента корреляции.

1. Коэффициент корреляции принимает значения на отрезке

2. Если случайные величины независимы, то их коэффициент корреляции равен нулю, т.е. ρ = 0.

3. Если коэффициент корреляции двух случайных величин равен (по абсолютной величине) единице, то между этими случайными величинами существует линейная функциональная зависимость.

Пример №9

Определить ковариацию и корреляционный момент случайных величин Х и Y.

Решение:

В примере были получены следующие распределения одномерных случайных величин

Найдем математические ожидания и средние квадратические отклонения этих случайных величин:

Для нахождения математического ожидания M(XY) произведения случайных величин Х и Y можно составить закон распределения произведения двух дискретных случайных величин, а затем по нему найти M(XY). Однако M(XY) можно найти непосредственно по табл. 8.2 распределения двумерной случайной величины (X, Y) по формуле:

где двойная сумма означает суммирование по всем mn клеткам таблицы (m – число строк, n – число столбцов):

Вычисляем ковариацию по формуле (8.26):

Вычисляем коэффициент корреляции по формуле (8.28):

т.е. между случайными величинами Х и Y существует отрицательная линейная зависимость.

Двумерной называют случайную величину

, возможные значения
которой есть пары чисел

. Составляющие

 и

, рассматриваемые
одновременно, образуют систему двух случайных величин. Двумерную величину
геометрически можно истолковать как случайную точку

 на плоскости

 либо как случайный вектор

.

Дискретной называют двумерную величину, составляющие которой дискретны.

Закон распределения дискретной двумерной СВ.
Безусловные и условные законы распределения составляющих

Законом распределения вероятностей двумерной случайной величины называют соответствие
между возможными значениями и их вероятностями.

Закон
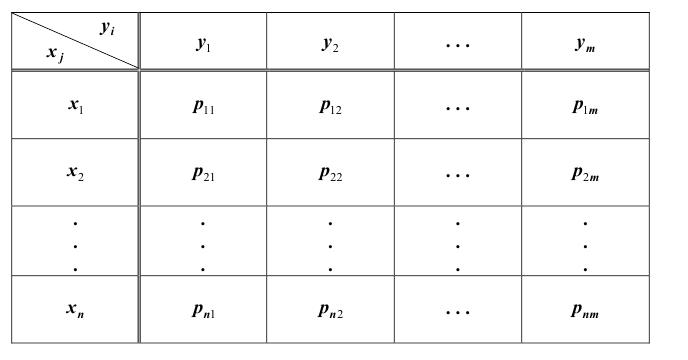
распределения дискретной двумерной случайной величины может быть задан:

а) в
виде таблицы с двойными входом, содержащей возможные значения и их вероятности;

б) аналитически, например в виде функции распределения.

Зная
закон распределения двумерной дискретной случайной величины, можно найти законы
каждой из составляющих. В общем случае, для того чтобы найти вероятность

, надо просуммировать
вероятности столбца

. Аналогично сложив
вероятности строки

 получим вероятность

.

Пусть
составляющие

 и

 дискретны и имеют соответственно следующие
возможные значения:

; 

.

Условным распределением составляющей

 при

 (j сохраняет одно и то же
значение при всех возможных значениях

) называют совокупность
условных вероятностей:

Аналогично
определяется условное распределение

.

Условные
вероятности составляющих

 и

 вычисляют соответственно по формулам:

Для
контроля вычислений целесообразно убедиться, что сумма вероятностей условного
распределения равна единице.

Ковариация (корреляционный момент)

Ковариация двух случайных величин характеризует степень зависимости случайных величин, так
и их рассеяние вокруг точки

.

Ковариацию
(корреляционный момент) можно найти по формуле:

Свойства ковариации

Свойство 1.

Ковариация двух независимых случайных величин равна нулю.

Свойство 2.

Ковариация двух случайных величин равна математическому ожиданию их
произведение математических ожиданий.

Свойство 3.

Ковариация двухмерной случайной величины по абсолютной случайной величине не
превосходит среднеквадратических отклонений своих компонентов.

Коэффициент корреляции

Коэффициент корреляции – отношение ковариации двухмерной случайной
величины к произведению среднеквадратических отклонений.

Формула коэффициента корреляции:

Две
случайные величины

 и

 называют коррелированными, если их коэффициент
корреляции отличен от нуля.

 и

 называют некоррелированными величинами, если
их коэффициент корреляции равен нулю

Свойства коэффициента корреляции

Свойство 1.

Коэффициент корреляции двух независимых случайных величин равен нулю. Отметим,
что обратное утверждение неверно.

Свойство 2.

Коэффициент корреляции двух случайных величин не превосходит по абсолютной
величине единицы.

Свойство 3.

Коэффициент корреляции двух случайных величин равен по модулю единице тогда и
только тогда, когда между величинами существует линейная функциональная
зависимость.

Линейная регрессия

Рассмотрим
двумерную случайную величину

, где

 и

 – зависимые случайные величины. Представим
одну из величины как функцию другой. Ограничимся приближенным представлением
величины

 в виде линейной функции величины

:

где

 и

 – параметры, подлежащие определению. Это можно
сделать различными способами и наиболее употребительный из них – метод
наименьших квадратов.

Линейная
средняя квадратическая регрессия

 на

 имеет вид:

Коэффициент

называют
коэффициентом регрессии

 на

, а прямую

называют
прямой среднеквадратической регрессии

 на

.

Аналогично
можно получить прямую среднеквадратической регрессии

 на

:

Смежные темы решебника:

• Двумерная непрерывная случайная величина
• Линейный выборочный коэффициент корреляции
• Парная линейная регрессия и метод наименьших квадратов

Задача 1

Закон
распределения дискретной двумерной случайной величины (X,Y) задан таблицей.

Требуется:

—
определить одномерные законы распределения случайных величин X и Y;

— найти
условные плотности распределения вероятностей величин;

—
вычислить математические ожидания m_x и m_y;

—
вычислить дисперсии σ_x и σ_y;

—
вычислить ковариацию μ_xy;

—
вычислить коэффициент корреляции r_xy.

Задача 2

Задана
дискретная двумерная случайная величина (X,Y).

а) найти
безусловные законы распределения составляющих; б) построить регрессию случайной
величины Y на X;  в) построить регрессию случайной величины X на Y;  г) найти коэффициент ковариации; д) найти
коэффициент корреляции.

Задача 3

Двумерная случайная величина (X,Y) задана
таблицей распределения. Найти законы распределения X и Y, условные
законы, регрессию и линейную регрессию Y на X.

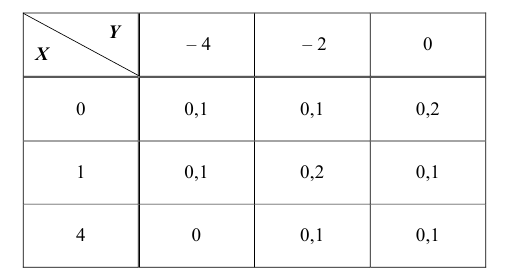
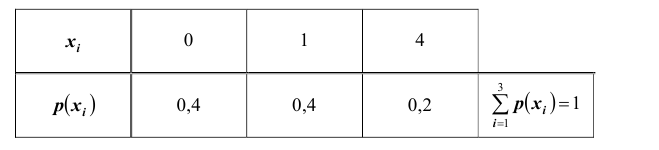
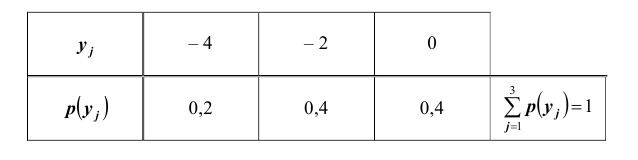
Задача 4

Двумерная
случайная величина (X,Y) распределена по закону

Найти
законы распределения случайных величины X и Y, условный закон
распределения Y при X=0 и вычислить ковариацию.
Исследовать зависимость случайной величины X и Y.

Задача 5

Случайные
величины ξ и η имеют следующий совместный закон распределения:

P(ξ=1,η=1)=0.14

P(ξ=1,η=2)=0.18

P(ξ=1,η=3)=0.16

P(ξ=2,η=1)=0.11

P(ξ=2,η=2)=0.2

P(ξ=2,η=3)=0.21

1)
Выписать одномерные законы распределения случайных величин ξ и η, вычислить
математические ожидания Mξ, Mη и дисперсии Dξ, Dη.

2) Найти
ковариацию cov(ξ,η) и коэффициент корреляции ρ(ξ,η).

3)
Выяснить, зависимы или нет события {η=1} и {ξ≥η}

4)
Составить условный закон распределения случайной величины γ=(ξ|η≥2) и найти Mγ и
Dγ.

Задача 6

Дан закон
распределения двумерной случайной величины (ξ,η):

1) Выписать одномерные законы
распределения случайных величин ξ и η, вычислить математические ожидания M_ξ,
M_η и дисперсии D_ξ, D_η

2) Найти ковариацию cov(ξ,η) и
коэффициент корреляции ρ(ξ,η).

3) Являются ли случайные события |ξ>0|
и |η> ξ | зависимыми?

4) Составить условный закон
распределения случайной величины γ=(ξ|η>0) и найти M_γ  и D_γ.

Задача 7

Дано
распределение случайного вектора (X,Y). Найти ковариацию X и Y.

Задача 8

Случайные
приращения цен акций двух компаний за день имеют совместное распределение,
заданное таблицей. Найти ковариацию этих случайных величин.

Задача 9

Найдите
ковариацию Cov(X,Y) для случайного дискретного вектора (X,Y),
распределенного по закону:

Задача 10

Совместный
закон распределения пары

 задан таблицей:

Найти
закон распределения вероятностей случайной величины xh и вычислить cov(2x-3h,x+2h).
Исследовать вопрос о зависимости случайных величин x и h.

Задача 11

Составить двумерный закон распределения случайной
величины (X,Y), если известны законы независимых составляющих. Чему равен коэффициент
корреляции r_xy?

и

Задача 12

Задано
распределение вероятностей дискретной двумерной случайной величины (X,Y):

Задача 13

Совместное
распределение двух дискретных случайных величин ξ и η задано таблицей:

Вычислить
ковариацию cov(ξ-η,η+5ξ). Зависимы ли ξ и η?

Задача 14

Рассчитать
коэффициенты ковариации и корреляции на основе заданного закона распределения
двумерной случайной величины и сделать выводы о тесноте связи между X и Y.

Задача 15

Задан
закон распределения случайного вектора (ξ,η). Найдите ковариацию (ξ,η)
и коэффициент корреляции случайных величин.

Задача 16

Для
случайных величин, совместное распределение которых задано таблицей
распределения. Найти:

а) законы
распределения ее компонент и их числовые характеристики;

b) условные законы распределения СВ X при условии Y=b и СВ Y при
условии X=a, где a и b – наименьшие значения X и Y.

с)
ковариацию и коэффициент корреляции случайных величин X и Y;

d) составить матрицу ковариаций и матрицу корреляций;

e) вероятность попадания в область, ограниченную линиями y=16-x² и y=0.

f) установить, являются ли случайные величины X и Y зависимыми;
коррелированными.

Задача 17

Совместный
закон распределения случайных величин X и Y задан таблицей:

Найдите:

а) закон
распределения случайной величины X и закон распределения
случайной величины Y;

б) EX, EY, DX, DY, cov(2X+3Y, X-Y), а
также математическое ожидание и дисперсию случайной величины V=6X-8Y+3.

Задача 18

Известен
закон распределения двумерной случайной величины (X,Y).

а) найти
законы распределения составляющих и их числовые характеристики (M[X],D[X],M[Y],D[Y]);

б)
составить условные законы распределения составляющих и вычислить
соответствующие мат. ожидания;

в)
построить поле распределения и линию регрессии Y по X и X по Y;

г)
вычислить корреляционный момент (коэффициент ковариации) μ_xy и
коэффициент корреляции r_xy.