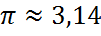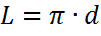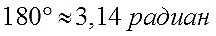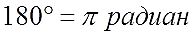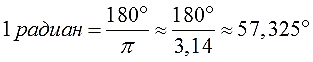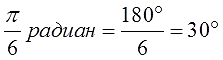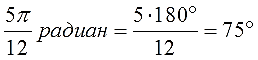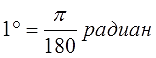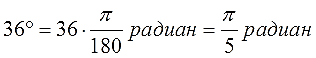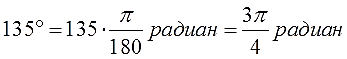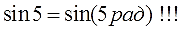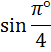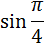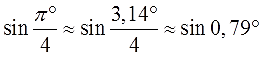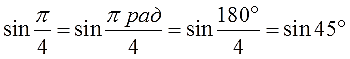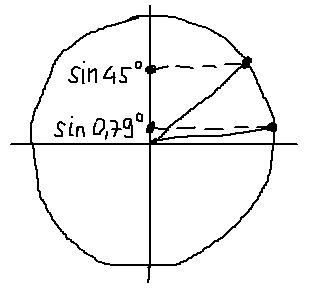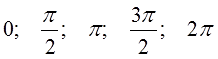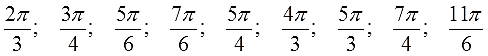Как найти один рад

Онлайн калькулятор для перевода углов из радиан в градусы и обратно, интерактивная таблица градусов и радиан.
Формула перевода радианов в градусы: x°=х_рад⋅180/π

Точное число чему равен 1 радиан в градусах:
1 радиан = 57.29577951308 градуса

Радиан (обозначение: рад, rad) — угол, соответствующий дуге, длина которой равна её радиусу.

        В прошлый раз мы с вами ответили на первый вопрос, касаемый работы с углами. А именно — как отсчитываются углы. Рассмотрели положительные и отрицательные углы, а также углы, большие 360 градусов. И на круге углы порисовали.)

        В этом же уроке настал черёд ответить на второй вопрос, связанный с измерением углов. Здесь мы разберёмся с загадочными радианами и особенно — с пресловутым числом «пи», которое будет мозолить нам глаза на протяжении всего дальнейшего изучения тригонометрии. Поймём, что это за число, откуда оно берётся и как с ним работать. И задания порешаем, само собой. Стандартные и не очень…)

        Разберёмся? Ну сколько же можно бояться числа «пи», в конце-то концов!)

        Итак, в чём же измеряются углы в математике? Начнём с привычного и знакомого. С градусов.

Что такое один градус? Градусная мера угла.

        К градусам вы уже попривыкли. Геометрию изучаете, да и в жизни постоянно сталкиваетесь. Например, «повернул на 90 градусов».) Короче, градус — штука простая и понятная.

        Вы и вправду так думаете? Тогда сможете сказать мне, что такое градус? Нет, гуглить и потрошить Википедию не надо. Ну как, слабо с ходу? Вот так-то…

        Начнём издалека. С древнейших времён. А именно — с двух очагов древних цивилизаций Вавилона и Египта.)

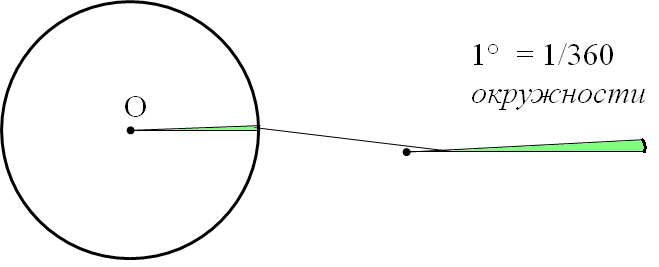
        Градус — это 1/360 часть окружности. И всё!

        Смотрим картинку:

        Придумали градусы в Древнем Вавилоне.) Как? Очень просто! Просто взяли да разбили окружность на 360 равных кусочков. Почему именно на 360? А не на 100 или на 1000? Вроде бы, число 100 поровнее, чем 360… Вопрос хороший.

        Основная версия — астрономическая. Ведь число 360 очень близко к числу дней в году! А для наблюдений за Солнцем, Луной и звёздами это было оч-чень удобно.)

        Кроме того, в астрономии (а также строительстве, землемерии и прочих смежных областях) очень удобно делить окружность на равные части. А теперь давайте прикинем чисто математически, на какие числа делится нацело 100 и на какие — 360? И в каком из вариантов этих делителей нацело больше? А людям такое деление очень удобно, да…)

Что такое число «пи»? Как оно возникло?

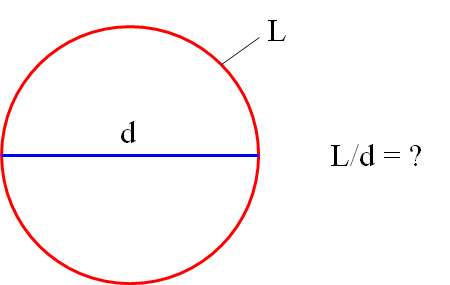
        А теперь переместимся из Древнего Вавилона в Древний Египет. Примерно в то же самое время там разгадывали другую загадку. Не менее интересную, чем вопрос, на сколько частей бить окружность. А именно — во сколько раз длина окружности больше её диаметра? Или по-другому: чему равна длина окружности с диаметром, равным единице?

        И так измеряли и сяк… Каждый раз получалось чуть-чуть больше трёх. Но как-то коряво получалось, неровно…

        Но они, египтяне, ни в чём не виноваты. После них математики всех мастей продолжали мучиться аж до 18 века! Пока в 1767 году окончательно не доказали, что, как бы мелко ни нарезать окружность на равные кусочки, из таких кусочков сложить точно длину диаметра нельзя. Принципиально нельзя. Только лишь примерно.

        Нет, конечно же, во сколько раз длина окружности больше её диаметра установили давным-давно. Но, опять же, примерно… В 3,141592653… раза.

        Это число — и есть число «пи» собственной персоной.) Да уж… Корявое так корявое… После запятой — бесконечное число цифр безо всякого порядка, безо всякой логики. В математике такие числа называются иррациональными. И на сегодняшний день доказательство факта иррациональности числа «пи» занимает аж десять (!) лекций на 4-м курсе мехмата МГУ… Этот факт, кстати, и означает, что из одинаковых кусочков окружности её диаметр точно не сложить. Никак. И никогда…

        Конечно, рациональные приближения числа «пи» известны людям ещё со времён Архимеда. Например:

        22/7 = 3,14285714…

        377/120 = 3,14166667…

        355/113 = 3,14159292…

        Сейчас, в век суперкомпьютеров, погоня за десятичными знаками числа «пи» не стихает, и на сегодняшний день человечеству известно уже два квадриллиона (!) знаков этого числа…

        Но нам для практического применения такая сверхточность совершенно не требуется. Чаще всего достаточно запомнить всего лишь две цифры после запятой.

        Запоминаем:

        Вот и всё. Раз уж нам ясно, что длина окружности больше её диаметра в «пи» раз, то можно записать (и запомнить) точную формулу для длины окружности:

        Здесь L — длина окружности, а d — её диаметр.

        В геометрии всяко пригодится.)

        Для общего развития скажу, что число «пи» сидит не только в геометрии или тригонометрии. Оно возникает в самых различных разделах высшей математики. В интегралах, например. Или в теории вероятностей. Или в теории комплексных чисел, а также рядов. Само по себе возникает, хотим мы того или нет… Поступите в ВУЗ — убедитесь лично.)

        Ну а теперь снова вернёмся к старым добрым градусам. Как мы помним, один градус — это 1/360 часть окружности. С исторической и практической точек зрения людям такое деление на 360 равных частей оказалось очень даже удобно, но…

        Как выяснилось гораздо позже Древнего Вавилона, градусы удобны далеко не всем. Например, высшей математике они ой как неудобны! Высшая математика — дама серьёзная. По законам природы устроена. И она справедливо заявляет: «Сегодня вы на 360 частей круг разбили, завтра — на 100 разобьёте, послезавтра — на 250… А мне что делать? Каждый раз под ваши хотелки подстраиваться?»

        Против природы не попрёшь… Пришлось прислушаться и уступить. И ввести новую меру угла, не зависящую от наших хотелок. )

        Итак, знакомьтесь — радиан!

Что такое один радиан? Радианная мера угла.

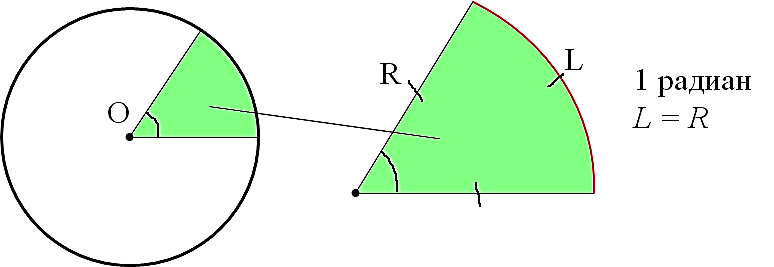
        В основе определения радиана — та же самая окружность. Угол в 1 радиан — это угол, который отсекает от окружности дугу, длина которой (L) равна радиусу окружности (R). И всё!

        Смотрим картинку:

        Причём величина угла в один радиан не зависит от радиуса окружности! Никак. Можно нарисовать очень большую окружность, можно очень маленькую. Но угол, отсекающий от окружности дугу, равную радиусу, никогда не изменит своей величины и будет составлять ровно один радиан. Всегда. Это важно.)

        Запоминаем:

        Угол в один радиан — это угол, вырезающий из окружности дугу, равную радиусу окружности. Величина угла в 1 радиан не зависит от радиуса окружности.

        Кстати говоря, градусная мера угла тоже не зависит от радиуса окружности. Большая окружность, маленькая — углу в один градус без разницы. Но градус — это величина, искусственно придуманная людьми для их личного удобства! Древними вавилонянами, если мы помним.) 1/360 часть окружности. Так уж сложилось чисто исторически. А если бы по каким-то причинам договорились на 100 частей разбить окружность? Или на 200? Кто знает, что тогда называлось бы градусом сегодня… Вот на сколько частей разобьём окружность, такой «градус» и получим. А вот радиан — штука универсальная!) К способу разбиения окружности никак не привязан. Строго дуга, равная радиусу! И чем больше радиус, тем больше (по длине) будет и соответствующая вырезаемая дуга. И наоборот. Но сама величина угла в один радиан не меняется. И разбиение окружности (любой!) радианами — всегда одинаковое. И сейчас мы в этом лично убедимся.)

Как переводить радианы в градусы и обратно?

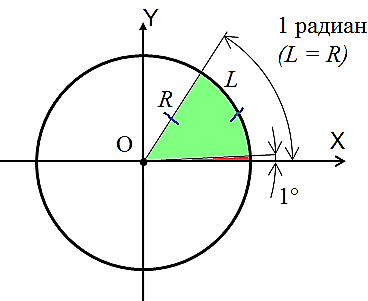
        К этому моменту вам уже должно быть интуитивно понятно, что один радиан существенно больше одного градуса. Всё-таки непонятно? Тогда смотрим снова на картинку:

        Будем считать, что малюсенький красный угол имеет величину примерно один градус. Совсем крохотный уголок, почти и нет его… А большой зелёный угол — примерно один радиан! Чувствуете разницу?) Конечно же, один радиан сильно больше одного градуса…

        А вот теперь начинается самое интересное! Вопрос: а во сколько раз один радиан больше одного градуса? Или сколько градусов в одном радиане? Сейчас выясним!)

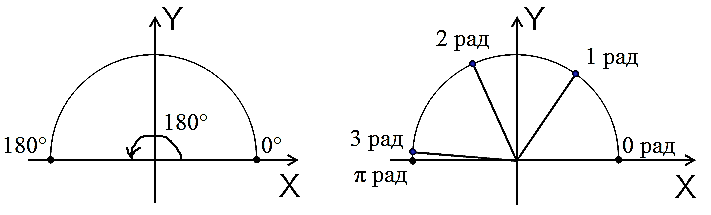
        Смотрим на очередные картинки:

        На картинке слева изображён полукруг. Обычный развёрнутый угол величиной 180°. А вот на картинке справа — тот же самый полукруг, но нарезанный радианами! Видно, что в 180° помещается примерно три с хвостиком радиана.

        Вопрос на засыпку: как вы думаете, чему равен этот хвостик?)

        Да! Он равен 0,141592653… Привет, число «пи», вот мы про тебя и вспомнили!)

        Стало быть, в 180° укладывается 3,141592653… радиан. Понятное дело, что каждый раз писать такое длинное число неудобно, поэтому пишут приближённо:

        Или точно:

        Вот и всё. Вот и весь секрет тотального присутствия числа «пи» в тригонометрии. Эту простую формулку надо знать железно. Уловили?)

        Так сколько же градусов в одном радиане? Не вопрос! Если в «пи» радианах содержится 180 градусов, то сколько же тогда градусов сидит в одном радиане? Правильно, в «пи» раз меньше! То есть меньше примерно в 3,14 раза.

        Вот и делим обе части нашего соотношения на «пи» и получаем один радиан в градусах:

        Это приближённое равенство также очень полезно запомнить. В одном радиане примерно 60 градусов. Такой грубой оценки бывает вполне достаточно для ответа на очень многие каверзные вопросы, связанные с углами. Бывает и недостаточно, конечно. В своё время мы такие хитрые задачки рассмотрим.)

        Но это не самое главное применение этой формулы!) А самое главное — перевод радианов в градусы и обратно.

        Переводим радианы в градусы!

        Чаще всего углы в тригонометрии заданы в радианах с числом «пи». Это — самая стандартная ситуация. Если угол задан в радианах с числом «пи», то всё очень просто. Мы знаем, что «пи» радиан — это 180 градусов. Вот и подставляем вместо «пи» радиан — число 180. Сокращаем всё что сокращается и получаем угол в градусах.

        Например:

        Или более мудрёный угол:

        Просто, правда?)

        Переводим градусы в радианы!

        Обратный перевод градусов в радианы чуть сложнее, но ненамного. Если угол задан в градусах, то сначала нам надо узнать, сколько составляет один градус в радианах. И умножить это значение на количество градусов.) И чему же равен 1° в радианах?

        Снова смотрим на нашу формулу и соображаем. Если 180° — это «пи» радиан, то 1° в 180 раз меньше. Вот и делим обе части формулы на 180! Получаем, что 1° в радианах равен:

        Вот и все дела. Умножаем дробь π/180 на количество градусов, сокращаем что сокращается и получаем угол в радианах. Например:

        Или аналогично:

        Вот и всё. Заменять «пи» на примерно 3,14 никакой необходимости нет: его всегда буквой пишут. Что правда, то правда: нас же в заданиях обычно точный ответ интересует! А не приближённый.) Кстати, кому интересен приближённый ответ, посчитайте на калькуляторе. Получите примерно 0,628 и 2,356 радиана соответственно.

        Итак, в непринуждённой беседе с лирическими отступлениями мы узнали, что радианы — это очень даже просто, не больно и не страшно.) Да и перевод туда-обратно несложен. И «пи» — не кусается… Так откуда же проблемы?

        Что ж, вскрою тайну. Всё дело в том, что в тригонометрии значок градусов — пишется. Всегда и везде. Например, cos30° — это косинус 30 градусов! А вот значок радианов («рад») — не пишется! Он — подразумевается. В чём причина — неизвестно. Может, обленились математики, может ещё что… Но договорились не писать. Например, sin5 — это синус пяти радианов!

        Это и приводит к казусам. Человек смотрит на пример, видит «пи» и автоматически считает, что это 180°. Везде и всюду. Кстати, это срабатывает. До поры до времени, пока примеры — типовые. Но любое отклонение примера от шаблона — тут же валит наповал! Почему?

        Потому, что само по себе «пи» — это число! А никакие не градусы! Это «пи» радиан = 180°!

        Ещё раз запоминаем:

        Просто «пи» — это число! «Пи» РАДИАН — это 180°!

        Это заклинание надо понимать железно. Причём не просто механически зазубрить, а именно понимать каждое слово и каждый значок! И особенно — слово «радиан». Я не шучу. Ибо, если на вопрос, «Что такое «пи» в тригонометрии?», вы, блистая знаниями, радостно заявляете:

        «Пи — это 180 градусов!!!» ,

        то это говорит о том, что вы не понимаете до конца смысла этой зелёной фразы. И все дальнейшие беседы уже бессмысленны, да…

        Ещё раз: «пи» — это число! Примерно равное 3,14. Точного значения этого числа не знает никто: оно бесконечно длинное, корявое, иррациональное. Но — число! Такое же, как 2 или 7. Можно пройти примерно «пи» километров. Три километра и ещё около 140 метров. Можно купить «пи» килограммов картошки. Если продавец образованный встретится.) Можно выпить «пи» литров кока-колы. Если здоровье не жалко… И так далее…

        Всё равно непонятна зелёная запись? Хорошо, вот вам простые житейские фразы:

        1 километр — это 1000 метров;

        3 часа — это 180 минут;

        2 года — это 730 дней;

        И тому подобное. Точно так же и с градусами/радианами:

        «Пи» радиан — это 180 градусов!

        Уяснили, что «пи» — это просто число? Или я уже достал вас этой заезженной фразой? Ну ладно, убедили. Тогда вот вам парочка нестандартных вопросов:

        1. Что больше?

        или

        2. Что меньше?

        cos5°

        или

        cos5

        Если у вас случился ступор, не беда. Вспоминаем нашу мантру: «Пи» — это число! В первом синусе нам чётко сказано, что угол — в градусах! Следовательно, машинально заменять «пи» на 180° — нельзя. «Пи» градусов — это примерно 3,14°. Вот и пишем:

        Во втором синусе никаких значков нет. Значит, там — радианы. И вот тут замена «пи» на 180° — вполне законна.) Переводим радианы в градусы и получаем:

        А теперь сравниваем эти два синуса. Как? По кругу, разумеется! Рисовать углы мы с вами уже умеем, что такое синус угла на круге — тоже знаем. Вперёд! Рисуем круг, углы примерно 0,79° и 45° и смотрим какие синусы у этих углов. Даже на самом корявом круге будет видно, что sin45° гораздо больше, чем sin0,79°.

        С косинусами — всё то же самое. Рисуем на круге в правильных четвертях углы примерно 5 градусов и 5 радианов (помним, чему примерно равен один радиан в градусах?). Круг нам всё и подскажет. А именно, что cos5 меньше, чем cos5°.

        Вообще, задачки с углами в радианах без «пи» (типа определить знак выражения sin10∙cos20) относятся к разряду нестандартных. В следующем уроке разберём парочку таких.)

        Ну что, потренируемся с переводом углов?) Решаем несложные задания.

        1. Переведите следующие углы из градусной меры в радианную:

        180°; 0°; 360°; 90°; 270°.

        Ответы (по возрастанию):

        Как вы думаете, что это были за углы? Да! Это углы, которые попадают на координатные оси! Эти опорные значения надо держать в голове надёжно. До автоматизма! Как в градусах, так и в радианах. Зачем? Да всё за тем же! Для правильного распределения любых углов по четвертям.) Это полезное умение — залог успеха в любом задании по тригонометрии. Любом! От примитивных примеров до вполне себе солидных ЕГЭшных задачек части 2 (уравнения с отбором корней, тригонометрические неравенства и прочие хитрые штучки).

        Продолжаем развлекаться.

        2. Переведите углы в радианную меру:

        30°; 45°; 60°.

        Ответы (в беспорядке):

        Получилось? Рад за вас. Почему я выделил именно эти три угла? По той же самой причине. Эти углы — особые личности в тригонометрии. Потому что именно про эти углы вы обязаны знать всё! И где они находятся и весь комплект их тригонометрических функций. Скажем, значение sin20° вы знать не обязаны. А вот sin30° — уж будьте так добры! Это обязательные значения, без которых во всей остальной тригонометрии делать вообще нечего. Но об этом — в отдельном уроке.)

        Продолжим тренировку.

        Переведите следующие углы из радианной меры в градусную:

        Ответы (в беспорядке):

        300°; 225°; 120°; 330°; 240°; 135°; 210°; 315°; 150°.

        А это что за углы? Правильно! Это углы, в пределах одного оборота, кратные предыдущим трём! Но не попадающие на оси координат. Такие углы вы также обязаны уметь просчитывать! И более того, все углы, кратные 30, 45 или 60 градусам, вы обязаны уметь просчитывать! Как в пределах одного оборота, так и за его пределами. Как положительные, так и отрицательные… В соответствующем уроке мы научимся с вами проделывать такие полезные вещи.

        Если и это получилось, то тогда можно считать, что перевод радианов в градусы и обратно — уже не ваша проблема. Но перевод углов из одной размерности в другую — это лишь ещё один шаг вперёд к успешному постижению тригонометрии. Шаг мощный, но недостаточный. Ведь, чаще всего, с углами надо потом ещё и что-то делать.) Рисовать на круге, например. Или синус/косинус считать. Да и тангенс/котангенс тоже…

        Второй серьёзный шаг — это умение правильно определять положение любого угла на тригонометрическом круге. Любого! Как в градусах, так и в радианах. С градусами на круге мы уже плотно поработали в предыдущем уроке. Теперь настал черёд набивать руку в работе с радианами.

        Об этом — в следующей теме.

Современный сумасшедший мир сделал наши отношения с противоположным полом одновременно проще и сложнее. Сейчас отношения завязываются легче, но разобраться и найти счастье в них стало сложнее. Это знакомства в интернете, бесконечные свидания, неудачные взаимоотношения, короткие интрижки, френдзоны, измены, возвращение к бывшим, расставания и так по новому кругу.

Страдаешь или наслаждаешься одиночеством, но потом решил найти себе половинку? Порой кажется, что найти себе подружку очень сложно, но не стоит переживать. Девушкам найти себе мужчину не легче. Давай подумаем над тем, где и как искать себе девушку в современном мире. Пора обустроить свою личную жизнь, найдя симпатичную и хорошую компанию.

Как правильно искать себе девушку?

Мечтаешь найти ту особенную девушку, с которой наконец все получится хорошо и счастливо, а не как обычно? В любом деле требуется опыт, а также задействование интеллектуальных способностей. Какие ошибки парни делают, когда ищут себе подружку? О чем следует обязательно помнить?

1. Не реагировать на ярких и плохих девушек

Вот подумай, как искать девушку нормальную, если ты тратишь свое время на не тех женщин? Безусловно любовь всей своей жизни найти сложно, тем более тебя будут отвлекать разные девушки, которые далеки от идеала. Это стервозные, инфантильные, недалекие, меркантильные, несостоявшиеся или гулящие бабы. Но самое печальное в таких девушках то, что такие будут попадать чаще, ведь они в вечном поиске мужчины.

Реагирование на ярких, но плохих девушек, приводит к мысли о том, что нормальных крошек совсем не осталось. Но это не так. Учись игнорировать токсичных девушек. Тогда ты заметишь, что вокруг множество отличных девушек, которых ранее не замечал.

2. Смотреть не на красоту тела, а красоту души

В отношениях следует выбирать не только по красоте лица, фигуре, длине ног или величине бюста. Здесь следует присматриваться к характеру и личности девушки. Часто за самой красивой оберткой кроется токсичная личность, а за обычной внешностью прекрасный человек и замечательная девушка. Смотри в глубину девушки, обращая внимание на ее слова, поведение, мышление, цели, образ жизни, подруг, семью. Это позволит избежать ошибок, которые выльются в трату времени, сил, денег, нервов. Утихомирь свою страсть и влечение, ведь это не дает тебе адекватно воспринимать свой объект влюбленности. Смотри на девушку без розовых очков влюбленности.

3. Быть в активном поиске девушки

Немаловажная ошибка в обустройстве личной жизни мужчин и парней исходит их стратегии поиска. Как искать девушку и найти, если ты практически не уделяешь этому внимания? Чудес не бывает, ведь подружка сама не появится у тебя на пороге квартиры.

При поиске второй половинки важно быть в действительно активном поиске. Если ты одинок, то одно свидание в месяц не сделает погоду на личном фронте. Шансы найти в таком слабом женском трафике хорошую подружку минимальны. Следует общаться с десятком девушек с помощью интернета или знакомств в реальной жизни, а ходить на свидание как минимум с 2-3 девушками в неделю. В таком случае шансы найти девушку и любовь значительно повышаются. Теперь магия больших цифр будет работать на тебя, когда рано или поздно встретится та, с которой все сложится почти идеально.

4. Не спешить с девушками

В отношениях не стоит спешить, ведь звать под венец через месяц или два знакомства – это безумие, которое заканчивается разводом, алиментами и разбитым сердцем. Тщательнее выбирай девушку, наслаждайся свиданиями, поцелуями, близостью. Предлагай девушке съехаться не раньше, чем через 3-6 месяцев, а жениться через 1-3 года. Если девушка тебя торопит, то она тебя не любит, а ей нужен не ты сам, а дежурный штамп в паспорте. Не спеши в отношениях, ведь это нешуточное дело, которое может испортить твою жизнь, но может сделать счастливым при грамотном поведении.

5. Адекватное покорение сердца

Тебе не нужно покупать девушку подарками, выслуживаться или бегать за ней, чтобы влюбить ее. Хватит мыслить шаблонами романтических фильмов. Тебе следует просто показать себя с лучшей стороны, продемонстрировав надежность, адекватность, эмоциональную стабильность. Яркие эмоции, интересные свидания, клевые развлечения, увлекательное общение, дерзки флирт и приятная близость дополнят ваше сближение. Все это сложится в отношения вполне естественно, если вы оба адекватных человека с адекватными ожиданиями и требованиями.

Как искать девушку на учебе или работе

Поиск второй половинки там, где ты проводишь много времени, может быть довольно успешным. Ты можешь присмотреться к девушке со стороны, лучше узнать ее, а затем сблизиться для отношений. Такие знакомства довольно перспективы, ведь многие из них заканчиваются длительными отношениями и браком.

Знакомство на учебе имеет некоторые особенности. В школах, колледжах, техникумах, университета есть такая вещь, что девушки предпочитают мутить с парнями постарше, а на одногодок не обращают внимание. Но кто сказал, что ты не можешь выбрать себе подружку младше на год, два или три?

На работе следует искать девушку тогда, когда это не противоречит политике компании, а также не принесет сложностей на работе. Служебные романы часто приносят неловкие ситуации, сложности и проблемы. Есть такое правило, которое гласит не мутить ни с кем на работе, чтобы не закончилось все расставаниями, а потом вам нужно каждый день вместе контактировать. Это довольно неприятно, а поэтому часто неудачи в служебных романах приводят к увольнениям по разными причинам. Но это не говорит, что служебные романы не имеют место быть для обустройства личной жизни.

Поиск девушки среди знакомых и друзей

В юные годы мы имеем много друзей, приятелей и знакомых, хотя с годами этот круг сужается. Мы развлекаемся, гуляем, общаемся. Так среди общего круга знакомства можно найти себе девушку, которая тебе понравится. Ты можешь разузнать о ней через друзей и пообщаться сам, прежде чем решать о то, чего ты хочешь.

Поиск девушки среди знакомых и друзей довольно комфортен для узнавания личности девушки. Это такой неторопливый подкат, когда ты узнаешь характер девушки хотя бы немного, прежде чем штурмовать ее сердце. Среди приятельской тусовки вам будет приятно сближаться и мутить, тем более ваши друзья скорей всего помогут в этом.

Как искать девушку в интернете

Современный мир знакомств – это уже скорее не улица, знакомые или работа, а онлайн-знакомства. С каждым годом все больше людей знакомиться через сайты и приложения для знакомств, ведь это очень удобно, быстро и практично. Ты можешь в любое время начать искать себе половинку и общаться с разными девушками, с которыми в реальной жизни шансы встретиться минимальны. Там тысячи потенциальных твоих будущих девушек на любой вкус и цвет.

Через приложения и сайты знакомств мы можем выбирать, лучше узнавать, общаться, ходить на свидания и пробовать завязать отношения. Вариантов, где это сделать довольно много, но самые популярные сайты знакомств по убыванию довольно известны.

• Badoo
• Tinder
• Мамба
• LovePlanet
• MyLove
• Teamo
• ДругВокруг

Проблема таких сайтов в том, что среди большого количества анкет тебе придется перебрать множество. Будет много неадекватных девушек, продающих любовь индивидуалок, меркантильных телок, стервозных дам и прочих подводных камней. Но среди всего этого можно отыскать себе замечательную девушку, с которой вы будете счастливы.

В знакомствах по интернету надо грамотно подойти к своей анкете, общаться с большим количеством девушек для лучшей выборки, проявлять оригинальность и активность. Как только находишь хороший вариант, то сразу бери номер и вытягивай на свидание. Дальше узнавай лучше, выбирай, смотри и бери на тест-драйв девушек.

Как искать девушку в социальных сетях: ВКонтакте, Одноклассниках и прочих местах? Здесь все схоже, но нужно выбирать девушек, которые из твоего города и свободны, хотя понять это порой довольно сложно. Но при должной сноровке многие парни находят себе девушек через социальные сети. В таком поиске главное терпение и упорство.

Как познакомиться с девушкой на улице или в общественном месте?

Кто сказал, что реальные знакомства прекратили существование? Есть множество возможностей найти себе подружку где-то на улице, в транспорте, на тренировке или на концерте. Для этого следует вести себя более активно, открыто, дружелюбно. Обычно проще всего знакомиться с девушками вместе с напарником другом, который поможет в общении. Так компании девушек легко общаться с компанией парней, когда те подкатывают.

Знакомиться с девушками можно прямо на улице, в транспорте, кафе, клубах, выставках, театрах, концертах, фестивалях, вечеринках. В клубах по интересам можно найти себе подружку, с которой вас будут разделять общие увлечения. В любом месте можно подойти и попытать удачу с обалденной незнакомкой. Здесь нет место сомнениям, стеснительности или трусости. Подходи и пробуй. Если из десятка одна тебе даст телефон, то это уже неплохо. Чем чаще ты пробуешь, тем чаще везет на номера телефонов, свидания, интрижки, отношения и любовь.

Многие девушки охотно общаются и знакомится в спортивных местах. Это тренажерный зал, беговой клуб, спортивные состязания, бассейн, велоклубы. Плюс знакомства в таких местах будет в том, что девушка будет фитоняшкой с красивым телом и попой с орех.

Как найти девушку на один раз или один вечер?

Это скорее для любителей непродолжительных отношений, сторонников близости на первом свидании, коротких романов и просто развлечений. Когда мужчины ищут девушку на один раз, то это обычно способ поразвлечься и взбодриться. Порой так мужчины убегают от одиночества, разочарования в женщинах или жизни.

Искать себе девушку на один вечер следует там, где они чаще всего обитают. Это приложения для знакомства Pure, а также частично Tinder. Если есть время, то проще выбраться вечером в какой-то клуб, бар или кабак, где сидят ищущие приключений одинокие дамы за бокалом вина или чего покрепче. Это обычно беззаботные студентки, одинокие, брошенные, разведенки или гулящие телки. Рано или поздно соблазнение таких девушек надоедает, но кто сказал, что это не будет приятно.

Лови лайфак, как не потратить деньги и снять себе телку на одну ночь. Один мой знакомый просто подкатывал на тачке к клубу или кабаку незадолго до его закрытия, чтобы познакомиться с выпившей и готовой на приключения девушкой. Потом он подвозил ее домой, приглашал к себе или кувыркался еще в тачке на заднем сидении. Просто, бесплатно, эффективно.

Как искать девушку для серьезных отношений?

Безусловно все девушки отличаются, ведь с одной можно только в постель, когда с другой хоть под венец. Девушки для отношений часто отличаются тем, что у них есть цели в жизни и планы, которые отличны от желания удачно выскочить замуж. У них насыщенная жизнь работой, учебой, хобби, увлечениями, друзьями, спортом, путешествиями.

Девушки для серьезных отношений имеют более правильные моральные принципы и не скачут в постель на 1-3 свидании. Такие девушки хорошо воспитаны, добры, нежны, заботливы. Они не требуют завоеваний с помощью дорогих подарков, открыты для общения и сами делают взаимные шаги навстречу. С такой девушкой чувствуешь себя счастливым, ведь это главный признак правильных отношений.

Когда ты решаешь наладить личную жизнь, то следует меньше заморачиваться над тем, как искать девушку в теории, а скорее приступать к практике. Чем больше ты пробуешь, тем больше получаешь опыта и больше шансы. Найти любовь и отношениях не всегда просто, но реально, ведь это делают тысячи людей каждый день. Удачи в поисках девушки!

Перевод градусов в радианы и обратно

Чтобы перевести градусы в радианы и обратно, воспользуйтесь нашим удобным онлайн конвертером:

Перевод градусов в радианы

Просто введите значение угла в градусах и получите результат в радианах с подробным решением.

Перевод радиан в градусы

Просто введите значение угла в радианах и получите результат в градусах с подробным решением.

Теория

Градусы в радианы

Радианы в градусы

Угол может измеряться следующими величинами:

1. Градусами (и соответствующими ему величинами: угловыми минутами и секундами);
2. Радианами.

Градусная мера угла

Если взять развернутый угол (это два прямых угла) и поделить его на 180 частей, то одна такая часть будет называться одним градусом. Для того, чтобы измерить градусную меру угла, необходимо посчитать, сколько раз 1 градус входит в данный угол. Полученное число и будет ответом.

Если угол таков, что его нельзя измерить целым числом, либо же он меньше единичного угла, то используют такие меры измерения как угловые минуты и секунды.

Если градус поделить на 60 частей, то одной такой частью будет минута. В свою же очередь, если минуту разделить на те же 60 частей, то полученным числом будет 1 секунда.

Радианная мера угла

Радианом называют угол, образованный дугой окружности длинной равной радиусу этой окружности.

Длина окружности равна:

где rr — радиус этой окружности.

Тогда, разделив на радиус, получаем, что полный угол в радианах равен:

lr=2⋅π⋅rr=2⋅π радианfrac{l}{r}=frac{2cdotpicdot r}{r}=2cdotpitext{ радиан}

В градусах этот же угол равен, как известно, 360∘360^{circ}.

Отсюда находим связь между радианами и градусами:

Это та главная формула, которая нужна, чтобы переводить градусы в радианы и наоборот.

Перевод градусов в радианы

Если по условию известна градусная мера угла, то чтобы перевести ее в радианную, нужно сделать следующие действия: умножить ее на πpi и разделить на 180.

Перевод радиан в градусы

Чтобы перевести радианы в градусы, нужно умножить угол в радианах на 180 и разделить на πpi.

Ищете, где можно заказать задачу по математике недорого? Обратитесь к нашим экспертам в данной области!

Тест по теме «Перевод градусов в радианы и наоборот»