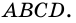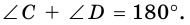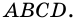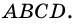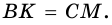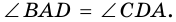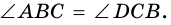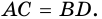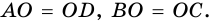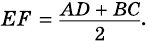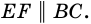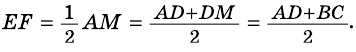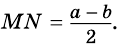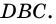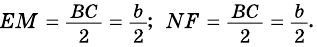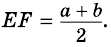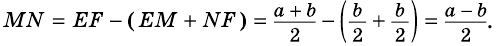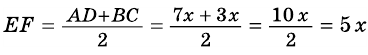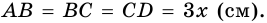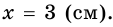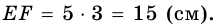Трапеция — геометрическая фигура представляет собой выпуклый четырехугольник с параллельными
противоположными сторонами. Они называются основаниями. Две другие стороны — боковые.
Трапеция, у которой они одинакового размера, называется равнобедренной. Если одна из боковых сторон
образует у основания угол в 90 градусов-прямоугольной.
Прямая линия, проведенная от одного основания
к другому, именуется высотой трапеции. Величина ее высчитывается делением суммы оснований на 2.
Диагонали — это отрезки, соединяющие противоположные углы фигуры. У равнобедренной трапеции
они равны по длине. Средняя линия-прямая, делящая пополам боковые стороны.
- Угол трапеции при основании через высоту и прилегающую
боковую сторону - Угол трапеции через нижнее основание, боковую сторону и
диагональ - Угол равнобедренной трапеции через нижнее основание,
среднию линию и боковую сторону - Угол равнобедренной трапеции через среднию линию, верхнее
основание и боковую сторону - Острый угол при нижнем основании прямоугольной трапеции
через высоту и два основания - Острый угол при нижнем основании прямоугольной трапеции
через два основания и боковую сторону
Угол трапеции при основании через высоту и прилегающую боковую сторону
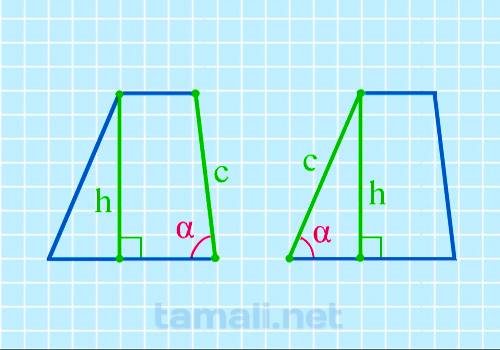
Введем обозначения: h-высота, с — боковая сторона. Угол трапеции α при основании вычисляется с
помощью формулы
sin α = h/с
где: h — высота трапеции, c — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Заменим буквенные обозначения условными цифрами. Пример: если высота равна
9см, боковая сторона-11см, получим: sin α = 9 / 11 = 0,818 , отсюда α =
55º. Указанное значение находим в таблице синусов. Данный показатель синуса угла соответствует
величине 55 градусов.
Через нижнее основание, среднию линию и боковую сторону в равнобедренной трапеции
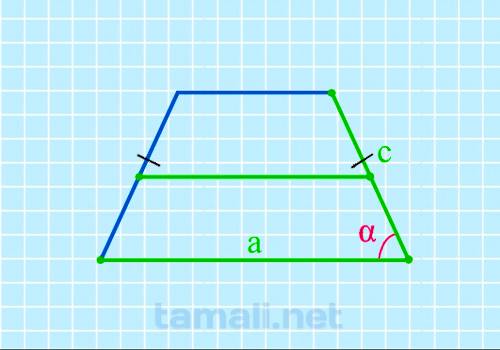
Угол равнобедренной трапеции через нижнее основание, среднюю линию и боковую сторону находится по
формуле:
cos α = (2a-2m) / 2c
где а — нижнее основание, m — средняя линия, с — боковая сторона.
Цифр после
запятой:
Результат в:
Пример.Заменим буквы условными цифровыми значениями. Если нижнее основание равно 8
см, средняя линия-6, а боковая сторона-4,8 см, то косинус угла равен 0,41666, что соответствует 65
градусам. cos α = (2 * 8 — 2 * 6) / 2 * 4,8 = 0, 41666, отсюда α =
65º. Равнобедренная трапеция — геометрическая фигура с нижними острыми углами. Это ее
особенность.
Угол трапеции, зная размер нижнего основания, боковой стороны и диагонали
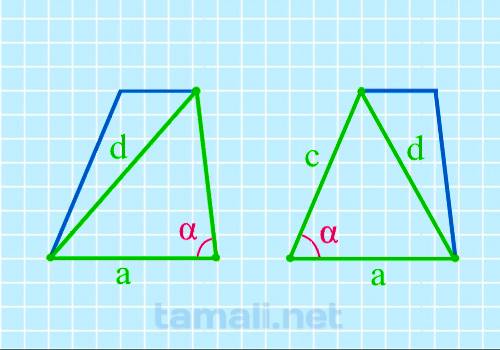
Если известны эти величины, воспользуемся формулой:
cos α= (a²+c²-d²) / 2ac
где а-нижнее основание, d-диагональ, с-боковая сторона.
Цифр после
запятой:
Результат в:
Пример. При условной величине нижнего основания 4 см, диагонали — 5.7 см,
боковой стороны — 4,4 см косинус равняется 0,081534, что соответствует углу 85 градусов по
таблице функций. cos α= (4² + 4,4² — 5,7²) / 2*4*4,4 = 0,081534,
отсюда α = 85º.
Через среднюю линию, верхнее основание и боковую сторону в равнобедренной трапеции
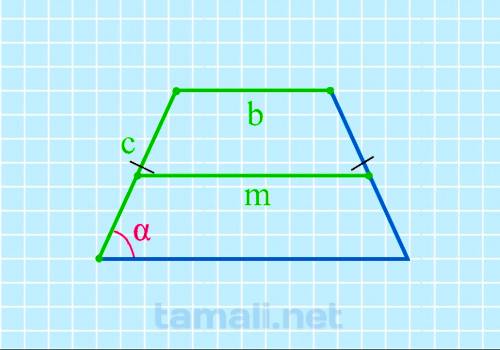
Нахождение угла равнобедренной трапеции через среднюю линию, верхнее основание и боковую сторону
выполняется по предложенной формуле:
cos α = (2m-2b) / 2c
где m — средняя линия, b — верхнее основание, c — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Введем условные цифровые значения. Допустим, что у равнобедренной трапеции
верхнее основание равно 4 см, средняя линия-6, боковая сторона-4 см. Косинус составляет 0,5.
Значение соответствует 60 градусам по таблице Брадиса. cos α = (2 * 6 — 2 * 4) / 2 * 4 = 0,5,
отсюда α = 60º
Вычисление острого угла при нижнем основании, если известны величины обоих оснований и боковой
стороны в прямоугольной трапеции
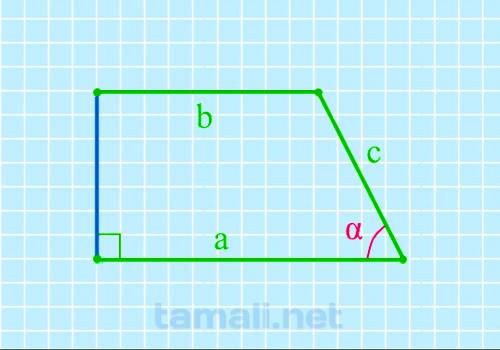
Находится по формуле
cos α = (a — b) / c
где a,b — основания, c — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Если буквенные выражения заменить условными цифровыми, получится наглядный
пример вычисления. Допустим, длина нижнего основания а 8 см, верхнего b-5,8 см, размер боковой
стороны с-4,8. Подставив в формулу цифровые значения, получим итог: косинус равен 0,45833.
Сравниваем показатель с таблицей вычисления Брадиса: он соответствует углу 63 градуса. cos α=(8 — 5,8) / 4,8 = 0,45833, отсюда α = 63º
Острый угол при нижнем основании, зная высоту и размеры двух оснований прямоугольной трапеции
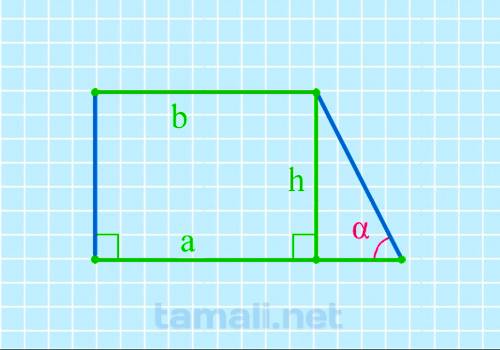
При известных указанных величинах воспользуемся следующей формулой:
tg(α) = h / (a-b)
где h — высота, a,b — верхнее и нижнее основания.
Цифр после
запятой:
Результат в:
Пример. Введя условные цифровые значения h = 15, a = 11, b = 10 получим tg(α) = 15 / (11-10) = 15. При вычислении получим значение тангенса: 15.
По таблице функций показатель соответствует 86 градусам.
Следует знать несколько закономерностей данной геометрической конструкции. У трапеции четыре угла,
общая сумма которых составляет 360 градусов.
Равнобедренная отличается двумя равными острыми, прилегающими к нижнему основанию, и тупыми
одинаковой величины-к верхнему. У прямоугольной трапеции два угла по 90 градусов, другие —
острый и тупой. Если он прилегает к нижнему основанию, величина такого угла определяется делением
высоты на разность между нижним и верхним основаниями. Угол трапеции при основании равен отношению
высоты к боковой стороне.
Как найти угол в трапеции
Трапеция — это плоский четырехугольник, у которого две противолежащие стороны параллельны. Они называются основаниями трапеции, а две другие стороны — боковыми сторонами трапеции.
Инструкция
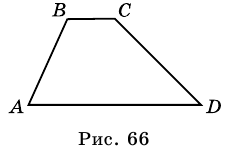
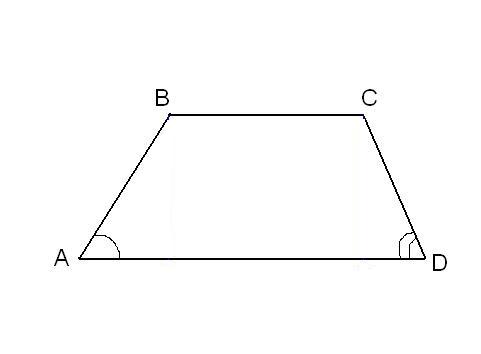
Задача нахождения произвольного угла в трапеции требует достаточного количества дополнительных данных. Рассмотрим пример, в котором известны два угла при основании трапеции. Пусть известны углы ∠BAD и ∠CDA, найдем углы ∠ABC и ∠BCD. Трапеция обладает таким свойством, что сумма углов при каждой боковой стороне равна 180°. Тогда ∠ABC = 180°-∠BAD, а ∠BCD = 180°-∠CDA.
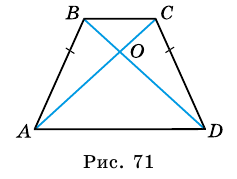
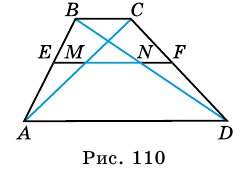
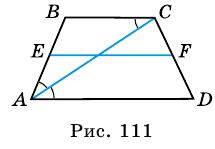
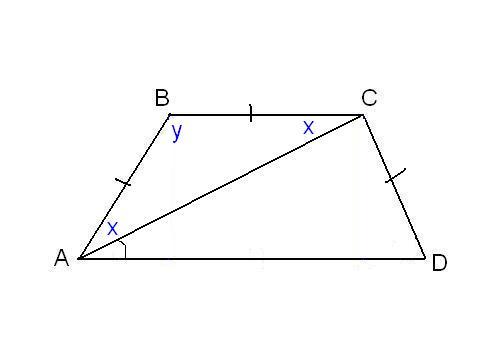
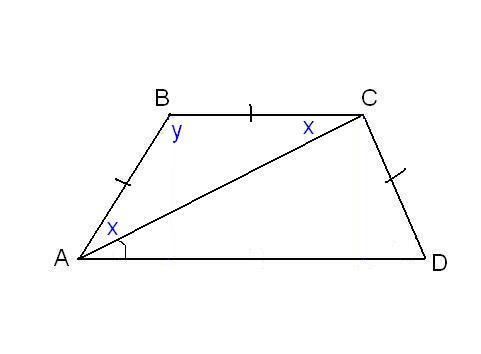
В другой задаче может быть указано равенство сторон трапеции и какие-нибудь дополнительные углы. Например, как на рисунке, может быть известно, что стороны AB, BC и CD равны, а диагональ составляет с нижним основанием угол ∠CAD = α.Рассмотрим треугольник ABC, он равнобедренный, так как AB = BC. Тогда ∠BAC = ∠BCA. Обозначим его x для краткости, а ∠ABC — y. Сумма углов любого треугольника равна 180°, из этого следует, что 2x + y = 180°, тогда y = 180° — 2x. В то же время из свойств трапеции: y + x + α = 180° и следовательно 180° — 2x + x + α = 180°. Таким образом, x = α. Мы нашли два угла трапеции: ∠BAC = 2x = 2α и ∠ABC = y = 180° — 2α.Так как AB = CD по условию, то трапеция равнобокая или равнобедренная. Значит, диагонали равны и равны углы при основаниях. Таким образом, ∠CDA = 2α, а ∠BCD = 180° — 2α.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Содержание:
Трапецией называют четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
На рисунке 66 изображена трапеция
Свойства трапеции
Рассмотрим некоторые свойства трапеции.
1. Сумма углов трапеции, прилежащих к боковой стороне, равна 180°.
Так как 
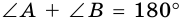
2. Трапеция является выпуклым четырехугольником.
Поскольку 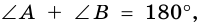
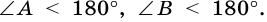
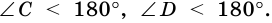
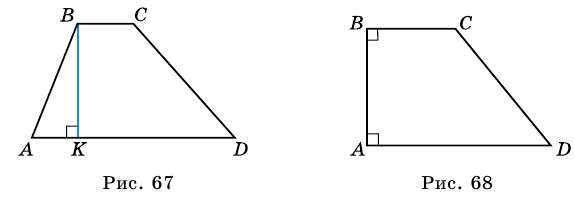
Высотой трапеции называют перпендикуляр, проведенный из любой точки основания трапеции к прямой, содержащей другое ее основание.
Как правило, высоту трапеции проводят из ее вершины. На рисунке 67 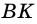
Трапецию называют прямоугольной, если один из ее углов -прямой. На рисунке 68 — прямоугольная трапеция 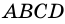
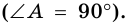
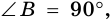
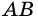
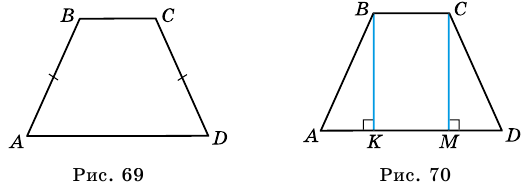
Трапецию называют равнобокой, если ее боковые стороны равны. На рисунке 69 — равнобокая трапеция
Свойства равнобокой трапеции
Рассмотрим некоторые важные свойства равнобокой трапеции.
1. В равнобокой трапеции углы при основании равны.
Доказательство:
1) Пусть в трапеции 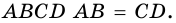
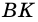
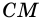
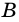
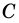
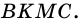
2) 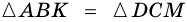
3) Также 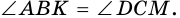
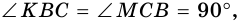
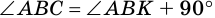
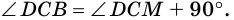
2. Диагонали равнобокой трапеции равны.
Доказательство:
Рассмотрим рисунок 71. 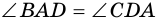
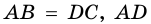
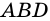
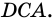
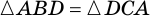
Пример:
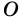
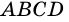
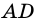
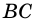
Доказательство:
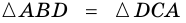
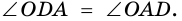
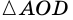
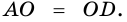
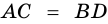
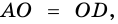
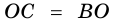
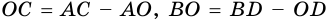
Теорема (признак равнобокой трапеции). Если в трапеции углы при основании равны, то трапеция — равнобокая.
Доказательство:
1) Пусть в 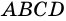
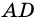
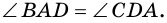
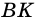
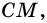
2) Тогда 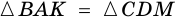
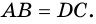
А еще раньше…
Термин «трапеция» греческого происхождения (по-гречески «трапед-зион» означает «столик», в частности столик для обеда; слова «трапеция» и «трапеза» — однокоренные).
В «Началах» Евклид под термином «трапеция» подразумевал любой четырехугольник, не являющийся параллелограммом. Большинство математиков Средневековья использовали термин «трапеция» с тем же смыслом.
Трапеция в современной трактовке впервые встречается у древнегреческого математика Посидония (I в.), но начиная только с XVIII в. этот термин стал общепринятым для четырехугольников, у которых две стороны параллельны, а две другие — не параллельны.
Свойство средней линии трапеции
Средней линией трапеции называют отрезок, соединяющий середины ее боковых сторон.
Рассмотрим свойство средней линии трапеции.
Теорема (свойство средней линии трапеции). Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство:
Пусть 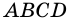
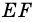
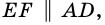
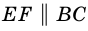
1) Проведем луч 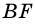
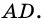
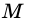
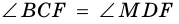
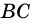
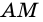
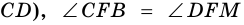
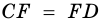
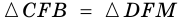
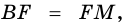
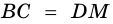
2) Поскольку 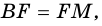
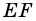
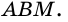
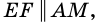
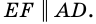
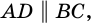
3) Кроме того,
Пример:
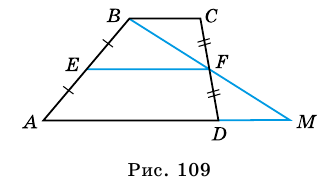
Докажите, что отрезок средней линии трапеции, содержащийся между ее диагоналями, равен полуразности оснований.
Доказательство:
Пусть 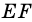
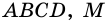
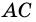
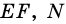
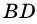
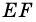
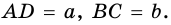
1) Так как 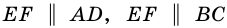
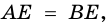
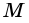
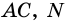
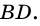
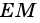
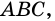
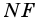
Тогда
2) 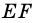
3)
Пример:
В равнобокой трапеции диагональ делит острый угол пополам. Найдите среднюю линию трапеции, если ее основания относятся как 3 : 7, а периметр трапеции — 48 см.
Решение:
Пусть 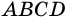
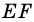
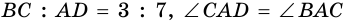
1) Обозначим 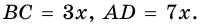
2) 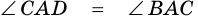
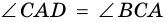
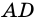
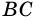
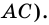
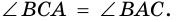
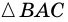
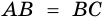
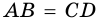
3) Учитывая, что 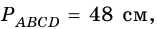
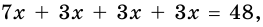
4) Тогда
Ответ. 15 см.
А еще раньше…
То, что средняя линия трапеции равна полусумме оснований, было известно еще древним египтянам; эту информацию содержал папирус Ахмеса (примерно XVII в. до н. э.).
О свойстве средней линии трапеции знали также и вавилонские землемеры; это свойство упоминается и в трудах Герона Александрийского (первая половина I в. н. э.).
- Площадь трапеции
- Центральные и вписанные углы
- Углы и расстояния в пространстве
- Подобие треугольников
- Площадь параллелограмма
- Прямоугольник и его свойства
- Ромб и его свойства, определение и примеры
- Квадрат и его свойства
Сколько градусов у трапеции?
360°
Трапеция 180 градусов?
Трапеция — это четырехугольник. Все четырехугольники имеют четыре угла, сумма которых равна 360 градусам. Если два угла прямые, что составляет 180 градусов от суммы. Следовательно, два других угла также должны составлять 180 градусов.
Трапеция это 360?
Объяснение: Сумма углов любого четырехугольника равна 360°, а свойства равнобедренной трапеции диктуют, что наборы углов, соединенные параллельными прямыми (в данном случае нижний набор и верхний набор углов), равны.
Имеют ли трапеции углы 90 градусов?
Трапеция может не иметь прямых углов или иметь два прямых угла. Большинство трапеций имеют два острых угла (под 90 градусов) и два…
Смотрите также, когда мигрируют воробьи
У трапеции есть угол 60 градусов?
Углы 60 градусов составляют для специальных треугольников и в этом случае специальная трапеция.
Как найти углы трапеции?
Есть ли у трапеции прямые углы?
Трапеция имеет два прямых угла.
Сколько углов в трапеции?
четыре угла
Трапеция — это замкнутая форма или многоугольник с четырьмя сторонами, четырьмя углами/вершинами и четырьмя углами. 25 августа 2020 г.
У трапеций 4 прямых угла?
Нет. Трапеция является четырехугольником, поэтому сумма внутренних углов должна быть равна 360 градусам. Любые тупые углы должны компенсироваться острыми, если только они не прямые/не прямоугольник.
Что такое трапеция с двумя прямыми углами?
Правильная трапеция (также называемая прямоугольной трапецией) имеет два смежных прямых угла. … Равнобедренная трапеция — это трапеция, у которой углы при основании имеют одинаковую меру.
Может ли трапеция иметь 3 прямых угла?
У трапеции не может быть трех прямых углов.
Сумма мер четырех внутренних углов любого четырехугольника всегда составляет 360 градусов. …
Сколько острых углов у трапеции?
два острых угла Подсказка: Поскольку трапецией называется выпуклый четырехугольник, у которого хотя бы одна из пар сторон параллельна. Это означает, что если это общая трапеция, то существуют два острых угла
и два тупых угла.
Как найти стороны трапеции?
Поскольку в этой задаче указана длина обоих оснований, а также общий периметр, недостающие стороны можно найти по следующей формуле: Периметр = основание один основание два (нога), где длина «ножки» — одна из двух эквивалентных непараллельных сторон.
См. также, как клеточная мембрана защищает клетку.
Сколько сторон у трапеции?
Трапеция/Количество ребер
Трапеция (также известная как трапеция) представляет собой плоскую двухмерную фигуру с четырьмя прямыми сторонами. Он имеет одну пару параллельных сторон, которые обычно являются верхней и нижней сторонами. Параллельные стороны называются основаниями, а непараллельные — катетами.
Как решить трапецию?
Сколько градусов в треугольнике?
180°
Сколько вершин у трапеции?
4
Как выглядит угол 180 градусов?
Как выглядит угол 180 градусов? 180 градусов выглядит как прямая линия потому что лучи или стороны угла, составляющего 180 градусов, полностью противоположны друг другу. Общая точка, соединяющая прямые, совершает половину оборота, т. е. угол 180 градусов.
У трапеции 4 равные стороны?
Трапеция, также известная как трапеция, представляет собой плоскую замкнутую форму, имеющую 4 прямые стороны, с одной парой параллельных сторон. Параллельные стороны трапеции называются основаниями, а непараллельные стороны – катетами.
Как найти диагональ трапеции?
Есть ли у трапеции угол?
Трапеция имеет четыре угла.
Может ли трапеция иметь 4 разных угла?
У трапеции не может быть четырех прямых углов. Трапеция – четырехугольник, а это значит, что у нее четыре стороны и четыре угла.
Может ли трапеция иметь 3 стороны?
Трехсторонняя трапеция – это равнобедренная трапеция, имеющая не менее трех равных сторон. Ниже приведено изображение трапеции с тремя сторонами. В некоторых диалектах английского языка (например, в британском английском) эта фигура называется трапецией с тремя сторонами.
У трапеции 2 тупых угла?
Трапеция ABCD имеет две пары дополнительных углов. Тогда Оба дополнительных угла не могут быть тупыми одновременно. Следовательно У трапеции может быть не более двух тупых углов.
Что такое правильная трапеция в математике?
Правильная трапеция это трапеция с двумя прямыми углами.
Как выглядят трапеции?
Трапеция – это четырехгранная плоская фигура с одной парой противоположных параллельных сторон. Это выглядит как треугольник, у которого вершина срезана параллельно основанию. Обычно трапеция располагается самой длинной стороной вниз, и у вас будут две наклонные стороны для краев.
Смотрите также, что означает слово «затвердевать»
Является ли квадрат трапецией?
Поскольку у квадрата 4 прямых угла, его также можно классифицировать как прямоугольник. … Противоположные стороны параллельны, поэтому квадрат также можно классифицировать как параллелограмм. Если он классифицируется как параллелограмм, то он также классифицируется как параллелограмм. трапеция.
Является ли ромб трапецией?
Трапеция – это четырехугольник хотя бы с одной парой параллельных сторон (называемых основаниями), а у ромба должно быть две пары параллельных сторон (частный случай параллелограмма). Второе отличие состоит в том, что у ромба все стороны равны, а у трапеции все 4 стороны могут быть разной длины.
У трапеции нет равных углов?
Трапеция, также известная как трапеция, может иметь либо ноль, либо две пары равных углов.
Можно ли нарисовать трапецию, являющуюся прямоугольником?
Если трапецию определить как многоугольник с четырьмя сторонами (то есть четырехугольник) и две его стороны параллельны друг другу, то прямоугольник можно рассматривать как тип трапеции. В этом случае все теоремы, доказанные для трапеции, справедливы. верно для прямоугольников.
Сколько диагоналей у трапеции?
две диагонали Трапеция, катеты которой не равной длины, не имеет диагоналей. Если ноги одинаковой длины, то фигура имеет две диагонали.