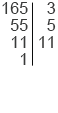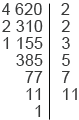Наибольший общий делитель
4.3
Средняя оценка: 4.3
Всего получено оценок: 224.
4.3
Средняя оценка: 4.3
Всего получено оценок: 224.
Наибольший общий делитель – это еще один показатель, позволяющий упростить работу с дробями. Очень часто в результате вычислений получаются дроби с очень большими значениями числителя и знаменателя. Сокращать поэтапно такие числа можно, но это крайне долго, поэтому проще сразу найти НОД и сократить на него. Разберемся в теме подробнее.
Что такое НОД?
Наибольший общий делитель (НОД) ряда чисел – это наибольшее число, на которое можно без остатка разделить каждое из чисел ряда.
Это значение чаще всего используется для ряда из двух чисел. Просто потому, что сокращаются обычно два числа: числитель и знаменатель дроби. Нахождение НОД для большего количества значений не всегда оправдано, но вырабатывает навык.
Как найти НОД?
Для того, чтобы найти НОД необходимо каждое из чисел разложить на простые множители и выделить общую часть.
Специальной формулы для этого не придумали, зато есть алгоритм вычисления.
Приведем пример нахождения наибольшего общего делителя двух натуральных чисел: 540 и 252. Разложим 640 на простые множители. Последовательность действий такова:
- Делим число на наименьший из возможных простых чисел. То есть, если число можно разделить на 2, 3 или 5, то сначала нужно делить на 5. Просто, чтобы не запутаться.
- Получившийся результат делим на наименьшее из возможных простых чисел.
- Повторяем деление каждого полученного результата, пока не получим простое число.
Теперь проведем ту же процедуру на практике.
- 540 : 2=270
- 270:2=135
- 135 : 3 =45
- 45 : 3=15
- 15 : 5 = 3
Запишем результат в виде равенства 540=2*2*3*3*3*5. Для того, чтобы записать результат, нужно последнее получившееся число умножить на все делители.
Аналогично поступим с числом 252:
- 252 : 2=126
- 126: 2=63
- 63 : 3=21
- 21 : 3 = 7
Запишем результат: 252=2*2*3*3*7.
В каждом разложении есть одинаковые числа. Найдем их, это два числа 2 и два числа 3. Отличаются только 7 и 3*5.
Для того, чтобы найти НОД нужно перемножить общие множетели. То есть в произведении будет две двойки и две тройки.
НОД=2*2*3*3=36
Как можно это использовать?
Задача: сократить дробь $$252over540$$.
НОД для двух этих чисел мы уже находили, теперь просто воспользуемся уже посчитанным значением.
НОД = 36
Сократим числитель и знаменатель дроби на 36 и получим ответ.
$${252over540} ={7over15}$$ – чтобы быстро сократить, достаточно посмотреть на разложение чисел.
Если 540=2*2*3*3*3*5, а НОД=36=2*2*3*3, то 540 = 36*3*5. И если мы поделим 540 на 36, то получим 3*5=15.
Без НОД нам пришлось бы в одну длинную строку писать сокращения. К тому же, бывают случаи, когда непонятно, можно ли сократить дробь вообще. Для таких ситуаций в математике и придумали разложение чисел на простые множители и НОД.
Что мы узнали?
Мы узнали, что такое наибольший общий делитель пары чисел, разобрались, как можно использовать показатель на практике, решили задачу на нахождение НОД и применение НОД для сокращения дробей. Поняли, что с использованием НОД можно проще и быстрее сократить громоздкие дроби, найдя НОД для числителя и знаменателя.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.3
Средняя оценка: 4.3
Всего получено оценок: 224.
А какая ваша оценка?
Наибольший общий делитель (сокращённо НОД) необходим для того, чтобы работать с обыкновенными дробями. Также он тесно связан с другим математическим понятием — наименьшим общим кратным. На этом уроке мы разберём способы нахождения НОД и рассмотрим признаки деления на разные числа.
Знакомство с наибольшим общим делителем
Наибольший общий делитель заданных чисел (НОД) – это наибольшее число, на которое все заданные числа делятся без остатка
При вычислениях нам помогут признаки деления на число. Они есть у многих чисел. Нам понадобятся вот эти четыре, если их запомнить, они станут нашими помощниками.
Признаки деления по последнему числу:
Число делится на $2$, если оно чётное, т.е. заканчивается на чётную цифру: $0, 2, 4, 6, 8$
Число делится на $5$, если его последняя цифра равна $0$ или $5$
Кроме того, существуют признаки деления и для других чисел, некоторые из них очень интересны:
Число делится на $3$, если сумма его цифр делится на $3$.
Например, $21 (2+1=3)$ и $69 (6+9=15)$
Число делится на $ 7 $, если утроенное число десятков плюс число единиц делится на $7$.
Например, число $154 (15cdot 3 + 4 = 49) $
Также нам нужно, чтобы число делилось без остатка. Если в итоге деления получается остаток, то такое число не является множителем данного числа.
Первый способ нахождения НОД
Существует три способа нахождения НОД. Эти способы имеют очень много общего между собой, но мы разберём их все.
Первый способ заключается в нахождении всех возможных делителей для числа.
Проще рассматривать сразу на примерах. Например, нам нужно сократить дробь $frac{12}{40}$.
Делители числа $12$: $2, 3, 4, 6, 12$
Мы не берём $1$, так как единица для нас бесполезна в качестве делителя, потому что даёт в результате то же число. Также мы отбросили $5, 7, 8, 9, 10, 11$ ( потому что число $12$ нельзя поделить на эти числа без остатка).
Делители числа $40$: $2, 4, 5, 8, 10, 20$
Теперь запишем все наши делители. Вот что получилось:
Теперь нам сразу видно, какие числа общие. Это $2$ и $4$. Так как $4$ больше, оно и является наибольшим общим делителем.
Второй способ нахождения НОД
Второй и третий способы базируются на том, что мы раскладываем числа не на делители, а на простые множители.
Для нахождения НОД нескольких чисел данные числа нужно разложить на множители и определить общие для обоих чисел. Если такой множитель один, он и будет являться наибольшим общим делителем. Если общих множителей несколько, то наибольшим общим делителем будет являться произведение этих множителей
Простой множитель — это простое число.
Простое число — это натуральное число больше единицы, которое делится без остатка только на два натуральных числа — единицу и само себя.
И так как для нахождения НОД нам нужны только простые множители, нашими делителями чаще всего будут только $ 2, 3, 5, 7 $.
Мы не будем делить на $4$ , потому что $4$ – это $2 cdot 2$, на $6$, потому что это $3cdot 2$. $8$ и $9$ также можно разложить на множители. Значит, выбор вариантов, на которые можно разделить число, невелик.
Сначала пробуем поделить число на $2$, затем на $3$, на $5$ и так далее.
При нахождении НОД этим способом мы будем записывать делители и промежуточные результаты деления в столбик. Так они остаются у нас на виду, и мы не запутаемся. Сначала пишем наше число, потом ставим вертикальную черту и напротив числа пишем первый делитель – то есть число, на которое собираемся разделить наше число.
Итак. Справа у нас $12$, слева – простой делитель, например, $2$.
$$12:2=6$$
Записываем частное под цифрой «12». Почему там? Потому что теперь мы будем делить уже «6», и так, пока будет возможно делить без остатка.
Получается вот такая запись:
Частные, которые получились слева, нам уже не нужны. Нам нужны числа справа, так как именно там у нас записаны делители. Но постойте, нам же были нужны множители?
Это и есть множители. Мы разобрали число на них, как конструктор разбирают на детальки, и из них же можем сложить. Давайте проверим:
$$2 cdot 3 cdot 2=12$$
Теперь таким же образом «разберём» число $40$.
$40$ делится без остатка также на $4, 8, 10$. Почему мы не можем использовать эти множители?
Показать ответ
Скрыть
Данные числа действительно являются множителями числа $40$, но они не являются простыми множителями. Простое число делится только на $1$ и на само себя, а все эти числа можно разложить на простые множители, например, $8$ является произведением $2$ и $4$, и т.д.
Теперь самое интересное. Находим среди множителей обоих чисел одинаковые числа и перемножаем их между собой. То, что получится, и будет НОД – наибольший общий делитель для обоих чисел.
Второй способ наиболее распространён, потому что позволяет удобно записывать промежуточные результаты деления и делители. При записи первым способом мы записываем только делители и легко «потерять» какие-то из них, особенно если их много и они повторяются.
Третий способ нахождения НОД
Третий способ похож на второй. Мы также пишем числа в столбик, но затем не выделяем общие, а берём множители одного числа и вычёркиваем из них те, которые не встречаются во втором числе.
Этот способ не сильно отличается от второго (да и от первого тоже): мы точно таким же образом ищем общие множители, только не выделяем общие, а вычёркиваем те, которые общими не являются.
Записывают наибольший общий делитель так:
НОД ($12$ и $40$) $= 4$
Теперь, когда мы знаем НОД, мы можем легко сократить дробь, разделив числитель и знаменатель на НОД. У нас получится так:
$$frac{12}{40} = frac{12:4}{40:4}=frac{3}{10}$$
Также мы можем использовать НОД для нахождения НОК (наименьшего общего кратного).
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Обыкновенные дроби
- Наибольший общий делитель
Число 36 имеет такие делители: 1, 2, 4, 6, 9, 12, 18, 36.
Число 126 имеет такие делители: 1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63, 126.
Синим цветом мы выделили числа 1, 2, 6, 9, 18, которые являются общими делителями чисел 36 и 126. Наибольшим из данных множителей является 18.
Наибольший общий делитель чисел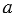 
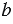
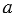
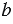
и 
обозначают так: НОД(; ), то есть мы можем записать НОД(36; 126) = 18.
Предварительно разложив числа на простые множители, мы упростим нахождение наибольшего общего делителя многозначных чисел.
Найдем НОД(240; 165).
240 = 2
22235 165 = 3511.
Синим мы выделили все общие простые делители рассматриваемых чисел, это 3 и 5. Значит, оба данных числа делятся и на произведение данных чисел, то есть на 35 = 15, оно и будет являться наибольшим общим делителем чисел 240 и 165, то есть НОД(240; 165) = 35 = 15.
Найдем НОД(2520; 4620).
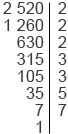
2 520 = 2223357 4 620 = 2235711.
Рассмотрев разложения данных чисел, мы можем заметить, что некоторые простые множители повторяются, например, число 2 в разложении числа 2520 повторяется трижды, а в разложении числа 4620 — дважды. Заметим, что число 4 = 22 является делителем и числа 2520, и числа 4620, а число 8 = 222, является делителем только числа 2520. Так же число 3 является множителем рассматриваемых чисел, а число 9 = 33 является только делителем числа 2520. Кроме чисел 4 и 3, общими делителями данных чисел являются числа 5 и 7.
Мы получили, что числа 2520 и 4620 делятся без остатка на каждое из чисел 4, 3, 5, 7, на их произведение 4357 рассматриваемые числа тоже делятся без остатка, то есть мы получили, что НОД(2520; 4620) = 4357 = 420.
Таким образом, можно найти НОД, разложив числа на простые множители и выписав те, что входят в разложение обоих чисел (или можно просто зачеркнуть те множители, которые есть только в разложении одного числа, например, в разложении числа 2520 нам надо вычеркнуть одну 2 и одну 3, а в разложении числа 4620 число 11).
Таким же образом можно найти НОД трех и более чисел.
Чтобы найти НОД нескольких натуральных чисел, надо:
- разложить их на простые множители;
- из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;
- найти произведение оставшихся множителей.
Заметим, что если все данные числа делятся на одно из них, то это число и является НОД данных чисел.
Натуральные числа называют взаимно простыми, если их наибольший общий делитель равен 1.
Нам известно, что разложение на простые множители, мы можем записать в виде произведения степеней, то есть в последнем примере мы можем записать, что:
2 520 = 23325171
4 620 = 22315171111.
Тогда НОД мы можем найти по следующему правилу:
- Определить степени, основания которых являются общими простыми делителями данных чисел.
- Из каждой пары степеней с одинаковыми основаниями выбрать степень с меньшим показателем.
- Перемножить выбранные степени. Полученное произведение является искомым наибольшим общим делителем.
Найдем НОД(2520; 4620):
- Выписываем общие основания: 2, 3, 5, 7.
- Выбираем наименьшие показатели данных степеней: 22, 31, 51, 71.
- Находим произведение данных степеней, то есть искомый наибольший общий делитель: НОД(2520; 4620) = 22
315171 = 420.
Советуем посмотреть:
Доли. Обыкновенные дроби
Сравнение дробей
Делители и кратные
Признаки делимости на 10, на 5 и на 2
Четные и нечетные числа
Признаки делимости на 9 и на 3
Простые и составные числа
Разложение на простые множители
Наименьшее общее кратное
Деление и дроби
Сложение и вычитание дробей с одинаковыми знаменателями
Смешанное число
Сложение и вычитание смешанных чисел
Основное свойство дроби
Решето Эратосфена
Приведение дробей к общему знаменателю
Сравнение, сложение и вычитание дробей с разными знаменателями
Умножение обыкновенных дробей
Деление обыкновенных дробей
Обыкновенные дроби
Правило встречается в следующих упражнениях:
6 класс
Номер 142,
Мерзляк, Полонский, Якир, Учебник
Номер 145,
Мерзляк, Полонский, Якир, Учебник
Номер 151,
Мерзляк, Полонский, Якир, Учебник
Номер 177,
Мерзляк, Полонский, Якир, Учебник
Номер 224,
Мерзляк, Полонский, Якир, Учебник
Задание 148,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 191,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 484,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 190,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 2,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
7 класс
Номер 351,
Мерзляк, Полонский, Якир, Учебник
Математика
5 класс
Урок № 52
Приведение дробей к общему знаменателю. Сокращение дробей
Перечень рассматриваемых вопросов:
— делитель двух чисел;
— НОД двух чисел;
— сокращение дробей.
Тезаурус
НОД двух чисел – наибольшее число, на которое будут делиться оба числа без остатка.
Сократить дробь – значит, разделить её числитель и знаменатель на их общий делитель.
Обязательная литература
- Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
На прошлом уроке мы научились приводить дробь к наименьшему общему знаменателю.
Чтобы ответить на этот вопрос разложим числитель и знаменатель на простые множители.
30 = 2 ∙ 3 ∙ 5
48 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 3
После этого мы видим, что наибольший общий делитель равен шести. Разделим и числитель, и знаменатель на шесть.
Итак, сегодня мы научились приводить дробь к несократимому виду, используя алгоритм сокращения дробей. Он подразумевает следующие действия: сначала надо найти наибольший общий делитель (НОД) числителя и знаменателя; а затем разделить числитель и знаменатель на их НОД.
Тренировочные задания
Сравним вторую пару дробей. Сократим их:
Разложим 18 и 36 на простые множители:
18 = 2 ∙ 3 ∙ 3
36 = 2 ∙ 2 ∙ 3 ∙ 3
Наибольший общий делитель НОК (18, 36) = 18.
Теперь сократим дробь на 18:
Как найти НОД
- Нахождение путём разложения на множители
- Алгоритм Евклида
Рассмотрим два способа нахождения наибольшего общего делителя.
Нахождение путём разложения на множители
Первый способ заключается в нахождении наибольшего общего делителя путём разложения данных чисел на простые множители.
Чтобы найти НОД нескольких чисел, достаточно, разложить их на простые множители и перемножить между собой те из них, которые являются общими для всех данных чисел.
Пример 1. Найти НОД (84, 90).
Решение: Раскладываем числа 84 и 90 на простые множители:
Итак, мы подчеркнули все общие простые множители, осталось перемножить их между собой:
2 · 3 = 6.
Таким образом, НОД (84, 90) = 6.
Пример 2. Найти НОД (15, 28).
Решение: Раскладываем 15 и 28 на простые множители:
Числа 15 и 28 являются взаимно простыми, так как их наибольший общий делитель — единица.
НОД (15, 28) = 1.
Алгоритм Евклида
Второй способ (иначе его называют способом Евклида) заключается в нахождении НОД путём последовательного деления.
Сначала мы рассмотрим этот способ в применении только к двум данным числам, а затем разберёмся в том, как его применять к трём и более числам.
Если большее из двух данных чисел делится на меньшее, то число, которое меньше и будет их наибольшим общим делителем.
Пример 1. Возьмём два числа 27 и 9. Так как 27 делится на 9 и 9 делится на 9, значит, 9 является общим делителем чисел 27 и 9. Этот делитель является в тоже время и наибольшим, потому что 9 не может делиться ни на какое число, большее 9. Следовательно:
НОД (27, 9) = 9.
В остальных случаях, чтобы найти наибольший общий делитель двух чисел используется следующий порядок действий:
- Из двух данных чисел большее число делят на меньшее.
- Затем, меньшее число делят на остаток, получившийся от деления большего числа на меньшее.
- Далее, первый остаток делят на второй остаток, который получился от деления меньшего числа на первый остаток.
- Второй остаток делят на третий, который получился от деления первого остатка на второй и т. д.
- Таким образом деление продолжается до тех пор, пока в остатке не получится нуль. Последний делитель как раз и будет наибольшим общим делителем.
Пример 2. Найдём наибольший общий делитель чисел 140 и 96:
1) 140 : 96 = 1 (остаток 44)
2) 96 : 44 = 2 (остаток 
3) 44 : 8 = 5 (остаток 4)
4) 8 : 4 = 2
Последний делитель равен 4 — это значит:
НОД (140, 96) = 4.
Последовательное деление так же можно записывать столбиком:
Чтобы найти наибольший общий делитель трёх и более данных чисел, используем следующий порядок действий:
- Сперва находим наибольший общий делитель любых двух чисел из нескольких данных.
- Затем находим НОД найденного делителя и какого-нибудь третьего данного числа.
- Затем находим НОД последнего найденного делителя и четвёртого данного числа и так далее.
Пример 3. Найдём наибольший общий делитель чисел 140, 96 и 48. НОД чисел 140 и 96 мы уже нашли в предыдущем примере (это число 4). Осталось найти наибольший общий делитель числа 4 и третьего данного числа — 48:
48 : 4 = 12
48 делится на 4 без остатка. Таким образом:
НОД (140, 96, 48) = 4.