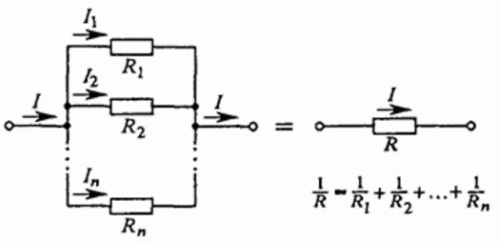
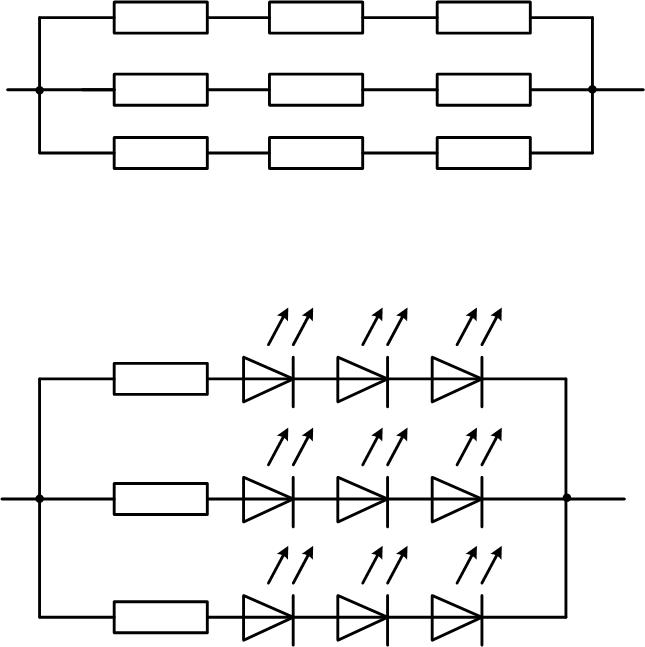
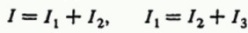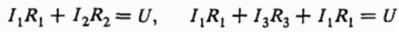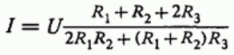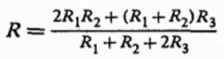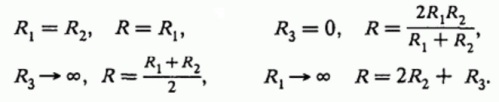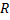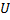Смешанное соединение резисторов. Расчет смешанного соединения
Здравствуйте, уважаемые читатели сайта sesaga.ru. Смешанное соединение резисторов представляет собой сложную электрическую цепь, в которой часть резисторов соединена последовательно, а часть параллельно.
В радиолюбительской практике такое включение резисторов встретить трудно, так как нет смысла подбирать сопротивление таким сложным способом. Достаточно соединить два, ну максимум три резистора последовательно или параллельно, чтобы подобрать нужный номинал.
Смешанное соединение встречается в основном в учебниках физики или электротехники в виде задач. Мне вспоминается такая задачка из школьной программы, но тогда она мне показалась сложной и правильно решить ее не получилось.
И вот, исходя из полученного опыта, хочу рассказать Вам, как вычислить общее сопротивление смешанного соединения резисторов. Вдруг кому-нибудь в жизни да и пригодится.
Расчет смешанного соединения резисторов.
Расчет начинают от дальнего участка цепи по отношению к источнику питания.
Определяют участок с параллельным или последовательным соединением двух резисторов и высчитывают их общее сопротивление Rобщ. Затем полученное сопротивление складывают с рядом стоящим резистором и т.д.
Суть данного метода заключается в уменьшении количества элементов в цепи с целью упрощения схемы и, соответственно, упрощению расчета общего сопротивления.
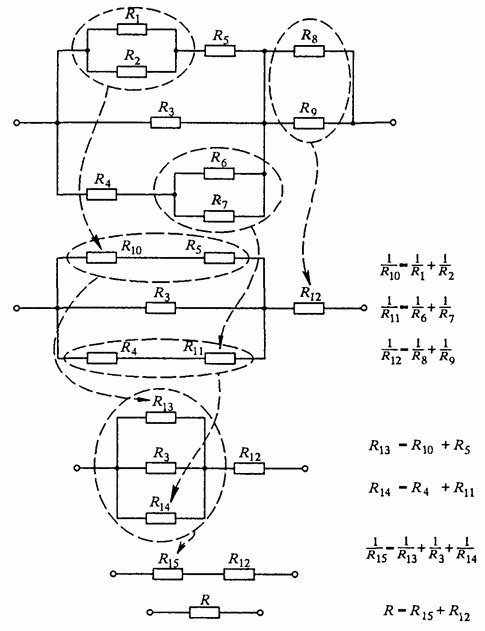
Разберем схему смешанного соединения из семи резисторов:
Самым дальним участком схемы оказались резисторы R6 и R7, соединенные параллельно:
Вычисляем их общее сопротивление используя формулу параллельного соединения:
Теперь если сравнить первоначальную схему с получившейся, то здесь мы видим, что она уменьшилась на один элемент и вместо двух резисторов R6 и R7 остался один R6 с суммарным сопротивлением равным 30, 709 кОм.
Продолжим расчет и следующим дальним участком схемы оказались резисторы R5 и R6, соединенные последовательно:
Вычисляем их общее сопротивление используя формулу последовательного соединения. Сопротивление резистора R5 составляет 27 Ом, а R6 = 30,709 кОм, поэтому для удобства расчета килоомы переводим в Омы (1 кОм = 1000 Ом):
Схема уменьшилась еще на один элемент и приняла вид:
Теперь дальним участком оказались резисторы R4 и R5 соединенные параллельно:
Вычисляем их общее сопротивление:
Первоначальная схема опять изменилась и теперь состоит всего из четырех резисторов соединенных последовательно. Таким образом мы максимально упростили схему и привели ее к удобному расчету.
Теперь все просто. Складываем сопротивления оставшихся четырех резисторов, используя формулу последовательного соединения, и получаем общее сопротивление всей цепи:
Вот в принципе и все, что хотел сказать о смешанном соединении резисторов и расчете смешанного соединения.
Удачи!
Источник
Ток и напряжение при параллельном, последовательном и смешанном соединении проводников

Если взглянуть на электрическую цепь, включающую в себя несколько разных проводников, и рассмотреть на ней пару точек (вход и выход), то в принципе остальная часть цепи может быть рассмотрена как одиночный резистор (по ее эквивалентному сопротивлению).
При таком подходе говорят, что если ток I – это ток в цепи, а напряжение U – напряжение на выводах, то есть разность электрических потенциалов между точками «входа» и «выхода», то тогда отношение U/I можно рассмотреть как величину эквивалентного сопротивления R цепи целиком.
Если закон Ома выполняется, то эквивалентное сопротивление можно вычислить довольно легко.
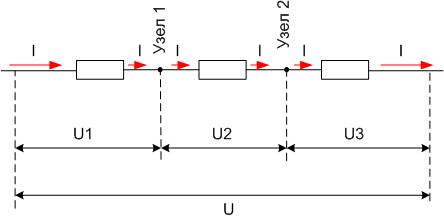
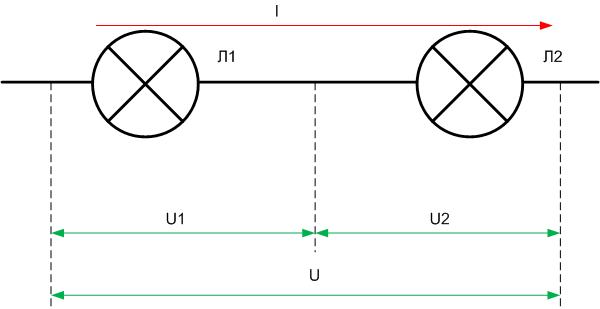
Ток и напряжение при последовательном соединении проводников
В простейшем случае, когда два и более проводников объединены друг с другом в последовательную цепь, ток в каждом проводнике окажется одним и тем же, а напряжение между «выходом» и «входом», то есть на выводах всей цепи, будет равным сумме напряжений на составляющих цепь резисторах. И поскольку закон Ома справедлив для любого из резисторов, то можно записать:
Итак, для последовательного соединения проводников характерны следующие закономерности:
Для нахождения общего сопротивления цепи, сопротивления составляющих цепь проводников складываются;
Ток через цепь равен току через любой из проводников, образующих цепь;
Напряжение на выводах цепи равно сумме напряжений на каждом из проводников, образующих цепь.
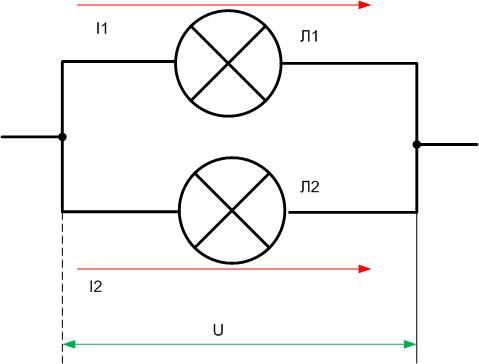
Ток и напряжение при параллельном соединении проводников
При параллельном соединении нескольких проводников друг с другом, напряжение на выводах такой цепи — это напряжение на каждом из проводников, составляющих цепь.
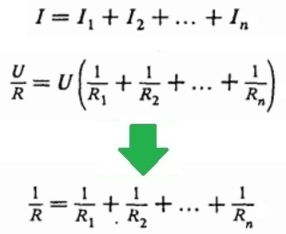
Напряжения на всех проводниках равны между собой и равны напряжению приложенному (U). Ток через всю цепь — на «входе» и «выходе» — равен сумме токов в каждой из ветвей цепи, параллельно объединенных и составляющих данную цепь. Зная, что I = U/R, получаем, что:
Итак, для параллельного соединения проводников характерны следующие закономерности:
Для нахождения общего сопротивления цепи — складываются обратные величины сопротивлений составляющих цепь проводников;
Ток через цепь равен сумме токов через каждый из проводников, образующих цепь;
Напряжение на выводах цепи равно напряжению на любом из проводников, образующих цепь.
Эквивалентные схемы простых и сложных (комбинированных) цепей
В большинстве случаев схемы цепей, являясь комбинированным соединением проводников, поддаются пошаговому упрощению.
Группы соединенных последовательно и параллельно частей цепи, заменяют эквивалентными сопротивлениями по приведенному выше принципу, шаг за шагом вычисляя эквивалентные сопротивления кусочков, затем приводя их к одному эквивалентному значению сопротивления всей цепи.
И если сначала схема выглядит довольно запутанной, то будучи упрощенной шаг за шагом, она может быть разбита на меньшие цепочки из последовательно и параллельно соединенных проводников, и так в конце концов сильно упрощена.
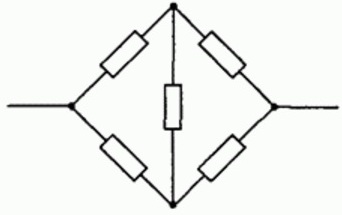
Между тем, не все схемы подаются упрощению таким простым путем. Простая с виду схема «моста» из проводников не может быть исследована таким образом. Здесь нужно применять уже несколько правил:
Для каждого резистора выполняется закон Ома;
В любом узле, то есть в точке схождения двух и более токов, алгебраическая сумма токов равна нулю: сумма токов втекающих в узел, равна сумме токов вытекающих из узла (первое правило Кирхгофа);
Сумма напряжений на участках цепи при обходе по любому пути от «входа» до «выхода» равна приложенному к цепи напряжению (второе правило Кирхгофа).
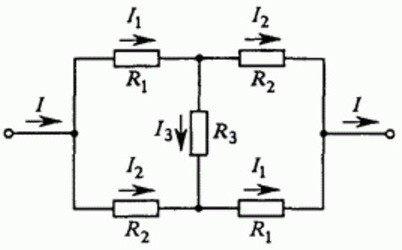
Мостовое соединение проводников
Дабы рассмотреть пример использования приведенных выше правил, рассчитаем цепь, собранную из проводников, объединенных в схему моста. Чтобы вычисления получились не слишком сложными, примем, что некоторые из сопротивлений проводников равны между собой.
Обозначим направления токов I, I1, I2, I3 на пути от «входа» в цепь — к «выходу» из цепи. Видно, что схема симметрична, поэтому токи через одинаковые резисторы одинаковы, поэтому обозначим их одинаковыми символами. В самом деле, если поменять у цепи местами «вход» и «выход», то схема будет неотличима от исходной.
Для каждого узла можно записать уравнения токов, исходя из того, что сумма токов втекающих в узел равна сумме токов вытекающих из узла (закон сохранения электрического заряда), получится два уравнения:
Следующим шагом записывают уравнения сумм напряжений для отдельных участков цепи при обходе цепи от входя к выходу различными путями. Так как схема является в данном примере симметричной, то достаточно двух уравнений:
В процессе решения системы линейных уравнений, получается формула для нахождения величины тока I между зажимами «входным» и «выходным», исходя из заданного приложенного к цепи напряжения U и сопротивлений проводников:
А для общего эквивалентного сопротивления цепи, исходя из того, что R = U/I, следует формула:
Можно даже проверить правильность решения, например приведя к предельным и к частным случаям величины сопротивлений:
Теперь вы знаете, как находить ток и напряжение при параллельном, последовательном, смешанном, и даже при мостовом соединении проводников, применяя закон Ома и правила Кирхгофа. Эти принципы очень просты, и даже самая сложная электрическая цепь с их помощью в конце концов приводится к элементарному виду путем нескольких несложных математических операций.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Источник
Решение задач на смешанное соединение проводников.
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
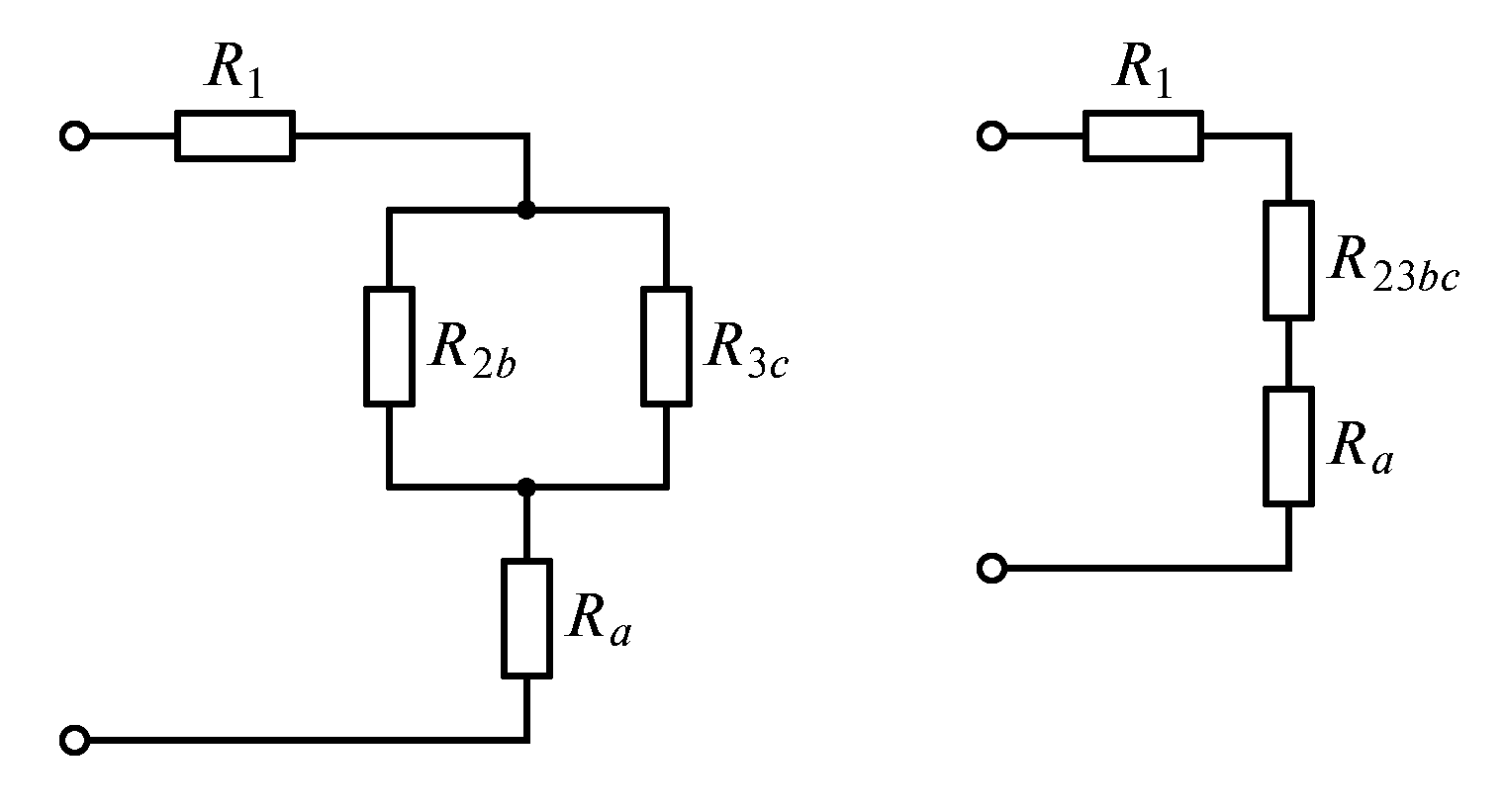
При решении задач на смешанное соединение проводников обычно составляют так называемые эквивалентные схемы, выделяя участки с последовательным и параллельным соединением.
Сопротивление R 1,2 заменило выделенный участок цепи, в котором два проводника соединены параллельно.
Тогда мы можем найти сопротивление этого участка с параллельным соединением проводников:
А теперь видно, что проводники R 1,2 и R 3 соединены последовательно. Общее сопротивление равно R = R 1,2 + R 3 = 4 + 2 = 6 .
В данном случае нужно развернуть схему, двигаясь от точки к точке. Видно, что в точке Б схема разветвляется, а в точке В ветви соединяются. Таким образом, эквивалентные схемы будут иметь вид:
R 2 , R 3 и R 4 соединены последовательно. Поэтому R 2,3,4 = R 2 + R 3 + R 4 = 1 + 10 + 1 = 12
R 2,3,4 и R 5 соединены параллельно. Поэтому
И в последней схеме проводники соединены последовательно. R = R 2-5 + R 1 + R 6 = 1 + 4,8 + 1 = 6,8.
Пример 3. Найти распределение токов и напряжений в цепи.
Так как известны сила тока и сопротивление на первом участке, то можно найти напряжение на нем: U 1 = I 1 R 1 = 1 ∙ 10 = 10 B .
Первый и второй проводники соединены параллельно. Значит, напряжение на них одинаково, т.е. U 1 = U 2 = 10 В. Так как первый и второй проводники имеют одинаковое сопротивление, то сила тока на них одинакова: I 2 = 1 А. При параллельном соединении I 1,2 = I 1 + I 2 = 2 А.
Найдем общее сопротивление участка 3-4-5:
R 3,4,5 = 3 Ом. Тогда можно найти напряжение на 3-4-5, при параллельном соединении оно одинаково на всех участках. U 3,4,5 = I 3,4,5 ∙ R 3,4,5 = 2 ∙ 3 = 6 В.
U 3 = U 4 = U 5 = 6 В. Зная напряжение на каждом из участков и сопротивление, можно найти силу тока на каждом участке.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс профессиональной переподготовки
Физика: теория и методика преподавания в образовательной организации
Курс повышения квалификации
Современные педтехнологии в деятельности учителя
Ищем педагогов в команду «Инфоурок»
Вам будут интересны эти курсы:
Оставьте свой комментарий
Путин поручил не считать выплаты за классное руководство в средней зарплате
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
В России планируют создавать пространства для подростков
Апробацию новых учебников по ОБЖ завершат к середине 2022 года
Утверждено стратегическое направление цифровой трансформации образования
ВПР для школьников в 2022 году пройдут весной
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Источник
Смешанное соединение проводников. Расчёт электрических цепей
Повторение. Факты про последовательное и параллельное соединение проводников.
1. При последовательном соединении проводников общее сопротивление участка равно сумме сопротивлений проводников:
2. При последовательном соединении проводников силы тока в каждом из проводников равны и равны общей силе тока на участке цепи:
3. При последовательном соединении проводников сумма напряжений равна общему напряжению на участке цепи:
4. При параллельном соединении проводников общая проводимость участка равна сумме проводимостей проводников:
5. При параллельном соединении проводников сумма сил токов равна общей силе тока на участке цепи:
6. При параллельном соединении проводников напряжения в каждом из проводников равны и равны общему напряжению на участке цепи:
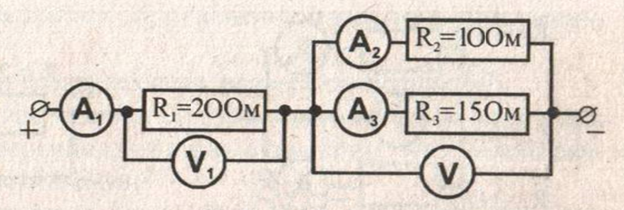
Задача 1
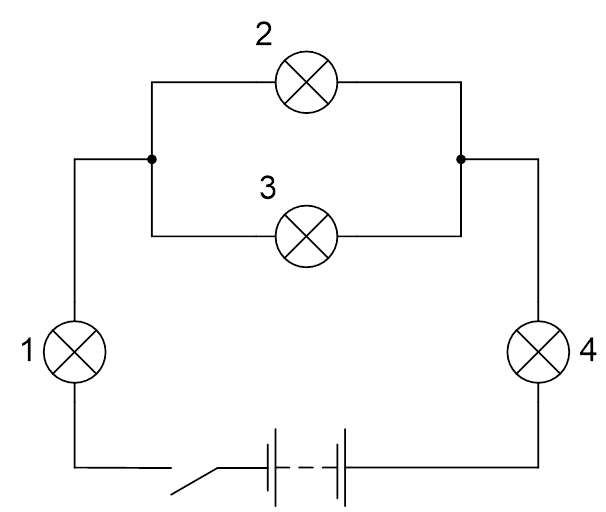
Четыре одинаковые лампы подключены к источнику постоянного напряжения (см. Рис. 1). Определите силу тока в каждой лампе, если напряжение на источнике составляет 30 В.
Дано: ;
Найти: ,
,
,
Решение
Рис. 1. Иллюстрация к задаче
На рисунке 1 изображена электрическая цепь со смешанным соединением проводников: лампы 2 и 3 соединены параллельно, а лампы 2 и 4 соединены последовательно с участком цепи, состоящим из ламп 2 и 3.
Проводимость участка цепи, состоящего из ламп 2 и 3, равна:
Следовательно, сопротивление этого участка равно:
Так как лампы 1 и 4 соединены последовательно с участком цепи, состоящим из ламп 2 и 3, то общее сопротивление ламп будет равно:
Согласно закону Ома, сила тока всей цепи равна:
Так как при последовательном соединении проводников силы тока в каждом из проводников равны и равны общей силе тока на участке цепи, то:
Необходимо найти силу тока на лампах 2 и 3. Для этого вычислим напряжение на участке цепи, который состоит из ламп 2 и 3:
Так как лампы 2 и 3 соединены параллельно, то напряжения на этих лампах равны:
Отсюда сила тока в каждой лампе равна:
Ответ: ;
Задача 2
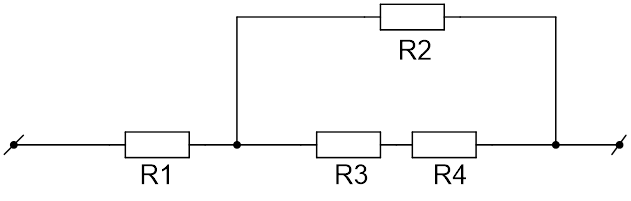
Участок цепи, который состоит из четырёх резисторов, подключён к источнику с напряжением 40 В (см. Рис. 2). Вычислите силу тока в резисторах 1 и 2, напряжение на резисторе 3. Сопротивление первого резистора равно 2,5 Ом, второго и третьего – по 10 Ом, четвёртого – 20 Ом.
Дано: ;
;
;
Найти: ,
,
Решение
Рис. 2. Иллюстрация к задаче
Через резистор течёт такой же ток, как и через весь участок (
), следовательно, согласно закону Ома:
То есть для нахождения нужно вычислить сопротивление (R) всего участка цепи, который состоит из двух последовательно подключённых частей, одна часть с резистором
, другая часть с резисторами
:
Резистор соединён параллельно резисторам
и
, следовательно:
Резисторы и
соединены последовательно, поэтому:
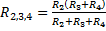
Следовательно, сопротивление всей цепи равно:
Подставим данное значение в формулу для нахождения тока в резисторе :
Так как при параллельном соединении проводников напряжения в каждом из проводников равны и равны общему напряжению на участке цепи, то:
Отсюда:
При последовательном соединении силы тока одинаковы, поэтому:
Получили систему уравнений:
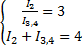
Решив эту систему получим, что:
Так как и
соединены последовательно:
Напряжение на резисторе равно:
Ответ: ;
;
Задача 3
Найдите полное сопротивление цепи (см. Рис. 3), если сопротивление резисторов ,
,
. Найдите силу тока, идущего через каждый резистор, если к цепи приложено напряжение 36 В.
Дано: ;
;
;
Найти: ,
, ,
,
,
,
;
Решение
Рис. 3. Иллюстрация к задаче
Резисторы ,
,
соединены последовательно, поэтому сопротивление на этом участке равно:
Резистор подключён параллельно участку с резисторами
,
,
, поэтому сопротивление на участке с резисторами
,
,
,
равно:
Резисторы и
соединены с участком цепи с резисторами
,
,
,
последовательно, то есть общее сопротивление цепи равно:
Через резистор и
(
) неразветвлённой цепи течёт весь ток цепи, поэтому:
По закону Ома этот ток равен:
Общее напряжение цепи будет состоять из напряжений , так как
,
,
соединены последовательно (
, потому что
и
параллельны):
Согласно закону Ома:
Резисторы ,
,
соединены последовательно, следовательно:
Ответ: ;
;
;
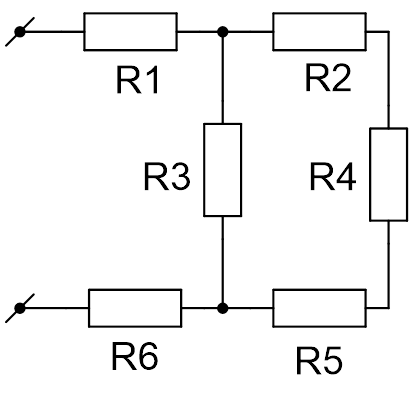
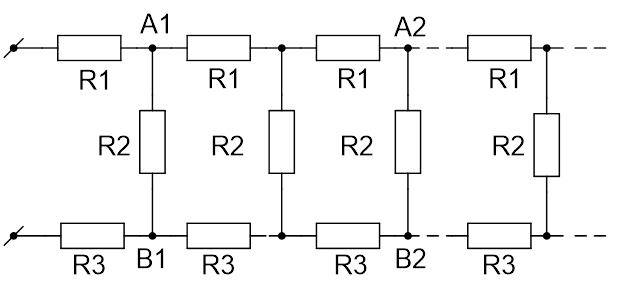
Разветвление: Задача на бесконечную электрическую цепь
Найдите сопротивление R бесконечной цепи, показанной на рисунке 4.
Рис. 4. Иллюстрация к задаче
Решение
Поскольку рассматриваемая в задаче цепь бесконечна, удаление одной «ячейки», состоящей из резисторов и
, не влияет на её сопротивление. Следовательно, вся цепь, находящаяся правее звена
, тоже имеет сопротивление R. Это позволяет нарисовать эквивалентную схему цепи (см. Рис. 5) и записать для неё уравнение.
Рис. 5. Иллюстрация к задаче
Получили квадратное уравнение относительно R. Решая это уравнение и отбрасывая отрицательный корень (отрицательного сопротивления не существует), получаем формулу для общего сопротивления цепи:
Проанализировав данную формулу, можно заметить, что если , то общее сопротивление цепи
. То есть резистор с малым сопротивление
практически закоротит всю последующую бесконечную цепь.
Ответ:
Итоги
Мы рассмотрели различные задачи на смешанное сопротивление проводников, а также на расчёт электрических цепей.
Разветвление: Задача из ЕГЭ
Сопротивление каждого резистора в цепи (см. Рис. 6) равно 100 Ом. Участок подключён к источнику постоянного напряжения выводами AиB. Напряжение на резисторе равно 12 В. Найти напряжение между выводами схемы на участке A–B(варианты ответа: а) 12 В; б) 18 В; в) 24 В; г) 36 В.
Дано: ;
Найти:
Решение
Рис. 6. Иллюстрация к задаче
Резисторы расположены последовательно, значит, силы тока на этих резисторах равны:
Так как, по условию, 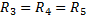
Следовательно, общее напряжения на участке, состоящем из резисторов , будет равно:
Так как участок с резисторами соединён с участком с резисторами
параллельно, то напряжения на этих участках равны между собой и равны общему напряжению на участке A–B:
Ответ: г) 36 В
Данную задачу, как видим, можно решить, не зная значений сопротивления, а зная только то, что они равны. Также эту задачу можно решить, зная значение сопротивлений , даже если они не равны.
Вопросы к конспектам
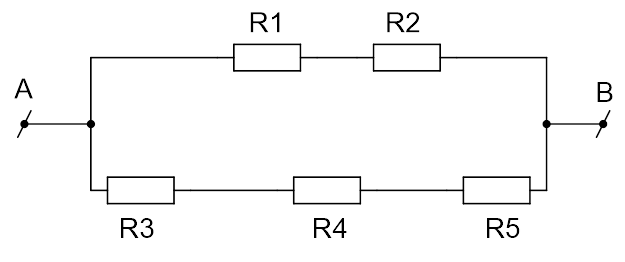
Участок электрической цепи состоит из трех сопротивлений: ;
;
(см. Рис. 7). Определите показания вольтметров
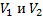
, если амперметр
показывает силу тока 2 А.
Рис. 7. Иллюстрация к задаче
Как нужно соединить четыре резистора, сопротивления которых 0,5 Ом, 2 ОМ, 3,5 Ом и 4 Ом, чтобы их общее сопротивление было 1 Ом?
Содержание
- Виды соединений электрических проводников
- Последовательное
- Параллельное
- Смешанное
- Как вычисляются напряжение, сила тока и электрическая мощность в зависимости от подключения
- При параллельном соединении
- При последовательном соединении
- Примеры расчетов
- Для резисторов
- Для лампочек
- Для светодиодов
При разработке электрических цепей применяется последовательное и параллельное соединение проводников. Умение анализировать (как количественно, так и качественно) и рассчитывать такие схемы является базовым принципом знаний электротехники.
Виды соединений электрических проводников
Основными схемами подключения являются параллельное и последовательное соединение. Также существуют комбинации из этих двух включений.
Последовательное
При последовательном (в зарубежной терминологии serial) соединении выводы элементов соединяются так, чтобы получилась цепочка. Один вывод устройства подключается к одному соседнему звену, а второй – к другому, с противоположной стороны.
Параллельное
При параллельном (parallel) включении одноименные выводы элементов цепи соединяются между собой. Практический пример – лампы в многорожковой люстре или повторители светового сигнала поворота в автомобиле.
Смешанное
В одной цепи схема подключения может быть комбинированной – serial+parallel. Часть элементов подключена в параллель, образуя звенья. Эти звенья могут быть включены в последовательную цепочку. Или наоборот – последовательные цепи включаются параллельно.
Как вычисляются напряжение, сила тока и электрическая мощность в зависимости от подключения
Параметры электрической цепи рассчитываются по-разному в зависимости от типа подключения. Чтобы разобраться, какова будет сила тока, проходящего через каждое сопротивление, можно воспользоваться первым законом Кирхгофа. Одна из его формулировок гласит, что алгебраическая сумма токов, втекающих в узел, равна сумме токов, вытекающих из узла. Остальные зависимости будут вытекать из данного рассуждения.
При параллельном соединении
Если рассмотреть параллельное соединение, например, трех резисторов, то можно отметить, что втекающий ток I в узле 1 распадается на три ветви I1, I2, I3, причем Кирхгоф утверждает, что их сумма I1+ I2+ I3 = I. В узле 2 все токи стекаются в один ток, и снова I= I1+ I2+ I3.
Очевидно, что напряжение на каждом резисторе одинаково и равно U, следовательно, по закону Ома:
- I1=U/R1;
- I2=U/R2;
- I3=U/R3;
- I=U/Rобщ.
Отсюда U/Rобщ= U/R1+ U/R2+ U/R3, после сокращения обеих частей на U получается формула для нахождения общего сопротивления при параллельном соединении резисторов:
1/Rобщ= 1/R1+ 1/R2+ 1/R3.
Отсюда следует, что при параллельном соединении общее сопротивление будет меньше наименьшего сопротивления в наборе. При соединении двух резисторов формула принимает вид Rобщ=R1* R2/(R1+ R2).
Также из равенства I=U/R1+U/R2+U/R3 следует, что токи через параллельно включенные резисторы распределяются обратно пропорционально значениям их сопротивлений – чем выше сопротивление, тем ниже ток, и наоборот. Если все резисторы имеют одинаковый номинал, то ток, текущий через каждый из них, находится делением общего тока на количество сопротивлений. Если элементов в сборке три, то через каждый течет треть общего тока, а если параллельно включены n одинаковых резисторов, то через каждый протекает I/n.
Так как электрическая мощность равна P=U*I, а напряжение на каждом резисторе равно, то мощность, выделяемая на каждом элементе, распределяется пропорционально току и обратно пропорционально сопротивлению резистора. Если все элементы одинаковы, то и мощность на них будет рассеиваться одинаковая.
Для наглядности видео.
При последовательном соединении
Если рассматривать последовательную цепь из трех элементов, можно заметить, что ток, втекающий в узел 1 будет равен вытекающему. В узле 2 выполняется то же самое соотношение и так до бесконечности.
Отсюда сила тока в последовательном соединении будет одинакова для любого элемента и равна I. Напряжение, приложенное к цепи и равное I*R, распределится между резисторами:
U=U1+U2+U3=I*R1+I*R2+I*R3 = I* Rобщ
После сокращения на I можно найти общее сопротивление цепи. Оно равно сумме составляющих, и общее значение сопротивления будет выше сопротивления любого элемента:
Rобщ=R1+R2+R3
Очевидно, что падение напряжения в последовательной цепи прямо пропорционально сопротивлению каждого элемента – чем выше сопротивление, тем выше на нем напряжение. Точно так же, эти соотношения выполняются для цепи из n элементов.
Примеры расчетов
В качестве практических примеров можно рассмотреть несколько вариантов расчетов параметров цепи в разных схемах соединения.
Для резисторов
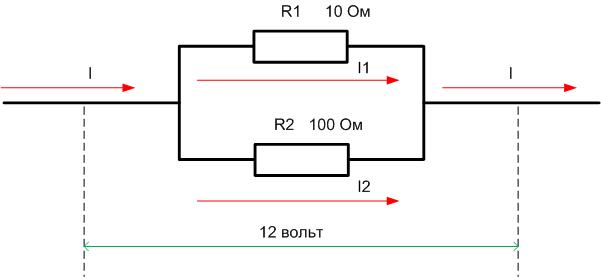
Самым простым примером расчета будет цепь из двух сопротивлений – 10 Ом и 100 Ом, соединенных в цепочку. К цепи приложено 12 вольт.
Сначала надо найти Rобщ, оно равно сумме R1 и R2. Rобщ=100+10=110 Ом. Отсюда ток в цепи I=U/R=12/110=0,109 ампер. Падение на каждом элементе можно вычислить исходя из равенств U1=I*R1 и U2=I*R2. Отсюда U1=1,1 В, а U2=10,9 В. Очевидно, что U1/U2=R1/R2. На первом элементе будет рассеиваться мощность P1=U1*I=1,1*0,109=0,12 ватт (для практики подойдет стандартный компонент на 0,125 ватт), а на втором – P2=U2*I=10,9*0,109=1,19 ватт (для практической реализации понадобится двухваттник).
Если соединить эти же два резистора параллельно и подать то же самое напряжение, то параметры распределятся по-другому.
Сначала надо определить Rобщ=R1*R2/(R1+R2)=110*10/(110+10)=1100/120=9,17 Ом (меньше наименьшего значения в 10 Ом). Общий ток составит I=U/Rобщ=12/9,17=1,31 ампер. Через первый элемент потечет I1=U/R1=12/10=1,2 ампер, через второй I2=U/R2=12/100=0,12. Очевидно, что I1+I2=I (с учетом погрешностей округления). Мощности потребуются такие:
- P1=I1*U=1,2*12=14,2 ватт;
- P2=I2*U=0,12*12=1,42 ватт.
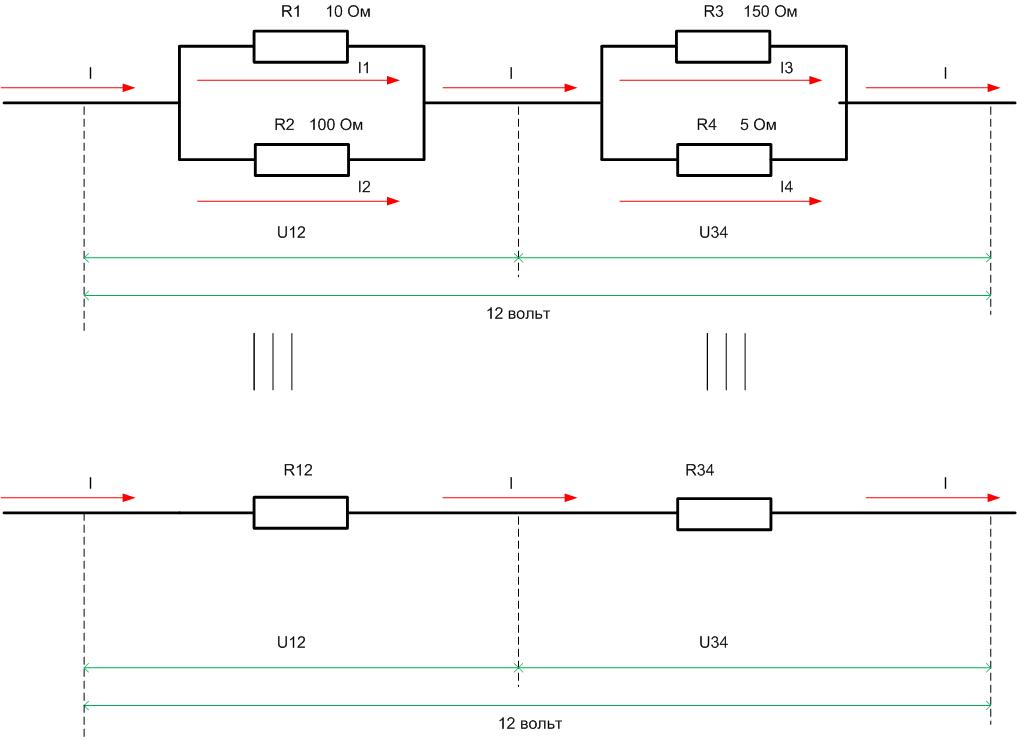
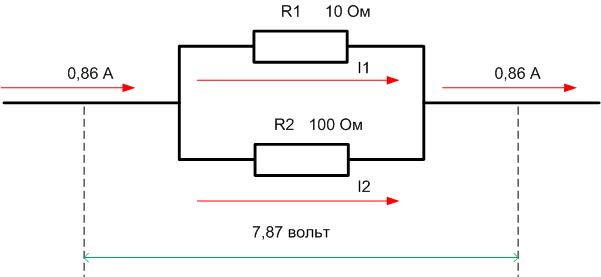
Если имеется смешанное соединение элементов, надо сначала преобразовать схему к однотипному виду – параллельному или последовательному. Пусть имеется схема следующего вида.
В данном случае удобно заменить параллельную сборку R1 и R2 на резистор с эквивалентным сопротивлением R12, а R3 и R4 – на R34. Сначала находится R12=R1*R2/(R1+R2)=9,17 Ом. Тем же способом рассчитывается R34=150*5/(150+5)=4,8 Ом. Тогда общее сопротивление эквивалентной цепи будет равно R12+R34=9,17+4,8=13,97 Ом.
Отсюда I=U/R=12/13,97=0,86 ампер. На “гирлянде» R1R2 падает U12=I*R12=0,86*9,17=7,87 вольт, а на R3R4 падение составит U34= I*R34=0,86*4,8=4,13 вольт. Дальше надо вернуться к исходной схеме и рассмотреть отдельно участок схемы R1R2 с найденными параметрами.
Отсюда I1=U/R1=7,87/10=0,787 ампер, I2=U/R2=7,87/100=0,0787 ампер. По мощностям – P1=U*I1=7,87*0,787=6,2 ватт, P2= U*I2=7,87*0,0787=0,62 ватт.
Аналогично рассчитывается и участок, содержащий элементы R3R4.
Читайте также
Последовательное и параллельное подключение аккумуляторных батарей
Для лампочек
Точно такими же способами можно рассчитать параметры цепи, состоящей из двух или более лампочек накаливания – на практике с такой ситуацией можно столкнуться чаще. Но есть две проблемы. Первая из них – на лампочках и в технических данных на них не указывается сопротивление нити. Его придется пересчитывать исходя из номинального напряжения и мощности. Так как P=U*I, а I=U*R, то P=U2/R, а R=U2/P. Так, для 10-ваттной лампочки на 12 вольт сопротивление нити будет равно 122/10=144/10=14,4 Ом. Можно рассчитать характеристики цепи для двух последовательно и параллельно соединенных лампочек.
В первом случае ток, текущий через каждую лампу будет общим, и равным I=U/Rобщ=12/(14,4+14,4)=12/28,8=0,42 А. На каждой лампе упадет U/2=6 вольт. А электрическая мощность каждого элемента составит 0,42*6=2,5 Вт, что составляет ¼ от номинала лампочки. Такое уменьшение произошло из-за двукратного снижения тока и двукратного снижения напряжения. Естественно, лампочки будут светиться далеко не в полный накал. Чтобы довести яркость свечения до нормальной, придется вдвое увеличивать напряжение, что одновременно вдвое увеличит ток.
Если лампочки соединить в параллель, то на каждой из них упадет номинальный уровень в 12 вольт. Через каждый элемент потечет I=U/R= 12/14,4=0,83 А, а мощность на каждой лампочке будет равна P=U*I=12*0,83=10 ватт, то есть, номинал. И каждая нить будет светить в полный накал. Но вся цепь будет потреблять 20 ватт и через нее потечет 0,83*2=1,66 А, что вдвое больше значения для одной лампы.
Есть и вторая проблема. В общем случае сопротивление зависит от тока и приложенного напряжения, но у ламп накаливания эта зависимость выражена ярко. Нить в холодном состоянии имеет низкое сопротивление, а номинального значения достигает при прогреве в номинальном режиме. Поэтому данные выше расчеты верны лишь для штатного напряжения 12 вольт. В других условиях характеристики лампы будут другими, и, по большому счету, расчет для параллельного случая неточен – сопротивление нити будет меньше 14,4 Ом. Зато это свойство позволяет применять лампу в качестве стабилизатора тока – при увеличении его значения нить нагреется, сопротивление вырастет, ток упадет примерно до прежнего уровня. При его уменьшении произойдет обратный процесс со снижением уровня накала нити лампочки.
Рекомендуем посмотреть видео урок «Просто физика»
Для светодиодов
Еще сложнее ситуация со светодиодами. В отличие от лампочек они стабилизируют напряжение, причем не всегда, а только после открывания. Иными словами, сначала при росте напряжения на последовательной цепочке (LED+резистор), она ведет себя согласно закону Ома. После того, как светодиод открылся (и начал светиться), увеличение падения на нем прекратилось, и рост напряжения на цепочке ведет к росту тока и увеличению U на резисторе. На полупроводниковом приборе напряжение остается стабильным (в зависимости от технологии изготовления – от 1,2 до 3 вольт или выше), хотя ток через него также растет.
По мере освоения приемов расчета можно научиться анализировать все более сложные схемы, содержащие как параллельное, так и последовательное подключение элементов. Потом можно переходить к следующему этапу – анализ и расчет устройств, содержащих реактивные (а впоследствии – и нелинейные) компоненты.
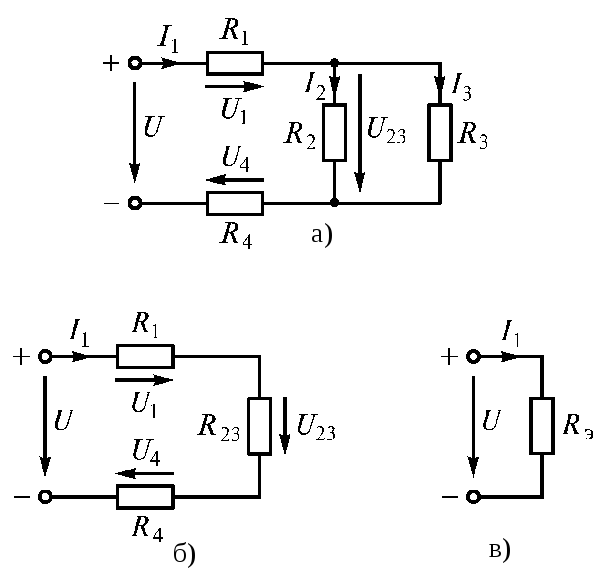
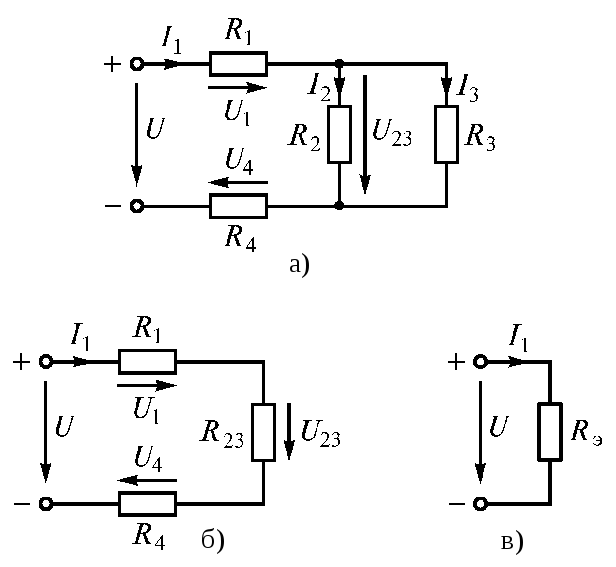
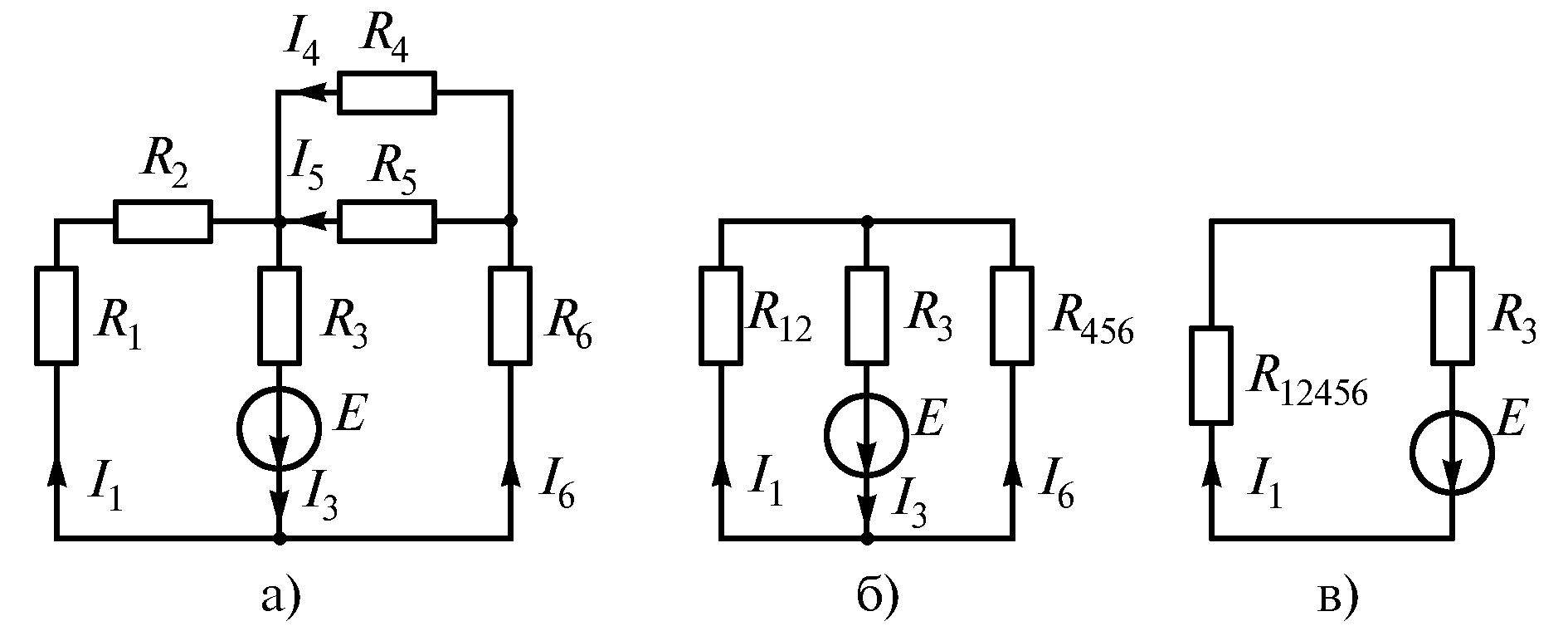
Смешаннымсоединением называют
сочетание последовательного и
параллельного соединений резисторов.
Большое разнообразие этих соединений
не позволяет вывести общую формулу для
определения эквивалентного сопротивления
цепи. Поэтому в каждом конкретном случае,
используя методы расчета при
последовательном и параллельном
соединениях, можно рассчитать
эквивалентное сопротивление при
смешанном соединении. Поясним это на
конкретном примере расчета электрической
цепи (рис. 1.20 а).
Электрическую цепь постепенно упрощают
и приводят к простейшему виду (рис. 1.20
б, в)
;
;
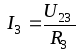
.
Рис. 1.20
Проверка: 1)2)
.
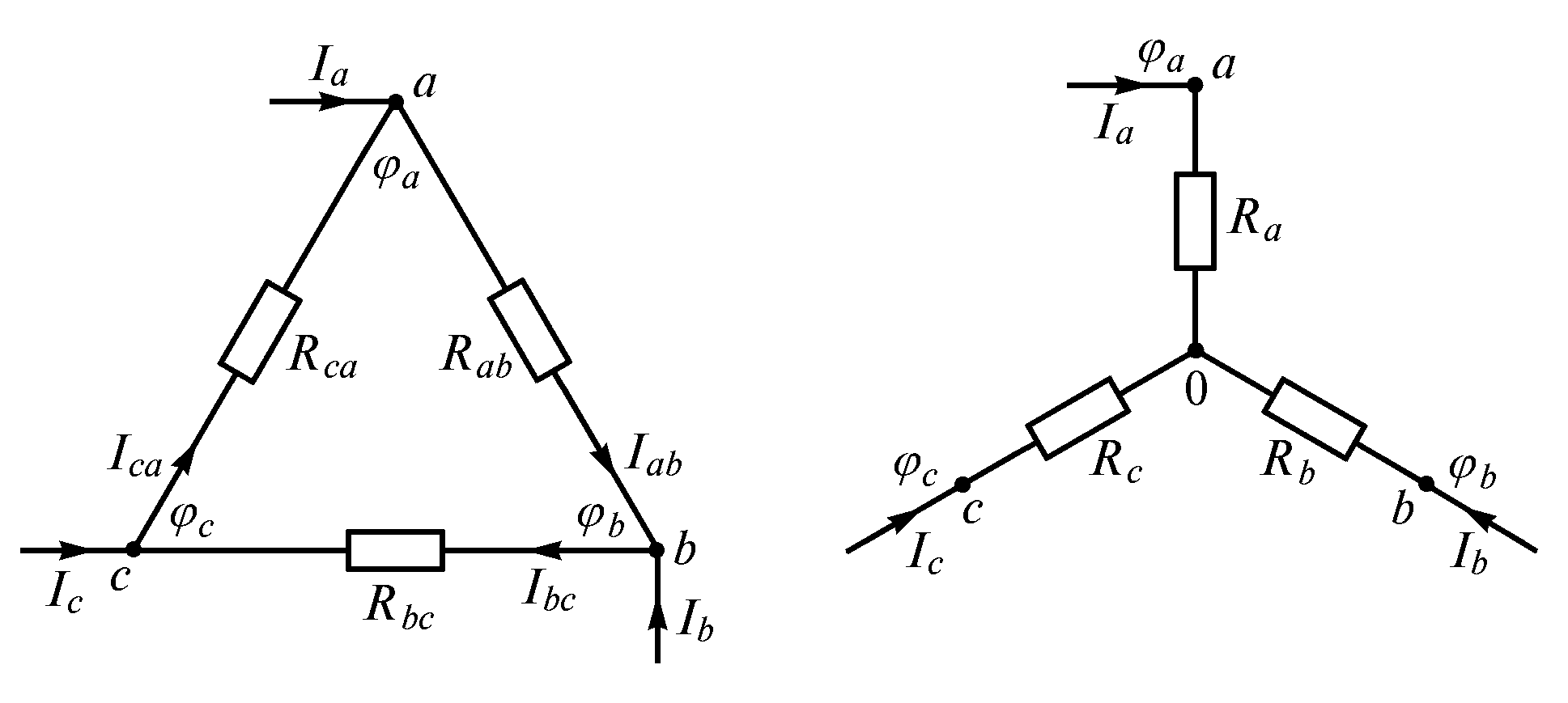
1.8.4. Метод преобразований треугольника резисторов в эквивалентную звезду и наоборот
Рассмотрим
две электрические цепи (рис. 1.21). Одна
из них имеет вид треугольника, другая
– трехлучевой звезды. В дальнейшем
такие соединения будем называть
соответственно соединением в треугольник
и соединением звездой.
Рис. 1.21
Соединения такого вида очень распространены
в трехфазных цепях, в которых часто
возникает необходимость перехода от
одного вида соединения к другому
(эквивалентному). Эквивалентность
треугольника и звезды резисторов
заключается в том, что их замена не
изменяет потенциалов узловых точек
(φа,
φb
иφс),
являющихся вершинами треугольника и
эквивалентной звезды. Не изменяются
также токи, напряжения и мощности в
остальной части схемы, не затронутой
преобразованием.
Формулы пересчета без вывода сопротивлений
ветвей треугольника
,
,
в эквивалентную звезду
,
,
имеют вид
(1.39)
При переходе от звезды к треугольнику
можно воспользоваться следующими
формулами
(1.40)
Если сопротивления всех ветвей цепи
по схеме треугольник одинаковы, т.е.
,
сопротивления эквивалентной звезды
будут также одинаковые:,
причем
.
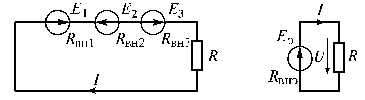
1.8.5. Последовательное соединение источников энергии
В практике последовательное и согласное
включение источников применяют для
увеличения напряжения. Рассмотрим схему
с двумя согласно и одним встречно
включенными источниками (рис. 1.22).
Рис. 1.22
По второму закону Кирхгофа запишем
.
(1.41)
Отсюда
,
(1.42)
где
.
Напряжения на зажимах источников и
приемника
.
При последовательном соединении
источников с одинаковыми параметрами
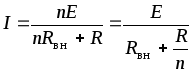
(1.43)
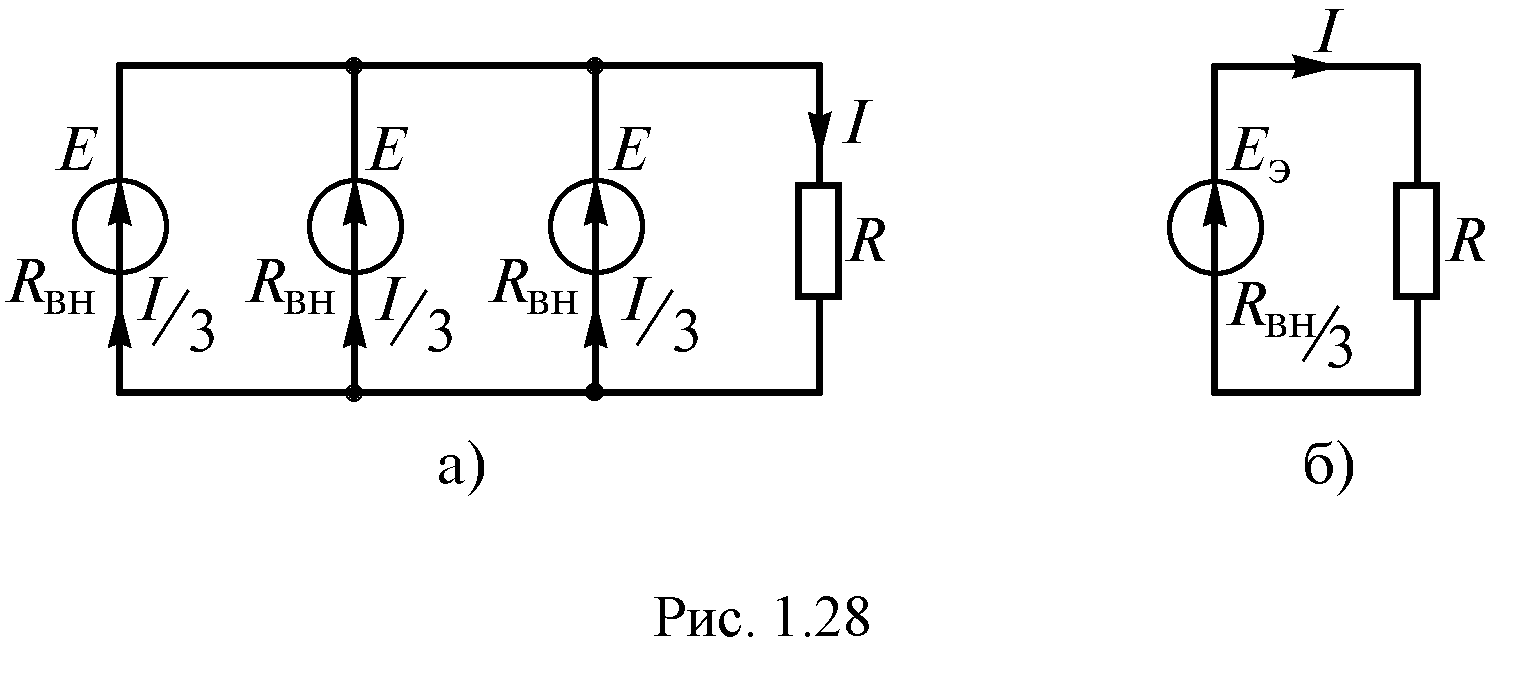
1.8.6. Параллельное соединение источников энергии
В тех случаях, когда номинальное
напряжение приемника равно напряжению
одного источника, а его ток больше
допустимого тока одного источника,
применяют параллельное соединение
источников (рис. 1.23 а).
При параллельном
соединении источников с одинаковыми
параметрами их общая ЭДС не изменится,
но уменьшатся токи через каждый источник
и внутреннее сопротивление общего
источника. Тогда эквивалентный источник
(рис. 1.23 б) имеет следующие параметры:
.
Рис. 1.23
Приисточниках
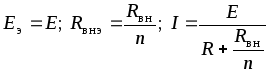
(1.44)
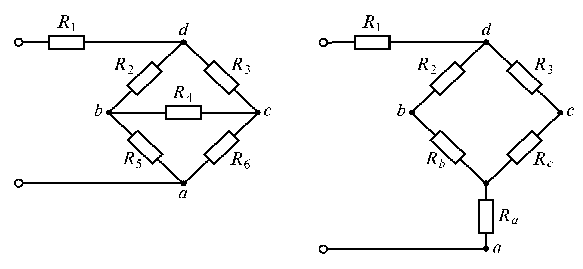
1.1. Определить
эквивалентное сопротивление цепи (рис.
1.24 а),
если
1Ом;
3Ом.
а) б)
в) г)
Рис. 1.24
Решение. Преобразуем
треугольник сопротивлений
в эквивалентную
звезду сопротивлений
(рис. 1.24 б).
Так как
,
то
Ом.
Дальнейшее решение
выполним преобразованием последовательно
или параллельно
соединенных сопротивлений резисторов
их эквивалентными сопротивлениями
«свертыванием» схемы. Резисторы
и
,
а такжеи
соединены последовательно, поэтому их
общие сопротивления
Ом;
Ом.
Полученная
схема приведена на рис. 1.24 в.
Резисторы
и
соединены параллельно, поэтому (рис.
1.24 г)
Ом.
Эквивалентное сопротивление всей цепи
Ом.
Пример 1.2.Определить токи в ветвях
цепи (рис. 1.25 а), если задано:Ом;
= 6Ом;
Ом;
= 2Ом;
= 100В.
Решение. Резисторы
и
соединены последовательно и образуют
ветвь с током.
Резисторыи
включены параллельно, а относительно
резистора– последовательно. Вычислим эквивалентные
сопротивления:
Ом;
Ом.
Рис. 1.25
Резисторы
и
соединены параллельно, а по отношению
к– последовательно, поэтому (рис. 1.25
б, в)
Ом.
Эквивалентное сопротивление цепи
Ом.
Ток в ветви с источником
А.
Так как сопротивления резисторов
и
одинаковы, то
А.
Аналогично, при
А.
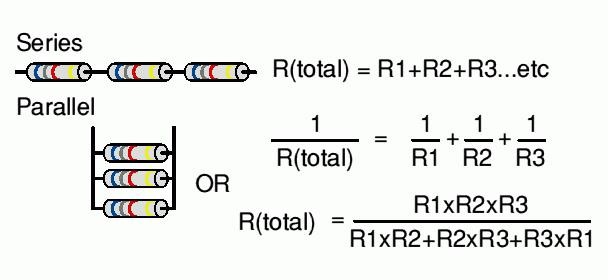
Все разнообразие схем построено на двух типах соединения — параллельном и последовательном. Для разных соединений действуют разные законы, что и дает возможность создания устройств с различными характеристиками. Рассмотрим последовательное и параллельное соединение резисторов.
Содержание статьи
- 1 Что такое резистор и для чего он нужен
- 2 Последовательное соединение сопротивлений
- 2.1 Теоретическая часть
- 2.2 Примеры расчета
- 3 Параллельное соединение резисторов
- 3.1 Теория и законы параллельного соединения
- 3.2 Примеры расчета параллельного соединения сопротивлений
- 4 Смешанное соединение
- 5 Практическое применение параллельного и последовательного соединения резисторов
Что такое резистор и для чего он нужен
Резистор — это радиоэлемент, который увеличивает сопротивление цепи. Ставят его обычно для того, чтобы понизить/ограничить напряжение или ток. Есть сопротивления постоянные и переменные.
Например, светодиоды требуют небольшого тока, иначе перегревается и быстро выходит из строя. Чтобы ограничить ток, перед светодиодом поставьте сопротивление. Ток в цепи станет меньше.
Для чего нужны резисторы: для подстройки параметров питания
Постоянные сопротивления — это те, которые не меняют своего номинала в процессе работы. Если это и происходит, то считается выходом из строя.
Так выглядят переменные и постоянные резисторы
Переменные резисторы, наоборот, отличаются тем, что их сопротивление можно изменять. Они имеют бегунок или поворотную ручку, при помощи которых и изменяется номинал. На основе таких устройств делают регуляторы. Например, регулятор громкости, накала греющего элемента и т.д.
Последовательное соединение сопротивлений
Последовательное соединение характеризуется тем, что элементы идут друг за другом. Конец одного подключается к началу другого. При подключении полученной цепочки к источнику тока получается кольцо.
Лампы накаливания соединенные последовательно, можно рассматривать как сопротивления
Теоретическая часть
Последовательное соединение характерно тем, что через все элементы протекает ток одинаковой силы. То есть, если цепочка состоит из двух резисторов R1 и R2 (как на рисунке ниже), то ток протекающий через каждое из них и любую другую часть цепи будет одинаковой (I = I1 = I2).
Последовательно соединенные сопротивления. I1 — ток протекающий через резистор R1, I2 — ток протекающий через резистор R2
Суммарное сопротивление всей цепи последовательно соединенных резисторов считается как сумма сопротивлений всех ее элементов. То есть, номиналы складывают.
R = R1 + R2 — это и есть формула расчета сопротивления при последовательном соединении резисторов. Если элементов больше двух, будет просто больше слагаемых.
Еще одно свойство последовательного соединения — на каждом элементе напряжение отличается. Ток в цепи одинаковый, а напряжение на резисторе зависит от его номинала.
Примеры расчета
Давайте рассмотрим пример. Цепь представлена на рисунке выше. Есть источник тока и два сопротивления. Пусть R1=1,2 кОм, R2= 800 Ом, а ток в цепи 2 А. По закону Ома U = I * R. Подставляем наши значения:
- U1 = R1 * I = 1200 Ом * 2 А = 2400 В;
- U2 = R2 * I = 800 Ом * 2А = 1600 В.
Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В.
Так понятнее, что такое последовательное соединение
Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток. R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом. Если подставить в формулу напряжения при последовательном соединении сопротивлений, получаем: U = R * I = 2000 Ом * 2 А = 4000 В. Получаем, что общее напряжение данной цепи 4000 В.
А теперь посмотрите на схему. На первом вольтметре (возле резистора R1) показания будут 2400 В, на втором — 1600 В. При этом напряжение источника питания — 4000 В.
Параллельное соединение резисторов
Параллельное соединение — это когда входы нескольких деталей соединяются в одной точке. Точно так же — в одну точку — соединяют их выходы.
Так выглядит параллельное соединение на схеме и в реальности
Теория и законы параллельного соединения
Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение. То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение.
U = U1 = U2 = U3.
Получается, что ток разделяется на несколько «ручейков». То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи. В случае с параллельным соединением резисторов — от их номинала.
Так выглядит параллельное соединение резисторов на схеме
Общее сопротивление участка цепи при таком соединении становится ниже. Его высчитывают по формуле:
1/R = 1/R1 + 1/R + 1/R3+…
Такая форма хоть и понятна, но неудобна. Формула расчета сопротивления параллельно подключенных резисторов получается тем сложнее, чем больше элементов соединены параллельно. Но больше двух-трех редко кто объединяет, так что на практике достаточно знать только две формулы приведенные ниже.
Формулы расчета сопротивления при параллельном подключении двух и трех резисторов
Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала.
Примеры расчета параллельного соединения сопротивлений
Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.
- Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом.
- Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом.
Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.
Как высчитывать сопротивление составных резисторов
Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом.
Еще один пример с лампочками
При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее. Но картина не отличается:
- Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом.
- Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом. Получим результирующее сопротивление 4,61 Ом.
Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.
Смешанное соединение
Как быть, если в схеме есть и параллельное, и последовательное соединение резисторов? В таком случае считают общее сопротивление по участкам. Можно при этом перерисовывать схему, заменяя составные сопротивления на один «прямоугольник», но проставляя над ним высчитанный результат.
Пример расчета сопротивления при смешанном соединении резисторов. Рассматриваем исходную схему как совокупность параллельных и последовательных соединений
Шаг 1. Нашли общее сопротивление последовательно соединенных резисторов R3 и R4:
R3-4 = 3 кОм + 3 кОм = 6 кОм;
Шаг 2. Рассчитали сопротивление параллельно соединенных резисторов R2 и R3-4:
R2-4 = 3 кОм * 6 кОм / (3 кОм + 6 кОм) = 18 кОм/9 кОм = 2 кОм;
Шаг 3. Рассчитали общее сопротивление последовательно соединенных резисторов R1 и R2-4:
R1-4 = R1 + R2-4 = 1 кОм + 2 кОм = 3 кОм.
Практическое применение параллельного и последовательного соединения резисторов
Для чего практически можно использовать параллельное и последовательное соединение резисторов? Случается, что при ремонте электронной аппаратуры, не всегда в наличии сопротивление нужного номинала. Ехать в магазин за одним копеечным элементом — накладно. Вот тут и могут пригодиться составные резисторы. Просто надо последовательно или параллельно соединить их, подобрав требуемый номинал.
Последовательное и параллельное соединение резисторов применяют для подбора требуемого номинала. Контролировать точное значение получившегося сопротивления можно при помощи цифрового мультиметра
При соединении резисторов, их ножки первоначально скручивают. Какой стороной разворачивать сопротивление — неважно (в отличие от диодов, резисторы одинаково пропускают ток в обоих направлениях). На концах скрутку слегка обжимают плоскогубцами, затем пропаивают. Следите за тем, чтобы корпуса были друг от друга подальше — так они будут лучше охлаждаться при работе.