Калькулятор НОД и НОК
При помощи данного калькулятора вы можете легко найти наибольший общий делитель НОД и наименьшее общее кратное НОК благодаря подробно расписанному решению. Вы можете найти НОД и НОК для двух, трех и четырех чисел
Выберите количество чисел для НОД и НОК
Наибольший общий делитель НОД
Наибольший общий делитель НОД(a, b) – это наибольшее натуральной число, на которое можно разделить без остатка числа a и b.
Если числа имеют только один общий делитель – единицу, то такие числа называют взаимно простыми.
Наибольший общий делитель НОД обозначают: НОД(a, b), (a, b), gcd(a, b), hcf(a, b).
Свойства НОД
- Наибольший общий делитель чисел a и b делится на любой общий делитель этих чисел.
Данное свойство означает, что если найти все общие делители чисел a и b, то НОД(a, b) будет делится на любой из этих делителей.
Например, возьмём два числа 15 и 30 и найдем все общие делители этих чисел: 1, 3, 5, 15. Наибольший из этих делителей – число 15. Тогда число 15 делится на 1, 3, 5, 15. - Если число a делится на b, то НОД(a, b) = b.
Например, число 20 делится на число 10, тогда НОД(20, 10) = 10. - При помощи наибольшего общего делителя можно привести дроби к несократимому виду.
Например, дробь 5/30 можно привести к несократимому виду, если найти НОД(30, 5). НОД(30, 5) = 5, следовательно число 5 – самое больше число из возможных делителей числа 30 и 5 на которое можно разделить эти числа, тогда 30:5 = 6, 5:5 = 1. Получаем дробь 5/30 = 1/6.
Любые действия с дробями и развернутое поэтапное решение можно вычислить, используя калькулятор дробей.
Как найти наибольший общий делитель НОД
Чтобы найти наибольший общий делитель НОД двух, трех и более чисел, необходимо:
- Разложить числа на простые множители.
- Найти общие множители чисел – такие числа, которые есть в разложении всех чисел и вычеркнуть их.
- Перемножить оставшиеся множители.
Приведем пример, найдем наибольший общий делитель двух чисел 24 и 58.
Способ №1
- Разложим числа на простые множители. Для этого проверим, является ли каждое из чисел простым (если число простое, то его нельзя разложить на простые множители, и оно само является своим разложением).
58 — составное число
Разложим число 24 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
24 : 2 = 12 — делится на простое число 2
12 : 2 = 6 — делится на простое число 2
6 : 2 = 3 — делится на простое число 2.
Завершаем деление, так как 3 простое числоРазложим число 58 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
58 : 2 = 29 — делится на простое число 2.
Завершаем деление, так как 29 простое число - Выделим синим цветом и выпишем общие множители.
24 = 2 ⋅ 2 ⋅ 2 ⋅ 3
58 = 2 ⋅ 29
У чисел (24, 58) только один общий множитель — 2 и он и будет наибольшим общим делителем этих чиселОтвет: НОД (24, 58) = 2
Способ №2
- Найдем все возможные делители чисел (24, 58). Для этого поочередно разделим число 24 на делители от 1 до 24, число 58 на делители от 1 до 58. Если число делится без остатка, то делитель запишем в список делителей.
Для числа 24 выпишем все случаи, когда оно делится без остатка:
24 : 1 = 24;
24 : 2 = 12;
24 : 3 = 8;
24 : 4 = 6;
24 : 6 = 4;
24 : 8 = 3;
24 : 12 = 2;
24 : 24 = 1;Для числа 58 выпишем все случаи, когда оно делится без остатка:
58 : 1 = 58;
58 : 2 = 29;
58 : 29 = 2;
58 : 58 = 1; - Выпишем все общие делители чисел (24, 58) и выделим зеленым цветом самый большой, это и будет наибольший общий делитель НОД чисел (24, 58)
Общие делители чисел (24, 58): 1, 2
Ответ: НОД (24, 58) = 2
Наименьшее общее кратное НОК
Наименьшее общее кратное НОК(a, b) – это наименьшее число, которое можно разделить на числа a и b без остатка.
Наименьшее общее кратное НОК обозначается: НОК(a, b), [a, b], LCM(a, b), lcm(a, b).
Как найти наименьшее общее кратное НОК
Чтобы найти НОК двух, трех и более чисел необходимо:
- Разложить эти числа на простые множители.
- Выписать множители одного из чисел и добавить к ним множители из разложения остальных чисел, которых нет в разложении.
- Умножить получившиеся множители.
Приведем пример, найдем наименьшее общее кратное НОК для чисел 30 и 225.
Способ №1
- Разложим числа на простые множители. Для этого проверим, является ли каждое из чисел простым (если число простое, то его нельзя разложить на простые множители, и оно само является своим разложением).
225 — составное число
30 — составное числоРазложим число 225 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
225 : 3 = 75 — делится на простое число 3
75 : 3 = 25 — делится на простое число 3
25 : 5 = 5 — делится на простое число 5.
Завершаем деление, так как 5 простое числоРазложим число 30 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
30 : 2 = 15 — делится на простое число 2
15 : 3 = 5 — делится на простое число 3.
Завершаем деление, так как 5 простое число - Прежде всего запишем множители самого большого числа, а затем меньшего числа. Найдем недостающие множители, выделим синим цветом в разложении меньшего числа множители, которые не вошли в разложение большего числа.
225 = 3 ∙ 3 ∙ 5 ∙ 5
30 = 2 ∙ 3 ∙ 53) Теперь, чтобы найти НОК нужно перемножить множители большего числа с недостающими множителями, которые выделены синим цветом
НОК (225 ; 30) = 3 ∙ 3 ∙ 5 ∙ 5 ∙ 2 = 450
Способ №2
- Найдем все возможные кратные чисел (225 ; 30). Для этого поочередно умножим число 225 на числа от 1 до 30, число 30 на числа от 1 до 225.
Выделим все кратные числа 225 зеленым цветом:
зеленым цветом:225 ∙ 1 = 225; 225 ∙ 2 = 450; 225 ∙ 3 = 675; 225 ∙ 4 = 900;
225 ∙ 5 = 1125; 225 ∙ 6 = 1350; 225 ∙ 7 = 1575; 225 ∙ 8 = 1800;
225 ∙ 9 = 2025; 225 ∙ 10 = 2250; 225 ∙ 11 = 2475; 225 ∙ 12 = 2700;
225 ∙ 13 = 2925; 225 ∙ 14 = 3150; 225 ∙ 15 = 3375; 225 ∙ 16 = 3600;
225 ∙ 17 = 3825; 225 ∙ 18 = 4050; 225 ∙ 19 = 4275; 225 ∙ 20 = 4500;
225 ∙ 21 = 4725; 225 ∙ 22 = 4950; 225 ∙ 23 = 5175; 225 ∙ 24 = 5400;
225 ∙ 25 = 5625; 225 ∙ 26 = 5850; 225 ∙ 27 = 6075; 225 ∙ 28 = 6300;
225 ∙ 29 = 6525; 225 ∙ 30 = 6750;Выделим все кратные числа 30 зеленым цветом:
30 ∙ 1 = 30; 30 ∙ 2 = 60; 30 ∙ 3 = 90; 30 ∙ 4 = 120;
30 ∙ 5 = 150; 30 ∙ 6 = 180; 30 ∙ 7 = 210; 30 ∙ 8 = 240;
30 ∙ 9 = 270; 30 ∙ 10 = 300; 30 ∙ 11 = 330; 30 ∙ 12 = 360;
30 ∙ 13 = 390; 30 ∙ 14 = 420; 30 ∙ 15 = 450; 30 ∙ 16 = 480;
30 ∙ 17 = 510; 30 ∙ 18 = 540; 30 ∙ 19 = 570; 30 ∙ 20 = 600;
30 ∙ 21 = 630; 30 ∙ 22 = 660; 30 ∙ 23 = 690; 30 ∙ 24 = 720;
30 ∙ 25 = 750; 30 ∙ 26 = 780; 30 ∙ 27 = 810; 30 ∙ 28 = 840;
30 ∙ 29 = 870; 30 ∙ 30 = 900; 30 ∙ 31 = 930; 30 ∙ 32 = 960;
30 ∙ 33 = 990; 30 ∙ 34 = 1020; 30 ∙ 35 = 1050; 30 ∙ 36 = 1080;
30 ∙ 37 = 1110; 30 ∙ 38 = 1140; 30 ∙ 39 = 1170; 30 ∙ 40 = 1200;
30 ∙ 41 = 1230; 30 ∙ 42 = 1260; 30 ∙ 43 = 1290; 30 ∙ 44 = 1320;
30 ∙ 45 = 1350; 30 ∙ 46 = 1380; 30 ∙ 47 = 1410; 30 ∙ 48 = 1440;
30 ∙ 49 = 1470; 30 ∙ 50 = 1500; 30 ∙ 51 = 1530; 30 ∙ 52 = 1560;
30 ∙ 53 = 1590; 30 ∙ 54 = 1620; 30 ∙ 55 = 1650; 30 ∙ 56 = 1680;
30 ∙ 57 = 1710; 30 ∙ 58 = 1740; 30 ∙ 59 = 1770; 30 ∙ 60 = 1800;
30 ∙ 61 = 1830; 30 ∙ 62 = 1860; 30 ∙ 63 = 1890; 30 ∙ 64 = 1920;
30 ∙ 65 = 1950; 30 ∙ 66 = 1980; 30 ∙ 67 = 2010; 30 ∙ 68 = 2040;
30 ∙ 69 = 2070; 30 ∙ 70 = 2100; 30 ∙ 71 = 2130; 30 ∙ 72 = 2160;
30 ∙ 73 = 2190; 30 ∙ 74 = 2220; 30 ∙ 75 = 2250; 30 ∙ 76 = 2280;
30 ∙ 77 = 2310; 30 ∙ 78 = 2340; 30 ∙ 79 = 2370; 30 ∙ 80 = 2400;
30 ∙ 81 = 2430; 30 ∙ 82 = 2460; 30 ∙ 83 = 2490; 30 ∙ 84 = 2520;
30 ∙ 85 = 2550; 30 ∙ 86 = 2580; 30 ∙ 87 = 2610; 30 ∙ 88 = 2640;
30 ∙ 89 = 2670; 30 ∙ 90 = 2700; 30 ∙ 91 = 2730; 30 ∙ 92 = 2760;
30 ∙ 93 = 2790; 30 ∙ 94 = 2820; 30 ∙ 95 = 2850; 30 ∙ 96 = 2880;
30 ∙ 97 = 2910; 30 ∙ 98 = 2940; 30 ∙ 99 = 2970; 30 ∙ 100 = 3000;
30 ∙ 101 = 3030; 30 ∙ 102 = 3060; 30 ∙ 103 = 3090; 30 ∙ 104 = 3120;
30 ∙ 105 = 3150; 30 ∙ 106 = 3180; 30 ∙ 107 = 3210; 30 ∙ 108 = 3240;
30 ∙ 109 = 3270; 30 ∙ 110 = 3300; 30 ∙ 111 = 3330; 30 ∙ 112 = 3360;
30 ∙ 113 = 3390; 30 ∙ 114 = 3420; 30 ∙ 115 = 3450; 30 ∙ 116 = 3480;
30 ∙ 117 = 3510; 30 ∙ 118 = 3540; 30 ∙ 119 = 3570; 30 ∙ 120 = 3600;
30 ∙ 121 = 3630; 30 ∙ 122 = 3660; 30 ∙ 123 = 3690; 30 ∙ 124 = 3720;
30 ∙ 125 = 3750; 30 ∙ 126 = 3780; 30 ∙ 127 = 3810; 30 ∙ 128 = 3840;
30 ∙ 129 = 3870; 30 ∙ 130 = 3900; 30 ∙ 131 = 3930; 30 ∙ 132 = 3960;
30 ∙ 133 = 3990; 30 ∙ 134 = 4020; 30 ∙ 135 = 4050; 30 ∙ 136 = 4080;
30 ∙ 137 = 4110; 30 ∙ 138 = 4140; 30 ∙ 139 = 4170; 30 ∙ 140 = 4200;
30 ∙ 141 = 4230; 30 ∙ 142 = 4260; 30 ∙ 143 = 4290; 30 ∙ 144 = 4320;
30 ∙ 145 = 4350; 30 ∙ 146 = 4380; 30 ∙ 147 = 4410; 30 ∙ 148 = 4440;
30 ∙ 149 = 4470; 30 ∙ 150 = 4500; 30 ∙ 151 = 4530; 30 ∙ 152 = 4560;
30 ∙ 153 = 4590; 30 ∙ 154 = 4620; 30 ∙ 155 = 4650; 30 ∙ 156 = 4680;
30 ∙ 157 = 4710; 30 ∙ 158 = 4740; 30 ∙ 159 = 4770; 30 ∙ 160 = 4800;
30 ∙ 161 = 4830; 30 ∙ 162 = 4860; 30 ∙ 163 = 4890; 30 ∙ 164 = 4920;
30 ∙ 165 = 4950; 30 ∙ 166 = 4980; 30 ∙ 167 = 5010; 30 ∙ 168 = 5040;
30 ∙ 169 = 5070; 30 ∙ 170 = 5100; 30 ∙ 171 = 5130; 30 ∙ 172 = 5160;
30 ∙ 173 = 5190; 30 ∙ 174 = 5220; 30 ∙ 175 = 5250; 30 ∙ 176 = 5280;
30 ∙ 177 = 5310; 30 ∙ 178 = 5340; 30 ∙ 179 = 5370; 30 ∙ 180 = 5400;
30 ∙ 181 = 5430; 30 ∙ 182 = 5460; 30 ∙ 183 = 5490; 30 ∙ 184 = 5520;
30 ∙ 185 = 5550; 30 ∙ 186 = 5580; 30 ∙ 187 = 5610; 30 ∙ 188 = 5640;
30 ∙ 189 = 5670; 30 ∙ 190 = 5700; 30 ∙ 191 = 5730; 30 ∙ 192 = 5760;
30 ∙ 193 = 5790; 30 ∙ 194 = 5820; 30 ∙ 195 = 5850; 30 ∙ 196 = 5880;
30 ∙ 197 = 5910; 30 ∙ 198 = 5940; 30 ∙ 199 = 5970; 30 ∙ 200 = 6000;
30 ∙ 201 = 6030; 30 ∙ 202 = 6060; 30 ∙ 203 = 6090; 30 ∙ 204 = 6120;
30 ∙ 205 = 6150; 30 ∙ 206 = 6180; 30 ∙ 207 = 6210; 30 ∙ 208 = 6240;
30 ∙ 209 = 6270; 30 ∙ 210 = 6300; 30 ∙ 211 = 6330; 30 ∙ 212 = 6360;
30 ∙ 213 = 6390; 30 ∙ 214 = 6420; 30 ∙ 215 = 6450; 30 ∙ 216 = 6480;
30 ∙ 217 = 6510; 30 ∙ 218 = 6540; 30 ∙ 219 = 6570; 30 ∙ 220 = 6600;
30 ∙ 221 = 6630; 30 ∙ 222 = 6660; 30 ∙ 223 = 6690; 30 ∙ 224 = 6720;
30 ∙ 225 = 6750; - Выпишем все общие кратные чисел (225 ; 30) и выделим зеленым цветом самое маленькое, это и будет наименьшим общим кратным чисел (225 ; 30).
Общие кратные чисел (225 ; 30): 450, 900, 1350, 1800, 2250, 2700, 3150, 3600, 4050, 4500, 4950, 5400, 5850, 6300, 6750
Ответ: НОК (225 ; 30) = 450
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажер по математике |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
| Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
|
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
|
Оптика |
| Калькулятор отражения и преломления света |
|
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
|
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
| Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Данный калькулятор предназначен для нахождения наибольшего общего делителя двух, трех и более чисел онлайн.
Делители числа n – это числа, на которые делится число n нацело, то есть без остатка. Натуральные числа могут иметь два, три и большее количество делителей. Число называется простым, если оно делится только на само себя и на единицу.
Несколько чисел могут иметь одинаковые делители, которые будут являться общими делителями. Если единица является единственным общим делителем чисел, то такие числа называются взаимно простыми.
Среди общих делителей чисел выделяют наибольший из них. Наибольший общий делитель (сокращенно НОД) двух, трех и более чисел – наибольшее число, на которое данные числа делятся без остатка. Наибольший общий делитель взаимно простых числе по определению равен единице.
Для тех пользователей, кого интересует вопрос, как находить наибольший общий делитель двух, трех и более чисел самостоятельно, представим последовательность решения данной задачи. Во-первых, необходимо разложить делители чисел на простые множители. Во-вторых, выделяются одинаковые простые множители данных чисел. В-третьих, необходимо перемножить найденные до этого одинаковые простые множители чисел. Найденное произведение одинаковых простых множителей будет являться наибольшим общим делителем натуральных чисел.
Чтобы быстро найти наибольший общий делитель чисел, необязательно самостоятельно проходить все этапы решения. Просто введите числа в соответствующие ячейки калькулятора и нажмите кнопку «Вычислить».
Найдите наибольший общий делитель чисел.
Калькулятор НОД.
Введите первое целое число — A.
Введите второе целое число — B.
Введите третье целое число — C.
Найдите наибольший общий делитель чисел 180, 240 и 200.
Ответ: Наибольший общий делитель чисел 180, 240 и 200 равен 20.
Найдите общие делители 3(трех) чисел 180, 240 и 200.
Ответ: Общие делители 3х чисел 180, 240 и 200 = 1, 2, 4, 5, 10, 20.
Сколько общих делителей имеют числа 180, 240 и 200?
Ответ: У чисел 180, 240 и 200 — 6(шесть) общих делителей.
Найдите наименьший общий делитель чисел 180, 240 и 200.
Ответ: Наименьший общий делитель чисел 180, 240 и 200 равен 1.
Четные общие делители чисел 180, 240 и 200 -> 20, 10, 4, 2.
Количество общих четных делителей чисел 180, 240 и 200 — 4(четыре).
Нечетные общие делители чисел 180, 240 и 200 -> 5, 1.
Количество общих нечетных делителей чисел 180, 240 и 200 — 2(два).
Как найти, НОД чисел 180, 240 и 200?
Наибольший общий делитель, НОД чисел 180, 240 и 200 — решение онлайн (первый способ).
Для решения задачи нахождения наибольшего общего делителя чисел 180, 240 и 200 необходимо найти все делители числа 180, 240 и 200.
Выпишем все делители числа 180.
1 2 3 4 5 6 9 10 12 15 18 20 30 36 45 60 90 180
Выпишем все делители числа 240.
1 2 3 4 5 6 8 10 12 15 16 20 24 30 40 48 60 80 120 240
Выпишем все делители числа 200.
1 2 4 5 8 10 20 25 40 50 100 200
Зная все делители чисел 180, 240 и 200 выпишем общие делители этих чисел.
Общими делителями чисел 180, 240 и 200 являются числа:
1 2 4 5 10 20
Наибольшим из этих чисел является число:
20
Таким образом:
НОД(180;240;200) = 20
Cумма трех чисел 180, 240 и 200
180+240+200=620
Cумма трех чисел равнв 620
Cумма квадратов трех чисел 180, 240 и 200
1802+2402+2002=130000
Cумма квадратов трех чисел равна 130000
Произведение трех чисел 180, 240 и 200
180*240*200=8640000
Произведение трех чисел равно 8640000
Произведение квадратов трех чисел 180, 240 и 200
1802*2402*2002=74649600000000
Произведение квадратов трех чисел равно 74649600000000
Квадрат суммы, квадрат разности трех чисел 180, 240 и 200
(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
(180+240+200)2=1802+2402+2002+2*180*240+2*180*200+2*240*200=384400
Квадрат суммы трех чисел равен 384400
(a-b+c)2=a2+b2+c2-2ab+2ac-2bc
(180-240+200)2=1802+2402+2002-2*180*240+2*180*200-2*240*200=19600
Квадрат суммы, разности трех чисел равен 19600
(a+b-c)2=a2+b2+c2+2ab-2ac-2bc
(180+240-200)2=1802+2402+2002+2*180*240-2*180*200-2*240*200=48400
Квадрат суммы, разности трех чисел равен 48400
(a-b-c)2=a2+b2+c2-2ab-2ac+2bc
(180-240-200)2=1802+2402+2002-2*180*240-2*180*200+2*240*200=67600
Сумма цифр трех чисел 180, 240 и 200.
(включая повторяющиеся)
Сумма цифр трех чисел равна 17
(исключая дубли)
Сумма цифр трех чисел равна 15
Произведение цифр трех чисел 180 и 240 и 200.
(включая повторяющиеся)
Произведение цифр тех чисел равна 0
(исключая дубли)
Произведение цифр трех чисел равна 0
Калькулятор онлайн.
Нахождение (вычисление) НОД и НОК
Наибольшим общим делителем (НОД) для двух целых чисел m и n называется наибольший из их общих делителей.
Пример: для чисел 6 и 9 наибольший общий делитель равен 3.
Наибольший общий делитель существует и однозначно определён, если хотя бы одно из чисел m или n не равно нулю.
В школьной программе обозначается так: НОД(m, n)
Понятие наибольшего общего делителя (НОД) распространяется на любой набор из более чем двух целых чисел.
Чаще всего НОД используется для сокращения дроби — если найти НОД числителя и знаменателя, то на это число можно сократить
числитель и знаменатель данной дроби.
Наименьшее общее кратное (НОК) двух целых чисел m и n это наименьшее натуральное число, которое делится на m и n без остатка.
В школьной программе обозначается так: НОК(m, n)
Пример: НОК(16, 20) = 80
Одно из наиболее частых применений НОК — приведение дробей к общему знаменателю.
С помощью данной математической программы вы можете найти (вычислить) НОД и НОК двух целых чисел.
Программа нахождения НОД и НОК не только выводит ответ задачи, но и отображает процесс вычисления НОД и НОК двух чисел.
Вводить можно только целые положительные числа.
Наши игры, головоломки, эмуляторы:
Немного теории.
Наибольший общий делитель (НОД). Взаимно простые числа
Определение. Наибольшее натуральное число, на которое делятся без остатка числа а и b, называют
наибольшим общим делителем (НОД) этих чисел.
Найдём наибольший общий делитель чисел 24 и 35.
Делителями 24 будут числа 1, 2, 3, 4, 6, 8, 12, 24, а делителями 35 будут числа 1, 5, 7, 35.
Видим, что числа 24 и 35 имеют только один общий делитель — число 1. Такие числа называют взаимно простыми.
Определение. Натуральные числа называют взаимно простыми, если их наибольший общий делитель (НОД) равен 1.
Наибольший общий делитель (НОД) можно найти, не выписывая всех делителей данных чисел.
Разложим на множители числа 48 и 36, получим:
48 = 2 * 2 * 2 * 2 * 3, 36 = 2 * 2 * 3 * 3.
Из множителей, входящих в разложение первого из этих чисел, вычеркнем те, которые не входят в разложение второго числа
(т. е. две двойки).
Остаются множители 2 * 2 * 3. Их произведение равно 12. Это число и является наибольшим общим делителем чисел 48 и 36.
Так же находят наибольший общий делитель трёх и более чисел.
Чтобы найти наибольший общий делитель нескольких натуральных чисел, надо:
1) разложить их на простые множители;
2) из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;
3) найти произ ведение оставшихся множителей.
Если все данные числа делятся на одно из них, то это число и является наибольшим общим делителем данных чисел.
Например, наибольшим общим делителем чисел 15, 45, 75 и 180 будет число 15, так как на него делятся все остальные числа: 45, 75 и 180.
Наименьшее общее кратное (НОК)
Определение. Наименьшим общим кратным (НОК) натуральных чисел а и b называют наименьшее натуральное число,
которое кратно и a и b.
Наименьшее общее кратное (НОК) чисел 75 и 60 можно найти и не выписывая подряд кратные этих чисел. Для этого разложим 75 и 60 на
простые множители: 75 = 3 * 5 * 5, а 60 = 2 * 2 * 3 * 5.
Выпишем множители, входящие в разложение первого из этих чисел, и добавим к ним недостающие множители 2 и 2 из разложения
второго числа (т.е. объединяем множители).
Получаем пять множителей 2 * 2 * 3 * 5 * 5, произведение которых равно 300. Это число является наименьшим общим кратным чисел 75 и 60.
Так же находят наименьшее общее кратное для трёх и более чисел.
Чтобы найти наименьшее общее кратное нескольких натуральных чисел, надо:
1) разложить их на простые множители;
2) выписать множители, входящие в разложение одного из чисел;
3) добавить к ним недостающие множители из разложений остальных чисел;
4) найти произведение получившихся множителей.
Заметим, что если одно из данных чисел делится на все остальные числа, то это число и является наименьшим общим кратным данных
чисел.
Например, наименьшим общим кратным чисел 12, 15, 20 и 60 будет число 60, так как оно делится на все данные числа.
Пифагор (VI в. до н. э.) и его ученики изучали вопрос о делимости чисел. Число, равное сумме всех его делителей (без самого числа),
они называли совершенным числом. Например, числа 6 (6 = 1 + 2 + 3), 28 (28 = 1 + 2 + 4 + 7 + 14) совершенные. Следующие совершенные
числа — 496, 8128, 33 550 336. Пифагорейцы знали только первые три совершенных числа. Четвёртое — 8128 — стало известно в I в. н. э.
Пятое — 33 550 336 — было найдено в XV в. К 1983 г. было известно уже 27 совершенных чисел. Но до сих пор учёные не знают, есть ли
нечётные совершенные числа, есть ли самое большое совершенное число.
Интерес древних математиков к простым числам связан с тем, что любое число либо простое, либо может быть представлено в виде
произведения простых чисел, т. е. простые числа — это как бы кирпичики, из которых строятся остальные натуральные числа.
Вы, наверное, обратили внимание, что простые числа в ряду натуральных чисел встречаются неравномерно — в одних частях ряда их больше,
в других — меньше. Но чем дальше мы продвигаемся по числовому ряду, тем реже встречаются простые числа. Возникает вопрос: существует
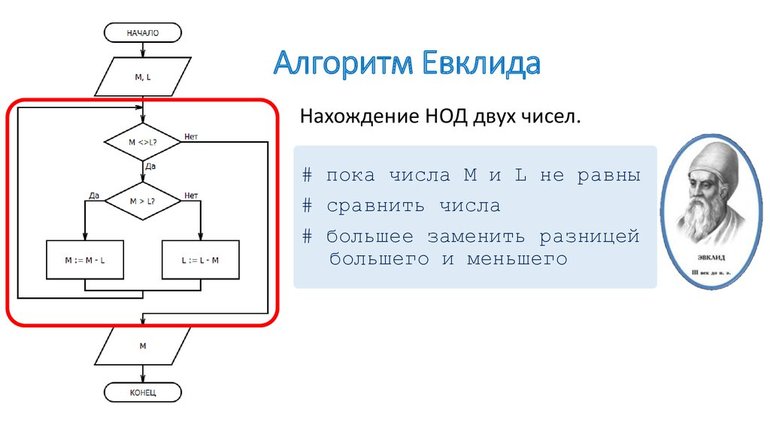
ли последнее (самое большое) простое число? Древнегреческий математик Евклид (III в. до н. э.) в своей книге «начала», бывшей на
протяжении двух тысяч лет основным учебником математики, доказал, что простых чисел бесконечно много, т. е. за каждым простым числом
есть ещё большее простое число.
Для отыскания простых чисел другой греческий математик того же времени Эратосфен придумал такой способ. Он записывал все числа
от 1 до какого-то числа, а потом вычёркивал единицу, которая не является ни простым, ни составным числом, затем вычёркивал через
одно все числа, идущие после 2 (числа, кратные 2, т. е. 4, 6, 8 и т. д.). Первым оставшимся числом после 2 было 3. Далее
вычёркивались через два все числа, идущие после 3 (числа, кратные 3, т. е. 6, 9, 12 и т. д.). в конце концов оставались
невычеркнутыми только простые числа.
Понятие НОД
Определение, что такое НОД в математике, звучит следующим образом: наибольший делитель, общий для чисел a и b, есть такое наибольшее число, на которое описанные значения смогут разделиться без остатка.
Для наилучшего понимания того, как найти НОД двух чисел, вместо указанных переменных достаточно подставлять простые числа, например, 12 и 9. То есть самым наименьшим делимым числом для 12 и 9 является то, которое позволяет найти решение без остатка.
Задача по нахождению НОД может решаться тремя способами. Каждый из них применяется в зависимости от того, насколько быстро требуется найти необходимый показатель:
- Первый метод схож с алгоритмом Евклида для нахождения НОД. Он достаточно трудоемкий и канонический. Необходимо искать все возможные делители, а через них — наибольший делитель, являющийся общим для значений. Если выписывать все показатели, на которые поделятся 12 и 9, наибольшим окажется 3.
- Второй способ предполагает разложение пары чисел на простые множители и перемножение наибольших из них между собой.
- Суть следующего способа: компоненты, которые подлежат поиску наибольшего общего делителя, начинают раскладывать на простые множители. Это значит, что из разложения первого нужно вычеркнуть множители, какие не попадают во второе значение. Остальные показатели в первом разложении перемножаются и оказываются НОД.
Лучше всего рассматривать применение указанных методов через определенный класс задач, которые помогают при дальнейшем изучении теорем, касающихся дробей. Формулы для указанной темы очень доступны для понимания ученикам и учителям.
Метод разложения
Суть второй методики заключается в разложении на простые множители и перемножении общих из них. В качестве примера можно рассмотреть представление НОД для показателей 18 и 24:
- Оба параметра раскладываются на множители — 24 на 1, 2, 3, 4, 6, 8, 12, 24, а 18 на 1, 2, 3, 6, 9, 18. Происходит поиск общих значений.
- Необходимо перемножать между собой общие множители. Если есть риск запутаться, то стоит подчеркивать общие значения.
- В результате поиска соотношений выделяют в качестве общих значений 2 и 3. После перемножения они дают число 6. Именно это линейное число и считается наибольшим объединенным делителем.
Способ является достаточно простым. Однако из-за некоторого объема операций можно оказаться в сложной ситуации с поиском общих делителей, поэтому следует рассмотреть еще один способ.
Вычеркивание показателей
Для третьей методики характерно вычеркивание из разложения тех показателей, которые не проходят во второе число. Есть такие виды НОД, которые могут сильно отличаться, но все равно позволяют найти нужный показатель. Например, нужно найти наибольший делитель для значений 28 и 16:
- Сначала раскладывают оба параметра на простые множители. Для 28 таковыми считаются 1, 2, 4, 7, 14, 28, для 16 это 1, 2, 4, 8,16.
- Из разложения первого объекта по формуле следует вычеркнуть показатель 7, так как он не входит в группу делителей второго.
- После перемножения наибольшим делителем оказывается 4. Проверка в виде деления на него 28 и 16 показывает, что именно он и является нужным НОДом.
Аналогично можно отыскать для других значений, например, 100 и 40. После разложения из первого перечеркивается лишняя пятерка. Перемножение дает 20, который после поверки оказывается наибольшим делителем.
Несколько значений
Несмотря на кажущуюся сложность, доказать, что возможно найти НОД для нескольких чисел без помощи онлайн-калькуляторов, вполне реально. Значения, подлежащие поиску, необходимо разложить на множители. После чего ищется произведение общих простейших множителей.
Есть такие числа как 18, 24 и 36. Разложение 18 дает такие коэффициенты как 1, 2, 3, 6, 9 и 18. Затем 24 и 36 необходимо править по аналогичному методу. Если составить таблицу, то можно найти следующие общие показатели в виде 2 и 3. Они считаются общими для всех трех чисел.
Перемножив между собой, получается делимое число 6. Оно также подходит под разложение 18, 24 и 36, а также считается наибольшим общим делителем для всех трех параметров. Аналогичный принцип срабатывает и для четырех и более чисел, когда потребуется найти делитель на любом уровне сложности вплоть до максимального.
Наименьшее общее кратное
Помимо НОД, существует еще и наименьшее общее кратное, или НОК. Если сказать по-другому, то таковым свойством можно считать число, которое без остатка будет разделяться на число a и число b.
Как и для НОД, поиск НОК может осуществляться тремя похожими с предшествующими способами. Каждым из них можно воспользоваться в зависимости от ситуации и удобства решения задания:
- Первый метод достаточно простой и распространенный. Необходимо записать кратные первых чисел, после чего подобрать такое число, чтобы оно являлось общим для всех и наименьшим.
- Также возможно раскладывать кратные на простые натуральные множители. В этом случае переписываются множители из первого разложения и прибавляются недостающие во второе. Получаемые значения перемножают между собой и получают НОК.
- Особняком стоит третий метод, который работает при соблюдении определенных условий. Одним из них является то, что НОК ищут для двух чисел, и на предыдущих этапах был найден наибольший общий делитель.
На последнем методе стоит остановиться несколько подробнее. Он является не только сравнительно менее громоздким, но и обладает определенным преимуществом в виде уже найденного НОД и более простого алгоритма решения.
Совмещение делителей
Такая методика характерна для тех примеров, в которых требуется единовременное нахождение НОД и НОК двух чисел. Например, необходимо отыскать для чисел 24 и 12 НОК и НОК. Действовать нужно в следующем порядке:
- Первым делом нужно найти НОД. Для этого надлежит раскладывать оба числа, отыскать общий показатель 12.
- После этого 24 и 12 перемножаются между собой. Результатом становится 288.
- Полученное число требуется разделять на НОД от 24 и 12. Полученный ответ 24 говорит о том, что именно оно является наименьшим общим кратным для 24 и 12.
Сходный механизм действует и при поиске НОК и НОД исходя из другой пары чисел. В каждом примере необходимо сначала отыскать наибольший делитель, перемножить два числа и получить наименьшее кратное.
Что касается решения с помощью интернет-ресурсов, то на сегодняшний день имеется много онлайн-калькуляторов и программ, которые дают возможность сравнительно быстро найти НОД и НОК и подсказать грамотные пути решения.
Нахождение наибольшего делителя и НОК является не только распространенной, но и сравнительно трудной задачей для учеников средней школы. Ведь если не рассмотреть подробно такую тему, то дальнейшее изучение дробей, которые включают в себя числитель и знаменатель, окажется практически невозможным.
Важно грамотно использовать ресурсы на специальных математических сайтах, где могут подробно и понятно объяснить разложение дробей и нахождение общих делителей. Бояться ошибиться в такой теме не стоит, поскольку при правильном подходе она пройдет достаточно быстро, а вычисление различных по уровню сложности примеров не составит особых сложностей.