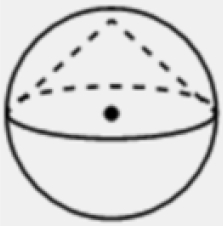
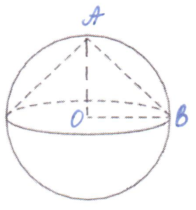
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен 10√2. Найдите образующую конуса.
Источники: fipi, os.fipi, Основная волна 2013.
Решение:
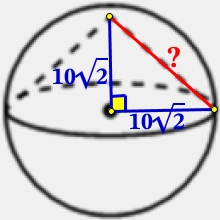
Радиус сферы равен радиусу конуса. Проведём два радиуса так, что бы они с образующей конуса создали прямоугольный треугольник.
По теореме Пифагора найдём образующую конуса l:
l2 = (10√2)2 + (10√2)2
l2 = 100·2 + 100·2
l2 = 200 + 200
l2 = 400
l = √400
l = 20
Ответ: 20.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 3
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Около конуса описана сфера (сфера содержит окружность
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Радиус сферы равен 28√2. Найдите образующую конуса.
Решение:
Всего: 9 1–9
Добавить в вариант
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна
Найдите радиус сферы.
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Радиус сферы равен
Найдите образующую конуса.
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна
Найдите радиус сферы.
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Радиус сферы равен
Найдите образующую конуса.
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен
Найдите образующую конуса.
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Образующая конуса равна
Найдите радиус сферы.
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен
Найдите образующую конуса.
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен
Найдите образующую конуса.
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен
Найдите образующую конуса.
Всего: 9 1–9
albina
2019-11-20 22:45:40
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен 10sqrt(2). Найдите образующую конуса.
математика 10-11 класс
3684
sova
2019-11-20 23:09:52
★
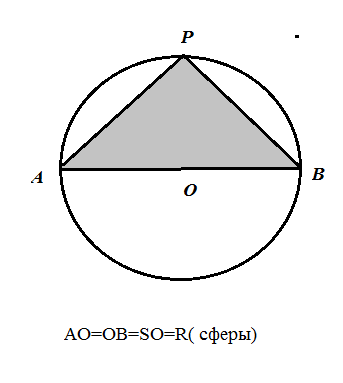
∠ APB=90 градусов, так как AB- диаметр
Δ АРВ — прямоугольный равнобедренный
H=R_(сферы)=10sqrt(2)
L^2=H^2+R^2=(10sqrt(2))^2+(10sqrt(2))^2=200+200=400
L=20
Skip to content
Около конуса описана сфера (сфера содержит окружность основание конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус конуса равен 10√2. Найдите образующую конуса.
Решение:
АВ- образующая конуса
( Отрезок, соединяющий вершину конуса с точкой окружности основания, называется образующей )
ОА=ОВ=10√2 радиусы сферы
Из прямоугольного треугольника АОВ найдем АВ по теореме Пифагора:
(В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов)
АВ2=АО2+ОВ2
АВ2=(10√2)2+(10√2)2
АВ2=(10)2(√2)2+(10)2(√2)2
АВ2=100•2+100•2
АВ2=400
АВ2=20
Ответ: 20
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Реклама