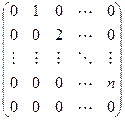
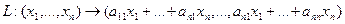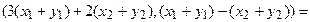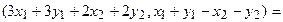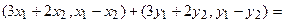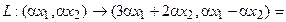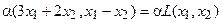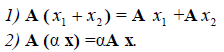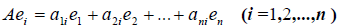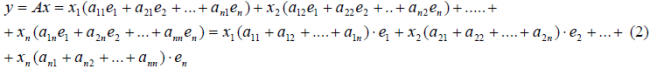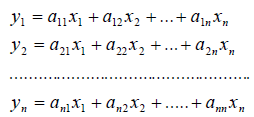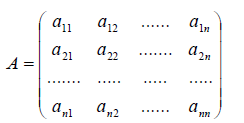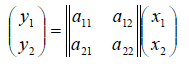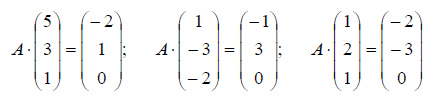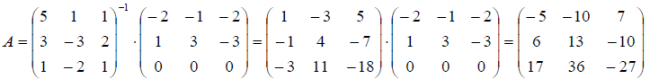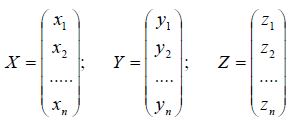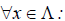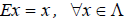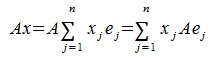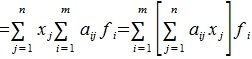Линейный
оператор ,
действующий из пространства
в пространство ,
ставит в соответствие каждому вектору
определенный вектор
из .
При этом вектор
называется образом
вектора
,
а вектор
— прообразом
вектора
при отображении .
Пусть
и
— некоторые базисы линейных пространств
и
соответственно. Тогда ,
и координаты вектора — образа
связаны с координатами вектора — прообраза
соотношением

(7.2.1)
в
котором
— матрица линейного оператора
в паре базисов
и .
В
случае, когда пространства
и
совпадают, базисы
и
также совпадают, и формула (7.2.1) принимает
вид

(7.2.2)
Образом
(областью
значений)
линейного
оператора
называется
множество всех элементов
вида .
Образ линейного оператора является
подпространством пространства
и обозначается .
Размерность образа называется рангом
оператора
и обозначается .
Ядром
линейного оператора
называется
множество всех векторов пространства
,
которые переводятся оператором
в нулевой вектор пространства .
Ядро линейного оператора является
подпространством пространства
и обозначается .
Размерность ядра называется дефектом
оператора
и обозначается .
Сумма
ранга и дефекта оператора
равна размерности пространства
.
Ранг
линейного оператора равен рангу матрицы
этого оператора.
Базис
системы векторов — столбцов матрицы
линейного оператора
образует систему координатных столбцов
базиса образа .
Базис подпространства решений однородной
системы линейных алгебраических
уравнений с матрицей оператора
образует базис ядра .
Пример
1.
Из пространства
с базисом
в пространство
с базисом
действует линейный оператор ,
имеющий в данной паре базисов матрицу

Найдите столбец координат в базисе
образа вектора
и столбец координат в базисе
прообраза вектора .
Решение.
Столбец координат образа вектора
в базисе находим
непосредственно по формуле (7.2.1):

Для
определения прообраза вектора
по той же формуле (7.2.1) имеем

или,
что то же самое,
Отсюда
находим все прообразы
вектора ,
где
— свободная переменная, принимающая
произвольные значения.
Пример
2.
В пространстве с
базисом линейный
оператор
переводит векторы ,
в
векторы ,
соответственно. Найдите матрицу оператора
в
базисе .
Решение.
Пусть 
матрица оператора в
базисе .
Тогда из условий ,
по формуле (7.2.2) имеем 
или,
в подробной записи,
Отсюда
получаем
Следовательно,
.
Пример
3.
Найдите базис ядра и базис образа
линейного оператора пространства ,
если этот оператор задан матрицей 
Решение.
При помощи элементарных преобразований
над строками матрицы
приведём её к ступенчатому виду:

Отсюда
следует, что .
Базис составляют,
например, векторы
и .
Дефект
оператора найдём по формуле
,
т.е.
фундаментальная система решений
однородной системы линейных алгебраических
уравнений с матрицей
будет состоять из одного вектора. Общее
решение однородной системы можно
записать в виде .
Полагая
получаем базисный вектор .
7.2.1.
Линейный оператор переводит
вектор
в вектор.
Найдите образ вектора
и прообраз вектора ,
если
,
,
;
,
,
;
,
,
.
7.2.2.
Линейный оператор в
паре базисов и
имеет матрицу .
Найдите прообраз вектора ,
если

;
б)
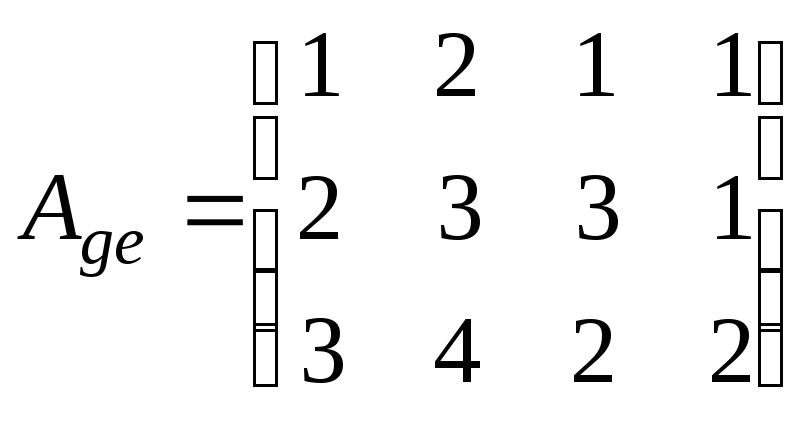
;
в)

.
7.2.3.
Выясните, существует ли линейный оператор
двумерного пространства, переводящий
векторы ,
соответственно в векторы ,
,
и найдите матрицу этого оператора в
базисе ,
:
а)
б)
в)
7.2.4.
Выясните, существует ли линейный оператор
трехмерного пространства, переводящий
векторы ,
,
соответственно в векторы ,
,
,
и найдите матрицу этого оператора в том
же базисе, в котором даны координаты
всех векторов:
а)
б)
7.2.5.
Для указанных линейных операторов
пространства
найдите дефект и ранг, а также постройте
базисы ядра и образа. Каждый оператор
описывается своим действием на
произвольный вектор :
а)
б)
в)
7.2.6.
Найдите образ и ядро оператора
дифференцирования в пространстве .
7.2.7.
В пространстве
рассмотрите разностный
оператор
где
— фиксированное
число, отличное от нуля. Найдите его
образ и ядро.
7.2.8.
Найдите образ и ядро оператора
проектирования (см. задачу 7.1.2) на
параллельно
и оператора отражения (см. задачу 7.1.3) в
параллельно .
7.2.9.
Найдите базис ядра и базис образа
линейного
оператора из ,
заданного в некотором базисе матрицей
:
а)
;
б)
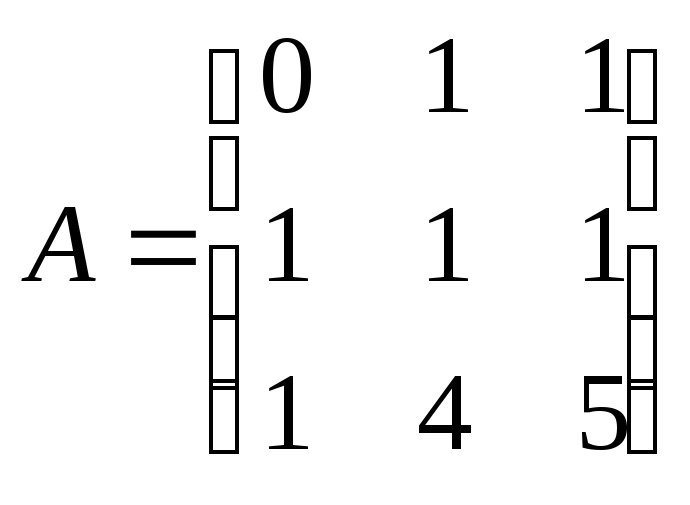
в)
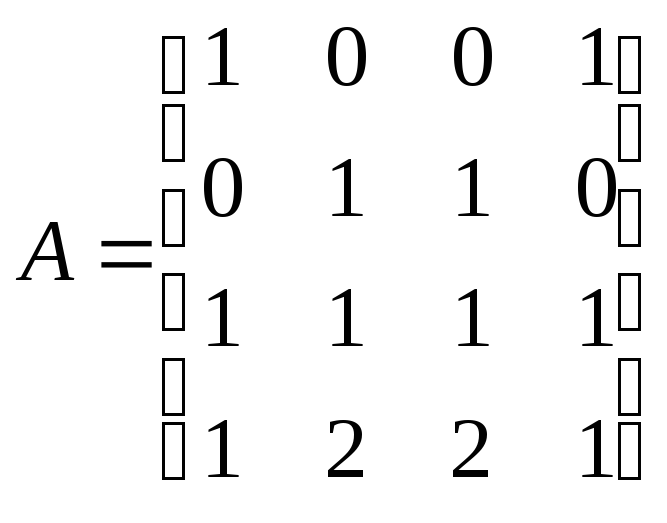
7.2.10.
Найдите размерность линейного пространства
всех линейных операторов, действующих
в
— мерном линейном пространстве
и постройте базис пространства .
Соседние файлы в папке Задачник-2
- #
- #
- #
- #
- #
- #
Матрица линейного оператора примеры
Построение матрицы по заданной формуле отображения.
Пусть отображение задано с помощью формулы:
то есть для координат произвольного исходного вектора определены координаты его образа. Тогда, рассматривая вместо произвольного вектора x вектор 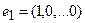
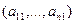
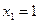
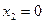
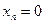
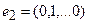
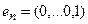
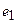
Пример 1. Пусть оператор задан с помощью формулы:
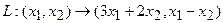
Прежде всего, докажем, что это отображение – действительно линейный оператор.
Отобразим сумму векторов:
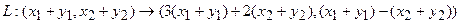
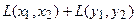
Аналогично для умножения на константу:
Для того чтобы найти матрицу этого линейного оператора, нужно, как было сказано выше, подставить значения x1 = 1, x2 = 0, а затем x1 = 0, x2 = 1. В этом примере образы базисных векторов – соответственно (3, 1) и (2, -1).
Поэтому матрица линейного оператора будет иметь вид:
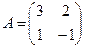
Аналогичным способом решается задача и для 3 и большего количества переменных.
Пример 2. 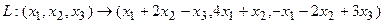
Построим матрицу оператора. Отображая вектор (1,0,0), получаем (1,4,-1), соответственно (0,1,0) переходит в (2,1,-2), а вектор (0,0,1) – в (-1,1,3).
Матрица линейного оператора:
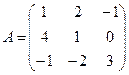
2.2. Построение матрицы оператора в случае, когда известен исходный базис и система векторов, в которую он отображается.
Если задана система 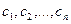
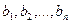
Матрицу этого оператора можно найти двумя способами: с помощью обратной матрицы и с помощью системы уравнений.
Пусть 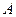
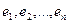
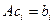
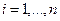
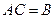
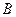
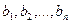
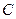
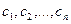
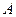
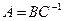
Пример. Найти матрицу линейного оператора, отображающего базис
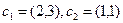
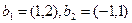
Здесь 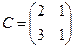
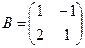
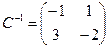
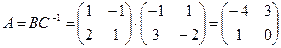
Проверка осуществляется умножением получившейся матрицы на каждый вектор: 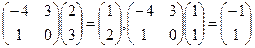
Аналогично решаются подобные задачи и для трёхмерного пространства. В приложении (§5) есть несколько вариантов таких задач.
2.3. Прочие способы нахождения матрицы оператора.
Существуют также примеры, где линейный оператор задаётся другими способами, отличными от рассмотренных в п. 2.1 и 2.2.
Пример. Линейными операторами являются как правое, так и левое векторное умножение на фиксированный вектор в трёхмерном пространстве, то есть отображения вида 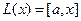
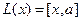
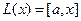
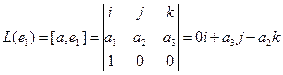
Аналогично, 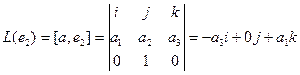
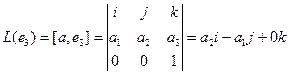
Координаты полученных векторов запишем в виде столбцов матрицы оператора.
Матрица оператора: 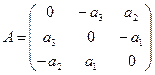
Аналогично можно построить матрицу линейного оператора 
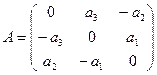
Пример. Линейный оператор дифференцирования в пространстве всех многочленов степени не более n. Это пространство размерности n + 1. Возьмём в качестве базиса элементы 
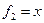
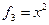
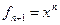
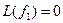
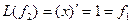
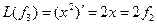
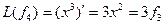
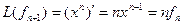
Матрица этого линейного оператора:
Линейные операторы могут отображать не только пространства конечной размерности, но и бесконечномерные пространства. Так, оператор дифференцирования может рассматриваться также в пространстве всех непрерывных функций. (В этом пространстве нет конечного базиса). В этом случае, очевидно, оператор не может быть задан матрицей конечного порядка.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10219 – 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Матрица линейного оператора
Определение 1. Если задан закон, который каждому вектору x?? ставит в соот ветствие вектор y . то говорят, что в линейном пространстве ? задан оператор A , при этом пишут:
Определение 2. Оператор A называется линейным, если для любых x 1 ?? и x 2 ?? и произвольного числа ? выполняются условия:
Рассмотрим теперь в евклидовом пространстве E n базис e 1 ,e 2 . e n и пусть в этом пространстве определён линейный оператор A : y = A x .
Разложим векторы x и y по базису e 1 ,e 2 . e n :
В силу линейности оператора A можно написать
Заметим, что каждый вектор 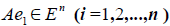
В силу единственности разложения по данному базису мы можем при равнять коэффициенты при базисных векторах в правых частях формул (1) и (2); тогда получим:
Получили, что линейному оператору A в данном базисе соответствует квадратная матрица
которая называется матрицей линейного оператора A , i -й столбец которой состоит из координат вектора Ae i (i = 1,2. n ) относительно данного базиса. Отметим, что матрица A оператора A зависит от выбора базиса e 1 ,e 2 . e n .
Итак, мы показали, что всякому линейному оператору A в евклидовом пространстве E n соответствует матрица A ; можно доказать и обратное утверждение: всякую квадратную матрицу A можно рассматривать как матрицу некоторого линейного оператора A в данном базисе e 1 ,e 2 . e n .
Представляют интерес невырожденные линейные операторы, т.е. такие операторы, матрицы которых имеют обратную A -1 , т.е. также являются невырожденными. В этом случае каждому вектору y (образу), определённому соотношением, отвечает единственный вектор x (прообраз) и при этом имеет место матричное равенство: X = A -1 ? Y .
Примеры линейных операторов
1. В пространстве 2-мерных векторов линейным оператором является правило
связывающее вектор-прообраз 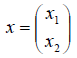
2. В пространстве бесконечно дифференцируемых функций линейным оператором является операция дифференцирования, ставящая в соответствие каждому элементу этого простран ства его производную функцию.
3. В пространстве многочленов P n (t) линейным оператором является операция умножения многочлена на независимую переменную t .
Пример: Известны образы базисных векторов E 3 под действием оператора A :
Найти матрицу этого оператора в исходном базисе.
Решение: По определению y = A x, значит в матричном виде можно записать, что A = X -1 Y . Для нашего примера получаем
Действия над операторами
Сложение линейных операторов. Пусть x?E n , A и B – два линейных оператора в этом пространстве.
Определение 1. Суммой линейных операторов A и B в E n называется оператор C, определяемый равенством Cx = A x + Bx , где x – любой вектор из E n .
Сумма линейных операторов является линейным оператором, причём его матрица C = A + B, где A и B – матрицы линейных операторов A и B .
Умножение линейного оператора на число. Пусть x?E n , линейный оператор A определён в E n , ? – некоторое число.
Определение 2. Произведением линейного оператора A на число ? называется оператор ?A , определяемый равенством 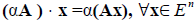
?A является линейным оператором, а матрица этого линейного оператора получается из матрицы A умножением её на число ? , т.е. она равна ? ? A.
Умножение линейных операторов. Пусть x? E n , y ? E n , z ? E n и кроме того в E n определены линейные операторы A и B таким образом, что y = Bx, z = A y .
Определение 3. Произведением A ? B линейных операторов A и B называется оператор C, определяемый соотношением Cx = A (Bx) .
Таким образом, перемножение линейных операторов состоит в последовательном их применении по отношению к вектору x .
Рассмотрим матрицы – столбцы:
и обозначим через A, B и C – соответственно матрицы линейных операторов A, B и C. Тогда Z = A ? (B ? X) = (A ? B) ? X = C ? X , таким образом, C = A ? B, т.е. матрица произведения линей ных операторов также является линейным оператором.
a) (A ? B)(x + y) = A (B(x + y)) = A (Bx + By) = A (Bx) + A (By) = = (A ? B) ? x + (A ? B) ? y
б) (A ? B)(? x) = A (B(? x)) = A (?Bx) =?A (Bx) =? (A ? B)x
Свойства умножения линейных операторов вытекают из свойств умножения матриц.
Определение 4. Линейные операторы A и В называются равными, если 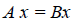
Определение 5. Оператор E называется единичным (или тождественным) оператором, если каждому элементу x линейного пространства 
1. Понятие линейного оператора
Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида 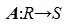
Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x1 и x2 пространства R и любого λ из числового поля K выполняются соотношения
Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.
Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы 

где A – m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:
Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов 

Пусть x − произвольный элемент в R. Тогда
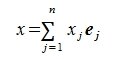 |
(3) |
является разложением x в по базису 
Применим оператор A к базисным векторам 
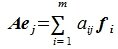 |
(4) |
где aij − координаты полученного вектора в базисе 
Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем
Сделаем следующее обозначение:
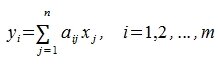 |
(6) |
Тогда равенство (5) примет следующий вид:
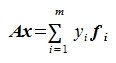 |
(7) |
Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе 
Построим матрицу A с элементами aij:
 |
(8) |
Тогда выражение (6) можно записать в матричном виде:
Матрица A называется матрицей линейного оператора в заданных базисах 

2. Сложение линейных операторов
Пусть A и B два линейных оператора действующих из R в S и пусть A и B – mxn − матрицы соответствующие этим операторам.
Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством
где x∈R означает, что x принадлежит пространстве R.
Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.
Применим оператор C к базисному вектору ej, тогда:
| Cej= Aej+ Bej= | n | (aij+bij) ej |
| ∑ | ||
| j= 1 |
Следовательно оператору C отвечает матрица 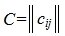
3. Умножение линейных операторов
Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.
Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:
Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.
Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C
можно записать в виде матричных равенств
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
Учитывая произвольность х, получим
Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.
4. Умножение линейного оператора на число
Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.
Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:
Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства
можно записать в виде матричных равенств
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
Учитывая произвольность х, получим
Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.
5. Нулевой оператор
Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:
6. Противоположный оператор
Противоположным оператору A называется оператор −A удовлетворяющий равенству:
7. Ядро линейного оператора
Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.
Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.
8. Образ линейного оператора
Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.
Образ линейного оператора обозначается символом im A.
9. Ранг линейного оператора
Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).
Ядро и образ линейного отображения
Ядром линейного отображения называется множество таких векторов , что , т.е. множество векторов из , которые отображаются в нулевой вектор пространства . Ядро отображения обозначается:
Образом линейного отображения называется множество образов всех векторов из . Образ отображения обозначается или
Заметим, что символ следует отличать от — мнимой части комплексного числа.
Примеры ядер и образов линейных отображений
1. Ядром нулевого отображения является все пространство , а образом служит один нулевой вектор, т.е.
2. Рассмотрим отображение , которое ставит в соответствие каждому вектору n-мерного линейного пространства его координатный столбец относительно заданного базиса . Ядром этого отображения является нулевой вектор пространства , поскольку только этот вектор имеет нулевой координатный столбец . Образ преобразования совпадает со всем пространством , так как это преобразование сюръективно (любой столбец из является координатным столбцом некоторого вектора пространства ).
3. Рассмотрим отображение , которое каждому вектору n-мерного евклидова пространства ставит в соответствие алгебраическое значение его проекции на направление, задаваемое единичным вектором . Ядром этого преобразования является ортогональное дополнение — множество векторов, ортогональных . Образом является все множество действительных чисел .
4. Рассмотрим отображение , которое каждому многочлену степени не выше ставит в соответствие его производную. Ядром этого отображения является множество многочленов нулевой степени, а образом — все пространство .
Свойства ядра и образа линейного отображения
1. Ядро любого линейного отображения является подпространством: .
В соответствии с определением требуется доказать, что множество является непустым и замкнутым относительно операций сложения векторов и умножения вектора на число. В самом деле, из однородности отображения следует, что
т.е. нулевой вектор отображается в нулевой вектор . Следовательно, ядро любого линейного отображения не является пустым и содержит, по крайней мере, нулевой элемент: . Покажем, что множество замкнуто по отношению к операциям сложения векторов и умножения вектора на число. Действительно:
Следовательно, множество является линейным подпространством пространства .
2. Образ любого линейного отображения является подпространством: .
В самом деле, докажем, например, замкнутость множества по отношению к операции умножения вектора на число. Если , то существует вектор такой, что . Тогда , то есть .
Поскольку ядро и образ линейного отображения являются линейными подпространствами (свойства 1 и 2), можно говорить об их размерностях.
Дефектом линейного отображения называется размерность его ядра: , а рангом линейного отображения — размерность его образа: .
3. Ранг линейного отображения равен рангу его матрицы (определенной относительно любых базисов).
В самом деле, если любой базис пространства , то . Поэтому максимальное число линейно независимых векторов системы (ранг системы векторов) равно максимальному числу линейно независимых столбцов матрицы отображения, т.е. рангу матрицы: .
4. Линейное отображение инъективно тогда и только тогда, когда , другими словами, когда дефект отображения равен нулю: .
Действительно, образом нулевого вектора служит нулевой вектор . Поэтому, если отображение инъективно, то ядро содержит только нулевой вектор , иначе два разных вектора имели бы один и тот же образ . Обратно, при условии разные векторы не могут иметь одинаковые образы , так как в этом случае из равенств , следует, что ненулевой вектор (приходим к противоречию).
5. Линейное отображение сюръективно тогда и только тогда, когда , другими словами, когда ранг отображения равен размерности пространства образов: .
6. Линейное отображение биективно (значит, обратимо) тогда и только тогда, когда и одновременно.
Теорема (9.1) о размерностях ядра и образа. Сумма размерностей ядра и образа любого линейного отображения равна размерности пространства прообразов:
Действительно, пусть . Выберем в подпространстве базис и дополним его векторами до базиса всего пространства . Покажем, что векторы образуют базис подпространства .
Во-первых, , так как образ любого вектора линейно выражается через векторы
Во-вторых, образующие линейно независимы. Если их линейная комбинация равна нулевому вектору:
то вектор принадлежит ядру (его образ — нулевой вектор). Однако, по построению этот вектор принадлежит алгебраическому дополнению . Учитывая, что , заключаем: . Получили разложение нулевого вектора по линейно независимой системе векторов, значит, все коэффициенты . Поэтому равенство справедливо только для тривиальной линейной комбинации, т.е. система векторов линейно независимая.
Таким образом, векторы образуют базис подпространства , а его размерность определяется количеством базисных векторов, т.е. , что равносильно (9.3).
Следствие. Линейное отображение биективно (значит, обратимо) тогда и только тогда, когда обратима его матрица (определенная относительно любых базисов).
Действительно, для обратимости преобразования (см. свойство 6) его матрица (размеров ) должна удовлетворять условиям (см. свойства 3,4,5):
Тогда по теореме 9.1 заключаем, что , т.е. матрица — квадратная n-го порядка и невырожденная , что и требовалось доказать.
Обратимые линейные отображения называются также невырожденными (имея в виду невырожденность их матрицы).
Линейные операторы
1. Понятие линейного оператора
Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида 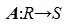
Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x1 и x2 пространства R и любого λ из числового поля K выполняются соотношения
Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.
Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы 

где A — m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:
Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов 

Пусть x − произвольный элемент в R. Тогда
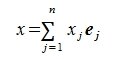 |
(3) |
является разложением x в по базису 
Применим оператор A к базисным векторам 
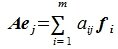 |
(4) |
где aij − координаты полученного вектора в базисе 
Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем
Сделаем следующее обозначение:
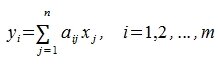 |
(6) |
Тогда равенство (5) примет следующий вид:
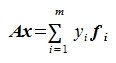 |
(7) |
Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе 
Построим матрицу A с элементами aij:
 |
(8) |
Тогда выражение (6) можно записать в матричном виде:
Матрица A называется матрицей линейного оператора в заданных базисах 

2. Сложение линейных операторов
Пусть A и B два линейных оператора действующих из R в S и пусть A и B — mxn − матрицы соответствующие этим операторам.
Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством
где x∈R означает, что x принадлежит пространстве R.
Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.
Применим оператор C к базисному вектору ej, тогда:
| Cej= Aej+ Bej= | n | (aij+bij) ej |
| ∑ | ||
| j= 1 |
Следовательно оператору C отвечает матрица 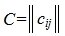
3. Умножение линейных операторов
Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.
Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:
Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.
Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C
можно записать в виде матричных равенств
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
Учитывая произвольность х, получим
Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.
4. Умножение линейного оператора на число
Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.
Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:
Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства
можно записать в виде матричных равенств
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
Учитывая произвольность х, получим
Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.
5. Нулевой оператор
Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:
6. Противоположный оператор
Противоположным оператору A называется оператор −A удовлетворяющий равенству:
7. Ядро линейного оператора
Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.
Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.
8. Образ линейного оператора
Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.
Образ линейного оператора обозначается символом im A.
9. Ранг линейного оператора
Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).
http://mathhelpplanet.com/static.php?p=yadro-i-obraz-linyeinogo-otobrazheniya
http://matworld.ru/linear-algebra/linear-operator.php
Линейные операторы
1. Понятие линейного оператора
Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида 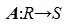
Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x1 и x2 пространства R и любого λ из числового поля K выполняются соотношения
- A(x1+x2)=Ax1+Ax2.
- A(λx)=λAx.
Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.
Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы 

где A — m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:
Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов 

Пусть x − произвольный элемент в R. Тогда
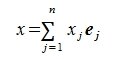 |
(3) |
является разложением x в по базису 
Применим оператор A к базисным векторам 
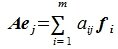 |
(4) |
где aij − координаты полученного вектора в базисе 
Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем
|
|
(5) |
Сделаем следующее обозначение:
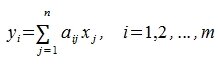 |
(6) |
Тогда равенство (5) примет следующий вид:
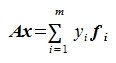 |
(7) |
Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе 
Построим матрицу A с элементами aij:
 |
(8) |
Тогда выражение (6) можно записать в матричном виде:
Матрица A называется матрицей линейного оператора в заданных базисах 

2. Сложение линейных операторов
Пусть A и B два линейных оператора действующих из R в S и пусть A и B — mxn − матрицы соответствующие этим операторам.
Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством
где x∈R означает, что x принадлежит пространстве R.
Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.
Применим оператор C к базисному вектору ej, тогда:
| Cej=Aej+Bej= | n | (aij+bij)ej |
| ∑ | ||
| j=1 |
Следовательно оператору C отвечает матрица 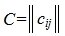
3. Умножение линейных операторов
Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.
Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:
Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.
Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C
можно записать в виде матричных равенств
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
Учитывая произвольность х, получим
Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.
4. Умножение линейного оператора на число
Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.
Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:
Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства
можно записать в виде матричных равенств
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
Учитывая произвольность х, получим
Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.
5. Нулевой оператор
Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:
6. Противоположный оператор
Противоположным оператору A называется оператор −A удовлетворяющий равенству:
7. Ядро линейного оператора
Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.
Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.
8. Образ линейного оператора
Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.
Образ линейного оператора обозначается символом im A.
9. Ранг линейного оператора
Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).
§ 1. Понятие отображения
Пусть Х и Y – множества элементов произвольной природы. Говорят, что задано Отображение (читается: отображение f множества X во множество Y), если задан закон, по которому каждому элементу
ставится в соответствие вполне определенный элемент
(рис. 1).
 |
Рис. 1.
Если , то
называется Образом элемента
,
– Прообразом элемента
при отображении F.
Примерами отображений являются функции, которые изучаются в школе и в математическом анализе, например, функция – это отображение
. Классный журнал является примером отображения множества учеников в классе во множество всех фамилий.
Отображение называется Тождественным, если оно любой элемент оставляет на месте. Тождественное отображение множества X на себя будем обозначать
. Таким образом,
.
Отображение называется Взаимно однозначным (или биективным, или биекцией), если оно удовлетворяет двум условиям:
1. такой, что
.
2.
Или одному, эквивалентному им, третьему условию:
3.Такой, что
Хороший пример взаимно однозначного отображения: в театре дают билет, каждому билету соответствует некоторое кресло, причем только одно.
Отображения и
называются Равными, если
.
Пусть заданы отображения и
. Произведением (или композицией) отображений F и G называется отображение
, такое, что
(рис. 2)
 |
Рис. 2.
Замечание. В произведении отображений сначала действует внутреннее, а затем внешнее отображение.
Примером произведения отображений является сложная функция.
Лемма. Произведение отображений ассоциативно, т. е., если заданы отображения ,
и
, то
.
UДля доказательства равенства отображений и
нужно показать, что
.
Итак, выберем произвольное . Тогда
; (1)
(2)
Сравнивая (1) и (2), видим, что
и, поэтому,
.t
Отображение называется Обратным к отображению
, если
и
(рис. 3).
 |
Рис. 3.
Упражнение. Докажите следующие утверждения:
1. Для того чтобы отображение F имело обратное необходимо и достаточно, чтобы F было взаимно однозначным.
2. Если отображение имеет обратное, то это обратное определяется однозначно.
§2. Определение линейного оператора и его простейшие свойства
Определение. Пусть и
– линейные пространства над одним и тем же полем
. Отображение
называется Линейным оператором, если оно удовлетворяет следующим условиям:
1*.
2*.
Следствие. При линейном операторе образ линейной комбинации векторов равен такой же линейной комбинации их образов, т. е. если – линейный оператор, то
(1)
UДоказательство проведем методом математической индукции по количеству векторов.
А) N=1: [2*]
– истинно.
Б) Предполагая, что утверждение верно для (N-1)-го вектора, доказываем его для N векторов.
= [1*] =
[2* и предположение индукции] =
=T
Примеры линейных операторов
1. Нулевой оператор :
. Очевидно, этот оператор удовлетворяет условиям 1* и 2*, значит, является линейным.
2. Тождественный оператор также, очевидно, является линейным.
3. Оператор дифференцирования , который каждой дифференцируемой функции ставит в соответствие ее производную, является линейным, т. к. производная суммы функций равна сумме их производных, а при умножении функции на число её производная умножается на это число.
4. Пусть – пространство свободных векторов,
.
Покажем, что оператор проектирования на ось также является линейным.
►В аналитической геометрии доказывалось, что . Тогда
=
=
=
=
;
=
=
=
Таким образом, условия 1* и 2* выполняются, а значит, оператор проектирования вектора на ось является линейным.◄
5. В пространстве
Векторов плоскости, закрепленных в начале координат О, рассмотрим оператор
поворота вектора на угол
против часовой стрелки и докажем его линейность.
►1*. Пусть – произвольные векторы,
,
(рис. 1). Построим
и
по правилу параллелограмма. Так как плоскость поворачивается
Рис.1. как жесткое целое, методами элементарной геометрии нетрудно показать, что при этом повороте диагональ
переходит в диагональ
. Значит,
.
2* . Пусть α>0,
,
,
,
(рис.2). Очевидно, вектор
получен из
поворотом на угол
, следовательно,
, а значит,
. Аналогично это свойство проверяется
И при , а при
оно очевидно.◄
Теорема. Пусть и
– линейные пространства над одним и тем же полем P и пусть в пространстве
задан базис
, (2)
А в пространстве – произвольная система векторов
. (3)
Тогда существует единственный линейный оператор , переводящий базис (2) в систему (3), то есть такой, что
. (4)
►Построение. Выберем произвольный вектор и разложим его по базису (2):
. Положим по определению
.
Линейность. Если — произвольные векторы, то
,
,
. Тогда
= [определение F ] =
;
.
Выполнение (4). Заметим, что все координаты вектора В базисе (2) равны нулю, за исключением K-й, которая равна 1. Таким образом, I-я координата вектора
равна
, то есть
. Тогда
,
Значит, условие (4) выполнено.
Единственность. Предположим, что существует еще один линейный оператор ,
, переводящий (2) в (3), то есть такой, что
. Тогда
– противоречие.◄
Простейшие свойства линейного оператора
1º. Линейный оператор переводит нейтральный элемент пространства
в нейтральный элемент пространства
.
►Пусть – линейный оператор. Тогда
.◄
2º. При линейном операторе линейно зависимые векторы пространства переходят в линейно зависимые векторы пространства
.
►Пусть — линейно зависимые векторы. Это значит, что существуют числа
, не все равные нулю, такие, что
. (5)
Подействуем линейным оператором на обе части равенства (5). Тогда
(5)
[(1) и 1º]
. (6)
Так как среди чисел есть отличные от нуля, то система {
} линейно зависима.◄
Упражнение. Верно ли утверждение: при линейном операторе линейно независимые векторы переходят в линейно независимые?
§ 3. Матрица линейного оператора
Определение матрицы линейного оператора
Пусть в линейном пространстве над полем
задан базис
(1)
И пусть – линейный оператор (читается так:
в себя). Построим систему векторов
(). (2)
Каждый из векторов системы (2) можно разложить по базису (1):

Сокращенно система (3) записывается одним равенством:
. (4)
Расположим числа в матрицу А по нашей договоренности: верхний индекс обозначает номер строки, а нижний – номер столбца:
Заметим, что столбцы полученной матрицы А являются координатными столбцами образов векторов базиса (1) в том же базисе. Обозначим
[]=
.
Равенство (4) можно переписать и так: , откуда, руководствуясь правилом цепочки, (4) записываем в матричном виде:
. (5)
Матрицей линейного оператора в некотором базисе называется матрица А, столбцами которой являются координатные столбцы образов базисных векторов в том же базисе. Это матрица
, элементы которой удовлетворяют системе равенств (3) или (4), а сама матрица удовлетворяет матричному равенству (5).
Примеры
1. Матрицей нулевого оператора в любом базисе является нулевая матрица; матрицей тождественного оператора
также в любом базисе является матрица единичная.
2. Пусть . Составим матрицу оператора проектирования на ось OX в базисе
. Для этого находим образы базисных векторов и разлагаем их по базису:

3. Составим матрицу оператора поворота плоскости на угол
(см.§2) в базисе
. Из рисунков 1 и 2 видно, что
Тогда

Рис. 1. Рис. 2.
Итак, если в пространстве задан какой-либо базис, то каждому линейному оператору
можно поставить в соответствие его матрицу в этом базисе, то есть квадратную матрицу A n-Ого порядка, причем эта матрица определяется однозначно.
Пусть теперь задана квадратная матрица А с элементами из поля P . Обозначим вектор, координатный столбец которого в базисе (1) совпадает с I-м столбцом матрицы А. Получим упорядоченную систему векторов
() (6)
Согласно теореме § 2 существует единственный линейный оператор такой, что
. По определению, матрица этого оператора в базисе (1) совпадает с А.
Обозначим — множество всех линейных операторов линейного пространства
над полем Р в себя. Из вышесказанного вытекает: если в
задан базис, то определяется отображение
,
Которое ставит в соответствие каждому линейному оператору его матрицу в этом базисе, причем это отображение взаимно однозначно. Это дает возможность в конечномерных линейных пространствах линейные операторы изучать с помощью их матриц.
Связь координат вектора с координатами его образа
Пусть в линейном пространстве задан базис (1), и пусть
–матрица линейного оператора
В этом базисе. Выберем произвольный вектор
и положим
. Обозначим
и
– координатные столбцы векторов
и
соответственно в базисе (1). Тогда
[(1) § 2] =
[(4)] =
,
И, т. о.,
. (7)
Равенство (7) есть не что иное, как разложение вектора по базису (1), а коэффициенты разложения – это координаты вектора
в этом базисе. В силу единственности координат вектора в данном базисе, получаем:
(8)
Записав (8) по правилу цепочки (), получаем
. (9)
Формула (8) и задает связь координат вектора и координат его образа при линейном операторе, а (9) – это её матричная запись.
Изменение матрицы линейного оператора при изменении базиса
Теорема. Пусть в линейном пространстве заданы два базиса:
(10)
И
, (11)
И пусть A= и
– матрицы линейного оператора
в базисах (10) и (11) соответственно. Тогда
, (12)
Где Т – матрица перехода от (10) к (11).
►Для того чтобы найти матрицу , следует образы векторов базиса (11) разложить опять же по этому базису. Имеем:
= [определение матрицы перехода] =
= [(1) § 2] =
= =[(4)]=
= [свойство 6º §9 гл. 3] =
.
Итак,
=
. (13)
Равенство (13) есть не что иное, как разложение вектора по базису (11). С другой стороны, по определению матрицы линейного оператора,
. (14)
В силу единственности координат вектора в данном базисе, из (13) и (14) получаем равенство
, (15)
Которое и дает нам связь элементов матриц линейного оператора в различных базисах. Запишем (15) по правилу цепочки:
. (16)
Так как (см. замечание в § 9 гл. 3), то из (16) получаем (12). ◄
Определение. Квадратные матрицы А и В называются Подобными, если существует невырожденная матрица Т такая, что .
Таким образом, мы видим, что матрицы линейного оператора в различных базисах подобны.
Лемма. Подобные матрицы имеют одинаковые определители. ►.◄
Определение. Определителем линейного оператора называется определитель его матрицы в некотором, а значит, и в любом базисе пространства
.
§4. Геометрический смысл определителя матрицы линейного
Оператора
Пусть – линейный оператор,
— его матрица в некотором ортонормированном базисе
, и пусть
– некомпланарные векторы, а
— их образы. Обозначим
и
координатные столбцы в выбранном базисе векторов
и
соответственно,
,
– объем параллелепипеда, построенного на векторах
, а
– объем параллелепипеда, построенного на векторах
. Тогда, учитывая (9) §3, получаем:
[(9) § 3]
[§ 5 главы 1] =
[§ 6 главы 1]
. (1)
Рассмотрим теперь пространство . Выберем в нем точку
и
линейно независимых векторов
,
. Параллелепипедом в
(
-мерным параллелепипедом) будем называть множество точек в
. (2)
Обозначим координатный столбец вектора
в каноническом базисе. По аналогии с трехмерным пространством, Объемом
— мерного параллелепипеда (2) будем называть число
.
Можно доказать, что при переходе от одного ортонормированного базиса к другому ортонормированному это число не меняется, т. е. определение объема параллелепипеда является корректным.
Точно так же, как и для трехмерного пространства, для пространства доказывается равенство (1).
Вывод: из формулы (1) на основании леммы §3 вытекает, что коэффициент изменения объема параллелепипеда при линейном операторе равен модулю определителя этого оператора.
§ 5. Операции над линейными операторами
Определения. Пусть и
— линейные пространства над одним и тем же полем
.
Суммой линейных операторов и
называется отображение
такое, что
.
Произведением линейного оператора на число
называется отображение
, такое что
.
Произведением линейных операторов и
называется отображение
такое, что
(т. е. произведение линейных операторов – это просто произведение или композиция отображений).
Теорема. Сумма линейных операторов, произведение линейного оператора на число, а также произведение линейных операторов также являются линейными операторами. При этом, если , А и В – матрицы линейных операторов F и G соответственно в некотором базисе пространства
, то матрицы операторов
,
и Gf в том же базисе совпадают соответственно с матрицами А+В, αА и ВА.
►Доказательство проведем для произведения линейных операторов.
Пусть и
— линейные операторы. Тогда
= [линейность F ] =
=
=[ линейность G ] = =
;
.
Таким образом, Gf – линейный оператор.
Пусть — матрицы линейных операторов
и
соответственно в базисе
пространства
, и пусть
— матрица оператора Gf В том же базисе. Тогда, по определению матрицы линейного оператора
. (1)
С другой стороны,
[линейность G] =
(2)
Сравнивая (1) и (2), на основании единственности координат вектора в данном базисе, делаем вывод: , откуда и получаем матричную запись: С=ВА.◄
Упражнение. Докажите, что множество
— линейный}
Всех линейных операторов пространства в пространство
есть линейное пространство над тем же полем, что и пространства
и
Относительно введенных операций сложения линейных операторов и умножения их на число. Найдите размерность
.
§ 6. Невырожденные линейные операторы
Определение. Линейный оператор называется невырожденным, если он любой ненулевой вектор переводит в ненулевой
Теорема 1. Для того чтобы линейный оператор был невырожденным необходимо и достаточно, чтобы его матрица в некотором, а значит, и в любом базисе пространства
была невырожденной
►Пусть А – матрица линейного оператора в некотором базисе, Х, как обычно, координатный столбец вектора
в том же базисе. Тогда
{F – невырожденный}
{однородная система линейных уравнений AX = O имеет единственное тривиальное решение}
{
}.
Так как определители подобных матриц совпадают, то утверждение справедливо и для любого базиса. ◄
Теорема 2. Для того чтобы линейный оператор был невырожденным необходимо и достаточно, чтобы он был взаимно однозначным.
►Пусть — линейный оператор, А— его матрица в некотором базисе, X и Y – координатные столбцы в том же базисе векторов
и
соответственно. Тогда
{ невырожденный}
{
Система
имеет единственное решение}
{
единственный
, что
}
{
единственный
, что
}
{F – взаимно однозначный}.◄
Теорема 3. Произведение невырожденных линейных операторов – невырожденный линейный оператор.
►Пусть и
— невырожденные линейные операторы. Тогда
{}
{
}
{
}.
Tаким образом, Gf – невырожденный линейный оператор.◄
§ 7. Обратный линейный оператор
Теорема. Для любого невырожденного линейного оператора существует единственный обратный оператор
, который также является линейным. При этом, если А – матрица оператора
в некотором базисе, то матрица оператора
в том же базисе совпадает с матрицей
.
►Единственность. Пусть некоторый оператор имеет два разных обратных:
И
. Тогда
—
Противоречие.
Существование. Пусть А — матрица оператора в некотором базисе. Тогда, по теореме 1 § 6,
, значит, существует
. Обозначим
— тот линейный оператор, матрица которого в выбранном базисе совпадает с
.
Так как , и т. к. произведению матриц соответствует произведение операторов, то
, и, таким образом,
.◄
Замечание. МОжно доказать, что любой взаимно однозначный линейный оператор имеет единственный обратный, который тоже является линейным.
§ 8. Изоморфизм линейных пространств
Определение. Изоморфизмом Линейных пространств называется взаимно однозначный линейный оператор. Если существует изоморфизм , то линейные пространства
и
называются изоморфными. Изоморфизм обозначается так:
.
Так как изоморфизм – взаимно однозначное отображение, то изоморфные объекты содержат одинаковое количество элементов. Кроме того, в силу линейности, действия, производимые над элементами пространства , одновременно производятся и над элементами пространства
. Поэтому в математике изоморфные объекты не различаются.
Свойства изоморфизма
1. — рефлективность (изоморфизм осуществляет тождественное отображение).
2.
— симметричность (если первый изоморфизм осуществляет с помощью отображения F, то второй — с помощью
).
3. {,
}
— транзитивность (если первый изоморфизм осуществляется с помощью отображения
, второй —
, то третий изоморфизм осуществляется с помощью отображения
).
Строгого доказательства этих свойств мы не приводим.
Теорема 1. Изоморфные линейные пространства имеют одинаковые размерности.
►Пусть и пусть
— изоморфизм. Выберем в
какой-либо базис
(1)
И покажем, что система
— (2)
Базис пространства . Действительно, в силу взаимной однозначности F,
единственный
такой, что
. Тогда, если
, то
. Значит, (2) – система образующих в
.
Докажем теперь линейную независимость (2).
[линейность F]
[взаимная однозначность F ]
[линейная независимость (1)]
{(2) — линейно независима}.
Таким образом, (2) – базис в , а значит,
. ◄
Теорема 2. Все N — мерные линейные пространства над полем Р изоморфны между собой, т. е. существует единственное с точностью до изоморфизма N-Мерное линейное пространство над полем Р.
►а) Докажем, что .
Выберем в какой-либо базис
. Тогда
. Обозначим
. Очевидно, отображение
— взаимно однозначное. Кроме того,
,
Поэтому F — линейный оператор, а значит, и изоморфизм. Итак, .
Б) Пусть теперь и
— N-Мерные линейные пространства над одним и тем же полем Р. Тогда
{ и
}
[симметричность]
{
и
}
[транзитивность]
{
}.◄
Таким образом, мы показали, что с точки зрения математики единственным N-Мерным линейным пространством над полем Р является .
§ 9. Образ и ядро линейного оператора
Определения. Образом Линейного оператора называется подмножество
линейного пространства
.
Ядром линейного оператора называется подмножество
линейного пространства
.
Теорема 1. Образ линейного оператора является подпространством пространства
, а его ядро – подпространством пространства
.
Упражнение. Докажите теорему 1.
Размерность подпространства называется Рангом оператора
и обозначается
, а размерность подпространства
называется Дефектом
и обозначается
.
Теорема 2. Если —
— мерное линейное пространство,
— линейный оператор, то
. (1)
►Обозначим . Так как
— подпространство пространства
, то
. Рассмотрим сначала случай, когда
. Выберем в
какой-либо базис
. (2)
По теореме 2 § 4 гл. 3 систему (1) можно дополнить до базиса
(3)
Пространства . Обозначим
. Очевидно,
— (4)
Базис пространства . Докажем, что
. Действительно,
Где , а
. Таким образом,
. Покажем, что сумма прямая. Пусть
. Тогда
можно разложить как по базису (2), так и по базису (4):
и
. Получаем
,
Откуда, в силу линейной независимости (3), вытекает, что . Поэтому
, а значит, сумма действительно прямая.
Покажем теперь, что . Построим отображение
.
Очевидно, — линейный оператор. Кроме того,
такой, что
. Так как
, то
где
,
. Тогда.
. Таким образом,
такой, что
. Предположим, что таких векторов два, т. е., что
, но
. Имеем:
. Отсюда вытекает, что
. Но
, следовательно,
, и поэтому
. Итак, мы показали, что
— взаимно однозначное отображение, следовательно, и изоморфизм. Так как изоморфные линейные пространства имеют одинаковые размерности, то
, откуда и вытекает доказываемое утверждение.
Рассмотрим теперь тривиальные случаи. Пусть , значит,
. Тогда
,
. Если же
, то
. В обоих случаях равенство (1), очевидно, выполняется. ◄
Следствие. Если — линейный оператор, то
(т. е.
). Если же оператор
— невырожденный, то
, следовательно,
, (т. е.
).