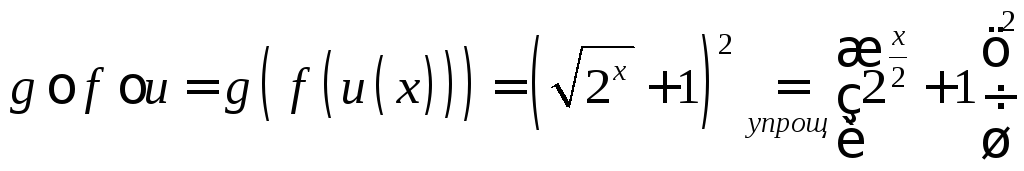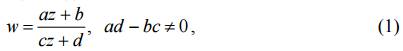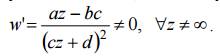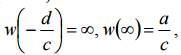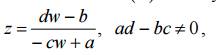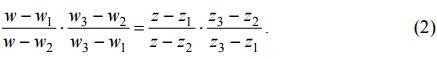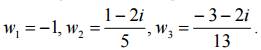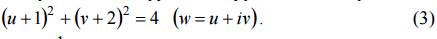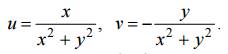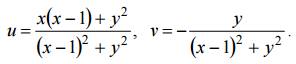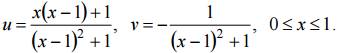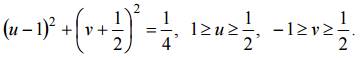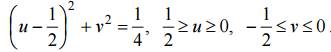Как найти образ при данном отображении

1. Образы и прообразы множеств при отображениях

Пусть
задана функция
и задано множество.

Образом
множества А при отображении f
называется множество всех,
являющихся значениями функцииfв точках.

Обозначается
.

В
частности,
,
то есть образом множества задания
функции является множество ее значений.

Если
множество,
то множество всех значений аргументах, для которых,
называетсяпрообразом
множества В при отображении f.

Записать кратко определение прообраза
можно так:
.

Пример
4 (образы
и прообразы множеств при различных
отображениях)

1) Множество является образом
множествапри отображении
функцией

Дирихле; множество
является прообразом
множествапри отображении
той же функцией;

2)

В — это образ множестваА при отображении функцией, A — это прообраз множества B при этом отображении функцией ;

2) найдем образ
множества
при отображении функцией:

, то есть

—это образ
множествапри отображении
функцией ;

3) найдем образ
множества
при отображении функцией.

или— это образ множестваАпри отображении функцией;

4) найдем прообраз
множества
при отображении функцией:

— это прообраз множестваВпри отображении функцией.

1. Понятие многозначного отображения

Отображениеназываетсямногозначным
отображением, еслитакие, что им соответствуют более одного
элемента(рис. 32).

Рис. 32

Многозначные функции рассматривать
будем пока только в исключительных
случаях, поэтому по умолчанию любая
функция
считается задающей однозначное
отображение.

1. Обратное отображение

Пусть
,
причем,
где(рис. 33).

Рис.
33

Функцияназываетсяобратным
отображением по отношению к отображению,
или— этообратная
функция по отношению к функции.

Обратная функция
является, вообще говоря, многозначной.

Если
отображение
является взаимно однозначным, т.е.
биективным, то отображениеявляется также взаимно однозначным
отображением множестваYна множествоX (рис.
34).

В этом случае функцияявляется обратной по отношению к функции,
а обе эти функцииfиназываютсявзаимно
обратными функциями.

Пример
5
(взаимно обратные функции)

Подробнее
о взаимно обратных функциях изложено
в §8 данного конспекта.

1. Суперпозиция отображений (сложная функция)

Если заданы два отображенияи,
то отображение,
ставящее в соответствие любому элементуединственный элемент,
называетсясуперпозицией
отображений f и g (другие
названия:композиция
отображений,сложное
отображение).

Обозначение
суперпозиции отображений:
или.

Иллюстрация
к сложному отображению приведена на
рис. 35.

Рис.
35

Пример
6 (сложные
отображения)

;

2)

Запись
сложных отображений как сложных функций:

.

Сложное отображение
(сложная функция) может получаться
суперпозицией любого количества
отображений.

Пример
7 (составление
сложных функций)

1) — сложная функция

;

2)

3)

,

1. Упражнения для самостоятельной работы

1. Найдите
образ
множествапри отображении функцией:
1),; 2),;
3),; 4),;

5) , ; 6)

,

;

2. Найдите
прообраз множества
при отображении функцией:
1),; 2),;
3),; 4),;
5),. 6)

3. Составьте
суперпозиции
идля заданныхии укажите множество задания и множество
значений каждого из составленных
отображений:
1),;
2),.

4. Запишите
суперпозиции
,,,
если,,;
укажите отображения множеств, которые
они задают.

Ответы
к упражнениям для самостоятельной
работы

1. 1) ; 2);

3) ; 4);

5) ; 6).

2. 1)
,; 2);
3); 4);
5); 6).

3. 1) ;;
2); .

4.fsdfsfsdfsdfsdfsdfsdfsdfsdfsdfsdfs

Образ окружности как найти

Конформные отображения. Дробно-линейная функция

Конформные отображения. Дробно-линейная функция

Определение 1. Функция вида

где a, b, c, d – комплексные числа, называется дробно-линейной.

Отображение, задаваемое этой функцией, называется дробно- линейным.

Условие ad − bc ≠ 0 означает, что w ≠ const . Функция (1) осуществляет конформное отображение расширенной комплексной плоскости Z на расширенную комплексную плоскость w, так как производная

Для 0 c ≠ предполагаем, что

для c = 0 функция (1) становится линейной, т. е. w = az + b и w(∞) = ∞. Функция

является обратной к функции (1). Она также является дробно-линейной и однозначной на расширенной комплексной плоскости, т. е. здесь функция (1) является однолистной.

Каждое дробно-линейное отображение может быть получено в результате последовательного выполнения трех отображений: линейного, отображения w = 1/z и снова линейного отображения.

Дробно-линейные отображения переводят:

1) окружность или прямую в окружность или прямую (круговое свойство);

2) пару точек, симметричных относительно окружности, – в пару то- чек, симметричных относительно образа этой окружности (свойство сохранения симметрии). Здесь «окружность», в частности, может быть прямой, если под последней понимать окружность бесконечного радиуса.

Существует единственное дробно-линейное отображение, которое три разных точки z₁, z₂, z₃ переводит соответственно в три разные точки w₁, w₂, w₃. Это отображение задается формулой

Если одна из точек z_k или w_k (k =1, 2, 3) является бесконечно удаленной точкой, то в формуле (2) разности, в которые входит z_k или w_k, требуется заменить единицами.

Существует бесконечно много дробно-линейных отображений, которые заданную окружность γ отображают на заданную окружность Г, причем область D, для которой γ является границей, отображается на одну из областей, для которой Г является границей.

Для обеспечения единственности дробно-линейного отображения достаточно выполнение одного из условий:

1) заданная точка z₀ ∈ D отображается в заданную точку w₀ ∈ D’, а любая кривая, выходящая из точки z₀, поворачивается на заданный угол α w₀ = f (z₀), α = arg(f ‘(z₀));

2) точки z₀ ∈ D и z₁ ∈ γ отображаются соответственно в заданные точки w₀ ∈ D’ и w₁ ∈ Γ.

Пример 1. Найти образ окружности, заданной уравнением

x 2 + y 2 + 2x − 4y + 1 = 0,

при отображении w = 1/z.

Решение. На основании кругового свойства дробно-линейного отображения окружность переходит в окружность. Для ее нахождения на заданной окружности x 2 + y 2 + 2x − 4y + 1 = 0, выберем три точки, например: z₁ = −1 z₂ = 1 + 2i, z₃ = −3 + 2i, образами которых при отображении w = 1/z будут точки

Точками w₁, w₂, w₃ однозначно определяется образ данной окружности, уравнение которой:

Для отображения w = 1/z имеем

Выразив отсюда x = x(u, v), y = (u, v) и подставив в уравнение заданной окружности, получим искомый образ (3).

Пример 2. Найти образ области D при отображении 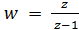, где D = 0 при данном отображении.

Решение. По условию имеем три пары соответствующих точек

Применяя формулу (2), получим искомое дробно-линейное отображение .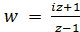

Найти образ и прообраз окружности

Введение в теорию множеств и комбинаторику

Практическая работа № 8. Отображения. Виды отображений

Вопросы к работе

1. Что такое «отображение множества в множество»?
2. Что такое «образ», что такое «прообраз» при данном отображении?
3. Что такое полный f — образ, что такое полный f — прообраз, при отображении f ?
4. Назовите типы отображений, дайте их определения и приведите примеры.
5. Какие два множества называются эквивалентными? Приведите примеры.
6. Какое множество называется счетным? Приведите примеры.

Образцы решения заданий

Пример 1. Пусть А = <1; 2; 3; 4; 5; 6; 7; 8; 9> N и В = <0; 1> Z Поставим в соответствие каждому числу x A его остаток при делении на 2.

Является ли это соответствие отображением? Какой тип у этого отображения? Какой элемент является образом элемента 6, 7? Найдем полный прообраз элемента 1.

Решение. Изобразим заданное соответствие с помощью графа:

1) каждый элемент множества А , является точкой исхода;

2) у каждой точки исхода, имеется только по одной точке прибытия. (Значит, указанное соответствие является отображением множества А в множество В);

3) Каждый элемент множества В является точкой прибытия. (Значит, это отображение «на»).

Так как в множестве В есть элемент (например, 0), для которого прообразом является ни один элемент из А , то это отображение не является взаимооднозначным.

Образом числа 6 является число 0 В , образом числа 7 – число 1 В . Полный прообраз числа 1 В есть множество чисел <1; 3; 5; 7; 9> А .

Пример 2. Пусть Х – множество треугольников плоскости, Y = R. Выберем единицу измерения длин и сопоставим каждому треугольнику число – периметр этого треугольника. Будет ли это соответствие отображением? Какой тип у заданного отображения? Каков полный прообраз числа у R ?

Решение. Каждый треугольник на плоскости имеет однозначно определенный периметр. Поэтому каждому треугольнику из множества Х сопоставляется единственное число из R , т. е. это соответствие является отображение Х в R . При этом у двух разных треугольников может быть одинаковый периметр. Другими словами, отображение не является взаимооднозначным. Кроме того, не существует треугольника, периметр которого равен отрицательному числу, т.е. отображение не является отображением «на». Пусть у R . Тогда:

1. у > 0, полный образ – множество всех треугольников плоскости, периметр которых равняется числу у , это множество бесконечное.
2. у ≤ 0, полный образ – пустое множество.

Пример 3. Х = <0; 1; 2; 3; 4> N , Y = Z. Отображение f множества Х в множество Y задано следующим образом:

Определим тип этого отображения и построим его график.

Решение. Для каждого x X найдем образ y Y. Соответствующие результаты запишем в таблицу:

Найти образ и прообраз окружности

Пример 1. Пусть y = sin x. За область определения функции можно принять множество действительных чисел. Тогда областью значений функции будет отрезок [-1, +1].

Пример 2. Пусть y = tg x. За область определения функции можно принять множество действительных чисел, отличных от чисел вида , где n пробегает все целые значения (т. к. для этих значений x функция не определена). Тогда областью значений функции будет множество всех действительных чисел.

Пример 3. Функция Дирихле:

Область определения здесь — множество действительных чисел, область значений — множество <0, 1>из двух элементов.

Замечательно, что гениальный русский математик Н. И. Лобачевский более ста лет назад дал определение функции, весьма близкое к приведенному. В противовес господствовавшему тогда взгляду на функцию как на аналитическое выражение (т. е. как на формулу) он подчеркивал значение идеи соответствия в определении понятия функции.

«Это общее понятие, — писал Лобачевский о понятии функции, — требует, чтобы функцией от x называть число, которое дается для каждого x и вместе с x постепенно изменяется. Значение функции может быть дано или аналитическим выражением или условием, которое подает средство испытать все числа и выбирать одно из них, или, наконец, зависимость может существовать и оставаться неизвестной».

Весьма близким к понятию функции является понятие отображения.

Определение. Пусть даны два множества X и Y. Такое соответствие, при котором каждому элементу соответствует (единственный) элемент , называется отображением множества X в множество Y; в частности, если каждый элемент соответствует по крайней мере одному элементу , то такое соответствие называется отображением X на Y.

Если элементу x соответствует y, то y называется образом элемента x, а x — прообразом элемента y. Пишут: или y = f(x). Множество A всех элементов , имеющих один и тот же образ , называется полным прообразом элемента y.

Конформные отображения. Дробно-линейная
функция

Определение 1. Функция
вида

где a, b, c, d – комплексные числа,
называется дробно-линейной.

Отображение, задаваемое
этой функцией, называется дробно- линейным.

Условие  ad − bc
≠ 0 означает, что w ≠ const . Функция (1) осуществляет конформное
отображение расширенной комплексной плоскости Z на расширенную комплексную
плоскость w, так как производная

Для 0 c ≠
предполагаем, что

для  c = 0 функция (1) становится
линейной, т. е. w = az + b и w(∞) = ∞. Функция

является обратной к функции (1). Она
также является дробно-линейной и однозначной на расширенной комплексной
плоскости, т. е. здесь функция (1) является однолистной.

Каждое дробно-линейное
отображение может быть получено в результате последовательного выполнения трех
отображений: линейного, отображения w = 1/z и снова линейного отображения.

Дробно-линейные
отображения переводят:

1) окружность или прямую
в окружность или прямую (круговое свойство);

2) пару точек,
симметричных относительно окружности, – в пару то- чек, симметричных
относительно образа этой окружности (свойство сохранения симметрии). Здесь
«окружность», в частности, может быть прямой, если под последней
понимать окружность бесконечного радиуса.

Существует единственное
дробно-линейное отображение, которое три разных точки  z₁, z₂,
z₃ переводит соответственно в три разные точки  w₁, w₂,
w₃. Это отображение задается формулой

Если одна из точек z_k или
w_k (k =1, 2, 3) является бесконечно удаленной точкой, то в формуле
(2) разности, в которые входит z_k или w_k, требуется
заменить единицами.

Существует бесконечно
много дробно-линейных отображений, которые заданную окружность γ
отображают на заданную окружность Г, причем область D, для которой γ
является границей, отображается на одну из областей, для которой Г является
границей.

Для обеспечения
единственности дробно-линейного отображения достаточно выполнение одного из
условий:

1) заданная точка z₀
∈
D отображается в
заданную точку  w₀ ∈ D’, а любая кривая, выходящая из точки z₀,
поворачивается на заданный угол α w₀ = f (z₀),
α = arg(f ‘(z₀));

2) точки z₀ ∈ D и z₁ ∈
γ отображаются
соответственно в заданные точки w₀ ∈ D’  и w₁ ∈
Γ.

Пример 1. Найти образ
окружности, заданной уравнением

x² + y² + 2x
− 4y + 1 = 0,

при отображении w  = 1/z.

Решение. На основании
кругового свойства дробно-линейного отображения окружность переходит в
окружность. Для ее нахождения на заданной окружности  x² + y²
+ 2x − 4y + 1 = 0,  выберем три точки, например: z₁ = −1
z₂ =  1 + 2i, z₃ = −3 + 2i, образами которых при
отображении w  = 1/z будут точки

Точками w₁, w₂,
w₃ однозначно определяется образ данной окружности, уравнение
которой:

Для отображения w  = 1/z 
имеем

Выразив отсюда x = x(u,
v), y = (u, v) и подставив в уравнение заданной окружности, получим искомый
образ (3).

Пример 2.  Найти образ
области D при отображении  ,   где   D = {z, 0 < Re(z) <
1, 0 < Im(z) < 1}.

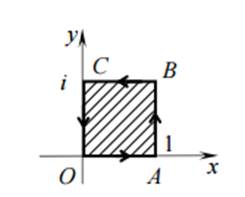
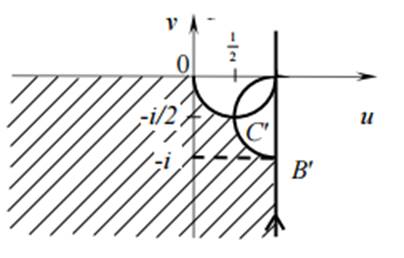
Будем искать образ границы
области D (рис. 1).

Сторона  OA: y = 0, 0
≤ x ≤ 1  отображается на отрицательную часть действительной оси (v
= 0, − ∞ < u ≤ 0) (рис. 2).

Рис. 1. Область D

Рис. 2. Образ области D

Сторона  AB: x = 1, 0
< y ≤ 1, отображается в линию  u = 1, −∞ < v ≤
−1.

Сторона  BC: y =1, 1 ≥
x ≥ 0, отображается в линию, параметрическое уравнение которой имеет вид

Исключив параметр x,
получим

Аналогично образ стороны
CO определяется уравнением

В соответствии с
принципом соответствия границ образом квадрата будет заштрихованная область на
рис. 1.

Пример 3. Найти
дробно-линейное отображение, которое точки z₁ = 1 и z₂ =
−1 оставляет неподвижными, а точку z₃ = i  переводит в точку 
w₃ = 0.

Найти образ полуплоскости
Im(z) > 0 при данном отображении.

Решение. По условию имеем
три пары соответствующих точек

z₁ = 1,  z₂ = -1, z₃ = i,

w₁ = 1, w₂ = -1, w₃ = 0,

Применяя формулу (2),
получим искомое дробно-линейное отображение.

Найдем теперь образ
верхней полуплоскости, границей которой является действительная ось. Согласно
круговому свойству действительная ось отображается в окружность. Чтобы найти
ее, на действительной оси выберем три точки, например: z₁ =1, z₂
= 0, z₃ = −1, образами которых бу- дут точки  w₁ =
1, w₂ = −i, w₃ = −1. Они лежат на окружности |w|
=1. По принципу соответствия границ получаем, что образом верхней полуплоскости
будет область D’= {w, |w| < 1}.

Пример 4. Найти
дробно-линейное отображение, которое круг  |z − 4i| < 2 отображает на
полуплоскость v > u так, что w(4i) = −4, w(2i) = 0.

Решение. Условие задачи
определяет две пары соответствующих точек. Третью пару найдем, пользуясь
свойством симметрии дробно линейного отображения, согласно которому точки z₁
= 4i и z₃ = ∞, симметричные относительно окружности  |z
− 4i| = 2, перейдут в точки w₁ = −4 и w₃ =
− 4i, симметричные относительно прямой u = v . Таким образом, найдена
третья пара точек z₃ = ∞ и w₃ = −4i. По
формуле (2) найдем искомое отображение .

Скачано с www.znanio.ru