From Wikipedia, the free encyclopedia
In algebra, given a polynomial
with coefficients from an arbitrary field, its reciprocal polynomial or reflected polynomial,[1][2] denoted by p∗ or pR,[2][1] is the polynomial[3]
That is, the coefficients of p∗ are the coefficients of p in reverse order. Reciprocal polynomials arise naturally in linear algebra as the characteristic polynomial of the inverse of a matrix.
In the special case where the field is the complex numbers, when
the conjugate reciprocal polynomial, denoted p†, is defined by,
where 

A polynomial p is called self-reciprocal or palindromic if p(x) = p∗(x).
The coefficients of a self-reciprocal polynomial satisfy ai = an−i for all i.
Properties[edit]
Reciprocal polynomials have several connections with their original polynomials, including:
- deg p = deg p∗ if
is not 0.
- p(x) = xnp∗(x−1).[2]
- α is a root of a polynomial p if and only if α−1 is a root of p∗.[4]
- If p(x) ≠ x then p is irreducible if and only if p∗ is irreducible.[5]
- p is primitive if and only if p∗ is primitive.[4]
Other properties of reciprocal polynomials may be obtained, for instance:
- A self-reciprocal polynomial of odd degree is divisible by x+1, hence is not irreducible if its degree is > 1.
Palindromic and antipalindromic polynomials[edit]
A self-reciprocal polynomial is also called palindromic because its coefficients, when the polynomial is written in the order of ascending or descending powers, form a palindrome. That is, if
is a polynomial of degree n, then P is palindromic if ai = an−i for i = 0, 1, …, n.
Similarly, a polynomial P of degree n is called antipalindromic if ai = −an−i for i = 0, 1, …, n. That is, a polynomial P is antipalindromic if P(x) = –P∗(x).
Examples[edit]
From the properties of the binomial coefficients, it follows that the polynomials P(x) = (x + 1)n are palindromic for all positive integers n, while the polynomials Q(x) = (x – 1)n are palindromic when n is even and antipalindromic when n is odd.
Other examples of palindromic polynomials include cyclotomic polynomials and Eulerian polynomials.
Properties[edit]
- If a is a root of a polynomial that is either palindromic or antipalindromic, then 1/a is also a root and has the same multiplicity.[6]
- The converse is true: If a polynomial is such that a is a root then if 1/a is also a root of the same multiplicity, then the polynomial is either palindromic or antipalindromic.
- For any polynomial q, the polynomial q + q∗ is palindromic and the polynomial q − q∗ is antipalindromic.
- It follows that any polynomial q can be written as the sum of a palindromic and an antipalindromic polynomial, since q = (q + q∗)/2 + (q − q∗)/2.[7]
- The product of two palindromic or antipalindromic polynomials is palindromic.
- The product of a palindromic polynomial and an antipalindromic polynomial is antipalindromic.
- A palindromic polynomial of odd degree is a multiple of x + 1 (it has –1 as a root) and its quotient by x + 1 is also palindromic.
- An antipalindromic polynomial over a field k with odd characteristic is a multiple of x – 1 (it has 1 as a root) and its quotient by x – 1 is palindromic.
- An antipalindromic polynomial of even degree is a multiple of x2 – 1 (it has −1 and 1 as roots) and its quotient by x2 – 1 is palindromic.
- If p(x) is a palindromic polynomial of even degree 2d, then there is a polynomial q of degree d such that p(x) = xdq(x + 1/x).[8]
- If p(x) is a monic antipalindromic polynomial of even degree 2d over a field k of odd characteristic, then it can be written uniquely as p(x) = xd(Q(x) − Q(1/x)), where Q is a monic polynomial of degree d with no constant term.[9]
- If an antipalindromic polynomial P has even degree 2n over a field k of odd characteristic, then its «middle» coefficient (of power n) is 0 since an = −a2n – n.
Real coefficients[edit]
A polynomial with real coefficients all of whose complex roots lie on the unit circle in the complex plane (that is, all the roots have modulus 1) is either palindromic or antipalindromic.[10]
Conjugate reciprocal polynomials[edit]
A polynomial is conjugate reciprocal if 

If p(z) is the minimal polynomial of z0 with |z0| = 1, z0 ≠ 1, and p(z) has real coefficients, then p(z) is self-reciprocal. This follows because
So z0 is a root of the polynomial 
for some constant c, i.e. 
A consequence is that the cyclotomic polynomials Φn are self-reciprocal for n > 1. This is used in the special number field sieve to allow numbers of the form x11 ± 1, x13 ± 1, x15 ± 1 and x21 ± 1 to be factored taking advantage of the algebraic factors by using polynomials of degree 5, 6, 4 and 6 respectively – note that φ (Euler’s totient function) of the exponents are 10, 12, 8 and 12.[citation needed]
Per Cohn’s theorem, a self-inversive polynomial has as many roots in the unit disk 
Application in coding theory[edit]
The reciprocal polynomial finds a use in the theory of cyclic error correcting codes. Suppose xn − 1 can be factored into the product of two polynomials, say xn − 1 = g(x)p(x). When g(x) generates a cyclic code C, then the reciprocal polynomial p∗ generates C⊥, the orthogonal complement of C.[14]
Also, C is self-orthogonal (that is, C ⊆ C⊥), if and only if p∗ divides g(x).[15]
See also[edit]
- Cohn’s theorem
Notes[edit]
- ^ a b *Graham, Ronald; Knuth, Donald E.; Patashnik, Oren (1994). Concrete mathematics : a foundation for computer science (Second ed.). Reading, Mass: Addison-Wesley. p. 340. ISBN 978-0201558029.
- ^ a b c Aigner, Martin (2007). A course in enumeration. Berlin New York: Springer. p. 94. ISBN 978-3540390329.
- ^ Roman 1995, pg.37
- ^ a b Pless 1990, pg. 57
- ^ Roman 1995, pg. 37
- ^ Pless 1990, pg. 57 for the palindromic case only
- ^ Stein, Jonathan Y. (2000), Digital Signal Processing: A Computer Science Perspective, Wiley Interscience, p. 384, ISBN 9780471295464
- ^ Durand 1961
- ^ Katz, Nicholas M. (2012), Convolution and Equidistribution : Sato-Tate Theorems for Finite Field Mellin Transformations, Princeton University Press, p. 146, ISBN 9780691153315
- ^ Markovsky, Ivan; Rao, Shodhan (2008), «Palindromic polynomials, time-reversible systems and conserved quantities» (PDF), Control and Automation: 125–130, doi:10.1109/MED.2008.4602018, ISBN 978-1-4244-2504-4, S2CID 14122451
- ^ Sinclair, Christopher D.; Vaaler, Jeffrey D. (2008). «Self-inversive polynomials with all zeros on the unit circle». In McKee, James; Smyth, C. J. (eds.). Number theory and polynomials. Proceedings of the workshop, Bristol, UK, April 3–7, 2006. London Mathematical Society Lecture Note Series. Vol. 352. Cambridge: Cambridge University Press. pp. 312–321. ISBN 978-0-521-71467-9. Zbl 1334.11017.
- ^ Ancochea, Germán (1953). «Zeros of self-inversive polynomials». Proceedings of the American Mathematical Society. 4 (6): 900–902. doi:10.1090/S0002-9939-1953-0058748-8. ISSN 0002-9939.
- ^ Bonsall, F. F.; Marden, Morris (1952). «Zeros of self-inversive polynomials». Proceedings of the American Mathematical Society. 3 (3): 471–475. doi:10.1090/S0002-9939-1952-0047828-8. ISSN 0002-9939.
- ^ Pless 1990, pg. 75, Theorem 48
- ^ Pless 1990, pg. 77, Theorem 51
References[edit]
- Pless, Vera (1990), Introduction to the Theory of Error Correcting Codes (2nd ed.), New York: Wiley-Interscience, ISBN 0-471-61884-5
- Roman, Steven (1995), Field Theory, New York: Springer-Verlag, ISBN 0-387-94408-7
- Durand, Émile (1961), «Masson et Cie: XV — polynômes dont les coefficients sont symétriques ou antisymétriques», Solutions numériques des équations algrébriques, vol. I, pp. 140–141
External links[edit]
- «The Fundamental Theorem for Palindromic Polynomials». MathPages.com.
- Reciprocal Polynomial (on MathWorld)
§
Будем обозначать через $ mathbb A_{} $ какое-либо из множеств $ mathbb Q, mathbb R_{} $ или
$ mathbb C_{} $.
Возвратным или взаимным полиномом называется такой полином $ a_0z^n+a_1z^{n-1}+dots+a_{n-1}z+a_n, a_0ne 0 $, у которого набор (вектор) коэффициентов
$ (a_0,a_1,dots, a_{n-1},a_n) $ симметричен относительно
середины:
$$ a_0=a_{n},a_1=a_{n-1},dots, a_{j}=a_{n-j} dots $$
П
Пример. Полиномы
$$ z^2-3,z+1,quad -sqrt{2}z^5+2,z^4+mathbf i z^3+2,z-sqrt{2},quad z^n+1 , quad z^n+z^{n-1}+z^{n-2}+dots + z^2 +z+1=sum_{j=1}^n z^{j} $$
будут возвратными.
Определение можно сделать более формальным, если ввести следующее преобразование.
Для произвольного полинома $ F(z)=A_0z^n+A_1z^{n-1}+dots+A_{n-1}z+A_n $ обозначим
$$F^{ast}(z)= A_0+A_1z+dots+A_{n-1}z^{n-1}+A_nz^n =sum_{j=0}^n A_jz^{j} , $$
т.е. полином $ F^{ast}(z) $ — это записанный «в обратном порядке» степеней мономов полином $ F(z) $: старший коэффициент стал свободным членом, коэффициент при $ z^{n-1} $ перешел в коэффициент при $ z_{} $ и т.д. Формально полином $ F^{ast}(z) $ связан с полиномом $ F(z) $ функциональным соотношением:
$$ F^{ast}(z)equiv z^n F(1/z) .$$
§
В литературе по теории кодирования полином $ F^{ast}(z) $ называется полиномом, двойственным к $ F_{}(z) $.
Имеется нестыковка в русскоязычном понятии возвратный полином (возвратное уравнение) и английским выражением reciprocal polynomial. Согласно ангоязычной Википедии reciprocal polynomial для произвольного полинома $ F(z) $ — это полином, обозначенный выше $ F^{ast}(z) $ (да еще с дополнительным сопряжением коэффициентов), а собственно возвратный — в приведенном выше определении — полином называется palindromic polynomial1).
Т
Теорема 1. Полином $ f_{}(z) $ будет возвратным тогда и только тогда, когда $ f(z)equiv f^{ast}(z) $.
=>
Если $ lambda_{} $ обозначает какой-то корень возвратного полинома, то корнем этого полинома будет и $ 1/lambda $.
Последнее следствие равносильно тому, что множество всех корней возвратного полинома можно разбить на пары корней $ {lambda,1/lambda } $. Геометрически: изобразив на комплексной плоскости $ z=x+mathbf i y $ корни возвратного полинома, находящиеся внутри единичного круга $ |z|<1 $, отображением $ w=1/z $ мы получим его корни, лежащие вне этого круга.
Отдельно следует исследовать значения $ z_{}=pm 1 $, т.к. они «остаются на своих местах» при таком отображении.
?
Доказать, что произведение двух возвратных полиномов является возвратным полиномом.
Т
Теорема 2. Возвратный полином $ f(z)in mathbb A[z] $ нечетной степени можно
представить в виде произведения $ f(z)equiv (z+1)f_1(z) $, где $ f_1(z)in mathbb A[z] $
является возвратным полиномом четной степени.
Доказательство производится формальной подстановкой $ z=-1 $ в функциональное равенство:
$$f(z)equiv z^nf(1/z)quad Rightarrow quad f(-1)=(-1)^n f(-1) ; $$
при $ n_{} $ нечетном это возможно только при $ f(-1)=0 $.
Следовательно, по теореме Безу,
$ f(z)equiv (z+1)f_1(z), deg f_1=deg f -1 $. Осталось показать, что
и полином $ f_1(z) $ будет возвратным. С помощью схемы Хорнера установим принцип формирования его коэффициентов на примере $ n_{}=7 $:
$$
begin{array}{c|c|c|c|c|c|c|c|c}
& a_0 & a_1 & a_2 & a_3 & a_3 & a_2 & a_1 & a_0 \
hline
-1 & a_0 & -a_0+a_1 & a_0-a_1+a_2 &-a_0+a_1-a_2+a_3 & a_0-a_1+a_2
& -a_0+a_1 & a_0
end{array}
$$
Для общего случая рассуждения аналогичны.
♦
Итак, возвратный полином нечетной степени обязательно имеет корень $ lambda=-1 $.
А для поиска остальных его корней мы получили возвратное уравнение четной степени. Покажем, что решение последнего
может быть сведено к решению подходящего уравнения в два раза
меньшей степени. Пусть $ deg f=2, m,, m in mathbb N $. Разделим уравнение
$ f(z)=0 $ на $ z^m $:
$$a_0z^m+a_1z^{m-1}+dots +a_{m-1}z+ a_{m}+a_{m-1}frac{1}{z}+ dots +
a_1frac{1}{z^{m-1}}+a_0frac{1}{z^{m}}=0 .$$
Сгруппируем члены с одинаковыми коэффициентами:
$$
a_0left(z^m + frac{1}{z^{m}} right)+a_1left(z^{m-1} + frac{1}{z^{m-1}} right)
+dots + a_{m-1}left(z + frac{1}{z} right)+a_m=0 .
$$
Введем новую переменную
$$w= z + frac{1}{z} .$$
Т
Теорема 3. Выражение $ z^k+1/z^k $ может быть представлено в виде полинома
степени $ k_{} $ от переменной $ w_{} $ с целыми коэффициентами:
$$ z^k+frac{1}{z^k} equiv P_k(w) in mathbb Z[w] . $$
Доказательство проводится индукцией по $ k_{} $. Для $ k_{}=1 $ утверждение очевидно.
Предположим, что оно доказано для всех показателей, меньших $ k_{} $. Разложим
$ w^k= (z+1/z)^k $ по формуле бинома Ньютона:
$$w^k=left(z + frac{1}{z} right)^k=left(z^k + frac{1}{z^k} right)
+C_k^1left(z^{k-2} + frac{1}{z^{k-2}} right)
+C_k^2left(z^{k-4} + frac{1}{z^{k-4}} right)+dots $$
Поскольку, по индукционному предположению, выражения из второй, третьей и т.д.
скобок правой части формулы могут быть выражены в виде полиномов от $ w_{} $,
то из этого равенства можно найти и выражение для $ z^k+1/z^k $.
♦
П
Пример.
$$
begin{array}{lcl}
w^2=z^2 + 2 + 1/z^2 &Rightarrow & z^2 + 1/z^2=w^2-2 , \
w^3=z^3 + 3,z +3/z+ 1/z^3 &Rightarrow & z^3 + 1/z^3=w^3-3,w , \
w^4=z^4 + 4,z^2 +6+ 4/z^2+ 1/z^4 &Rightarrow & z^4 + 1/z^4=w^4-4,(w^2-2) — 6= w^4-4,w^2 + 2 \
dots
end{array}
$$
Последняя теорема позволяет свести решение возвратного уравнения $ f(z)=0 $ четной степени $ 2, m $ к решению уравнения
$$Phi(w)equiv a_0P_m(w)+a_1P_{m-1}(w)+dots+ a_{m-1}w+a_m=0 $$
степени $ m_{} $. Если $ mu_{} $ — произвольный корень последнего, то уравнение $ z+1/z=mu $ даст значения двух корней возвратного уравнения.
П
Пример. Решить уравнение
$$z^6-6,z^5+14,z^4-18,z^3+14,z^2-6,z+1 =0 .$$
Решение. Разделив уравнение на $ z^3 $, формируем уравнение
$$ left(z^3+frac{1}{z^3} right)-6,left( z^2+frac{1}{z^2} right)+14left(z+frac{1}{z} right)-18=0 . $$
Затем, с помощью формул предыдущего примера, выписываем
уравнение относительно $ w_{} $:
$$(w^3-3,w)-6, (w^2-2)+14,w -18 =0 Rightarrow w^3-6, w^2+11, w -6 =0
.$$
Легко проверить, что корнями последнего уравнения являются
$ mu_1=1,, mu_2=2,, mu_3=3 $. Остается решить три квадратных уравнения
$$z+1/z=1, z+1/z=2, z+1/z=3 .$$
Ответ.
$$1 mbox{ (кратности 2)}, frac{1}{2} pm mathbf i frac{sqrt{3}}{2},
frac{3}{2}pm frac{sqrt{5}}{2} . $$
Частным случаем возвратного уравнения является уравнение
$$sum_{j=0}^{n-1} z^{n-1-j}= z^{n-1}+z^{n-2}+dots + z + 1=0 , $$
которое получается из уравнения деления круга
$ z^n-1=0 $, задающего значения корней n-й
степени из 1.
?
Найти выражения для $ sin {2pi}/5 $ и $ cos {2pi}/5 $, решив уравнение
$ z^4+z^3+z^2+z+1=0 $.
Имеется способ непосредственного построения полинома $ Phi(w) $, являющегося результатом подстановки
$ w=z+1/z $ в выражение для $ f(z)/z^m $. Этот способ основан на вычислении результанта двух полиномов.
Т
Теорема 4. Для возвратного полинома $ f(z) $ четной степени имеет место тождество
$$ mathcal R_z (f(z),z^2-wz+1) equiv Phi^2(w) ; $$
здесь результант рассматривается для полиномов относительно переменной $ z_{} $.
=>
$ Phi^2(0)=f(mathbf i)f(-mathbf i) $.
Это следует из представления результанта полиномов через корни одного из них — в данном случае, через корни полинома $ z^2+1 $.
Здесь мы встретились с отдельной интересной проблемой: известно, что некоторый полином $ Psi(z) $ является квадратом какого-то другого полинома $ Phi(z) $; как найти $ Phi(z) $, т.е. извлечь квадратный корень из $ Psi(z) $ ? Имеются разные подходы к решению этой задачи. Наиболее просто реализуемый заключается в вычислении наибольшего общего делителя полинома $ Psi(z) $ и его производной (см. теорию
☞
ЗДЕСЬ ):
$$ operatorname{HOD} (Psi(z),Psi'(z)) ; $$
поскольку $ operatorname{HOD} $ вычисляется с точностью до домножения на константу, следует зафиксировать один из коэффициентов — например, потребовать чтобы свободный член $ operatorname{HOD} (Psi(z),Psi'(z)) $ был равен $ sqrt{Psi(0)} $. Тогда, как правило, этот $ operatorname{HOD} $ и будет искомым полиномом:
$$ Phi(z) equiv operatorname{HOD} (Psi(z),Psi'(z)) . $$
Имеются, однако, исключительные случаи (например, предлагаемый алгоритм засбоит на полиноме $ z^8+4,z^6+6,z^4+4,z^2+1 $), но эти вырождения мне лень сейчас описывать…
П
Пример. Для полинома
$$ f(z)=z^6-6,z^5+14,z^4-18,z^3+14,z^2-6,z+1 $$
из последнего примера представим результант в форме Сильвестра:
$$
mathcal R_z (f(z),z^2-wz+1)=-
left|begin{array}{rrrrrrrr}
1 & -6 & 14 &-18 & 14 & -6 & 1 & 0 \
0 & 1 & -6 & 14 &-18 & 14 & -6 & 1 \
0 & 0 & 0 & 0 & 0 & 1 & -w & 1 \
0 & 0 & 0 & 0 & 1 & -w & 1 & 0 \
0 & 0 & 0 & 1 & -w & 1 & 0 & 0 \
0 & 0 & 1 & -w & 1 & 0 & 0 & 0 \
0 & 1 & -w & 1 & 0 & 0 & 0 & 0\
1 & -w & 1 & 0 & 0 & 0 & 0 & 0
end{array}right|
=(-w^3+6,w^2-11,w+ 6)^2 .
$$
Альтернативный метод сведения возвратного уравнения к уравнению вдвое меньшей степени основан на следующем результате.
Т
Теорема 5. Замена переменной
$$
w=left(frac{z+1}{z-1} right)^2
$$
в возвратном уравнении $ f(z)=0 $ четной степени $ 2n_{} $ приводит к алгебраическому уравнению $ Xi(w)=0 $ степени $ le n $.
Доказательство. Отображение комплексной плоскости $ mathbb C $, задаваемое формулой
$$
u=frac{z+1}{z-1}
$$
отображает пару точек $ { z, 1/z } $ в пару точек $ { u,-u} $. Полином
$$
mathfrak F(u)equiv (u-1)^{2n} f((u+1)/(u-1))
$$
будет четным по $ u $. Действительно,
$$
mathfrak F(-u)equiv (-u-1)^{2n} f((-u+1)/(-u-1))equiv (u+1)^{2n} f((u-1)/(u+1))equiv (u+1)^{2n} f(1/z)equiv
$$
$$
equiv (u+1)^{2n} f(1/z)z^{2n} frac{1}{z^{2n}}equiv (u-1)^{2n} f(z)equiv (u-1)^{2n} f((u+1)/(u-1))equiv mathfrak F(u) , .
$$
Замена $ u^2=w $ в $ mathfrak F(u) $ приводит к полиному $ Xi(w) $.
♦
П
Пример. Для полинома
$$ f(z)=z^6-8,z^5+16,z^4-32,z^3+16,z^2-8,z+1 $$
замена переменной
$$ z= frac{sqrt{w}+1}{sqrt{w}-1} $$
приводит к дроби
$$
-2frac{-41+9,w-7,w^2+7,w^3}{(sqrt{w}-1)^6} quad Rightarrow quad Xi(w)=7,w^3-7,w^2+9,w-41 , .
$$
=>
$ deg Xi(w) < n $ тогда и только тогда, когда $ f(1)=0 $. Если $ f(1) ne 0 $ то
$$ Xi(w) = b_0x^n+dots+b_n quad mbox{ при } b_n/b_0 = f(-1)/f(1) , . $$
Т
Теорема 6. Полином $ f(z) in mathbb C[z] $ четной степени $ 2n_{} $ является возвратным тогда и только тогда, когда его можно представить в виде произведения2)
$$ f(z) equiv f_1(z) f_1^{ast}(z) quad npu quad f_1(z) in mathbb C[z], deg f_1=n . $$
Полином $ f(z) in mathbb C[z] $ нечетной степени $ 2n_{}+1 $ является возвратным тогда и только тогда, когда его можно представить в виде произведения
$$ f(z) equiv (z+1)f_1(z) f_1^{ast}(z) quad npu quad f_1(z) in mathbb C[z], deg f_1=n . $$
Доказательство достаточности очевидно ввиду теоремы $ 1 $. Необходимость следует из следствия к той же теореме: корни возвратного полинома четной степени $ 2,n $ можно разбить на пары $ { lambda, 1/lambda } $. В результате разложение $ f_{}(z) $ на линейные множители будет иметь вид
$$ f(z)equiv a_0underbrace{(z-lambda_1)(z-lambda_2)times dots times (z-lambda_n)}_{equiv f_{_1}(z)} times
underbrace{(z-1/lambda_1)(z-1/lambda_2)times dots times (z-1/lambda_n)}_{equiv f_{_2}(z)} . $$
Согласно свойству
3
из пункта
☞
ПРЕОБРАЗОВАНИЕ КОРНЕЙ имеет место тождество $ f_2(z) equiv f_1^{ast}(z) $.
♦
Т
Теорема. Если характеристический полином $ det (P-lambda E) $ вещественной ортогональной матрицы $ P $ не имеет корнем $ lambda= +1 $ или же кратность этого корня — четная, то этот полином является возвратным. Если же кратность корня $ lambda=+1 $ нечетная, то частное
$$ frac{det (P-lambda E)}{lambda-1} $$
является возвратным полиномом.
Доказательство
☞
ЗДЕСЬ.
Рассмотрим полином $ a_0z^n+a_1z^{n-1}+dots+a_{n-1}z+a_n, a_0ne 0 $, у которого набор коэффициентов
$ (a_0,a_1,dots, a_{n-1},a_n) $ «симметричен с комплексным сопряжением» относительно середины этого набора:
$$ a_0=overline{a_{n}},a_1=overline{a_{n-1}},dots, a_{j}=overline{a_{n-j}} dots $$
В отечественной литературе я встречал для подобного полинома название симметрический только в [2]. Не очень удобное название, поскольку возникает коллизия с другим объектом, за которым это название прочно закрепилось. В англоязычной литературе он называется self-reciprocal (см. замечание о терминологии в предыдущем пункте ). В настоящем ресурсе буду называть его сопряженно-возвратным.
П
Пример.
$$ f(z)=(1+mathbf i)z^5+ 3,z^4+(-sqrt{3}-2mathbf i)z^3 +(-sqrt{3}+2mathbf i)x^2+3,z+ (1-mathbf i) , .$$
В случае, когда все коэффициенты полинома $ f_{}(z) $ вещественны, то сопряженно-возвратный полином совпадает с возвратным. По аналогии со случаем возвратного полинома, выводится функциональное тождество, определяющее сопряженно-возвратный полином:
$$ f(z)equiv z^noverline{f(1/z)} ; $$
здесь знак $ overline{ cdot } $ над полиномом означает, что все его коэффициенты меняются на комплексно-сопряженные:
$$ overline{ (3-mathbf i)z^2+2mathbf i , z — 178} equiv (3+mathbf i)z^2-2mathbf i , z — 178 . $$
=>
Если $ lambda_{} $ — корень сопряженно-возвратного полинома $ f_{}(z) $, то и $ 1/ overline{lambda} $ также является корнем этого полинома.
Т
Теорема [Кон]. Число корней сопряженно-возвратного полинома внутри единичного круга равно числу различных корней его производной вне этого круга.
[1]. Журавский А.М. Сборник задач по высшей алгебре. М.-Л.ГТТИ. 1933
[2]. Крейн М., Наймарк М. Метод симметрических и эрмитовых форм в теории отделения корней
алгебраических уравнений.-Харьков, ГТТИ, 1936, 39 с.
В алгебре, обратный многочлен или отраженный многочлен p или p, полинома p степени n с коэффициентами из произвольного поля , например
- p (x) = a 0 + a 1 x + a 2 Икс 2 + ⋯ + тревога, { Displaystyle р (х) = а_ {0} + а_ {1} х + а_ {2} х ^ {2} + cdots + а_ {п} х ^ {п}, , !}
— многочлен
- p ∗ (x) = an + an — 1 x + ⋯ + a 0 xn = xnp (x — 1). { displaystyle p ^ {*} (x) = a_ {n} + a_ {n-1} x + cdots + a_ {0} x ^ {n} = x ^ {n} p (x ^ {- 1}).}
По сути, коэффициенты записываются в обратном порядке. Они естественным образом возникают в линейной алгебре как характеристический многочлен для , обратный матрице.
. В частном случае, когда многочлен p имеет комплексные коэффициенты, то есть
- p (z) = a 0 + a 1 z + a 2 z 2 + ⋯ + anzn, { displaystyle p (z) = a_ {0} + a_ { 1} z + a_ {2} z ^ {2} + cdots + a_ {n} z ^ {n}, , !}
сопряженный обратный многочлен, p, заданный как,
- p † (z) = an ¯ + an — 1 ¯ z + ⋯ + a 0 ¯ zn = znp (z ¯ — 1) ¯, { displaystyle p ^ { dagger} (z) = { overline {a_ {n}}} + { overline {a_ {n-1}}} z + cdots + { overline {a_ {0}}} z ^ {n} = z ^ {n} { overline {p ({ bar {z}} ^ {- 1})}},}
где ai ¯ { displaystyle { overline {a_ {i}}}}

Многочлен p называется самовзаимным или палиндромным, если p (x) = p (x). Коэффициенты самовзаимного полинома удовлетворяют a i = a n-i. В сопряженном обратном случае коэффициенты должны быть действительными, чтобы удовлетворять условию.
Содержание
- 1 Свойства
- 2 Палиндромные и антипалиндромные многочлены
- 2.1 Примеры
- 2.2 Свойства
- 2.3 Действительные коэффициенты
- 3 Сопряженные взаимные многочлены
- 4 Применение в теории кодирования
- 5 См. Также
- 6 Примечания
- 7 Ссылки
- 8 Внешние ссылки
Свойства
Взаимные многочлены имеют несколько связей со своими исходными многочленами, включая:
- p (x) = xp (x)
- α является корнем многочлена p тогда и только тогда, когда α является корнем p.
- Если p (x) ≠ x, то p неприводимо тогда и только тогда, когда p неприводимо.
- p является примитивным тогда и только тогда, когда p примитивно.
Могут быть получены другие свойства обратных многочленов, например:
- Если многочлен самовзаимодействующий и неприводимый, то он должен иметь четную степень.
Палиндромные и антипалиндромные многочлены
Самовзаимный многочлен также называется палиндромным, потому что его коэффициенты, когда многочлен записывается в порядке восходящей или нисходящей p owers, образуют палиндром. То есть, если
- P (x) = ∑ i = 0 naixi { displaystyle P (x) = sum _ {i = 0} ^ {n} a_ {i} x ^ {i}}
является многочленом степени n, тогда P палиндромный, если a i = a n — i для i = 0, 1,…, n. Некоторые авторы используют термины палиндромный и взаимозаменяемый.
Точно так же P, многочлен степени n, называется антипалиндромным, если a i = −a n — i для i = 0, 1,… п. То есть многочлен P антипалиндромен, если P (x) = — P (x).
Примеры
Из свойств биномиальных коэффициентов следует, что многочлены P (x) = (x + 1) являются палиндромными для всех натуральных чисел n, в то время как многочлены Q (x) = (x — 1) являются палиндромными, когда n четно, и антипалиндромными, когда n нечетно.
Другие примеры палиндромных многочленов включают циклотомические многочлены и эйлеровы многочлены.
Свойства
- Если a является корнем полинома, который является палиндромным или антипалиндромным, то 1 / a также является корнем и имеет ту же самую кратность.
- Верно и обратное: если многочлен таков, что если a является корнем, то 1 / a также является корнем той же кратности, тогда многочлен равен либо палиндромный, либо антипалиндромный.
- Для любого многочлена q многочлен q + q является палиндромным, а многочлен q — q антипалиндромным.
- Любой многочлен q может быть записан как сумма палиндромного и антипалиндромный полином.
- Произведение двух палиндромных или антипалиндромных полиномов является палиндромным.
- Произведение палиндромного полинома и антипалиндромного полинома является антипалиндромным полиномом.
- Палиндромный полином. нечетной степени делится на x + 1 (корень имеет –1), и его частное по x + 1 также палиндромно.
- Антипалиндромный многочлен делится на x — 1 (у него 1 в качестве корня), а его частное по x — 1 является палиндромным.
- Антипалиндромный многочлен четной степени делится на x — 1 (он имеет -1 и 1 как корень), а его фактор по x — 1 палиндромный.
- Если p (x) — палиндромный многочлен четной степени 2d, то существует многочлен q степени d такой, что p (x) = xq (x + 1 / x) (Durand 1961).
- Если p (x) — монический антипалиндромный многочлен четной степени 2d над полем k с нечетной характеристикой, то его можно однозначно записать как p (x) = x (Q (x) — Q (1 / x)), где Q — монический многочлен степени d без постоянного члена.
- Если антипалиндромный многочлен P имеет четную степень 2n, тогда его «средний» коэффициент (степени n) равен 0, поскольку a n = −a 2n — n.
Действительные коэффициенты
Многочлен с действительными коэффициентами, все комплексные корни которого лежат на единичной окружности в комплексной плоскости (все корни унимодулярны), либо pal индромный или антипалиндромный.
Сопряженные обратные многочлены
Многочлен является сопряженным обратным, если p (x) ≡ p † (x) { displaystyle p (x) Equiv p ^ { dagger} (x)}

Если p (z) — минимальный многочлен of z 0 с | z 0 | = 1, z 0 ≠ 1 и p (z) имеет действительные коэффициенты, тогда p (z) взаимно взаимно. Это следует потому, что
- z 0 np (1 / z 0 ¯) ¯ = z 0 np (z 0) ¯ = z 0 n 0 ¯ = 0. { displaystyle z_ {0} ^ {n} { overline { p (1 / { bar {z_ {0}}})}} = z_ {0} ^ {n} { overline {p (z_ {0})}} = z_ {0} ^ {n} { bar {0}} = 0.}
Итак, z 0 является корнем многочлена znp (z ¯ — 1) ¯ { displaystyle z ^ {n} { overline { p ({ bar {z}} ^ {- 1})}}}
- cp (z) = znp (z ¯ — 1) ¯ { displaystyle cp (z) = z ^ {n} { overline {p ({ bar {z}) } ^ {- 1})}}}
для некоторой константы c, т.е. cai = an — i ¯ = an — i { displaystyle ca_ {i} = { overline {a_ {ni}}} = a_ {ni}}
Следствием этого является то, что циклотомические многочлены Φnвзаимно обратны для n>1. Это используется в специальном числовом поле сито, чтобы разрешить факторизацию чисел вида x ± 1, x ± 1, x ± 1 и x ± 1 с использованием алгебраических факторов с использованием полиномов степени 5, 6, 4 и 6 соответственно — обратите внимание, что φ (функция Эйлера ) экспонент равняется 10, 12, 8 и 12.
Применение в теории кодирования
Обратный многочлен находит применение в теории циклических кодов исправления ошибок. Предположим, что x — 1 можно разложить на произведение двух многочленов, скажем, x — 1 = g (x) p (x). Когда g (x) генерирует циклический код C, то обратный многочлен p генерирует C, ортогональное дополнение к C. Кроме того, C самоортогонален (то есть C ⊆ C), если и только если p делит g (x).
См. также
- Теорема Кона
Примечания
Ссылки
- Плесс, Вера (1990), Введение в теорию Коды исправления ошибок (2-е изд.), Нью-Йорк: Wiley-Interscience, ISBN 0-471-61884-5
- Роман, Стивен (1995), Теория поля, New Йорк: Springer-Verlag, ISBN 0-387-94408-7
- Эмиль Дюран (1961) Solutions numériques des équations algrébriques I, Masson et Cie: XV — полиномы не имеют коэффициентов sont symétriques ou antisymétriques, стр. 140-141.
Внешние ссылки
- «Основная теорема для палиндромных многочленов». MathPages.com.
- Взаимный многочлен (на MathWorld )
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
В поле Q(a) найти обратный элемент
|
|
15/12/07 |
|
|
|
|
|
maxal |
|
||
11/01/06 |
|||
|
|
|||
|
Еленаm15 |
|
|
15/12/07 |
Ну да,я и имела ввиду такое разложение.Просто невнимательно писала и вместо х написала а. Добавлено спустя 1 час 32 минуты 16 секунд: Помогите поссчитать НОД этих многочленов пожалуйста.
|
|
|
|
|
Brukvalub |
|
||
01/03/06 |
Еленаm15 писал(а): Помогите поссчитать НОД этих многочленов пожалуйста. Так Вам все уже сосчитал maxal maxal писал(а): У многочленов
|
||
|
|
|||
|
Еленаm15 |
|
|
15/12/07 |
Я понимаю,что он равен 1 у этих многочленов.Но в итоге надо получить разложение с U(X) и V(x),поэтому надо знать само разложение.А у меня не получается по алгоритму Евклида,что последний ненулевой остаток равен 1.
|
|
|
|
|
RIP |
|
||
11/01/06 |
Ну НОД ведь определён с точностью до умножения на ненулевую постоянную, поэтому если у Вас вдруг получается другая постоянная, то ничего страшного.
|
||
|
|
|||
|
Еленаm15 |
|
|
15/12/07 |
Точно?Спасибо…
А еще вопрос :Зачем сказано,что найти обратный в поле
|
|
|
|
|
Dan B-Yallay |
|
||
11/12/05 |
Это значит, что обратным элементом к заданному будет многочлен от
|
||
|
|
|||
|
RIP |
|
||
11/01/06 |
|||
|
|
|||
|
Еленаm15 |
|
|
15/12/07 |
RIP А почему Вы записали многочлен третьей степени?
|
|
|
|
|
Dan B-Yallay |
|
||
11/12/05 |
Кстати, Добавлено спустя 5 минут 13 секунд: Цитата: RIP Любой многочлен степени 4 и выше может быть представлен как
|
||
|
|
|||
|
Еленаm15 |
|
|
15/12/07 |
Цитата: Кстати, является «неприводимым» согласно критерия Ейзенштайна. Так что даже делить по Евклиду не обязательно
Ну я делю по алгоритму Евклида ,чтобы как раз получить разложение,потом подставив вместо
А как по другому найти это
|
|
|
|
|
Brukvalub |
|
||
01/03/06 |
Еленаm15 писал(а): Ну я делю по алгоритму Евклида Я тоже, ради интереса, попробовал поделить, но скис — полезли дробные коэффициенты.. А проделать вычисления в каком-либо пакете символьных вычислений Вы не пробовали?
|
||
|
|
|||
|
Еленаm15 |
|
|
15/12/07 |
Цитата: А проделать вычисления в каком-либо пакете символьных вычислений Вы не пробовали? А что это значит?
А еще вопрос .Можно ведь решать вот таким методом.Записать ,что 1-
Но почему-то получается система,где
|
|
|
|
|
RIP |
|
||
11/01/06 |
|||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы
В заголовке упомянуто кольцо [math]mathbb{Z}_p[x][/math]/[math](x^N-1)[/math]. Это, конечно, не конечное поле, но в нем уже есть обратные для элементов [math]g(x)[/math], взаимно простых с [math]x^N-1[/math]. Сравнения в нем, если писать формально, писались бы как [math]g(x)equiv h(x) pmod{p, x^N-1}[/math]. Т.е. нужно только задать [math]N[/math]. В примере [math]N=11[/math].
Возвращаясь к исходной задаче: она решается алгоритмом Евклида для многочленов. Т.е. у Вас дан [math]f(x)[/math], Вам нужно найти [math]g(x)equiv f^{-1}(x)[/math] такой, что [math]f(x)g(x)equiv 1pmod{3,x^N-1}[/math], т.е. [math]f(x)g(x)+(x^N-1)q(x)equiv 1pmod{3}[/math]. Сразу предполагаем, что [math]f(x), x^N-1[/math] взаимно просты. Ну и дальше применяете алгоритм Евклида к ним, получаете [math]g(x)[/math], [math]mathbb{Z}_3[/math] — поле, так что считать удобно.











 и
и  НОД равен 1,
НОД равен 1, ?
? . А как вы уже знаете, такие многочлены с рациональными коэффициентами — элементы
. А как вы уже знаете, такие многочлены с рациональными коэффициентами — элементы 
 где степень
где степень 
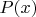 …
…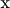
 ,обнулить первое произведение и таким образом найти ,что
,обнулить первое произведение и таким образом найти ,что и найти
и найти 
 *
* =
=  и перемножить первую скобку,а потом разделить на
и перемножить первую скобку,а потом разделить на  ,а так как должно получиться какое-то
,а так как должно получиться какое-то  ),то в остатке приравнять все скобки при каждой степени к 0 и потом подставить в
),то в остатке приравнять все скобки при каждой степени к 0 и потом подставить в  зависят друг от друга и она не решается.
зависят друг от друга и она не решается.