Как найти обратный дирекционный угол в геодезии - AvtoShod.ru

8,Дирекционные
углы и румбы линий, зависимость между
ними. Прямые и обратные дирекционные
углы.

дирекционным
углом
является угол в горизонтальной плоскости,
отсчитываемый от северного направления
осевого меридиана по ходу часовой
стрелки до данной линии.

Осевым
румбом называется
острый горизонтальный угол, отсчитываемый
от ближайшего направления осевого
меридиана (северного или южного) до
данной линии.

Зависимость
между дирекционными углами и румбами
определяется
для четвертей по следующим формулам:

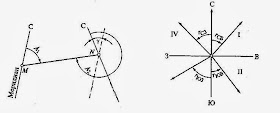
I
четверть (СВ) r
= α

II
четверть (ЮВ) r
= 180° – α

III
четверть (ЮЗ) r
= α
– 180°

IV
четверть (СЗ) r
= 360° – α

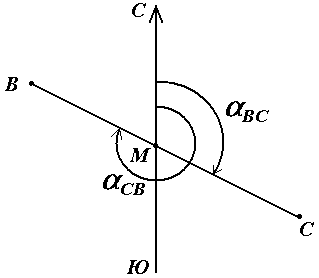
α_BC
является прямым дирекционным углом
линии ВС
в точке М,
а угол α_CB
– обратным дирекционным углом этой же
линии в той же точке.

Рис.
17. Прямое и обратное направление линии

Из
рисунка видно, что α_CB
= α_BC
+ 180°, т.е. прямой и обратный дирекционные
углы отличаются друг от друга на 180°.

Источник

При выполнении
геодезических работ на местности, работ с картой или чертежом необходимо
определить положение линии (ориентировать линию) относительно стран света или
какого-нибудь направления, принимаемого за исходное.

Ориентирование
заключается в том, что определяют угол между исходным направлением и
направлением данной линии. За исходное направление для ориентирования
принимают истинный (географический), магнитный меридианы или ось абсцисс прямоугольной
системы координат плана. В качестве углов, определяющих направление линии,
служат истинный и магнитный азимуты, румбы и дирекционные углы.

Азимутом называется угол между северным направлением меридиана и
направлением данной линии MN.
Азимут измеряется от севера через восток, юг и запад, т.е. по направлению
движения часовой стрелки, и может иметь значения 0… 360°. Азимут А, измеряемый
относительно истинного меридиана, называется истинным.

Азимуты и румбы

В
геодезии принято различать прямое и обратное направления линии. Если
направление линии MN от точки М к точке N считать прямым, то NM— обратное направление той же линии. В соответствии с этим угол А₁
— прямой азимут линии MN в точке М, а А₂ — обратный азимут этой же
линии в точке N.

Меридианы разных
точек не параллельны между собой, так как они сходятся в точках полюсов. Отсюда
азимут линии в разных ее точках имеет разное значение.

Угол между
направлениями двух меридианов называется сближением
меридианов и обозначается γ. Зависимость между прямым и
обратным азимутами линии MN выражает следующая формула: A₂ = A_t + 180⁰ + γ .

Истинные
азимуты линий местности определяются путем астрономических наблюдений или с
помощью приборов — гиротеодолитов.

Иногда для
ориентирования линии местности пользуются не азимутами, а румбами.

Румбом называется острый угол между ближайшим (северным С или
южным Ю) направлением меридиана и направлением данной линии.

Румбы
обозначают буквой r с индексами, указывающими четверть, в которой находится
румб. Названия четвертей составлены из соответствующих обозначений стран света.
Так, I четверть —
северо-восточная (СВ), II — юго-восточная (ЮВ), III — юго-западная (ЮЗ), IV — северо-западная (СЗ). Соответственно
обозначают румбы в четвертях, например: в первой — г_св, во второй —
г_юв. Румбы измеряют в градусах (0… 90°).

В прямоугольной системе координат ориентирование линии
производят относительно оси абсцисс. Углы, отсчитываемые в направлении хода
часовой стрелки от положительного (северного) направления оси абсцисс до линии, направление которой определяется, называются дирекционными.
Дирекционные углы обозначаются буквой ά и подобно азимуту изменяются от 0 до 360⁰. Дирекционный угол какого-либо направления непосредственно на местности не измеряют, его значение можно вычислить, если для данного направления определен истинный азимут (рис. 2). В
данном случае у — сближение меридианов —
представляет собой угол между истинным
меридианом М и осью абсцисс в этой точке.

Зависимость между дирекционным углом и истинным
азимутом линии

Ось абсцисс параллельна осевому
меридиану зоны, в которой расположена линия MN. Как видно из рисунка, =А — γ. Также как и для азимута, различают прямой и обратный
дирекционные углы: — прямой, ά — обратный дирекционные углы линии MN: ά = + 180°.

Румбы
дирекционных углов обозначают и вычисляют так же, как румбы истинных азимутов,
только отсчитывают от северного и южного направлений оси абсцисс (табл.).

Четверть	*А,⁰*	r
I (СВ)	0…90	А
II (ЮВ)	90.. .180	180°-А
III (ЮЗ)	180…270	А -180°
IV (СЗ)	270… 360	360° -А

Направление
магнитной оси свободно подвешенной магнитной стрелки называется магнитным меридианом. Угол между северным направлением магнитного
меридиана и направлением данной линии называют магнитным
азимутом. Магнитный азимут, так же как и истинный, считают по
направлению движения часовой стрелки; он также изменяется от 0 до 360°. Зависимость между
магнитными азимутами
и магнитными румбами такая же, как между истинными румбами. Так как магнитный полюс не совпадает с
географическим,
направление магнитного меридиана в данной точке не совпадает с направлением истинного
меридиана. Горизонтальный угол между этими направлениями называют склонением
магнитной стрелки 5. В
зависимости от того, в какую сторону уклоняется северный конец стрелки от направления
истинного меридиана, различают восточное и западное склонения.

Зависимости: а —
между истинным и магнитным азимутами;

б —
магнитным азимутом и дирекционным углом

Перед значением
восточного склонения
обычно ставят знак «плюс», западного — «минус». Зависимость (рис. 3 ) между
истинным А и магнитным А_м азимутами выражается
формулой А – А_м + δ. При использовании этой формулы
учитывают знак склонения. Если известно склонение δ магнитной стрелки и сближение
меридианов γ, то по измеренному магнитному азимуту А_м линии MN можно
вычислить дирекционный угол а этой линии (рис. 3, б): α = А_м + (δ — γ), где разность (δ -γ ) — поправка на склонение стрелки и
сближение меридианов (учитывают при ориентировании топографической карты).

В
различных точках Земли магнитная стрелка имеет разное склонение. Так, на территории
Российской Федерации оно колеблется в
диапазоне (0 ± 15)°.

Склонение магнитной стрелки не остается постоянным
и в данной точке Земли
(различают вековые, годовые и суточные изменения склонений). Больше всего изменяются суточные склонения,
колебания которых достигают 15′. Следовательно, магнитная стрелка указывает положение магнитного меридиана
приближенно и ориентировать линии
местности по магнитным азимутам можно тогда, когда не требуется высокой точности.

Источник

Собрание уникальных книг, учебных материалов и пособий, курсов лекций и отчетов по геодезии, литологии, картированию, строительству, бурению, вулканологии и т.д.
Библиотека собрана и рассчитана на инженеров, студентов высших учебных заведений по соответствующим специальностям. Все материалы собраны из открытых источников.

Ориентирование линий. Прямая и обратная.

ГЕОДЕЗИЧЕСКИЕ ЗАДАЧИ НА ПЛОСКОСТИ

3.1. Углы ориентирования

Ориентировать линию – значит определить её направление относительно исходного направления, например, меридиана или оси абсцисс х системы плоских прямоугольных координат.

Угол, измеряемый по ходу часовой стрелки от северного направления меридиана до заданного направления, называется азимутом.

Если исходным направлением служит геодезический меридиан, то азимут называют геодезическим азимутом. Если – астрономический, то — астрономическим азимутом. Обобщением обоих понятий служит термин — географический азимут или просто — азимут.

Значения азимута лежат в пределах от 0° до 360°. На рис. 3.1, а обозначено: С – северное направление меридиана, угол А₁ – азимут направления на точку 1 и А₂ – азимут направления на точку 2.

[image]

Рис. 3.1. Углы ориентирования: а — азимуты географические; б — магнитный азимут

На местности азимут заданного направления можно определить астрономическим методом — измерив горизонтальный угол между направлением на небесное светило (Солнце, звезду) и заданным направлением. Зная азимут светила, вычисляемый с использованием астрономического ежегодника, и измеренный угол, соображают азимут заданного направления.

Угол, отсчитываемый от северного направления магнитной стрелки до заданного направления, называется магнитным азимутом.

Магнитная стрелка компаса отклоняется от направления истинного меридиана на угол d, который называется склонением магнитной стрелки (рис. 3.1, б).

Если северный конец магнитной стрелки отклоняется от меридиана к востоку, то склонение называют восточным и считают положительным, а если — к западу, то называют западным и считают отрицательным.

Азимут с магнитным азимутом связывает формула:

где А — азимут, А_м — магнитный азимут и d – склонение магнитной стрелки.

Магнитные азимуты в геодезии измеряют буссолью (рис. 3.2). Однако точность этих измерений невысока (несколько минут), так как склонение магнитной стрелки непостоянно. На территории России оно меняется от места к месту в пределах от –15° до 25°. В аномальных районах (например, в районе Курской магнитной аномалии) эти изменения так велики, что магнитной стрелкой пользоваться нельзя. Кроме того, склонение изменяется во времени, испытывая суточные, годовые и вековые изменения.

[image]

Рис. 3.2. Буссоль

Углом ориентирования, применяемым при использовании системы плоских прямоугольных координат Гаусса-Крюгера, является дирекционный угол.

Дирекционным углом называется угол между северным направлением осевого меридиана или линии ему параллельной и заданным направлением (рис. 3.3).

Угол g между северным направлением меридиана и направлением оси абсцисс х прямоугольных координат (то есть линии, параллельной осевому меридиану) называется сближением меридианов.

[image]

Рис. 3.3. Углы ориентирования: а — дирекционные углы a₁, a₂; б — азимут A и дирекционный угол a

При отклонении оси абсцисс от меридиана к востоку, сближение меридианов считают положительным, а при отклонении к западу — отрицательным. При этом справедлива формула (рис. 3.3 б)

А = a + g,

где a — дирекционный угол, g — сближение меридианов.

Приближенно сближение меридианов равно

g = Dl sinj,

где Dl = l-l₀, причем l -долгота географического данной точки и l₀— долгота осевого меридиана; j — широта точки.

На рис. 3.4 показано соотношение между азимутами и дирекционными углами в пределах одной координатной зоны. Легко заметить, что для точек, расположенных к востоку от осевого меридиана зоны, сближение меридианов положительное, а к западу – отрицательное. При этом дирекционные углы в разных точках прямой линии равны a₁= a₂= a₃. Поэтому обратный дирекционный угол в точке 3 отличается от прямого в точке 1 ровно на 180°, то есть a_1-3= a_3-1 ± 180°. Азимуты же в разных точках прямой различаются: А₁¹ А₂ ¹ А₃, что обусловлено различием сближения меридианов. Поэтому и А_1-3¹ А_3-1 ± 180°.

[image]

Рис. 3.4. Связь между азимутами и дирекционными углами: 1 – в западной половине зоны; 2 – на осевом меридиане; 3 – в восточной половине зоны; Р – полюс; 1Р, 3Р – меридианы; 2Р – осевой меридиан.

При использовании местной системы прямоугольных координат направление оси абсцисс x не связано с направлением осевого меридиана координатной зоны, и тогда дирекционные углы отсчитывают от положительного направления оси абсцисс х.

В практике вычислений находят применение также вспомогательные углы ориентирования – румбы. Румбом называют острый угол, измеряемый от ближайшего направления меридиана (северного или южного). Румбу приписывают название координатной четверти (СВ, ЮВ, ЮЗ, СЗ), в которой расположено заданное направление. Например, для a = 240°36¢ румб равен r = ЮЗ: 60°36¢.

Закрепленные

Понравившиеся

Источник

Актуальные цены на услуги геодезистов в Москве и Московской области в 2022 году.

Решение обратной геодезической задачи онлайн

Обратная геодезическая задача заключается в том, что при известных координатах точек А( X_A, Y_A ) и В( X_B, Y_B ) необходимо найти длину S_AB и направление линии АВ: румб r_AB и дирекционный угол α_AB

Ниже представлена форма в которую можно ввести исходные значения и получить искомые данные. Это простое решение, которым может воспользоваться любой кому лень разбираться с формулами.

Если же говорить о сути решения задачи, то обратная геодезическая задача решается следующим образом.

Сначала находим приращения координат:

ΔX = X_B – X_A ;

ΔY = Y_B – Y_A .

Величину угла r_AB определяем из отношения

По знакам приращений координат вычисляют четверть, в которой располагается румб, и его название. Используя зависимость между дирекционными углами и румбами, находим α_AB.

Для контроля расстояние S_AB дважды вычисляют по формулам:

Источник

Закрепленные

Понравившиеся

Решение обратной геодезической задачи онлайн

Не пропустите также: