Инверсия комплексного числа
protection click fraud
Число, обратное числу, означает замену числителя знаменателем и наоборот, если эта дробь или число отличны от нуля. В комплексном числе это происходит так же: чтобы комплексное число имело обратное значение, оно должно быть ненулевым, например:
Для любого ненулевого комплексного числа z = a + bi его обратное будет представлено как z–1.
См. Вычисление обратной величины комплексного числа z = 1 — 4i.
Следовательно, комплексное число, обратное к z = 1 — 4i, будет:
Мы заключаем, что обратное к ненулевому комплексному числу будет иметь следующую общность: г = а + би
Когда мы умножаем комплексное число на обратное, результат всегда будет равен 1, z * z–1 = 1. Обратите внимание на умножение комплекса z = 1 — 4i на обратное:
Умножение комплексных чисел происходит следующим образом:
(a + bi) * (c + di) = ac + adi + bci + bdi² = ac + (ad + bc) i + bd (–1) = ac + (ad + bc) i — bd = (ac — bd) + (ad + bc) я
Не останавливайся сейчас… После рекламы есть еще кое-что;)
Марк Ноа
Окончил математику
Бразильская школьная команда
Комплексные числа — Математика — Бразильская школа
Хотели бы вы использовать этот текст в учебе или учебе? Посмотрите:
СИЛЬВА, Маркос Ноэ Педро да. «Инверсия комплексного числа»; Бразильская школа. Доступно в: https://brasilescola.uol.com.br/matematica/inverso-um-numero-complexo-1.htm. Доступ 29 июня 2021 г.
Teachs.ru
How to find the reciprocal of a complex number?
Let z = x + iy be a non-zero complex number. Then
(frac{1}{z})
= (frac{1}{x + iy})
= (frac{1}{x + iy}) × (frac{x — iy}{x — iy}), [Multiplying numerator and denominator by conjugate of denominator i.e., Multiply both numerator and denominator by conjugate of x + iy]
= (frac{x — iy}{x^{2} — i^{2}y^{2}})
= (frac{x — iy}{x^{2} + y^{2}})
= (frac{x}{x^{2} + y^{2}}) + (frac{i(-y)}{x^{2} + y^{2}})
Clearly, (frac{1}{z}) is equal to the multiplicative inverse of z. Also,
(frac{1}{z}) = (frac{x — iy}{x^{2} + y^{2}}) = (frac{overline{z}}{|z|^{2}})
Therefore, the multiplicative inverse of a non-zero complex z is equal to its reciprocal and is represent as
(frac{Re(z)}{|z|^{2}}) + i(frac{(-Im(z))}{|z|^{2}})= (frac{overline{z}}{|z|^{2}})
Solved examples on reciprocal of a complex number:
1. If a complex
number z = 2 + 3i, then find the reciprocal of z? Give your answer in a + ib
form.
Solution:
Given z = 2 + 3i
Then, (overline{z}) = 2 — 3i
And |z| = (sqrt{x^{2} + y^{2}})
= (sqrt{2^{2} + (-3)^{2}})
= (sqrt{4 + 9})
= (sqrt{13})
Now, |z|(^{2}) = 13
Therefore, (frac{1}{z}) = (frac{overline{z}}{|z|^{2}}) = (frac{2 — 3i}{13}) = (frac{2}{13}) + (-(frac{3}{13}))i, which is the required a + ib form.
2. Find the
reciprocal of the complex number z = -1 + 2i. Give your answer in a + ib form.
Solution:
Given z = -1 + 2i
Then, (overline{z}) = -1 — 2i
And |z| = (sqrt{x^{2} + y^{2}})
= (sqrt{(-1)^{2} + 2^{2}})
= (sqrt{1 + 4})
= (sqrt{5})
Now, |z|(^{2})= 5
Therefore, (frac{1}{z}) = (frac{overline{z}}{|z|^{2}}) = (frac{-1 — 2i}{5}) = (-(frac{1}{5})) + (-(frac{2}{5}))i, which is the required a + ib form.
3. Find the
reciprocal of the complex number z = i. Give your answer in a + ib form.
Solution:
Given z = i
Then, (overline{z}) = -i
And |z| = (sqrt{x^{2} + y^{2}})
= (sqrt{0^{2} + 1^{2}})
= (sqrt{0 + 1})
= (sqrt{1})
= 1
Now, |z|(^{2})= 1
Therefore, (frac{1}{z}) = (frac{overline{z}}{|z|^{2}}) = (frac{-i}{1}) = -i
= 0 + (-i), which is the required a + ib form.
Note: The reciprocal of i is its own conjugate —
i.
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 27 октября 2012;
проверки требуют 12 правок.
Обра́тное число́ (обратное значение, обратная величина) — это число, на которое надо умножить данное число, чтобы получить единицу. Два числа, произведение которых равно единице, называются взаимно обратными.
Содержание
- 1 Обратное к действительному числу
- 1.1 Обратное к нулю
- 2 Обратное к комплексному числу
- 2.1 Обратное к мнимой единице
- 3 Примечания
- 4 См. также
Обратное к действительному числу [править]
Для любого действительного (или комплексного) числа, отличного от нуля, существует число, обратное ему. Обратное к действительному числу можно подать в виде дроби или степени с показателем -1. Но, как правило, используется запись через дробь.
| Примеры | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Число |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Обратное |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Не стоит путать термины «обратное число» и «противоположное число». Два числа называются противоположными, если их сумма равна нулю. Например, число, противоположное к 3, это -3, а обратное 1/3.
Обратное к нулю [править]
В арифметике, которая оперирует действительными (или комплексными) числами, нет понятия бесконечности (нет числа «бесконечность»). Поэтому в ней считается, что на ноль делить нельзя. Таким образом, ноль не имеет обратного числа. Но, с момента ввода предельного перехода (в математическом анализе), появились такие понятия как бесконечно малая и бесконечно большая величины, которые являются взаимно обратными.
Используя предельный переход, получаем: 
![left ( frac{1}{x} right ) xrightarrow[x xrightarrow{} 0]{} infty](https://web.archive.org/web/20130530180445im_/http://upload.wikimedia.org/math/d/6/5/d6520b00c55fd4bb1d387c79e7d56519.png)
Таким образом, обратной величиной для нуля формально является бесконечность.
Обратное к комплексному числу [править]
Числа, обратные к комплексным, выглядят несколько сложнее нежели обратные к действительным. Существует три формы комплексного числа: алгебраическая, тригонометрическая и показательная.
| Формы комплексного числа | Число  |
Обратное  [1] [1] |
| Алгебраическая |  |
 |
| Тригонометрическая |  |
 |
| Показательная |  |
 |
__________Обозначение и доказательство__________
Таким образом, при нахождении обратного к комплексному числу, удобнее пользоваться его показательной формой.
Пример:
| Формы комплексного числа | Число  |
Обратное  [1] [1] |
| Алгебраическая |  |
 |
| Тригонометрическая | 
или |

или |
| Показательная |  |
 |
Обратное к мнимой единице [править]
Существует лишь два числа (комплексно-сопряженные), обратное и противоположное числа к которым равны. Это 
| Число | Равенство обратного и противоположного | |
| Запись обратного через дробь | Запись обратного через степень | |
 |
 |
 |
 |
 |
 |
__________Доказательство__________
Примечания [править]
- ↑ 1 2 Обратное
к комплексному числу
записывается в такой же форме, как и это число
.
- ↑ 1 2 Запись комплексного числа в тригонометрической форме с использованием конкретного значения косинуса и синуса аргумента:
См. также [править]
- Обратный элемент
- Обратная матрица
- Деление
- Дробь
- Противоположное число
Сразу хочу сказать, что здесь никакой воды про комплексные числа, и только нужная информация. Для того чтобы лучше понимать что такое
комплексные числа, комплексное число, комплексного числа, мнимая единица , настоятельно рекомендую прочитать все из категории Алгебра.
комплексные числа (от лат. complex — совокупный, тесно связанный ; о двойном ударении см. примечание[K 1]) — числа вида , где
— вещественные числа,
—
мнимая единица , то есть число, для которого выполняется равенство: Множество комплексных чисел обычно обозначается символом
Вещественные числа можно рассматривать как частный случай комплексных, они имеют вид
. Главное свойство
— в нем выполняется основная теорема алгебры, то есть любой многочлен
-й степени (
) имеет
корней. Доказано[⇨], что система комплексных чисел логически непротиворечива[K 2].
Так же как и для вещественных чисел, для комплексных чисел определены операции сложения, вычитания[⇨], умножения[⇨] и деления[⇨]. Однако многие свойства комплексных чисел отличаются от свойств вещественных чисел; например, нельзя указать, какое из двух комплексных чисел больше или меньше[⇨]. Удобно представлять комплексные числа точками на комплексной плоскости[⇨]; например, для изображения сопряженных чисел используется операция отражения относительно горизонтальной оси[⇨]. Альтернативное представление
комплексного числа в тригонометрической записи оказалось полезным для вычисления степеней и корней[⇨]. Функции комплексного аргумента изучаются в комплексном анализе[⇨].
Первоначально идея о необходимости использования комплексных чисел возникла в результате формального решения кубических уравнений, при котором в формуле Кардано под знаком квадратного корня получалось отрицательное число . Большой вклад в исследование комплексных чисел внесли такие математики, как Эйлер, который ввел общепризнанное обозначение для мнимой единицы, Декарт, Гаусс[⇨]. Сам термин «
комплексное число » ввел в науку Гаусс в 1831 году .
Уникальные свойства комплексных чисел и функций нашли широкое применение для решения многих практических задач в различных областях математики, физики и техники: в обработке сигналов, теории управления, электромагнетизме, теории колебаний, теории упругости и многих других [⇨]. Преобразования комплексной плоскости оказались полезны в картографии и гидродинамике. Современная физика полагается на описание мира с помощью квантовой механики, которая опирается на систему комплексных чисел.
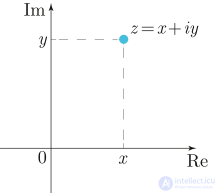
Комплексным числом называется выражение вида z = a + bi, где a, b — любые действительные числа, i — мнимая единица, удовлетворяющая условию i2 = -1. При этом обозначают a = Re z — действительную часть числа, b = Im z — мнимую его часть.
Основные соглашения:
- Действительное число a записывается также в виде a + 0i .
- Чисто мнимое число bi, т.е. 0 + bi .
- Два комплексных числа z1 = a + bi и z2 = c + di считаются равными, если a = c и b = d.
Число z1 = a — bi называется сопряженным числу z = a + bi.
Известно также несколько обобщений комплексных чисел — например, кватернионы
Определения
Комплексное число — это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен –1, то есть i2 = –1. Число a называется действительной частью, а число b — мнимой частью комплексного числа z = a + bi. Если b = 0, то вместо a + 0i пишут просто a. Видно, что действительные числа — это частный случай комплексных чисел.
Почему для расчетов в цепях переменного тока используются комплексные числа
Арифметические действия над комплексными числами те же, что и над действительными: их можно складывать, вычитать, умножать и делить друг на друга. Сложение и вычитание происходят по правилу (a + bi) ± (c + di) = (a ± c) + (b ± d)i, а умножение — по правилу (a + bi) · (c + di) = (ac – bd) + (ad + bc)i (здесь как раз используется, что i2 = –1). Число 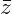
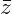
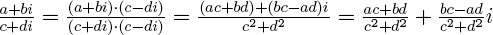
(Например, 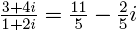
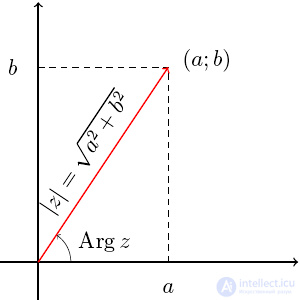
У комплексных чисел есть удобное и наглядное геометрическое представление: число z = a + bi можно изображать вектором с координатами (a; b) на декартовой плоскости (или, что почти то же самое, точкой — концом вектора с этими координатами). При этом сумма двух комплексных чисел изображается как сумма соответствующих векторов (которую можно найти по правилу параллелограмма). По теореме Пифагора длина вектора с координатами (a; b) равна 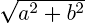
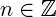
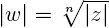
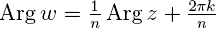
Формы записи комплексных чисел и действия над ними
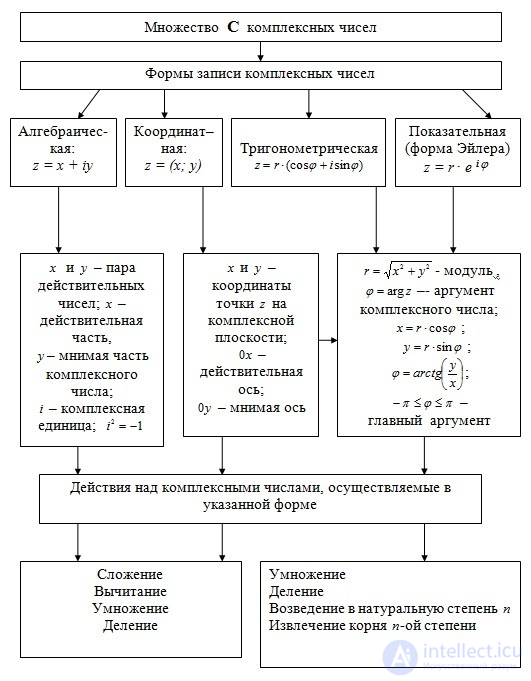
Комплексная арифметика
Связанные определения
Всякое комплексное число состоит из двух компонентов :
Противоположным для комплексного числа является число
Например, для числа
противоположным будет число
Четыре арифметические операции для комплексных чисел имеют те же свойства, что и аналогичные операции с вещественными числами. В отличие от последних, комплексные числа нельзя сравнивать на больше/меньше; доказано, что нет способа распространить порядок, заданный для вещественных чисел, на все комплексные так, чтобы порядок был согласован с арифметическими операциями (например, чтобы из вытекало
). Однако комплексные числа можно сравнивать на равно/не равно) :
Сложение и вычитание
Определение сложения и вычитания комплексных чисел :
Следующая таблица показывает основные свойства сложения для любых комплексных
| Свойство | Алгебраическая запись |
|---|---|
| Коммутативность (переместительность) | |
| Ассоциативность (сочетательность) | |
| Свойство нуля | |
| Свойство противоположного элемента | |
| Выполнение вычитания через сложение |
Умножение
Определим произведение комплексных чисел и
:
.
Следующая таблица показывает основные свойства умножения для любых комплексных .
| Свойство | Алгебраическая запись |
|---|---|
| Коммутативность (переместительность) | |
| Ассоциативность (сочетательность) | |
| Свойство единицы | |
| Свойство нуля | |
| Дистрибутивность (распределительность) умножения относительно сложения |
Правила для степеней мнимой единицы:
и т. д.
Деление
Комплексное число называется сопряженным к комплексному числу
(см. подробнее ниже).
Для каждого комплексного числа , кроме нуля, можно найти обратное к нему комплексное число
. Для этого умножим числитель и знаменатель дроби на число
, комплексно сопряженное знаменателю
Определим результат деления комплексного числа на ненулевое число
:
Как и для вещественных чисел, деление можно заменить умножением делимого на число, обратное к делителю.
Другие операции
Для комплексных чисел определены также извлечение корня, возведение в степень и логарифмирование.
Возведение в степень
Если x > 0 вещественное, а z комплексное, возведение в степень определяется как
где ln обозначает натуральный логарифм.
Кажется естественным распространить эту формулу на комплексные значения x , но возникают некоторые трудности, связанные с тем, что комплексный логарифм на самом деле не функция, а многозначная функция .
Комплексный логарифм
В реальном случае натуральный логарифм может быть определен как величина, обратная экспоненциальной функции. Чтобы распространить это на комплексную область, можно начать с формулы Эйлера. Это означает, что если комплексное число z записано в полярной форме
тогда его комплексный логарифм должен быть
Однако, поскольку косинус и синус являются периодическими функциями, добавление кцелого числа, кратного 2 π . не меняет z . Например,
возможные значения натурального логарифма
.
Следовательно, комплексный логарифм необходимо определять как многозначную функцию :
В качестве альтернативы, для определения истинной функции можно использовать разрез ветви . Если z не является отрицательным действительным числом, главное значение комплексного логарифма получается с помощьюЭто аналитическая функция вне отрицательных действительных чисел, но она не может быть продолжена до функции, которая является непрерывной при любом отрицательном действительном числе.
Отсюда следует, что если z такое же, как указано выше, и если t — другое комплексное число, то возведение в степень — это многозначная функция
Целые и дробные показатели
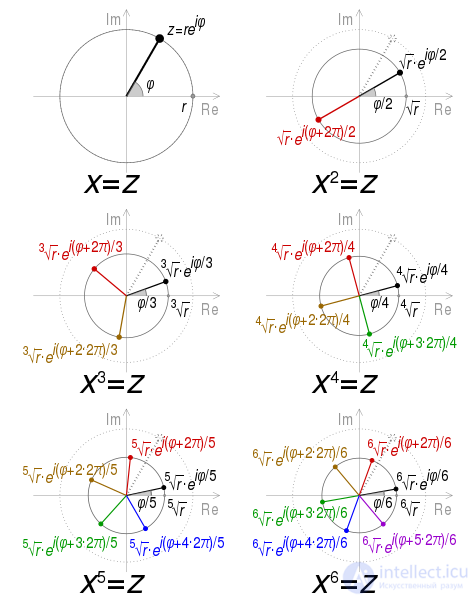
Геометрическое представление корней 2–6 комплексного числа z в полярной форме re iφ, где r = | z | и φ = arg z . Если z вещественное число, φ = 0 или π . Основные корни показаны черным.
Если в предыдущей формуле t — целое число, то синус и косинус не зависят от k . Таким образом, если показатель степени n является целым числом, тохорошо определена, и формула возведения в степень упрощается до формулы де Муавра :
П п й корни из комплексного числа г задается
для 0 ≤ k ≤ n — 1 . (Вотявляется обычным (положительным) корнем n- й степени из положительного действительного числа r .) Поскольку синус и косинус периодичны, другие целые значения k не дают других значений.
Хотя корень n- й степени положительного действительного числа r выбирается как положительное действительное число c, удовлетворяющее условию c n = r , естественного способа отличить один конкретный комплексный корень n- й степени комплексного числа не существует. Следовательно, корень n- й степени является n- значной функцией от z . Это означает, что, в отличие от положительных действительных чисел, мы имеем
поскольку левая часть состоит из n значений, а правая часть — одно значение.
Основные отличия комплексных чисел от вещественных
Уже упоминалось, что комплексные числа нельзя сравнивать на больше-меньше. Другое отличие: любой многочлен с вещественными или комплексными коэффициентами имеет, с учетом кратности, столько корней (вообще говоря, комплексных), какова его степень (основная теорема алгебры) .
В системе вещественных чисел из отрицательного числа нельзя извлечь корень четной степени. Для комплексных чисел возможно извлечение корня из любого числа любой степени, однако результат неоднозначен — комплексный корень -й степени из ненулевого числа имеет
различных комплексных значений[10]. См., например, корни из единицы.
Дополнительные отличия имеют функции комплексного переменного[⇨]..
Замечание
Число не является единственным числом, квадрат которого равен
. Число
также обладает этим свойством.
Следует также заметить, что выражение , ранее часто использовавшееся вместо
, не вполне корректно, так как арифметический корень определяется только для неотрицательных чисел. Во избежание ошибок, выражение с квадратными корнями из отрицательных величин в настоящее время принято записывать как
, а не
, несмотря на то, что даже в XIX веке второй вариант записи считался допустимым[11].
Пример возможной ошибки при неосторожном использовании устаревшей записи:
.
При использовании современной записи такой ошибки не возникло бы:
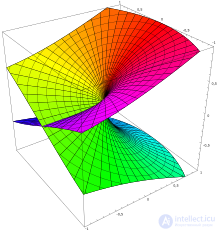
Риманова поверхность для √z. По вертикали откладывается действительная часть функции. Чтобы получить поверхность соответствует мнимой части, надо развернуть фигуру на 180 ° вокруг вертикальной оси
Геометрическое представление
Комплексная плоскость
Геометрическое представление комплексного числа
Комплексные числа можно представить на плоскости с прямоугольной системой координат: числу соответствует точка плоскости с координатами
(а также радиус-вектор, соединяющий начало координат с этой точкой). Такая плоскость называется комплексной. Вещественные числа на ней расположены на горизонтальной оси, мнимая единица изображается единицей на вертикальной оси; по этой причине горизонтальная и вертикальная оси называются соответственно вещественной и мнимой осями[12].
Модуль и аргумент
комплексного числа
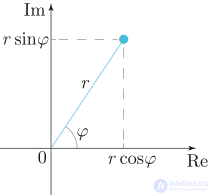
Бывает удобно рассматривать на комплексной плоскости также полярную систему координат (см. рисунок справа), в которой координатами точки являются расстояние до начала координат (модуль[⇨]) и угол
радиус-вектора точки с горизонтальной осью (аргумент[⇨]).
В этом представлении сумма комплексных чисел соответствует векторной сумме соответствующих радиус-векторов, а вычитанию чисел соответствует вычитание радиус-векторов. При перемножении комплексных чисел их модули перемножаются, а аргументы складываются. Если модуль второго сомножителя равен 1, то умножение на него соответствует повороту радиус-вектора первого числа на угол, равный аргументу второго числа[13]. Этот факт объясняет широкое использование комплексного представления в теории колебаний, где вместо терминов «модуль» и «аргумент» используются термины «амплитуда» и «фаза»[14].
Пример: умножение на поворачивает радиус-вектор числа на прямой
продолжение следует…
Продолжение:
Часть 1 Комплексные числа, определение и применение, операции над ними, физический смысл
Часть 2 Формы представления комплексного числа — Комплексные числа, определение и применение,…
Часть 3 Место в общей алгебре, топологии и теории множеств — Комплексные…
Часть 4 Вариации Обобщения и связанные с ними понятия — Комплексные числа,…
Евгений Машеров в сообщении #842252 писал(а):
Эээ… Искать в виде 
Выписать уравнения отдельно для действительной и мнимой частей и решить их относительно x, y.
Но при введении поля комплексных чисел не определено, когда два числа равны. Разве можно будет утверждать, что мнимые части и реальные части равны по отдельности?
— 28.03.2014, 16:51 —
Или все таки можно сделать так, а потом из утверждения единственности обратного элемента, согласится, что это и есть обратный элемент

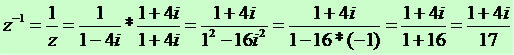
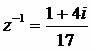
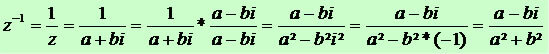
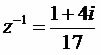


 [2]
[2] [2]
[2]