Загрузить PDF
Загрузить PDF
В каждой функции есть две переменные – независимая переменная и зависимая переменная, значения которой зависят от значений независимой переменной. Например, в функции y = f(x) = 2x + y независимой переменной является «х», а зависимой – «у» (другими словами, «у» – это функция от «х»). Допустимые значения независимой переменной «х» называются областью определения функции, а допустимые значения зависимой переменной «у» называются областью значений функции.[1]
-
1
Определите тип данной вам функции. Областью значений функции являются все допустимые значения «х» (откладываются по горизонтальной оси), которым соответствуют допустимые значения «у». Функция может быть квадратичной или содержать дроби или корни. Для нахождения области определения функции сначала необходимо определить тип функции.
- Квадратичная функция имеет вид: ax2 + bx + c:[2]
f(x) = 2x2 + 3x + 4 - Функция, содержащая дробь: f(x) = (1/x), f(x) = (x + 1)/(x — 1) (и так далее).
- Функция, содержащая корень: f(x) = √x, f(x) = √(x2 + 1), f(x) = √-x (и так далее).
- Квадратичная функция имеет вид: ax2 + bx + c:[2]
-
2
Выберите соответствующую запись для области определения функции. Область определения записывается в квадратных и/или круглых скобках. Квадратная скобка применяется в том случае, когда значение входит в область определения функции; если значение не входит в область определения, используется круглая скобка. Если у функции несколько несмежных областей определения, между ними ставится символ «U».[3]
- Например, область определения [-2,10) U (10,2] включает значения -2 и 2, но не включает значение 10.
- С символом бесконечности ∞ всегда используются круглые скобки.
-
3
Постройте график квадратичной функции. График такой функции представляет собой параболу, ветви которой направлены либо вверх, либо вниз. Так как парабола возрастает или убывает на всей оси Х, то областью определения квадратичной функции являются все действительные числа. Другими словами, областью определения такой функции является множество R (R обозначает все действительные числа).[4]
- Для лучшего уяснения понятия функции выберите любое значение «х», подставьте его в функцию и найдите значение «у». Пара значений «х» и «у» представляют собой точку с координатами (х,у), которая лежит на графике функции.
- Нанесите эту точку на плоскость координат и проделайте описанный процесс с другим значением «х».
- Нанеся на плоскость координат несколько точек, вы получите общее представление о форме графика функции.
-
4
Если функция содержит дробь, приравняйте ее знаменатель к нулю. Помните, что делить на нуль нельзя. Поэтому, приравняв знаменатель к нулю, вы найдете значения «х», которые не входят в область определения функции.[5]
- Например, найдите область определения функции f(x) = (x + 1)/(x — 1).
- Здесь знаменатель: (х — 1).
- Приравняйте знаменатель к нулю и найдите «х»: х — 1 = 0; х = 1.
- Запишите область определения функции. Область определения не включает 1, то есть включает все действительные числа за исключением 1. Таким образом, область определения функции: (-∞,1) U (1,∞).
- Запись (-∞,1) U (1,∞) читается так: множество всех действительных чисел за исключением 1. Символ бесконечности ∞ означает все действительные числа. В нашем примере все действительные числа, которые больше 1 и меньше 1, включены в область определения.
-
5
Если функция содержит квадратный корень, то подкоренное выражение должно быть больше или равно нулю. Помните, что квадратный корень из отрицательных чисел не извлекается. Поэтому любое значение «х», при котором подкоренное выражение становится отрицательным, нужно исключить из области определения функции.[6]
- Например, найдите область определения функции f(x) = √(x + 3).
- Подкоренное выражение: (х + 3).
- Подкоренное выражение должно быть больше или равно нулю: (х + 3) ≥ 0.
- Найдите «х»: х ≥ -3.
- Область определения этой функции включает множество всех действительных чисел, которые больше или равны -3. Таким образом, область определения: [-3,∞).
Реклама
-
1
Убедитесь, что вам дана квадратичная функция. Квадратичная функция имеет вид: ax2 + bx + c: f(x) = 2x2 + 3x + 4. График такой функции представляет собой параболу, ветви которой направлены либо вверх, либо вниз. Существуют различные методы нахождения области значений квадратичной функции.[7]
- Самый простой способ найти область значений функции, содержащей корень или дробь, – это построить график такой функции при помощи графического калькулятора.
-
2
Найдите координату «х» вершины графика функции. В случае квадратичной функции найдите координату «х» вершины параболы. Помните, что квадратичная функция имеет вид: ax2 + bx + c. Для вычисления координаты «х» воспользуйтесь следующим уравнением: х = -b/2a. Это уравнение является производной от основной квадратичной функции и описывает касательную, угловой коэффициент которой равен нулю (касательная к вершине параболы параллельна оси Х).[8]
- Например, найдите область значений функции 3x2 + 6x -2.
- Вычислите координату «х» вершины параболы: х = -b/2a = -6/(2*3) = -1
-
3
Найдите координату «у» вершины графика функции. Для этого в функцию подставьте найденную координату «х». Искомая координата «у» представляет собой предельное значение области значений функции.
- Вычислите координату «у»: y = 3x2 + 6x – 2 = 3(-1)2 + 6(-1) -2 = -5
- Координаты вершины параболы этой функции: (-1,-5).
-
4
Определите направление параболы, подставив в функцию по крайней мере одно значение «х». Выберите любое другое значение «х» и подставьте его в функцию, чтобы вычислить соответствующее значение «у». Если найденное значение «у» больше координаты «у» вершины параболы, то парабола направлена вверх. Если же найденное значение «у» меньше координаты «у» вершины параболы, то парабола направлена вниз.
- Подставьте в функцию х = -2: y = 3x2 + 6x – 2 = y = 3(-2)2 + 6(-2) – 2 = 12 -12 -2 = -2.
- Координаты точки, лежащей на параболе: (-2,-2).
- Найденные координаты свидетельствуют о том, что ветки параболы направлены вверх. Таким образом, область значений функции включает все значения «у», которые больше или равны -5.
- Область значений этой функции: [-5, ∞)
-
5
Область значений функции записывается аналогично области определения функции. Квадратная скобка применяется в том случае, когда значение входит в область значений функции; если значение не входит в область значений, используется круглая скобка. Если у функции несколько несмежных областей значений, между ними ставится символ «U».[9]
- Например, область значений [-2,10) U (10,2] включает значения -2 и 2, но не включает значение 10.
- С символом бесконечности ∞ всегда используются круглые скобки.
Реклама
-
1
Постройте график функции. Во многих случаях проще найти область значений функции, построив ее график. Областью значений многих функций с корнями является (-∞,0] или [0,+∞), так как вершина параболы, направленной вправо или влево, лежит на оси Х. В этом случае область значений включает все положительные значения «у», если парабола возрастает, или все отрицательные значения «у», если парабола убывает. Функции с дробями имеют асимптоты, которые определяют область значений.[10]
- Вершины графиков некоторых функций с корнями лежат выше или ниже оси Х. В этом случае область значений определяется координатой «у» вершины параболы. Если, например, координата «у» вершины параболы равна -4 (у = -4), а парабола возрастает, то область значений равна [-4,+∞).
- Самый простой способ построить график функции – это воспользоваться графическим калькулятором или специальным программным обеспечением.
- Если у вас нет графического калькулятора, постройте приблизительный график, подставив в функцию несколько значений «х» и вычислив соответствующие значения «у». Нанесите найденные точки на координатную плоскость, чтобы получить общее представление о форме графика.
-
2
Найдите минимум функции. Построив график функции, вы увидите на нем точку, в которой функция имеет минимальное значение. Если наглядного минимума нет, то он не существует, а график функции уходит в -∞.
- Область значений функции включает все значения «у» за исключением значений асимптот. Зачастую, области значений таких функций записываются так: (-∞, 6) U (6, ∞).
-
3
Определите максимум функции. Построив график функции, вы увидите на нем точку, в которой функция имеет максимальное значение. Если наглядного максимума нет, то он не существует, а график функции уходит в +∞.
-
4
Область значений функции записывается аналогично области определения функции. Квадратная скобка применяется в том случае, когда значение входит в область значений функции; если значение не входит в область значений, используется круглая скобка. Если у функции несколько несмежных областей значений, между ними ставится символ «U».[11]
- Например, область значений [-2,10) U (10,2] включает значения -2 и 2, но не включает значение 10.
- С символом бесконечности ∞ всегда используются круглые скобки.
Реклама
Об этой статье
Эту страницу просматривали 352 576 раз.
Была ли эта статья полезной?
Общая информация
У каждой функции y = f (x) есть два типа переменных: зависимые и независимые. Переменная «х» является независимой, поскольку она может принимать любые значения, кроме тех, которые «превращают» функцию в пустое множество (этого необходимо избегать). Они бывают с одной или несколькими независимыми переменными. Необходимо выяснить все значения зависимой переменной.
Существует несколько методов решения задач такого типа. К ним относятся следующие способы: автоматизированный и ручной. Решение первым подразумевает использование специальных программных оболочек и web-приложений, позволяющих найти область значения функции. Онлайн-калькулятор с решением применяется для тех, кто выполняет большое количество вычислений или проверку вычислений.
В различных дисциплинах необходимо исследовать поведение функций. Например, при проектировании какого-либо программного продукта. Программисты занимаются поиском «багов», при которых происходит некорректная работа приложения. Если заданы недопустимые параметры независимой переменной, то произойдет ошибка. Это называется исключением, и его всегда следует обрабатывать. При проектировании различных устройств нужно также уметь находить область значения функции.
Основные понятия
Руководствуясь некоторыми данными, можно сделать вывод: областью значений некоторой функции называются все ее допустимые значения. Обозначается она буквой «E», т. е. E (f) или E (y). Когда y = f (x) является сложной (w = f (x, y, z)), тогда можно ее обозначить «E (w)».
Независимая переменная, принимающая некоторые значения, называется аргументом. Для конкретного случая существует определенный алгоритм. Можно сразу определить E (f), но в некоторых ситуациях нужно выполнить некоторые преобразования.
Например, нужно найти область значений квадратичной функции y = 3x 2 — 2x — 1. Следует записать уравнение 3x 2 — 2x — 1 = 0. Ордината вычисляется таким образом: y0 = -D / 4a = -[b 2 — 4ac] / 4a = -[(-2)^2 — 4 * 3 * (-1)] / (4 * 3) = -16 / 12 = -4/3. Если коэффициент а>0, то ветви параболы направлены вверх. Следовательно, E (y) = (-4/3;+бесконечность).
Специалисты-математики утверждают, что важным аспектом является определение типа функции. Следовательно, следует разобраться в их классификации. Для этого необходимо знать их графики и названия.
Типы функций
Перед тем, как найти все допустимые значения, нужно знать область значения некоторых элементарных функций. Для каждой из них существует свой промежуток:
- (-бесконечность;+бесконечность): y =kx + b, y = x^(2n+1), y = x^(1/(2n+1)), y = log (x) с основанием а, y = tg (x) и y = ctg (x).
- [0;+бесконечность): y = x^(2n), y = x^(1/(2n)) и y = a^x.
- (-бесконечность;0] U [0;+бесконечность) только для y = k / x (гипербола).
- [-1;1]: y = sin (x) и y = cos (x).
- [0;Pi]: y = arccos (x) и arcsin (x).
- [-Pi/2;Pi/2]: y = arctg (x) и arcsin (x).
Если функция является многочленом четной степени, то для нее существует интервал [m;+бесконечность). Значение «m» — наименьшее значение многочлена. На промежутке (-бесконечность;n) число n — наибольшее его значение.
Довольно сложной задачей считается нахождение области значений тригонометрических функций. Примером одной из них считается y = cos (2x) + 2cos (x). Кроме того, при нахождении E (f) необходимо руководствоваться не только табличными значениями. Этих данных мало, поскольку нужно также знать о свойствах некоторых функций и способы нахождения E.
Важные свойства
Для качественного исследования нужно знать свойства простых функций: монотонность, непрерывность, дифференцируемость, четность или нечетность, периодичность, область определения и значения. Среди свойств можно выделить несколько основных:
- В случае, когда функция f (x) является непрерывной, и наблюдается ее возрастание или убывание на отрезке [a;b], то множество значений — интервал [f (a);f (b)].
- Если y = f (x) обладает непрерывностью на промежутке [a;b], и существует некоторое минимальное m и максимальное М ее значения, то множеством ее значений является интервал [m;M].
- При непрерывности и дифференцируемости функции на промежутке [a;b], она имеет минимальное и максимальное значения на данном промежутке.
Последние два свойства применяются для непрерывных функций. Простое решение позволяет получить первое свойство. При этом очень важно доказать ее монотонность. Задача существенно упрощается, когда удается доказать четность или нечетность функции, а также ее периодичность. По необходимости следует проверять и использовать некоторые ее свойства: непрерывность (при разрыве нужно определить его точку или интервал), монотонность, дифференцируемость, периодичность, четность или нечетность и т. д.
Методы нахождения
Существует много способов нахождения области значений. Однако для решения задач нужно подбирать оптимальный метод, поскольку следует избегать лишних вычислений. Например, если функция является простой, то нет необходимости применять сложные алгоритмы решения. К методам нахождения относятся следующие:
- Отдельное нахождение значений элементов сложной функции.
- Оценочный.
- Учет непрерывности и монотонности.
- Взятие производной.
- Использование max и min функции.
Для каждого из методов существует определенный алгоритм. Хотя встречаются случаи, когда целесообразно применить два простых метода. Нужно руководствоваться минимальным количеством вычислений и затраченным временем.
Для каждого элемента
Иногда в задачах следует найти E (f) при условии, когда функция является сложной. Очень распространенная методика разбиения задачи на подзадачи, которая применяется не только в дисциплинах с физико-математическим уклоном, но в экономике, бизнесе и других направлениях. Решение с помощью метода последовательного нахождения E (f) каждой из функций. Алгоритм имеет такой вид:
- Выполнить необходимые преобразования — упростить выражение.
- Разбить выражение на элементы.
- Выполнить поиск E (f) для каждого элемента.
- Произвести замену.
- Анализ.
- Результат решения.
Однако довольно сложно ориентировать по данному алгоритму, поскольку нужно разобрать решение примера с его помощью. Дана функция y = log0.5 (4 — 2 * 3^x — 9^x). Решается задача таким образом:
- Упростить (выделить квадрат): y = log0.5 (4 — 2 * 3^x — 9^x) = log0.5 [5 — (1 — 2 * 3^x — 9^x)] = log0.5 [5 — (3^x + 1)].
- Разбить на элементарные функции: y = 3^x, y = 3^x + 1, y = [-(3^x + 1)]^2 и y = [5 — (3^x + 1)]^2.
- Определить для каждого элемента E (f): E (3^x) = (0;+бесконечность), E (3^x + 1) = (1;+бесконечность), E ([-(3^x + 1)]^2) = (-бесконечность;-1) и E ([5 — (3^x + 1)]^2) = (-бесконечность;4).
- Произвести замену: t = 5 — (3^x + 1)]^2 (-бесконечность <= t <=4).
- Анализ: поскольку E (f) на луче (-бесконечность;4) совпадает с интервалом (0;4), то функция непрерывна и убывает. Необходимо отметить, что интервал (0;4) получен при пересечении луча (-бесконечность;4) с областью определения функции логарифмического типа (0;+бесконечность). На интервале (0;4) эта функция непрерывна и убывает. Если t>0, то она стремится к бесконечности. Когда t = 4, ее значение равно -2.
- Результат решения — искомый интервал: E (f) = (-2;+бесконечность).
Необходимо обратить внимание на пункты 1, 3 и 5. Они являются очень важными, поскольку от них зависит правильность решения. Очень важно уметь анализировать полученную функцию в 4 пункте.
Оценочный способ
Еще одним методом определения E (f) является способ оценки. Необходимо оценить непрерывную функцию в нижнем и верхнем направлениях. Еще следует доказать достижение нижней и верхней границ. Для этой цели существует также алгоритм. Он немного проще предыдущего. Суть его заключается в следующем:
- Доказать непрерывность.
- Составить неравенство или неравенства для нескольких функций.
- Узнать оценку.
- Записать интервал.
Необходимо разобрать алгоритм на примере функции y = cos (7x) + 5 * cos (x). Следует учитывать, что известен только один знак неравенства. Второй нужно доказать оценочным методом. Решение задачи имеет такой вид:
- Функция вида y = cos (x) является непрерывной.
- Неравенства: -1<=cos (7x)?1 и -5<=5 * cos (x)?5.
- Оценка получает при объединении неравенств: -6<=y?6. При значениях независимой переменной x = Pi и x = 0 функция принимает значения -6 и 6 соответственно (нижняя и верхняя границы). Функция состоит из двух элементов, следовательно, она является линейной и непрерывной.
- Интервал: E (y) = [-6;6].
Метод позволяет найти решение без использования дополнительных вычислений. Но при его использовании легко ошибиться.
Учет непрерывности и монотонности
Одним из простых способов решения, который специалисты рекомендуют новичкам, является метод учета непрерывности и монотонности. Для этого существует специальный алгоритм:
- Упростить выражение.
- Выполнить замену при необходимости.
- Найти вершину графика.
- Определить промежуток.
- Вычислить максимальное и минимальное значения.
- Записать E (f).
Например, существует некоторая функция y = cos (2x) + 2cos (x). Необходимо найти ее E. Искать следует по алгоритму решения методом учета монотонности и непрерывности:
- Упростить (по формуле двойного угла): y = 2 * (cos (x))^2 + 2cosx — 1.
- Замена t = cos (x): y = 2 * t 2 + 2 * t — 1 = 2 * (t + 0,5)^2 — 1,5.
- Показательная функция является параболой. Она монотонна, непрерывна и имеет вершину по оси ОУ -1,5. Промежуток, который рассматривается — [-1;1], поскольку E (cos (x)) = [-1;1].
- Минимальное значение равно -1,5, так как ветви направлены вверх. Максимальное на промежутке [-1;1] — MAX (y) = 3. Для его нахождения нужно построить график параболы y = 2 * (t + 0,5)^2 — 1,5.
- Искомый интервал — E (cos (2x) + 2cos (x)) = [-1,5;3].
Чтобы построить график параболы, нужно найти ее вершину и точки пересечения с осью абсцисс. Последние находятся при решении уравнения 2 * (t + 0,5)^2 — 1,5 = 0. Однако существует способ намного проще. Для этого следует привести выражение к виду 2 * (t + 0,5)^2 = 1,5. Отсюда t = — 0,5. Следовательно, координаты вершины — (-0,5;-1,5). Корни уравнения при его решении: t1 = -[(1 + (3)^0.5)] / 2 и t2 = -[(1 — (3)^0.5)] / 2.
Производная, min и max
Одним из простейших способов нахождения E (f) является взятие производной функции. Этот метод можно комбинировать с определением максимального и минимального значений. Математики рекомендуют простейший алгоритм:
- Найти производную.
- Анализ.
- Указать MAX (f) и MIN (f).
- Запись интервала в формате (MIN (f);MAX (f)).
Практическое применение алгоритма — решение задачи этим методом. Например, нужно найти E (arcsin (x)). Решение выполняется по нескольким этапам:
- Производная: y’ = [arcsin (x)]’ = 1 / [(1 — x 2 )^0.5].
- Функция возрастает на интервале (-1;1).
- Минимум и максимум на отрезке (-1;1): MIN (arcsin (-1)) = -Pi/2 MAX (arcsin (1)) = Pi/2.
- Интервал: E (arcsin (x)) = [-Pi/2;Pi/2].
В некоторых случаях рекомендуется вычислять пределы, поскольку часть задач решается только с их применением. Существует определенный тип задач, в которых нужно доказать, что отрезок является E (f) конкретной функции. Например, следует выяснить принадлежность [-1;1] функции sin (x). Для этого необходимо воспользоваться вышеописанным алгоритмом:
- Производная: y’ = [sin (x)]’ = cos (x).
- Период функции равен 2Pi. Следует взять отрезок [0;2Pi]. Для нахождения множества значений на нем нужно приравнять производную функции к 0, т. е. cos (x) = 0. Найти х = Pi/2 + Pi * к, где «к» принадлежит Z. Точки экстремума равны Pi/2 и 3Pi/2.
- Минимум и максимум на отрезке [0;2Pi): MIN ([sin (3Pi/2)]) = -1 и MAX ([sin (3Pi/2)]) = 1.
- E (sin (x)) = [-1;1].
Отрезок [-1;1] является E (sin (x)). Оптимальный метод — нахождение производной и определение E (f). В этом примере необходимо знать и проверить периодичность.
Таким образом, существует несколько способов нахождения E (f), но всегда необходимо выбирать метод, приводящий к минимуму вычислений. Нет смысла усложнять решение, поскольку большинство алгоритмов направлены на оптимизацию вычислений.
Всем здравствуйте! Тренируемся находить область значений функции! Кто еще не понял, что такое область определения (а она нам тоже понадобится непременно), тому сюда.
Что же такое область значений функции? Это та «часть» оси ординат, та область, где можно наткнуться на какие-либо точки, принадлежащие функции. То есть можно сказать, что если область значений найдена, то все точки функции находятся в ней, не выше и не ниже. Это почти тоже самое, что и область определения, только теперь это «область определения по оси ординат». Здесь никаких особых ограничений нет, поэтому, чтобы найти область значений, нужно иметь представление об элементарных функциях — например, как выглядят парабола или гипербола, как определить, направлены ли ветви параболы вверх или вниз и т.п. Все это рассказано и показано здесь.
Ну, поехали!
Примеры.
1. Найдите область значений функции 
Решение: функция – квадратичная, представляет собой параболу с положительным старшим коэффициентом, ветви направлены вверх. Понятно тогда, что весь график располагается выше координаты своей вершины (вершина — самая низшая точка). Ордината вершины: 
, тогда 
.
2. Найдите область значений функции 
Решение: область определения функции 
( 
] 
[
).
В точках (-7) и (3) двучлен обращается в ноль. Поскольку результат извлечения корня — величина положительная, то вся функция располагается выше оси абсцисс, и ее область значений 
[
)
3. Найти область значений функции 
Область определения – вся числовая ось, кроме ноля. Можем подставить любое число из области определения, при этом функция всегда отрицательна.
Из графика также видно, что 
4. Найти область значений функции: 
Решение. Область определения:
На концах отрезка функция принимает значение 1, под корнем имеем квадратный двучлен, наибольшее значение он принимает в вершине, при 
, значит, функция будет принимать в этой точке наименьшее значение.
Подставив 1, получаем 
Ответ: ![E(f)=[{1/3};1]](https://easy-physic.ru/img_formuls/math_985.5_1886f49c79f1ee64a352b2c46dc2c867.png "E(f)=[{1/3};1]")
5. Найдите область значений функции: 
Очевидно, что график данной функции может быть получен из графика обычной параболы 
, область значений которой легко найти: ветви направлены вверх, поэтому низшая точка – вершина параболы. Однако заметим также, что если аргумент функции под знаком модуля, то график такой функции может быть построен с помощью отражения части графика, лежащей в правой вертикальной полуплоскости, в левую полуплоскость(см. рисунок). Тогда от нашей параболы останется только часть, лежащая правее оси ординат, и именно она будет отражена относительно оси y, и тогда низшей точкой окажется та, в которой график пересечет ось ординат, а это — значение свободного члена (коэффициента с), который у нас равен (-6).
Область значений нашей функции [
)
6. Найдите область значений функции: 
Очевидно, что график данной функции может быть получен из графика обычной параболы . Так как все выражение находится под знаком модуля, то для того, чтобы построить такой график, нужно отразить всю часть графика, расположенную ниже оси х, вверх, поэтому [).
7. Найдите область значений функции: 
Данная функция получена преобразованием обычной гиперболы. Данная функция не существует при 
, или 
. При 
второе слагаемое обращается в ноль, и функция стремится к значению 
, причем можно заметить, что при положительных больших значениях х данная функция приближается к 2 снизу, а при отрицательных — сверху.
Ответ: 
8. Найти область значений функции: 
Решение. Область определения:
При 
функция принимает наибольшее значение 
,
При x, стремящемся к бесконечности, функция стремится к нулю. Но мы запишем область значений от меньшего к большему:
Ответ: 
(
]
Мы знакомы с примерами функций и способами их задания. Рассмотрим понятия области определения и области значения функции, а также свойства функции.
1. Область определения и область значений функции
Найти область определения функции можно как по формуле, задающей функцию, так и по графику.
Определение:
Область определения функции — это допустимые значения независимой переменной (переменной x). Обозначается область определения функции D(f).
Чтобы лучше понять что такое область определения функции рассмотрим несколько примеров.
Если функция задана аналитически:
Найти область определения функции, если она задана формулой:
1) y=12x+7
2)f(x)=(5x-3)/(8x-16)
Функция задана формулой значит, для того чтобы найти ее область определения, нужно ответить на вопрос: «Какие значения можно подставлять в формулу вместо х?»
1) В формулу функции вместо х можно подставлять
любые
действительные числа. Значит область определения функции — любые действительные числа. Записывают следующим образом:
D(y)=(-ထ; +ထ)
2) Поскольку знаменатель функции не должен равняться нулю:
8x-16≠0
х≠2
Значит, D(y)=(-ထ; 2)U(2; +ထ)
Найти область определения функции если она задана графически еще проще, для этого необходимо обратить внимание на то, какие значения принимает «х» на графике. Попробуйте выполнить задание самостоятельно, а затем сравните с решением.
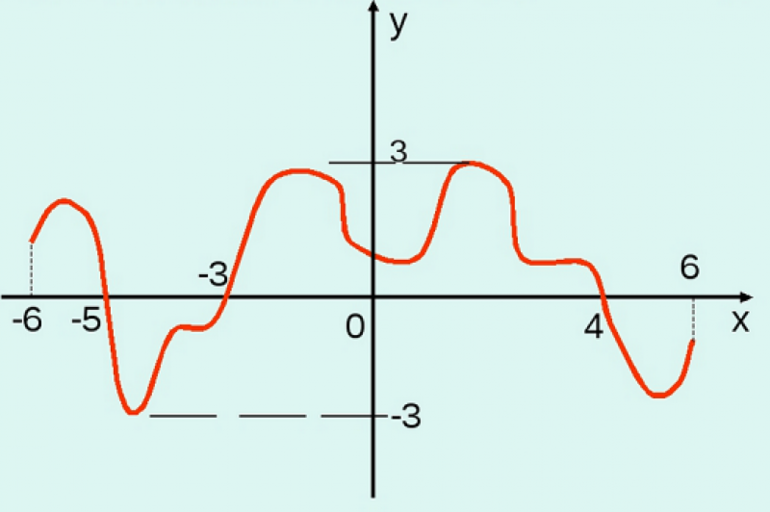
По графику видно что D(f)=[-7;7]
Далее рассмотрим понятие область значений функции
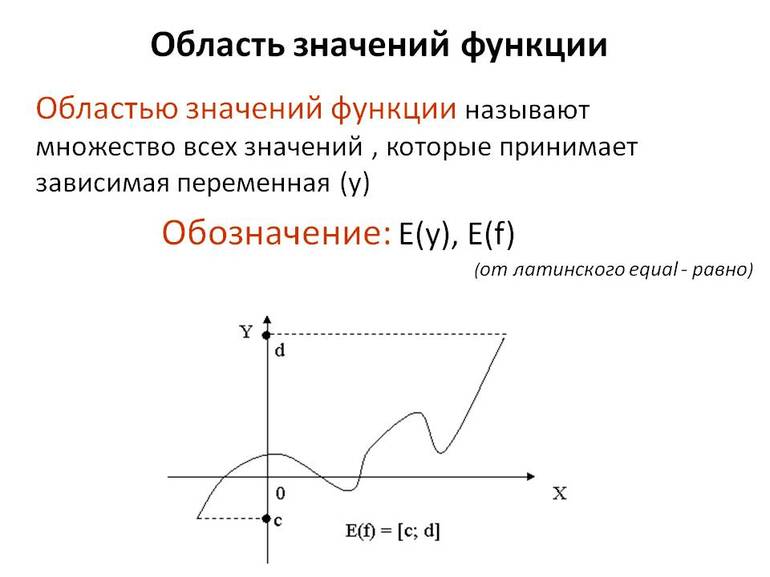
Определение:
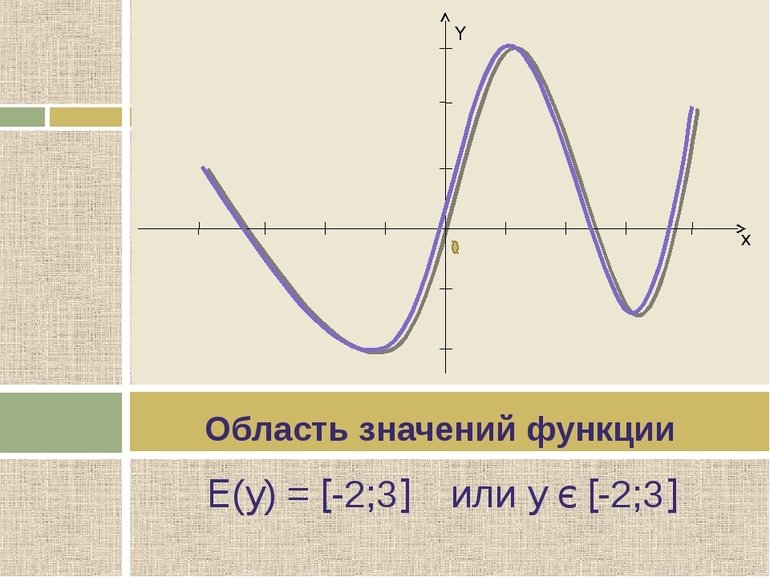
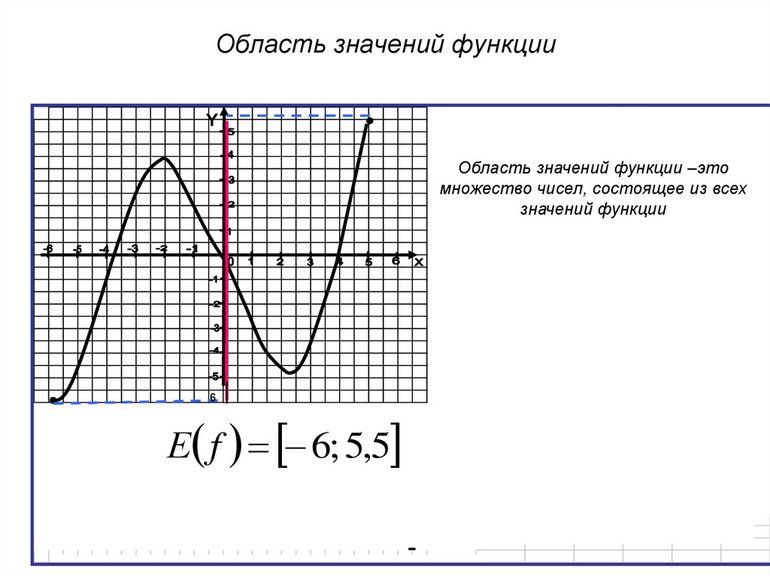
Область значений функции — это множество всех действительных значений y, которые принимает функция. Обозначается область значений функции E(f).
Рассмотрим примеры на нахождение области определения если функция задана аналитически и графически.
Для того чтобы найти область значений функции необходимо ответить на вопрос: » какие значения может принимать у«
1) Если вместо х любое действительное число, то у, в данном случае, также может принимать любые значения, следовательно
E(y)=(-ထ; +ထ)
2) Так как, при подстановке любого действительного числа вместо х, функция (у) из-за модуля будет принимать только неотрицательные значения, то
E(y)=[0; +ထ)
Для нахождения области значений функции, если она задана графически необходимо обратить внимание на то, какие значения принимает «у» на графике. Попробуйте выполнить задание самостоятельно, а затем сравните с решением.
По графику видно что E(f)=[-7;7]
2. Нули функции
Нули функции можно найти как по формуле, задающей функцию, так и по графику.
Определение:
Нули функции– это значение аргумента, при которых функция обращается в ноль.
Если необходимо найти нули функции по графику, то нужно определить точки пересечения графика с осью ОХ:
На данном примере график функции пересекает ось ОХ при х=-4; х=5,5 и х=8. Эти точки пересечения выделены красным цветом.
Обратите внимание!:
Существуют функции, которые не будут иметь точек пересечения с осью ОХ, следовательно нулей у такой функции нет
Для того чтобы найти нули функции заданной аналитически нужно:
- Прировнять «у» к нулю
- Решить получившееся уравнение
а. y=-11х+22
б. y=(х+76)(х-95)
а. y=-11х+22
1) у=0
т.е:
-11х+22=0
2) Решим получившееся уравнение
-11х+22=0
-11х=-22
х=2
Ответ: 2
б. y=(х+76)(х-95)
1) у=0
получим:
(х+76)(х-95)=0
2) Решим уравнение
(х+76)(х-95)=0
х+76=0 или х-95=0
х=-76 х=95
Ответ: -76; 95
3. Промежутки знакопостоянства
Промежутки знакопостоянства функции также можно определить как по формуле, задающей функцию, так и по графику.
Определение:
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
Если необходимо найти промежутки знакопостоянства у функции заданной графически, то достаточно определить по графику где функция принимает положительные и отрицательные значения. Для примера возьмем график функции для которой мы находили нули функции :
На рисунке синим цветом выделены части графика в промежутках [-8; -4) U (-4; 5,5) U (8;9] , которые расположены выше оси ОХ. Зеленым цветом выделены части графика в промежутке (5,5 ; 
который расположен выше оси х.
Значит, что в промежутках [-8; -4) U (-4; 5,5) U (8;9] функция принимает положительные значения, а в промежутке (5,5 ; она принимает отрицательные значения. Это и есть промежутки знакопостоянства.
Что делать если функция задана аналитически?
Чтобы определить знаки постоянства достаточно понимать как решаются неравенства и запомнить алгоритм:
- Рассматриваем случай когда у>0
- Решаем получившееся неравенство, полученный промежуток показывает при каких «х» функция положительна
- Аналогично рассматриваем случай у<0
- Решаем неравенство, полученный промежуток показывает при каких «х» функция отрицательна
Рассмотрите пример с решением или попробуйте выполнить задание самостоятельно с помощью алгоритма описанного выше:
а. y=-11х+22
1) y>0
Следовательно
-11х+22>0
2)
-11(x+2)>0
x+2<0
x<-2
3) y<0
Следовательно
-11х+22<0
4)
-11(x+2)<0
x+2>0
x>2
Ответ: Функция положительна (у>0) при х∈ (-∞;-2)
Функция отрицательна (у<0) при х∈ (-2;+∞)
б. y=|x+14|
1) y>0
Следовательно
|x+14|>0
2) |x+14|>0
Неравенство верно при любых «х» кроме х=-14
3) y<0
Следовательно
|x+14|<0
4) |x+14|<0
Неравенство неверно при любых «х»
Ответ: Функция положительна (у>0) при х∈ (-∞;-14) U (-14;+∞)
Функция не принимает отрицательных значений
4. Монотонность
В курсе средней школы монотонность функции будем определять исключительно по ее графическому заданию, но в старших классах промежутки возрастания и убывания можно определить и аналитически с помощью производной
Определение:
Функцию у=f(x) называют возрастающей на промежутке, если для любых двух точек x1 и x2 промежутка, таких, что x1 < x2, выполняется неравенство f(x1) < f(x2)
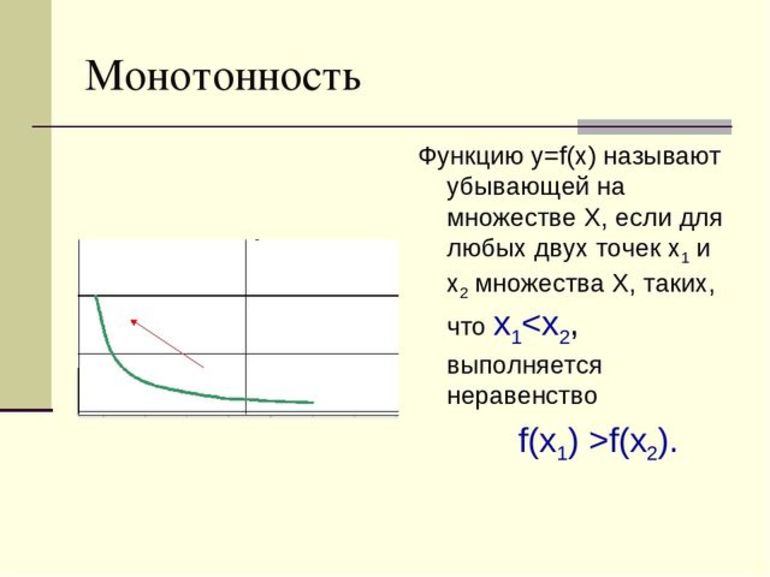
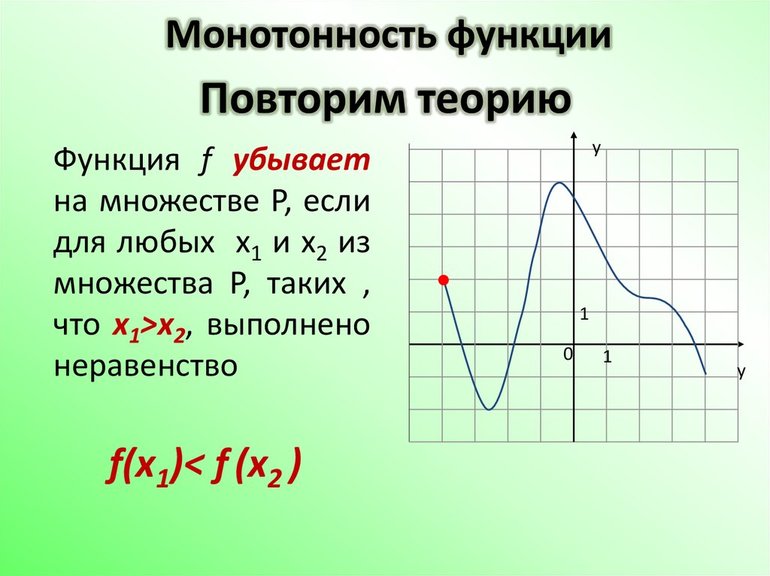
Функцию у=f(x) называют убывающей на промежутке, если для любых двух точек x1 и x2 промежутка, таких, что x1 < x2, выполняется неравенство f(x1) > f(x2)
Иными словами формальное определение можно интерпретировать следующим образом:
Функция называется возрастающей на промежутке если график визуально «идет наверх», аналогично функция называется убывающей если график визуально «идет вниз».
В качестве примера найдем промежутки монотонности графика функции, рассматриваемого выше:
На рисунке голубым цветом выделены части графика в промежутках (-4; 1) U (7;9) на которых график функции возрастает. Розовым цветом выделены части графика в промежутке (-8 ; 4) U (1;7) на которых график функции убывает. Это и есть промежутки монотонности исходной функции.
5. Четность и нечетность
Исследовать функцию на четность и нечетность можно как аналитически так и графически. Рассмотрим определения четной и нечетной функции, а также алгоритмы для ее проверки.
Определение:
Функцию у=f(x) называют четной, если для любого значения «х» выполняется равенство f(-x)=f(x)
Функцию у=f(x) называют нечетной, если для любого значения «х» выполняется равенство f(-x)=-f(x)
Важно!
Существуют четные функции, нечетные функции, а также функции которые не являются ни четными, ни нечетными.
Не существует функций которые одновременно являются четными и нечетными
Если функция y=f(x) задана аналитически, то для ее исследования на четность и нечетность применим следующий алгоритм:
- Записать выражение y=f(-x). Для этого необходимо в формуле задания функции заменить «х» на «-х»;
- Сопоставить выражения f(-x) и f(x):
Если f(-x) = f(x), то функция является четной;
Если f(-x) = -f(x), то функция является нечетной;
Если ни первое, ни второе условие не выполняется то функция не является ни четной, ни нечетной.
Рассмотрим пример:
а. y=-11х+22
1) f(-x)= -11·(-x)+22=11х+22
2) Сравним f(x) и f(-x)
-11х+22 ≠ 11х+22, то есть f(-x) ≠ f(x)
-11х+22 ≠ -(-11х-22), то есть f(-x) ≠ -f(x)
Значит, функция не является четной и не является нечетной
б. y=|x|
1) f(-x)=|-x|
2) Сравним f(x) и f(-x)
|x|=|-x|, то есть f(-x) = f(x)
Значит функция является четной
Если функция y=f(x) задана графически, то для ее исследования на четность и нечетность будем применять следующие правила:
Четная и нечетная функция y=f(x) имеет симметричную область определения D(f)
Если график функции y=f(x) симметричен относительно оси ординат, то y=f(x) — четная функция
Например:
Если график функции y=f(x) симметричен относительно начала координат, то y=f(x) — четная функция
Например:
На этом рассмотрение свойств функций закончено. Помимо тех свойств, которые разобраны в данном разделе существуют и другие, такие как ограниченность и неограниченность функции, периодичность функции и так далее, которые в курсе алгебры 7-9 класса не рассматриваются.
Александр Мельник
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение 1
Функцией, заданной на множестве $X$ и принимающей значения из множества $Y$ называют некую закономерность, по которой каждому элементу из множества $X$ соответствует лишь один и только один элемент из множества $Y$.
Из этого определения следует, что множество (область) значений функции — это те значения функции $y(x)$, которые она может принимать соответственно области её определения. Теперь перейдём к следующему определению.
Определение 2
Область (множество) значений функции на некотором рассматриваемом отрезке — это интервал значений, которые функция принимает на этом рассматриваемом отрезке.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Чаще всего в учебной литературе встречается термин «множество значений функции». Кратко его обозначают $E(f)$.
Как определить область значения функции
Для определения множества значений функции пользуются графическим методом, методом поисков минимума и максимума, вычислением производной и другими.
Определение множества значений функции графическим методом
Графический метод подразумевает построение графика функции и изучение этого графика. Этот метод наиболее удобен, если не известна какая-либо закономерность изменения функции $f(x)$, а есть только набор произвольных точек или собственно сам график.
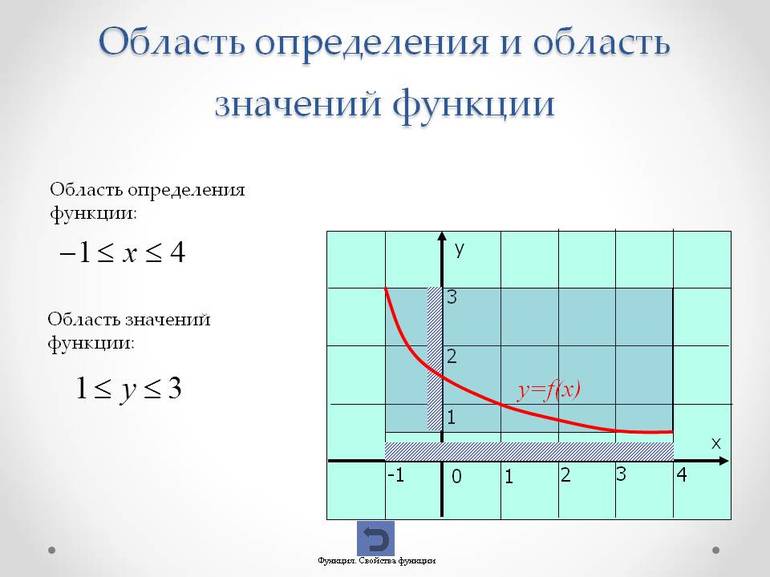
Пример 1
Рисунок 1. Определение множества значений функции графическим методом
На данном рисунке область значений функции $y=f(x)$ равна $E(y)=3$, так как на протяжении всего отрезка функция $y$ не меняет своего значения и всегда равна $3$, тогда как область определения функции $D(y)=[0;3.5]$.
Скобки в данном случае для области определения функции необходимо использовать квадратные, так как обе точки закрашены, то есть включены в отрезок. В случае если точки не закрашены, они не включаются в отрезок и тогда применяются круглые скобки.
«Множество значений функции» 👇
Метод нахождения области значения функции через производную
Метод нахождения области значения функции через производную состоит в том, чтобы сначала оценить область её определения (то есть определить те значения, которые может принимать аргумент $x$, а затем осуществить процедуру нахождения самой производной. После этого осуществляют поиск значений $x$, при которых производная функции равна нулю и при которых производная не существует.
Рассмотрим пример нахождения области значений функции через производную.
Пример 2
Дана функция $f(x)=sqrt{16-x^2}$. Найдите область её значений.
Сначала определяем, какие значения может принимать $x$ для существования функции.
При значении $x^2>16$ под корнем получается отрицательное число, а это значит, что область определения функции от $[-4;4]$ включительно.
Теперь найдём производную функции:
$(sqrt{16-x^2})’=-frac{x}{sqrt{16-x^2}}$
Если в знаменателе производной нуль, то производной не существует, в данном случае это условие выполняется при $x=±4$.
Приравниваем производную к нулю и находим значения $x$. Производная данной функции принимает нулевое значение при $x=0$. Теперь подставляем найденные значения производной в нашу функцию, и получаем, что наименьшее значение функции — это $f(4)$ и $f(-4)$, при этих значениях функция равна нулю, а наибольшее значение $f(x)$ — при $x=0$, в этой точке функция равна $16$.
Метод поиска минимума и максимума
Метод поиска минимума и максимума основан на том, чтобы найти максимальное и и минимальное значение, которые функция принимает на изучаемой области.
Пример 3
Определите область значений функции:
$y=6-4sinx$
Проанализируем данную функцию. Так как минимальное значение синуса равно минус единице, а а максимальное — единице, то подставив эти значения получаем, что $max(f(x))=10$ при $x=frac{3π}{2}$, а минимум $min(f(x))=2$ при $x=frac{π}{2}$. Следовательно, множество значений, которые может принимать данная функция — $E(x)=[2;10]$.
Разница между областью значения и областью определения функции
Стоит обратить внимание, что область значений функции — не одно и то же с термином «область определения функции».
Определение 3
Область определения функции $D(y)$ — это диапазон таких значений переменной $x$, при которых существует функция $y(x)$.
Например, рассмотрим функцию $y(x)=x^2$. В данном случае область определения этой функции будет множеством вещественных (действительных) чисел $mathbb{R}$, а сама функция будет принимать значения только положительных действительных чисел $mathbb{R}^+$, так как вещественное число, возведённое в квадрат, не может давать отрицательное значение. То есть, в этом примере множество значений функции — это множество положительных вещественных чисел $mathbb{R}^+$.
Также имеют место случаи, когда область определения функции совпадает с областью значений.
В качестве иллюстрации можно рассмотреть функцию $y(x)=2x$. За аргумент $x$ данная функция может принимать любое действительное число из множества $mathbb{R}$, а значения, которые будет принимать сама функция — это удвоенные числа из множества всех действительных чисел. То есть, в данном случае областью значений $E(y)$ будет также всё множество вещественных чисел $mathbb{R}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме