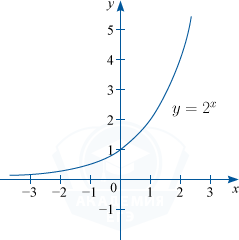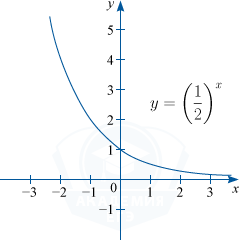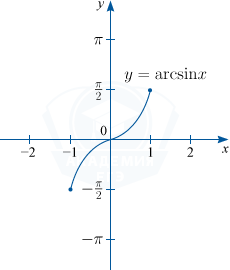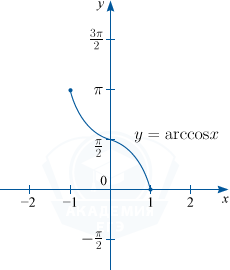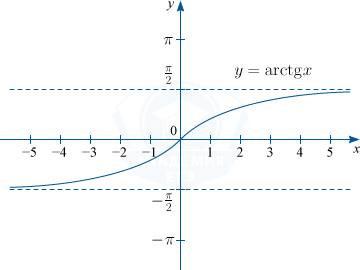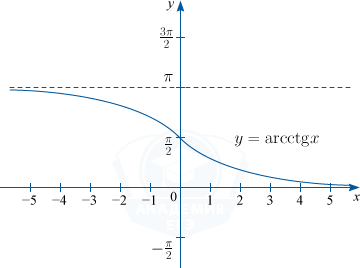- Развертка котангенса движения точки по числовой окружности в функцию от угла
- Свойства функции y=ctgx
- Примеры
п.1. Развертка котангенса движения точки по числовой окружности в функцию от угла
При движении точки по числовой окружности на горизонтальной касательной, проведенной через точку (0;1), отображаются значения котангенсов соответствующих углов (см. §3 данного справочника).
Рассмотрим, как изменяется котангенс, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=ctgx на этом отрезке.
Если мы продолжим движение по окружности для углов x > 2π, кривые продолжатся вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x<0, кривые продолжатся влево.
В результате получаем график y=ctgx для для всех x из области допустимых значений.
График котангенса называют «тагненцоидой», термин «котангенцоида» не используют.
Часть графика c (0lt xltpi) называют главной ветвью графика котангенса.
п.2. Свойства функции y=ctgx
1. Область определения (xnepi k) — множество действительных чисел, кроме точек, в которых (sinx=0).
2. Функция не ограничена сверху и снизу. Область значений (yinmathbb{R})
3. Функция нечётная $$ ctg(-x)=-ctgx $$
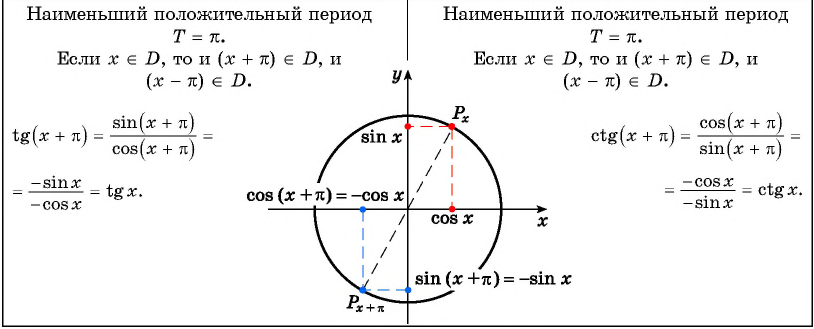
4. Функция периодическая с периодом π $$ ctg(x+pi k)=ctgx $$
5. Функция стремится к (-infty) при приближении слева к точкам (x=pi k).
Приближение к точке a слева записывается как (xrightarrow a-0) $$ lim_{xrightarrow pi k-0} ctgx=-infty $$ Функция стремится к (+infty) при приближении справа к точкам (x=pi k).
Приближение к точке a справа записывается как (xrightarrow a+0) $$ lim_{xrightarrow pi k+0} ctgx=+infty $$ Нули функции (y_{0}=0) достигаются в точках (x_0=fracpi2+pi k)
6. Функция убывает на всей области определения.
7. Функция имеет разрывы в точках (x=pi k), через эти точки проходят вертикальные асимптоты. На интервалах между асимптотами ((pi k; pi+pi k)) функция непрерывна.
п.3. Примеры
Пример 1.Найдите наименьшее и наибольшее значение функции y=ctgx на заданном промежутке:
a) (left[frac{2pi}{3}; piright)) $$ y_{min}=lim_{xrightarrowpi-0}ctgx=-infty, y_{max}=ctgleft(frac{2pi}{3}right)=-frac{1}{sqrt{3}} $$ б) (left(0; frac{pi}{4}right]) $$ y_{min}=ctgleft(frac{pi}{4}right)=1, y_{max}=lim_{xrightarrow +0}ctgx=+infty $$ в) (left[frac{7pi}{6}; frac{7pi}{4}right]) $$ y_{min}=ctgleft(frac{7pi}{4}right)=-1, y_{max}=ctgleft(frac{7pi}{6}right)=sqrt{3} $$
Пример 2. Решите уравнение:
a) (ctgx=-sqrt{3})
Бесконечное множество решений: (x=frac{5pi}{6}+pi k, kinmathbb{Z})
б) (ctgleft(x+fracpi2right)=0)
(x+fracpi2=fracpi2+pi k)
Бесконечное множество решений: (x=pi k, kinmathbb{Z})
в) (ctg(2x)=1)
(2x=fracpi4+pi k)
Бесконечное множество решений: (x=frac{pi}{8}+frac{pi k}{2}, kinmathbb{Z})
г) (ctgleft(frac{x}{3}-1right)=-1)
(frac{x}{3}-1=-frac{pi}{4}+pi k)
(frac{x}{3}=1-frac{pi}{4}+pi k)
Бесконечное множество решений: (x=3-frac{3pi}{4}+3pi k, kinmathbb{Z})
Пример 3. Постройте графики функций: a) (y(x)=x^2-2tgxcdot ctgx)
 |
Произведение (tgxcdot ctgx=1). При этом ограничивается область определения функции (y(x)), т.к. (tgx) и (ctgx) имеют разрывы. Точки разрыва отмечены на числовой окружности: (xnefrac{pi k}{2}). |
Получаем: $$ begin{cases} x^2-2\ xnefrac{pi k}{2}, kinmathbb{Z} end{cases} $$ Строим график параболы и выкалываем точки, не входящие в ОДЗ.
б) (y(x)=sin^2(tgx)+cos^2(tgx)-x)
 |
Сумма (sin^2(tgx)+cos^2(tgx)=1). При этом ограничивается область определения функции (y(x)), т.к. (tgx) имеeт разрывы. Точки разрыва отмечены на числовой окружности: (xnefrac{pi}{2}+pi k). |
Получаем: $$ begin{cases} 1-x\ xnefrac{pi}{2}+pi k, kinmathbb{Z} end{cases} $$ Строим график прямой и выкалываем точки, не входящие в ОДЗ.
Рейтинг пользователей
Область определения и
множество значений
тригонометрических
функций
ОГЛАВЛЕНИЕ:
1.
Определение
«функция»;
2.
Какие функции
называются тригонометрическими;
3.
Что такое область
определения и множество значений функций. Как найти область определения и множество значений
тригонометрических функций;
4. Таблица «Область определения и множество
значений тригонометрических функций».
1. Функция — это зависимость одной переменной
величины от другой. То есть, это зависимость между величинами.
«x» называют
аргументом функции (переменной), «y» называют значением функции.
Рассмотрим
на простом примере (y=2x), как мы видим «y»
зависит от «х», так
как «х» переменный
аргумент, вместо него мы выбираем любые значения и подставляем в уравнение,
получая при этом значение «у».
2. Какие же
функции называются тригонометрическими?
Тригонометрические функции — это элементарные функции, с переменным аргументом, в которых служит угол, то есть «х»
является определённым углом.
Зачастую
тригонометрические функции обозначают отношением сторон прямоугольного
треугольника либо длины конкретных отрезков в единичной окружности. Такие
функции имеют вид:
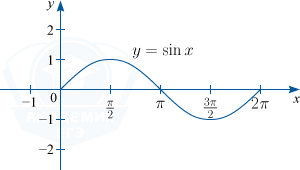
1. y=sinx
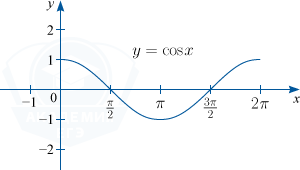
2. y=cosx
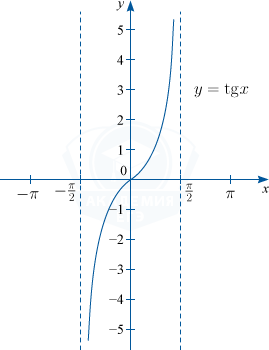
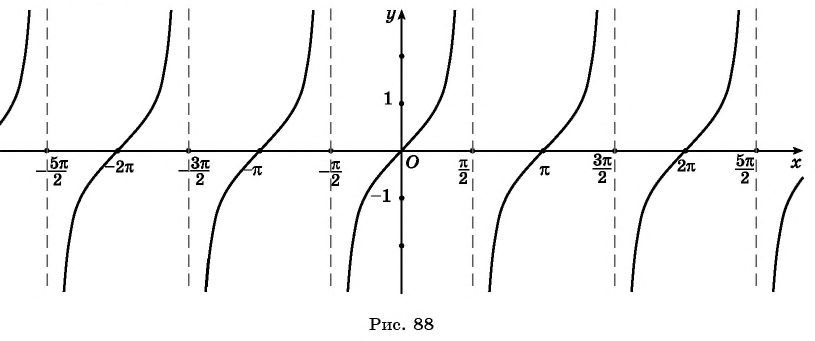
3. y=tgx
4.
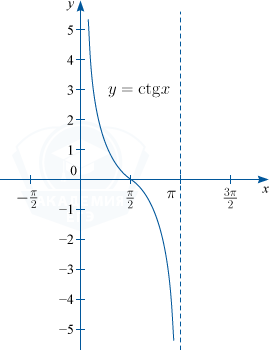
y=ctgx
3. Начнем с
области определения.
Областью
определения функции называется множество значений аргумента «х», на
котором можно задать эту функцию «у».
Множеством значения функций называют множество, состоящее их всех
значений, которые принимает функция.
Рассмотрим
функции y=tgx, у=ctg, sinx, cosx на единичной окружности.
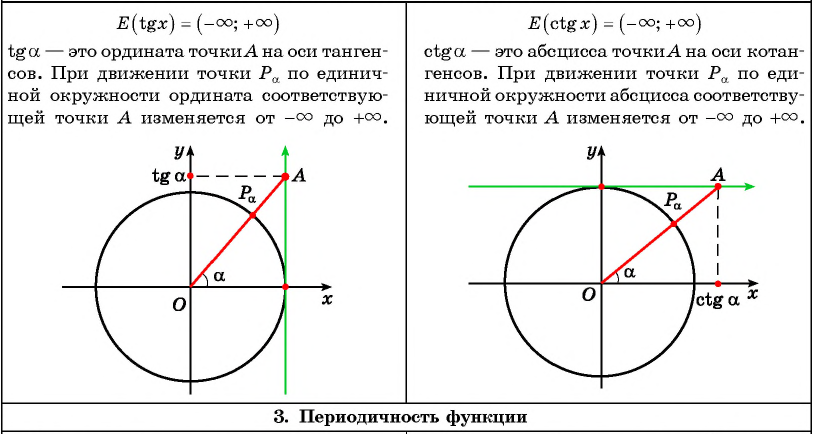
Функция
y=tgx определяется из ΔOAB как tgx=AB/OB=sinx/cosx.
Эта
функция определена при тех значениях, для которых cosx≠0.
Следовательно,
областью определения функции y=tgx является всё множество действительных чисел,
исключая x=π/2+πn, n∈Z.
Множеством
значений функции y=tgx является множество всех действительных чисел R.
Функция y=ctg определяется из ΔOAB как ctgx=OB/AB=cosx/sinx.
Эта функция
определена при тех значениях, для которых sinx≠0.
Следовательно,
областью определения функции y=ctgx является всё множество действительных
чисел, исключая x=πn, n∈Z.
Множеством
значений функции y=ctgx является множество всех действительных чисел R.
AB=sinx;OB=cosx .
Тем
самым каждому действительному числу x поставлены в соответствие числа sinx и
cosx, то есть на множестве R всех действительных чисел определены функции
y=sinx и y=cosx.
Таким
образом, областью определения функций y=sinx и y=cosx является множество R всех
действительных чисел.
Множеством
значений функций y=sinx и y=cosx является интервал [−1;1].
4. Таблица:
«Область определения и множество значений тригонометрических функций»
Источники:
1.
https://videouroki.net/video/01-oblast-opredeleniya-i-mnozhestvo-znachenij-trigonometricheskih-funkcij.html
2.
https://www.yaklass.ru/p/algebra/10-klass/trigonometricheskie-funktcii-10781/trigonometricheskie-funktcii-chislovogo-argumenta-10782/re-90ce54f0-d7df-47e5-becb-006ab01487e9
Преподаватель который помогает студентам и школьникам в учёбе.
Содержание:
Определение функции y=tg x
Определение:
Зависимость, при которой каждому действительному числу
Пример:
Определите, принадлежит ли графику функции 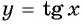
Решение:
а) Подставим в формулу 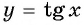
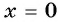
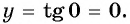
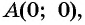
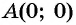
б) При 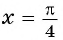
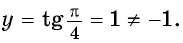
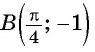
в) При 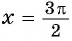
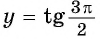
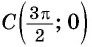
Определение функции y=ctg x
Определение:
Зависимость, при которой каждому действительному числу 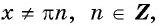
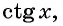
Пример:
Верно ли, что график функции 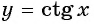
Решение:
а) Подставим в формулу 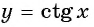
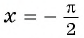
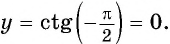
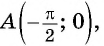
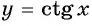
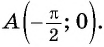
б) При 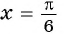
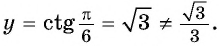
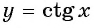
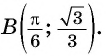
в) При 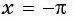
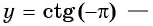
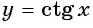
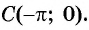
Свойства функций y=tg x и y=ctg x
Рассмотрим свойства этих функций:
График функции y=tg x
График функции 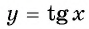
График функции y=ctg x
График функции 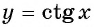
Примеры заданий и их решения
Пример №1
Найдите область определения функции:
Решение:
а) Так как область определения функции 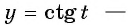
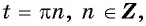
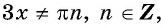
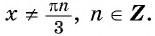
б) Областью определения функции 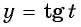
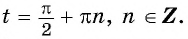
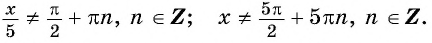
Пример №2
Найдите множество значений функции:
Решение:
а) Так как множество значений функции 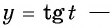
б) Так как множество значений функции 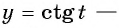
Пример №3
Используя свойство периодичности функций 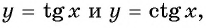
Решение:
Так как число 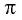
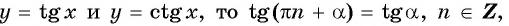
- Заказать решение задач по высшей математике
Пример №4
Используя свойство нечетности функций 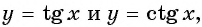
Решение:
Так как функции 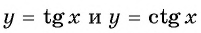
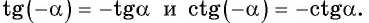
Пример №5
Определите знак произведения
Решение:
Так как 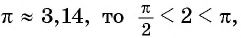
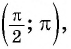
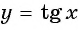
Угол 4,5 радиана принадлежит промежутку 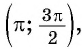
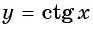
Угол 7 радиан принадлежит промежутку 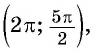
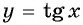
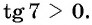
Пример №6
Что больше:
Решение:
Поскольку углы 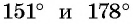
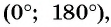
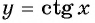
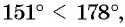
Пример №7
Постройте график функции:
Решение:
а) График функции 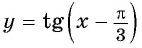
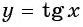
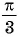
б) График функции 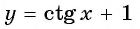
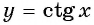
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Тригонометрические уравнения
- Тригонометрические неравенства
- Формулы приведения
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Функция y=sin x и её свойства и график
- Функция y=cos x и её свойства и график
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
Voprosy_k_ekzamenu_po_distsipline_matematika2.docx
Скачиваний:
30
Добавлен:
23.12.2018
Размер:
390.79 Кб
Скачать
Функция котангенс
|
|
||||||||||
Множество значений функции —
Функция Функция периодическая с наименьшим
|
18.
Свойства и график тригонометрической
функции y=tg
x.
Функция тангенс
|
|
||||||||||
Множество значений функции — Функция нечетная: tg(−x)=−tg x для Функция периодическая с наименьшим
|
19.
Свойства и график тригонометрической
функции y=cos
x.
Функция косинус
|
|
||||||||||||||
|
Множество значений функции — Функция четная: cos(−x)=cos x для График функции симметричен Функция периодическая с наименьшим cos(x+2π·k) = cos x, где
|
20.
Простейшие тригонометрические уравнения
cos
x=a,
ctg
x=a.
Частные
случаи
Частные
случаи
21.
Простейшие тригонометрические уравнения
sin
x=a,
tg
x=a.
Частные
случаи
Частные
случаи
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Графики элементарных функций
Линейная функция
Линейная функция — это функция вида y=kx+b, где k и b некоторые действительные числа.
Если b=0, то функция примет вид y=kx и будет называться прямой пропорциональностью.
D(f) : x in R;enspace E(f) : y in R
График линейной функции — прямая.
Угловой коэффициент k прямой y=kx+b вычисляется по следующей формуле:
k= tg alpha , где alpha — угол наклона прямой к положительному направлению оси Ox.
1) Функция монотонно возрастает при k > 0.
Например: y=x+1
2) Функция монотонно убывает при k < 0.
Например: y=-x+1
3) Если k=0, то придавая b произвольные значения, получим семейство прямых параллельных оси Ox.
Например: y=-1
Обратная пропорциональность
Обратной пропорциональностью называется функция вида y=frac {k}{x}, где k — отличное от нуля, действительное число
D(f) : x in left { R/x neq 0 right }; : E(f) : y in left {R/y neq 0 right }.
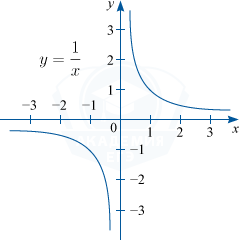
Графиком функции y=frac {k}{x} является гипербола.
1) Если k > 0, то график функции будет располагаться в первой и третьей четверти координатной плоскости.
Например: y=frac{1}{x}
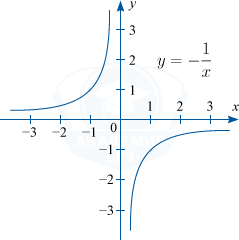
2) Если k < 0, то график функции будет располагаться во второй и четвертой координатной плоскости.
Например: y=-frac{1}{x}
Степенная функция
Степенная функция — это функция вида y=x^n, где n — отличное от нуля, действительное число
1) Если n=2, то y=x^2. D(f) : x in R; : E(f) : y in [0; +infty) .
Графиком функции y=x^2 является парабола.
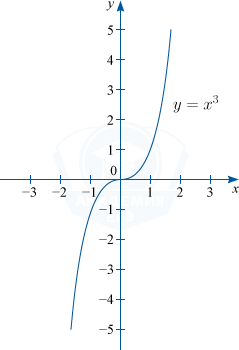
2) Если n=3, то y=x^3. D(f) : x in R; : E(f) : y in R .
Графиком функции y=x^3 является кубическая парабола.
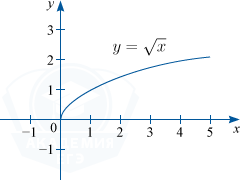
3) Если n=frac{1}{2}, то y=x^tfrac{1}{2} или y=sqrt{x}. D(f) : x in [0; +infty ); : E(f) : y in [0; +infty )
4) Если n=frac{1}{3}, то y=x^tfrac{1}{3} или y=sqrt[3]{x}. D(f) : x in R; : E(f) : y in R
Показательная функция
Показательная функция — это функция вида y=a^x, где a=const, a > 0, a neq 1
D(f) : x in R; : E(f) : y in (0; +infty ).
Графиком показательной функции является экспонента.
1) Функция будет монотонно возрастать при a > 1.
Например: y=2^x
2) Функция монотонно убывает при 0 < a < 1.
Например: y=left (frac{1}{2} right )^{x}
Логарифмическая функция
Логарифмическая функция — это функция вида y=log_{a}x, где a — действительное число, a > 0, : a neq 1
D(f) : x in (0; +infty ); : E(f) : y in R.
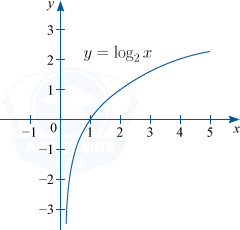
1) Функция монотонно возрастает при a > 1.
Например: y=log_{2}x
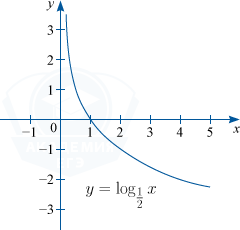
2) Функция будет монотонно убывать при 0 < a < 1.
Например: y=log_{tfrac{1}{2}}x
Тригонометрическая функция
К тригонометрическим функциям относят функции вида:
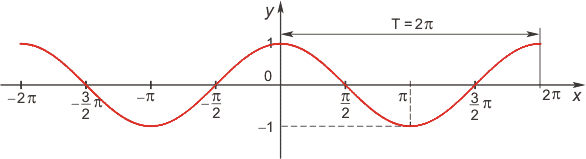
1) y=sin x. D(f) : x in R; : E(f) : y in [-1; 1]; основной период функции T=2 pi
2) y = cos x. D(f) : x in R; : E(f) : y in [-1; 1]; основной период функции T=2 pi
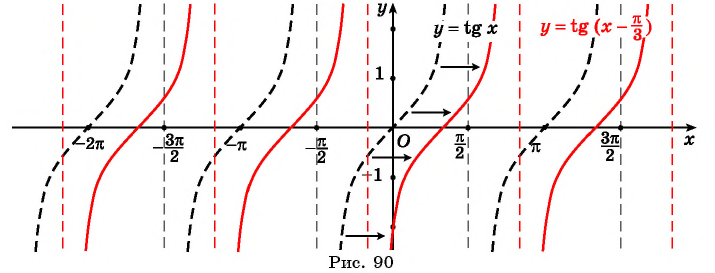
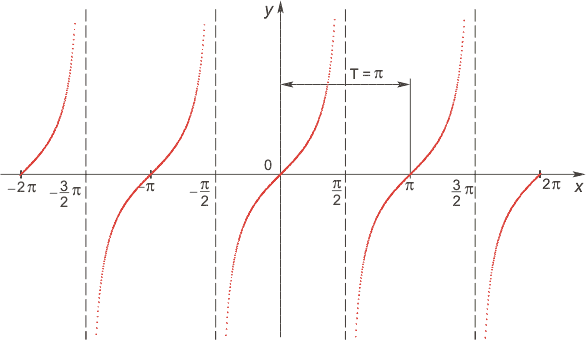
3) y = tg x. D(f) : x in left { R /x neq frac{pi}{2}+pi nright }, n in mathbb{Z}; : E(f) : y in R; основной период функции T= pi
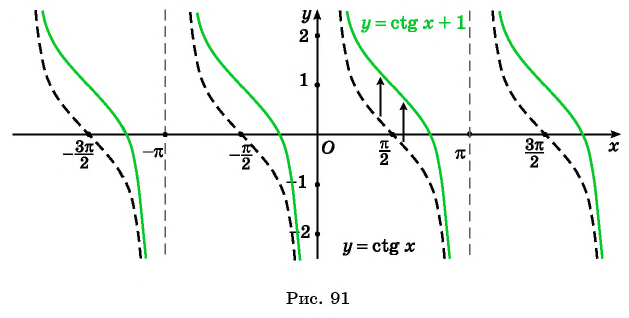
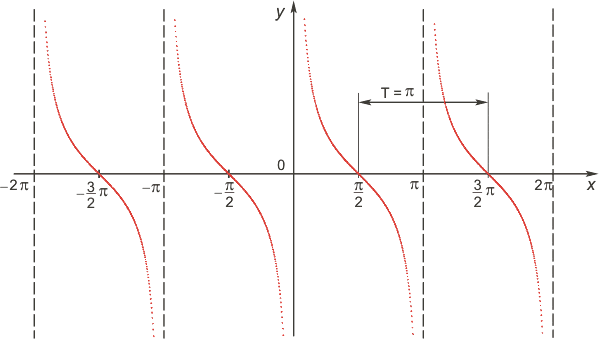
4) y = ctg x. D(f) : x in left { R /x neq 0+pi nright }, n in mathbb{Z}; : E(f) : y in R; основной период функции T= pi
Обратные тригонометрические функции
К обратным тригонометрическим функциям относят функции вида:
1) y=arcsin x. D(f) : x in [-1; 1], : E(f) : y in left [ -frac{pi}{2}; frac{pi}{2} right ]
2) y=arccos x. D(f) : x in [-1; 1], : E(f) : y in [0; pi]
3) y=arctg x. D(f) : x in R, : E(f) : y in left (-frac{pi}{2}; frac{pi}{2} right )
4) y= arcctg x. D(f) : x in R, : E(f) : y in left (0; pi right )










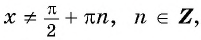
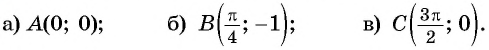
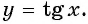
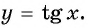
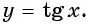
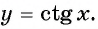
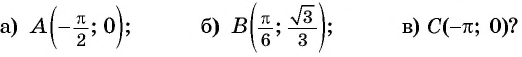



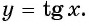


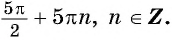

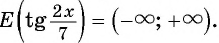
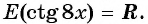
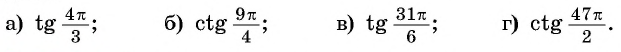
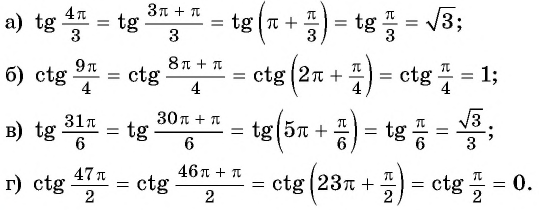


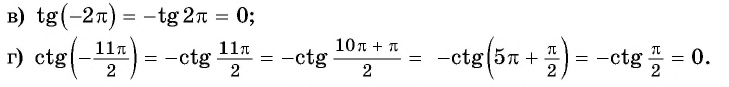
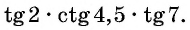
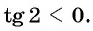
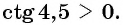
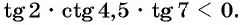
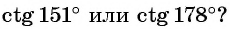
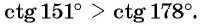


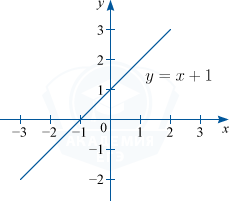
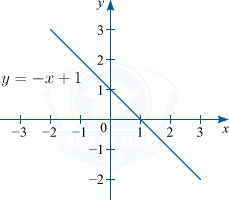
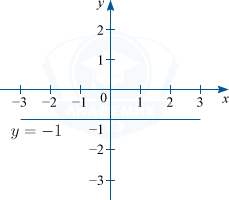
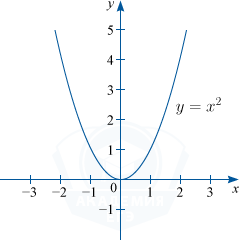
![График степенной функции y=x^{frac 13} или y=sqrt[3]x](https://egeguru.com/i/grafik-stepennoj-funkcii-yxfrac-13-ili-ysqrt3x.png)