Функции комплексного переменного
Основные понятия функций комплексного переменного
Основные понятия, связанные с функцией комплексного переменного, находятся так же, как и в действительной области.
Пусть заданы два множества и
комплексных чисел.
Если каждому значению ставится в соответствие число
, то говорят, что на множестве
задана функция
комплексного переменного, т.е.
Если записать числа и
в алгебраической форме:
, то замечаем, что действительная
и мнимая
части функции
являются функциями переменных
и
и
.
Задание функции эквивалентно заданию на множестве
двух функций
двух действительных переменных.
Кроме того, если для числа записать модуль
и аргумент
для
и
при
(
при
и
при
), то получим аналогичное утверждение. Задание функции комплексного переменного
равносильно заданию двух функций двух действительных переменных. Первая из функций определяет модуль функции:
, вторая — аргумент функции:
, где
в точках, в которых
при
и
при
.
Пример 2.1. Найти значение функции в точках
и
.
Решение
Пример 2.2. Найти , если а)
; б)
.
Решение
Отображения на комплексной плоскости
Задание функции комплексного переменного с областью определения
и областью значений
есть отображение множества
на множество
,
(рис. 2.1).
Точка называется образом точки
при отображении
, точка
— прообразом.
По определению предполагается однозначность отображения, т.е. каждому числу соответствует единственное значение
, но при этом может оказаться, что точка
является образом двух или более точек
(на рис. 2.1 это точка
, так как
и
).
Если любое значение является образом только одной точки
, то отображение называется однолистным в
, в противном случае — неоднолистным. Из определения следует, что однолистное отображение является взаимно однозначным отображением.
Простейшими однолистными (во всей комплексной плоскости) отображениями являются отображения . Первое отображает любую область, в том числе и всю комплексную плоскость, на себя, второе — верхнюю полуплоскость на нижнюю, а нижнюю на верхнюю.
Примером неоднолистного в отображения является
. Действительно, различным точкам, например
и
, соответствует одно значение
, а точкам
— одно значение
. Неоднолистным отображением является и
. Каждой точке
, соответствуют
значений
. В силу этого отображение
при
называют n-листным, а отображение
— двулистным.
Из определения получаем и условие однолистности отображения, отображение является однолистным на множестве , если для любых точек
и
, принадлежащих
, равенство
выполняется тогда и только тогда, когда
. Иначе: отображение однолистно на множестве
, если множество не содержит ни одной пары чисел
и
, таких, что
и выполняется условие
.
Пример 2.3. Найти область однолистности функции .
Решение
Во всей комплексной плоскости отображение не является однолистным. Но можно найти множество, где условие однолистности будет выполняться, т.е. множество, которое не содержит двух различных точек и
, для которых
.
Рассмотрим две произвольные точки и
и разность значений функции в них:
. При
равенство
выполняется, если
. Таким образом, отображение
будет однолистным в любой области, в которой не лежат одновременно две точки
и
, такие, что
. Эти точки нужно расположить на границе области. Так как указанному условию удовлетворяют точки, симметрично расположенные относительно начала координат, то в качестве границы можно выбрать любую прямую, доходящую через
.
Отображение однолистно в любой полуплоскости, границей которой является прямая, проходящая через начало координат, например или
. При этом каждую такую полуплоскость
отображает на всю плоскость.
Рассмотрим подробнее отображение области . На границе выберем точки
(рис. 2.2,с), а обход границы в направлении от
к
. Образами точек
и
на плоскости w является одна точка
(рис. 1.2,б). При этом и левая, и правая полуоси действительной оси отображаются в действительную положительную полуось. Любая область
, принадлежащая верхней полуплоскости, взаимно однозначно отображается на соответствующую область
.
Взаимная однозначность отображения нарушается на границе. Чтобы отображение было взаимно однозначным (однолистным) и на границе, сделаем «разрез» действительной положительной полуоси. Будем считать, что эта полуось состоит из двух «частей» — верхнего «берега» и нижнего «берега» (рис. 2.2,б). Полуось как граница пробегается точкой дважды, скачала по нижнему «берегу» в направлении от точки к
, потом по верхнему — от
к
.
Функция взаимно однозначно отображает верхнюю полуплоскость на плоскость с разрезом по действительной положительной полуоси.
Также на всю плоскость с разрезом по действительной положительной полуоси функция отображает и нижнюю полуплоскость (на рис. 2.2,с обход от
к
), только при этом образом точки
будет точка нижнего «берега» разреза (
на рис. 2.2,б). Заметим также, что правая
и левая
полуплоскости переходят при отображении
в плоскость с разрезом по отрицательной действительной полуоси.
В силу указанной особенности отображение является двулистным в .
Пример 2.4. Исследовать на однолистность отображения: а) ; б)
; в)
.
Решение
Обратные и многозначные функции комплексного переменного
Понятие обратной функции для функции комплексного переменного вводится, как и в действительной области.
Пусть задана функция . Тогда по определению любому числу
из области
соответствует одно или несколько значений
из области
таких, что
, т.е. для любого
уравнение
имеет решения и области
. В таком случае говорят, что уравнение
определяет функцию
, обратную функции
.
Существование функции, согласно определению, предполагает ее однотипность, т.е. для случая обратной функции — это единственность решения уравнения при всяком фиксированном
из
. Очевидно, в общем случае уравнение определяет неоднозначную функцию.
Достаточным условием однозначности обратной функции является однолистность функции .
Пример 2.5. Найти функции, обратные к следующим однолистным функциям:
a) ; б)
; в)
.
Решение
а) Из равенства получаем
, или
. Обратная к линейной функции также является линейной, однозначной. Линейная функции взаимно однозначно отображает комплексную плоскость на себя:
. Если положить
, то можно говорить о взаимно однозначном отображении расширенной плоскости на себя:
.
б) Из , получаем
. Функция сама себе обратная, однозначная; осуществляет взаимно однозначное соответствие плоскости с выброшенной точкой
на всю комплексную плоскость. Если положить
, a
, то получим отображение
.
в) Отображение , очевидно, однолистное, так как из
, или иначе
, получаем, что для любых значений
и
значения функции не совпадают, т.е.
. Функция
, обратная к функции
, является однозначной.
Функции, обратные к неоднолистным. Выделение однозначных ветвей
С неоднозначными функциями приходится встречаться в математическом анализе. Например, уравнение на множестве
определяет двухзначную функцию
, точнее, две функции:
и
. Геометрически — это две части окружности, верхняя и нижняя полуокружности. Эти функции можно назвать двумя однозначными ветвями функции, определяемой неявно уравнением
. Отделение этих функций — выделение однозначных ветвей — здесь не представляет затруднений. Говоря о верхней полуокружности, подразумеваем то решение уравнения
, где
, поэтому ветвь
можно выделить, задавая значения функции во внутренней точке промежутка
, например
; говоря о нижней, можем задать
.
Аналогично в комплексной области предполагаем однозначность функции, однако термин «функция» применяем и к случаю неоднозначных отображений.
Примерами неоднозначных отображений являются функции, обратные к неоднолистным. Например, функция , обратная к функции
, неоднозначная.
Вопрос о возможности выделения в соответствующих областях однозначных ветвей — однозначных, непрерывных функций и построении таких функций связан с исследованием простейшей многозначной функции .
Функция аргумента Arg(z)
Функция является многозначной, что следует из способа введения полярных координат, а именно аргумент числа
определяется с точностью до слагаемого, кратного
.
При перемещении любой точки по произвольной непрерывной кривой аргумент числа
непрерывно изменяется. При этом, если кривая замкнутая, то возможны два случая. В одном случае точка после обхода возвращается в исходное положение с прежним значением аргумента. Так будет для любой кривой, не совершающей обхода вокруг начала координат (рис. 2.4,а). В другом случае аргумент изменяется на
или
в зависимости от направления обхода, а при n-кратном обходе — на
или
. Это имеет месте в случае, когда точка при перемещении обходит начало координат (рис. 2.4.б).
Аргумент как функция точки будет однозначной функцией в области, которая не содержит кривых, совершающих обход точки . В качестве такой области можно взять плоскость с разрезом по любому лучу, выходящему из начала координат, в частности, с разрезом по действительной отрицательной полуоси — область
; можно выбрать разрез по действительной положительной полуоси — область
, где главное значение аргумента определяется равенством
(рис. 2.5). Заметим, что аргументы числа, геометрически соответствующего одной и той же точке областей
и
, могут быть различны. Например. в области
, а в области
.
Границами каждой из областей и
являются два «берега» соответствующей полуоси, обход границ на рисунках указан стрелками.
Пример 2.6. Исследовать возможность выделения однозначных ветвей неоднозначной, функции .
Решение
Функция является неоднозначной как обратная к неоднолистной . Её неоднозначность (двузначность), согласно правилу извлечения корня, связана с неоднозначностью аргумента:
.
Для каждого получаем два значения
, для одного из которых
, для другого
. При этом в силу равенства
эти значения функции отличаются только знаком,
, то есть
. Например, значению
(точка
в плоскости
на рис. 2.6 и 2.7) соответствуют два значения
(точки
в плоскости w на рис. 2.6 и 2.7).
В плоскости с разрезом по лучу (
на рис. 2.5) возможно выделение однозначных ветвей аргумента. Можно рассмотреть две функции:
Первая из них переводит область — плоскость с разрезом — в область
, где
(на рис. 2.6 точка
принадлежит области
), так как для
имеем неравенство
.
Положительный обход границ указан стрелками. В точках границы области однозначность нарушается, но в силу сделанного разреза действительные положительные значения
рассматриваются дважды: на верхнем «берегу» и на нижнем «берегу». Например, при
это точки
— верхнего «берега» и
— нижнего, а при
точки
— верхнего «берега» и
— нижнего (рис. 2.6). При отображении
точкам верхнего «берега» соответствуют положительные значения
(точки
и
), а точкам нижнего — отрицательные (точки
и
).
Вторая функция переводит область
— плоскость с разрезом
на нижнюю полуплоскость
(рис. 2.7), так как для
имеем неравенство
. На рис. 2.7 точка
принадлежит области
.
Граничным точкам верхнего «берега» соответствуют отрицательные значения (точка
), а точкам нижнего «берега» — положительные (точка
).
Отображение и разрез плоскости
Из приведенных рассуждений сформулируем следующее утверждение.
Утверждение 2.1. Двузначная функция отображает плоскость с разрезом по действительной положительной полуоси (область
) на верхнюю полуплоскости (область
) и нижнюю (область
). В области
возможно выделение однозначных ветвей — двух однозначных функций, одна из которых отображает
на
, другая —
на
. Однозначное отображение всей плоскости
невозможно.
Замечание 2.1. Проведение разреза в плоскости позволило получить однозначные функции, с которыми можно производить обычные операции (нахождение значений функции, дифференцирование, интегрирование). Указание определенной ветви осуществляется заданием функции в некоторой точке области. Например, при задании условия рассматривается ветвь
; при условии
— ветвь
(на рис. 2.6 и 2.7 (см. решение примера 2.6) точка
). Но, с другой стороны, проведение разреза нарушило непрерывность отображения. Нарушенную непрерывность можно восстановить следующим образом. На основе приведенных рассуждений имеем, что значения
на верхнем «берегу» границы области
совпадают со значением функции
на нижнем «берегу» той же области, и наоборот (точки
и
на рис. 2.6 и 2.7 (см. решение примера 2.6)). Поэтому можно построить следующую модель.
Возьмем два экземпляра (листа) плоскости (плоскость с разрезом), а именно
и
и «склеим» верхний «берег» разреза
с нижним для
, a нижний
— с верхним для
. В плоскости
при этом получим полную плоскость
. Построенная модель называется римановой поверхностью функции
.
Если в плоскости точка описывает простую замкнутую кривую, обходя начало координат, то в плоскости
ей будет соответствовать кривая, совершающая дважды обход вокруг
, а на римановой поверхности — простая кривая, по которой точка, взятая, например, на первом листе, перемещается по этому листу, потом по второму и возвращается в исходное положение, совершив один обход. Непрерывность и однозначность отображения соблюдены.
Точка , при обходе вокруг которой по замкнутой кривой точка переходит с одного листа на другой, называется точкой ветвления
. Также точкой ветвления
является точка
.
Утверждение 2.2. Функция взаимно однозначно и непрерывно отображает полную плоскость
на риманову поверхность этой функции. Обратная функция
также взаимно однозначно и непрерывно отображает риманову поверхность функции
на полную плоскость
.
Аналогично можно исследовать n-листную функцию и обратную к ней
.
Предел функции комплексного переменного
Число называется пределом функции
в точке
, если для любого числа
найдется число
такое, что для
, удовлетворяющих неравенству
, выполняется неравенство
для
.
Геометрически это означает, что для точек из проколотой δ-окрестности точки соответствующие значения функции принадлежат ε-окрестности точки
.
Напомним, что окрестность точки на комплексной плоскости — это круг с центром в этой точке. Так, или
есть круг радиуса
с центром в точке
, а проколотая окрестность точки
или
, или
— круг радиуса
с центром в точке
за исключением точки
.
Если записать числа в алгебраической форме, то нетрудно доказать справедливость следующего утверждения.
Условия существования предела функции комплексного переменного
Утверждение 2.3 (необходимое и достаточное условие существования предела функции комплексного переменного).
Для того чтобы в точке существовал предел функции
, необходимо и достаточно, чтобы в точке
существовали пределы двух функций действительных переменных
, где
; при этом имеет место равенство
Иначе: .
Замечания 2.2
1. Из сформулированного критерия следует, что в комплексной области имеют место правила и свойства пределов такие же, как и в действительной области (за исключением, разумеется, свойств, связанных со знаками неравенств).
Например, (при условии, что существуют пределы в правой части равенства).
2. Можно определить понятие предела функции в точке, рассматривая не всю окрестность этой точки, а только некоторое связное множество точек из этой окрестности — предельный переход по множеству:
для
.
Здесь точки принадлежат пересечению множества
и проколотой окрестности точки
. В частности, это имеет место, если
— множество точек кривой, или
— замкнутое множество
. Так, на рис. 2.8,а множество
— кривая
, функция
определена на
и
— дута
, за исключением точки
. На рис. 2.8,б множество
— множество
, функция определена в области
(или
),
— заштрихованная часть области
.
Непрерывность в точке функции комплексного переменного
Функция комплексного переменного называется непрерывной в точке , если бесконечно малому приращению аргумента в точке соответствует бесконечно малое в этой точке приращение функции, т.е.
Это эквивалентно следующему определению: функция непрерывна в точке
, если предел функции в точке равен ее значению в этой точке, т.е.
Так как понятие непрерывности определяется через понятие предела, то, учитывая сформулированный выше критерий существования предела функции (утверждение 2.3), нетрудно убедиться в справедливости следующего утверждения.
Утверждение 2.4 (необходимое и достаточное условие непрерывности функции в точке). Для того чтобы функция была непрерывна в точке
, необходимо и достаточно, чтобы в точке
были непрерывны функции
, где
.
Функция, непрерывная в каждой точке области , называется непрерывной в этой области.
Замечание 2.3. Как и в действительной области, справедливы свойства непрерывности в точке для суммы, произведения, частного двух функций, а также свойство непрерывности сложной функции.
▼ Примеры 2.7-2.12
Пример 2.7. Исследовать функцию на непрерывность.
Решение. Функция , очевидно, непрерывна во всей комплексной плоскости. Поэтому непрерывными во всей плоскости являются функции
при любом
, согласно свойству непрерывности произведения.
Пример 2.8. Исследовать на непрерывность многочлен n-й степени , где
— любые комплексные числа, если
Решение. Функция , очевидно, непрерывна во всей комплексной плоскости. Поэтому, учитывая непрерывность суммы и произведения непрерывных функций и результат примера 2.7, заключаем, что многочлен
есть функция, непрерывная во всей комплексной плоскости.
Пример 2.9. Исследовать на непрерывность рациональную функцию , где
и
— многочлены.
Решение. Согласно замечанию 2.3 рациональная функция непрерывна во всей комплексной плоскости, за исключением точек, где
.
Пример 2.10. Исследовать на непрерывность функции .
Решение. Функции непрерывны во всей комплексной плоскости (всюду в
), что нетрудно установить, используя утверждение 2.4.
Пример 2.11. Исследовать на непрерывность функции и
.
Решение. Функция непрерывна всюду в
, за исключением точки
, а функция
— за исключением точек
и
. Этот вывод следует из решения примера 2.9.
Пример 2.12. Найти пределы функций комплексного переменного:
Решение. В первых двух случаях в силу непрерывности функций в предельных точках получаем
Так как функция является бесконечно малой в точке
, то обратная ей дробь — функция
бесконечно большая в этой точке. Поэтому
.
Производная функции комплексного переменного
Производная функции комплексного переменного в точке вводится так же, как и в действительной области, а именно
(2.1)
Здесь стремится к нулю по любой кривой, по любому направлению.
Функция, имеющая производную в точке, называется дифференцируемой в этой точке; функция, дифференцируемая в каждой точке области, называется дифференцируемой в области.
Из равенства (2.1) и свойств пределов получаем, что приращение дифференцируемой в точке функции можно записать в виде
(2.2)
где — бесконечно малая при
.
Очевидно, справедливо и обратное утверждение. Поэтому равенство (2.2) является необходимым и достаточным условием дифференцируемости функции в точке .
Кроме того, из равенства (2.2) следует, что непрерывность функции в точке является необходимым условием дифференцируемости ее в этой точке, т.е. если функция дифференцируема в точке, то она непрерывна в этой точке.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Вопрос
№1
Необходимые и достаточные условия
дифференцируемости функции комплексной
переменной
Теорема
3. Пусть
функция
определена в некоторой области G.
Для того, чтобы функция f(z)
была дифференцируемой в точке z
области G
необходимо и достаточно, чтобы
-
функции
u(x;y)
и v(x;y)
были дифференцируемы в точке z
как функции двух действительных
переменных; -
в
точке z
выполнялись равенства
и
. (1)
При
выполнении всех условий теоремы
производная может быть представлена в
одном из следующих видов:
. (2)
Равенства
(1) называются условиями Коши-Римана
(или Даламбера-Эйлера).
Доказательство.
1)
Необходимость.
Пусть
функция f(z)
дифференцируема в точке z
области G.
Тогда по теореме 1 ее приращение может
быть представлено в виде
,
где
.
—
комплексная функция от z.
Следовательно,
,
где
.
—
комплексное
число,
значит,
,
a,b
.
Тогда
f(z)=u+iv=(a+ib)(x+iy)+(1+i2)(x+iy)=ax—by+i(ay+bx)+
+1x-2y+i(1y+2x)=(ax—by+1x-2y)+i(ay+bx+1y+2x).
Отсюда
u=ax—by+1x-2y,
v=bx+ay+2x+1y,
где
. (3)
Из
(3) следует, что
1)
функции u(x;y)
и v(x;y)
дифференцируемы в точке (x;y),
2)
их частные производные в точке (x;y):
,
,
,
.
Отсюда
,
,
т.е. удовлетворяют условиям Коши-Римана.
Тогда
для производной получаем:
.
2)
Достаточность.
Пусть
в точке z
области G
выполнены условия 1) и 2) теоремы. Придадим
точке z=(x;y)
приращение z=x+iy0.
По условию
где
. (4)
Приращение
функции
,
соответствующее приращению
,
имеет вид:
.
Разделим на
:
.
Используя условия Коши-Римана, перейдём
к частным производным по x:
. (5)
Т.к.
,
,
и
,
то
и
(огр.БМФ).
Следовательно,
переходя в (5) к
,
получим:
,
т.е. f(z)
дифференцируема в точке z.

Формулами
(2) можно пользоваться для вычисления
производных.
Вопрос
№2 Понятие функции аналитической в
точке и области. Гарм. функции. Необх. и
достат. условие.
Определение.
Функция f(z)
называется аналитической
(голоморфной,
регулярной,
правильной)
в точке
,
если она дифференцируема в каждой точке
некоторой окрестности точки
.
Заметим,
что необходимо различать понятие
дифференцируемости в точке и понятие
аналитичности в точке:
f(z)
дифференцируема в точке
,
f(z)
аналитическая в точке

Определение.
Функция
f(z)
называется аналитической
в области G,
если она дифференцируема в каждой точке
этой области. Т.е. понятия дифференцируемости
и аналитичности в области совпадают.
Примеры.
1)
— аналитическая на
.
2)
аналитическая
на
.
3)
аналитическая
на
.
4)
нигде
не является аналитической, так производная
существует только в точке
(см. пример 2 п.2).
Гармонические
функции
Определение.
Дифференциальное уравнение с частными
производными второго порядка
называется уравнением
Лапласа.
Обозначим
тогда
-краткая
запись уравнения Лапласа.
Определение.
Действительная
функция двух действительных переменных
называется гармонической
на области
G,
если она имеет непрерывные частные
производные второго порядка и на G
удовлетворяет уравнению Лапласа.
Определение.
Две гармонические функции, связанные
условиями Коши – Римана, называются
сопряжёнными
гармоническими функциями.
Позже
будет доказано, что производная
аналитической функции сама является
аналитической функцией. Используем
этот факт при доказательстве следующей
теоремы.
Теорема
5.
Для того чтобы функция f(z)=u(x,y)+iv(x,y)
была аналитической в области G
необходимо и достаточно, чтобы её
действительная и мнимая часть были
сопряжёнными гармоническими функциями.
Доказательство.
1)
Пусть
f(z)=u(x,y)+iv(x,y)
аналитическая в некоторой области G.
Тогда по теореме 2 u(x,y)
и v(x,y)-дифференцируемые
функции двух действительных переменных
и удовлетворяют условиям Коши – Римана:
.
Производная
может
быть представлена в одном из видов:
или
.
Так
как производная аналитической функции
является аналитической функцией, то
и
тоже дифференцируемые функции двух
действительных переменных и удовлетворяют
условиям Коши – Римана.
Применим
к паре функций
и
первое условие Коши– Римана, а для
функций
и
— второе:
,
,
, (7)
, (8)
т.е.
u
и v
удовлетворяют
уравнению Лапласа.
Покажем,
что u(x,y)
и v(x,y)
имеют непрерывные частные производные
второго порядка. Т.к. f(z)
— аналитическая функция, то
-тоже
аналитическая функция.
Дифференцируя
по x,
получим
.
Из
(7), (8)
.
Дифференцируя
по y,
получим
,
т.е.
является аналитической функцией и может
быть представлена в одном из видов:
.
Значит,
все частные производные второго порядка
являются (по теореме 2) дифференцируемыми
в области G
функциями, следовательно, они непрерывны.
Итак,
u(x,y)
и v(x,y)
имеют в G
непрерывные частные производные второго
порядка, удовлетворяют уравнению Лапласа
и условиям Коши – Римана. Значит, они
являются сопряжёнными гармоническими
функциями.
2.
Пусть
u(x,y)
и v(x,y)
какие – либо сопряжённые гармонические
в области G
функции. Так как они дифференцируемы и
удовлетворяют условиям Коши – Римана,
то по теореме 2 функция f(z)=u(x,y)+iv(x,y)
является дифференцируемой в G
и, следовательно, она аналитическая в
G.
.
Из
теоремы 5 следует, что действительной
или мнимой частью аналитической функции
может быть только гармоническая функция.
Например,
не существует аналитической функции
f(z),
у которой
Действительно,
функция
не является гармонической ни в какой
области G.
,
,
,
.
.
Следовательно,
только
на прямой
(не
является областью). Значит, u(x,y)
не является гармонической ни в какой
области G
из
.
Вопрос
№3. Теорема о восстановление
аналитической функции по заданной
действительной или мнимой части
Теорема
6. Для
заданной функции u(x,y),
гармонической в односвязной области
G,
существует бесконечное множество
аналитических в G
функций, действительной частью которых
является u(x,y).
Все они выражаются формулой

и
отличаются между собой на чисто мнимую
постоянную
.
Доказательство.
Пусть
дана гармоническая функция u(x,y).
Для нахождения аналитической функции
f(z)=u(x,y)+iv(x,y)
необходимо найти мнимую часть v(x,y),
которая дифференцируема в G
и связана с u(x,y)
условиями Коши – Римана:
,
.
Так
как u(x,y)
известна, то известны её частные
производные. Обозначим
, 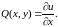
Тогда
условия Коши – Римана запишутся в виде:
. (9)
Т.к.
u
гармоническая функция, то она имеет
непрерывные производные второго порядка,
следовательно, существуют
и
непрерывны в G.
Тогда уравнение Лапласа для функции u
примет вид
. (10)
Т.к.
непрерывны
в G
и удовлетворяют условию (10), то выражение
P(x,y)dx+Q(x,y)dy
является полным дифференциалом некоторой
функции v0(x,y):
dv0(x,y)=P(x,y)dx+Q(x,y)dy
и
,
где
интеграл по кривой, соединяющий точки
(x0,y0)
и (x,y)
в
,
не зависит от пути интегрирования. Имеем
.
Надо найти функцию v(x,y)
удовлетворяющую условиям (9). Следовательно,
.
Учитывая
обозначения, получим
. (11)
Следовательно,
функция f(z)=
u(x,y)+iv(x,y),
где v(x,y)
определяется соотношением (11), является
аналитической функцией (u
и v-дифференцируемы
и связаны условиями Коши-Римана). Итак,
.
Аналогично
можно показать, что для любой функции
v(x,y),
гармонической на области G
существует аналитическая в G
функция f(z)=u(x,y)+iv(x,y),
мнимая часть которой равна v(x,y).
Эта функция определяется с точностью
до постоянного слагаемого
.
Вопрос
№4. Линейная
и дробно-линейная функция комплексного
переменного. Свойства.
Определение.
Линейной
функцией
называется функция вида
, (1)
где
а,
b—
комплексные постоянные.
Эта
функция определена
,
.
Следовательно, если
,то
линейная функция производит конформное
отображение всей плоскости комплексного
переменного. При этом касательные ко
всем кривым поворачиваются на один и
тот же угол Arga,
а растяжение во всех точках равно
.
Если a=1,
то
,
значит, растяжение и поворот отсутствуют.
В этом случае получаем w=z+b.
Это отображение осуществляет сдвиг
всей плоскости на вектор
.
В
общем случае, переходя к показательной
форме записи комплексного числа
,
получим
.
Следовательно, линейное отображение
является композицией трех геометрических
преобразований:
—
поворот на угол
вокруг точки О;
—
подобие с коэффициентом r;
—
параллельный перенос на вектор
.
Подойдем
с другой стороны. Найдем число с,
такое что
.
Отсюда, т.к.
,
то
.
Значит, при
(и
)
отображение (1) сводится к повороту всей
плоскости вокруг точки
на угол
с последующим растяжением относительно
этой точки в
раз, (т.е. подобие с центром в точке
и коэффициентом подобия
).
Дробно-линейная
функция
Рассмотрим
функцию вида
, (2)
где
a,b,c,d—
комплексные числа.
Если
,
то получаем
-линейную
функцию.
Если
,
выделим в дроби целую часть
.
Если
,то
получаем, что
.
В дальнейшем будем считать, что
,
.
Определение.
Функция вида (2), где a,
b,
c,
d — комплексные
числа, такие что
,
,
называется дробно-линейной.
Свойства
дробно-линейного преобразования
1
Конформность
.
существует
во всех конечных точках комплексной
плоскости, кроме точки
и
0
(т.к.
).
Функция
является
аналитической во всех конечных точках
плоскости, кроме
.
Следовательно, отображение
является конформным во всех конечных
точках к плоскости, кроме
.
Т.к.
,
.
Таким
образом, функция
определена
на
.
Итак,
дробно-линейная функция
отображает взаимно однозначно и конформно
расширенную комплексную плоскость саму
на себя.
2
Круговое
свойство.
Рассмотрим
астный случай
. (3).
Положим
,
.Тогда
(3) примет вид

Следовательно,
отображение (3) разбивается на два
отображения. Сначала точка
переходит в точку
.Т.к.
эти точки лежат на одном луче, выходящем
из начала координат и их модули связаны
соотношением
,
то это преобразование инверсии
относительно единичной окружности.
Затем точка
переходит
в точку
,
симметричную ей относительно действительной
оси.

Теорема.
При отображении
совокупность прямых и окружностей на
комплексной плоскости
переходит в себя.
Доказательство.
Уравнение
для любой прямой или окружности имеет
вид:
А(x2+y2)+2Bx+2Cy+D=0.
(4)
При
А=0
и В,
С
0
одновременно это уравнение определяет
прямую, при А=0
и В2+С2
-AD>0
– окружность.
Заменим
,
,
, (5)
получим
.
Обозначим
,
тогда
. (6)
Если
А=0,
а Е0,
то уравнение (6) определяет прямую, если
А0
и
,
то окружность. Т.е. любая окружность или
прямая на комплексной плоскости
определяется уравнением (6).
Верно
и обратное: уравнение вида (6) определяет
прямую или окружность на комплексной
плоскости. Для доказательства надо в
(6) сделать замену по формулам (5). Получим
(4) , которое является уравнением либо
прямой, либо окружности.
При
преобразовании
имеем
.
Линия (6) перейдет в линию:
. (7)
Уравнение
(7) имеет тот же вид, что и (6), с заменой A
на D,
D
на А,
E
на
.
Следовательно, при D=0
– это уравнение прямой, а при
—
уравнение окружности.
Теорема
2.
Образом прямой или окружности при
дробно-линейном отображении w=L(z)
является прямая или окружность, (причем
образом прямой может быть как окружность,
так и прямая, и образом окружности –
как прямая, так и окружность).
Доказательство.
.
Следовательно,
w=L(z)
является композицией трех отображений:
t=cz+d,
,
w=kq+l,
где
,
.
Первое и третье — линейные отображения.
Они и отображение
переводят в себя совокупность прямых
и окружностей.
Замечание.
Несложно установить, что при отображении
w=L(z)
все прямые и окружности, проходящие
через точку
переходят в прямые плоскости (w),
а все прямые или окружности, не проходящие
через точку ,
— в окружности плоскости (w).
3
Инвариантность двойного отношения
Дробно-линейное
преобразование однозначно определяется
заданием трех параметров (например,
если с0,
то ими могут быть
).
Поэтому это отображение определяется
заданием образов трех точек. Выведем
формулу дробно-линейного преобразования.
Пусть
,
k=1,2,3.
Пусть
.
Образуем разности
,
,
,
,
.
Разделим
почленно первое уравнение на второе и
третье и на четвертое.
,
.
Разделим
теперь снова первое уравнение на второе:
. (8)
Это
и есть искомое линейное преобразование.
Т.к.
за z1,
z2,
z3,
z
и w1,
w2,
w3,
w
могут быть приняты любые четверки точек,
соответствующие друг другу при
дробно-линейном преобразовании, то (8)
выражает следующее свойство:
отношение
сохраняется при дробно-линейном
отображении, т.е является его инвариантом.
Это отношение называется двойным
отношением четырех точек.
4
Сохранение симметрии
Если
точки z1
и z2
симметричны относительно некоторой
прямой или окружности ,
то при любом дробно-линейном отображении
w=L(z)
их образы w1
и w2
будут симметричны относительно образа
:
.
В
случае, когда
— окружность, преобразование называют
инверсией.
5
Принцип соответствия обхода границ
(отображение областей, ограниченных
прямыми или окружностями)
Е
сли
при дробно-линейном отображении прямая
или окружность
переходит в прямую или окружность
,то область D,
которую ограничивает ,
преобразуется в одну из двух областей,
которые ограничивает .
При этом имеет место принцип соответствия
обхода границ: если при каком-то обходе
линии
область D
оказывается слева (справа), то при
соответствующем
обходе линии
область D
тоже должна оказаться слева (справа).
Вопрос
№5. Определение
показательной функции и ее свойства.
Показательной
функцией комплексного переменного
называется
функция вида
.
Свойства
expz
1
Если
,
то expz=expx=ex,
т.е. на действительной оси показательная
функция комплексного переменного
совпадает с показательной функцией
действительного переменного.
2


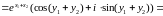
.
С
другой стороны,
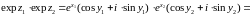
.
Следовательно,
.
Аналогичное
свойство имеет место для функции
действительного переменного:
.
Назовём
комплексное число z
показателем
функции expz.
Следовательно, при перемножении двух
значений показательной функции показатели
можно складывать. В связи с этим можно
вместе с обозначением expz
использовать обозначение ez:
.
3
Из свойства 2
следует
.
С другой стороны
.
Следовательно,
.
4
.
.
Т.к.
,
то
.
.
5
expz
-периодическая функция с основным
периодом 2i,
т.е.
exp(z+2i)=expz.
.
Покажем
что 2i
-основной период функции expz,
т.е. любой другой период имеет вид
2ki,где
.
Действительно,
пусть
—
период expz.
Тогда exp(z+w)=expz
z.
Значит и при z=0
это равенство выполнено.
Для
z=0:
.
Отсюда
что
и требовалось доказать.
6
Если
так,
что
,то
.
Если
так, что
,
то
.
(6
следует из того, что
).
Выражение
лишено смысла. Отсюда, в частности,
следует, что expz
не совпадает ни с одним многочленом
.
Целые функции, отличные от многочленов,
называются трансцендентными
целыми функциями.
Следовательно expz
— трансцендентная целая функция.
7
Показательная
функция является аналитической на
,
(expz)=expz.
Вопрос
№6.
Тригонометрические функции. Гиперболические
функции.
Т.
к.
,
то при сложении и вычитании соответственно
получим:
, (14)
Формулы
(14) – формулы Эйлера, верные
.
Если
,
то функции
,
определены
и являются аналитическими, следовательно
они целые. При
они принимают действительные значения,
совпадающие соответственно с cosx
и sinx.
Поэтому по определению первую обозначают
через cosz,
а вторую – sinz
и называют косинусом и синусом z.
Определение.
(15)
Формулы
(15) тоже называются формулами Эйлера.
Если вторую умножить на i
и сложить с первой, то получим
– (16)
– тоже формула Эйлера.
Свойства
cosz
и
sinz
1
Из (15) следует cos(-z)=cosz,
sin(-z)=sinz
, следовательно cosz
– чётная, sinz
– нечётная.
2
cosz
и sinz
– периодические с периодом 2.
,
т.
к. 2i–
основной период expz.

Покажем,
что 2
– основной период cosz
и sinz.
Пусть
w
– период cosz.
Следовательно, cos(z+w)=cosz.
Если
,
то
.
Следовательно,
(по определению cosz).
Отсюда
.
Тогда,
поскольку из expz=w
следует
,
то
.
Значит w=k.
Если
z=0,
то
(чётное число).
Значит
w=2m.
Следовательно,
2
– основной период функции cosz.
Для
sinz
аналогично.
3
Для sinz
и cosz
справедливы основные формулы тригонометрии:
а)
(17)
Заменяя
в (16) z
на
,
получим

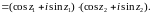
Следовательно,
.
Заменяя
здесь z1
и z2
на -z1
и -z2
и учитывая свойство 1, получим
.
Складывая
и вычитая две последних формулы, получим
(17).
Формулы
(17) являются основными в теории
тригонометрических функций.
б)
Из них следуют «формулы приведения».
Положим
в (17) z1=z,
.
Тогда
,
.
Положим
в (17) z1=z,
.
Следовательно,
,
.
в)
Положим в 1-й из формул (17) z1=z,
z2=-z,
получим
. (18)
4
Из (18) не следует, что
.
5
cosz=0
при
, sinz=0
при
.
cosz=0



Следовательно,
.
Для
sinz=0
аналогично.
6
Функции cosz
и sinz
аналитические в
.
,
.
Определение.
.
Свойства
tgz
и ctgz
1.
,
.
2.
tgz=tgx,
ctgz=ctgx
при
.
3.
tg(-z)=-tgz, ctg(-z)=-ctgz
.
4.
tgz
и ctgz
– периодические с периодом .
5.
tgz
и ctgz
– непрерывны в своих областях определения.
6.
tgz
и ctgz
– аналитические в своих областях
определения,
,
.
7.
Нули tgz
совпадают с нулями sinz,
нули ctgz
– с нулями cosz.
8.
tgz
и ctgz
принимают любые значения из
,
кроме z=i
и z=-i.

.
Следовательно,

. (*)
Если
w=i,
то (*) примет вид
– нет решений;
если
w=-i,
то (*): 0=2 – не имеет смысла. Т. е.
.
Пусть
w=A
(
),
тогда
.
Следовательно,
существует точка z0:
.
Т. к.
,
то, следовательно, существует
.
Гиперболические
функции
Определение. Гиперболический
косинус
,
гиперболический
синус
. (19)
Свойства
chz
и shz
1
Для
chz=chx
и shz=shx.
2
ch(-z)=chz
и sh(-z)=-shz.
3
chz=cos(iz)
и
shz=-isin(iz) (20)
(или
sin(iz)=ishz)
,

.
4
Из (20) следует
.
5
chz
и shz
аналитические в


6
chz
и shz
— периодические с периодом
.
Вернемся к sinz
и cosz.
Определим их
действительные, мнимые части и модули.
Покажем,
что
и
—
неограниченные функции.



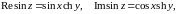

,
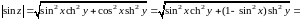
.
Отсюда
следует
,
.
(эти
соотношения можно получить из (15)).
Т.к.
,
то из последних соотношений заключаем:
при
,
т. е. sinz
и cosz—
неограниченные функции.
Пусть
функция w=f(z)
— аналитическая в области D.
Пусть G
— образ области D
при отображении
w=f(z),
т.е. G=f(D).
Определение.
Если
(т.е. в различных точках области D
функция принимает различные значения),
то аналитическая функция w=f(z)
называется однолистной
в
области D.
Другими
словами, однолистная функция w=f(z)
взаимно однозначно отображает область
D
на G.
При
однолистном отображении w=f(z)
прообраз любой точки wG
состоит из единственного элемента:
:
.
Поэтому
z
можно рассматривать как функцию от
переменной
,
определенную на G.
Она обозначается
и
называется обратной
функцией.
Справедливы
тождества:

и
имеет место
Теорема.
Если f(z)-
однолистная и аналитическая на D,
и
на
D,
то
—
аналитическая
на G=f(D).
Определение.
Если
в области D
существует, по крайней мере, одна пара
точек
,
то функцию f(z)
называют многолистной
в области
D.
Если
отображение w=f(z)
является многолистным на D
(например, w=ez,
w=sinz,
w=cosz,
w=zn),
то в этом случае некоторым значениям
wG
соответствует более, чем одна точка
zD:
f(z)=w.
Следовательно,
обратное отображение
не является однозначным, оно является
многозначной функцией.
Определение.
Функция w=f(z)
называется многозначной
функцией
на
множестве E,
если некоторыми значениям zE
соответствует более чем одно значение
w.
Теорема.
Если аналитическая функция w=f(z)
многолистна в области D,
то эту область можно разбить на конечное
или счетное множество областей, в каждой
из которых функция f(z)
является однолистной.
К
многозначным функциям неприменимы
понятия аналитичности и непрерывности.
Они могут применяться только к однозначным
функциям. Для того, чтобы их использовать,
выделяют однозначные ветви многозначных
функций.
Определение.
Однозначная на области D
функция w=f(z)
называется
ветвью
многозначной функции F,
если значение f
в любой точке zD
совпадает с одним из значений F
в этой точке.
Е
сли
функция w=f(z)
многолистна на D,
то обратная функция
будет
многозначной. Чтобы выделить однозначную
ветвь этой функции поступают, следующим
образом: область D
разбивают на области однолистности
функции w=f(z)
так, что никакие две из областей не имеют
общих внутренних точек и так, чтобы
каждая точка zD
принадлежала одной из этих областей
или границе некоторых из них. В каждой
из этих областей однолистности определяют
функцию, обратную к w=f(z).
Она и является однозначной ветвью
многозначной функции
.
Н
айдем
области однолистности функции expz.
Выберем
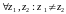

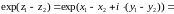
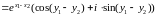
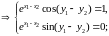

.
Тогда
областью однолистности функции
будут полоса шириной не больше
,
параллельная действительной оси.
Разобьем
плоскость
на области однолистности:
.
Если,
например,
,
то
.
Логарифмическая
функция
Как
было сказано, множество всех корней
уравнения w=ez
(w
)
представляется формулой
z=ln|w|+iArgw=ln|w|+i(argw+2k)
),
.
Значит,
функция, обратная к z=ew=eu(cosv+isinv),
определена z0,
z
и задается формулой
w=ln|z|+iArgz.
Эта
функция многозначная (бесконечнозначная),
называется логарифмической
и обозначается Lnz:
w=Lnz=ln|z|+iArgz=ln|z|+i(аrgz+2k).
Назовем
значение логарифма ln|z|+iargz
главным
значением
и обозначим через lnz:
lnz=ln|z|+iargz.
Тогда
Lnz=lnz+2ki,
.
Следовательно,
любое комплексное число z0,
z
имеет бесконечное множество логарифмов
(значений логарифмической функции), из
которых любые два отличаются на целое
кратное 2
i.
Если
,
то Lnz=ln|z|
.
Но для этих
существует еще бесконечно много значений
логарифма. Например, Ln2=ln2+2ki,
.
Все
логарифмы комплексного числа z
имеют одну и ту же действительную часть
ln|z|,
а мнимые части отличаются на кратное
2.
Следовательно, все логарифмы комплексного
числа z
расположены на комплексной плоскости
на одной прямой параллельной оси Оy на
расстоянии 2
друг от друга.
Пример.
Ln1=ln1+2k
i=2k
i,
.
Свойства
логарифмической функции
1
Ln(z1
z2)=Lnz1+Lnz2.
Ln(z1
z2)=ln|z1
z2|+i
Arg(z1
z2)=ln|z1|+ln|z2|+i(Argz1+Argz2)=Lnz1+Lnz2.
2
.
.
Замечание.
Эти равенства означают равенство
множеств (в том смысле, что множества
состоят из одних и тех же элементов).
Отсюда следует что, например, Lnz2
2Lnz
Например, Ln(-1)2=Ln1=2ki,
2Ln(-1)=2(+2k)i=i(2+4k),
Ln(-1)2
2Ln(-1):
4i
Ln(-1)2,
но
4i2Ln(-1).
Степенная
функция и радикал
Определение.
Степенной
называется функция вида
.
Если
,
то
.
Следовательно,
—
многолистная функция.
,
при
.
Следовательно,
-аналитическая
в
функция.
Функция
обладает основными свойствами функции
действительного переменного:
.
Найдем
области однолистности функции
.
Выберем
произвольные
,


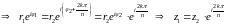
С
ледовательно,
областью однолистности функции
будет любой угол с вершиной в начале
координат и раствором
:
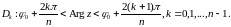
Если
,
то
.
Радикал
определяется как функция, обратную к
функции
.
Пусть
т.е.
,
тогда
.
Следовательно,
радикал имеет n
различных значений, которые выражаются
формулой
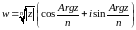
Следовательно,
функция
является
многозначной (n
– значной). Эти n
значений располагаются в вершинах
правильного n
– угольника, вписанного в окружность
.
При
и
получаем по одному значению функции
и
.
Чтобы
выделить однозначную ветвь, достаточно
указать, в какой области однолистности
изменяется w.
Мы установили выше, что областью
однолистности функции
является
угол с вершиной в начале координат и
раствором
:

Любой
луч плоскости (
)
при
отображении
переходит
в луч плоскости (z):
.
Если луч
пробегает
область
против хода часовой стрелки, то луч
пробежит всю плоскость (z)
от
до
.
Следовательно, любая из областей
однолистности
перейдет в одну и ту же область
плоскости (z):
угол раствора 2π, границей которой служит
луч
.
Т
аким
образом, в области
получаем n
однозначных ветвей функции
Каждая из них определяется условием,
что ее значения
принадлежат области
.
Будем
обозначать эти ветви
.
Вопрос
№8. Достаточное условие существования
интеграла
Определение.
Если
существует конечный предел интегральной
суммы (1) при
(или
при
),
не зависящий ни от способа разбиения T
кривой L,
ни от выбора точек
,
то этот предел называется интегралом
от функции f(z)
по кривой L
и обозначается
.
Таким
образом,
.
В
этом случае функция f(z)
называется интегрируемой
по кривой
L.
Теорема
1 (достаточное
условие существования интеграла от
функции комплексного переменного).
Пусть L
– простая гладкая кривая на
,
f(z)=u(x;y)+iv(x;y)
непрерывна на L.
Тогда существует
,
причем справедливо равенство:
. (2)
Доказательство.
Выберем
произвольно разбиение T
кривой L
на дуги
,
на каждой
выберем произвольно точку
.
Составим интегральную сумму
.
Выделим в
действительную и мнимые части:
z=x+iy,
f(z)=u(x;y)+iv(x;y),
,
,
,
,
.
Тогда

. (3)
В
правой части (3) стоят интегральные суммы
для криволинейных интегралов II типа
двух действительных функций u(x;y)
и v(x;y).
Если
и
,
то и
(или
).
Т.к.
L
– гладкая кривая, а функции u(x;y)
и v(x;y)
непрерывны на L,
то
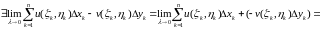

и
.
Тогда
существует предел при
левой части (3), т.е. существует
.
Переходя
в (3) к пределу при
,
получим (2).
Вычисление
интеграла от функции комплексного
переменного
Пусть
вначале f(t)=u(t)+iv(t)
–комплексно-значная функция действительной
переменной. Тогда интеграл от f(t)
по отрезку [a;b]
определяется следующим образом:
.
Рассмотрим
теперь интеграл от функции комплексного
переменного по кривой L.
Теорема
2.Пусть
L
– простая гладкая кривая, заданная
параметрически:
L:
z(t)=x(t)+iy(t),
t,
функция f(z)
непрерывна на L.
Тогда справедливо равенство:
(где
).
Доказательство.
Т.к.
выполнены условия теоремы 1, то имеет
место равенство (2) . Каждый криволинейный
интеграл II типа можно заменить по
формуле, сводящей его вычисление к
вычислению обычного определенного
интеграла:
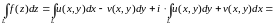

=
.
Вопрос
№9. Необходимое и достаточное условие
независимости интеграла. Интегральная
теорема Коши.
Рассмотрим
.
Он зависит от функции f(z)
и от вида кривой L.
Возникает вопрос: каким условиям должна
удовлетворять функция f(z),
чтобы интеграл не зависел от пути
интегрирования L,
а определялся начальной и конечной
точками кривой.
Как
и в случае криволинейного интеграла II
рода независимость интеграла от пути
интегрирования равносильна равенству
нулю этого интеграла по любому замкнутому
контуру.
Теорема.
не
зависит от пути интегрирования на
области D
тогда и только тогда, когда
по любому кусочно-гладкому контуру
.
Доказательство.
(
)
Пусть
,
где
и
-кривые,
лежащие в D
и соединяющие точки A
и B.
Тогда
,
где
.
(
)
Пусть
,
где C
— кусочно-гладкий замкнутый контур,
.
Разобьем C
точками A
и B
на кривые
и
так, что
.
Тогда
Для
доказательства интегральной теоремы
Коши нам понадобится следующая
Л
емма.
Пусть
f(z)-
непрерывная в области G
функция, L
— произвольная кусочно — гладкая линия,
LG.
Тогда >0
существует ломаная P,
вписанная в L,
PG,
такая что
.
Доказательство.
Разобьём
L
на частичные дуги
,
,…,
sk
– длина
).
Впишем в L
ломаную P,
звенья которой стягивают дуги
.
Точки z0,
z1,…,zn
– вершины ломаной P.
Звенья ломаной (и их длины) обозначим
через lk
,
k=
Рассмотрим
сумму
S=f(z1)z1+f(z2)z2+…+f(zn)zn
. (4)
S
является интегральной суммой для
интеграла
,
в которой в качестве точек k
взяты точки zk.
Так
как f(z)
– непрерывна в G,
а L
–
кусочно – гладкая линия, то
(
),
т.е. >0
1>0:
T:
<1
. (5),
Оценим
.
Так как
,
то (4) примет вид:
.
(6)
С
другой стороны,
. (7)
Вычтем
(6) из (7):
.
Так
как функция f(z)
непрерывна
в G,
то она равномерно непрерывна на любом
ограниченном замкнутом множестве точек
из G.
Следовательно, она непрерывна на ломаной
P.
По определению равномерной непрерывности:
для выбранного числа >0
2>0:
z,
zP:
|z-z|<2
выполнено
.
Пусть <2.
Так как k
на звене lk
|z—zk|<
lk<<2,
то
.
Тогда
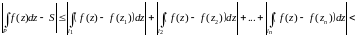
.
(8)
Выберем
=min{1;2}.
Из (5) и (8) получим: >0
>0:
T:
<
выполнено
.
Итак,
в линию L
всегда можно вписать ломаную P
так, что разность значений
будет
меньше любого наперёд заданного числа.

I.
Случай
односвязной области
Теорема
(Коши для односвяз.). Если
f(z)
аналитическая в односвязной области G
функция, то
,
где L—
любой замкнутый контур, лежащий в G.
Доказательство.
Согласно
лемме в линию L
можно вписать ломаную P
так, что
.
Следовательно,
если мы докажем, что
,
то отсюда будет следовать что
и, значит,
.
Следовательно,
теорему достаточно доказать для случая,
когда контуром интегрирования является
ломаная P.
Далее:
данный многоугольник с периметром P
можно разбить на треугольники. Тогда
,
так как по AC,
DA
интегрирование совершается два раза в
противоположных направлениях.
Следовательно, если допустить, что
теорема Коши доказана для случая, когда
контуром интегрирования является любой
треугольник, то из последнего равенства
будет следовать, что
.
И
так,
докажем, что если f(z)
– аналитическая в области G
функция, то
,
где -
периметр любого треугольника, лежащего
в G.
Положим
и докажем, что M=0.
Р
азделим
стороны треугольника пополам и соединим
точки деления. Треугольник, таким
образом, разобьётся на четыре равных
треугольника 1,
2,
3,
4.
.
Так
как
,
то существует периметр k:
.
С
этим треугольником k=(1)
поступим так же, как и с ,
разбив на четыре разных треугольника.
Следовательно, существует треугольник
с периметром (2)(1):
.
Этот
процесс продолжим неограниченно, получим
последовательность треугольников с
периметрами =(0),
(1),
(2),…,
(n),…,
из которых каждый содержит следующий
и таких, что:
(n=0,1,…). (9)
Обозначим
периметр
через U.
Тогда периметр
.
Оценим
.
Имеем {(n)}
– последовательность вложенных
треугольников. Их периметры стремятся
к 0 при n.
Следовательно, существует точка z0,
принадлежащая всем треугольникам
последовательности {(n)}.
Так как z0G,
а f(z)-аналитическая
в G,
то
.
Следовательно, >0
()>0:
z:
|z-z0|<
выполнено
,
отсюда
. (10)
Начиная
с достаточно большого номера n0,
треугольник (n)
будет находиться в круге
и, следовательно, для оценки
можно использовать (10). Заметим, что

,
так
как
и
(см.
пример о
).
Тогда
.
Так
как z0(n),
то
(расстояние между z
и z0
меньше периметра).
Следовательно,
. (11)
Из
(9) и (11) следует
.
Так как —
произвольное сколь угодно малое число,
то переходя к пределу при
0,
получим M=0.
Следовательно,
.
II.
Случай
многосвязной области
Пусть
D—
многосвязная область, граница которой
L
состоит из внешнего контура L0
и внутренних L1,
L2,…
Ln,
,
(D—
(n+1)-связная
область).
Определение.
Положительным обходом границы L
многосвязной области D
называется такое направление обхода
каждого контура, при котором область D
остаётся всё время слева.
Теорема
(Коши для многосвяз.). Пусть
f(z)
– аналитическая в области G,
D
– многосвязная область, которая вместе
со своей границей L
целиком лежит в G.
Т
огда
,
где интеграл берётся в положительном
направлении.
Доказательство.
Рассмотрим
случай n=2:
.
Соединим контуры L1
и L2
c
внешним контуром L0
линиями l1,
l2
(l1
и l2
выберем
так, чтобы они не пересекались). Т.о., мы
получим односвязную область D*,
которая ограничена кривыми
L0,
L1,
L2,
l1,
l2,
причём
l1,
l2
проходятся
дважды в противоположных направлениях.
.
– граница D*.
По предыдущей теореме
Пользуясь свойством аддитивности
интеграла получим:
Следствие.
Если l1
и l2
кусочно – гладкие замкнутые кривые
ограничивающие кольцеобразную область
в области G,
и функция f(z)
– аналитическая в G,
то
.
Вопрос
№10. Первообразная. Формула ньютона-Лейбница.
Если
f(z)
аналитическая в односвязной области D
функция, то, как было установлено,
значение
,
взятого по любой кусочно – гладкой
кривой LD,
не зависит от вида кривой, а определяется
лишь начальной и конечной точками
кривой. Поэтому для интеграла вдоль
произвольной кусочно – гладкой кривой
L,
соединяющей точки z0
и z,
используют обозначение
,
где z0
и z
называются соответственно, нижним и
верхним пределами интегрирования.
Зафиксируем
z0,
тогда
зависит только от точки z,
т.е. является однозначной функцией,
определённой на D,
т.е.
.
Теорема
1.
Пусть f(z)-функция,
непрерывная в области D,
для которой интеграл
вдоль любой кусочно – гладкой кривой
LD
не
зависит от вида кривой, а определяется
только начальной и конечной точками
кривой. Тогда
является аналитической на D
функцией и F’(z)=f(z)
.
Доказательство.
Пусть
L
D-кусочно-гладкая
кривая, соединяющая точки z0
и z.
Выберем ∆z≠0
так, чтобы z+∆z
D.
.
. (1)
Т.к.
,
то
. (2)
Интегралы
(1) и (2) не зависят от пути интегрирования,
поэтому в качестве пути от z
до z+∆z
можно взять прямолинейный отрезок,
соединяющий эти точки. Из (1) и (2) следует:
. (3)
Зафиксируем
>0.
Так как f(z)
непрерывна на D,
то для
любой точки
z
D
выполнено
. (4)
В
равенстве (3)
.
Следовательно,
.
Поэтому если
,
то
,
значит, выполнено
(4).
Тогда
из (3) следует
.
Таким
образом,
.
По
определению это означает, что
,
то
есть F’(z)=f(z)
.
Замечание
1. Теорему
1 можно было сформулировать следующим
образом:
если
f(z)
аналитическая в области D
функция, то
— аналитическая функция и F’(z)=f(z),
где интеграл берётся по любой
кусочно-гладкой кривой, соединяющей
точки z0
и z.
Действительно,
если f(z)
– аналитическая функция, то
не
зависит от пути интегрирования.
Определение.
Функция
F(z)
называется первообразной
для функции f(z)
на области G,
если F’(z)=f(z)
.
Из
определения следует, что если F(z)
первообразная для f(z)
на D,
то и функция F(z)+C
является первообразной для f(z)
на D
(
).
Следовательно,
если выполнены условия теоремы 1, то
функция f(z)
имеет первообразную.
Теорема
2.
Если f(z)-аналитическая
на односвязной области D,
и F(z),
(z)-две
первообразные для f(z)
на D,
то
справедливо
F(z)-Φ(z)=С=const.
Доказательство.
Пусть
F(z)
и Φ(z)
— две первообразные функции f(z)
на D.
Рассмотрим функцию w(z)=F(z)-Φ(z)
,
w(z)=u(x,y)+iv(x,y).
Тогда
w(z)=F’(z)-Φ’(z)=f(z)-f(z)=0
.
Так
как
,
то
и
.
Так
как w(z)
— аналитическая
функция, то
и
.
Итак,
,
u=aconst,
,
v=bconst.
Тогда
w(z)=a+ibconst.
Значит,
F(z)-Φ(z)=С.
Следствие
1. Если
f(z)-аналитическая
на односвязной области D,
то любая её первообразная имеет вид
,
где
. (5)
Следствие
2. Положим
в (5) z=z0,
тогда C=F(z0).Заменяя
в (5) C
на F(z0)
получим:
—
формула Ньютона-Лейбница.
Таким
образом, интеграл от аналитической
функции комплексной переменной
вычисляется с помощью тех же методов и
формул, что и в случае функции действительной
переменной.
Вопрос
№11. Интегральная
формула Коши и ее следствия
Интегральная
формула Коши
Теорема.
Пусть
функция f(z)
аналитическая в односвязной области
D,
L-произвольный
замкнутый кусочно-гладкий контур,
лежащий в D.
Тогда для любой точки z0,
лежащей внутри контура L,
справедлива формула:
, (1)
где
L
обходится в положительном направлении.
(1)
— интегральная формула Коши. Она выражает
значения аналитической функции внутри
контура через её значения на контуре.
Доказательство.
Пусть
z0—
произвольная точка, лежащая внутри
контура L.
Рассмотрим окружность γr:
|z-z0|=r
, где r
выберем так, чтобы γr
лежала внутри L.
В двусвязной области, ограниченной
контурами L
и
γr,
функция
является
аналитической, следовательно, она
аналитическая и на области
.
Тогда по следствию из теоремы Коши:
. (2)
Из
(2) следует, что значение
не
зависит от радиуса окружности γr.
Из
(2) следует, что для доказательства (1)
достаточно показать, что
. (3)
Так
как
,
то
или
. (4)
Из
(3) и (4) следует, что для доказательства
(1) надо доказать, что
. (5)
Заметим,
что интеграл в (5) не зависит от r
.
Возьмем
.
Так как f(z)
аналитическая на D,
то f(z)
непрерывна в точке z0D.
Тогда
выполнено
.
Если
γr
такая, что r<δ,
то
выполнено
|z-z0|=r<δ
|f(z)-f(z0)|<ε.
. (6)
Так
как ε>0
– произвольное сколь угодно малое
число, а значение интеграла не зависит
от r,
то (6) может быть выполнено только если
,
то есть
выполнено (5),
а значит,
выполнено (1).
Следствие
. Если
две аналитические в односвязной области
D
функции f(z)
и g(z)
совпадают на замкнутом контуре LD,
то они совпадают и внутри контура L.
Замечание.
Если
точка z0
лежит вне контура L,
то
.
Действительно,
в этом случае
является
аналитической не только на L,
но и внутри L,
следовательно, применима интегральная
формула Коши, согласно которой этот
интеграл равен 0.
Итак,
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Область однолистности функции
|
|
01/11/09 |
В комплекном анализе столкнулся с проблемами при решении следующей задачи: Мое решение: Область аналитичности нетрудно установить используя условия Коши-Римана (http://en.wikipedia.org/wiki/Cauchy%E2%80%93Riemann_equations). А вот с однолистностью возникают проблемы: По теореме о неявной функции, в окрестности любой точки, кроме нуля, существует обратная функция. Но это не дает нам возможности сказать, что функция однолистна во всех точках, кроме нуля.
|
|
|
|
|
g______d |
Re: Область однолистности функции
|
||
08/11/11 |
Ну как, берете в окрестности любой точки, кроме нуля, обратную функцию, т. е.
|
||
|
|
|||
|
ex-math |
Re: Область однолистности функции
|
||
24/02/12 |
|||
|
|
|||
|
Fidd |
Re: Область однолистности функции
|
|
01/11/09 |
Ну как, берете в окрестности любой точки, кроме нуля, обратную функцию, т. е. Спасибо за отзыв, а не могли бы вы несколько более формально описать способ?
|
|
|
|
|
g______d |
Re: Область однолистности функции
|
||
08/11/11 |
Спасибо за отзыв, а не могли бы вы несколько более формально описать способ? По-видимому, проще сказать как ex-math и не мучиться с продолжением корня. Более формально с корнем — нужна конструкция аналитического продолжения вдоль кривой, прочитайте где-нибудь про нее. Далее если есть область, то она связна, следовательно линейно связна, следовательно, можно продолжить корень в любую ее точку. Проблема может быть, если разные кривые дают разные продолжения в одну и ту же точку. Но тогда можно из них составить замкнутую кривую и убедиться, что эта кривая обходит вокруг нуля.
|
||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы
18
Лекция 4(23 сентября 2002 года).
20. Функция Жуковского.
Определение. Функцией Жуковского называется (рациональная функция 2ого порядка).
Она осуществляет непрерывное отображение: . В каких точках отображение конформно?
— конформное отображение.
т.е. в 0 и
отображение конформно. Рассмотрим остальные точки:
здесь конформность нарушается.
Вывод. Функция Жуковского конформна в , за исключением точек
.
Найдём области однолистности функции (биективности). Это любая область, не содержащая одновременно точек . Почему? С одной стороны они переходят в 2 точки, с другой это биекция, следовательно, такого не может быть.
Пример однолистности области. А) Единичный круг. .
Б) Верхняя полуплоскость. . Почему? Рассмотрим инверсию.
Задача. Функция Жуковского ? Найти эту область.
Решение. Рассмотрим расслоение единичного круга на окружности радиуса r.


, куда переходит окружность? Уравнение окружности:
, вычислим:
.


Фокусы находятся в точках
. Предельные случаи такие:
Пусть
область стягивается к отрезку.
искомая область, т.е. доказано.
Теорема. Функция Жуковского осуществляет конформное отображение единичного круга на область G, равную
с разрезом
.
Хотим выразить z через w (функцией Жуковского). — функция, обратная функции Жуковского. Знак выбрали так, чтобы z лежало в единичном круге (помним, что
).
Задача. Куда функция Жуковского отображает верхнюю полуплоскость?
30. Экспонента, логарифм и степенная функция.
Рассмотрим — голоморфизм во всём С (но не расширенном). В каких точках отображение конформно?
Вывод. Отображение конформно в каждой точке.
Область однолистности – любая область, не содержащая различных точек, отличающихся на период. (Период: ).
Пример. 1) Рассмотрим Куда экспонента отображает эту область?
Решение.
, а угол меняется от 0 до
.


Ответ: На области z: семейство прямых. На области w: семейство полуокружностей с радиусом от 1 до 2. Можно было фиксировать у. Экспонента переводит прямоугольную декартову сетку координат в полярную.
2) . С помощью отображения
можно отобразить сетку с углом
в сетку с углом
.
— это используется для
.
ИНТЕГРИРОВАНИЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
10. Спрямляемые и гладкие кривые.
Пусть — произвольная кривая на плоскости.
, введём обозначение:
Обозначим:
— длина произвольной ломанной.
.
Определение. Величина — длина кривой.
Определение. Если конечно, то кривая называется спрямляемой.
Замечание. В терминах действительного анализа спрямляемая кривая – непрерывная функция ограниченной вариации.
Задача. 1) Доказать, что длина кривой не зависит от выбора параметризации.
Пусть — строго возрастающая и непрерывная функция на
т.ч.
— имеют одну и ту же длину.
2) Доказать, что ,
параметр разбиения, т.е.
.
3) Привести пример не спрямляемой кривой.
Определение. — гладкая кривая, если функция непрерывна, дифференцируема на отрезке [a,b] и
.
Задача. Доказать, что длина гладкой кривой вычисляется по формуле:
20. Определение интеграла.
Пусть — произвольная кривая, т.е.
,
,
— это обозначения.
Пусть Ф: — произвольная комплексно-значная функция на отрезке [a,b]. Рассмотрим разбиение с отмеченными точками:
. Составим интегральную сумму:
.
Определение. Интегралом называется: , если этот предел существует. Обозначение интеграла:
— интеграл от Ф по
.
Замечание. В терминах действительного анализа мы дали определение интеграла Римана-Стильтьеса.
Задача. 1) Доказать, что интеграл не зависит от выбора параметризации.
2) Теорема — ния: Если кривая
спрямляема, а функция Ф непрерывна, то
существует.
3) Если Ф – непрерывна, а — гладкая кривая, то
— с помощью введения параметризации.
Замечание. 1) Обычно интеграл используется в следующих частных случаях. Дана — множество точек на комплексной плоскости. Положим:
— это важно для кривых с самопересечениями.
2) , т.е. интеграл от функции комплексного переменного = сумме двух криволинейных интегралов 2-ого рода.
30. Свойства интеграла.
-
Интеграл от единичной функции.
, где интеграл берётся по любой кривой, соединяющей точку А и В.
-
Линейность интеграла.
.
-
Ориентированность интеграла.
.
-
Аддитивность.
-
Оценка интеграла. Пусть
— длина
.
на
, тогда
.
Замечание. 1) Предположим, что все интегралы
2) Все свойства доказываются по стандартной схеме: написать их для интегральных сумм и перейти к пределу. Рассмотрим на примере 1-ого свойства: .
3) Уточним, что такое ? Кривая – функция на отрезке. Без ограничения общности пусть это будет [0,1]. Тогда
.
4) Свойство аддитивности мы берём в качестве определения интеграла по формальной сумме кривых.
40. Примеры.
(

1) , где интеграл берётся по любой спрямляемой кривой, соединяющей точки А и В. Посчитаем, исходя из определения. Если кривая спрямляема, то предел существует. Интегральные суммы:
знаем, что сходятся к I.
Возьмём среднее арифметическое:
.
(2) Вычислим интеграл: Это гладкая кривая, следовательно введём параметризацию и тогда посчитаем. Уравнение окружности (параметризуемое):
.
т.к. это интеграл от sin, cos по периоду.
ИНТЕГРАЛЬНАЯ ТЕОРЕМА КОШИ
Замечание. Если замкнутая и спрямляемая кривая, то
.
Почему? Т.к. и
Гипотеза: Поскольку равенство 0 верно для линейной функции (по замкнутой кривой), тогда верно для любой голоморфной функции.
10. Интегральная теорема Коши для односвязной области.
Теорема1. Если: 1) D – односвязная область
2) — замкнутая и спрямляемая кривая, лежащая в области D.
3) f(z) – голоморфная функция в D. Тогда
Доказательство(НЕ ПРАВИЛЬНОЕ). По теореме Грина
в силу 2ого условия Коши-Римана.
— непрерывны в D для условия теоремы Грина, а мы не знаем на самом деле того, что они непрерывны ,
так доказывать теорему нельзя…
Доказательство(ПРАВИЛЬНОЕ).
Замечание. 1) Теорему достаточно доказать для замкнутых ломаных.
Т.к. любую кривую можно приближать ломаной сколько угодно точно (по теореме Кантора о равномерной непрерывности) и интегралы по ломаным стремятся к длине кривой.
2) Теорему достаточно доказать для многоугольника (замкнутой ломанной без самопересечений). Т.к. точка пересечения разбивает любую замкнутую на многоугольники.
3) Теорему достаточно доказать для . Т.к. в любом многоугольнике
диагонали,
многоугольник разбивается на
-ки.

Лемма (Турса). Если — замкнутый, функция f – голоморфна на
, то
.
Доказательство. Обозначим: проведём средние линии
.
. Обозначим
. К нему применим те же рассуждения.
,
. И т.д.
т.е. оценка снизу существует.
Оценка сверху: по определению производной:
Тогда
(т.к. интеграл от линейной функции = 0). Оценим этот интеграл. Напишем определение о («о» малого)
(меньше диаметра, меньше периметра). Т.е. мы доказали, что
лемма доказана,
теорема доказана.



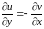
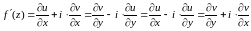
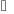



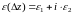













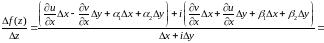
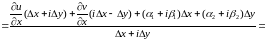






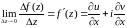
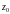




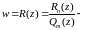




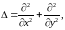


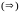


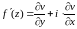











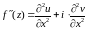


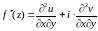





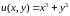


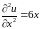




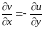
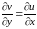




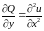
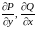

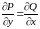
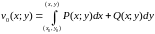



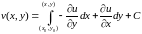



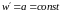


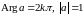





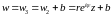


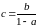
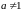

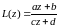



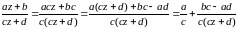
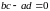

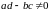




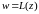


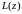

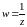

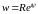




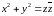
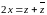


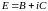
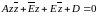


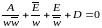

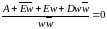

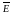







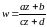






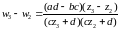






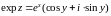


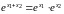





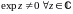



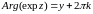
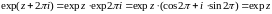
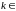
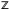

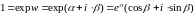



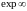
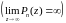
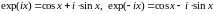

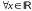



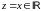


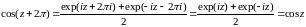



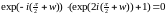
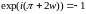



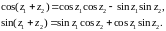


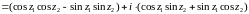
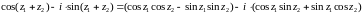
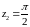



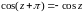
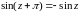
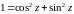
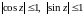



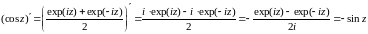
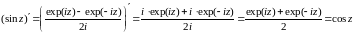
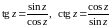
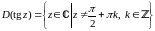

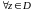


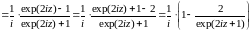
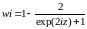





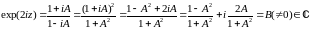

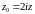





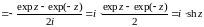
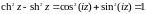
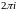




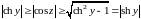

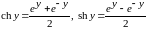


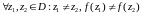


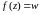
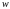
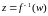



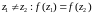
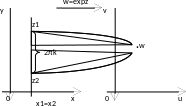
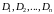







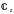
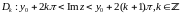

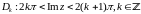
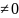



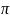

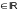







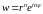
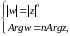

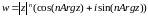
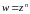







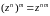


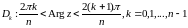
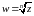


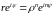


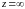
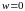
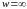


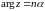
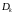






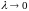
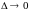


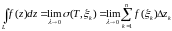


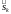

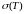
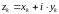
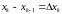

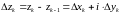
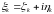
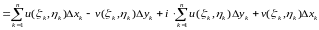



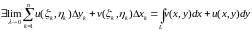

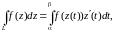
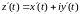
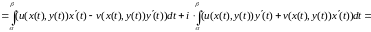


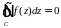

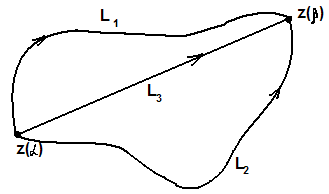
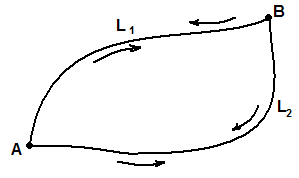




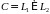







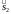
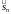





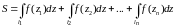






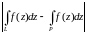


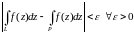


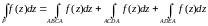




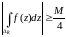



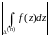
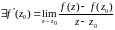

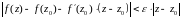
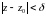

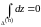





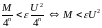


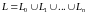

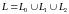


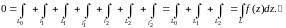
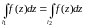






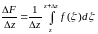





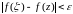







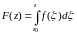
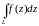
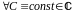




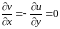


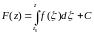





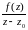
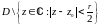
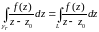
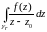
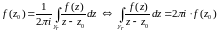
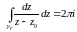



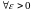

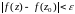



 . Нужно определить области аналитичности и однолистности.
. Нужно определить области аналитичности и однолистности. , где
, где  ,
, -действительные. Тогда несложно представить
-действительные. Тогда несложно представить 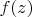 в виде
в виде  :
: . То есть
. То есть  ,
,  .
. . Выбираете одну из двух ветвей. Тогда вопрос про однолистность — это вопрос о том, на какую максимальную область нужно можно продолжить эту ветвь
. Выбираете одну из двух ветвей. Тогда вопрос про однолистность — это вопрос о том, на какую максимальную область нужно можно продолжить эту ветвь