Как найти объем влажного воздуха

В
воздухе всегда содержится то или иное
количество водяного пара. Такую смесь
сухого воздуха и водяного пара называют
влажным воздухом. Обычно расчеты,
связанные с влажным воздухом, выполняют
при давлениях, близких к атмосферному,
и парциальное давление пара в нем
невелико, то с достаточной точностью в
расчетах можно применять формулы,
полученные для идеальных газов. Поэтому
принимаем, что влажный воздух подчиняется
уравнению состояния идеальных газов
(2.5) и закону Дальтона (3.4)

р=
р_в
+ р_п, (14.1)

где
р
– давление влажного воздуха;

р_в
– парциальное давление сухого воздуха;

р_п
– парциальное давление пара.

Абсолютной
влажностью воздуха называют массу
водяного пара, содержащегося в 1 м³
влажного воздуха (или плотность пара
_п
при его парциальном давлении и температуре
воздуха).

, (14.2)

где
R_в
– газовая
постоянная воздуха, Дж/(кг·К);

Т
– температура воздуха, К.

Отношение
абсолютной влажности воздуха при данной
температуре к его максимально возможной
абсолютной влажности при той же
температуре, называют относительной
влажностью.

, (14.3)

где
р_н
– давление насыщения водяного пара при
температуре влажного воздуха.

Отношение
массы пара во влажном воздухе к массе
сухого воздуха называется влагосодержанием

,
м/м, (14.4)

Из этого уравнения
следует

. (14.5)

Аналогично
уравнению (14.5) можно написать

, (14.6)

где
d_max
– максимально возможное влагосодержание
влажного воздуха.

Отношение
влагосодержания к максимально возможному
влагосодержанию называется степенью
насыщения

. (14.7)

Температура,
при которой влажный воздух при постоянном
давлении становится насыщенным (
= 100 %) называется температурой
точки росы t_р.
Плотность влажного воздуха определяется
по формуле

,
кг/м³. (14.8)

Упрощенно плотность
воздуха можно определить по формуле

,
кг/м³. (14.9)

Энтальпию
влажного воздуха относят к 1 кг сухого
воздуха и определяют по формуле

i
= i_в
+ i_пd, (14.10)

где
i_в
– энтальпия сухого воздуха, кДж/кг;

i_п
– энтальпия водяного пара, кДж/кг;

d
– влагосодержание в кг/кг.

Энтальпия сухого
воздуха

i_в
= с_рt
≈ 1·t
≈ t, (14.11)

где
с_р
≈1 кДж/(кг·ºС) – удельная теплоемкость
воздуха.

Энтальпия
водяного пара, содержащегося во влажном
воздухе, определяется по эмпирической
формуле

i_п
= 2490 +
1,97·t_н. (14.12)

Следовательно,
энтальпия влажного воздуха

i
= t
+ (2490 +
1,97·t_н)d. (14.13)

Примеры

П-14.1

Определить
влагосодержание воздуха при температуре
t
= 60 ºС и
барометрическом давлении В
= 99325 Па (745
мм рт.ст.), если относительная влажность
воздуха

= 60 %.

Решение.

По
формуле (13.4)

а
так как по уравнению (13.3)

то


.

р_н
определяются по приложению А насыщенного
водяного пара для температуры t
= 60 ºС. Из
этой таблицы р_н
= 0,019917 МПа и, следовательно,

МПа.

По
таблицам перегретого пара для р
= 0,012 МПа и t
= 60 ºС находим
v
= 12,78 м³/кг.
Тогда

кг/м³.

Парциальное
давление воздуха

Па.

Плотность влажного
воздуха

кг/м³,

поэтому

кг/кг=85,4
г/кг.

П-14.2

Начальное
состояние воздуха задано параметрами:
t=20
ºС, d=8
г/кг, р
=993,3
гПа. Воздух сжимается адиабатически до
давления 6 бар и затем охлаждается.

Определить,
при какой температуре начнется выделение
влаги из этого воздуха. Для решения
задачи воспользоваться таблицами
водяного пара.

Решение.

По
I—d
диаграмме находим, что относительная
влажность φ=54
%. Следовательно,
парциальное давление водяных паров
р_п=
=0,54·9933=53640
Па, здесь
значение давления насыщения взято из
таблиц водяного пара. Так как парциальное
давление водяных паров будет увеличиваться
пропорционально общему давлению влажного
воздуха, то парциальное давление водяного
пара при р=6
бар составит:

Па.

Это
давление водяного пара соответствует
температуре насыщения 135,56 ºС, при которой
и начнется выпадение воды из воздуха.

П-14.3

Определить
плотность влажного воздуха при параметрах

t=320
ºС, d=30
г/кг, р=0,3
МПа.

Решение.

Находим
газовую постоянную влажного воздуха
R_вл.в.:

R_вл.в.=m
_c.вR_c.в+
m
_в.пR_в.п

где
индексы «с.в.» и «в.п.» относятся к сухому
воздуху и водяному пару:

Дж/(кг·К).

Плотность
влажного воздуха определяется из
уравнения Клайперона-Менделеева:

кг/м³.

Задачи

З-14.1

Состояние
влажного воздуха характеризуется
температурой

t=25
ºС и относительной влажностью

=0,8.
Барометрическое давление В
=99325 Па (745 мм
рт.ст.)

Найти
парциальное давление пара в воздухе и
его влагосодержание.

Ответ:
р_П
=0,0025 МПа, d
=16,3 г/кг.

З-14.2

При
определении состояния влажного воздуха
с помощью психрометра зафиксировано,
что «сухой» термометр показывает 20 ºС,
а «мокрый» 15 ºС.

Найти
влагосодержание d,
относительную влажность

,
энтальпию I,
а также температуру точки росы для этого
воздуха.

Ответ:
d
=9,2 г/кг,

=62 %, I
= 43 кДж/кг,
t_р
=12,6 ºС.

З-14.3

Состояние
влажного воздуха при температуре 20 ºС
определяется с помощью гигрометра,
которым измерена точка росы, равная 10
ºС.

Определить
относительную влажность

,
влагосодержание
d
и
энтальпию
I
влажного воздуха.

Ответ:

=52 %, d
=7,8 г/кг, I
=40 кДж/кг.

З-14.4

Определить
удельный объем влажного воздуха при
следующих параметрах: t
=200 ºС, р
=0,2 МПа, d
=40 г/кг.

Ответ:
v
=0,695 м³/кг.

З-14.5

Воздух
с параметрами t₁
=15 ºС,
р₁ =1
кгс/см²
и d₁=10
г/кг сжимается с отводом теплоты.
Параметры воздуха в конце процесса
сжатия t₂
=60 ºС, р₂
=7 кгс/см².

Определить
относительную влажность в конце процесса
сжатия.

Ответ:

=55 %.

94

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

6.4. Характеристики влажного воздуха

Отношение абсолютной влажности ненасыщенного воздуха при данной температуре к
абсолютной влажности насыщенного воздуха при той же температуре называется

относительной влажностью

воздуха

j = с_п / с_н
или j = с_п / с_н
·100% , (6.10)

j = r_П
/ Р_Н или r = Р_П / Р_Н
·100% . (6.11)

Плотность влажного воздуха
слагается из масс, содержащихся в 1 м³ сухого воздуха и водяных
паров:

r = r_в
+ r_п = P_B/(R_B·T)
+ j/n^»
. (6.12)

Молекулярная
масса влажного воздуха определяют по формуле:

m = 28,95 – 10,934j
P_Н/P (6.13)

d = М_П / М_В , (6.14)

d = 0,622 j·Р_Н·/(Р
— j·Р_Н). (6.15)

Газовая
постоянная:

R = 8314/м = 8314/(28,95 – 10,934·m·Р_Н/P).
(6.16)

Объем
влажного воздуха, приходящегося на 1 кг сухого воздуха:

V_ВЛ.В =
R·T/P. (6.17)

Удельный
обьем влажного воздуха:

n = V_ВЛ.В/(1
+ d). (6.17)

Удельная
массовая теплоемкость паровоздушной смеси:

с_см = с_В + d·с_П .
(6.18)

    Удельный объем влажного воздуха (отнесенный к 1 кг сухого воздуха) Ууд (м /кг) рассчитывается по формуле [c.297]

    Удельный объем влажного воздуха по (10.8) [c.305]

    Объем влажного воздуха, подаваемого в печь (в м кг)  [c.54]

    ОБЪЕМ ВЛАЖНОГО ВОЗДУХА (м ), СОДЕРЖАЩЕГО 1 кг СУХОГО ВОЗДУХА, ПРИ ДАВЛЕНИИ 745 мм рт. ст. [c.34]

    ОБЪЕМ ВЛАЖНОГО ВОЗДУХА [c.642]

    Объем влажного воздуха, отнесенный к 1 кг сухого воздуха, может быть найден ио таблице или вычислен по формуле  [c.642]

    Рассмотрим некоторый объем влажного воздуха V, в котором содержится 1 кг сухого воздуха и д кг водяных паров. Общее давление воздуха Р, парциальное давление водяных паров р . По уравнению состояния объем V равен  [c.738]

    При известных температуре воздуха и относительной влажности по таблицам можно определить также влагосодержание и теплосодержание воздуха [63, 64]. Удельный объем влажного воздуха находят по таблицам [63, 64] в зависимости от и ф. [c.265]

    Кроме л , ф и / при расчетах процесса сушки необходимо знать плотность пли обратную ей величину — удельный объем влажного воздуха. Плотность влажного воздуха равна сумме плотностей абсолютно сухого воздуха рс.в и водяного пара р . Учитывая, что, согласно выражению (XV,5), плотность водяного пара р = хрс в, плотность влажного воздуха [c.586]

    Удельный объем влажного воздуха Э, (м кг) равен [c.930]

    Удельный объем влажного воздуха рассчитывают по формуле [c.282]

    Объем влажного воздуха (м ), содержащего 1 кг сухого воздуха при давлении 99,2 кПа [c.45]

    Объем влажного воздуха — объем (в кубических метрах) 1 кг сухого воздуха с содержащимся в нем водяным паром. [c.471]

    Объем насыщенного воздуха — объем влажного воздуха, когда он насыщен водяным паром. [c.471]

    По. данным предыдущей задачи определить уд. объем влажного воздуха. [c.216]

    Здесь Oi и 2 — удельный объем влажного воздуха, приходящийся на I кас сухого воздуха, при начальных параметрах воздуха ( 1=120° С и di = =0,00893 кгс/кгс) в конечных параметрах его ( 2 = 60° G и 2= 19%). [c.341]

    Барометрическое давление воздуха 740 мм рт. ст. и температура 30° С. Парциальное давление водяных паров в нем при этой температуре равно 22 мм рт. ст. После охлаждения воздуха до 15° С часть водяных паров сконденсировалась и парциальное давление их понизилось до 12,5 мм рт. ст. Подсчитать а) объем воздуха после охлаждения б) вес сконденсированной воды, если первоначальный объем влажного воздуха (до охлаждения) равен [c.90]

    Vi = 1,28 м /кг — объем влажного воздуха на 1 кг сухих газов при 4= 160° С и 1= 13,9 [77, 78, 49]. [c.324]

    Общий объем влажного воздуха будет равен 455 + 6 = 461 ж. Тогда состав и количество продуктов сгорания будут равны (на 100 ж газа)  [c.261]

    Объем влажного воздуха [c.150]

    Удельный объем влажного воздуха (приходящийся на 1 кг сухого воздуха) (в м Укг) рассчитывается по формуле  [c.403]

    Пример 10-5. По Данным предыдущего примера определить удельный объем влажного воздуха, приходящийся на 1 кг сухого воздуха, т. е. на (1 4- ) кг воздушно-паровой смеси. [c.411]

    Решение. Удельный объем влажного воздуха находим по формуле (10-12)  [c.412]

    Шкалы А— относительная влажность воздуха, г/кг В — удельный объем воздуха, м /кг С— энтальпня влажного воздуха, ккал/кг В — упругость паров воды в воздухе, мм рт. ст. Е — влагосодержание насыщенного влагой воздуха, г/м. Кривые А — насыщения (температуры точки росы) В — удельный объем влажного воздуха, м /кг В — удельный объем сухого воздуха, м /кг С — энтальпия влажного воздуха, ккал/кг В — упругость паров воды, мм рт. ст. Е — влагосодержание воздуха, г/м  [c.172]

    На диаграмме, изображенной на рис. УП1-3, показан ход этой кривой в зависимости от температуры. Кривые для 0<Х<Хнас при данной температуре на диаграмму не нанесены, но объем влажного воздуха V в состоянии 1, X легко вычислить найдя по диаграмме значения У и У л При температуре нужно затем линейно интерполировать значение V  [c.600]

    Определить удельный объем влажного воздуха при следующих парамефах t = 200 °С, р = 0,2 МПа, d= АО г/кг с.в. [c.285]

    Удельный вес сухого воздуха при 0°и760лш рт. ст.—То.в. 1,293, поэтому объем влажного воздуха можно выразить формулой  [c.658]

    Пример 4, Пересчитать объем влажного воздуха, равный Qi=2000 при / =50°С, дазлении pi=3 мм Hg, барометрическом давлении 722 лш Hg, давлении паров Pd =92,75 мм Hg на состояние, определяемое параметрами /2=Ю°С, Р2=6 мм Hg, 2=750 мм Hg и ра=9,21 мм Hg. После подстановки в уравнение (195) получим  [c.110]

    П = 760 мм рт. ст. — общее давление паро-воздушной смеси. Объем влажного воздуха при ос = 95° С и9ос = 14%  [c.271]

---

Справочник инженера — химика том первый (1969) — [

c.471

]

Справочник химика Том 5 Издание 2 (1966) — [

c.642

]

Сушильные установки (1952) — [

c.17

]

Справочник химика Изд.2 Том 5 (1966) — [

c.642

]

---

АВОК

СПРАВОЧНОЕ ПОСОБИЕ

Влажный воздух

НП «Инженеры по отоплению, вентиляции,
кондиционированию воздуха, теплоснабжению и
строительной теплофизике» (НП «АВОК»)

Москва — 2004

Разработан
творческим коллективом Некоммерческого Партнерства «Инженеры по отоплению,
вентиляции, кондиционированию воздуха, теплоснабжению и строительной
теплофизике» (НП «АВОК») канд. техн. наук М.Г. Тарабанов (НИЦ «Инвент»),
канд. техн. наук В.Д. Коркин (СПбГАИЖСА), В.Ф. Сергеев (НИЦ «Инвент»)

Внесен
Комитетом по техническому нормированию, стандартизации и сертификации НП
«АВОК».

ПРЕДИСЛОВИЕ

В
справочном пособии изложены основные законы термодинамики идеальных газов и
смесей, используемые в технике вентиляции и кондиционирования воздуха, даны
определения основных параметров влажного воздуха и расчётные зависимости для их
вычисления с примерами расчётов. Подробно рассмотрены построения процессов
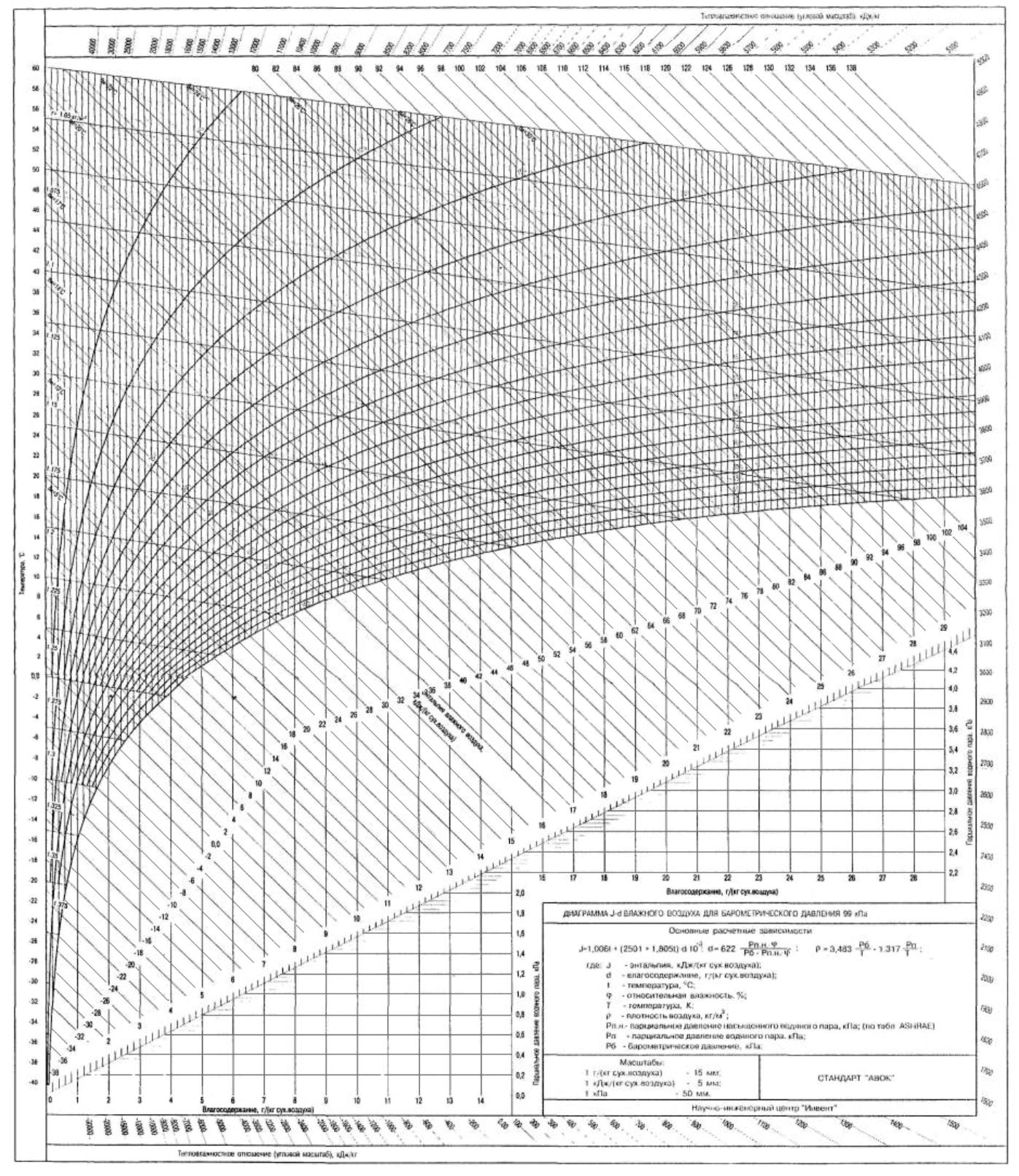
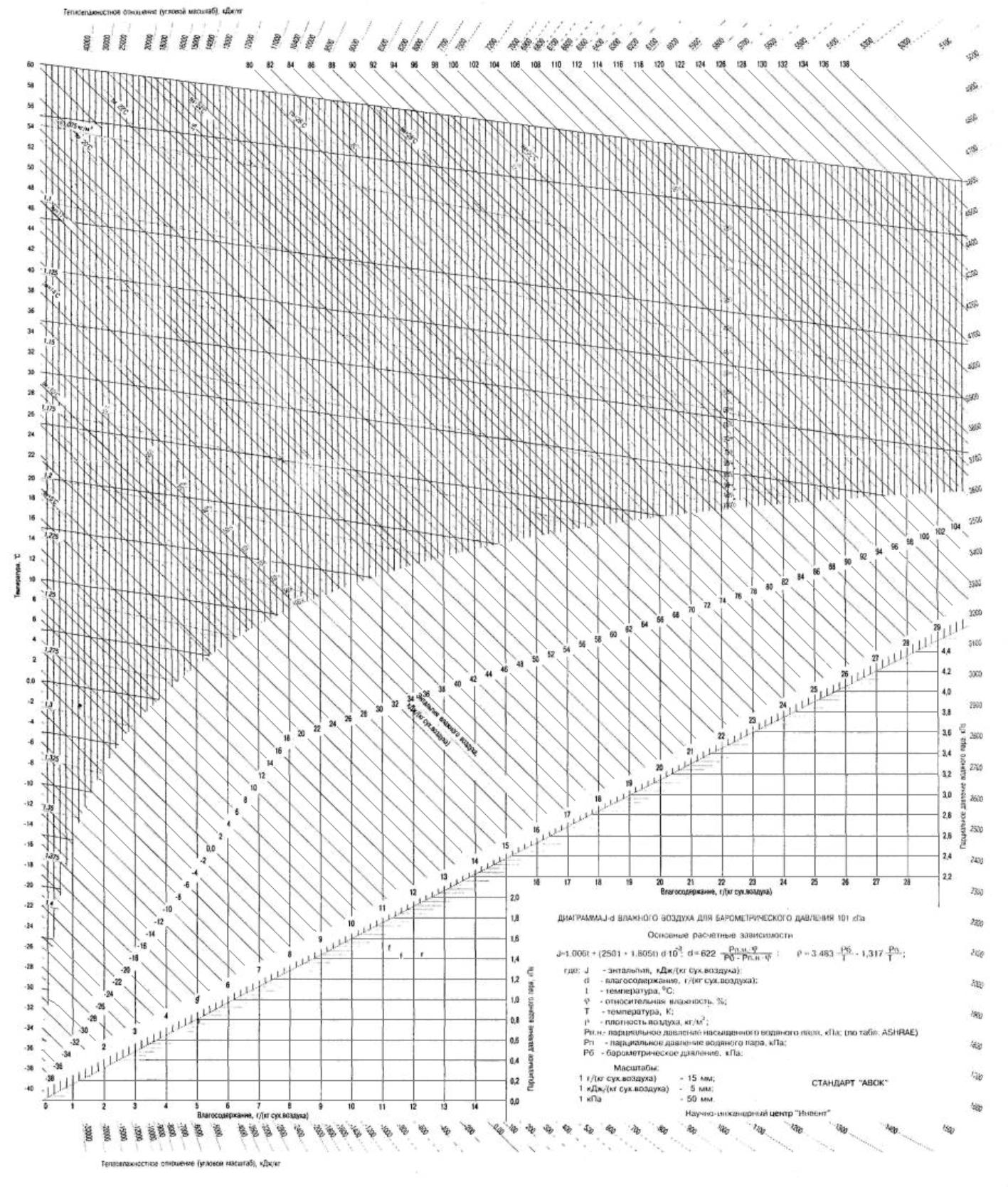
тепловлажностной обработки влажного воздуха на J — d диаграмме. Приведены таблицы значений
давления насыщенного водяного пара над поверхностью льда и чистой воды, а также
значений влагосодержания насыщенного влажного воздуха при барометрическом
давлении 99 и 101 кПа.

К
стандарту приложены J — d диаграммы влажного воздуха для интервала
температур от -40 до +60 °С и значения влагосодержания до 30 г/кг с.в. при
барометрическом давлении 99 и 101 кПа. При построении J — d диаграмм масштабы J и d выбраны таким образом, чтобы получить
широкое рабочее поле для построения процессов изменения параметров влажного
воздуха наиболее характерных для систем вентиляции и кондиционирования воздуха
жилых, общественных и промышленных зданий.

В
справочном пособии использованы некоторые расчётные зависимости и табличные
материалы из справочника ASHRAE .

Настоящее
справочное пособие является первой в отечественной практике попыткой
систематизировать определения и расчётные зависимости основных параметров
влажного воздуха и привести их в соответствие с международными стандартами.

Справочное
пособие предназначено для специалистов по проектированию, наладке и
эксплуатации систем вентиляции и кондиционирования воздуха и студентов высших
учебных заведений.

СОДЕРЖАНИЕ

1 .
ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕРМОДИНАМИКИ ИДЕАЛЬНЫХ ГАЗОВ

1.1 . ОСНОВНЫЕ ПОНЯТИЯ

Термодинамической
системой называется совокупность материальных тел в
ограниченной области пространства, являющихся объектом изучения и находящихся
во взаимодействии с окружающей средой.

Система
отделяется от внешней среды материальной или
воображаемой поверхностью — границей системы, которая
может быть закрытой, т.е. непроницаемой для вещества, или открытой,
если граница системы проницаема для вещества.

Если
граница системы непроницаема для вещества и не допускает обмена с окружающей
средой как теплотой, так и работой, то такая термодинамическая система
называется изолированной.

Система
называется неизолированной, если она допускает обмен с внешней
средой и теплотой, и работой.

Система,
имеющая во всех своих частях однородный состав и физические свойства,
называется однородной.

Однородная
термодинамическая система, внутри которой нет поверхности раздела фаз,
называется гомогенной.

Система
из двух или более фаз называется гетерогенной.

Примером
гомогенной системы является атмосферный воздух, состоящий из смеси различных
газов и водяного пара, а гетерогенной системы — туман, когда наряду с газовой
фазой в системе присутствует жидкая (взвешенные капли воды) или твердая
(кристаллы льда) фазы.

Термодинамическая
система описывается рядом термодинамических величин, характеризующих ее
свойства.

При
устойчивом состоянии системы эти величины называются параметрами
состояния.

Внутренние
параметры характеризуют внутреннее состояние
системы, к ним относятся давление, температура, объем и др.

Внешние
параметры определяют положение системы (ее
координаты) во внешних силовых полях и ее скорость.

Внутренние
параметры подразделяются на интенсивные и экстенсивные. Интенсивные
— это те параметры, величина которых не зависит от размеров или массы системы,
например, давление, температура, удельный объем, удельная теплоемкость.

Параметры
состояния, значения которых определяются суммой параметров состояния
составляющих частей условно разделенной системы, называются экстенсивными.
Примером экстенсивных параметров состояния являются объем и масса.

Для
характеристики конкретных условий, в которых находится данная система, или
процесса, идущего в системе, обычно необходимо знать такие интенсивные
параметры состояния, как удельный объем, давление, абсолютная температура.

Удельный
объем v — это отношение объема к его массе, т.е.
объем единицы массы

,                                                            ( 1.1 )

где V — объем, занимаемый системой, м³;

m — масса вещества системы, кг.

Масса
вещества, содержащаяся в единице объема, или величина, обратная удельному
объему, называется плотностью (ρ, кг/м³)

                                                       ( 1.2)

Давление
— отношение нормальной
составляющей силы, действующей на заданную поверхность, к площади этой
поверхности (Р, Па = Н/м²)

                                                         ( 1.3 )

где F _н — нормальная
составляющая силы, Н;

S — площадь поверхности, нормальной к
действующей силе, м².

Температура
(Т, К) — величина,
характеризующая степень нагретости тела. Она представляет собой меру средней
кинетической энергии поступательного движения молекул.

В
настоящее время используются температурная шкала Цельсия и термодинамическая
шкала температур, основанная на втором законе термодинамики. Между
температурами, выраженными в Кельвинах и градусах Цельсия, имеется следующее
соотношение

T, K = 273,15 + t
° С .                                                ( 1.4)

Заметим,
что параметром состояния является абсолютная температура, выраженная в
Кельвинах, но градус абсолютной шкалы численно равен градусу шкалы Цельсия, так
что dT
= dt .

Состояние
термодинамической системы может быть равновесным и неравновесным. Равновесным
называют такое состояние системы, при котором во всех точках ее объема
все параметры состояния и физические свойства одинаковы (давление, температура,
удельный объем и др.), иными словами, система находится в термодинамическом
равновесии, если при изоляции ее от воздействия внешней среды параметры
состояния системы не изменяются.

1.2 . ИДЕАЛЬНЫЙ ГАЗ

Простая
гомогенная система в равновесном состоянии характеризуется определенными
значениями параметров состояния v , P и T . Уравнение, устанавливающее связь между
давлением, температурой и удельным объемом системы, называется термическим
уравнением состояния и имеет вид

F ( Р , v, T) = 0.                                                       ( 1.5)

Состояние
системы вполне определяется заданием двух из указанных параметров, т.к. любой
из трех параметров является для каждого равновесного состояния однозначной
функцией двух заданных. Поэтому можно записать, что

P = f₁ (v , T); v = f₂ (P, T); T = f₃
(v, P).

Термическое
уравнение состояния газов при малых давлениях принимает простое выражение. Если
по измеренным значениям Р, v
и T рассчитать величину P
×
v
/ T ,
то получим

lim_p→0 = Const = R _{г .}                                                ( 1.6)

Константа
R _г
называется газовой постоянной и имеет для каждого газа
свое значение. Она представляет собой работу 1 кг газа при постоянном давлении
и при изменении температуры на 1 градус. Используя понятие газовой постоянной,
уравнение состояния можно записать в виде

Pv = R _г
· T.                                                         ( 1.7)

Газ,
состояние которого точно описывается уравнением ( 1.7), называется идеальным,
а само уравнение — термическим уравнением состояния идеальных газов, или
уравнением Клапейрона.

Для
m
кг идеального газа уравнение состояния имеет вид

PV = m · R _г
· T,                                                      ( 1.8)

где V — объем газа, м³.

Умножая
обе части уравнения ( 1.8) на молекулярную массу μ,
получим

PV _μ = μ · R _г · T ,                                                     ( 1.9)

где V _μ
= v
· μ — объем, занимаемый одним молем газа.

Молем
или киломолем называется
количество газа, масса которого в килограммах численно равна его молекулярной
массе.

Произведение
μ · R _г
= R
называется универсальной газовой постоянной. Ее значение при
нормальных условиях для 1 кмоль любого газа равно 8314,41 Дж/(кмоль·К).

Каждый
идеальный газ характеризуется также удельной теплоемкостью. Теплоемкостью
называется количество теплоты, которое нужно подвести к газу или отнять
от него для изменения температуры газа на 1 °С. Под удельной
теплоемкостью газа понимают отношение теплоты, полученной единицей
количества вещества при бесконечно малом изменении его состояния, к изменению
температуры.

Теплоемкость
является функцией процесса и не входит в число термодинамических параметров.

Различают
массовую и объемную теплоемкости.

Теплоемкость,
отнесенную к 1 кг газа, называют удельной массовой и обозначают
с, Дж/кг·К.

Теплоемкость,
отнесенную к 1 м³ газа при нормальных физических условиях называют удельной
объемной и обозначают с’, Дж/м³·К.

Между
указанными удельными теплоемкостями существует зависимость

c = c ‘ · v ₀ ,

где v ₀ — удельный
объем газа при нормальных условиях.

Теплоемкость,
отнесенную к 1 кмоль газа, называют удельной мольной и обозначают
c_μ
= μ
· c ,
кДж/(кмоль·К).

Теплоемкость
зависит от характера процесса. В термодинамике большое значение имеют удельная
теплоемкость при постоянном объеме c_v (изохорная
теплоемкость), равная отношению количества теплоты к
изменению температуры газа в процессе при постоянном объеме, и удельная
теплоемкость при постоянном давлении c_p (изобарная
теплоемкость), равная отношению количества теплоты к
изменению температуры газа в процессе при постоянном давлении.

Для
идеального газа связь между изобарной и изохорной теплоемкостями определяется
уравнением Майера

c_p — c_v
= R _г ,

или

μ c_p — μ c_v = R = 8314,41, Дж/(кмоль·К).

Удельные
теплоемкости идеальных газов c_p
и c_v ,
в общем случае представляют собой сложные функции температуры, поэтому в
расчетах используют средние значения удельных теплоемкостей, обычно заданные в
табличной форме для определенных значений температур. Средней удельной
теплоемкостью данного процесса в интервале температур от t ₁ до t ₂ называют
отношение количества теплоты, переданного в процессе, к конечной разности
температур t ₂
— t ₁ .
Методика определения средних значений c_p и c_v и примеры расчета
приведены в [ 2].

Из
первого закона термодинамики следует, что теплота, подведенная к рабочему телу,
затрачивается на изменение внутренней энергии и на совершение работы.

Внутренняя
энергия — это энергия, заключенная в системе. Она
состоит из кинетической энергии, вращательного и колебательного движения
молекул, потенциальной энергии взаимодействия молекул, энергии внутриатомных и
внутриядерных движений частиц и др.

Внутренняя
энергия является однозначной функцией внутренних параметров состояния
(температуры, давления) и состава системы.

Для
упрощения расчетов термодинамических процессов У. Гиббсом введена функция J для m кг массы, называемая энтальпией и
i
для 1 кг массы, называемая удельной энтальпией.

Энтальпия
J относится к экстенсивным параметрам, т.к. ее величина пропорциональна массе.

Удельная
энтальпия i
представляет собой сложную функцию и может быть выражена формулой

i = u + Pv ,

где u — удельная внутренняя энергия газа.

Поскольку
входящие в формулу величины u ,
P
и v
являются параметрами состояния, то и сама удельная энтальпия также будет
параметром состояния.

Физический
смысл энтальпии состоит в том, что в изобарных процессах изменение энтальпии
равно количеству теплоты, поглощенной или отданной системой.

Удельная
энтальпия идеального газа, также как и внутренняя энергия, является функцией
только температуры и не зависит от объема и давления.

В
термодинамике не требуется знание абсолютного значения энтальпии, поэтому ее
отсчитывают от некоторого условного нуля. Для идеального газа принято считать
энтальпию равной нулю при температуре t ₀ = 0 °С.

Приращение
энтальпии для любого процесса изменения состояния идеального газа в пределах
одной фазы (газообразной, жидкой или твердой) определяется по формуле

∆i_1-2 = i₂ — i₁
= .

Если
считать, что i_{t
= 0} = 0, то энтальпия газа при температуре t

i = , кДж / кг .                                                      ( 1.10)

Формула
( 1.10)
показывает, что удельная энтальпия идеального газа численно равна количеству
теплоты, которая подведена к 1 кг газа при нагревании его от 0 °С до
температуры 1 °С при постоянном давлении.

1.3 . СВОЙСТВА ГАЗОВЫХ СМЕСЕЙ

Под
газовой смесью понимают механическую смесь отдельных газов, не
вступающих между собой ни в какие химические реакции. Каждый газ в смеси,
независимо от других газов, полностью сохраняет свои свойства и ведет себя так,
как если бы он один занимал весь объем смеси.

Все
реальные газы в диапазоне температур, характерном для систем кондиционирования
воздуха, и атмосферном или близком к нему давлении полностью подходят под
понятие идеального газа, поэтому каждый отдельный газ, входящий в смесь,
считается идеальным газом.

Так
как смесь состоит из нескольких компонентов, то ее состояние не может быть
определено лишь двумя параметрами, и необходимы дополнительные величины,
характеризующие состав смеси.

Обычно
состав смеси идеальных газов задают массовыми долями g_i , т.е. отношением
массы компонента смеси m_i
к массе всей смеси m _см

g₁ = ; g₂ = ; … g_n = .

При этом m ₁ + m ₂ + … + m_n = m _см ;

g ₁ + g ₂ + … + g_n = 1.

Иногда
состав смеси задают объемными долями r_i , т.е. отношением парциального объема
компонента V_i к объему смеси V _см

r₁ = ; r₂ = ; … r_n = .

При
этом

V₁ + V₂ + … + V_n = V _см ;

r₁ + r₂ + … + r_n =
1.

Под
парциальным объемом газа понимают объем,
который занимал бы этот газ, если бы его температура и давление соответствовали
температуре и давлению смеси.

Соотношение
между массовыми и объемными концентрациями имеют вид

g_i =  =  =  = ,

или

r_i =  =  =  = .

По
закону Дальтона общее давление идеальных газов P _см равно сумме
парциальных давлений отдельных газов P_i , составляющих смесь,

P _см
= P₁ + P₂ + … + P_n =                                             ( 1.11)

Под
парциальным давлением понимают такое
давление, которое имел бы газ, входящий в состав смеси, если бы он находился в
этом же количестве, в том же объеме и при той же температуре, что и в смеси.

Для
отдельных компонентов и для смеси в целом справедливо уравнение Клапейрона

P_iV _см = m_iR_iT _см ;                                                        ( 1.12)

P _см V _см = m _см R _см T _см .                                                   ( 1.13)

Если
просуммировать уравнение ( 1.12) по всем компонентам, то получим

V _см
= T _см                                              ( 1.14)

Согласно
закону Дальтона ( 1.11) левые части
уравнений ( 1.12)
и ( 1.13)
равны, следовательно, равны и правые. Тогда, можно получить следующее выражение
для газовой постоянной смеси:

R _см =                                                       ( 1.15)

Или,
если задан объемный состав смеси, то

R _см =                                                           ( 1.16)

Понятие
универсальной газовой постоянной распространяется и на смеси

μ ₁ R₁
= μ
₂ R₂ = … =
μ _n R_n = μ_см R _см = 8314,41
Дж/(кмоль·К).

Если
известна величина газовой постоянной смеси, то средняя
молекулярная масса, представляющая собой условную величину и
относящаяся к такому условно однородному газу, у которого число молекул и общая
масса равны числу молекул и массе смеси газов, определяется из выражения

μ_см =                                                         ( 1.17 )

Парциальное
давление газа в смеси можно определить:

— через массовые доли — из уравнения Клапейрона

P_i =  = P _см · g_i = P _см · g_i                                   ( 1.18)

— через объемные доли — из закона Бойля-Мариотта

P_i = P _см = r_i · P _см .                                                    ( 1.19)

Значения
удельных теплоемкостей газовых смесей определяются по следующим формулам:

— смесь газов задана массовыми долями

c_{v см}
= g₁ · c_v1 + g₂ · c_v2 + … + g_n
· c_vn =                               ( 1.20)

c_{p см} = g₁ · c_p1
+ g₂ · c_p2 + … + g_n · c_pn =                               ( 1.21)

— смесь газов задана объемными долями

c ‘ _{v см} = r₁ · c ‘ _v1 + r₂ ·
c ‘ _v2 + … + r_n · c ‘ _vn =                               ( 1.22)

c ‘ _{p см} = r₁ ·
c ‘ _p1 + r₂ · c ‘ _p2 + … + r_n · c ‘ _pn =

Аддитивность
объема и внутренней энергии идеальной газовой смеси предопределяет это свойство
и для энтальпии смеси

J _см = J₁ + J₂ + … + J_n =

Тогда для удельных величин энтальпии

i _см = g₁ ·
i₁ + g₂
· i₂ + … + g_n
· i_n =                                   ( 1.23)

2 . СУХОЙ ВОЗДУХ

Атмосферный
воздух представляет собой смесь не взаимодействующих между собой газов,
водяного пара и различных загрязнителей (дым, пыль, промышленные, транспортные
и другие газовые выбросы).

Смесь
газов, содержащихся в атмосферном воздухе, без водяного пара и загрязнителей
называется сухим воздухом.

Состав
сухого воздуха относительно стабилен (табл. 1), однако в зависимости от
времени года, географического положения, высоты местности и погоды возможны
небольшие изменения количества некоторых компонентов.

Таблица
1

Состав
сухой части атмосферного воздуха 1

Наименование компонента	Химическое обозначение	Содержание по объему, %
Азот	N2	78,084
Кислород	О2	20,9476
Аргон	Ar	0,934
Углекислый газ	СО2	0,0314
Неон	Ne	0,001818
Гелий	He	0,000524
Метан	CH4	0,00015
Водород	H 2	0,00005
Двуокись серы	SO 2	от 0 до 0,0001
Озон	O 3	1 · 10 -6
Криптон	Kr	1 · 10 -4
Ксенон	Xe	8 · 10 -6
Радон	Rn	6 · 10 -18

Задачей
расчета газовых смесей, в т.ч. и сухого воздуха, является определение газовой
постоянной, молекулярной массы, плотности и удельного объема, удельных
теплоемкостей и других величин на основе заданного состава смеси.

Для
сухого воздуха указанные величины определяют на основе уравнений и соотношений
для идеального газа.

Мольная
масса газов, составляющих сухой воздух, по шкале углерода-12 равна 28,9645
кг/кмоль.

Газовая
постоянная для сухого воздуха R_c
может быть определена по формуле

R_c =  =  = 287,055,                                      ( 2.1)

где R — универсальная газовая постоянная,
Дж/кмоль·К;

μ _c — мольная масса сухого воздуха, кг/кмоль.

Плотность
сухого воздуха ρ _с
в кг/м³ и его удельный объем можно определить из уравнения
Клапейрона

ρ _c
=  = 3,483                                                 ( 2.2)

где P _с — давление
сухого воздуха, кПа;

T _с — температура
сухого воздуха, К.

Удельные
массовые теплоемкости сухого воздуха c_{p . c} и c_{v . c} зависят от
температуры. Значения средней удельной теплоемкости при постоянном давлении
сухого воздуха 101,325 кПа для определенного интервала температур приведены
ниже в табл. 2.

Из
табл. 2
видно, что в интервале температур от -40 до +60 °С удельную теплоемкость
сухого воздуха при постоянном давлении можно считать постоянной:

c_{p . c} = 1,006 кДж/(кг·К).

Массовая
удельная теплоемкость при постоянном объеме может быть определена по формуле
Майера

c_{v . c} = c_{p . c} — R_c = 1,006 — 0,2871 =
0,7189 кДж/(кг·К).

Удельную
энтальпию сухого воздуха кДж/кг при различных температурах можно определить по
формуле ( 1.10):

i_c
= c_p.c · t = 1,006t                                                      ( 2.3 )

3 . ВОДА И ВОДЯНОЙ ПАР

3.1 . ОБЩИЕ ПОЛОЖЕНИЯ

Вода,
как и любое другое вещество, может находиться в твердом (лед), жидком (вода) и
газообразном (пар) состояниях, а в зависимости от соотношения давления и
температуры — одновременно в двух и даже в трех состояниях.

Таким
образом, вода может быть гомогенной системой (лед, вода, пар) и гетерогенной
системой (пар — вода, вода — лед, пар — лед, пар — вода — лед).

Каждая
гомогенная часть гетерогенной системы, ограниченная поверхностью раздела и
характеризующаяся одинаковыми физическими свойствами во всех своих точках,
называется фазой.

Фазовым
переходом называется процесс, сопровождающийся затратой
теплоты и изменением объема, в котором происходит изменение агрегатного
состояния вещества. Переход вещества из одной фазы в другую происходит через
поверхность раздела фаз.

Переход
вещества из твердого состояния в жидкое называют плавлением, из
твердого в газообразное — сублимацией, из жидкого в газообразное
— парообразованием. Обратные процессы соответственно называют затвердеванием,
десублимацией и конденсацией.

В
свою очередь, процесс парообразования реализуется в виде испарения и кипения.

Испарением
называется парообразование, которое происходит
только с поверхности жидкости. Кипение — процесс
превращения жидкости в пар, который происходит не только с поверхности
жидкости, но и внутри нее, т.е. это процесс парообразования во всей массе
жидкости.

Газообразная
фаза воды в зависимости от температуры и давления может быть в виде сухого
насыщенного, перегретого и влажного насыщенного пара.

Сухой
насыщенный пар — это пар, находящийся
в равновесном состоянии с жидкостью на границе раздела фаз, не содержащий
частиц жидкой фазы.

Если
к сухому насыщенному пару подводить теплоту, то его температура будет
возрастать и пар становится перегретым. Разность между
температурой перегретого пара и температурой сухого насыщенного пара называется
степенью перегрева.

Перегретый
пар является ненасыщенным. При данном давлении его плотность меньше плотности
сухого ненасыщенного пара, а удельный объем больше.

Влажный
пар является гетерогенной системой, которая может
быть двух- или трехфазной.

Таблица
2

Интервал температур, °С	-40 … -21	-20 … -1	0 … 19	20 … 29	30 … 39	40 … 49	50 … 59
Значения c p . c , кДж/(кг·К)	1,0057	1,0058	1,006	1,0061	1,0063	1,0064	1,0066

При
температуре выше 0 °С и давлении больше 0,61 кПа (для плоской поверхности
раздела фаз) влажный пар состоит из водяного пара и воды; при температуре 0 °С
и давлении 0,61 кПа влажный пар состоит из водяного пара, воды и льда, а при
температуре ниже 0 °С и давлении меньше 0,61 кПа — из водяного пара и льда.

Указанные
выше параметры характеризуют тройную точку воды, которой
соответствует давление 0,61 кПа и температура 0,01 °С. В тройной точке
внутренняя энергия, энтальпия и энтропия воды условно принимаются равными нулю.

3.2 . ОСНОВНЫЕ ПАРАМЕТРЫ ВОДЫ И ВОДЯНОГО ПАРА

Вода,
как и все капельные жидкости, практически несжимаема. Поэтому для воды, не
находящейся в состоянии насыщения, принимают удельный объем v _в , равный удельному объему в состоянии насыщения v ‘ _в .

Значения
удельного объема воды в состоянии насыщения приведены в табл. 3 [ 4].

Изменение
удельного объема v ‘ _в
в диапазоне температур от 0 до 50 °С составляет 1,2 %. Поэтому для практических
расчетов можно считать удельный объем постоянным и равным среднему значению

v _в
= v ‘ _{в ср.} =  = 0,001006 м³/кг.

Таблица 3

Температура t , °С	Удельный объем v ‘ в , м 3 /кг	Температура t , °С	Удельный объем v ‘ в , м 3 /кг
0	0,0010002	40	0,0010078
5	0,0010000	45	0,0010099
10	0,0010003	50	0,0010121
15	0,0010008	60	0,0010171
20	0,0010017	70	0,0010228
25	0,0010029	80	0,0010292
30	0,0010043	90	0,0010361
35	0,0010060	100	0,0010437

В
этом случае плотность воды ρ_в = 994,04 кг/м³.

Средние
значения удельной массовой теплоемкости воды в интервале температур от 0 до 100
°С изменяются от 4,179 до 4,217 кДж/(кг·К) [ 4]. В расчетах систем
кондиционирования воздуха принимают

c _{ср. в} = 4,186
кДж/(кг·К).

Состояние
сухого ненасыщенного пара определяется одним параметром — давлением насыщения,
которое является функцией только температуры.

Давление
насыщенного водяного пара над плоской поверхностью воды или льда можно
определить по формулам 3.1 и 3.2 [ 3] или по таблице приложения 1.

Для
насыщающей упругости водяного пара над поверхностью льда при температуре от
-100 до 0 °С:

ln ( P _н ) =  = С₂ + С₃ T + C ₄ T ² + C ₅ T ³ + C ₆ T ⁴ + C ₇ lnT ,                             ( 3.1)

где P _н — давление
насыщенного водяного пара над поверхностью льда, Па;

T = t + 273,15 — абсолютная температура по
шкале Кельвина;

C ₁
= -5,6745359 ·
10³;

C ₂
= 6,3925247;

C ₃
= -9,677843 · 10^-3;

C ₄
= 6,2215701 · 10^-7;

C ₅
= 2,0747825 · 10^-9;

C ₆
= -9,484024 ·
10^-13;

C ₇
= 4,1635019.

Для
насыщающей упругости водяного пара над поверхностью чистой воды при температуре
от 0 до 200 °С:

ln ( P _н ) =  + C ₉ + С₁₀ T + C ₁₁ T ² + C ₁₂ T ³ + C ₁₃ lnT ,                                ( 3.2)

где C ₈ = -5,8002206 ·
10³;

C ₉
= 1,3914993;

C ₁₀
= -4,8640239 · 10^-2;

C ₁₁
= 4,1764768 · 10^-5;

C ₁₂
= -1,4452093 · 10^-8;

C ₁₃
= 6,5459673.

Для
инженерных расчетов более удобными являются формулы, предложенные в работе [ 7].

Для
насыщающей упругости водяного пара над поверхностью льда при температуре от -60
до 0 °С:

P _н = exp                                                ( 3.3)

Для
насыщающей упругости водяного пара над поверхностью чистой воды при температуре
от 0 до 83 °С:

P _н = exp                                                 ( 3.4)

Отметим,
что в интервале температур от -5 до -60 °С значения P _н , полученные по
формуле ( 3.3),
отличаются от табличных в пределах от 0 до 0,00046 кПа. В интервале температур
от 0 до 43 °С максимальная разность между значениями P _н , полученными
по формуле ( 3.4),
и табличными не превышает 0,0017 кПа.

Мольная
масса воды и водяного пара по шкале углерода-12 равна

µ_п =
18,01528 кг/кмоль.

Значение
газовой постоянной для водяного пара

R _п =  = 461,520,

Сухой
насыщенный пар при значениях температуры и давления, характерных для систем
кондиционирования воздуха, незначительно отклоняется от поведения идеального
газа, что позволяет использовать уравнение Клапейрона для определения удельного
объема и плотности пара. Например, при t = 0 °С давление насыщения P _п = 611,2 Па,
тогда:

v «_п =  = 206,26 м³/кг;

ρ _п = 0,00485 кг/м³.

Экспериментальные
табличные значения v «_п для
насыщенного водяного пара в интервале температур от -60 до 160 °С приведены в [ 3], а
для условий кондиционирования воздуха — в табл. 4.

Значения
средней удельной теплоемкости насыщенного водяного пара при постоянном давлении
по данным [ 4]
приведены в табл. 5.

Для
диапазона температур от минус 50 до 50 °С удельную теплоемкость насыщенного
водяного пара принято считать постоянной и равной

c _рп = 1,86 кДж/(кг·К).

Удельная
энтальпия сухого насыщенного водного пара i _п при t _н > 0 °С
определяется по формуле

i _п = i _в + r = c _рв · t _н + r ,                                                   ( 3.5)

где i _в — энтальпия
кипящей воды, кДж/кг;

c _рв — удельная
массовая теплоемкость воды, кДж/(кг·К);

r — удельная теплота парообразования,
кДж/кг.

Удельной
теплотой парообразования называется количество
теплоты, затрачиваемое на превращение в пар 1 кг воды, нагретой до температуры
кипения.

Удельная
теплота парообразования r
является функцией температуры насыщения и для диапазона температур от 0 до 60
°С хорошо аппроксимируется линейной зависимостью

r = 2501 — 2,36 t _н .                                                        ( 3.6)

В
табл. 6
приведены значения r
по данным [ 4]
и по формуле 3.6.

При
температуре t _н
< 0 °С удельная энтальпия сухого насыщенного пара определяется по формуле

i _п = c _Рл — r _пл0 + r _суб ,                                                     ( 3.7)

где c _Рл — удельная массовая теплоемкость льда,
кДж/(кг·К);

r _пл0 = 334,11
кДж/кг — удельная теплота плавления льда при t _н = 0 °С;

r _суб — удельная
теплота сублимации льда, кДж/кг.

Экспериментальные
значения удельной энтальпии сухого насыщенного водяного пара в интервале
температур от -60 до 160 °С приведены в [ 3].

Значение
удельной энтальпии перегретого водяного пара определяется по уравнению

i _п.п = i _н.п + c _р.п ( t _п — t _н ),                                                       ( 3.8)

где i _н.п — удельная
энтальпия насыщенного водяного пара, кДж/кг;

c _р.п = 1,86
кДж/(кг·К) — удельная средняя теплоемкость перегретого пара;

Таблица
4

Удельный
объем и плотность насыщенного водяного пара

Температура t , °С	Давление насыщения Рн, Па	Удельный объем v » п , м3/кг	Плотность ρ нп , кг/м3 по табл. [ 3 ]
Табл. [ 3 ]	По уравнению Клапейрона
-50	3,94	26145,0	26139,0	0,0000382
-40	12,85	8376,3	8373,8	0,0001194
-30	38,02	2951,6	2951,6	0,000339
-20	103,26	1131,3	1131,4	0,000884
-10	259,9	467,14	467,29	0,002141
0	611,2	206,14	206,26	0,004851
5	872,5	147,03	147,13	0,00680
10	1228,0	106,33	106,42	0,00940
15	1705,5	77,898	77,98	0,01284
20	2338,8	57,773	57,85	0,01731
25	3169,2	43,351	43,42	0,02307
30	4246,0	32,889	32,95	0,03041
35	5627,8	25,213	25,27	0,03966
40	7383,5	19,521	19,58	0,05123
45	9593,2	15,256	15,31	0,06555
50	12349,9	12,029	12,08	0,08313

Таблица
5

Температура t , °С	0	10	20	30	40	50	60
Удельная теплоемкость c рп , кДж/(кг·К)	1,864	1,868	1,874	1,883	1,894	1,907	1,924

t _п и t _н — температура
соответственно перегретого и насыщенного пара, °С.

4 . ВЛАЖНЫЙ ВОЗДУХ

В
термодинамике атмосферный воздух рассматривают как смесь, состоящую из сухого
воздуха и водяного пара, который может быть в перегретом, насыщенном или в
сконденсированном взвешенном состоянии в виде капельного или ледяного (при отрицательной температуре) тумана.

Последнее состояние является неустойчивым и
изучается обычно при решении некото рых специальных задач,
например, в холодильной технике.

При
расчетах систем вентиляции и кондиционирования атмосферный воздух считают
бинарной гомогенной смесью, в состав которой входят сухой воздух и водяной пар.

Смесь
сухого воздуха с перегретым водяным паром называется ненасыщенным влажным
воздухом, а смесь сухого воздуха с насыщенным водяным паром — насыщенным
влажным воздухом. При этом условие насыщения рассматривается как
равновесное состояние между водяным паром во влажном воздухе и водой в жидкой
или твердой фазах при одинаковой температуре на плоской
поверхности раздела.

Таблица
6

Температура t н , °С	Удельная теплота парообразования r , кДж/кг	Погрешность, %
По данным [ 4 ]	По формуле 3.6
0	2501	2501	0
1	2498,6	2498,6	0
2	2496,3	2496,3	0
3	2493,9	2493,9	0
5	2489,2	2489,2	0
10	2477,4	2477,4	0
15	2465,7	2465,6	0,004
20	2453,8	2453,8	0
25	2442,0	2442,0	0
30	2430,2	2430,2	0
35	2418,4	2418,4	0
40	2406,5	2406,6	0,004
45	2394,5	2394,8	0,013
50	2382,5	2383,0	0,021
55	2370,5	2371,2	0,03
60	2358,4	2359,4	0,06

Количество
водяного пара во влажном воздухе изменяется от нуля (сухой воздух) до некоторого
максимального значения, которое зависит от температуры и барометрического
давления, и в процессах кондиционирования обычно не превышает 3 … 4 %.

Поэтому
с достаточной для технических расчетов точностью влажный воздух можно считать
идеальным газом, который подчиняется всем законам смеси идеальных газов, хотя в
ряде случаев необходимо учитывать реальные свойства водяного пара.

Термодинамические
свойства сухого воздуха и водяного пара различны, поэтому свойства влажного
воздуха зависят от его количественного состава.

В
технике вентиляции и кондиционирования свойства влажного воздуха
характеризуются следующими основными параметрами: температура по сухому
термометру t ,
влагосодержание d ,
относительная влажность φ, плотность
ρ ,
температура по мокрому термометру t _м , температура
точки росы t _р ,
барометрическое давление P _б , удельная
теплоемкость с и удельная энтальпия J (здесь и далее используются обозначения, принятые в
кондиционировании воздуха).

Согласно
закону Дальтона, барометрическое давление влажного воздуха равно сумме
парциальных давлений сухого воздуха и водяного пара

P _б
= P_c + P _п .                                                            ( 4.1)

Величины
P _б ,
P _с
и P _п
измеряют в Па или кПа.

Температура
и барометрическое давление атмосферного воздуха зависят от высоты над уровнем
моря, географического расположения и погодных условий. На уровне моря в
качестве стандартных приняты [ 3]: температура 15 °С и барометрическое
давление 101,325 кПа. Значения температуры и барометрического давления для
стандартной атмосферы на высоте от -500 до 20000 м можно вычислить по формулам
[ 3]:

P _б
= 101,325 · (1 — 2,25577 · 10^-5 · Z)^5,2559;                                     ( 4.2)

t = 15 — 0,0065 ·
Z,                                                        ( 4.3)

где Z — высота над уровнем моря, м;

Р_б
— барометрическое давление, кПа;

t — температура воздуха, °С.

Парциальные
давления сухого воздуха и водяного пара, входящих в состав влажного воздуха,
можно определить в Па по уравнению Клапейрона:

P _с =                                                         ( 4.4)

P _п =
                                                         ( 4.5)

где M _с — масса сухой
части влажного воздуха;

M _п — масса водяного пара во влажном
воздухе;

V — общий объем смеси;

Т
— абсолютная температура смеси, К.

При
тепловлажностной обработке и изменении свойств влажного воздуха количество его
сухой части остается неизменным, поэтому при рассмотрении тепловлажностного
состояния воздуха принято его показатели относить к 1 кг сухой части.

Масса
водяного пара во влажном воздухе, приходящаяся на 1 кг массы сухой его части,
называется влагосодержанием влажного воздуха

d = ,
                                                        ( 4.6)

Для
(1 + d )
кг влажного воздуха, т.е. для смеси, содержащей 1 кг сухого воздуха и d кг водяного пара, уравнения состояния
имеют вид:

P _с
· V = R _с
· T;                                                              ( 4.7)

P _п · V
=                                                        ( 4.8)

Разделив
первое уравнение на второе, и подставив значения R _с и R _п , получим

d = 622 = 622 ,                                             ( 4.9)

Из
уравнения ( 4.9)
можно получить зависимость

P _п =                                                             ( 4.10)

Как
видно, парциальное давление водяного пара в ненасыщенном влажном воздухе при
определенном барометрическом давлении однозначно определяется влагосодержанием
и не зависит от температуры.

Относительной
влажностью воздуха называется отношение парциального
давления водяного пара, содержащегося во влажном воздухе заданного состояния, к
парциальному давлению насыщенного водяного пара при той же температуре:

φ = %.                                                            ( 4.11 )

Давление
насыщенного водяного пара над поверхностью воды или льда Р_н
отличается от давления водяного пара в насыщенном влажном воздухе Р_п.н
при той же температуре. Это связано с тем, что в присутствии инертного газа,
которым является сухой воздух, равновесное давление водяного пара над свободной
поверхностью воды зависит не только от температуры, но и от общего давления
влажного воздуха. Поскольку на воду воздействует дополнительное давление сухого
воздуха, то должно увеличиться давление насыщенного водяного пара во влажном
воздухе. Однако удельный объем водяного пара значительно больше удельного
объема воды, и если давление жидкой фазы возрастает пропорционально увеличению
давления воздуха, то давление насыщенного водяного пара изменяется
незначительно.

В
общем случае давление насыщенного водяного пара в многокомпонентной системе
(например, в атмосферном воздухе) можно рассчитать по формуле [ 1]

Р_п.н = Р_н · χ,                                                                ( 4.12 )

где χ —
корректирующая функция, зависящая от состава сухой части парогазовой смеси, ее
общего давления, температуры и агрегатного состояния воды.

Значения
функции χ приведены в прил. 6 [ 1].

В
диапазоне температуры от -40 до +50 °С и давлении 100 кПа относительная
погрешность при определении давления насыщенного водяного пара в воздухе без
учета коэффициента χ носит систематический характер и не превышает 0,55 %.

Поэтому
при расчетах систем кондиционирования воздуха можно считать, что Р_п.н
= Р_н.

Удельная
энтальпия влажного воздуха обычно используется в виде уравнения ( 1.10),
поэтому в технике кондиционирования общепринятым является следующее
определение: удельная энтальпия влажного воздуха J — это
количество теплоты, содержащееся во влажном воздухе при заданных температуре и
давлении, отнесенное к 1 кг сухого воздуха.

Энтальпия
смеси газов равна сумме энтальпий компонентов, входящих в смесь. Следовательно,
удельная энтальпия влажного воздуха представляет сумму энтальпий сухого воздуха
и водяного пара.

J = J _с
+ J _п
· d,                                                           ( 4.13)

где J _с — удельная
энтальпия сухого воздуха, кДж/кг с.в.;

J _п — удельная
энтальпия водяного пара, кДж/кг п.

С
учетом зависимостей 2.3 и 3.5 формулы для расчета
энтальпии влажного воздуха имеют вид:

— для ненасыщенного воздуха

J = c _с · t + ( r + c _рп · t )                                           ( 4.14)

— для насыщенного воздуха

J _н = c _с · t _н + ( r + c _рп · t _н )                                          ( 4.15)

Для
диапазона температур от -50 до +50 °С в работе [ 2] предложена зависимость:

J = 1,006 ·
t + (2500,64 +
1,86 · t ) , кДж/кг с. в.                         ( 4.16)

Более точные результаты дает формула [ 3]:

J = 1,006 ·
t + (2501 +
1,805 ·
t ) , кДж/кг с.в.                           ( 4.17)

За
нулевую точку принята энтальпия сухого воздуха ( d = 0) при температуре 0 °С.

Уравнение
( 4.17)
можно записать в следующем виде:

J = (1,006 + 1,805d) · t + 2501d = c ·
t + 2501d,                              ( 4.18)

где c = 1,006 + 1,805 d , кДж/(К·кг с.в.) представляет собой
теплоемкость влажного воздуха, отнесенную к 1 кг сухой его части.

В
ненасыщенном влажном воздухе водяной пар находится в перегретом состоянии, т.е.
его температура выше температуры насыщения. Если влажный воздух охлаждать без
изменения давления, то количество содержащегося в нем водяного пара будет
оставаться неизменным, следовательно, процесс охлаждения будет идти при
постоянном влагосодержании и парциальном давлении пара. Такой процесс может
протекать до тех пор, пока температура воздуха и пара не понизится до
температуры насыщения, т.к. при дальнейшем охлаждении воздуха из него начнет
выпадать влага в виде капель или инея.

Температура,
соответствующая состоянию насыщения влажного воздуха при заданном значении
влагосодержания или парциального давления, называется температурой точки
росы. Температура точки росы является предельной температурой, до
которой можно охлаждать влажный воздух при постоянном влагосодержании без
выпадения конденсата.

Значения
температуры точки росы при известном парциальном давлении можно определить по
приложению 1
или, с достаточной для инженерных расчетов точностью, вычислить по формулам [ 7]:

при
температуре от 0 до -60 °С

t _р =                                            ( 4.19)

при
температуре от 0 до 87 °С

t _р =                                            ( 4.20)

где t _р — температура
точки росы, °С;

P _н — парциальное
давление насыщенного водяного пара, кПа.

Заметим,
что в интервале температур от 5 до 87 °С расчетные значения t _р отличаются от
табличных не более, чем на 0,02 °С, а в интервале от 0 до -40 °С не более, чем
на 0,03 °С.

Рассмотрим
замкнутую систему, в которой ненасыщенный влажный воздух контактирует с
открытой поверхностью воды.

Начальные
параметры воздуха: t ₁ ,
J ₁ ,
d ₁ ,
P _п1 ,
φ₁.

Начальная
температура воды в поддоне t _р1
< t_{w 1}
< t ₁ .

Система
теплоизолирована от окружающей среды и не имеет потерь или поступлений тепла
извне. Общее давление воздуха в системе не изменяется.

Т.к.
температура воздуха не равна температуре воды, а парциальное давление
насыщенного водяного пара над поверхностью воды выше, чем в ненасыщенном
воздухе, то между воздухом и водой будет идти процесс — тепло- и массообмена,
направленный в сторону более низкого потенциала, т.е. испарение воды и
охлаждение воздуха.

Процесс
продолжается до тех пор, пока не выйдет на стационарный режим.

На
испарение воды требуется тепло (скрытая теплота парообразования), которое
вначале поступает от воздуха и воды.

Однако
через некоторое время температура воды достигнет такого уровня, когда тепло,
передаваемое от воздуха к воде, уравновесится с теплом, затрачиваемым на
испарение воды, и ее температура будет оставаться постоянной, равной t _м .

Т.к.
система теплоизолирована от внешней среды, то дальше в процессе тепло- и
массообмена будет понижаться только температура воздуха при одновременном
увеличении его влагосодержания и относительной влажности.

Изменение
состояния влажного воздуха завершится, когда его температура станет равна
температуре воды и воздух станет насыщенным, т.е. t ₂ = t _н = t _м .

Процесс
насыщения воздуха, в котором отсутствует взаимодействие с окружающей средой, в
термодинамике называют процессом адиабатного насыщения.

В
результате такого процесса происходит следующее:

— влагосодержание влажного воздуха увеличивается от
начального d ₁ до конечного d _н , соответствующего насыщению при температуре t _м ;

— энтальпия воздуха возрастает от J ₁ до J _н , соответствующей насыщению при температуре t _м , за счет энтальпии испарившейся воды, J_w .

При
фиксированном значении барометрического давления значения J _н , d _н и J_w являются функцией
только температуры t _м ,
которую примут воздух и вода в результате адиабатного процесса. Эта температура
и является температурой мокрого термометра.

Температура
мокрого термометра — это температура,
которую принимает ненасыщенный влажный воздух с начальными параметрами J ₁ и d ₁ в результате
адиабатного тепло- и массообмена с водой в жидком или твердом состоянии,
имеющей постоянную температуру t_w
= t_м после достижения им насыщенного состояния, удовлетворяющего
равенству

J _н = J ₁ + ( d _н — d ₁ ) · c_w · t _м ,                                                 ( 4.21)

где с _w = 4,186 — удельная
теплоемкость воды, кДж/кг·°С.

Разность
J _н
— J ₁
обычно невелика, поэтому процесс адиабатного насыщения часто называют
изоэнтальпийным, хотя в действительности J _н = J ₁ только при t _м = 0.

Температуру
мокрого термометра при известных значениях d ₁ или J₁
и t ₁
можно определить по формулам:

J ₁ = 1,006 t _м + 2501 d _н + (4,186 d ₁ — 2,381 d _н ) · t _м , кДж/кг с.в.;                 ( 4.22)

d ₁ = , кг/кг с.в.                          ( 4.23)

В
уравнениях ( 4.22) и ( 4.23) по два неизвестных ( t _м и d _н ), однако
каждому значению t _м
при заданном барометрическом давлении соответствует только одно табличное
значение d _н ,
поэтому уравнения легко решаются методом последовательных приближений.

Для
упрощения расчетов в приложениях 2 и 3 приведены значения
влагосодержания насыщенного влажного воздуха при барометрическом давлении 99 и
101 кПа.

Плотность
влажного воздуха ρ_в в кг/м³ представляет
собой отношение массы влажного воздуха к объему:

ρ _в
=  =                                                   4.24

Значения
р_в вычисляют по формулам:

ρ _в = 3,483 ;                                                 ( 4.25)

ρ _в =                                              ( 4.26)

где Р_б —
барометрическое давление воздуха, кПа;

Р_п
— парциальное давление водяного пара, кПа;

d — влагосодержание влажного воздуха,
кг/кг с.в.;

Т
= t
+ 273,15 — абсолютная температура воздуха, К.

Удельный
объем влажного воздуха v _в
принято определять, относя объем влажного воздуха v _в
к массе сухого воздуха М_с

v _в =  = .                                                    ( 4.27)

Эта
величина отличается от удельного объема v ‘_в , отнесенного к общей массе влажного воздуха

v ‘_в =  = .                                               ( 4.28)

Приведенные
выше расчетные зависимости, а также таблица давления насыщенного водяного пара
над поверхностью чистой воды и льда (приложение 1) и таблицы значений
влагосодержания насыщенного влажного воздуха при барометрическом давлении 99 и 101
кПа (приложения 2 и 3) позволяют аналитически
определять требуемые параметры воздуха при двух заданных.

Порядок
вычислений рассмотрен в примерах 1.1 … 1.4.

Пример
1.1 .

Дано:
температура воздуха по сухому термометру t = 24 °С; относительная влажность φ
= 50 %; барометрическое давление Р_б = 99 кПа.

Определить:
энтальпию J ,
влагосодержание d ,
температуру точки росы t _р ,
температуру мокрого термометра t _м ,
парциальное давление водяного пара P _п и плотность влажного
воздуха ρ_в.

Решение.

1 . По прил. 1 находим
значение парциального давления насыщенного водяного пара при t = 24 °С:

P _н = 2,9851 кПа.

2 . По формуле 4.11 определяем
парциальное давление водяного пара:

Р_н =
φ · P _н
= 0,5 · 2,9851 = 1,4926 кПа.

3 . По формуле 4.20 вычисляем
значение температуры точки росы:

t _р =  = 12,946 °С

(по прил. 1 t _р = 12,947 °С).

4 . По формуле 4.9 вычисляем
значение влагосодержания:

d = 622
= 9,521 г/кг с.в.

5 . Определяем значение удельной энтальпии по формуле
4.17 :

J = 1,006 · 24 + (2501 + 1,805 · 24) = 48,368, кДж/кг
с.в.

6 . Значение температуры мокрого термометра
определяем методом последовательных приближений. Для ускорения вычислений
воспользуемся приближенным выражением:

t _м
≈  =                                  ( 4.29)

Задаемся
значениями t _м
= 18 °С и t _м
= 17 °С, по таблице прил. 2 находим значения d _н(18) = 13,2458 г/кг
с.в.; d _н(17)
= 12,4189 г/кг с.в.

Вычисляем:

t _м =  = 15,03 < 18 °С;

t _м =  = 17,065 > 17 °С;

Как
видно, значение t _м действительно
находится в интервале температур 17 … 18 °С, причем очень близко к 17 °С.

Задаемся
значением t _м = 17,01 °С; по прил. 2
находим значение d _н
= 12,427 г/кг с.в и проверяем равенство по формуле 4.22:

J ₁ ·
V = 1,006 · 17,01 + 2,501 ·
12,427 + (4,186
· 9,521
— 2,381 · 12,427) ·
 =
48,367 .

Следовательно,
действительно t_м = 17,01 °С.

7 . По формуле 4.25 вычисляем
плотность влажного воздуха:

ρ _в
= 3,483 — 1,317 = 1,154, кг/м³.

Пример
1.2 .

Дано:
температура воздуха по сухому термометру t = 33 °С; удельная энтальпия J = 60 кДж/кг с.в.; барометрическое
давление Р_б = 101 кПа.

Определить:
относительную влажность φ, влагосодержание d , температуру точки росы t _р , температуру
мокрого термометра t _м ,
парциальное давление водяного пара Р_п и плотность влажного воздуха
ρ_в.

Решение.

1 . Используя формулу 4.17 , определяем
значение d :

d =  =  = 10,467 г/кг с.в.

2 . По формуле 4.10 вычисляем
значение P _п :

P _п =  = 1,671 кПа.

3 . По прил. 1 находим
значение парциального давления насыщенного водяного пара при t = 33 °С:

P _н = 5,0343 кПа.

4 . По формуле 4.11 определяем
относительную влажность воздуха:

φ =  ≈
33 %.

5 . По прил. 1 находим
значение температуры точки росы при P _п = 1,671 кПа:

t_р = 14,7 °С.

6 . Методом последовательных приближений определяем
температуру мокрого термометра. Задаемся значениями t _м = 20 °С и t _м = 21 °С. По таблице прил. 3 находим
значения

d _н(20) = 14,7448 г/кг
с.в.; d _н(21)
= 15,7070 г/кг с.в.

t _м1 =  = 22,80 > 20 °С.

Вычисляем
по формуле 4.29:

t _м2 =  = 20,43 < 21 °С.

Значение
t _м находится в заданном интервале
температур ближе к 21 °С.

Задаемся
значением t _м = 20,84 °С, по прил. 3
находим значение d _н
= 15,5494 г/кг с.в. и проверяем равенство по формуле 4.22:

J ₁ = 1,006 · 20,84 + 2,501 · 15,5494 + (4,186 · 10,467 — 2,381 · 15,5494) ·  = 59,996
≈ 60 кДж/кг с.в.

7 . По формуле 4.25 определяем
плотность влажного воздуха:

ρ_в
= 3,483 — 1,317 = 1,142 кг/м³.

Пример
1.3 .

Дано:
температура мокрого термометра t _м
= 17 °С; относительная влажность φ = 20 %; барометрическое давление Р_б
= 99 кПа.

Определить:
удельную энтальпию J ;
влагосодержание d; температуру воздуха по сухому термометру t ; парциальное давление водяного пара P _п и температуру
точки росы t _р
влажного воздуха.

Решение.

Данная
задача является одной из наиболее сложных для расчета, т.к. нет аналитических
зависимостей, связывающих два заданных параметра.

1 . По прил. 2 находим
значение влагосодержания насыщенного воздуха при t _м = 17 °С:

d _н = 12,4189 г/кг с.в.

2 . Вычисляем значение энтальпии J _{н(17 °С)}

J _н = 1,006 · 17 + (2501 +
1,805 · 17) = 48,5427 кДж/кг с.в.

3 . Вычисляем значение энтальпии при t _м = 17 °С и d = 0 г/кг с.в.:

J _с = J _н —  = 47,6589 кДж/кг с.в.
1000.

4 . Значение энтальпии для искомой точки находится в
интервале от 47,6589 до 48,5427 кДж/кг с.в.; d — от 0 до 12,4189 г/кг с.в.

5 . Дальше задачу решаем методом последовательных
приближений. Задаемся значением:

J ₁ =  = 48,1 кДж/кг с.в.

Вычисляем
значение d ₁
по формуле, полученной из формулы 4.22:

d ₁ =  =  = 6,197
г/кг с.в.

По
формуле 4.10
вычисляем значение:

P _п =  = 0,9766 кПа.

По
формуле 4.11
определяем:

P _п.н. =  = 4,8830 кПа.

По
прил. 1
находим соответствующее значение температуры: t = 32,46 °С.

Вычисляем:

J ₁ = 1,006 ·
32,46 + (2501 + 1,805 · 32,46) = 48,52 > 48,1.

Заданное
значение J ₁
несколько меньше расчетного, поэтому фактические значения температуры t ₁ и
влагосодержания d ₁
должны быть немного ниже.

Дальнейшее
приближение удобнее выполнять, используя температуру сухого термометра.

Задаемся
значением: t₁ = 32,24 °С.

По
прил. 1
находим:

P _п.н = 4,8235 кПа.

Вычисляем:

P _п = 4,8235 · 0,2
= 0,9647 кПа;

d ₁ = 622 ·  = 6,1207 г/кг с.в.

J ‘₁ = 1,006 · 32,24 + (2501 +
1,805 · 32,24) = 48,097 кДж/кг с.в.

Определяем
значение J ₁
по формуле 4.22:

J ₁ = 1,006 · 17 + 2,501 · 12,4189 + (0,004186 · 6,1207 — 0,002381 · 12,4189) · 17 = 48,095 кДж/кг с.в.

Значения J ‘₁ и J ₁ практически
совпали, т.е. заданное значение t ₁
= 32,24 °С является правильным, и окончательно получаем:

J ₁ = 48,097 кДж/кг с.в.; d ₁ = 6,1207 г/кг с.в.; P _п = 0,9647 кПа; t _р = 6,45 °С.

Пример
1.4 .

Дано:
энтальпия внутреннего воздуха J
= 60 КДж/кг с.в. относительная влажность φ = 50 %; барометрическое
давление Р_б = 99 кПа.

Определить:
температуры t ,
t _р ,
t _м ;
влагосодержание d
и парциальное давление водяного пара P_п.

Решение:

Настоящая
задача не имеет прямого решения, поскольку в формулах для φ и J количество неизвестных больше, чем число
уравнений. Поэтому задача может быть решена только методом последовательных
приближений. Приведенная в примере методика позволяет решить задачу с
наименьшим объемом вычислений.

1 . Задаемся двумя произвольными значениями
влагосодержания. Чем ближе эти значения окажутся от действительной величины и
чем меньше будет разность между ними, тем скорее будет решена задача.

Принимаем:
d ₁
= 10; d ₂
= 13 г/кг с.в.

2 . По формулам 4.10 и 4.11 вычисляем
соответствующие значения парциального давления водяного пара:

P _п1 =  = 1,5665 кПа

P _п2 =  = 2,0268 кПа

P _н1 = 3,1330 кПа;
P_н2 = 4,0536 кПа.

3 . По прил. 1 находим
значения температуры сухого термометра:

t _н1 = 24,81 °С;

t _н2 = 29,19 °С.

4 . Вычисляем значения энтальпии:

J ₁ = 1,006 · 24,81 + (2501 + 1,805 · 24,81) = 50,4167 кДж/кг с.в.;

J ₂ = 1,006 · 29,19 + (2501 + 1,805 · 29,19) = 62,5631 кДж/кг с.в.

Как
видно, заданное значение энтальпии находится в интервале:

50 ,4167 < 60 < 62,5631.

5 . С помощью линейной интерполяции находим
приближенное значение влагосодержания:

d ‘ = 13 —  = 12,3669 г/кг с.в.

6 . С учетом нелинейной зависимости энтальпии от
влагосодержания принимаем: d
= 12,345 г/кг с.в. и повторяем вычисления по пунктам 2 ,
3 и 4 :

P _п =  = 1,9266 кПа;

P _{п .н} = 1,9266 · 2 = 3,8533 кПа;

t = 28,32 °С;

J = 1,006 · 28,32 + (2501 + 1,805 ·
28,32) = 59,996 кДж/кг с.в.

Значение
энтальпии практически равно заданному J = 60 кДж/кг с.в., т.е. значения d и t соответствуют искомым.

7 . По прил. 1 находим
значение температуры точки росы при P _п = 1,9266 кПа:

t _р = 16,9 °С.

8 . Значение t _м определяем методом
последовательных приближений так же, как в примерах 1.1 и 1.2 , поэтому
промежуточные расчеты не приводим.

Задаемся
t _м
= 20,57 °С; по прил. 2 находим d _н = 15,6031 г/кг
с.в.

Вычисляем:

J ₁ = 1,006 · 20,57 + 2501 · 15,6031 + (4,186 · 12,345 — 2,381 · 15,6031) = 60,016 ≈ 60 кДж/кг с.в.,

т.е.
t _м
= 20,57 °С.

5 .
J- d ДИАГРАММА ВЛАЖНОГО ВОЗДУХА

5.1 . ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ВЛАЖНОГО ВОЗДУХА С
ПОМОЩЬЮ J- d ДИАГРАММЫ

Используя
систему уравнений, включающую зависимости 4.9, 4.11,
4.17,
а также функциональную связь P _н
= f ( t ), Л.К. Рамзин построил J — d диаграмму влажного воздуха, которая
широко применяется в расчетах систем вентиляции и кондиционирования воздуха.
Эта диаграмма представляет собой графическую зависимость между основными параметрами
воздуха t ,
φ, J ,
d
и P _п
при определенном барометрическом давлении воздуха P _б .

Построение
J — d диаграммы подробно описано в работах [ 5, 6, 8].

Состояние
влажного воздуха характеризуется точкой, нанесенной на поле J — d диаграммы, ограниченном линией d = 0 и кривой φ = 100 %.

Положение
точки задается любыми двумя параметрами из пяти, указанных выше, а также температурами
точки росы t _р
и мокрого термометра t _м .
Исключение составляют сочетания d
— P _п
и d
— t _р ,
т.к. каждому значению d
соответствует только одно табличное значение P _п и t _р , и сочетание J — t _м .

Схема
определения параметров воздуха для заданной точки 1 приведена на рис. 1.

Пользуясь
J — d диаграммой в прил. 4 и схемой на рис. 1, решим конкретные примеры для
всех 17 возможных сочетаний заданных начальных параметров воздуха, конкретные
значения которых указаны в табл. 7.

Схемы
решений и полученные результаты показаны на рис. 2.1 … 2.17.
Известные параметры воздуха выделены на рисунках утолщенными линиями.

5.2 . УГЛОВОЙ КОЭФФИЦИЕНТ ЛУЧА ПРОЦЕССА НА J- d ДИАГРАММЕ

Возможность
быстрого графического определения параметров влажного воздуха является важным,
но не основным фактором при использов а нии J — d диаграммы.

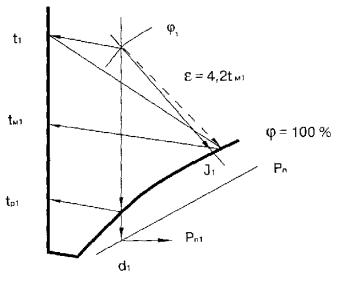
Рис. 1 . Схема
определения параметров влажного воздуха на J — d диаграмме

Таблица 7

Номер рисунка	Известные параметры воздуха
t1, °С	φ1, %	d 1 , г/кг с.в.	J 1 , кДж/кг с.в.	P п1 , кПа	t р1 , °С	t м1 , °С
2.1	30	50	—	—	—	—	—
2.2	32	—	—	—	—	12	—
2.3	24	—	10	—	—	—	—
2.4	28	—	—	—	2,0	—	—
2.5	26	—	—	38	—	—	—
2.6	33	—	—	—	—	—	20
2.7	—	25	—	—	1,6	—	—
2.8	—	50	—	60	—	—	—
2.9	—	—	8	64	—	—	—
2.10	—	—	—	—	—	10	22
2.11	—	30	15	—	—	—	—
2.12	—	—	—	—	2,2	—	24
2.13	—	25	—	—	—	14	—
2.14	—	55	—	—	—	—	20
2.15	—	—	9	—	—	—	23
2.16	—	—	—	62	1,2	—	—
2.17	—	—	—	60	—	8	—

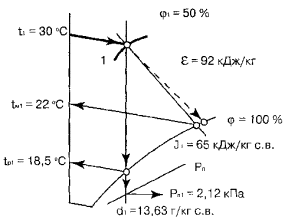
Рис.
2.1 .

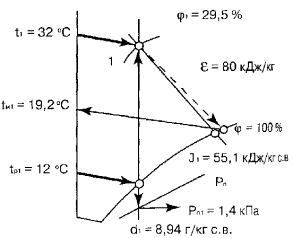
Рис.
2.2 .

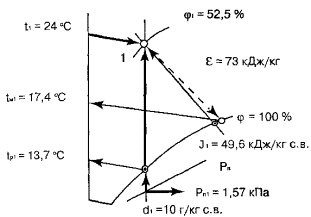
Рис.
2.3 .

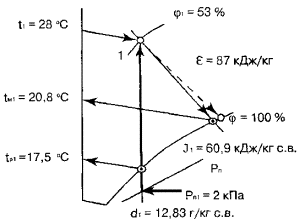
Рис.
2.4 .

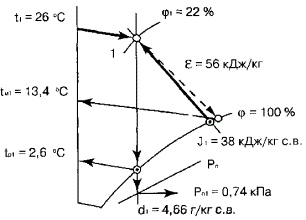
Рис.
2.5 .

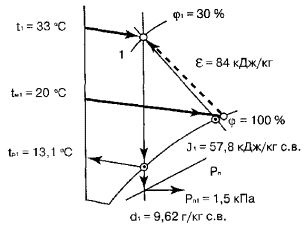
Рис.
2.6 .

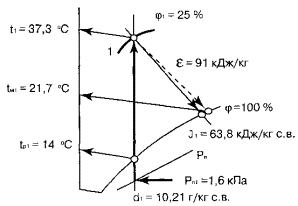
Рис.
2.7 .

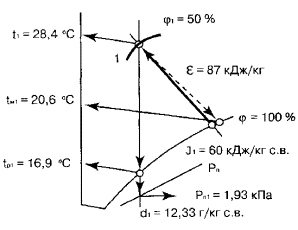
Рис.
2.8 .

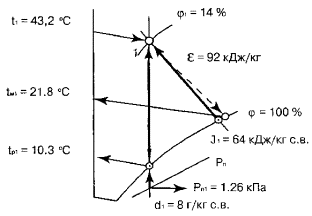
Рис.
2.9 .

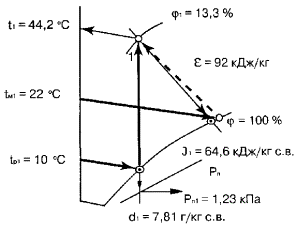
Рис.
2.10 .

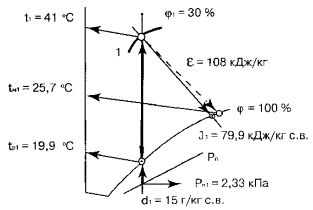
Рис.
2.11 .

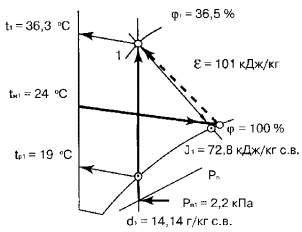
Рис.
2.12 .

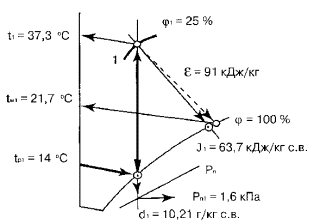
Рис.
2.13 .

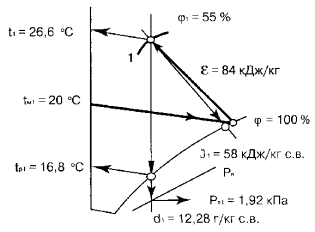
Рис.
2.14 .

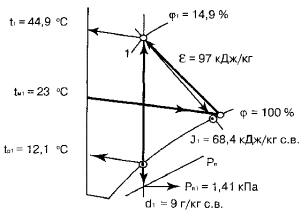
Рис.
2.15 .

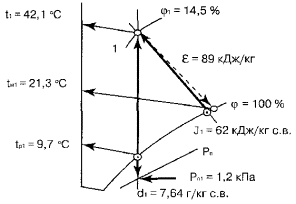
Рис.
2.16 .

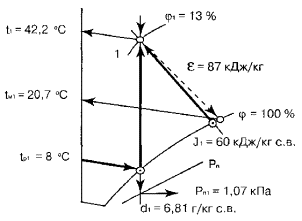
Рис. 2.17 .

В
результате нагревания, охлаждения, осушения или увлажнения влажного воздуха
изменяется его тепловлажностное состояние. Процессы изменения изображаются на J — d диаграмме прямыми линиями, которые
соединяют точки, характеризующие начальные и конечные состояния воздуха.

Эти
линии называются лучами процессов изменения состояния воздуха.
Направление луча процесса на J — d диаграмме определяется угловым
коэффициентом ε . Если
параметры начального состояния воздуха J ₁ и
d ₁ ,
а конечного — J ₂
и d ₂ ,
то угловой коэффициент выражается отношением Δ J / Δ d , т.е.:

ε
=   · 100.                                                        ( 5.1)

Величина
углового коэффициента измеряется в кДж/кг влаги.

Если
в уравнении ( 29) числитель и знаменатель
умножить на массовый расход обрабатываемого воздуха G , кг/ч, то получим:

ε
=  · 1000 = ,                                           ( 5.2)

где: Q _п — полное
количество тепла, переданное при изменении состояния воздуха, кДж/ч;

W — количество влаги, переданное в процессе
изменения состояния воздуха, кг/ч.

В
зависимости от соотношения Δ J
и Δ d
угловой коэффициент ε может изменять свой знак и величину от 0 до ±
∞.

На
рис. 3
показаны лучи характерных изменений состояния влажного воздуха и
соответствующие им значения углового коэффициента.

1 . Влажный воздух с начальными параметрами J ₁ и d ₁ нагревается при постоянном
влагосодержании до параметров точки 2, т.е. d ₂ = d ₁ , J ₂ > J ₁ . Угловой
коэффициент луча процесса равен:

ε =  · 1000 = +∞.

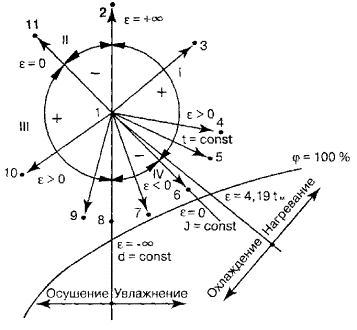
Рис. 3 . Угловой
коэффициент на J — d диаграмме

Такой
процесс осуществляется, например, в поверхностных воздухонагревателях, когда
температура и энтальпия воздуха возрастают, относительная влажность
уменьшается, но влагосодержание остается постоянным.

2 . Влажный воздух одновременно нагревается и
увлажняется и приобретает параметры точки 3. Угловой коэффициент луча процесса ε ₃ > 0. Такой
процесс протекает, когда приточный воздух ассимилирует тепло- и влаговыделения
в помещении.

3 . Влажный воздух увлажняется при постоянной
температуре до параметров точки 4, ε₄ > 0. Практически такой
процесс осуществляется при увлажнении приточного или внутреннего воздуха
насыщенным водяным паром.

4 . Влажный воздух увлажняется и нагревается с
повышением энтальпии до параметров точки 5. Так как энтальпия и влагосодержание
воздуха увеличиваются, то ε₅ > 0.
Обычно такой процесс происходит при непосредственном контакте воздуха с
отепленной водой в камерах орошения и в градирнях.

5 . Изменение состояния влажного воздуха происходит
при постоянной энтальпии J ₆ = J ₁ = const . Угловой коэффициент такого луча
процесса ε₆ = 0, т.к. Δ J = 0.

Процесс
изоэнтальпийного увлажнения воздуха циркуляционной водой широко используется в
системах кондиционирования. Он осуществляется в камерах орошения или в
аппаратах с орошаемой насадкой.

При
контакте ненасыщенного влажного воздуха с мелкими каплями или тонкой пленкой
воды без отвода или подвода тепла извне, вода в результате испарения увлажняет
и охлаждает воздух, приобретая температуру мокрого термометра.

Как
следует из уравнения 4.21, в общем случае угловой коэффициент луча
процесса при изоэнтальпийном увлажнении не равен нулю, т.к.

ε₆
=  · 1000 =
t _м
· с _w
= 4,186 · t _м ,

где с _w = 4,186 — удельная
теплоемкость воды, кДж/кг·°С.

Действительный
изоэнтальпийный процесс, при котором ε = 0 возможен только при t _м = 0.

6 . Влажный воздух увлажняется и охлаждается до точки
7. В этом случае угловой коэффициент ε₇ < 0, т.к. J ₇ — J ₁ < 0, а d ₇ — d ₁ > 0. Такой
процесс протекает в форсуночных камерах орошения при контакте воздуха с
охлажденной водой, имеющей температуру выше точки росы обрабатываемого воздуха.

7 . Влажный воздух охлаждается при постоянном
влагосодержании до параметров точки 8. Так как Δ d = d ₈ — d ₁ = 0, а J ₈ — J ₁ < 0, то ε ₈ = — ∞ . Процесс
охлаждения воздуха при d = const происходит в поверхностных
воздухоохладителях при температуре поверхности теплообмена выше температуры
точки росы воздуха, когда нет конденсации влаги.

8 . Влажный воздух охлаждается и осушается до
параметров точки 9. Выражение углового коэффициента в этом случае имеет вид:

ε₉ =  · 1000 =  · 1000 > 0.

Охлаждение
с осушкой происходит в камерах орошения или в поверхностных воздухоохладителях
при контакте влажного воздуха с жидкой или твердой поверхностью, имеющей
температуру ниже точки росы.

Отметим,
что процесс охлаждения с осушкой при непосредственном контакте воздуха и охлажденной
воды ограничен касательной, проведенной из точки 1 к кривой насыщения φ =
100 %.

9 . Глубокая осушка и охлаждение воздуха до
параметров точки 10 происходит при прямом контакте воздуха с охлажденным
абсорбентом, например, раствором хлористого лития в камерах орошения или в
аппаратах с орошаемой насадкой. Угловой коэффициент ε₁₀ > 0.

10 . Влажный воздух осушается, т.е. отдает влагу, при
постоянной энтальпии до параметров точки 11. Выражение углового коэффициента
имеет вид

ε₁₁
=  · 1000 = 0.

Такой
процесс можно осуществить с помощью растворов абсорбентов или твердых
адсорбентов. Заметим, что реальный процесс будет иметь угловой коэффициент
ε₁₁ = 4,186 t ₁₁ ,
где t ₁₁
— конечная температура воздуха по сухому термометру.

Из
рис. 3.
видно, что все возможные изменения состояния влажного воздуха располагаются на
поле J — d диаграммы в четырех секторах, границами
которых являются линии d
= const
и J
= const .
В секторе I
процессы происходят с увеличением энтальпии и влагосодержания, поэтому значения
ε > 0. В секторе II
происходит осушение воздуха с увеличением энтальпии и значения ε < 0. В
секторе III
процессы идут с уменьшением энтальпии и влагосодержания и ε > 0. В
секторе IV
происходят процессы увлажнения воздуха с понижением энтальпии, поэтому ε
< 0.

5.3 . ПОСТРОЕНИЕ ПРОЦЕССОВ ИЗМЕНЕНИЯ СОСТОЯНИЯ
ВЛАЖНОГО ВОЗДУХА НА J- d ДИАГРАММЕ

5.3.1 . Нагревание и охлаждение влажного воздуха в поверхностных
теплообменниках

Нагревание
влажного воздуха при его контакте с сухой поверхностью, имеющей более высокую
температуру, происходит при постоянном влагосодержании.

Если
известно начальное состояние воздуха (точка 1), то новое его состояние после
нагревания на J — d диаграмме определится как точка
пересечения линии d ₁
= d ₂
= const
и линии изотермы t ₂
(рис. 4).
Для точки 2, так же как и для точки 1, можно определить все необходимые
параметры и, в частности, начальное и конечное значения энтальпии J ₁ и J ₂ . Зная разность
J ₂
— J ₁
и количество сухого воздуха, которое надо нагреть в единицу времени, G _с , кг/ч, можно
определить количество теплоты, необходимое для нагревания воздуха Q _т :

Q _т = G _с ·
(J₂ — J ₁ ).

Напомним,
что G _с
— масса сухой части воздуха, равная

G _{с =}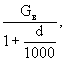

где G _в — масса
влажного воздуха.

При
охлаждении влажного воздуха в поверхностных воздухоохладителях до температуры t ₃ выше
температуры точки росы t _р ,
процесс изображается линией d ₃
= d ₁
= const
(рис. 5).

Количество
теплоты, отводимой от воздуха при охлаждении от состояния 1 до состояния 3,
определяется по формуле

Q _х = G _с · ( J ₁ — J ₃ ).

Это
количество теплоты составляет расчетную холодопроизводительность поверхностного
воздухоохладителя.

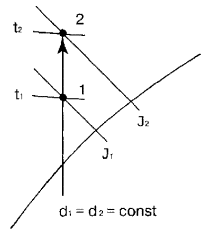
Рис.
4 .

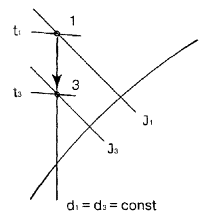
Рис. 5 .

Если
охлаждение влажного воздуха осуществляется до температуры, которая ниже
температуры точки росы, то на поверхности воздухоохладителя происходит
частичная конденсация водяного пара, находящегося во влажном воздухе.

В
работе [ 10]
рассмотрены два предельных случая такого процесса.

При
постоянной температуре охлаждающей стенки изменение состояния воздуха
изображается на J — d диаграмме прямой линией, соединяющей
точку начального состояния воздуха с точкой на линии насыщения при постоянной
температуре поверхности t _п
(рис. 6).

Однако
температура охлаждающей поверхности может считаться постоянной и близкой к
температуре холодильного агента t _а
только в воздухоохладителях непосредственного испарения с медными гладкими
трубками.

Второй
предельный случай возможен, если тепловое сопротивление на наружной оребренной
поверхности близко к нулю, т.е. температура поверхности t _п равна
температуре воздуха t _в .
Тогда в начале процесса температура t _п выше температуры
точки росы t _р ,
и охлаждение воздуха происходит без его осушения. Такой процесс изображается на
J — d диаграмме линией d = const до ее пересечения с линией насыщения.
После этого начинается конденсация влаги, и процесс охлаждения и осушения
воздуха идет по линии насыщения.

При
большой поверхности охлаждения температура выходящего воздуха будет
приближаться к температуре холодильного агента:

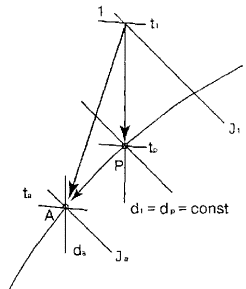
Рис. 6 .

Расчетную
холодопроизводительность поверхностного воздухоохладителя определяют по формуле

Q _х = G _с · ( J ₁ — J _а ).

Массу
сконденсированной влаги вычисляют по формуле

M _в = G _с · ( d ₁ — d _а ).

Рассмотренных
предельных случаев в действительности не бывает. Реальный процесс изменения
состояния воздуха в воздухоохладителе протекает по кривой, расположенной внутри
треугольника 1-Р-А, и относительная влажность охлажденного воздуха обычно
меньше 100 %.

5.3.2 . Изменение состояния ненасыщенного влажного
воздуха при контакте с водой

В
кондиционировании воздуха широко используются аппараты, в которых воздух
взаимодействует с пленкой или распыленными каплями воды, имеющими различную
температуру.

Обычно
предполагают, что непосредственно над поверхностью капель или пленки воды
находится тонкий слой воздуха, полностью насыщенный водяным паром и имеющий
температуру, равную температуре воды.

В
этом случае процесс тепло- и массообмена между влажным воздухом и водой можно рассматривать
как процесс смешения основного потока воздуха с насыщенным воздухом над
поверхностью воды.

Используя
указанное предположение, А.А. Гоголин [ 10] сформулировал правило,
называемое законом прямой линии: при взаимодействии влажного воздуха с водой,
имеющей постоянную температуру, изменение его состояния изображается на J — d диаграмме прямой, проходящей через точку
начального состояния воздуха и точку на линии насыщения (φ = 100 %) с
температурой, равной температуре воды.

При
большой поверхности и длительном времени контакта процесс продолжается до тех
пор, пока воздух не станет насыщенным и не примет температуру воды.

Вся
область возможных изменений параметров воздуха начального состояния, заданного
на J — d диаграмме точкой А, ограничивается
прямыми AB
и AC ,
проведенными из точки А касательно к кривой насыщения (рис. 7). При
этом в зависимости от температуры воды можно выделить следующие зоны.

Зона
1. Температура воды ниже температуры точки росы обрабатываемого воздуха. В
результате взаимодействия влажного воздуха с водой такой температуры уменьшаются:
энтальпия, температура и влагосодержание воздуха, т.е. происходят процессы
охлаждения и осушения воздуха.

Зона
2. Температура воды равна температуре точки росы. В этом процессе уменьшаются
энтальпия и температура воздуха при постоянном влагосодержании.

Зона
3. Температура воды выше температуры точки росы воздуха, но ниже его
температуры по мокрому термометру. При обработке воздуха увеличивается его
влагосодержание, но уменьшаются энтальпия и температура, следовательно, воздух
увлажняется и охлаждается.

Зона
4. Температура воды равна температуре воздуха по мокрому термометру. Такой
процесс называют адиабатным увлажнением воздуха циркулирующей водой. Это
единственный реальный процесс, при котором температура воды остается
постоянной.

Зона
5. Температура воды выше температуры воздуха по мокрому термометру, но ниже его
температуры по сухому термометру. При контакте с такой водой влагосодержание и
энтальпия воздуха возрастают, а его температура по сухому термометру снижается.
Однако, поскольку процесс увлажнения сопровождается ростом энтальпии, такой
процесс следует считать процессом увлажнения и нагревания.

Зона
6. Температура воды равна температуре воздуха по сухому термометру. В этом
случае происходит рост влагосодержания и энтальпии воздуха, а его температура
по сухому термометру остается постоянной.

Зона
7. Температура воды выше температуры воздуха по сухому термометру. Процесс
протекает так же, как в зоне 6, но одновременно происходит повышение
температуры воздуха.

В
реальных аппаратах расход воды и поверхность контакта имеют конечные значения,
и температура воды в процессе тепло- и массообмена не может быть постоянной
(кроме режима адиабатного увлажнения).

Поэтому
фактические процессы изменения состояния влажного воздуха при его обработке
водой изображаются кривыми линиями, направленными из точки начального состояния
воздуха к точке на кривой насыщения, соответствующей конечной температуре воды.
Причем относительная влажность воздуха, выходящего из контактного аппарата,
практически равна 85 … 95 %.

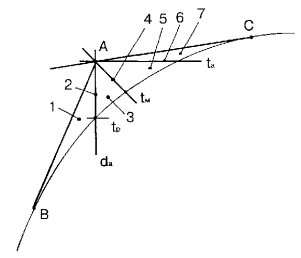
Рис.
7 . Возможные процессы взаимодействия влажного
воздуха и воды: 1 … 7 — зоны процессов

5.3.3 . Увлажнение влажного воздуха паром

Увлажнение
приточного или внутреннего воздуха насыщенным водяным паром достаточно широко
используется в современных установках кондиционирования.

Выражение
углового коэффициента луча процесса увлажнения воздуха паром можно получить,
используя уравнения балансов теплоты и влаги.

Примем,
что начальные параметры воздуха — J ₁ и d ₁ , а конечные
после увлажнения — J ₂
и d ₂ .
Количество сухой части увлажняемого воздуха — G _с и количество
насыщенного пара — G _п ,
его удельная энтальпия — J _п .

Уравнения
балансов теплоты и влаги имеют вид:

G _с · J ₁ + G _п · J _п = G _с · J ₂ ;

G _с ·  + G _п = G _с ·

Разделив
первое уравнение на второе, и произведя сокращения, получим выражение для
углового коэффициента:

ε =  · 1000 =
J _п .

Построение
процесса на J — d диаграмме показано на рис. 8.
Исходными данными являются начальное d ₁ , и конечное d ₂ ,
влагосодержание обрабатываемого воздуха, его конечная φ₂
относительная влажность и удельная энтальпия подаваемого пара J _п .

При
отсутствии технологических данных с достаточной точностью можно принять J _п ≈ 2680
кДж/кг.

Построение
процесса начинают с нанесения на J — d диаграмме точки 2, характеризующей
требуемые параметры приточного или внутреннего воздуха. Через точку 2 проводят
луч процесса с угловым коэффициентом ε = J _п до пересечения
с линией d ₁
= const .
Полученная точка 1 характеризует параметры воздуха до его увлажнения.

Количество
пара, требуемое для увлажнения воздуха, равно:

G _п = , кг/ч.

Отметим,
что процесс увлажнения паром протекает с небольшим повышением температуры
воздуха.

Например,
если d ₁
= 0,4 г/кг с.в. и t
= 20 °С, то после увлажнения до d ₁
= 6,4 г/кг с.в. температура воздуха t ₂ = 20,9 °С.

5.3.4 . Осушение воздуха адсорбентами

При
необходимости глубокого осушения и одновременного нагревания влажного воздуха в
технике кондиционирования применяют твердые поглотители влаги (адсорбенты),
которые позволяют получить практически сухой воздух. Такими поглотителями могут
быть активированный уголь, силикагель, алюмогель и др.

Рассмотрим
построение процесса адсорбции на J — d диаграмме. Для вывода выражения углового
коэффициента луча процесса адсорбции запишем уравнения баланса теплоты и влаги:

G _с · J ₂ = G _с · J ₁ — G _п · c _в · t ₂ — q · G _п + 420 G _п ;

G _с ·  = G _с ·  — G _п ,

где G _п — количество водяного
пара, кг, сконденсировавшегося в адсорбере;

c _в — удельная
теплоемкость воды;

q — расход теплоты на нагревание
адсорбента (принимается 420 кДж/кг адсорбированной влаги);

420 — удельная теплота смачивания,
кДж/кг адсорбированной влаги;

J ₁ , d ₁ , t ₁ — начальные
параметры воздуха;

J ₂ , d ₂ , t ₂ — конечные параметры воздуха. Разделив первое
уравнение на второе, после преобразований получим

ε = 1000
=  = с_в · t ₂ + q —
420 ≈ c _в · t ₂ = 4,19 t ₂ .

Таким
образом, угловой коэффициент луча процесса очень близок к изоэнтальпе J ₁ = const , т.е. осушение воздуха адсорбентом
представляет собой практически адиабатный процесс, направленный в сторону,
противоположную процессу адиабатного увлажнения воздуха водой.

В
процессе осушения температура воздуха значительно возрастает и, в зависимости
от начального состояния, может достигать 40 … 50 °С и больше.

С
достаточной для практических расчетов точностью конечную температуру воздуха t ₂ можно
определить по формуле

t₂ = t₁ + ,

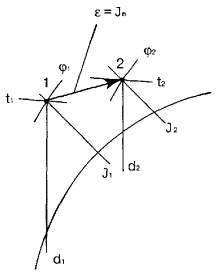
Рис. 8 .

где r — удельная теплота парообразования,
вычисляемая по формуле ( 3.6) при температуре воздуха t ₁ ;

c _вл = 1,006 +
1,805 d ₁ ,
кДж/(кг·К) — удельная теплоемкость влажного воздуха.

Построение
процесса на J — d диаграмме показано на рис. 9.

На
J — d диаграмме наносят точку 1,
характеризующую начальное состояние влажного воздуха d ₁ и t ₁ .

Зная
требуемое значение влагосодержания d ₂ в точке 2, вычисляют
конечную температуру воздуха t ₂
и угловой коэффициент луча процесса ε = 4,19 t ₂ .

Через
точку 1 проводят луч процесса до пересечения с линией d ₂ — const и получают точку 2, параметры которой
характеризуют конечное состояние воздуха J ₂ , d ₂ , t ₂ .

Если
полученное значение t ₂
значительно отклоняется от расчетного, то построение процесса можно повторить,
изменив исходное значение t ₂ .

Количество
влаги, отводимой от воздуха в адсорбере, кг/ч, определяют по формуле

G _п =

Минимальное
значение d ₂
может быть 0,03 г/кг с.в.

5.3.5 . Осушение воздуха абсорбентами

Для
осушения влажного воздуха с понижением энтальпии применяют жидкие поглотители
влаги — абсорбенты.

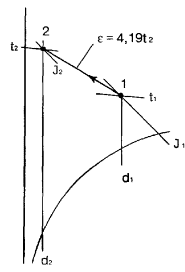
Рис. 9 .

Наибольшее
применение в системах кондиционирования воздуха получили водные растворы солей
хлористого кальция CaCl ₂
+ 6 H ₂ O и хлористого лития LiCl .

Особенность
указанных растворов заключается в том, что при равных температурах давление
насыщенного водяного пара в пограничном слое над поверхностью раствора ниже
давления насыщенного водяного пара над поверхностью воды.

Применение
жидких сорбентов позволяет осуществлять непрерывную регенерацию раствора и
получать осушенный воздух относительно низкой температуры, т.к. в контур ре циркуляции
раствора кроме осушителя (контактного аппарата) могут быть включены кипятильник
(для восстановления концентрации раствора) и охладитель (для охлаждения
раствора перед подачей его в воздухоосушитель).

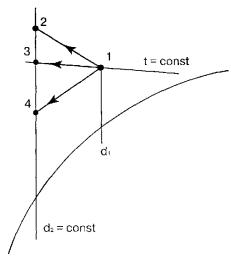
Рис. 10 .

Регулируя
степень охлаждения жидкого сорбента, можно осушать воздух с повышением
температуры (луч 1-2 рис. 10), изотермически (луч 1-3) и с понижением
температуры (луч 1-4).

Изотермическое
осушение влажного воздуха можно произвести при одинаковых начальных
температурах воздуха и орошающего раствора. Причем расход последнего должен
быть таким, чтобы теплота конденсации водяного пара и теплота разбавления
незначительно повышали температуру раствора.

Для
осушения воздуха с повышением температуры раствор должен иметь более высокую
температуру, чем обрабатываемый воздух, однако при этом упругость водяного пара
над поверхностью раствора должна быть меньше упругости водяного пара в
осушаемом воздухе.

Для
осушения воздуха с одновременным понижением его температуры необходимо, чтобы
температура раствора была ниже, чем при изотермическом процессе.

Заметим,
что абсорбенты осушают воздух не так глубоко, как твердые поглотители,
например, конечное влагосодержание воздуха при применении раствора хлористого
лития не менее 1 г/кг с.в.

Рис. 11 .

5.3.6 . Процессы смешения различных масс воздуха с разными
параметрами

В
системах кондиционирования очень часто осуществляется смешение двух потоков
воздуха с различными начальными параметрами. Предположим, что смешиваются G ₁ (кг) влажного
воздуха с параметрами J ₁ ,
d ₁ ,
и G ₂
(кг) влажного воздуха с параметрами J ₂ , d ₂ (рис. 11).

В
общем случае, количество сухого воздуха G _с (кг),
содержащегося в G
(кг) влажного воздуха может быть выражено отношением:

G _с = , кг.

Тогда,
баланс влаги, участвующей в процессе смешения, имеет вид:

G _с1 · d ₁ + G _с2 · d ₂ = ( G _с1 + G _с2 ) · d ₃ ,

где d ₃ —
влагосодержание смеси.

Аналогично
можно записать уравнение для теплового баланса:

G _с1 · J ₁ + G _с2 · J ₂ = ( G _с1 + G _с2 ) · J ₃ ,

где J ₃ — энтальпия
смеси.

Представим
два последних выражения в виде:

G _с1 ( J ₁ — J ₃ ) = G _с2 ( J ₃ — J ₂ );

G _с1 ( d ₁ — d ₃ ) = G _с2 ( d ₃ — d ₂ ).

Разделив
первое уравнение на второе, получим:

 =

В
координатной сетке J
и d
это выражение представляет собой уравнение прямой, проходящей через заданные
точки 1 и 2. Величины J ₃
и d ₃
— координаты точки смеси 3, лежащей на прямой 1-2.

Положение
точки 3 на прямой 1-2 определяют путем деления отрезка 1-2 на части в
отношении:

 и .

Из
уравнений материального и теплового баланса можно получить зависимость:

 =  =

Аналитически
значения влагосодержания и энтальпии смеси следует определять по формулам:

d ₃ =

J ₃ =

В
практике кондиционирования воздуха значения G и G_с отличаются обычно на 1
… 2 %, поэтому некоторые авторы предлагают вести построения и расчеты при
смешении влажного воздуха, используя значение G , однако в некоторых случаях это может
привести к значительной погрешности.

При
построении процесса смешения для холодного периода года точка смеси 6′ (рис. 11)
может оказаться ниже кривой φ = 100 %, т.е. процесс смешения
сопровождается конденсацией части содержащегося в смеси водяного пара.

Вместе
со сконденсировавшимся водяным паром из воздуха уйдет часть тепла, равная Q _кон. :

Q _кон. =  · t _м · c _ж ,

где Δ d = d ‘₆ — d ₆ — количество
выделившегося конденсата, г/кг с.в.;

t _м — температура конденсата, равная температуре мокрого термометра, °С;

c _ж — теплоемкость
конденсата, кДж/кг·°С.

Из
теплового баланса следует, что энтальпия воздуха после выпадения конденсата
уменьшается, т.е.:

J₆ = J ‘ ₆ —   · t _м · c _ж .

Учитывая,
что величина Δ d
обычно очень мала, в практических расчетах последним слагаемым можно пренебречь
и считать, что J ₆
= J ‘₆.

5.3.7 . Изменение состояния воздуха в помещениях с
тепло- и влаговыделениями

В
общем случае при проектировании систем вентиляции и кондиционирования воздуха
необходимо учитывать поступление в помещение теплоты, влаги, пыли и газовых
вредностей.

Однако
при выделении пыли и газов тепловлажностное состояние воздуха обычно не
изменяется. Поэтому рассмотрим процесс изменения состояния воздуха в помещении
с тепло- и влаговыделениями.

Источниками
выделения явной и скрытой теплоты являются: технологическое оборудование, люди,
ограждающие конструкции, искусственное освещение, солнечная радиация, система
отопления и теплота от поступающего в помещение пара и испаряющейся воды. Часть
теплоты может теряться на нагревание поступающих в помещение материалов и
продуктов и через ограждающие конструкции.

Одновременно
в помещении выделяется водяной пар от технологического оборудования и от людей,
а также влага со смоченной поверхности с температурой, близкой к температуре
мокрого термометра внутреннего воздуха.

Не
останавливаясь на методах расчета отдельных составных частей теплового и
влажностного балансов, запишем в общем виде уравнения для определения
избыточных тепло- и влаговыделений:

Q _изб = Q _я + Q _п + Q _л — Q _пот ,

где Q _я — суммарное
количество явной теплоты;

Q _п — суммарное
количество полной теплоты;

Q _л — полные
тепловыделения от людей;

Q _пот — теплопотери
помещения.

Величина
Q _п
определяется по формуле:

Q _п = G _п · i _п ,

где G _п — количество
выделяющегося от оборудования водяного пара;

i _п — удельная энтальпия
водяного пара.

Количество
избыточной влаги в помещении находится из уравнения:

G _в = G _п + G _п.л + G _с.п ,

где G _п.л —
влаговыделения от людей;

G _с.п — количество
влаги, испаряющейся со смоченной поверхности.

Пусть
t ₂ ,
J ₂
и d ₂
— нормируемые параметры воздуха внутри помещения.

Для
ассимиляции (поглощения) выделяющейся в помещении теплоты и влаги в помещение
необходимо подавать приточный воздух в количестве G _с , имеющий более
низкие значения параметров J ₁ ,
d ₁ ,
t ₁ .

Запишем
уравнения баланса по теплу и по влаге:

G _с · J ₁ + Q _изб = G _с · J ₂ ;

G _с ·  + G _в = G _с ·

Разделив
первое выражение на второе, после соответствующих преобразований получим
угловой коэффициент луча процесса ε, характеризующий изменение состояния
влажного воздуха в помещении с тепло- и влаговыделениями:

ε =  · 1000 =  = .

Получив
значение ε из теплового и влажностного балансов помещения, можно построить
процесс на J — d диаграмме.

На
J — d диаграмме наносим точку 2,
характеризующую параметры внутреннего воздуха, которые определяются по
санитарным или технологическим требованиям и задаются обычно значениями t ₂ и φ₂,
и определяем значения J ₂
и d ₂ .

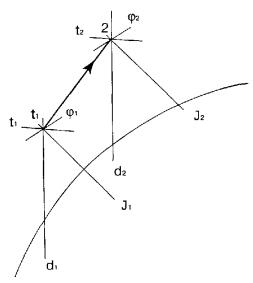
Рис. 12 .

Через
точку 2 проводим луч процесса с известным угловым коэффициентом ε до
пересечения с линией какого-либо заданного параметра приточного воздуха J ₁ , d ₁ , t ₁ или φ₁
и получаем точку 1, для которой определяем все указанные выше параметры (рис. 12).

Ассимилирующая
способность приточного воздуха по теплоте и по влаге определяется
соответственно разностью энтальпий J ₂ — J ₁ и
влагосодержаний d ₂
— d ₁ .

Требуемое
количество приточного воздуха можно найти по формулам:

G _с = ;

G _с =  · 1000.

ЛИТЕРАТУРА

1 . Таблицы психрометрические. ГОСТ 8.524-85. — М., 1985.

2 . Бурцев С.И., Цветков Ю.Н. Влажный воздух. Состав
и свойства: Учебное пособие. — СПб.; СПбГАХПТ, 1998.

3 . ASHRAE HANDBOOK. FUNDAMETALS. ASHRAE , Atlanta , 2001.

4 . Ривкин С.Л., Александров А.А. Теплофизические
свойства воды и водяного пара. — М.: Энергия, 1980.

5 . Нестеренко А.В. Основы термодинамических расчетов
вентиляции и кондиционирования воздуха. — М.: «Высшая школа», 1971.

6 . Богословский В.Н., Кокорин О.Я., Петров Л.В.
Кондиционирование воздуха и холодоснабжение. — М.: Стройиздат, 1985.

7 . Тарабанов М.Г. J — d диаграмма
влажного воздуха. Методические указания. — Волгоград, 2003.

8 . Стефанов Е.В. Вентиляция и кондиционирование
воздуха. — Л., ВВИТКУ, 1970.

9 . Воронец Д., Косич Д. Влажный воздух. — М.:
Энергоатомиздат, 1984.

10 . Гоголин А.А. Кондиционирование воздуха в мясной
промышленности. — М., «Пищевая промышленность», 1966.

6 . УСЛОВНЫЕ ОБОЗНАЧЕНИЯ

с	удельная массовая теплоемкость	Дж/(кг·К)
с’	удельная объемная теплоемкость	Дж/(м3·К)
c µ	удельная мольная теплоемкость	кДж/(кмоль·К)
с v	изохорная теплоемкость	кДж/(м3·К)
с p	изобарная теплоемкость	кДж/(кг·К)
cp .с	удельная массовая теплоемкость сухого воздуха	кДж/(кг·К)
cv .с	удельная объемная теплоемкость сухого воздуха	кДж/(м3·К)
ср.в	удельная массовая теплоемкость воды	кДж/(кг·К)
с p .п	удельная теплоемкость насыщенного водяного пара при постоянном давлении	кДж/(кг · К)
ср.л	удельная массовая теплоемкость льда	кДж/(кг · К)
d	влагосодержание влажного воздуха	г/кг с.в
F н	нормальная составляющая силы	Н
gi	массовая доля
J	энтальпия	Дж
i	удельная энтальпия	Дж/кг
i с	удельная энтальпия сухого воздуха	кДж/кг
i п	удельная энтальпия сухого насыщенного водяного пара	кДж/кг
i в	энтальпия кипящей воды	кДж/кг
i п.п	удельная энтальпия перегретого водяного пара	кДж/кг
i н.п	удельная энтальпия насыщенного водяного пара	кДж/кг
M с	масса сухой части влажного воздуха
M п	масса водяного пара во влажном воздухе
m	масса вещества	кг
m см	масса смеси	кг
mi	масса компонента смеси	кг
P	давление	Н/м2 (Па)
P см	общее давление смеси идеальных газов	Па
Pi	парциальное давление отдельного газа	Па
P с	давление сухого воздуха	Па
P н	давление насыщенного водяного пара	Па
P б	барометрическое давление	Па
P п.н	давление насыщенного водяного пара	Па
R г	газовая постоянная	Дж/(кг · К)
R с	газовая постоянная для сухого воздуха	Дж/(кг · К)
R п	газовая постоянная водяного пара	Дж/(кг · К)
R	универсальная газовая постоянная	Дж/(кмоль · К)
r	удельная теплота парообразования	кДж/кг
r пл0	удельная теплота плавления льда	кДж/кг
r суб	удельная теплота сублимации льда	кДж/кг
ri	объемная доля
S	площадь поверхности, нормальной к действующей силе	м2
T	абсолютная температура	К
Тс	температура сухого воздуха	К
t н	температура насыщения °С
t п	температура перегретого пара	° C
u	удельная внутренняя энергия газа	Дж/кг
V	объем	м3
Vm	объем, занимаемый одним молем газа
Vi	парциальный объем компонента	м3
V см	объем смеси	м3
v	удельный объем	м3 /кг
v 0	удельный объем газа при нормальных условиях	м3 /кг
v в	удельный объем воды	м3 /кг
v ‘ в	удельный объем воды в состоянии насыщения	м3 /кг
v п	удельный объем водяного пара	м3 /кг
φ	относительная влажность воздуха
ρ	плотность	кг/м3
ρ с	плотность сухого воздуха	кг/м3
ρ в	плотность воды	кг/м3
ρ п	плотность водяного пара	кг/м3
µ	молекулярный вес	кмоль
µсм	средняя молекулярная масса
µс	мольная масса сухого воздуха	кг/моль
µ п	мольная масса водяного пара
χ	корректирующая функция

УСЛОВНЫЕ
ОБОЗНАЧЕНИЯ

в	вода		п.п	перегретый пар
г	газ	с	сухой воздух
л	лед	см	смесь
н	насыщение	суб	сублимация
н.п	насыщенный пар	i	порядковый номер компонента
0	нормальные условия	р	изохорный процесс
п	пар	v	изобарный процесс
пл	плавление

Приложение 1

Давление насыщенного водяного пара над
поверхностью льда ( t < 0) и чистой воды (t
> 0), кПа

Температура °С	Десятые доли,°С
0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
-40	0,01285	0,01270	0,01256	0,01242	0,01228	0,01214	0,01200	0,01186	0,01173	0,01160
-39	0,01438	0,01422	0,01406	0,01390	0,01375	0,01359	0,01344	0,01329	0,01314	0,01299
-38	0,01608	0,01590	0,01572	0,01555	0,01538	0,01520	0,01504	0,01487	0,01470	0,01454
-37	0,01796	0,01776	0,01757	0,01737	0,01718	0,01699	0,01681	0,01662	0,01644	0,01626
-36	0,02004	0,01983	0,01961	0,01940	0,01919	0,01898	0,01877	0,01856	0,01836	0,01816
-35	0,02235	0,02211	0,02187	0,02163	0,02140	0,02117	0,02094	0,02071	0,02049	0,02026
-34	0,02490	0,02463	0,02437	0,02411	0,02385	0,02359	0,02334	0,02309	0,02284	0,02259
-33	0,02771	0,02742	0,02713	0,02684	0,02656	0,02627	0,02599	0,02572	0,02544	0,02517
-32	0,03082	0,03050	0,03018	0,02986	0,02954	0,02923	0,02892	0,02861	0,02831	0,02801
-31	0,03424	0,03389	0,03353	0,03318	0,03284	0,03249	0,03215	0,03181	0,03148	0,03115
-30	0,03802	0,03762	0,03723	0,03685	0,03646	0,03608	0,03571	0,03534	0,03497	0,03461
-29	0,04217	0,04173	0,04130	0,04088	0,04046	0,04004	0,03963	0,03922	0,03881	0,03841
-28	0,04673	0,04625	0,04578	0,04532	0,04485	0,04439	0,04394	0,04349	0,04304	0,04260
-27	0,05174	0,05122	0,05070	0,05019	0,04968	0,04918	0,04868	0,04819	0,04770	0,04721
-26	0,05725	0,05668	0,05611	0,05554	0,05499	0,05443	0,05389	0,05334	0,05280	0,05227
-25	0,06329	0,06266	0,06204	0,06142	0,06081	0,06020	0,05960	0,05900	0,05841	0,05783
-24	0,06991	0,06922	0,06854	0,06786	0,06719	0,06652	0,06586	0,06521	0,06457	0,06392
-23	0,07716	0,07641	0,07566	0,07492	0,07418	0,07345	0,07273	0,07202	0,07131	0,07061
-22	0,08510	0,08427	0,08345	0,08264	0,08184	0,08104	0,08025	0,07947	0,07869	0,07792
-21	0,09378	0,09287	0,09198	0,09109	0,09021	0,08934	0,08848	0,08762	0,08677	0,08593
-20	0,10326	0,10227	0,10130	0,10033	0,09937	0,09841	0,09747	0,09653	0,09561	0,09469
-19	0,11362	0,11254	0,11147	0,11041	0,10937	0,10833	0,10729	0,10627	0,10526	0,10426
-18	0,12492	0,12375	0,12258	0,12143	0,12028	0,11915	0,11802	0,11691	0,11580	0,11470
-17	0,13725	0,13597	0,13470	0,13344	0,13219	0,13095	0,12972	0,12851	0,12730	0,12611
-16	0,15068	0,14928	0,14790	0,14653	0,14517	0,14382	0,14248	0,14116	0,13984	0,13854
-15	0,16530	0,16378	0,16228	0,16078	0,15930	0,15783	0,15638	0,15493	0,15350	0,15208
-14	0,18121	0,17956	0,17792	0,17630	0,17469	0,17309	0,17151	0,16993	0,16838	0,16683
-13	0,19852	0,19672	0,19494	0,19317	0,19142	0,18969	0,18796	0,18625	0,18456	0,18288
-12	0,21732	0,21537	0,21344	0,21152	0,20961	0,20773	0,20585	0,20400	0,20216	0,20033
-11	0,23774	0,23562	0,23352	0,23144	0,22937	0,22732	0,22529	0,22327	0,22127	0,21929
-10	0,25990	0,25760	0,25533	0,25306	0,25082	0,24860	0,24639	0,24420	0,24203	0,23988
-9	0,28394	0,28144	0,27897	0,27652	0,27409	0,27168	0,26928	0,26691	0,26456	0,26222
-8	0,30998	0,30728	0,30461	0,30195	0,29931	0,29670	0,29410	0,29153	0,28898	0,28645
-7	0,33819	0,33527	0,33237	0,32949	0,32664	0,32381	0,32100	0,31821	0,31545	0,31270
-6	0,36873	0,36557	0,36243	0,35932	0,35623	0,35316	0,35012	0,34710	0,34411	0,34114
-5	0,40176	0,39834	0,39495	0,39158	0,38824	0,38492	0,38163	0,37837	0,37513	0,37192
-4	0,43748	0,43378	0,43011	0,42647	0,42286	0,41927	0,41572	0,41219	0,40869	0,40521
-3	0,47606	0,47206	0,46810	0,46417	0,46027	0,45639	0,45255	0,44874	0,44496	0,44120
-2	0,51772	0,51341	0,50913	0,50488	0,50067	0,49649	0,49234	0,48822	0,48414	0,48008
-1	0,56267	0,55802	0,55341	0,54883	0,54428	0,53977	0,53529	0,53085	0,52644	0,52206
0	0,61115	0,60614	0,60116	0,59622	0,59132	0,58646	0,58163	0,57683	0,57208	0,56736
0	0,6112	0,6157	0,6202	0,6247	0,6292	0,6338	0,6384	0,6430	0,6477	0,6524
1	0,6571	0,6618	0,6666	0,6714	0,6763	0,6811	0,6860	0,6910	0,6959	0,7009
2	0,7060	0,7110	0,7161	0,7212	0,7264	0,7316	0,7368	0,7421	0,7474	0,7527
3	0,7580	0,7634	0,7688	0,7743	0,7798	0,7853	0,7909	0,7965	0,8021	0,8078
4	0,8135	0,8192	0,8250	0,8308	0,8366	0,8425	0,8484	0,8544	0,8604	0,8664
5	0,8725	0,8786	0,8847	0,8909	0,8971	0,9034	0,9097	0,9160	0,9224	0,9288
6	0,9352	0,9417	0,9483	0,9548	0,9614	0,9681	0,9748	0,9815	0,9883	0,9951
7	1,0020	1,0089	1,0158	1,0228	1,0298	1,0369	1,0440	1,0511	1,0583	1,0656
8	1,0728	1,0802	1,0875	1,0950	1,1024	1,1099	1,1175	1,1251	1,1327	1,1404
9	1,1481	1,1559	1,1637	1,1716	1,1795	1,1875	1,1955	1,2035	1,2116	1,2198
10	1,2280	1,2362	1,2445	1,2529	1,2613	1,2697	1,2782	1,2868	1,2954	1,3040
11	1,3127	1,3215	1,3303	1,3391	1,3481	1,3570	1,3660	1,3751	1,3842	1,3934
12	1,4026	1,4119	1,4212	1,4306	1,4400	1,4495	1,4591	1,4687	1,4783	1,4880
13	1,4978	1,5076	1,5175	1,5275	1,5375	1,5475	1,5576	1,5678	1,5780	1,5883
14	1,5987	1,6091	1,6195	1,6301	1,6407	1,6513	1,6620	1,6728	1,6836	1,6945
15	1,7054	1,7165	1,7275	1,7387	1,7499	1,7611	1,7725	1,7839	1,7953	1,8069
16	1,8184	1,8301	1,8418	1,8536	1,8654	1,8774	1,8893	1,9014	1,9135	1,9257
17	1,9379	1,9503	1,9627	1,9751	1,9876	2,0002	2,0129	2,0257	2,0385	2,0513
18	2,0643	2,0773	2,0904	2,1036	2,1168	2,1301	2,1435	2,1570	2,1705	2,1841
19	2,1978	2,2116	2,2254	2,2393	2,2533	2,2673	2,2815	2,2957	2,3100	2,3244
20	2,3388	2,3533	2,3679	2,3826	2,3974	2,4122	2,4272	2,4422	2,4572	2,4724
21	2,4877	2,5030	2,5184	2,5339	2,5495	2,5652	2,5809	2,5967	2,6127	2,6287
22	2,6448	2,6609	2,6772	2,6935	2,7100	2,7265	2,7431	2,7598	2,7766	2,7935
23	2,8104	2,8275	2,8446	2,8619	2,8792	2,8966	2,9141	2,9318	2,9495	2,9672
24	2,9851	3,0031	3,0212	3,0393	3,0576	3,0760	3,0944	3,1130	3,1316	3,1504
25	3,1692	3,1882	3,2072	3,2263	3,2456	3,2649	3,2844	3,3039	3,3235	3,3433
26	3,3631	3,3831	3,4031	3,4233	3,4435	3,4639	3,4844	3,5050	3,5256	3,5464
27	3,5673	3,5883	3,6094	3,6306	3,6520	3,6734	3,6949	3,7166	3,7383	3,7602
28	3,7822	3,8043	3,8265	3,8488	3,8713	3,8938	3,9165	3,9393	3,9622	3,9852
29	4,0083	4,0315	4,0549	4,0784	4,1020	4,1257	4,1495	4,1735	4,1975	4,2217
30	4,2460	4,2705	4,2950	4,3197	4,3445	4,3694	4,3945	4,4197	4,4450	4,4704
31	4,4959	4,5216	4,5474	4,5734	4,5994	4,6256	4,6519	4,6784	4,7050	4,7317
32	4,7585	4,7855	4,8126	4,8399	4,8672	4,8948	4,9224	4,9502	4,9781	5,0062
33	5,0343	5,0627	5,0911	5,1197	5,1485	5,1774	5,2064	5,2356	5,2649	5,2943
34	5,3239	5,3537	5,3835	5,4136	5,4437	5,4740	5,5045	5,5351	5,5659	5,5968
35	5,6278	5,6590	5,6904	5,7219	5,7535	5,7853	5,8173	5,8494	5,8817	5,9141
36	5,9466	5,9794	6,0122	6,0453	6,0785	6,1118	6,1453	6,1790	6,2128	6,2468
37	6,2810	6,3153	6,3498	6,3844	6,4192	6,4542	6,4893	6,5246	6,5601	6,5957
38	6,6315	6,6674	6,7036	6,7399	6,7763	6,8130	6,8498	6,8868	6,9239	6,9612
39	6,9987	7,0364	7,0743	7,1123	7,1505	7,1889	7,2274	7,2662	7,3051	7,3442
40	7,3835	7,4229	7,4626	7,5024	7,5424	7,5826	7,6229	7,6635	7,7042	7,7452
41	7,7863	7,8276	7,8691	7,9108	7,9527	7,9947	8,0370	8,0794	8,1221	8,1649
42	8,2080	8,2512	8,2946	8,3382	8,3821	8,4261	8,4703	8,5147	8,5593	8,6042
43	8,6492	8,6944	8,7398	8,7855	8,8313	8,8773	8,9236	8,9701	9,0167	9,0636
44	9,1107	9,1580	9,2055	9,2532	9,3011	9,3493	9,3976	9,4462	9,4950	9,5440
45	9,5932	9,6427	9,6923	9,7422	9,7923	9,8426	9,8932	9,9439	9,9949	10,0462
46	10,0976	10,1493	10,2012	10,2533	10,3056	10,3582	10,4110	10,4641	10,5174	10,5709
47	10,6246	10,6786	10,7328	10,7873	10,8419	10,8969	10,9520	11,0074	11,0631	11,1190
48	11,1751	11,2315	11,2881	11,3449	11,4020	11,4594	11,5170	11,5748	11,6329	11,6913
49	11,7499	11,8087	11,8678	11,9272	11,9868	12,0467	12,1068	12,1672	12,2278	12,2887
50	12,3499	12,4113	12,4730	12,5349	12,5971	12,6596	12,7223	12,7853	12,8486	12,9121
51	12,9759	13,0400	13,1043	13,1690	13,2338	13,2990	13,3645	13,4302	13,4962	13,5624
52	13,6290	13,6958	13,7629	13,8303	13,8980	13,9659	14,0342	14,1027	14,1715	14,2406
53	14,3100	14,3797	14,4496	14,5199	14,5904	14,6613	14,7324	14,8038	14,8755	14,9476
54	15,0199	15,0925	15,1654	15,2387	15,3122	15,3860	15,4601	15,5346	15,6093	15,6844
55	15,7597	15,8354	15,9113	15,9876	16,0642	16,1411	16,2184	16,2959	16,3738	16,4519
56	16,5304	16,6093	16,6884	16,7678	16,8476	16,9277	17,0082	17,0889	17,1700	17,2514
57	17,3331	17,4152	17,4976	17,5803	17,6634	17,7468	17,8305	17,9146	17,9990	18,0838
58	18,1689	18,2543	18,3401	18,4262	18,5126	18,5994	18,6866	18,7741	18,8619	18,9501
59	19,0387	19,1276	19,2168	19,3065	19,3964	19,4867	19,5774	19,6685	19,7599	19,8516
60	19,9438	20,0362	20,1291	20,2223	20,3159	20,4099	20,5042	20,5989	20,6940	20,7894

Приложение 2

Влагосодержание насыщенного влажного воздуха
при барометрическом давлении 99 кПа

Температура °С	Десятые доли, °С
0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
-40	0,0807	0,0798	0,0789	0,0780	0,0771	0,0763	0,0754	0,0746	0,0737	0,0729
-39	0,0903	0,0893	0,0883	0,0873	0,0864	0,0854	0,0844	0,0835	0,0826	0,0816
-38	0,1010	0,0999	0,0988	0,0977	0,0966	0,0955	0,0945	0,0934	0,0924	0,0914
-37	0,1129	0,1116	0,1104	0,1092	0,1080	0,1068	0,1056	0,1044	0,1033	0,1022
-36	0,1260	0,1246	0,1232	0,1219	0,1206	0,1192	0,1179	0,1166	0,1154	0,1141
-35	0,1405	0,1389	0,1374	0,1360	0,1345	0,1330	0,1316	0,1302	0,1287	0,1273
-34	0,1565	0,1548	0,1531	0,1515	0,1499	0,1483	0,1467	0,1451	0,1435	0,1420
-33	0,1742	0,1723	0,1705	0,1687	0,1569	0,1651	0,1634	0,1616	0,1599	0,1582
-32	0,1937	0,1917	0,1896	0,1876	0,1857	0,1837	0,1818	0,1798	0,1779	0,1760
-31	0,2152	0,2130	0,2108	0,2085	0,2064	0,2042	0,2021	0,1999	0,1978	0,1958
-30	0,2389	0,2365	0,2340	0,2316	0,2292	0,2268	0,2244	0,2221	0,2198	0,2175
-29	0,2650	0,2623	0,2596	0,2569	0,2543	0,2517	0,2491	0,2465	0,2440	0,2414
-28	0,2937	0,2907	0,2878	0,2848	0,2819	0,2790	0,2762	0,2734	0,2706	0,2678
-27	0,3253	0,3220	0,3187	0,3155	0,3123	0,3091	0,3060	0,3029	0,2998	0,2968
-26	0,3599	0,3563	0,3527	0,3492	0,3457	0,3422	0,3387	0,3353	0,3319	0,3286
-25	0,3979	0,3939	0,3900	0,3861	0,3823	0,3785	0,3747	0,3709	0,3672	0,3635
-24	0,4395	0,4352	0,4309	0,4266	0,4224	0,4182	0,4141	0,4100	0,4059	0,4019
-23	0,4852	0,4804	0,4757	0,4710	0,4664	0,4618	0,4573	0,4528	0,4483	0,4439
-22	0,5351	0,5299	0,5248	0,5196	0,5146	0,5096	0,5046	0,4997	0,4948	0,4900
-21	0,5897	0,5840	0,5784	0,5728	0,5673	0,5618	0,5564	0,5510	0,5456	0,5404
-20	0,6494	0,6432	0,6371	0,6310	0,6249	0,6189	0,6130	0,6071	0,6013	0,5955
-19	0,7147	0,7079	0,7012	0,6945	0,6879	0,6813	0,6748	0,6684	0,6620	0,6557
-18	0,7858	0,7784	0,7711	0,7638	0,7566	0,7495	0,7424	0,7354	0,7284	0,7215
-17	0,8635	0,8554	0,8474	0,8395	0,8316	0,8238	0,8161	0,8084	0,8008	0,7933
-16	0,9481	0,9393	0,9306	0,9220	0,9134	0,9049	0,8965	0,8881	0,8798	0,8716
-15	1,0403	1,0307	1,0212	1,0118	1,0025	0,9932	0,9840	0,9749	0,9659	0,9570
-14	1,1406	1,1302	1,1199	1,1096	1,0995	1,0894	1,0794	1,0695	1,0597	1,0499
-13	1,2498	1,2384	1,2272	1,2161	1,2050	1,1941	1,1832	1,1724	1,1617	1,1511
-12	1,3684	1,3561	1,3439	1,3318	1,3198	1,3079	1,2960	1,2843	1,2727	1,2612
-11	1,4973	1,4839	1,4707	1,4575	1,4445	1,4315	1,4187	1,4060	1,3933	1,3808
-10	1,6372	1,6227	1,6083	1,5940	1,5799	1,5658	1,5519	1,5381	1,5244	1,5108
-9	1,7891	1,7733	1,7577	1,7422	1,7268	1,7116	1,6965	1,6815	1,6666	1,6519
-8	1,9537	1,9366	1,9197	1,9029	1,8862	1,8697	1,8533	1,8371	1,8209	1,8049
-7	2,1321	2,1136	2,0953	2,0771	2,0590	2,0411	2,0233	2,0057	1,9882	1,9709
-6	2,3253	2,3053	2,2855	2,2657	2,2462	2,2268	2,2076	2,1885	2,1695	2,1507
-5	2,5345	2,5128	2,4913	2,4700	2,4488	2,4279	2,4070	2,3864	2,3659	2,3455
-4	2,7608	2,7373	2,7141	2,6910	2,6681	2,6454	2,6229	2,6005	2,5783	2,5563
-3	3,0054	2,9801	2,9550	2,9300	2,9053	2,8807	2,8564	2,8322	2,8082	2,7844
-2	3,2698	3,2425	3,2153	3,1884	3,1616	3,1351	3,1087	3,0826	3,0567	3,0310
-1	3,5554	3,5258	3,4965	3,4674	3,4385	3,4099	3,3814	3,3532	3,3252	3,2974
0	3,8636	3,8317	3,8001	3,7687	3,7375	3,7066	3,6759	3,6454	3,6152	3,5852
0	3,8640	3,8923	3,9209	3,9496	3,9785	4,0076	4,0368	4,0663	4,0960	4,1258
1	4,1559	4,1861	4,2165	4,2472	4,2780	4,3090	4,3403	4,3717	4,4033	4,4352
2	4,4672	4,4995	4,5320	4,5646	4,5975	4,6306	4,6639	4,6975	4,7312	4,7652
3	4,7993	4,8337	4,8683	4,9032	4,9382	4,9735	5,0090	5,0447	5,0807	5,1169
4	5,1533	5,1899	5,2268	5,2639	5,3013	5,3389	5,3767	5,4148	5,4531	5,4916
5	5,5304	5,5695	5,6087	5,6483	5,6881	5,7281	5,7684	5,8089	5,8497	5,8907
6	5,9320	5,9736	6,0154	6,0575	6,0998	6,1424	6,1853	6,2285	6,2719	6,3156
7	6,3595	6,4037	6,4482	6,4930	6,5381	6,5834	6,6290	6,6749	6,7211	6,7676
8	6,8143	6,8614	6,9087	6,9563	7,0042	7,0525	7,1010	7,1498	7,1989	7,2483
9	7,2980	7,3480	7,3984	7,4490	7,4999	7,5512	7,6027	7,6546	7,7068	7,7593
10	7,8122	7,8653	7,9188	7,9726	8,0268	8,0812	8,1360	8,1912	8,2466	8,3024
11	8,3586	8,4150	8,4718	8,5290	8,5865	8,6444	8,7026	8,7611	8,8200	8,8793
12	8,9389	8,9989	9,0592	9,1199	9,1809	9,2424	9,3042	9,3663	9,4289	9,4918
13	9,5551	9,6187	9,6828	9,7472	9,8120	9,8772	9,9428	10,0087	10,0751	10,1419
14	10,2090	10,2766	10,3445	10,4129	10,4817	10,5508	10,6204	10,6904	10,7608	10,8316
15	10,9029	10,9745	11,0466	11,1191	11,1920	11,2654	11,3392	11,4134	11,4881	11,5632
16	11,6387	11,7147	11,7911	11,8680	11,9453	12,0231	12,1014	12,1801	12,2592	12,3388
17	12,4189	12,4994	12,5805	12,6620	12,7439	12,8264	12,9093	12,9927	13,0766	13,1609
18	13,2458	13,3311	13,4170	13,5033	13,5902	13,6775	13,7654	13,8537	13,9426	14,0320
19	14,1219	14,2123	14,3032	14,3947	14,4867	14,5792	14,6723	14,7658	14,8600	14,9546
20	15,0498	15,1456	15,2419	15,3388	15,4362	15,5341	15,6327	15,7318	15,8314	15,9316
21	16,0324	16,1338	16,2358	16,3383	16,4414	16,5451	16,6494	16,7543	16,8598	16,9659
22	17,0726	17,1799	17,2878	17,3964	17,5055	17,6152	17,7256	17,8366	17,9483	18,0605
23	18,1734	18,2870	18,4012	18,5160	18,6315	18,7476	18,8644	18,9818	19,0999	19,2187
24	19,3381	19,4583	19,5790	19,7005	19,8227	19,9455	20,0690	20,1933	20,3182	20,4438
25	20,5701	20,6972	20,8249	20,9534	21,0826	21,2125	21,3431	21,4745	21,6066	21,7394
26	21,8730	22,0074	22,1424	22,2783	22,4149	22,5522	22,6904	22,8293	22,9689	23,1094
27	23,2506	23,3926	23,5354	23,6790	23,8234	23,9686	24,1147	24,2615	24,4091	24,5576
28	24,7069	24,8570	25,0079	25,1597	25,3123	25,4658	25,6201	25,7753	25,9313	26,0882
29	26,2460	26,4047	26,5642	26,7246	26,8859	27,0481	27,2111	27,3751	27,5400	27,7058
30	27,8725	28,0401	28,2087	28,3782	28,5486	28,7200	28,8923	29,0655	29,2398	29,4149
31	29,5911	29,7682	29,9463	30,1253	30,3054	30,4864	30,6684	30,8515	31,0355	31,2206
32	31,4066	31,5937	31,7819	31,9710	32,1612	32,3525	32,5447	32,7381	32,9325	33,1280
33	33,3245	33,5221	33,7209	33,9207	34,1216	34,3236	34,5267	34,7309	34,9362	35,1427
34	35,3503	35,5590	35,7689	35,9799	36,1921	36,4054	36,6199	36,8356	37,0525	37,2705
35	37,4898	37,7102	37,9319	38,1548	38,3789	38,6042	38,8307	39,0585	39,2875	39,5178
36	39,7494	39,9822	40,2163	40,4516	40,6883	40,9262	41,1655	41,4060	41,6479	41,8911
37	42,1356	42,3815	42,6287	42,8772	43,1272	43,3785	43,6311	43,8852	44,1406	44,3974
38	44,6556	44,9153	45,1764	45,4388	45,7028	45,9681	46,2350	46,5033	46,7730	47,0442
39	47,3169	47,5912	47,8669	48,1441	48,4228	48,7031	48,9849	49,2682	49,5531	49,8395
40	50,1275	50,4171	50,7083	51,0011	51,2955	51,5915	51,8891	52,1883	52,4892	52,7918
41	53,0960	53,4018	53,7094	54,0186	54,3295	54,6422	54,9565	55,2726	55,5904	55,9100
42	56,2313	56,5544	56,8793	57,2059	57,5344	57,8646	58,1967	58,5306	58,8663	59,2039
43	59,5433	59,8846	60,2278	60,5729	60,9199	61,2688	61,6196	61,9724	62,3271	62,6838
44	63,0424	63,4030	63,7656	64,1303	64,4969	64,8656	65,2363	65,6090	65,9838	66,3607
45	66,7397	67,1208	67,5040	67,8893	68,2768	68,6664	69,0582	69,4521	69,8483	70,2466
46	70,6472	71,0500	71,4550	71,8623	72,2719	72,6837	73,0979	73,5143	73,9331	74,3542
47	74,7777	75,2035	75,6318	76,0624	76,4954	76,9308	77,3687	77,8091	78,2519	78,6972
48	79,1450	79,5953	80,0482	80,5036	80,9616	81,4221	81,8852	82,3510	82,8194	83,2904
49	83,7641	84,2404	84,7195	85,2012	85,6857	86,1729	86,6629	87,1557	87,6513	88,1497
50	88,6509	89,1549	89,6619	90,1717	90,6844	91,2001	91,7186	92,2402	92,7647	93,2922
51	93,8228	94,3564	94,8930	95,4327	95,9755	96,5215	97,0705	97,6228	98,1782	98,7368
52	99,299	99,864	100,432	101,004	101,579	102,157	102,738	103,323	103,912	104,503
53	105,099	105,697	106,299	106,905	107,514	108,127	108,743	109,363	109,987	110,614
54	111,245	111,880	112,518	113,160	113,806	114,456	115,109	115,766	116,428	117,093
55	117,762	118,435	119,112	119,793	120,478	121,167	121,861	122,558	123,260	123,965
56	124,676	125,390	126,108	126,831	127,558	128,290	129,026	129,766	130,511	131,261
57	132,014	132,773	133,536	134,304	135,076	135,853	136,635	137,422	138,213	139,009
58	139,810	140,616	141,427	142,243	143,064	143,890	144,721	145,557	146,399	147,246
59	148,097	148,955	149,817	150,685	151,558	152,437	153,321	154,211	155,106	156,007
60	156,914	157,826	158,744	159,668	160,598	161,533	162,475	163,423	164,376	165,336

Приложение 3

Влагосодержание насыщенного влажного воздуха
при барометрическом давлении 101 кПа

Температура °С	Десятые доли, °С
0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
-40	0,0791	0,0782	0,0773	0,0765	0,0756	0,0748	0,0739	0,0731	0,0722	0,0714
-39	0,0886	0,0876	0,0866	0,0856	0,0847	0,0837	0,0828	0,0818	0,0809	0 , 0800
-38	0,0990	0,0979	0,0968	0,0958	0,0947	0,0937	0,0926	0,0916	0,0906	0,0896
-37	0,1106	0,1094	0,1082	0,1070	0,1058	0,1047	0,1035	0,1024	0,1012	0,1001
-36	0,1235	0,1221	0,1208	0,1195	0,1182	0,1169	0,1156	0,1143	0,1131	0,1118
-35	0,1377	0,1362	0,1347	0,1333	0,1318	0,1304	0,1290	0,1276	0,1262	0,1248
-34	0,1534	0,1517	0,1501	0,1485	0,1469	0,1453	0,1438	0,1422	0,1407	0,1392
-33	0,1707	0,1689	0,1671	0,1653	0,1636	0,1618	0,1601	0,1584	0,1567	0,1550
-32	0,1899	0,1879	0,1859	0,1839	0,1820	0,1801	0,1782	0,1763	0,1744	0,1726
-31	0,2110	0,2088	0,2066	0,2044	0,2023	0,2002	0,1981	0,1960	0,1939	0,1919
-30	0,2342	0,2318	0,2294	0,2270	0,2246	0,2223	0,2200	0,2177	0,2154	0,2132
-29	0,2598	0,2571	0,2545	0,2519	0,2493	0,2467	0,2441	0,2416	0,2391	0,2367
-28	0,2879	0,2850	0,2821	0,2792	0,2763	0,2735	0,2707	0,2679	0,2652	0,2625
-27	0,3188	0,3156	0,3124	0,3092	0,3061	0,3030	0,2999	0,2969	0,2939	0,2909
-26	0,3528	0,3492	0,3457	0,3423	0,3388	0,3354	0,3320	0,3287	0,3254	0,3221
-25	0 , 3900	0,3861	0,3823	0,3785	0,3747	0,3710	0,3673	0,3636	0,3599	0,3563
-24	0,4308	0,4266	0,4224	0,4182	0,4140	0,4099	0,4059	0,4019	0,3979	0,3939
-23	0,4755	0,4709	0,4663	0,4617	0,4572	0,4527	0,4482	0,4438	0,4395	0,4351
-22	0,5245	0,5194	0,5144	0,5093	0,5044	0,4995	0,4946	0,4898	0,4850	0,4802
-21	0,5780	0,5725	0,5670	0,5615	0,5561	0,5507	0,5453	0 ,5401	0,5348	0,5296
-20	0,6366	0,6305	0,6244	0,6185	0,6125	0,6067	0,6008	0, 5951	0,5893	0,5837
-19	0,7005	0,6938	0,6873	0,6807	0,6743	0,6678	0,6615	0,6552	0, 6489	0,6427
-18	0,7703	0,76 3 0	0,7558	0,7487	0,7416	0,7346	0,7277	0,7208	0,7140	0,7072
-17	0,8464	0,8385	0,8306	0,8228	0,8151	0, 8075	0,7999	0,7924	0,7850	0,7776
-16	0,9293	0,9207	0,9122	0,9037	0,8953	0,8870	0,8787	0,8705	0,8624	0,8543
-15	1,0197	1,0103	1,0010	0,9917	0,9826	0, 9735	0,9645	0,9556	0,9468	0,9380
-14	1,1180	1,1078	1,0977	1,0876	1,0777	1,0678	1,0580	1,0483	1,03 87	1,0291
-13	1,2250	1,2139	1,2029	1,1919	1,1811	1,1704	1,1597	1,1492	1,1387	1,1283
-12	1,3412	1,3292	1,3172	1,3053	1,2936	1,2819	1,2703	1,2588	1,2475	1,2362
-11	1,4676	1,4545	1,4415	1,4286	1,4158	1,4031	1,3905	1,3781	1,3657	1,3534
-10	1,6047	1,5905	1,5764	1,5624	1,5485	1,5347	1,5211	1,5075	1,4941	1,4808
-9	1,7535	1,7381	1,7228	1,7076	1,6925	1,6776	1,6628	1,6481	1,6335	1,6191
-8	1,9149	1,8982	1,8816	1,8651	1,8488	1,8326	1,8165	1,8006	1,7848	1,7691
-7	2,0897	2,0716	2,0536	2,0358	2,0181	2,0006	1,9831	1,9659	1,9487	1,9317
-6	2,2791	2,2595	2,2400	2,2207	2,2016	2,1825	2,1637	2,1450	2,1264	2,1080
-5	2,4841	2,4629	2,4418	2,4209	2,4002	2,3796	2,3592	2,3389	2,3188	2,2989
-4	2,7059	2,6829	2,6601	2,6375	2,6151	2,5928	2,5707	2,5488	2,5271	2,5055
-3	2,9456	2,9208	2,8962	2,8717	2,8475	2,8234	2,7995	2,7759	2,7523	2,7290
-2	3,2047	3,1779	3,1513	3,1249	3,0987	3,0727	3,0469	3,0213	2,9959	2,9707
-1	3,4846	3,4556	3,4269	3,3984	3,3701	3,3420	3,3141	3,2864	3,2590	3,2318
0	3,7867	3,7554	3,7244	3,6936	3,6631	3,6327	3,6027	3,5728	3,5432	3,5138
0	3,7870	3,8148	3,8427	3,8709	3,8992	3,9277	3,9564	3,9853	4,0143	4,0436
1	4,0730	4,1027	4,1325	4,1625	4,1927	4,2231	4,2537	4,2845	4,3155	4,3468
2	4,3782	4,4098	4,4416	4,4736	4,5058	4,5383	4,5709	4,6038	4,6368	4,6701
3	4,7036	4,7373	4,7712	4,8053	4,8397	4,8742	4,9090	4,9440	4,9793	5,0147
4	5,0504	5,0863	5,1225	5,1588	5,1954	5,2323	5,2693	5,3066	5,3442	5,3819
5	5,4200	5,4582	5,4967	5,5354	5,5744	5,6136	5,6531	5,6928	5,7328	5,7730
6	5,8135	5,8542	5,8952	5,9364	5,9779	6,0196	6,0616	6,1039	6,1464	6,1892
7	6,2323	6,2756	6,3192	6,3631	6,4073	6,4517	6,4964	6,5413	6,5866	6,6321
8	6,6779	6,7240	6,7704	6,8171	6,8640	6,9112	6,9588	7,0066	7,0547	7,1031
9	7,1518	7,2008	7,2501	7,2997	7,3497	7,3999	7,4504	7,5012	7,5524	7,6038
10	7,6556	7,7077	7,7601	7,8128	7,8658	7,9192	7,9729	8,0269	8,0812	8,1359
11	8,1909	8,2462	8,3018	8,3578	8,4142	8,4708	8,5279	8,5852	8,6429	8,7010
12	8,7594	8,8181	8,8772	8,9367	8,9965	9,0567	9,1172	9,1781	9,2394	9,3010
13	9,3630	9,4254	9,4881	9,5512	9,6147	9,6786	9,7428	9,8074	9,8724	9,9378
14	10,0036	10,0698	10,1364	10,2033	10,2707	10,3384	10,4066	10,4751	10,5441	10,6135
15	10,6833	10,7534	10,8240	10,8951	10,9665	11,0384	11,1106	11,1833	11,2565	11,3300
16	11,4040	11,4785	11,5533	11,6286	11,7044	11,7805	11,8572	11,9342	12,0118	12,0897
17	12,1682	12,2471	12,3264	12,4062	12,4865	12,5672	12,6484	12,7301	12,8123	12,8949
18	12,9780	13,0616	13,1457	13,2302	13,3153	13,4008	13,4869	13,5734	13,6604	13,7480
19	13,8360	13,9246	14,0136	14,1032	14,1933	14,2839	14,3750	14,4667	14,5588	14,6515
20	14,7448	14,8385	14,9328	15,0277	15,1231	15,2190	15,3155	15,4125	15,5101	15,6083
21	15,7070	15,8062	15,9061	16,0065	16,1074	16,2090	16,3111	16,4138	16,5171	16,6210
22	16,7255	16,8305	16,9362	17,0424	17,1493	17,2568	17,3648	17,4735	17,5828	17,6927
23	17,8033	17,9144	18,0262	18,1386	18,2517	18,3654	18,4797	18,5947	18,7103	18,8266
24	18,9435	19,0611	19,1794	19,2983	19,4179	19,5381	19,6591	19,7807	19,9030	20,0259
25	20,1496	20,2740	20,3990	20,5248	20,6512	20,7784	20,9063	21,0349	21,1642	21,2942
26	21,4250	21,5565	21,6887	21,8217	21,9554	22,0898	22,2250	22,3609	22,4976	22,6351
27	22,7733	22,9123	23,0521	23,1927	23,3340	23,4761	23,6190	23,7627	23,9072	24,0525
28	24,1986	24,3455	24,4932	24,6418	24,7911	24,9413	25,0923	25,2442	25,3969	25,5504
29	25,7048	25,8601	26,0161	26,1731	26,3309	26,4896	26,6492	26,8097	26,9710	27,1332
30	27,2964	27,4604	27,6253	27,7911	27,9579	28,1255	28,2941	28,4636	28,6341	28,8055
31	28,9778	29,1511	29,3253	29,5005	29,6766	29,8537	30,0318	30,2109	30,3909	30,5720
32	30,7540	30,9370	31,1210	31,3061	31,4921	31,6792	31,8673	32,0564	32,2466	32,4378
33	32,6300	32,8233	33,0177	33,2131	33,4096	33,6072	33,8058	34,0055	34,2064	34,4083
34	34,6113	34,8155	35,0207	35,2271	35,4346	35,6432	35,8530	36,0639	36,2760	36,4892
35	36,7036	36,9192	37,1359	37,3538	37,5730	37,7933	38,0148	38,2375	38,4615	38,6866
36	38,9130	39,1406	39,3695	39,5996	39,8310	40,0636	40,2975	40,5327	40,7691	41,0069
37	41,2459	41,4863	41,7279	41,9709	42,2152	42,4608	42,7078	42,9561	43,2058	43,4568
38	43,7092	43,9630	44,2182	44,4747	44,7327	44,9920	45,2528	45,5150	45,7786	46,0437
39	46,3102	46,5782	46,8476	47,1185	47,3909	47,6647	47,9401	48,2170	48,4953	48,7752
40	49,0566	49,3396	49,6241	49,9101	50,1977	50,4869	50,7777	51,0701	51,3640	51,6596
41	51,9567	52,2555	52,5560	52,8580	53,1618	53,4671	53,7742	54,0829	54,3934	54,7055
42	55,0193	55,3349	55,6522	55,9712	56,2920	56,6145	56,9388	57,2648	57,5927	57,9224
43	58,2538	58,5871	58,9222	59,2592	59,5980	59,9386	60,2812	60,6256	60,9719	61,3201
44	61,6703	62,0223	62,3763	62,7323	63,0902	63,4501	63,8119	64,1758	64,5416	64,9095
45	65,2794	65,6514	66,0254	66,4015	66,7796	67,1599	67,5422	67,9267	68,3132	68,7020
46	69,0928	69,4859	69,8811	70,2785	70,6781	71,0800	71,4840	71,8903	72,2989	72,7097
47	73,1229	73,5383	73,9560	74,3761	74,7985	75,2232	75,6504	76,0799	76,5118	76,9461
48	77,3828	77,8220	78,2636	78,7077	79,1543	79,6034	80,0551	80,5092	80,9659	81,4252
49	81,8870	82,3514	82,8185	83,2882	83,7605	84,2355	84,7131	85,1935	85,6765	86,1623
50	86,6509	87,1422	87,6362	88,1331	88,6328	89,1353	89,6407	90,1489	90,6600	91,1741
51	91,6910	92,2109	92,7338	93,2596	93,7885	94,3203	94,8552	95,3932	95,9342	96,4783
52	97,026	97,576	98,129	98,686	99,246	99,809	100,376	100,945	101,518	102,094
53	102,674	103,257	103,843	104,433	105,026	105,622	106,222	106,826	107,433	108,043
54	108,657	109,275	109,896	110,521	111,150	111,782	112,418	113,057	113,701	114,348
55	114,999	115,654	116,312	116,975	117,641	118,312	118,986	119,664	120,347	121,033
56	121,724	122,418	123,117	123,820	124,527	125,238	125,954	126,673	127,397	128,126
57	128,859	129,596	130,338	131,084	131,834	132,590	133,349	134,114	134,883	135,656
58	136,434	137,218	138,005	138,798	139,595	140,398	141,205	142,017	142,834	143,656
59	144,484	145,316	146,153	146,996	147,844	148,697	149,555	150,419	151,288	152,162
60	153,042	153,927	154,818	155,715	156,617	157,525	158,438	159,357	160,282	161,213

Приложение 4.

J- d диаграммы влажного воздуха