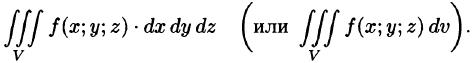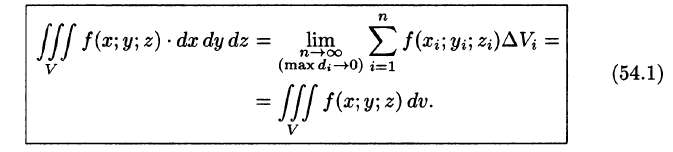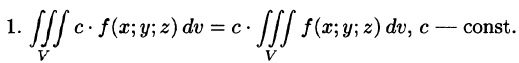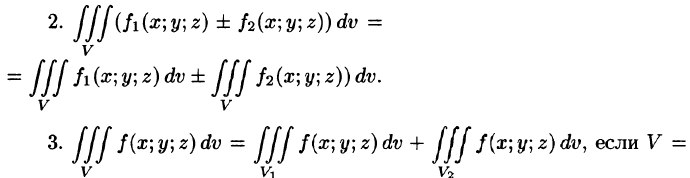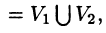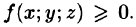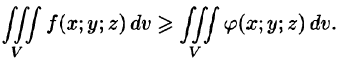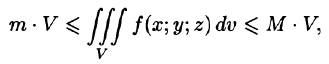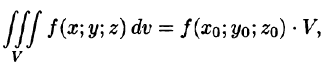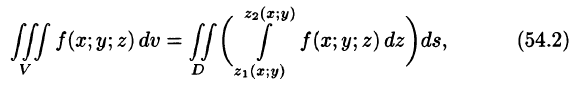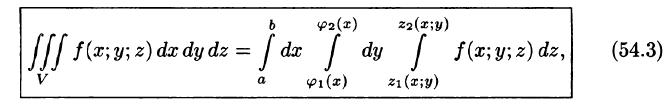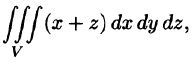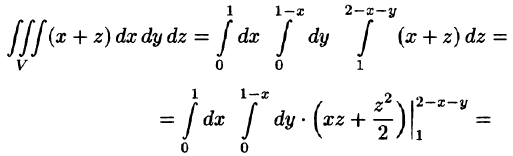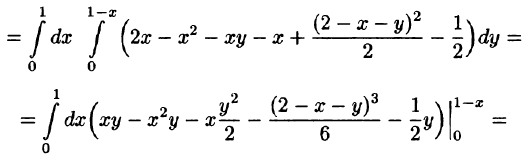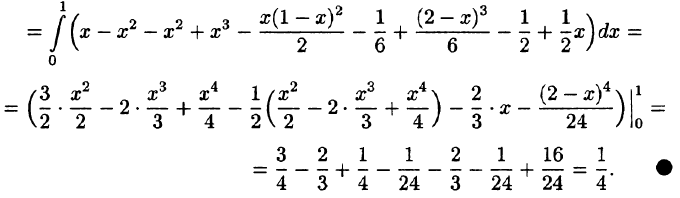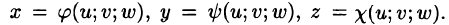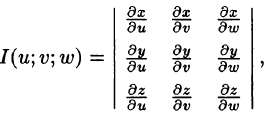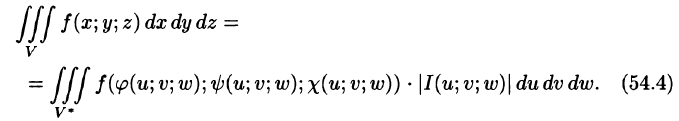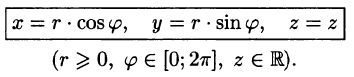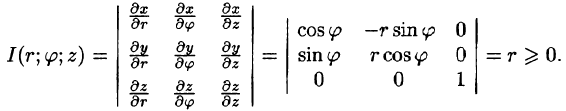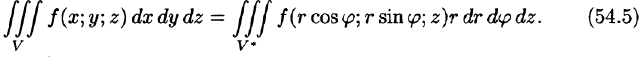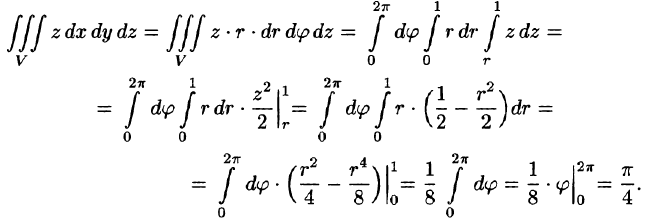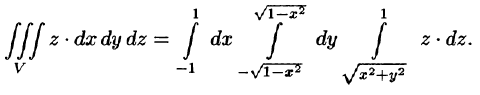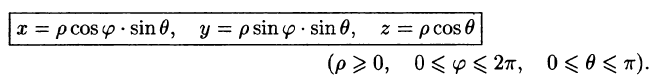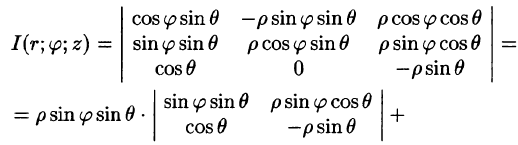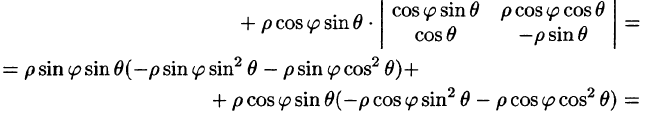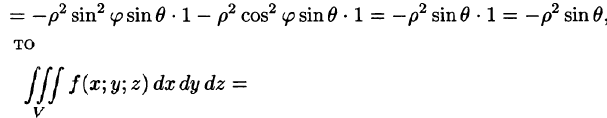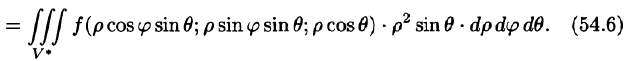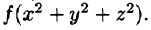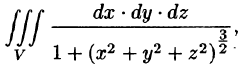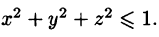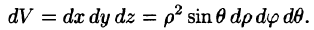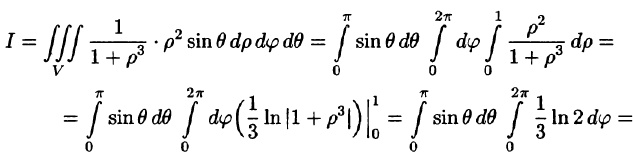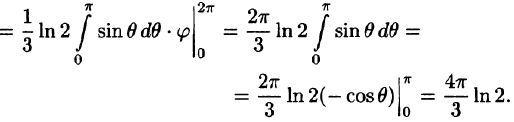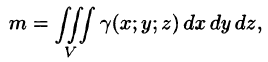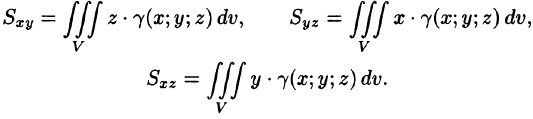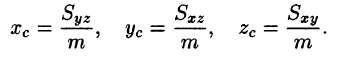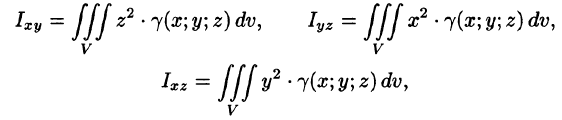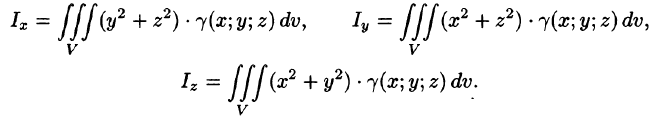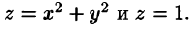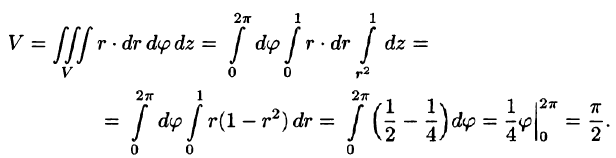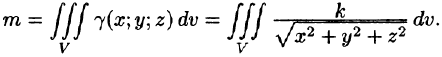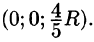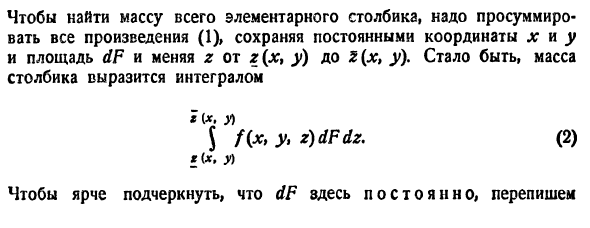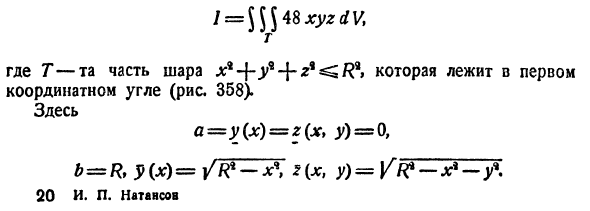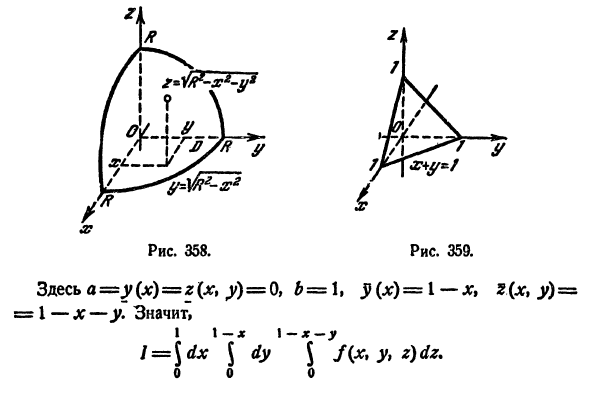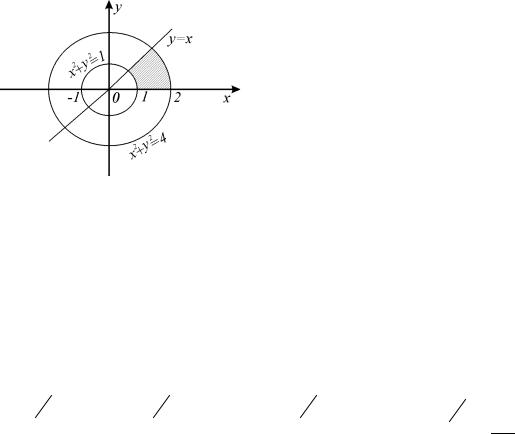
Как найти объем тройным интегралом - AvtoShod.ru

Пример 1.8. Найти площадь области D , ограниченной окружностями x2 + y2 =1 и x2 + y2 = 4 и прямыми x = y и y = 0, y ≥ 0.

Решение. Так как область D (рис. 1.13) есть часть круга, то площадь ее области вычислим по формуле (1.14), то есть воспользуемся полярными координатами. Пределы внешнего интеграла по переменной ϕ

	определяются	прямыми:	y = 0 ,
	следовательно,	ϕ = 0	и	y = x ,
	следовательно,	ϕ = π .		Пределы
		4
	внутреннего интеграла по переменной ρ
	определим так: фиксируем произвольное
Рис. 1.13	значение ϕ (0,	π		полюса О
	4 ) , затем	из

под углом ϕ проведем луч. Точка входа этого луча в область D лежит на

дуге окружности x2 + y2 = 4, уравнение которой в полярных координатах ρ = 2, а точка выхода этого луча из области D лежит на дуге окружности

x2 + y2 =1, уравнение которой в полярных координатах ρ =1. Значит, пределами интегрирования по ρ, соответственно, будут 1 и 2. Поэтому

π 4	2	π 4	ρ	2			2		1	π 4	3	π	4


S = ∫	dϕ∫ρdρ = ∫	dϕ				=	∫(4	−1)dϕ =	ϕ
	2		2	2	0
0	1	0					1			0

2. ТРОЙНЫЕ ИНТЕГРАЛЫ

Тройной интеграл является аналогом двойного интеграла и вводится для функций трех переменных.

2.1. Определение тройного интеграла. Пусть функция f (x, y, z)

определена в ограниченной замкнутой области V . Разобьем эту область с помощью сети поверхностей на конечное число частичных областей

V1,V2 ,…Vn , объемы которых соответственно	обозначим	через
∆v1, ∆v2,…∆vn . В каждой частичной области	Vi , i =
1, n	выберем

произвольную точку M i (xi , yi , zi ) , i =1, n и умножим значение функции f (x, y, z) в точке Mi на объем∆vi этой области, а затем составим сумму

n
σn = ∑ f (xi , yi , zi )∆vi ,	(2.1)

i =1

которая называется интегральной суммой для функции f (x, y, z) по об-

ласти V .

Если существует конечный предел I интегральной суммы (2.1) при стремлении к нулю наибольшего λ из диаметров всех частичных областей

Vi , i =		,		зависящий ни от способа разбиения области V , ни от
1, n	не
выбора	точек	Mi (xi , yi , zi ), то этот предел называется тройным
интегралом	функции	f (x, y, z) по	области V и	обозначается	так
∫∫∫ f (x, y, z)dv . Таким образом, по определению
V					n

				I = lim	∑ f (xi , yi , zi )∆vi = ∫∫∫ f (x, y, z)dv .	(2.2)
					λ→0 i =1	V
Функция	f (x, y, z) называется в	этом случае	интегрируемой по
области	V ,	V	— областью интегрирования, x, y, z — переменными
интегрирования, dv — элементом объема, а λ = max d (Vi ) .
							1≤i≤n

Если разбиение области V на частичные области проводить плоскостями, параллельными координатным плоскостям (в дальнейшем

будем предполагать, что это всегда имеет место), то частичные области Vi


—	есть	прямоугольные	параллелепипеды	и,	следовательно,
∆vi	= ∆xi ∆yi ∆zi , i =		. Тогда dv = dxdydz и
1, n

I = ∫∫∫ f (x, y, z)dv = ∫∫∫ f (x, y, z)dxdydz.

	V	V
Замечание 2.1. Если в (2.2) положить f (x, y, z) ≡1 при (x, y, z) V ,
то получим	выражение	для объема V области V в виде тройного
интеграла		V = ∫∫∫dxdydz .

		V
		#
Достаточные условия существования тройного интеграла можно
сформулировать в виде следующей теоремы.
Теорема. Всякая непрерывная в замкнутой ограниченной области
V функция	f (x, y, z) интегрируема в этой области.

Замечание 2.2. Можно указать менее жесткие условия существования тройного интеграла. Но мы ограничимся рассмотрением только непрерывных в замкнутой области функций.

Тройные интегралы обладают свойствами, аналогичными свойствам двойных интегралов (см. пункт 1.2).

2.2. Вычисление тройных интегралов сводится к трехкратному интегрированию, то есть к последовательному вычислению трех


обыкновенных	(однократных)	определенных
интегралов по каждой из трех переменных
координат точки трехмерного пространства.
Пусть	функция	f (x, y, z)	непрерывна	в
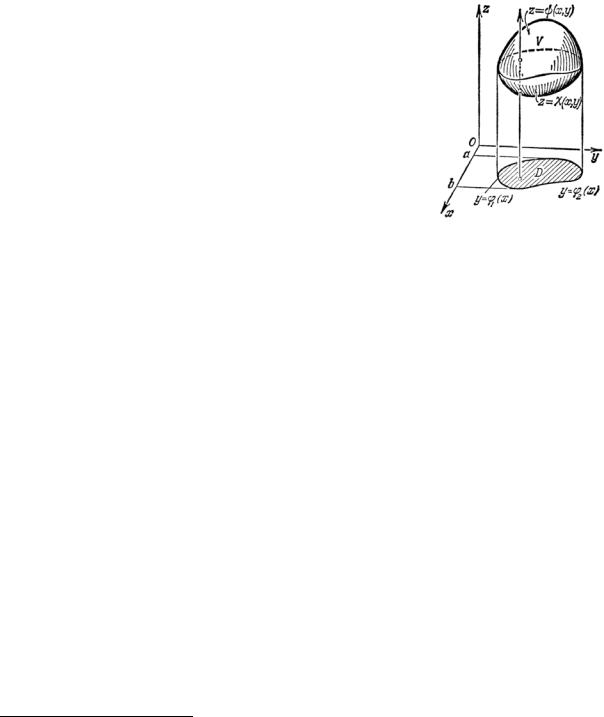
области V . Пусть поверхность S , ограничивающая
тело V , пересекается не более, чем в двух точках
любой	прямой,	параллельной	одной	из
координатных осей1, например, оси Oz, и
проходящей через любую внутреннюю точку
области (рис. 2.1), и проектируется в правильную
двумерную область D плоскости xOy .Такая	Рис. 2.1
область	V	называется	правильной трехмерной

областью. Пусть нижняя часть поверхности	S задана	уравнением
z = χ( x, y ), верхняя – уравнением	z =ψ(x, y) ,	где	χ(x, y),ψ(x, y) —
однозначные непрерывные функции, определенные в	областиD ,
являющейся проекцией тела V на плоскостьxOy . Тогда
	ψ ( x, y)
∫∫∫ f (x, y, z)dxdydz = ∫∫dxdy	∫ f (x, y, z)dz ,		(2.3)
V	D	χ( x, y)
					ψ ( x, y)
причем сначала вычисляется	внутренний интеграл	∫ f (x, y, z)dz по
переменной z , в котором переменные x			χ( x, y)
и	y считаются постоянными, а
пределы интегрирования есть	функции	от	x и	y ,	а затем внешний

двойной интеграл по области D .

Если область D является правильной в направлении оси Oy , то интеграл по области V вычисляется по формуле

	b	ϕ2 ( x)	ψ( x, y)
∫∫∫ f (x, y, z)dxdydz = ∫dx	∫	dy ∫ f (x, y, z)dz,	(2.4)
V	a	ϕ1 ( x)	χ( x, y)

1 Более сложные области V часто удается сводить к рассматриваемому виду путем разбиения их на конечное число областей V1,…,Vn, каждая из которых удовлетворяет условиям, изложенным выше.

то есть сводится к последовательному вычислению трех определенных интегралов. В (2.4) сначала вычисляется внутренний интеграл по переменной z при постоянных x и y , затем внутренний интеграл по

переменной y при постоянной x и, наконец, интеграл по переменнойx —

пределы интегрирования внешнего интеграла постоянны.

Разумеется, порядок интегрирования, при выполнении известных условий может быть избран другим, как в двойном интеграле по области D в формуле (2.4)

	d	ψ2 ( y)	ψ( x, y)
∫∫∫ f (x, y, z)dxdydz = ∫dy ∫	dx ∫ f (x, y, z)dz,	(2.5)
V	c	ψ1 ( y)	χ( x, y)
также и в тройном интеграле: для этого тело V нужно проектировать на
плоскость yOz или на плоскость	xOz ,	тогда в (2.3) соответственно
поменяются	ролями переменные x ,	y , z .

Наиболее простой вид формула вычисления тройного интеграла принимает в случае, когда V есть прямоугольный параллелепипед, ограниченный плоскостями x = a, x = b, y = c, y = d, z = e, z = h :

	b	d	h
∫∫∫ f ( x, y, z )dxdydz = ∫dx∫dy∫ f ( x, y, z )dz.	(2.6)
V	a	c	e
Пример 2.1. Вычислить	∫∫∫( x + z )dxdydz по	области V,

ограниченной плоскостями x = 0, x = 1, y = 0, y = 1, z = 0, z = 1. Решение. Так как область интегрирования есть прямоугольный

параллелепипед, то для вычисления данного интеграла воспользуемся формулой (2.6)

				1	1	1				1	1			z2		1

∫∫∫(x + z)dxdydz = ∫dx∫dy∫(x + z)dz = ∫dx∫dy(xz +				)		=
2
V				0	0	0				0	0				0
				1
1	1	1		1		1		1	1		x2			x	1

= ∫dx∫( x +		)dy = ∫dx(x +		) y	= ∫(x +		)dx = (		+			)	=1.
2	2	2	2	2
0	0		0			0	0					0

Пример.2.2. Вычислить∫∫∫	x2dxdydz по области V , ограниченной
плоскостями z = 0,	x = 0,	V		x + y + z −2 = 0.
y = 0,

Решение. Область интегрирования V есть тетраэдр, расположенный в первом октанте (рис.2.2). Область V является правильной, так как прямая, проведенная через любую ее внутреннюю точку параллельно оси Oz пересекает поверхность ограничивающую пространственную область лишь в двух точках (рис.2.2), поэтому для вычисления заданного интеграла воспользуемся формулой (2.3).

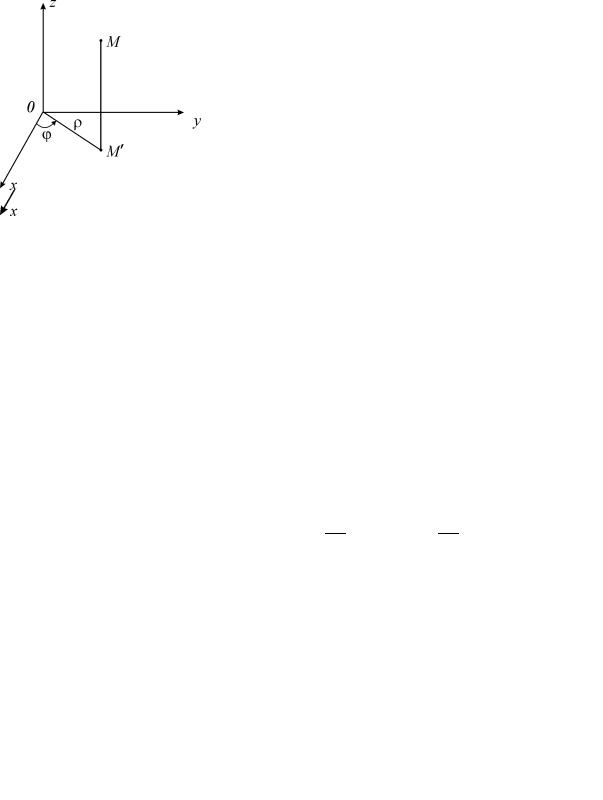
Рис. 2.3

Определим пределы внутреннего интеграла по
переменной	z . Так как прямая,	параллельная оси
Oz , входит в область V	через плоскость,
уравнение	которой z = 0	(нижний предел

интегрирования), а выходит из области через
плоскость, уравнение	которой	z = 2 − x − y
(верхний предел интегрирования), то
	2−x−y
∫∫∫x2dxdydz = ∫∫dxdy	∫x2dz ,
V	D	0
где D — проекция области V на плоскость xOy. D	Рис. 2.2
есть треугольник, образованный прямыми

x = 0, y = 0 и y = 2 − x . Следовательно, по формуле (2.4) имеем

	2−x−y	2	2−x	2−x −y	2	2−x						02−x −y =
∫∫dxdy	∫x2dz = ∫x2dx ∫	dy	∫dz = ∫x2dx ∫dy z


D	0	0	0			0	0	0				2−x
2	2−x			2				y	2

= ∫x2dx ∫(2 − x − y)dy = ∫x2dx ((2 − x) y −				)	=

0	0			0			2				0
		2
2			(2 − x)	2						x	4
= ∫x2 ((2 − x)2 −		)dx = ∫(2x2 − 2x3 +			) dx =
2
0					0						2

= (	2x3	−	2x	4	+	x5	)	2


3	4		10		0

= 163 −8 +165 = 158 .

2.3. Тройной интеграл в цилиндрических координатах. Как и в двумерном случае, для тройных интегралов имеют место формулы преобразования интеграла от прямоугольных координат к новым системам координат. Наиболее употребительные из них – цилиндрические и сферические координаты. Мы рассмотрим только преобразование к цилиндрическим координатам.

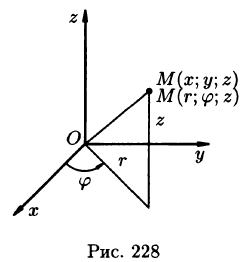
В цилиндрической системе координат положение точки M пространства определяется полярными координатами ϕ и ρ точки M ′ (проекции точки

Mна плоскость xOy ) и аппликатой z самой точки M (рис. 2.3). Числа

ϕ, ρ, z называют цилиндрическими координатами точки M , причем

ρ ≥ 0, ϕ [0,2π] z — любое. Цилиндрические координаты связаны с

декарторыми соотношениями:
x = ρ cosϕ, y = ρ sin ϕ, z = z .	(2.7)
Преобразование тройного интеграла от декартовых	координат

x , y, z к цилиндрическим координатам ϕ, ρ, z осуществляется по

следующей формуле перехода

∫∫∫ f (x, y, z)dxdydz =∫∫∫ f (ρ cosϕ, ρsin ϕ, z)ρdρdϕdz ,

V V

где dv = ρdρdϕdz — элемент объема в цилиндрических координатах.

Выразим уравнения нижней и верхней частей поверхности S , ограничивающей данную область V , в цилиндрических координатах —

z = z1(ρ,ϕ) и z = z2 (ρ,ϕ) соответственно и запишем формулу для вычисления интеграла в цилиндрических координатах, аналогичную (2.3)

∫∫∫ f (ρ cosϕ, ρsinϕ, z)ρdρdϕdz = ∫∫ρdρdϕ	z2 ( ρ,ϕ)
∫ f (ρ cosϕ, ρsinϕ, z)dz,
V		D	z1 ( ρ,ϕ)
где D есть проекция области V на плоскость xOy.Воспользовавшись
заданием плоской области D в полярных координатах (пункт 1.4) получим
	z2	( ρ,ϕ)
∫∫ρdρdϕ	∫ f (ρ cosϕ, ρsinϕ, z)dz =
D	z1 ( ρ,ϕ)
β	ρ2 (ϕ)	z2 ( ρ,ϕ)
= ∫dϕ	∫ ρdρ	∫ f (ρ cosϕ, ρsinϕ, z)dz .	(2.8)

αρ1 (ϕ) z1 ( ρ,ϕ)

Формулу (2.8) удобно использовать, если область V проектируется в круг или часть круга.

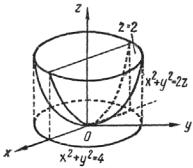
Пример 2.3. Вычислить ∫∫∫(x2 + y2 )dxdydz по области, ограни-

ченной плоскостью z = 2 и параболоидом x2 + y2 = 2z.

Решение. Область V (рис. 2.4) снизу ограничена параболоидом x2 + y2 = 2z , сверху

плоскостью z = 2 . Эта область проектируется на плоскость xOy в облстьD , ограниченную

	окружностью	x2 + y2 = 4,	уравнение которой
	получено	при	исключении	переменной z	из
	уравнений	параболоида	x2 + y2 = 2z	и
Рис. 2.4	плоскости z = 2 .	x2 + y2 = ρ2 ,
Введем цилиндрические координаты. Так как	то

уравнение

параболоида

примет вид z =

ρ2

;

уравнение плоскости при

изменится . В области D

переходе

к цилиндрическим

координатам

не

0 ≤ϕ ≤ 2π , а 0 ≤ ρ ≤ 2 . Тогда, следуя формуле (2.8), имеем

2π

∫∫∫(x2 + y2 )dxdydz =∫∫∫ρ2 ρdρdϕdz = ∫ dϕ∫ρ3dρ ∫dz =

ρ2

2π

ρ5

= ∫ dϕ∫ρ3dρ z

2 =

∫

dϕ∫

(2ρ3 −

)dρ =

2π		ρ	4		ρ	6		2	2π	(23 −	2	4	8ϕ

= ∫	dϕ(		−		)		= ∫		)dϕ =
2	12		3	3
0				0	0

= 163π .

2.4. Вычисление объемов. С помощью тройных интегралов можно вычислить объем пространственной области, массу тела, занимающего область V , а также координаты центра тяжести этого тела и моменты инерции его относительно координатных осей и начала координат. Мы рассмотрим только геометрическое приложение тройного интеграла – вычисление объема пространственной области.

Как установлено в замечании 2.1 объем V пространственной области V может быть вычислен с помощью тройного интеграла по формуле

	V = ∫∫∫dx dy dz.	(2.9)
		V
В цилиндрической системе координат имеем
	V = ∫∫∫ρ dρ dϕ dz.	(2.10)
		V
Пример 2.4. Вычислить объем тела, ограниченного параболоидом
6 − x2 − y2 = z	и конусом	x2 + y2 = z2
(z ≥ 0) .
Решение. Тело (рис.2.5), объем которого
нужно найти,	ограничено	снизу конусом
x2 + y2 = z2 ,	сверху –	параболоидом
6 − x2 − y2 = z	и проектируетcя на плоскость
xOy в область D , ограниченную окружностью	Рис. 2.5
x2 + y2 = 4. Уравнение окружности получено

в результате исключения z из уравнения конуса и параболоида.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Вычисление тройного интеграла в декартовых координатах
- Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах
Некоторые приложения тройного интеграла Объем тела
- Масса тела
- Статические моменты
- Центр тяжести тела
- Моменты инерции тела
Тройной интеграл

Обобщением определенного интеграла на случай функции трех переменных является так называемый «тройной интеграл».

Теория тройного интеграла аналогична теории двойного интеграла. Поэтому изложим ее в несколько сокращенном виде.

Пусть в замкнутой области V пространства Oxyz задана непрерывная функция и = f(x;y;z). Разбив область V сеткой поверхностей на п частей и выбрав в каждой из них произвольную точку , составим интегральную сумму для функции по области V (здесь — объем элементарной области ).

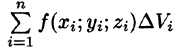
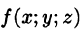
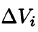
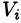
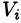
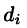
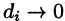
Если предел интегральной суммы существует при неограниченном увеличении числа п таким образом, что каждая «элементарная область» стягивается в точку (т. е. диаметр области стремится к нулю, т.е. ), то его называют тройным интегралом от функции и = f(х;у;z) по области V и обозначают

Таким образом, по определению, имеем:

Здесь dv = dx dy dz — элемент объема.

Теорема:

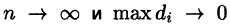
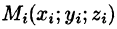
Если функция и = f(x;y,z) непрерывна в ограниченной замкнутой области V, то предел интегральной суммы (54.1) при существует и не зависит ни от способа разбиения области V на части, ни от выбора точек в них.
Тройной интеграл обладает теми же свойствами, что и двойной интеграл:

а пересечение 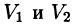состоит из границы, их разделяющей.
4. если в области V функция

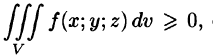
Если в области интегрирования 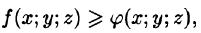то и

5.так как в случае любая интегральная сумма имеет вид и численно равна объему тела.

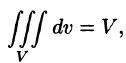
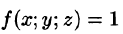
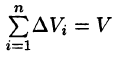
6. Оценка тройного интеграла:

где m и М — соответственно наименьшее и наибольшее значения функции f(x;y;z) в области V.

7. Теорема о среднем значении: если функция f(x; у, z) непрерывна в замкнутой области V, то в этой области существует такая точка 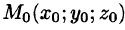, что

где V — объем тела.

Вычисление тройного интеграла в декартовых координатах

В декартовых координатах вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов.

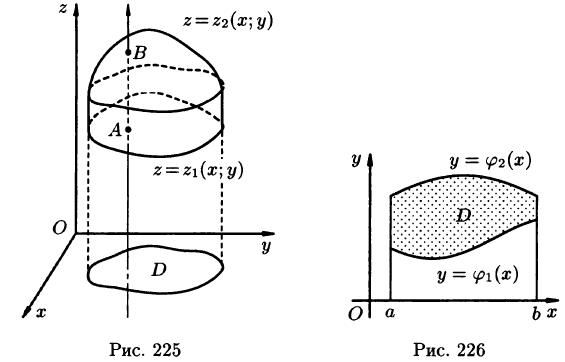
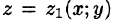
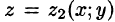
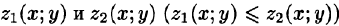
Пусть областью интегрирования V является тело, ограниченное снизу поверхностью , сверху — поверхностью , причем — непрерывные функции в замкнутой области D, являющейся проекцией тела на плоскость Оху (см. рис. 225). Будем считать область V — правильной в направлении оси Oz: любая прямая, параллельная оси Oz, пересекает границу области не более чем в двух точках. Тогда для любой непрерывной в области V функции f(х; у, z) имеет место формула

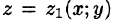
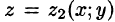
сводящая вычисление тройного интеграла к вычислению двойного интеграла от однократного (доказательство формулы (54.2) не приводим). При этом сначала вычисляется внутренний интеграл по переменной г при постоянных х и у в пределах изменения z. Нижней границей интеграла является аппликата точки А — точки входа прямой, параллельной оси Oz в область V, т. е. ; верхней границей — аппликата точки В — точки выхода прямой из области V, т. е. . Результат вычисления этого интеграла есть функция двух переменных: х и у.

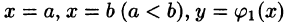
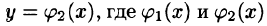
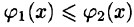
Если область D ограничена линиями и — непрерывные на отрезке [а, b] функции, причем (см. рис. 226), то, переходя от двойного интеграла по области D к повторному, получаем формулу

по которой вычисляется тройной интеграл в декартовых координатах.

Замечания:

Если область V более сложная, чем рассмотренная, то ее следует разбить на конечное число таких областей (правильных), к которым можно применить формулу (54.3).
Порядок интегрирования в формуле (54.3), при определенных условиях, может быть иным.

Пример:

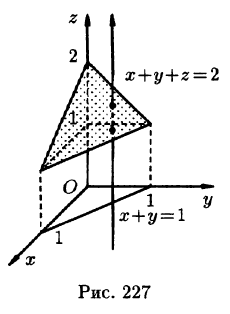
Вычислить

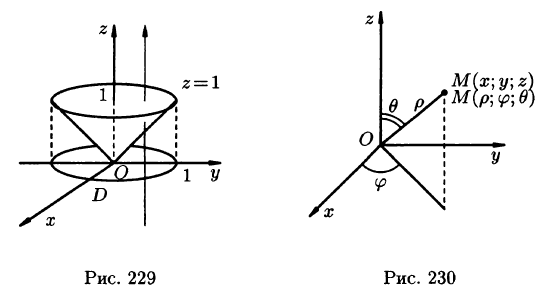
где V ограничена плоскостями х = 0, у =0, z = 1, x + y + z = 2 (рис. 227).

Решение:

Область V является правильной в направлении оси Oz (как, заметим, и в направлении осей Ох и Оу). Ее проекция на плоскость Оху является правильной в направлении оси Оу (и оси Ох). Согласно формуле (54.3), имеем:

Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах

При вычислении тройного интеграла, как и двойного, часто применяется метод подстановки, т. е. совершается преобразование переменных.

Пусть совершена подстановка

Если эти функции имеют в некоторой области 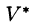пространства Ouvw непрерывные частные производные и отличный от нуля определитель

то справедлива формула замены переменных в тройном интеграле:

Здесь I(u; v;w) — определитель Якоби, или якобиан преобразования (примем без доказательства).

Для вычисления тройного интеграла часто используют так называемые цилиндрические координаты.

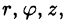
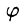
Положение точки М(х; у; z) в пространстве Oxyz можно определить заданием трех чисел где r — длина радиуса-вектора проекции точки М на плоскость Оху, — угол, образованный этим радиусом-вектором с осью Ox, z — аппликата точки М (см. рис. 228).

Эти три числа (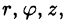) называются цилиндрическими координатами точки М.

Цилиндрические координаты точки связаны с ее декартовыми координатами следующими соотношениями:

Возьмем в качестве и, v, w цилиндрические координаты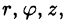 и вычислим якобиан преобразования:

Формула замены переменных (54.4) принимает вид

Таким образом, вычисление тройного интеграла приводится к интегрированию по r, по 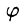и по z аналогично тому, как это делается в декартовых координатах.

Замечание:

К цилиндрическим координатам бывает удобно перейти в случае, если область интегрирования образована цилиндрической поверхностью.

Пример:

Вычислить 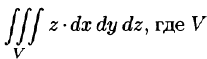— область, ограниченная верхней частью конуса и плоскостью z = 1.

Решение:

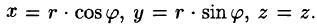
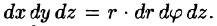
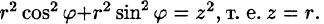
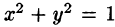
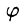
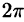
На рис. 229 изображена область интегрирования V. Вычислим интеграл путем перехода к цилиндрическим координатам: Здесь Уравнение конуса примет вид Уравнение окружности (границы области D) запишется так: r= 1. Новые переменные изменяются в следующих пределах: r— от 0 до 1, — от 0 до , a z — от r до 1 (прямая, параллельная оси Oz, пересекающая область D, входит в конус z =r и выходит из него на высоте z = 1).

Таким образом, согласно формуле (54.5), получаем:

Заметим, что, не переходя к цилиндрическим координатам, получим:

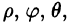
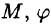
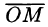
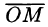
Сферическими координатами точки М(х; у; z) пространства Oxyz называется тройка чисел где р — длина радиуса-вектора точки — угол, образованный проекцией радиуса-вектора на плоскость Оху и осью Ох, в — угол отклонения радиуса-вектора от оси Oz (см. рис. 230).

Сферические координаты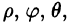 связаны с декартовыми координатами х, у, z соотношениями:

В некоторых случаях вычисление тройного интеграла удобно производить, перейдя к сферическим координатам. Для этого нужно воспользоваться формулой замены переменных в тройном интеграле (54.4). Так как якобиан преобразования

Замечание:

Переходить к сферическим координатам удобно, когда область интегрирования V есть шар (уравнение его границы 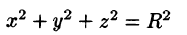в сферических координатах имеет вид р = R) или его часть, а также если подынтегральная функция имеет вид
Пример 54.3. Вычислить

где V — шар

Решение:

Вычислим интеграл путем перехода к сферическим координатам: 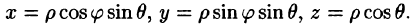Тогда

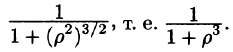
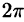
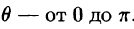
Граница области V — сфера и ее уравнение имеет вид р = 1, подынтегральная функция после замены переменных примет вид Новые переменные изменяются в следующих пределах: р —от 0 до 1, у — от 0 до , Таким образом, согласно формуле (54.6),

Некоторые приложения тройного интеграла Объем тела

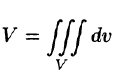
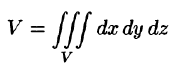
Объем области V выражается формулой или — в декартовых координатах,

Масса тела

Масса тела m при заданной объемной плотности вычисляется с помощью тройного интеграла как

где — объемная плотность распределения массы в точке M{x;y;z).

Статические моменты

Моменты 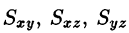тела относительно координатных плоскостей Оху, Oxz, Oyz вычисляются по формулам

Центр тяжести тела

Координаты центра тяжести тела V находятся по формулам

Моменты инерции тела

Моменты инерции тела относительно координатных плоскостей вычисляются по формулам

а моменты инерции относительно координатных осей:

Пример:

Найти объем тела, ограниченного поверхностями

Решение:

Данное тело ограничено сверху плоскостью z = 1, снизу — параболоидом 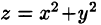(см. рис. 231). Объем тела находим, используя цилиндрические координаты:

Пример:

Найти массу шара 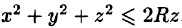, если плотность в каждой точке шара обратно пропорциональна расстоянию от нее до начала координат (дополнительно: найти координаты центра тяжести).

Решение:

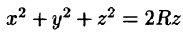
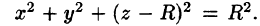
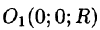
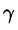
Уравнение сферы можно записать так: Центр шара расположен в точке (см. рис. 232). Пусть M(x;y;z) — произвольная точка шара. Тогда, по условию, плотность определяется формулой

где k — коэффициент пропорциональности, 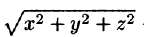— расстояние от точки М до начала координат.
Итак,

Вычислять интеграл будем в сферических координатах. Уравнение сферы 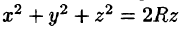примет вид

Поэтому сферические координаты будут изменяться в следующих пределах:

Подынтегральная функция примет вид 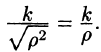Поэтому

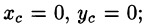
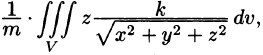
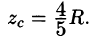
Из соображений симметрии следует, что вычислив интеграл найдем Итак, координаты центра тяжести

Тройной интеграл

Смотрите также:

Предмет высшая математика

Решение заданий и задач по предметам:

Математика
Высшая математика
Математический анализ
Линейная алгебра

Дополнительные лекции по высшей математике:

Тождественные преобразования алгебраических выражений
Функции и графики
Преобразования графиков функций
Квадратная функция и её графики
Алгебраические неравенства
Неравенства
Неравенства с переменными
Прогрессии в математике
Арифметическая прогрессия
Геометрическая прогрессия
Показатели в математике
Логарифмы в математике
Исследование уравнений
Уравнения высших степеней
Уравнения высших степеней с одним неизвестным
Комплексные числа
Непрерывная дробь (цепная дробь)
Алгебраические уравнения
Неопределенные уравнения
Соединения
Бином Ньютона
Число е
Непрерывные дроби
Функция
Исследование функций
Предел
Интеграл
Двойной интеграл
Интегрирование
Неопределённый интеграл
Определенный интеграл
Криволинейные интегралы
Поверхностные интегралы
Несобственные интегралы
Кратные интегралы
Интегралы, зависящие от параметра
Квадратный трехчлен
Производная
Применение производной к исследованию функций
Приложения производной
Дифференциал функции
Дифференцирование в математике
Формулы и правила дифференцирования
Дифференциальное исчисление
Дифференциальные уравнения
Дифференциальные уравнения первого порядка
Дифференциальные уравнения высших порядков
Дифференциальные уравнения в частных производных
Тригонометрические функции
Тригонометрические уравнения и неравенства
Показательная функция
Показательные уравнения
Обобщенная степень
Взаимно обратные функции
Логарифмическая функция
Уравнения и неравенства
Положительные и отрицательные числа
Алгебраические выражения
Иррациональные алгебраические выражения
Преобразование алгебраических выражений
Преобразование дробных алгебраических выражений
Разложение многочленов на множители
Многочлены от одного переменного
Алгебраические дроби
Пропорции
Уравнения
Системы уравнений
Системы уравнений высших степеней
Системы алгебраических уравнений
Системы линейных уравнений
Системы дифференциальных уравнений
Арифметический квадратный корень
Квадратные и кубические корни
Извлечение квадратного корня
Рациональные числа
Иррациональные числа
Арифметический корень
Квадратные уравнения
Иррациональные уравнения
Последовательность
Ряды сходящиеся и расходящиеся
Тригонометрические функции произвольного угла
Тригонометрические формулы
Обратные тригонометрические функции
Теорема Безу
Математическая индукция
Показатель степени
Показательные функции и логарифмы
Множество
Множество действительных чисел
Числовые множества
Преобразование рациональных выражений
Преобразование иррациональных выражений
Геометрия
Действительные числа
Степени и корни
Степень с рациональным показателем
Тригонометрические функции угла
Тригонометрические функции числового аргумента
Тригонометрические выражения и их преобразования
Преобразование тригонометрических выражений
Комбинаторика
Вычислительная математика
Прямая линия на плоскости и ее уравнения
Прямая и плоскость
Линии и уравнения
Прямая линия
Уравнения прямой и плоскости в пространстве
Кривые второго порядка
Кривые и поверхности второго порядка
Числовые ряды
Степенные ряды
Ряды Фурье
Преобразование Фурье
Функциональные ряды
Функции многих переменных
Метод координат
Гармонический анализ
Вещественные числа
Предел последовательности
Аналитическая геометрия
Аналитическая геометрия на плоскости
Аналитическая геометрия в пространстве
Функции одной переменной
Высшая алгебра
Векторная алгебра
Векторный анализ
Векторы
Скалярное произведение векторов
Векторное произведение векторов
Смешанное произведение векторов
Операции над векторами
Непрерывность функций
Предел и непрерывность функций нескольких переменных
Предел и непрерывность функции одной переменной
Производные и дифференциалы функции одной переменной
Частные производные и дифференцируемость функций нескольких переменных
Дифференциальное исчисление функции одной переменной
Матрицы
Линейные и евклидовы пространства
Линейные отображения
Дифференциальные теоремы о среднем
Теория устойчивости дифференциальных уравнений
Функции комплексного переменного
Преобразование Лапласа
Теории поля
Операционное исчисление
Системы координат
Рациональная функция
Интегральное исчисление
Интегральное исчисление функций одной переменной
Дифференциальное исчисление функций нескольких переменных
Отношение в математике
Математическая логика
Графы в математике
Линейные пространства
Первообразная и неопределенный интеграл
Линейная функция
Выпуклые множества точек
Система координат

Источник

Содержание:

Вычисление тройного интеграла в декартовых координатах
Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах.
Некоторые приложения тройного интеграла

Обобщением определенного интеграла на случай функции трех переменных является так называемый «тройной интеграл».

Пусть в замкнутой области пространства задана непрерывная функция Разбив область сеткой поверхностей на частей Vt (г — 1 , п) и выбрав в каждой из них произвольную точку составим интегральную сумму для функции по области (здесь — объем элементарной области

Если предел интегральной суммы существует при неограниченном увеличении числа таким образом, что каждая «элементарная область» стягивается в точку (т. е. диаметр области стремится к нулю, т.е. то его называют тройным интегралом от функции но области и обозначают

Таким образом, по определению, имеем:

Здесь — элемент объема.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Теорема 54.1 (существования). Если функция непрерывна в ограниченной замкнутой области то предел интегральной суммы (54.1) при и существует и не зависит ни от способа разбиения области на части, ни от выбора точек

в них.

Тройной интеграл обладает теми же свойствами, что и двойной интеграл:

а пересечение состоит из границы, их разделяющей.

4. если в области функция

Если в области интегрирования то и

5. , так как в случае любая интегральная сумма имеет вид численно равна объему тела.

Возможно вам будут полезны данные страницы:

6. Оценка тройного интеграла:

где и — соответственно наименьшее и наибольшее значения функции в области

7. Теорема о среднем значении: если функция непрерывна в замкнутой области то в этой области существует такая точка

что

где — объем тела.

Вычисление тройного интеграла в декартовых координатах

В декартовых координатах вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов.

Пусть областью интегрирования является тело, ограниченное снизу поверхностью сверху — поверхностью причем и — непрерывные функции в замкнутой области являющейся проекцией тела на плоскость

(см. рис. 225). Будем считать область — правильной в направлении оси : любая прямая, параллельная оси , пересекает границу области не более чем в двух точках. Тогда для любой непрерывной в области функции имеет место формула

сводящая вычисление тройного интеграла к вычислению двойного интеграла от однократного (доказательствоформулы (54.2) не приводим).

При этом сначала вычисляется внутренний интеграл по переменной при постоянных и в пределах изменения . Нижней границей интеграла является аппликата точки — точки входа прямой, параллельной оси в область , т. е. ; верхней границей — аппликата точки — точки выхода прямой из области , т. е. — Результат вычисления этого интеграла есть функция двух переменных: и

Если область ограничена линиями и где — непрерывные на отрезке функции, причем (см. рис. 226), то, переходя от двойного интеграла по области к повторному, получаем формулу по которой вычисляется тройной интеграл в декартовых координатах.

Замечания.

1. Если область более сложная, чем рассмотренная, то ее следует разбить на конечное число таких областей (правильных), к которым можно применить формулу (54.3).

2. Порядок интегрирования в формуле (54.3), при определенных условиях, может быть иным.

Пример с решением 54-1

Вычислить

где ограничена плоскостями (рис. 227).

Решение:

Область является правильной в направлении оси (как, заметим, и в направлении осей и ). Ее проекция на плоскость является правильной в направлении оси (и оси ). Согласно формуле (54.3), имеем:

Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах.

При вычислении тройного интеграла, как и двойного, часто применяется метод подстановки, т. е. совершается преобразование переменных.

Пусть совершена подстановка Если эти функции имеют в некоторой области пространства непрерывные частные производные и отличный от нуля определитель

то справедлива формула замены переменных в тройном интеграле:

Здесь — определитель Якоби, или якобиан преобразования (примем без доказательства).

Для вычисления тройного интеграла часто используют так называемые цилиндрические координаты.

Положение точки в пространстве можно определить заданием трех чисел где — длина радиуса-вектора проекции точки на плоскость — угол, образованный .этим радиусом-вектором с осью — аппликата точки (см. рис. 228).

Эти три числа называются цилиндрическими координатами точки

Цилиндрические координаты точки связаны с ее декартовыми координатами следующими соотношениями:

Возьмем в качестве цилиндрические координаты и вычислим

Формула замены переменных (54.4) принимает вид

Таким образом, вычисление тройного интеграла приводится к интегрированию по по и по аналогично тому, как это делается в декартовых координатах.

Замечание. К цилиндрическим координатам бывает удобно перейти в случае, если область интегрирования образована цилиндрической поверхностью.

Пример 54-2.

Вычислить где — область, ограниченная верхней частью конуса и плоскостью

Решение:

На рис. 229 изображена область интегрирования Вычислим интеграл путем перехода к цилиндрическим координатам: Здесь Уравнение конуса примет вид т.е. Уравнение окружности (границы области ) запишется так: Новые

переменные изменяются в следующих пределах: — от (прямая, параллельная оси пересекающая область входит в конус и выходит из него на высоте

Таким образом, согласно формуле (54.5), получаем:

Заметим, что, не переходя к цилиндрическим координатам, получим:

Сферическими координатами точки пространства называется тройка чисел где — длина радиуса-вектора точки — угол, образованный проекцией радиуса-вектора на плоскость и осью — угол отклонения радиуса-вектора оси (см. рис. 230).

Сферические координаты связаны с декарювыми координатами соотношениями:

Замечание. Переходить к сферическим координатам удобно, когда область интегрирования есть шар (уравнение его границы в сферических координатах имеет вид или его часть, а также если подынтегральная функция имеет вид

Пример 54-3.

Вычислить

где — шар

Решение:

Вычислим интеграл путем перехода к сферическим координатам: Тогда

Граница области — сфера и ее уравнение имеет вид подынтегральная функция после замены переменных примет вид т.е. Новые переменные изменяются в следующих пределах: -от до — от до — от до Таким образом, согласно формуле (54.6),

Некоторые приложения тройного интеграла

Объем тела

Объем области выражается формулой или

— в декартовых координатах,

— в цилиндрических координатах,

— в сферических координатах.

Масса тела

Масса тела при заданной объемной плотности вычисляется с помощью тройного интеграла как

где — объемная плотность распределения массы в точке

Статические моменты

Моменты тела отностельно координатных плоскостей вычисляются по формулам

Центр тяжести тела

Координаты центра тяжести тела находятся по формулам

Моменты инерции тела

Моменты инерции тела относительно координатных плоскостей вычисляются по формулам

а моменты инерции относительно координатных осей:

Пример 54 4.

Найти объем тела, ограниченного поверхностями

Решение:

Данное тело ограничено сверху плоскостью снизу — параболоидом (см. рис. 231). Объем тела находим, используя цилиндрические координаты:

Лекции:

Равномерное распределение
Признак Даламбера: пример решения
Производящие функции
Сложение и вычитание пределов
Логарифмические неравенства
Таблица истинности логических выражений
Элементы векторной алгебры
Асимптоты графика функции
Разложение в ряд маклорена
Частные производные второго порядка

Источник

Вычисление тройного интеграла

Содержание:

Что такое тройной интеграл
Свойства тройного интеграла
Геометрический смысл тройного интеграла, как вычислить

Что такое тройной интеграл

В процессе решения задач по алгебре, геометрии, физике и другим дисциплинам часто встречается такое понятие как интеграл. С помощью интегрирования можно упростить достаточно громоздкие и сложные расчеты. Отдельно стоит рассмотреть тройной интеграл. При формулировке термина и расшифровке его смысла целесообразно воспользоваться алгоритмом действий, аналогичным введению понятия двойного интеграла.

Предположим, что имеется некоторая функция. Обозначим ее как (u=fleft( x; y; z right)). Введем условие, по которому область определения рассматриваемой функции соответствует ограниченной области (Omega) в трехмерном измерении и декартовой системой с координатами по осям (Oxyz). В замкнутом пространстве можно выделить некоторое количество фрагментов, равное n частям ({{Omega }_{i}}). Эти сегменты не обладают едиными точками внутри области, а для вычисления их объемов стоит воспользоваться соотношением:

(Delta {{V}_{i}}, i=overline{1; n}).

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

На следующем шаге необходимо отметить в каждой из выделенных ранее частей какую-либо точку ({{P}_{i}}left( {{x}_{i}}; {{y}_{i}}; {{z}_{i}} right)). Используя записанное выражение, несложно сформулировать соотношение для интегральной суммы в случае конкретной функции (u=fleft( x; y; z right)) по области (Omega). Выражение примет следующий вид:

(sumlimits_{i=1}^{n}{fleft( {{x}_{i}}; {{y}_{i}}; {{z}_{i}} right)Delta {{V}_{i}}})

Рассмотрим детально фрагменты ограниченного пространства, которые записаны как ({{Omega }_{i}}). Эти простейшие части имеют точки, которые ранее были обозначены, удаленные друг от друга на расстояние, вычисляемое по формуле:

(lambda =underset{1le ile n}{mathop{max }},dleft( {{Omega }_{i}} right))

Допустим, что имеется некий предел: (underset{lambda to 0}{mathop{lim }},sumlimits_{i=1}^{n}{fleft( {{x}_{i}}; {{y}_{i}}; {{z}_{i}} right)Delta {{V}_{i}}}.)

Этот предел определен вне зависимости от метода деления области пространства (Omega) на простейшие части ({{Omega }_{i}}). Значение также не имеет обозначение в рассматриваемых фрагментах точек ({{P}_{i}}). Если перечисленные условия выполнимы, то записанный предел является тройным интегралом по области (Omega). При обозначении данного понятия целесообразно обратиться к такому соотношению:

(iiintlimits_{Omega }{f(x;y;z)dV} text{ }text{ } , text{ }text{ } iiintlimits_{Omega }{f(x;y;z)dxdydz})

Из уже рассмотренного примера можно заключить, что область Omega ограничена в пространстве. Представим, что на нижней и верхней границе расположены следующие поверхности:

(z={{phi }_{1}}left( x; y right));
(z={{phi }_{2}}left( x; y right)).

В соответствии с этой информацией (({{phi }_{2}}left( x; y right)ge {{phi }_{1}}left( x; y right))). С боковых сторон относительно исследуемой области находится поверхность в форме цилиндра, образующие которой расположены параллельно по отношению к оси Oz. В плоскости D можно наблюдать изменения переменных х и у. Данную плоскую область допустимо считать проекцией (Omega) на плоскость с координатами Оху.

С целью определения элемента объема dv в условиях декартовой координатной системы стоит воспользоваться следующим соотношением: (dv=dxdydz). Таким образом, в случае рассматриваемого ограниченного пространства (Omega) тройной интеграл соответствует справедливому равенству:

(iiintlimits_{Omega}{f(x; y; z)dxdydz}=iintlimits_{D}{dxdy}intlimits_{{{phi }_{1}}left( x right)}^{{{phi }_{2}}left( x right)}{fleft( x; y; z right)dz})

Заметим, что интеграл внутри выражения (intlimits_{{{phi }_{1}}left( x right)}^{{{phi }_{2}}left( x right)}{fleft( x; y; z right)dz}) зависит и рассчитывается с учетом значения, которое принимает z. При этом х и у не меняют свои значения. В итоге операции интегрирования получают функцию переменных х и у, которую можно обозначить за (Fleft( x;y right)) . Таким образом, алгоритм определения тройного интеграла представляет собой процесс расчета двойного интеграла (iintlimits_{D}{Fleft( x; y right)dxdy}). Стоит отметить, что допустимо нахождение внутреннего интеграла по х или по у, что формирует определенный порядок действий при интегрировании.

Свойства тройного интеграла

Тройной интеграл обладает рядом характерных свойств. Такие закономерности позволяют существенно упростить и сократить объем расчетов в процессе интегрирования. Каждая из характеристик сопровождается формулой или соотношением. Сформулированные математические записи применимы к условиям какой-либо задачи. При поиске ответа нужно лишь привести расчеты под установленный формат записи или подставить в готовую формулу известные значения для вычисления искомых величин.

Тройной интеграл имеет следующие свойства:

Линейность. Когда некоторая функции (mathbf { textit { f } } (mathbf { textit { x } }, mathbf { textit { y } }, mathbf { textit { z } } ), mathbf { textit { g } } (mathbf { textit { x } }, mathbf { textit { y } }, mathbf { textit { z } } )) можно найти через интегралы по ограниченному пространству (mathbf { textit { V } }), линейная комбинация рассматриваемых функций (alpha f(x,y,z)+beta g(x,y,z)) аналогично поддается интегрированию по (mathbf { textit { V } }, а также iiintlimits_V { ,left[ { alpha f(P)+beta g(P) }right]dv } = alpha iiintlimits_V { f(P)dv } +beta iiintlimits_V { g(P)dv }.)
Аддитивность. При условии, что некоторое ограниченное пространство (mathbf { textit { V } }) представляет собой совмещение пары областей (mathbf { textit { V } } _ { 1 } и mathbf { textit { V } } _ { 2 }) , которые не обладают едиными точками, выполняется следующее равенство: (iiintlimits_V { f(P)dv } =iiintlimits_ { V_1 } { f(P)dv } +iiintlimits_ { V_2 } { f(P)dv }).
Интеграл от единичной функции по области можно рассчитать, используя такое соотношени (mathbf { textit { V } } quad textbf { равен объёму этой области: } iiintlimits_V { dv } =v(V)textbf { . })
Интегрирование неравенств. Представим, что для каких-либо точек (Pin V) справедливо выражение со знаком неравенства (f(P)leqslant g(P)), а также функции (mathbf { textit { f } } (mathbf { textit { P } } ), mathbf { textit { g } } (mathbf { textit { P } } ) ) можно интегрировать относительно ограниченного пространства (mathbf { textit { V } }). В таком случае (iiintlimits_V { f(P)dv } leqslant iiintlimits_V { g(P)dv }).
Теоремы об оценке интеграла. В той ситуации, когда функция (mathbf { textit { f } } (mathbf { textit { P } } ))имеет интеграл по некоторому ограниченному пространству (mathbf { textit { V } }), а также при условии (forall Pin V ) справедливо, что (mleqslant f(P)leqslant M), работает следующее соотношение (mcdot v(V)leqslant iiintlimits_V { f(P)dv } leqslant Mcdot v(V)). При условии, что функцию (mathbf { textit { f } } (mathbf { textit { P } } )) допустимо интегрировать по области (mathbf { textit { V } }) , можно записать такое выполняемое выражение (left| { iiintlimits_V { f(P)dv } }right|leqslant iiintlimits_V { ,vert f(P)vert dv }).
Теорема о среднем. Когда исследуемая функция (mathbf { textit { f } } (mathbf { textit { P } } )) не прерывается на области (mathbf { textit { V } }), можно говорить о существовании некоторой точки (P_0 in V), при наличии которой выполняется следующее равенство (iiintlimits_V { f(P)dv } =f(P_0 )cdot v(V)).

Геометрический смысл тройного интеграла, как вычислить

Заметим, что в процессе определения тройного интеграла речь идет о поиске числа, выражающего объем некоторой фигуры V, то есть фактически ограниченного пространства V. В этом заключается геометрический смысл тройного интеграла. С помощью рассмотренного ранее понятия достаточно просто вычислить объем какого-то тела, относительно которого рассчитывается этот интеграл.

Процесс интегрирования очень интересен с прикладной точки зрения. Например, рассмотреть понятие можно с помощью изучения работы органов дыхания человека, а именно, легких. Известно, что эти функциональные и жизненноважные структуры включают в себя более семи сотен миллионов альвеол, которые представляют собой пузырьки, защищенные капиллярными сетками. Данные образования обеспечивают необходимый газовый обменный процесс.

Представим, что объем газообразного вещества во внутреннем пространстве легких является какой-то ограниченной областью с компактными размерами. В этот объем включено некоторое количество объемов габаритами поменьше, то есть альвеол. Смысл этого сравнения заключается во множестве пузырьковых образований, составляющих объем дыхательных органов. Таким образом, большое число малостей с точки зрения математики определяет значение термина тройного интеграла.

Предположим, что имеется некоторое замкнутое пространство с границами. Обозначим его как V. Такая область считается простейшей правильной при выполнении пары условий:

проекция (mathbf { textit { V } }) на некоторую плоскость с координатами, в том числе, (mathbf { textit { Оху } }), представляет собой простую область (mathbf { textit { D } });
произвольная прямая линия, расположенная перпендикулярно относительно рассматриваемой плоскости, пересекает точку (mathbf { textit { V } })внутри области и границу (mathbf { textit { V } }) в паре точек.

Тогда справедливым является следующее выражение:

(V=left( { (x,y,z)vert (x,y)in D,;psi _1 (x,y)leqslant zleqslant psi _2 (x,y) }right))

При этом целесообразно выделить пару граничных поверхностей:

(z=psi _1 (x,y));
(z=psi _2 (x,y)).

схема

Источник: 3dstroyproekt.ru

Теорема 1

При условии наличия некоторой примитивной области (mathbf { textit { V } }), граница которой является кусочно-гладкой, а функция (mathbf { textit { f } } (mathbf { textit { P } } )) не прерывается, можно заключить, что: (iiintlimits_V { f(P)dv } =iintlimits_D { dxdyintlimits_ { psi _1 (x,y) } ^ { psi _2 (x,y) } { f(x,y,z)dz } }) .

Исходя из записанной теоремы и полезных свойств, перечисленных ранее, допустимо представить следующую формулу для расчета тройного интеграла:

(iiintlimits_V { f(P)dv } =iintlimits_D { dxdyintlimits_ { psi _1 (x,y) } ^ { psi _2 (x,y) } { f(x,y,z)dz } } =intlimits_a^b { dxintlimits_ { varphi _1 (x) } ^ { varphi _2 (x) } { dyintlimits_ { psi _1 (x,y) } ^ { psi _2 (x,y) } { f(x,y,z)dz } } }.)

Если при решении задачи требуется сформулировать тройной интеграл через двойной, но при измененном порядке интегрирования, то целесообразно обратиться к такому соотношению:

(iiintlimits_V { f(P)dv } =intlimits_ { z_ { min } } ^ { z_ { max } } { dziintlimits_ { D_z } { f(x,y,z) } } dxdy.)

В теоретическом материале достаточно емко изложен смысл тройного интеграла. Однако при решении практических заданий порой сложно сразу сориентироваться в применении той или иной формулы интегрирования. Важно владеть основными приемами вычисления тройного интеграла и помнить о характерных для этого понятия свойствах, которые помогают справиться с самыми сложными примерами.

Задача 1

С применением понятия и свойств интегрирования необходимо вычислить следующий пример: (I=iiintlimits_V { frac { dxdydz } { left( { 1+x+y+z }right)^3 } } ,;V:left[{ begin{array} { l } x=0,;y=0,;z=0, \ x+y+z=1. \ end{array} }right.)

К заданию прилагается рисунок для наглядной демонстрации описанных в задаче величин:

рисунок

Источник: 3dstroyproekt.ru

Решение

Заметим, что при проектировании фрагмента ограниченного пространства (mathbf { textit { V } }) на плоскость (mathbf { textit { Оху } }) получается геометрическая фигура в виде треугольника (D:left[{ x=0,;y=0,;x+y=1 }right]). Исходя из этого, запишем следующее справедливое соотношение:

(I=iiintlimits_V { frac { dxdydz } { left( { 1+x+y+z }right)^3 } } =iintlimits_D { dxdyintlimits_0^ { 1-x-y } { frac { dz } { (1+x+y+z)^3 } } } =iintlimits_D { left. { left[ { -frac { 1 } { 2 } cdot frac { 1 } { (1+x+y+z)^2 } }right] }right|_0^ { 1-x-y } dxdy })

Для наглядности представим такое изображение:

рисунок2

Источник: 3dstroyproekt.ru

Продолжим вычисления:

(I=-frac { 1 } { 2 } intlimits_0^1 { dx } intlimits_0^ { 1-x } { left[ { frac { 1 } { 4 } -frac { 1 } { (1+x+y)^2 } }right]dy } =-frac { 1 } { 2 } intlimits_0^1 { left. { left[ { frac { y } { 4 } +frac { 1 } { 1+x+y } }right] }right|_0^ { 1-x } dx } =-frac { 1 } { 2 } intlimits_0^1 { left[ { frac { 1-x } { 4 } +frac { 1 } { 2 } -frac { 1 } { 1+x } }right]dx } = \ =-frac { 1 } { 2 } intlimits_0^1 { left[ { frac { 1-x } { 4 } +frac { 1 } { 2 } -frac { 1 } { 1+x } }right]dx } =-frac { 1 } { 2 } left( { frac { 3x } { 4 } -frac { x^2 } { 8 } -ln (1+x) }right)_0^1 =-frac { 1 } { 2 } left( { frac { 3 } { 4 } -frac { 1 } { 8 } -ln 2 }right)=frac { 1 } { 2 } left( { ln 2-frac { 5 } { 8 } }right))

Ответ: (frac { 1 } { 2 } left( { ln 2-frac { 5 } { 8 } }right)).

Задача 2

Известно, что ограниченный фрагмент пространства обозначен за (Omega). Эта область имеет форму геометрической фигуры тетраэдра, граница которого представляет собой плоскость (2x+2y+z-6=0). Остальные границы являются плоскостями с координатами. Требуется определить значение тройного интеграла: (I=iiintlimits_{Omega }{xdxdydz}) I

Решение

(I=intlimits_{0}^{3}{dx}intlimits_{0}^{3-x}{dy}intlimits_{0}^{6-2x-2y}{xdz}=intlimits_{0}^{3}{xdx}intlimits_{0}^{3-x}{left. z_{{}}^{{}} right|_{0}^{6-2x-2y}dy}=intlimits_{0}^{3}{xdx}intlimits_{0}^{3-x}{left( 6-2x-2y right)dy}= intlimits_{0}^{3}{xleft. cdot left( 6y-2xy-{{y}^{2}} right) right|_{0}^{3-x}dx}=intlimits_{0}^{3}{xleft( 6left( 3-x right)-2xleft( 3-x right)-{{left( 3-x right)}^{2}} right)dx=} intlimits_{0}^{3}{left( {{x}^{3}}-6{{x}^{2}}+9x right)dx=}left. left( frac{{{x}^{4}}}{4}-frac{6{{x}^{3}}}{3}+frac{9{{x}^{2}}}{2} right) right|_{0}^{3}=frac{81}{4}-54+frac{81}{2}=frac{27}{4}.)

Ответ: (frac{27}{4}).

Источник

Тройные интегралы в прямоугольных координатах

Краткая теория

Тройным
интегралом от функции

, распространенным на
область

, называется предел
соответствующей трехкратной суммы:

Вычисление
тройного интеграла сводится к последовательному вычислению трех обыкновенных
(однократных) интегралов или к вычислению одного двойного и одного
однократного.

Основные
свойства тройных интегралов аналогичны свойствам двойных интегралов.

Объем
тела

в декартовых координатах

выражается формулой:

Примеры решения задач

Задача 1

Вычислить
тройной интеграл:

Решение

Ответ:

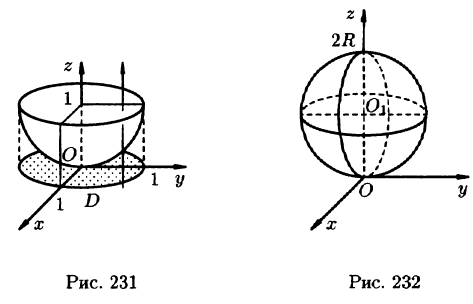
Задача 2

Вычислить
объем тела, ограниченного данными поверхностями. Сделать чертежи данного тела и
его проекции на плоскость

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Сделаем
чертеж тела:

Проекция
тела на

Искомый объем тела будет выражаться
интегралом:

Ответ:

Задача 3

Вычислить объем тела,
ограниченного заданными поверхностями:

Решение

Сделаем чертеж тела:

Проекция тела на

Искомый объем тела
будет выражаться интегралом:

Ответ:

Источник

2. ТРОЙНЫЕ ИНТЕГРАЛЫ

2.1. Определение тройного интеграла. Пусть функция f (x, y, z)

2.2. Вычисление тройных интегралов сводится к трехкратному интегрированию, то есть к последовательному вычислению трех

Вычисление тройного интеграла в декартовых координатах

Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах

Некоторые приложения тройного интеграла Объем тела

Масса тела

Статические моменты

Центр тяжести тела

Моменты инерции тела

Тройной интеграл

Вычисление тройного интеграла в декартовых координатах

Пример с решением 54-1

Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах.

Пример 54-2.

Пример 54-3.

Некоторые приложения тройного интеграла

Пример 54 4.

Вычисление тройного интеграла

Что такое тройной интеграл

Свойства тройного интеграла

Геометрический смысл тройного интеграла, как вычислить

Тройные интегралы в прямоугольных координатах

Краткая теория

Примеры решения задач

Задача 1

Задача 2

Задача 3

Не пропустите также: