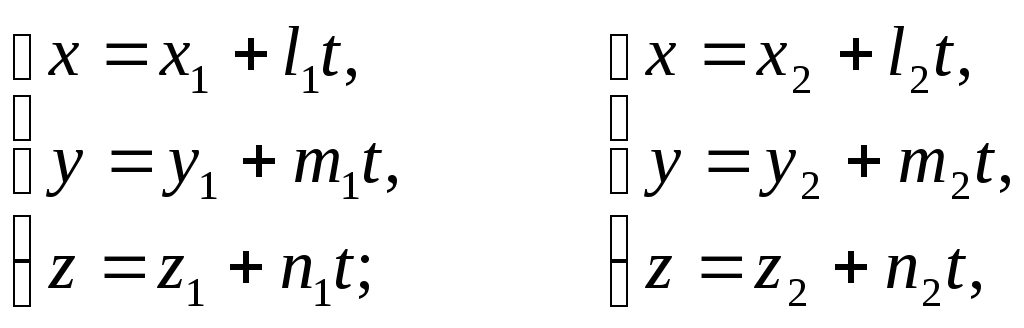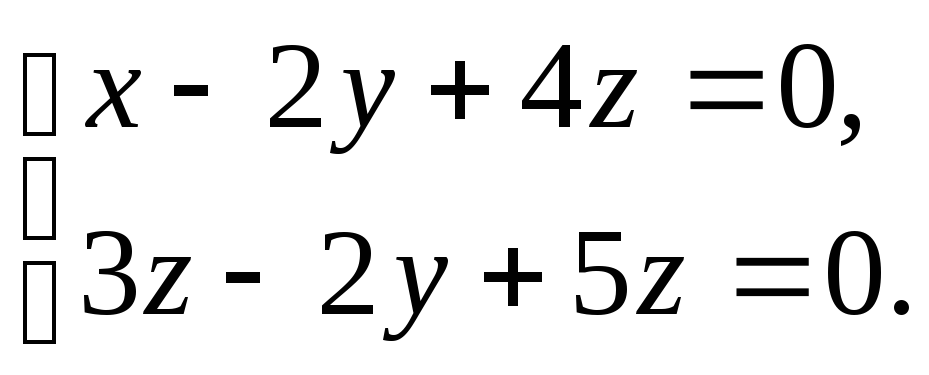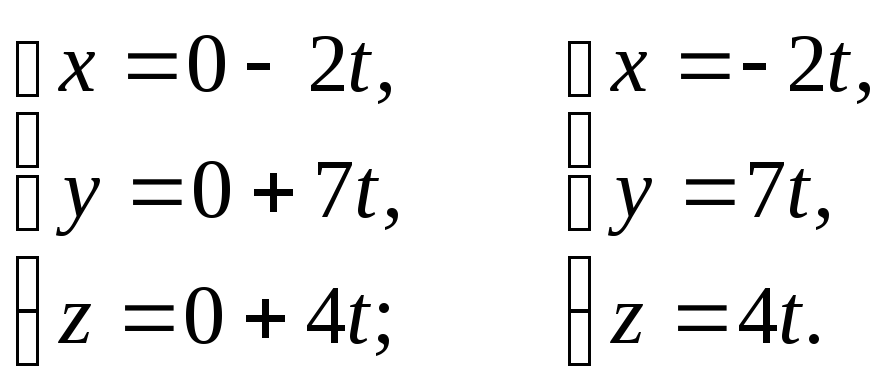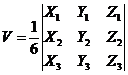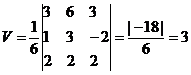Как найти объем тетраэдра отсекаемого плоскостью - AvtoShod.ru

Задача:
Чему равен объем треугольной пирамиды, отсекаемой плоскостью 3x+ 4y+ 5z = 60 от осей координат?

Решение:
Объем пирамиды, отсекаемой плоскостью

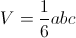
от осей координат, вычисляется по формуле:
.

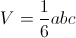
Приведем данное нам уравнение плоскости к виду уравнения плоскости в отрезках. Для этого обе части уравнения разделим на 60.
Получим уравнение:

,
.
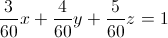
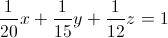
Отсюда,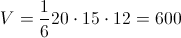
квадратных единиц.

Ответ:

квадратных единиц.

Источник

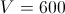
Справедливо
следующее утверждение: если в пространстве
дана произвольная декартова прямоугольная
система координат
,
то всякое линейное уравнение с тремя
переменными

и

определяет относительно этой системы
плоскость, уравнение которой имеет вид:

,
(23)

где

не равны нулю одновременно.

Уравнение (23)
называется общим
уравнением плоскости,
причём числа

являются координатами
некоторого вектора
,
который нормален к плоскости.

Уравнение

(24)

эквивалентно
уравнению (23) и определяет плоскость,
проходящую через заданную точку

и перпендикулярную вектору
.
Вектор

мы будем называть нормальным
вектором плоскости.

Уравнение плоскости
в отрезках на осях таково:

,
(25)

где
отрезки,
отсекаемые плоскостью соответственно
на осях
.

Уравнение плоскости,
проходящей через точку
,
параллельно двум неколлинеарным векторам

и
,
записывается так:

.
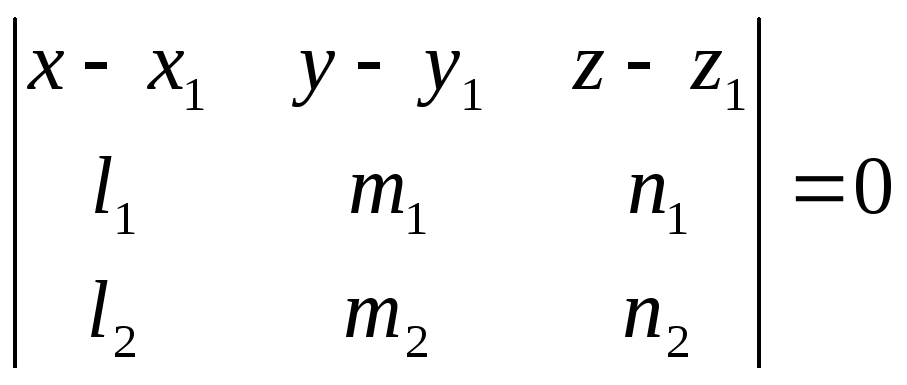
(26)

Уравнение плоскости,
проходящей через точки

и
,
параллельно вектору
,
неколлинеарному вектору

пишется в виде:

.
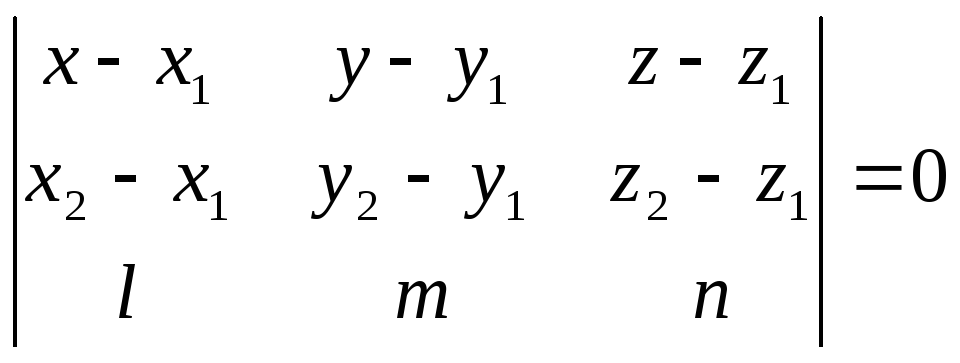
(27)

Уравнение плоскости,
проходящей через 3 точки, не лежащие на
одной прямой,

записывается так:

.
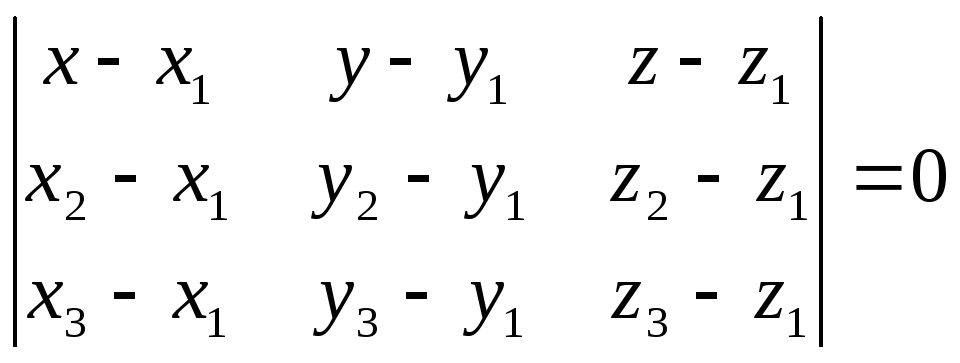
(28)

Угол между
плоскостями

и

с векторами нормалей

и

определяется по формуле:

.
(29)

Необходимым и
достаточным условием совпадения двух
плоскостей является пропорциональность
всех коэффициентов их общих уравнений,
т.е.

.
(30)

Необходимым и
достаточным условием параллельности
двух плоскостей является пропорциональность
коэффициентов при
:

причём
.
(31)

Необходимым и
достаточным условием того, что три
плоскости

имеют одну общую
точку, является условие

.
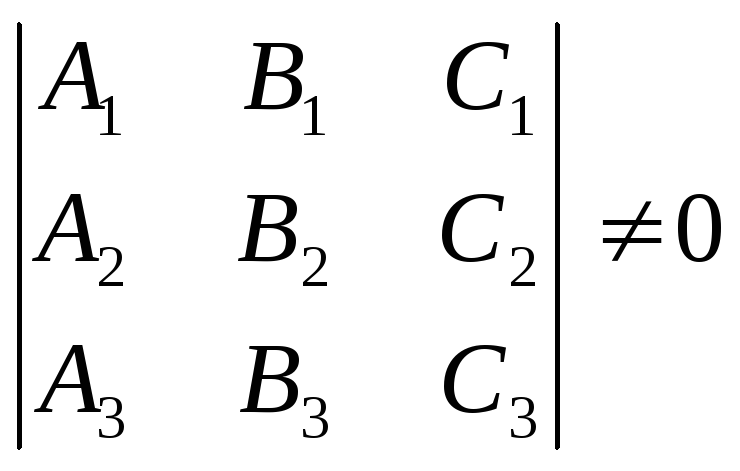
(32)

Необходимым и
достаточным условием перпендикулярности
двух плоскостей является условие
,
т.е.

.
(33)

Расстояние

от точки

до плоскости

в прямоугольной системе координат
находится по формуле:

.
(34)

Если плоскость не
проходит через начало координат и
углы
вектора нормали
,
имеющего начало в начале координат с
осями
,
то нормальное уравнение плоскости имеет
вид:

.
(35)

Чтобы общее
уравнение (23) плоскости привести к
нормальному виду (35), нужно общее уравнение
плоскости умножить на
.
Знак перед дробью выбирается противоположным
знаку
.

Прямая в пространстве

—
линия пересечения 2-х непараллельных
плоскостей, если плоскости заданы общими
уравнениями, то прямая в общем виде
задаётся, как результат пересечения
этих плоскостей, то есть системой
уравнений

(36)

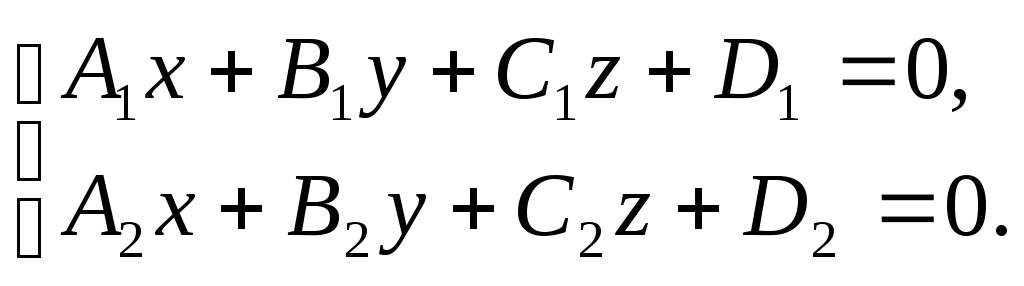
Прямая, проходящая
через точку
,
параллельно вектору

(направляющий вектор прямой), определяется
уравнениями:

,
(37)

или

,
(38)

где (37) –
параметрические
уравнения
прямой, (38) – канонические
уравнения.

Если прямая задана
двумя точками

и
,
то канонические уравнения прямой
запишутся в виде:

.
(39)

Необходимое и
достаточное условие того, что две прямые

лежат в одной
плоскости, записывается в виде:

.
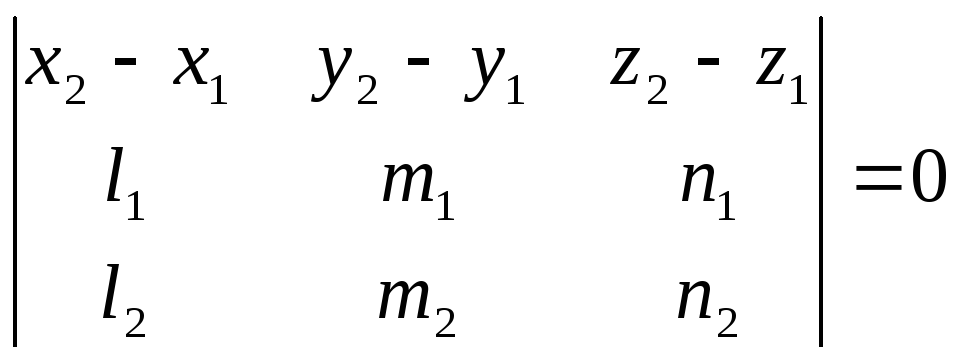
(40)

Условие параллельности
двух прямых имеет вид:

.
(41)

Условие
перпендикулярности двух прямых:

.
(42)

Углы между двумя
прямыми в прямоугольной системе координат
определяются соотношениями:

.
(43)

ПРИМЕРЫ РЕШЕНИЯ
ЗАДАЧ

Задача 1. Составить
уравнение плоскости, проходящей через
три точки
.

Решение.
Воспользуемся уравнением плоскости
(28), проходящей через три точки:

Раскрыв определитель
по элементам первой строки, получаем
уравнение плоскости:

или

Задача 2. Определить
объём тетраэдра, ограниченного
координатными плоскостями и плоскостью

Решение.
Пусть
объём
тетраэдра.
,
где
площадь
основания,
высота.

В основании
тетраэдра лежит прямоугольный треугольник,
катеты которого есть отрезки, отсекаемые
плоскостью

на осях

и
.
Высота

тетраэдра, опущенная на основание, есть
отрезок, отсекаемый плоскостью на оси

.
Поэтому, чтобы найти объём тетраэдра,
нужно записать уравнение плоскости

в виде
,
где
отрезки,
отсекаемые этой плоскостью на осях

соответственно.

Разделив обе части
на 18, получим
.
Итак,
.

(ед³).

Задача 3. Составить
уравнение плоскости, проходящей через
две точки

и

и параллельной вектору
.

Решение.
Векторы

и

неколлинеарны, так как их координаты
не пропорциональны.

Следовательно,
можно воспользоваться уравнением (27).
Подставив вместо

и

координаты точек

и вектора

соответственно, получим:

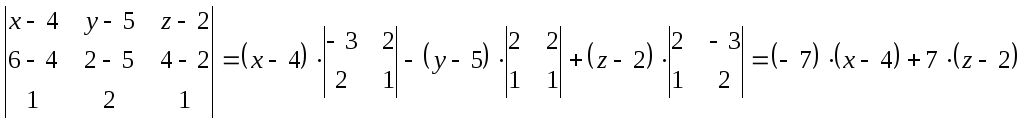
Таким образом,
получили уравнение:

Разделим обе части
полученного уравнения на

и приведём подобные, окончательно
получаем:

Задача 4. Даны две
точки
.
Составить уравнение плоскости, проходящей
через точку

и перпендикулярной к прямой
.

Решение.
Уравнение плоскости будем искать по
формуле (24).

Вектор

перпендикулярен искомой плоскости, так
как прямая

перпендикулярна плоскости.

Следовательно,
.
Вместо

подставим координаты точки
.

уравнение
искомой плоскости.

Задача 5. Определить
расстояние от точки

до плоскости
.

Решение.
Запишем уравнение плоскости в нормальном
виде. Выпишем нормирующий множитель
.
В нашем случае
.
Следовательно,
.

Так как свободный
член в уравнении плоскости

положительный, то обе части уравнения
умножим на
:

Пусть
расстояние
от точки

до плоскости
.
Тогда

Задача 6. Составить
уравнение прямой, проходящей через
точки
,

Решение.
В уравнения (38) подставим вместо

и

координаты точек

и

соответственно:

Канонические
уравнения искомой прямой:

Задача 7. Составить
параметрические уравнения прямой

Решение.
Прямая задана как результат пересечения
двух плоскостей. Чтобы записать
параметрические уравнения прямой, нужно
знать координаты какой-нибудь точки,
принадлежащей прямой, и вектор,
параллельный прямой, то есть её
направляющий вектор.

Точку, принадлежащую
прямой, можно найти, если решить систему
уравнений, задающих прямую. Так как
уравнений два, а неизвестных три, то
одно неизвестное, например
,
нужно определить произвольным образом,
положив его равным какому-либо числу.
Но в данной задаче обе плоскости проходят
через начало координат, то есть через
точку
,
так как их свободные члены равны нулю.
Следовательно, в качестве точки,
принадлежащей прямой, можно взять точку

В качестве
направляющего вектора прямой возьмём
вектор
,
где

и

нормальные векторы плоскостей. Здесь
мы воспользовались тем фактом, что
результат векторного произведения двух
ненулевых векторов перпендикулярен
плоскости этих векторов. То есть

и
,
следовательно, вектор

параллелен прямой.

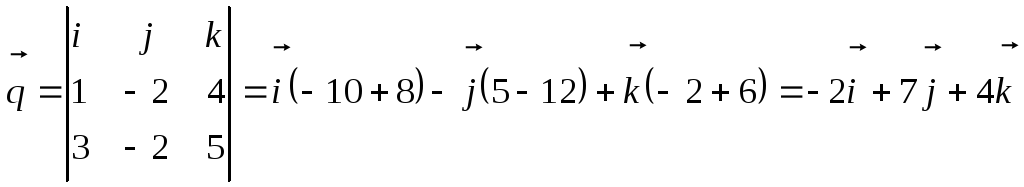
Искомые уравнения
прямой:

Задача 8. Установить,
лежат ли следующие точки на одной прямой:

Решение.
Напишем канонические уравнения прямой,
проходящей, например, через точки

и
:

Если три точки
лежат на одной прямой, то координаты
третьей точки должны удовлетворять
полученным уравнениям прямой. Вместо

подставим

соответственно:

Следовательно,
все три заданные точки лежат на одной
прямой.

Задача 9. Найти
точку пересечения прямой

с плоскостью
.

Решение.
Подставим вместо

в уравнение плоскости:

соответственно:

Отсюда
.
Найденное значение параметра
,
соответствующее общей точке прямой и
плоскости, подставим в параметрические
уравнения прямой:

координаты
точки пересечения.

Задача 10. Составить
уравнение плоскости, проходящей через
точку

и через прямую
.

Решение.
Решение данной задачи сводится к
написанию уравнения плоскости, проходящей
через две заданные точки, параллельно
некоторому вектору.

Так как прямая
принадлежит плоскости, то точка
,
через которую проходит эта прямая, также
принадлежит плоскости. Направляющий
вектор прямой

параллелен плоскости.

Подставляя
координаты точек и вектора в уравнение
(27), получим:

;

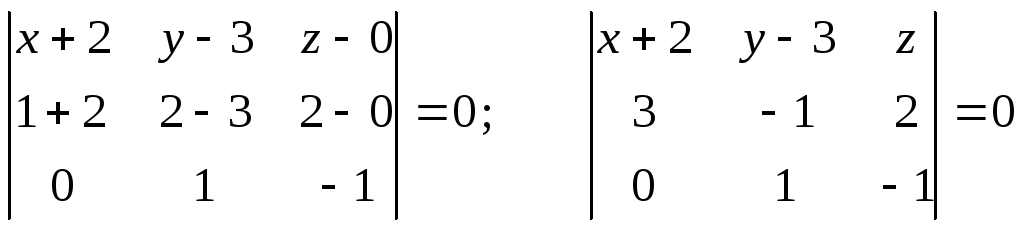
Уравнение плоскости:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Объем пирамиды

Если заданы координаты точек вершин пирамиды, то координаты векторов находятся по формуле:
X = x_j — x_i; Y = y_j — y_i; Z = z_j — z_i
где x_i, y_i, z_i — координаты точки А_i; x_j, y_j, z_j — координаты точки А_j;

Пример №2 . Найти объем пирамиды, отсекаемой от угла плоскостью, проходящей через точки А(0,2,-1), В(3,4,2), С(-3,0,4).

Онлайн калькулятор. Объем пирамиды (объем тетраэдра) построенной на векторах.

Этот онлайн калькулятор позволит вам очень просто найти объем пирамиды или объем тетраэдра построенных на векторах.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление объема пирамиды построенной на векторах и закрепить пройденый материал.

Калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторах

Выберите каким образом задается пирамида (тетраэдр):

Введите значения векторов: Введите координаты вершин пирамиды:

Инструкция использования калькулятора для вычисления объема пирамиды (объема тетраэдра) построенной на векторах

Ввод данных в калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторах

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора вычисления объема пирамиды (объема тетраэдра) построенной на векторах

Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.

Теория. Объем пирамиды (объем тетраэдра) построенной на векторах

Определение Объем пирамиды (объем тетраэдра) построенной на векторах a , b и c равен шестой части модуля смешанного произведения векторов составляющих пирамиду:

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Как рассчитать объем пирамиды по координатам вершин? Методика и пример задачи

Часто в задачах школьного курса геометрии приходится решать задания, которые требуют использования комплексного подхода. Одной из таких задач является вычисление объема пирамиды по координатам вершин. Как решить эту геометрическую задачу — ответит приведенная ниже статья.

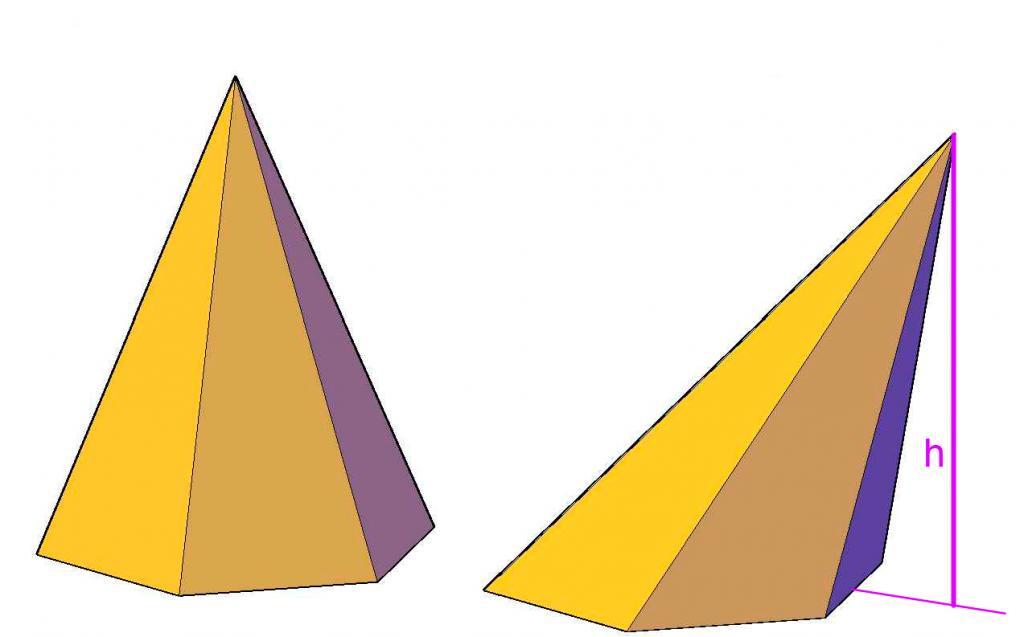
Что представляет собой пирамида?

Говоря простыми словами, под этой фигурой понимают пространственный объект, ограниченный треугольными сторонами и одной многоугольной гранью, которая называется основанием. Многоугольное основание может быть произвольным n-угольником на плоскости, например, правильным треугольником, параллелограммом и так далее.

Вам будет интересно: Какую роль играет репродуктивная клетка животных и растений?

Любая пирамида имеет n + 1 грань, 2 * n ребер и n + 1 вершину. Вершины фигуры не являются равноправными. Так, существует единственная вершина, которая не принадлежит основанию. Она называется главной. Расстояние от нее до плоскости основания — это высота фигуры.

Пирамиды могут быть наклонными, если высота пересекает основание не в его центре, или прямыми, когда высота с основанием пересекается в геометрическом центре последнего. Также фигуры могут быть неправильными и правильными. Пирамиды правильные состоят из равноугольного и равностороннего основания и нескольких равнобедренных треугольников, которые друг другу равны.

Как рассчитывается объем пирамиды?

Прежде чем приводить методику вычисления по координатам вершин объема пирамиды, следует привести формулу, при помощи которой можно рассчитать эту величину для фигуры любого типа из рассматриваемого класса. Итак, объем пирамиды рассчитывается так:

Здесь So — это основания площадь, h — расстояние от главной вершины до основания, то есть высота пирамиды.

Таким образом, любая геометрическая задача на нахождение объема пирамиды сводится к расчету величин So и h.

Как найти объем пирамиды по координатам вершин: методика

Пирамида может быть представлена произвольным n-угольным основанием. Чтобы рассчитать его площадь, следует внимательно изучить условие задачи, в котором должно быть сказано, о каком типе n-угольника идет речь. Если это треугольник или параллелограмм, то расчет его площади по известным координатам очень прост: необходимо лишь найти векторное произведение соответствующих векторов сторон.

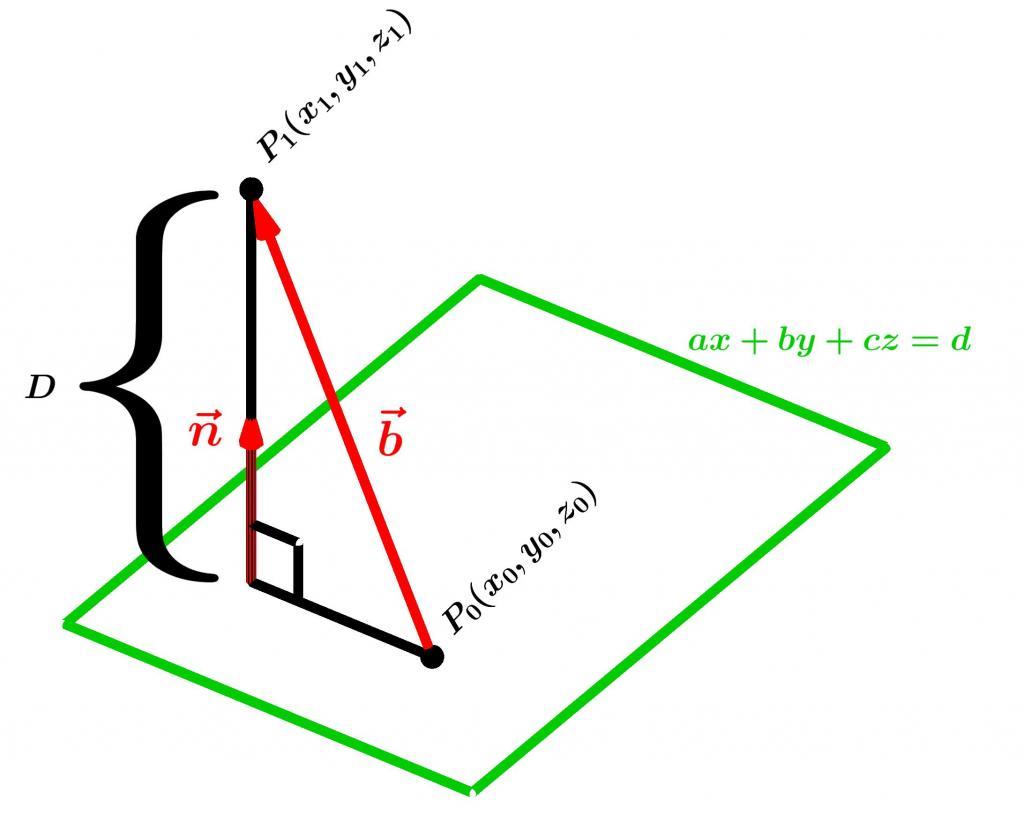
Вычислить высоту пирамиды также не представляет особого труда. Для этого следует из любых трех точек основания получить уравнение плоскости в общем виде, а затем нужно воспользоваться формулой расстояния между плоскостью и точкой (вершиной пирамиды). Формула имеет вид:

d = |(A * x1 + B * y1 + C * z1 + D)| / √(A2 + B2 + C2).

Здесь (x1; y1; z1) — координаты точки.

Уравнение плоскости имеет вид:

A * x + B * y + C * z + D = 0.

Задача с треугольной пирамидой

Решим задачу на примере самой простой пирамиды — треугольной. Условие простое: ниже даны координаты вершин пирамиды, объем найти нужно для фигуры, которая на этих координатах построена:

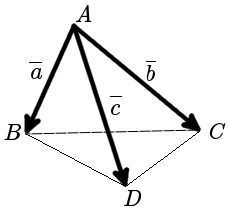
Положим, что основание пирамиды является треугольником ABC. Найдем длины векторов AB¯ и AC¯:

Векторное произведение AB¯ и AC¯ даст нам, с одной стороны, двойную площадь треугольника, то есть 2 * So, а с другой стороны, мы получим координаты нормального к плоскости вектора n¯, имеем:

n¯ = [AB¯ * AC¯] = (8; -10; -7).

Площадь треугольного основания равна полудлине вектора n¯, то есть:

So = √(82 + 102 + 72) / 2 = 7,3.

Прежде чем рассчитывать расстояние от D до плоскости ABC, необходимо записать уравнение плоскости. Три его коэффициента (A, B, C) мы уже знаем, они соответствуют координатам нормали n¯. Свободный член можно получить, подставив в уравнение координаты любой точки плоскости, например точки A, имеем:

D = -1 * (A * x1 + B * y1 + C * z1) = -1 * (8 * 1 + (-10) * 0 + (-7) * 3) = 13.

Тогда уравнение плоскости основания пирамиды принимает форму:

8 * x — 10 * y — 7 * z + 13 = 0.

Теперь применяем приведенную выше формулу для расчета расстояния от точки D(4; 3; 4) до найденной плоскости, получаем:

d = |(8 * 4 — 10 * 3 — 7 * 4 + 13)| / √(82 + 102 + 72) = 0,89.

Поскольку найденное значение расстояния d соответствует высоте пирамиды треугольной h, то можно воспользоваться формулой для объема фигуры:

V = 1 / 3 * So * h = 1 / 3 * 7,3 * 0,89 ≈ 2,166.

Полученное значение объема выражено в кубических единицах выбранной координатной системы.

источники:

http://ru.onlinemschool.com/math/assistance/vector/pyramid_volume/

http://1ku.ru/obrazovanie/51574-kak-rasschitat-obem-piramidy-po-koordinatam-vershin-metodika-i-primer-zadachi/

Источник

Условие

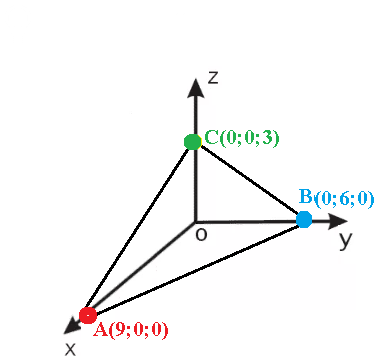
Определить объем тетраэдра, ограниченного координатными плоскостями и плоскостью а, проходящей через точки А (0; 4; 1), В (6; 2; 0), С (3; 0; 2). Найти угол между плоскостью а и плоскостью ХОУ.

математика ВУЗ
286

Решение

★

Составим уравнение плоскости, проходящей через точки А (0; 4; 1), В (6; 2; 0), С (3; 0; 2)

Общий вид уравнения:
ax+by+cz+d=0

Подставляем координаты точек
А (0; 4; 1)
a*0+b*4+c*1+d=0
В (6; 2; 0)
a*6+b*2+c*0+d=0
С (3; 0; 2)
a*3+b*0+c*2+d=0

Решаем систему уравнений:
{4b+c+d=0 ⇒ c=-4b-d
{6a+2b+d=0
{3a+2c+d=0

{ c=-4b-d
{6a+2b+d=0
{3a+2(-4b-d)+d=0

{ c=-4b-d
{6a+2b+d=0
{3a-8b-d=0

Складываем два последних

{ c=-4b-d
{6a+2b+d=0
{9a-6b=0 ⇒ 3a=2b ⇒ 6a=4b и подставляем во второе

{ c=-4b-d
{4b+2b+d=0 ⇒ b=(-1/6)d
{ 6a=4b

{ c=(-1/3)d
{4b+2b+d=0 ⇒ b=(-1/6)d
{ a=-(1/9)d

(-1/9)dx+(-1/6)dy+(-1/3)dz+d=0

Делим на D

(-1/9)x-(1/6)y-(1/3)z+1=0 ⇒ (-1/9)x-(1/6)y-(1/3)z+1=0

[b]2x+3y+6z-18=0[/b] — общее уравнение плоскости α с нормальным вектором vector{n_(1)}=(2;3;6}

(x/9)x+(y|6)+(z/3)=1 — уравнение плоскости в отрезках

Объем тетраэдра

V=(1/3)*S_( осн)*H=(1/3)*((1/2)*9*6)*3=27

S_( осн)=S_( Δ AOB)

H=OC

Уравнение плоскости ХОУ:

z=0

Нормальный вектор
vector{n_(2)}=(0;0;1}

Угол между плоскостями — угол между их нормальными векторами.

Находим угол между vector{n_(1)}=(2;3;6} и vector{n_(2)}=(0;0;1}

cos φ =vector{n_(1)}* vector{n_(1)}/(|vector{n_(1)}|* |vector{n_(1)}|)

Скалярное произведение:

vector{n_(1)}* vector{n_(1)}=2*0+3*0+6*1=6

|vector{n_(1)}|=sqrt(2^2+3^2+6^2)=7

|vector{n_(2)}|=1

cos φ =vector{n_(1)}* vector{n_(1)}/(|vector{n_(1)}|* |vector{n_(1)}|)=6/(1*7)=6/7

φ= arccos(6/7)

Написать комментарий

Источник

Определение тетраэдра

Тетраэдр – простейшее многогранное тело, гранями и основанием которого являются треугольники.

Онлайн-калькулятор объема тетраэдра

Тетраэдр имеет четыре грани, каждая их которых образована тремя сторонами. Вершин у тетраэдра четыре, из каждой выходит по три ребра.

Данное тело разделяется на несколько видов. Ниже приведена их классификация.

Равногранный тетраэдр — у него все грани являются одинаковыми треугольниками;
Ортоцентрический тетраэдр — все высоты, проведенные из каждой вершины на противолежащую грань, являются одинаковыми по длине;
Прямоугольный тетраэдр — ребра, исходящие из одной вершины, образуют друг с другом угол в 90 градусов;
Каркасный;
Соразмерный;
Инцентрический.

Формулы объема тетраэдра

Объем данного тела можно найти несколькими способами. Разберем их более подробно.

Через смешанное произведение векторов

Если тетраэдр построен на трех векторах с координатами:

a⃗=(ax,ay,az)vec{a}=(a_x, a_y, a_z)
b⃗=(bx,by,bz)vec{b}=(b_x, b_y, b_z)
c⃗=(cx,cy,cz)vec{c}=(c_x, c_y, c_z),

тогда объем этого тетраэдра это смешанное произведение этих векторов, то есть такой определитель:

Объем тетраэдра через определитель

V=16⋅∣axayazbxbybzcxcycz∣V=frac{1}{6}cdotbegin{vmatrix}
a_x & a_y & a_z \
b_x & b_y & b_z \
c_x & c_y & c_z \
end{vmatrix}

Задача 1

Известны координаты четырех вершин октаэдра. A(1,4,9)A(1,4,9), B(8,7,3)B(8,7,3), C(1,2,3)C(1,2,3), D(7,12,1)D(7,12,1). Найдите его объем.

Решение

A(1,4,9)A(1,4,9)
B(8,7,3)B(8,7,3)
C(1,2,3)C(1,2,3)
D(7,12,1)D(7,12,1)

Первым шагом является определение координат векторов, на которых построено данное тело.
Для этого необходимо найти каждую координату вектора путем вычитания соответствующих координат двух точек. Например, координаты вектора AB→overrightarrow{AB}, то есть, вектора, направленного от точки AA к точке BB, это разности соответствующих координат точек BB и AA:

AB→=(8−1,7−4,3−9)=(7,3,−6)overrightarrow{AB}=(8-1, 7-4, 3-9)=(7, 3, -6)

Далее, аналогично:

AC→=(1−1,2−4,3−9)=(0,−2,−6)overrightarrow{AC}=(1-1, 2-4, 3-9)=(0, -2, -6)
AD→=(7−1,12−4,1−9)=(6,8,−8)overrightarrow{AD}=(7-1, 12-4, 1-9)=(6, 8, -8)

Теперь найдем смешанное произведение данных векторов, для этого составим определитель третьего порядка, при этом принимая, что AB→=a⃗overrightarrow{AB}=vec{a}, AC→=b⃗overrightarrow{AC}=vec{b}, AD→=c⃗overrightarrow{AD}=vec{c}.

∣axayazbxbybzcxcycz∣=∣73−60−2−668−8∣=7⋅(−2)⋅(−8)+3⋅(−6)⋅6+(−6)⋅0⋅8−(−6)⋅(−2)⋅6−7⋅(−6)⋅8−3⋅0⋅(−8)=112−108−0−72+336+0=268begin{vmatrix}
a_x & a_y & a_z \
b_x & b_y & b_z \
c_x & c_y & c_z \
end{vmatrix}=
begin{vmatrix}
7 & 3 & -6 \
0 & -2 & -6 \
6 & 8 & -8 \
end{vmatrix}=7cdot(-2)cdot(-8) + 3cdot(-6)cdot6 + (-6)cdot0cdot8 — (-6)cdot(-2)cdot6 — 7cdot(-6)cdot8 — 3cdot0cdot(-8) = 112 — 108 — 0 — 72 + 336 + 0 = 268

То есть, объем тетраэдра равен:

V=16⋅∣axayazbxbybzcxcycz∣=16⋅∣73−60−2−668−8∣=16⋅268≈44.8 см3V=frac{1}{6}cdotbegin{vmatrix}
a_x & a_y & a_z \
b_x & b_y & b_z \
c_x & c_y & c_z \
end{vmatrix}=frac{1}{6}cdot
begin{vmatrix}
7 & 3 & -6 \
0 & -2 & -6 \
6 & 8 & -8 \
end{vmatrix}=frac{1}{6}cdot268approx44.8text{ см}^3

Ответ

44.8 см3.44.8text{ см}^3.

Формула объема равногранного тетраэдра по его стороне

Эта формула справедлива только для вычисления объема равногранного тетраэдра, то есть такого тетраэдра, у которого все грани являются одинаковыми правильными треугольниками.

Объем равногранного тетраэдра

V=2⋅a312V=frac{sqrt{2}cdot a^3}{12}

aa — длина ребра тетраэдра.

Задача 2

Определить объем тетраэдра, если дана его сторона, равная 11 см11text{ см}.

Решение

a=11a=11

Подставляем aa в формулу для объема тетраэдра:

V=2⋅a312=2⋅11312≈156.8 см3V=frac{sqrt{2}cdot a^3}{12}=frac{sqrt{2}cdot 11^3}{12}approx156.8text{ см}^3

Ответ

156.8 см3.156.8text{ см}^3.

На нашем сайте вы можете оформить выполнение контрольных работ на заказ онлайн!

Тест по теме «Объем тетраэдра»

Источник

Объем пирамиды

Онлайн калькулятор. Объем пирамиды (объем тетраэдра) построенной на векторах.

Калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторах

Инструкция использования калькулятора для вычисления объема пирамиды (объема тетраэдра) построенной на векторах

Ввод данных в калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторах

Дополнительные возможности калькулятора вычисления объема пирамиды (объема тетраэдра) построенной на векторах

Теория. Объем пирамиды (объем тетраэдра) построенной на векторах

Как рассчитать объем пирамиды по координатам вершин? Методика и пример задачи

Что представляет собой пирамида?

Как рассчитывается объем пирамиды?

Как найти объем пирамиды по координатам вершин: методика

Задача с треугольной пирамидой

Условие

Решение

Написать комментарий

Онлайн-калькулятор объема тетраэдра

Формулы объема тетраэдра

Через смешанное произведение векторов

Формула объема равногранного тетраэдра по его стороне

Тест по теме «Объем тетраэдра»

Не пропустите также: