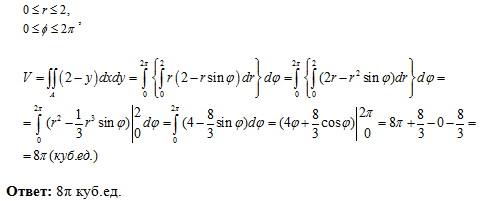Как найти объем тела ограниченного поверхностью онлайн - AvtoShod.ru

Undo

Square

Power

Square Root

−

≤

≥

(

)

Absolute Value

Источник

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	— twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{»}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Радианы}	mathrm{Степени}	square!	(	)	%	mathrm{очистить}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	—
pi	e	x^{square}	0	.	bold{=}	+

Подпишитесь, чтобы подтвердить свой ответ

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

объем:y=(3x+1)^{frac{1}{4}},:x=0,:x=8,:y=0
объем:y=sqrt{49-x^{2}},:y=0
объем:y=x+1,:y=0,:x=0,:x=2
объем:y=11e-x^{2},:y=0,:x=0,:x=1
объем:около:x=-1,:y=sqrt[3]{x},:y=1
Показать больше

Описание

Найдите объем тела вращения шаг за шагом

volume-calculator

объем y=(3x+1)^{frac{1}{4}}, x=0, x=8, y=0

Блог-сообщения, имеющие отношение к Symbolab

Practice Makes Perfect

Learning math takes practice, lots of practice. Just like running, it takes practice and dedication. If you want…

Введите Задачу

Сохранить в блокнот!

Войти

Источник

Калькулятор для нахождения объема тела, ограниченного поверхностями, заданными уравненинями.

Найдите объем тела, ограниченного поверхностями, заданными уравненинями `x^2+y^2=1,x^2+y^2=z,z=0`.

Для решения задач необходимо зарегистрироваться.

Источник

Вычислить объем тела, ограниченного поверхностями.

Пример 1:

Вычислить объем тела, ограниченного поверхностями (по площадям сечений).

Решение от преподавателя:

Строим графики функций:

Тогда объем тела вращения вокруг оси будем находить по формуле:

Ответ:.

Пример 2:

Найти объем тела, полученного вращением криволинейной трапеции вокруг оси ОХ.

Решение от преподавателя:

Пример 3:

Решение от преподавателя:

Пример 4:

Вычислить объем тела, ограниченного поверхностями:

Решение от преподавателя:

Изобразим поверхность:

то есть z меняется от

Пример 5:

Вычислить объемы тел, ограниченных поверхностями.

Решение от преподавателя:

Пример 6:

Объем тела, ограниченного поверхностью, полученной от вращения дуги кривой вокруг оси Ох.

Решение от преподавателя:

Объем фигуры, образованной в результате вращения вокруг оси Ox криволинейной трапеции, ограниченной непрерывной кривой y = f(x) (a ≤ x ≤ b), Осью Ox и прямыми x= a и x = b, вычисляется по формуле:

Построим график функции:

Пример 7:

Вычислить с помощью двойного интеграла объем тела, ограниченного указанными поверхностями:

Решение от преподавателя:

Пример 8:

Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной кривыми

Решение от преподавателя:

Работа вам нужна срочно. Не волнуйтесь, уложимся!

Заполните, пожалуйста, данные для автора:

22423 авторов готовы помочь тебе.
2402 онлайн

Источник

18:22

Объем тела вращения

Вычисление объема тела вращения вокруг оси Ох

Пусть график функции y = f(x) вращается вокруг оси Ox, образуя так называемую поверхность вращения. Определим объем тела, ограниченного этой поверхностью и плоскостями x = a, x = b.

Объем тела вращения, образованного вращением графика y=f(x) вокруг оси Ox, может быть вычислен по формуле

Пример 1. Вычислить объем тела, образованного вращением дуги кривой y=x², x∈[1,3] вокруг оси Оx.

Решение. Данные a=1, b=3, f(x)=x², подставляем в формулу, получаем

С помощью калькулятора проверяем правильность вычисления объема , а также получаем рисунок тела вращения.

Вычисление объема тела вращения вокруг оси Оy

Пусть график функции x=φ(y) вращается вокруг оси Oy, образуя так называемую поверхность вращения. Определим объем тела, ограниченного этой поверхностью и плоскостями y = c, y = d.

Объем тела вращения, образованного вращением графика x=φ(y) вокруг оси Oy, может быть вычислен по формуле

Пример 2. Вычислить объем тела, образованного вращением дуги кривой x=3y-y², x∈[1,2] вокруг оси Оx.

Решение. Данные c=1, d=2, φ(y)=3y-y², подставляем в формулу, получаем

В калькулятор вставляем функцию x=3y-y², x меняем на y, границы от 1 до 2, проверяем правильность вычисления объема , а также получаем рисунок тела вращения.

Следующая тема: Вычислить длину кривой

Категория: Вычислить интеграл | Просмотров: 109978 | | Теги: приложение интегралов | Рейтинг: 3.6/17

Источник

Номер Строки

Калькулятор для нахождения объема тела, ограниченного поверхностями, заданными уравненинями.

Найдите объем тела, ограниченного поверхностями, заданными уравненинями `x^2+y^2=1,x^2+y^2=z,z=0`.

Для решения задач необходимо зарегистрироваться.

Вычислить объем тела, ограниченного поверхностями.

Пример 1:

Решение от преподавателя:

Пример 2:

Решение от преподавателя:

Пример 3:

Решение от преподавателя:

Пример 4:

Решение от преподавателя:

Пример 5:

Решение от преподавателя:

Пример 6:

Решение от преподавателя:

Пример 7:

Решение от преподавателя:

Пример 8:

Решение от преподавателя:

Работа вам нужна срочно. Не волнуйтесь, уложимся!

Заполните, пожалуйста, данные для автора:

Объем тела вращения

Не пропустите также: