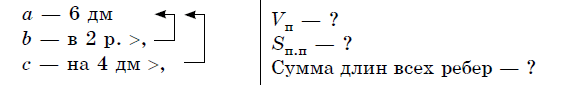Как найти объем прямоугольного параллелепипеда задачи - AvtoShod.ru

Индивидуальное
задание

1. Пример. Чему равен объем параллелепипеда с измерениями 2 см, 3 см и 4 см?

Решение. Воспользуемся формулой для нахождения объема прямоугольного
параллелепипеда V = a · b
· c, где a, b, c – измерения прямоугольного параллелепипеда.

V = 2 ·3 · 4 = 24 см³

Ответ:
V = 24 см³

Выполни по
образцу: вычислите объем прямоугольного
параллелепипеда, измерения которого равны 5 см, 11 см и 12 см.

Попробуй сам: Ширина прямоугольного параллелепипеда равна 7 м, длина – на 2 метра
больше ширины, а высота – в 3 раза меньше длины. Найдите объем данного параллелепипеда?

2. Пример. Чему равен объем куба, ребро которого равно 3 см?

Решение. Воспользуемся формулой для нахождения объема куба V = a³ = a
· a · a, где a – ребро
куба.

V = 3 ·3 · 3 = 27 см³

Ответ:
V = 27 см³

Выполни по
образцу. Чему равен объем куба, ребро которого равно 7
см?

3. Пример. Объем прямоугольного параллелепипеда равен 560 см³, длина –
14 см, ширина – 8 см. Найдите высоту данного параллелепипеда.

Решение. Воспользуемся формулой для нахождения объема прямоугольного параллелепипеда
V = a · b · c, где a, b, c – измерения прямоугольного параллелепипеда. Подставим в формулу все
известные значения. Пусть a =14 см, b = 8 см. Тогда

14 ·
8 · с = 560 см³

112
· с = 560 см³

с =
560 : 112

с =
5 см

Ответ: высота прямоугольного
параллелепипеда равна 5 см.

Выполни по
образцу. Объем прямоугольного параллелепипеда равен
420 см³, длина – 12 см, ширина – 7 см. Найдите высоту данного
параллелепипеда.

4. Прочитай пример параграфа 23 на странице 156 и реши задачу: объем комнаты,
имеющей форму прямоугольного параллелепипеда равен 156 м³, высота –
3 м. Найдите площадь комнаты.

5. Пример. Найдите объем фигуры, изображенной на рисунке:

Решение. Фигура представляет собой прямоугольный параллелепипед с измерениями 3
см, 5 см и 3 см, из которого вырезали прямоугольный параллелепипед с
измерениями 2 см, 1 см и 1 см. Чтобы найти объем фигуры, нужно из объема
исходного параллелепипеда вычесть объем вырезанного параллелепипеда.

V = 3 · 5 · 3 – 2 ·
1 · 1 = 43 см³.

Попробуй сам. Найдите объем фигуры, изображенной на рисунке:

Источник

8. Геометрия в пространстве (стереометрия)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задачи по теме «Прямоугольный параллелепипед»

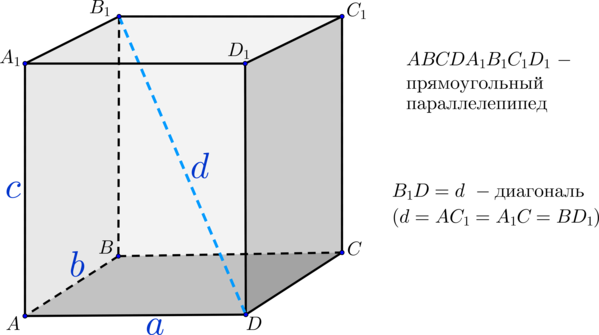
(blacktriangleright) Прямоугольный параллелепипед – это параллелепипед, все грани которого являются прямоугольниками.
Другими словами, это прямая призма, основания которой – прямоугольники.
(эти определения эквивалентны).

Тогда:

1) противоположные грани равны между собой;

2) боковые ребра перпендикулярны основаниям, то есть являются высотами;

3) как следствие, формула для объема принимает вид: ({Large{V=abc}}), где (a, b, c) – три различных боковых ребра.

(blacktriangleright) Диагональ прямоугольного параллелепипеда – это отрезок, соединяющий две противоположные (не лежащие в одной грани) вершины.

1) Все диагонали равны, пересекаются в одной точке и делятся ею пополам;

2) Диагональ (d) можно найти по формуле: ({Large{d^{,2}=a^2+b^2+c^2}}).

Задание
1

#2863

Уровень задания: Легче ЕГЭ

Дан прямоугольный параллелепипед, стороны основания которого равны (4) и (5), а боковое ребро равно (3). Найдите наибольшую площадь его грани.

Заметим, что все варианты для площадей его граней – это всевозможные попарные произведения чисел (3,4,5), то есть (3cdot
4), (4cdot 5) или (3cdot 5). Среди этих произведений наибольшим является (4cdot 5=20).

Ответ: 20

Задание
2

#2864

Уровень задания: Легче ЕГЭ

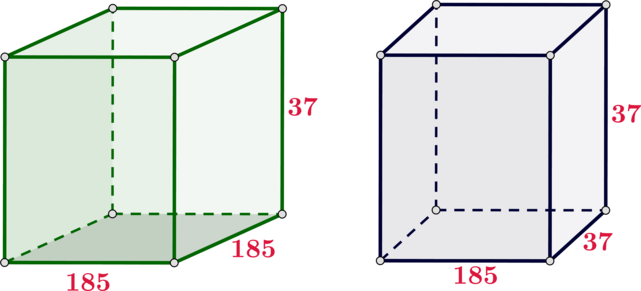
Даны два прямоугольных параллелепипеда: ребра одного равны (185), (185) и (37); а ребра другого равны (185, 37) и (37). Во сколько раз объем первого параллелепипеда больше объема второго параллелепипеда?

Отношение их объемов равно: [dfrac{V_1}{V_2}=dfrac{185cdot 185cdot 37}{185cdot 37cdot 37}=
dfrac{185}{37}=5.]

Ответ: 5

Задание
3

#2865

Уровень задания: Легче ЕГЭ

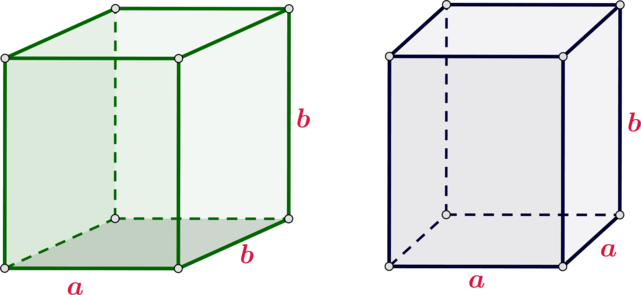
Даны два прямоугольных параллелепипеда: ребра одного равны (a, b) и (b), а ребра другого равны (a, a) и (b). На сколько площадь полной поверхности первого параллелепипеда больше, чем площадь поверхности второго параллелепипеда, если (a=1000, b=1001).

Площадь полной поверхности первого параллелепипеда [S_1=2(ab+b^2+ab)] Площадь полной поверхности второго параллелепипеда [S_2=2(ab+ab+a^2)] Следовательно, [S_1-S_2=2(b^2-a^2)=2(b-a)(b+a)=2(1001-1000)(1001+1000)=4002.]

Ответ: 4002

Задание
4

#3974

Уровень задания: Равен ЕГЭ

Дан прямоугольный параллелепипед (ABCDA_1B_1C_1D_1). Во сколько раз объем пирамиды (AA_1BD) меньше объема этого параллелепипеда?

Пусть (AB=x), (AD=y), (AA_1=z). Тогда объем параллелепипеда равен [V_{par}=S_{ABCD}cdot AA_1=xycdot z.] Так как (S_{ABD}=0,5S_{ABCD}) (потому что по определению прямоугольного параллелепипеда в основании лежит прямоугольник), то объем пирамиды [V_{pir}=dfrac13cdot S_{ABC}cdot AA_1=
dfrac13cdot dfrac12xycdot z=dfrac16xyz.] Следовательно, объем пирамиды в 6 раз меньше объема параллелепипеда.

Ответ:

Задание
5

#2867

Уровень задания: Равен ЕГЭ

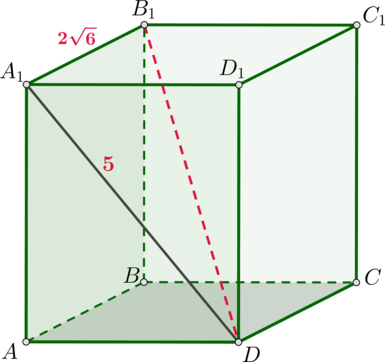
В прямоугольном параллелепипеде диагональ грани (AA_1D_1D) равна (5), а (AB=2sqrt6). Найдите диагональ параллелепипеда.

Так как параллелепипед прямоугольный, то все его грани – прямоугольники, а у прямоугольника обе диагонали равны. Следовательно, (A_1D=AD_1). Рассмотрим диагональ (A_1D) и диагональ параллелепипеда (B_1D). Треугольник (A_1B_1D) прямоугольный, так как ребро (A_1B_1) перпендикулярно грани (AA_1D_1D) (по определению прямоугольного параллелепипеда). Следовательно, гипотенуза [B_1D=sqrt{A_1B_1^2+A_1D^2}=sqrt{5^2+(2sqrt6)^2}=7.]

Ответ: 7

Задание
6

#2641

Уровень задания: Равен ЕГЭ

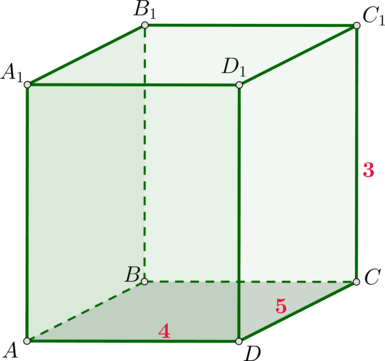
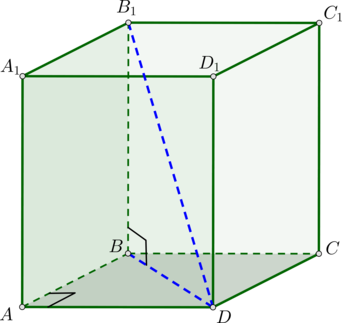
Дан прямоугольный параллелепипед с ребрами (2, 3) и (6). Найдите его диагональ.

Пусть (AB=2, AD=3 , AA_1=6).

По теореме Пифагора из прямоугольного треугольника (ABD) ((angle
A=90^circ)) имеем: (BD^2=AB^2+AD^2).

Из прямоугольного треугольника (BB_1D) ((angle B=90^circ)) по теореме Пифагора (B_1D^2=BD^2+BB_1^2).

Подставляя (BD^2) из первого равенства во второе, получим:

[B_1D^2=AB^2+AD^2+BB_1^2=2^2+3^2+6^2=4+9+36=49 quad Leftrightarrow quad B_1D=7.]

Ответ: 7

Задание
7

#2689

Уровень задания: Равен ЕГЭ

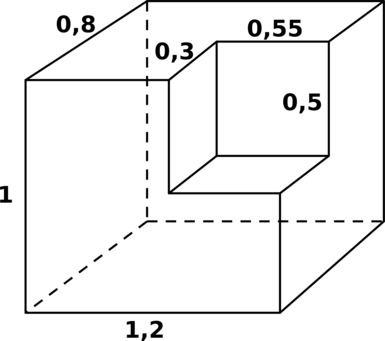
Найдите объём фигуры, получившейся после удаления маленького прямоугольного параллелепипеда из большого.

Объём оставшейся фигуры равен разности объёмов большого прямоугольного параллелепипеда (каким он был до удаления) и маленького (удалённого).

Таким образом, искомый объём равен [0,8cdot 1cdot 1,2 — 0,3cdot 0,5cdot 0,55 = 0,8775,.]

Ответ: 0,8775

Учащимся старших классов будет полезно научиться решать задачи ЕГЭ на нахождение объема и других неизвестных параметров прямоугольного параллелепипеда. Опыт предыдущих лет подтверждает тот факт, что подобные задания являются для многих выпускников достаточно сложными.

При этом понимать, как найти объем или площадь прямоугольного параллелепипеда, должны старшеклассники с любым уровнем подготовки. Только в этом случае они смогут рассчитывать на получение конкурентных баллов по итогам сдачи единого госэкзамена по математике.

Основные нюансы, которые стоит запомнить

Параллелограммы, из которых состоит параллелепипед, являются его гранями, их стороны — ребрами. Вершины этих фигур считаются вершинами самого многогранника.
Все диагонали прямоугольного параллелепипеда равны. Так как это прямой многогранник, то боковые грани представляют собой прямоугольники.
Так как параллелепипед — это призма, в основании которой находится параллелограмм, эта фигура обладает всеми свойствами призмы.
Боковые ребра прямоугольного параллелепипеда перпендикулярны основанию. Следовательно, они являются его высотами.

Готовьтесь к ЕГЭ вместе со «Школково»!

Чтобы занятия проходили легко и максимально эффективно, выбирайте наш математический портал. Здесь вы найдете весь необходимый материал, который потребуется на этапе подготовки к единому государственному экзамену.

Специалисты образовательного проекта «Школково» предлагают пойти от простого к сложному: сначала мы даем теорию, основные формулы и элементарные задачи с решением, а затем постепенно переходим к заданиям экспертного уровня. Вы можете потренироваться, например, с решением задач на тему “Призма”.

Нужную базовую информацию вы найдете в разделе «Теоретическая справка». Вы также можете сразу приступить к решению задач по теме «Прямоугольный параллелепипед» в онлайн-режиме. В разделе «Каталог» представлена большая подборка упражнений разной степени сложности. База заданий регулярно пополняется.

Проверьте, легко ли вы сможете найти объем прямоугольного параллелепипеда, прямо сейчас. Разберите любое задание. Если упражнение дается вам легко, переходите к более сложным задачам. А если возникли определенные сложности, рекомендуем вам планировать свой день таким образом, чтобы ваше расписание включало занятия с дистанционным порталом «Школково».

УСТАЛ? Просто отдохни

Источник

Рассказываем, как решать задачи на нахождение объема прямоугольного параллелепипеда и куба. Приводим алгоритм и примеры решения.

Задачи на нахождение объема прямоугольного параллелепипеда и куба – это геометрические задачи на построение и нахождение неизвестноых параметров прямоугольного параллелепипеда и куба используя формулы объема.

Алгоритм решения задач на нахождение объема прямоугольного параллелепипеда и куба:

Выполняем краткую запись задачи;
Определяем способ и решаем задачу;
Выписываем полный ответ.

Определяем способ решения:

Задача 1. Одно ребро прямоугольного параллелепипеда равно 6 дм, второе — в 2 раза больше первого, а третье — на 4 дм больше первого. Найти объем прямоугольного параллелепипеда, площадь его поверхности и сумму длин всего его ребер.

Краткая запись:

Решение:

(6⋅2=12) (дм) — b;
(6+4=10) (дм) — c;
(V_п =a⋅b⋅c)
(6⋅12⋅10=720) (дм3) — V;
(S_п= 2⋅)((ab+bc+ac))
(2)((6⋅12+6⋅10+12⋅10))(=2)((72+60+120))(=2⋅252=504) (дм²) — S;
(4)((a+b+c)) — сумма длин всех ребер
(4⋅)((6+12+10))(=4⋅28=112) (дм).

Ответ: объем прямоугольного параллелепипеда равен 720 дм³, площадь его поверхности — 504 дм², сумма длин всех ребер — 112 дм.

Источник

В данной публикации мы рассмотрим, как можно найти объем параллелепипеда и разберем примеры решения задач для закрепления материала.

Формула вычисления объема параллелепипеда
- 1. Общая формула
- 2. Объем прямоугольного параллелепипеда
Примеры задач

Формула вычисления объема параллелепипеда

1. Общая формула

Объем любого параллелепипеда равняется произведению площади его основания на высоту.

V = S_осн ⋅ h

S_осн – площадь основания (ABCD или EFHG, равны между собой);
h – высота.

Данная формула справедлива для всех видов геометрической фигуры:

наклонной – боковые грани не перпендикулярны основаниям;
прямой – все боковые грани (4 шт.) являются прямоугольниками;
прямоугольной – все грани (боковые и основания) являются прямоугольниками;
ромбоэдра – все грани являются равными ромбами;
куба – все грани представляют собой равные квадраты.

2. Объем прямоугольного параллелепипеда

Объем фигуры равен произведению его длины на ширину на высоту.

V = a ⋅ b ⋅ c

Формула следует из следующих утверждений:

Основанием фигуры является прямоугольник, площадь которого считается как произведение его длины (a) на ширину (b).
Высота фигуры – это длина боковой грани (c).

Примеры задач

Задание 1
Найдите объем параллелепипеда, если известно, что площадь его основания равняется 20 см², а высота – 7 см.

Решение:
Используем первую формулу, подставив в нее известные нам значения:
V = 20 см² ⋅ 7 см = 140 см³.

Задание 2
Дан прямоугольный параллелепипед. Длина и ширина его основания равны 9 см и 5 см, соответственно, а высота составляет 6 см. Найдите объем фигуры.

Решение:
Воспользуемся формулой для данного типа фигуры:
V = 9 см ⋅ 5 см ⋅ 6 см = 270 см³.

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.

Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.