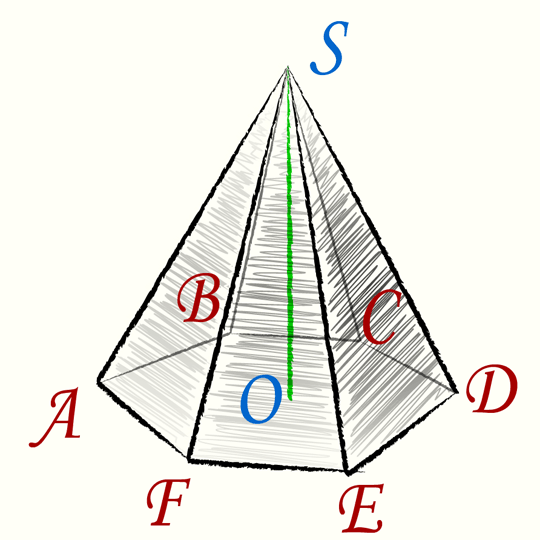
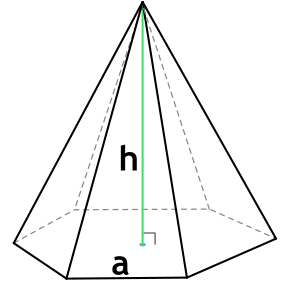
Шестиугольной пирамидой называется многогранник, в основании которого лежит правильный шестиугольник, а боковые грани образуются одинаковыми равнобедренными треугольниками.
Такие пирамиды обладают множеством уникальных свойств:
- Все стороны основания одинаковой длины;
- Все боковые ребра равны между собой;
- Все углы в основании равны, а также двугранные углы, образующиеся ребрами равны;
- Каждая боковая грань одинаковой площади.
Площадь шестиугольной пирамиды рассчитывается из площади ее основания и боковой развертки. Для расчета объема достаточно знать высоту пирамиды и площадь ее основания. Для начала разберемся с формулой площади правильного шестиугольника.
Одним из самых весомых отличий правильного шестиугольника от остальных фигур является равенство его стороны радиусу описанной окружности. Благодаря этому свойству площадь основания правильной шестиугольной пирамиды рассчитывается по формуле:
Для расчета можно использовать как радиус описанной окружности, так и длину стороны правильного шестиугольника.
Теперь вернемся к формуле объема шестиугольной пирамиды. Она представляет собой одну треть произведения площади основания на высоту пирамиды, опущенную к этому основанию:
Теперь рассмотрим пример расчета объема шестиугольной пирамиды.
Пусть дана правильная шестиугольная пирамида, высота которой равна h = 8 см. вокруг основания описана окружность с радиусом R = 6 см. Найдите объем.
В вычислении требуемого параметра не будет ничего сложного – ведь все необходимые величины заданы условиями. Поэтому найдем площадь основания нашего многогранника. Помним, что радиус описанной вокруг правильного шестиугольника окружности равен его сторонам. Подставим данные в формулу:
Теперь можем использовать найденную площадь для расчета объема нашей шестиугольной пирамиды:
Вот таким образом, зная свойства правильного шестиугольника и формулу объема для шестиугольной пирамиды, мы нашли все необходимые параметры.
В данной публикации мы рассмотрим, как можно найти объем пирамиды и разберем примеры решения задач для закрепления материала.
-
Формула вычисления объема пирамиды
- 1. Общая формула
- 2. Объем правильной треугольной пирамиды
- 3. Объем правильной четырехугольной пирамиды
- 4. Объем правильной шестиугольной пирамиды
- Примеры задач
Формула вычисления объема пирамиды
1. Общая формула
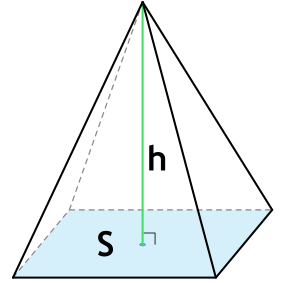
Объем (V) пирамиды равняется одной третьей произведения ее высоты на площадь основания.
- ABCD – основание;
- E – вершина;
- h – высота, перпендикулярная основанию.
2. Объем правильной треугольной пирамиды
Основанием правильной треугольной пирамиды является равносторонний треугольник (ABC), площадь которого вычисляется так (а – сторона треугольника):
Подставляем данное выражение в формулу расчета объема фигуры и получаем:
3. Объем правильной четырехугольной пирамиды
Основанием правильной четырехугольной пирамиды является квадрат, площадь которого считается так: S = a2, где а – длина его стороны.
Следовательно, формулу объема можно представить в виде:
4. Объем правильной шестиугольной пирамиды
Основанием правильной шестиугольной пирамиды является правильный шестиугольник, площадь которого вычисляется по формуле (а – сторона основания):
С учетом этого, объем фигуры считается так:
Примеры задач
Задание 1
Найдите объем правильной треугольной пирамиды, если известно, что ее высота составляет 16 см, а длина стороны ее основания – 8 см.
Решение:
Воспользуемся соответствующей формулой, подставив в нее известные значения:
Задание 2
Высота правильной четырехугольной пирамиды равна 12 см, а сторона ее основания – 3 см. Найдите объем фигуры.
Решение:
Площадь квадрата, который является основанием пирамиды, равна 9 см2 (3 см ⋅ 3 см). Следовательно, объем равен:
Шестиугольная пирамида представляет собой фигуру с правильным шестиугольником в основании, каждое из
ребер которого одинаковой длины. Объемом является физическое значение части пространства, занимаемой
пирамидой и вычисляется по формуле:
V = (a²/2) * (h√3)
где а- ребро основания, h- высота.
Цифр после
запятой:
Результат в:
Согласно этой формуле вычислить объем правильной шестиугольной пирамиды не составит труда.
Пример. При высоте пирамиды h = 4, а длине ребра основания а = 2, объем составит:
V = (2²/2) * (4√3) = 13,8
Говоря о пирамидах, первым на ум приходит пирамида Хеопса. Это настоящий пример совершенства
математических пропорций. Однако пирамида – это не только геометрическая фигура, это еще и тайна,
над разгадкой которой работают ученые всего мира. Людям давно известно об их чудодейственных
свойствах, позволяющих сохранять быстро портящиеся продукты, уменьшать боль. Даже цветы внутри
пирамиды будут стоять долго. Однако самый податливый элемент на земле для работы с энергетикой –
вода. Простояв под пирамидой всего несколько часов, она приобретает полезные качества, благотворно
влияющие на наш организм. Это можно понять уже по тому, как изменится ее вкус в лучшую сторону.
Можно и самим провести эксперимент и проверить свойства правильной шестиугольной пирамиды. Здесь не
лишней будет формула вычисления ее объема – например, чтобы использовать пирамиду в качестве сосуда
для воды.
Объем правильной шестиугольной пирамиды, формула
Объем правильной шестиугольной пирамиды
Правильная шестиугольная пирамида — это многогранник, у которого одна грань — основание пирамиды — правильный шестиугольник, а остальные — боковые грани — равные треугольники с общей вершиной. Высота опускается в центр правильного шестиугольника — основания из вершины.
Объем правильной шестиугольной пирамиды равен одной трети произведения площади правильного шестиугольника, являющегося основанием S (ABCDEF) на высоту h (OS)
[ V = frac{sqrt{3}}{2} h a^2 ]
a — сторона правильного шестиугольника — основания правильной шестиугольной пирамиды
h — высота правильной шестиугольной пирамиды
Вычислить, найти объем правильной шестиугольной пирамиды
Объем правильной шестиугольной пирамиды |
стр. 356 |
|---|

{V= S cdot h}
На этой странице собраны формулы и калькуляторы для нахождения объема пирамиды. Просто введите известные данные в калькулятор и получите результат. Либо рассчитайте объем пирамиды по приведенным формулам самостоятельно.
Пирамида — многогранник, в основании которого лежит многоугольник, а остальные грани представляют собой треугольники, имеющие общую вершину.
Содержание:
- калькулятор объема пирамиды
- формула объема пирамиды
- объем правильной треугольной пирамиды
- объем правильной четырехугольной пирамиды
- объем правильной шестиугольной пирамиды
- объем правильной n-угольной пирамиды
- объем тетраэдра
- примеры задач
Формула объема пирамиды
{V= dfrac{1}{3} S cdot h}
S — площадь основания пирамиды
h — высота пирамиды
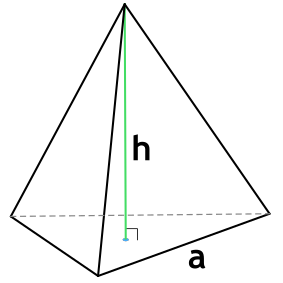
Формула объема правильной треугольной пирамиды
Правильная треугольная пирамида — пирамида, в основании которой лежит равносторонний треугольник, а грани являются равнобедренными треугольниками.
{V= dfrac{h cdot a^2}{4 sqrt{3}}}
a — длина стороны основания пирамиды
h — высота пирамиды
Формула объема правильной четырехугольной пирамиды
Правильная четырехугольная пирамида — пирамида, в основании которой лежит квадрат, а грани являются равнобедренными треугольниками.
{V= dfrac{1}{3} cdot h cdot a^2}
a — длина стороны основания пирамиды
h — высота пирамиды
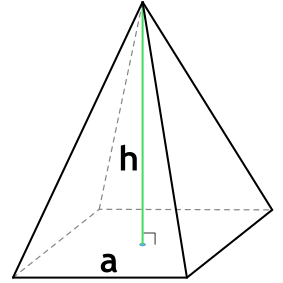
Формула объема правильной шестиугольной пирамиды
Правильная шестиугольная пирамида — пирамида, в основании которой лежит правильный шестиугольник, а грани являются равнобедренными треугольниками.
{V= dfrac{sqrt{3}}{2} cdot h cdot a^2}
a — длина стороны основания пирамиды
h — высота пирамиды
Формула объема правильной n-угольной пирамиды
Правильная пирамида имеет в основании правильный многоугольник (все стороны и углы равны между собой), а высота проходит через центр этого основания.
{V= dfrac{n cdot h cdot a^2}{12 cdot tg(dfrac{180°}{n} )}}
a — длина стороны основания пирамиды
h — высота пирамиды
n — число сторон многоугольника в основании пирамиды
Формула объема тетраэдра
Тетраэдр — правильный многогранник (четырехгранник), имеющий четыре грани, каждая из которых является правильным треугольником. У тетраэдра кроме четырех граней также 4 вершины и 6 ребер.
{V= dfrac{sqrt{2} a^3}{12}}
a — длина стороны тетраэдра
Примеры задач на нахождение объема пирамиды
Задача 1
Найдите объем пирамиды с высотой 2м, а основанием ее служит квадрат со стороной 3м.
Решение
Так как в основании пирамиды лежит квадрат, то воспользуемся формулой объема правильной четырехугольной пирамиды и подставим в нее значения высоты и стороны основания.
V= dfrac{1}{3} cdot h cdot a^2 = dfrac{1}{3} cdot 2 cdot 3^2 = dfrac{1}{3} cdot 2 cdot 9 = dfrac{1}{3} cdot 18 = 6 : м^3
Ответ: 6 м³
Используем калькулятор для проверки полученного ответа.
Задача 2
Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1см, а высота равна √3см.
Решение
Из условия следует, что пирамида правильная треугольная. Это значит, что для решения задачи необходимо воспользоваться формулой для правильной треугольной пирамиды. Подставим в нее значения и рассчитаем объем.
V= dfrac{h cdot a^2}{4 sqrt{3}} = dfrac{sqrt{3} cdot 1^2}{4 sqrt{3}} = dfrac{sqrt{3} cdot 1}{4 sqrt{3}} = dfrac{sqrt{3}}{4 sqrt{3}} = dfrac{cancel{sqrt{3}}}{4 cancel{sqrt{3}}} = dfrac{1}{4} = 0.25 : м^3
Ответ: 0.25 см³
Для проверки с помощью калькулятора извлечем квадратный корень из 3: √3 = 1.73205. Теперь можем подставить значения в калькулятор и проверить полученный ответ.