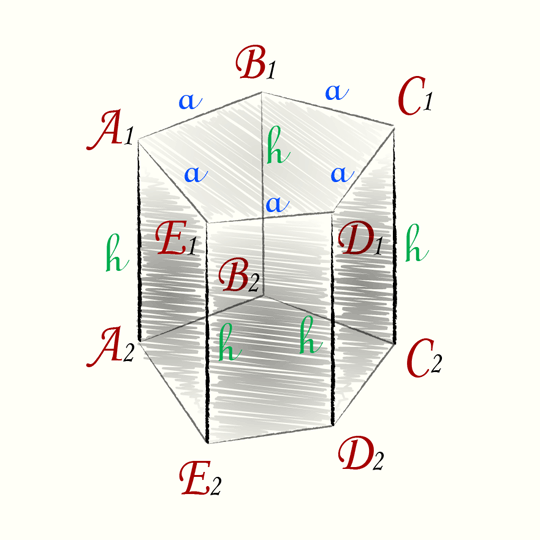
Объем правильной пятиугольной призмы
У правильной пятиугольной призмы в основании лежит правильный пятиугольник.
Объем правильной пятиугольной призмы
Объем правильной пятиугольной призмы равен произведению площади правильного пятиугольника лежащего в основании на высоту призмы.
[ V = frac{5}{2} a h sqrt{bigg(frac{a}{2 sin(π/5)}bigg)^2-frac{a^2}{4}} ]
[ V = frac{5}{4} a^{2} h sqrt{frac{1}{sin^{2}(π/5)}-1} ]
Вычислить, найти объем правильной пятиугольной призмы
Объем правильной пятиугольной призмы |
стр. 361 |
|---|
-
Вы здесь:
- Главная
- Правильная пятиугольная призма
Правильная пятиугольная призма
Пятиугольная призма — это многогранник, две грани которого являются равными пятиугольниками, лежащими в параллельных плоскостях, а остальные грани (боковые грани) — параллелограммами, имеющими общие стороны с этими пятиугольниками.
Правильная пятиугольная призма — это пятиугольная призма у которой основания правильные пятиугольники (все стороны которых равны, углы между сторонами основания составляют 108 градусов), а боковые грани прямоугольники.
Основания призмы являются равными правильными пятиугольниками.
Боковые грани призмы являются прямоугольниками.
Боковые рёбра призмы параллельны и равны.
Размеры призмы можно выразить через длину стороны a и высоту h.
Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.
Формула площади поверхности пятиугольной призмы:
Объём призмы равен произведению её высоты на площадь основания.
Формула объема правильной пятиугольной призмы:
Правильная пятиугольная призма может быть вписана в цилиндр.
Формула радиуса цилиндра вписанной пятиугольной призмы:
Двойственным многогранником прямой призмы является бипирамида.
Исторически понятие «призма» возникло из латыни и означало — нечто отпиленное.
Анимация демонстрирует как две параллельные плоскости отрезая лишнее формируют два основания призмы. Из одной заготовки можно получить как правильную призму, так и наклонную призму.
Геометрические размеры готовой призмы (мм):
Длина = 80
Ширина = 76
Высота = 50
Геометрические размеры готовой призмы (мм):
Длина = 68
Ширина = 65
Высота = 72
Геометрические размеры готовой призмы (мм):
Длина = 55
Ширина = 52
Высота = 93
посмотреть другие призмы
Популярное
Многогранники на почтовых марках
Почтовые марки охватывают все значимые события в мире. Не обошли вниманием художники-филателисты и изображения многогранников.
Почтовая марка, посвященная Леонарду Эйлеру с…
Практическое применение многогранников
Когда мы демонстрируем многогранники, собранные из наборов «Волшебные грани», люди часто задают один и тот же вопрос, – а какое это имеет практическое применение?
Естественные многогранники
В естественной среде правильные многогранники можно встретить в виде кристаллов (минералов).
Форму тетраэдра передает сурьмянистый сернокислый натрий.
3D – календарь ромбододекаэдр на 2021 год
Изобретение календаря замечательное событие для человечества. То, что год состоит из 12ти месяцев ни для кого не секрет.
С тех пор люди самыми различными способами группируют…
Многогранники для Хэллоуина
Если ты не любишь математику, опасайся хэллоуина! Злые силы придут за тобой в хэллоуин! Создай двух стражей, которые будут оберегать тебя от злых сил! Ну, или,…
МАТЕМАТИКА
Калькулятор для Объем пятиугольной призмы
Альтернативное название: Калькулятор объема пятигранной коробки
Этот калькулятор поможет вам найти объем формы пятиугольная призма. Формула, используемая в этом калькуляторе, приведена ниже.
Чтобы использовать этот калькулятор, вам нужно знать базовый край и высота.
Чтобы дать вам лучшую мысленную модель пятиугольная призма, вы можете взглянуть на визуализацию ниже. Вы можете перемещаться по 3D-модели пятиугольная призма как хотите.
CALCULATOR.RESULTS.HEADER
Объем = 1,720.477
Формула Пятиугольная Призма Объем
Объяснение переменной формулы:
- P представляет объем.
- e представляет Базовый край.
- h представляет Высота.
Формула LaTeX
Если вы работаете в редакторе на основе TeX, вы можете использовать эту формулу TeX для вычисления пятиугольная призма объем.
P:=frac{1}{4}cdotsqrt{5cdotleft(5+2cdotsqrt{5}right)}cdot{ e}^{2}cdotmathrm{h}
Как Рассчитать Пятиугольная Призма Объем Для Себя
Расчет объем довольно просто, если знать приведенную выше формулу. Выполните следующие действия:
-
Затем измените следующие переменные своими значениями:
- e следует заменить на Базовый край вашего пятиугольная призма. Например, e можно изменить на 10.
- h следует заменить на Высота вашего пятиугольная призма. Например, h можно изменить на 10.
- Теперь вы можете ввести это в калькулятор и получить ответ.
Объем пятиугольной призмы Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Базовая длина ребра пятиугольной призмы: 10 метр —> 10 метр Конверсия не требуется
Высота пятиугольной призмы: 15 метр —> 15 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
2580.71610088345 Кубический метр —> Конверсия не требуется
4 Пятиугольная призма Калькуляторы
Объем пятиугольной призмы формула
Объем пятиугольной призмы = sqrt(5*(5+(2*sqrt(5))))/4*Базовая длина ребра пятиугольной призмы^2*Высота пятиугольной призмы
V = sqrt(5*(5+(2*sqrt(5))))/4*le(Base)^2*h
Что такое пятиугольная призма?
В геометрии пятиугольная призма представляет собой призму с пятиугольным основанием. Этот многогранник имеет 7 граней, 15 ребер и 10 вершин.
Что такое Призма?
В математике призма — это многогранник с двумя многоугольными основаниями, параллельными друг другу. В физике (оптике) призмой называют прозрачный оптический элемент с плоскими полированными поверхностями, преломляющими свет. Боковые грани соединяются с двумя многоугольными основаниями. Боковые грани в основном прямоугольные. В некоторых случаях это может быть параллелограмм.
Призма — многогранное тело, основаниями которого являются два равных многоугольника, лежащие в параллельных плоскостях. Остальными гранями являются параллелограммы.
Такие параллелограммы в призме называются боковыми.
Онлайн-калькулятор объема призмы
Призмы разделяют на некоторые типы:
- Треугольная призма — у нее основания — треугольники;
- Четырехугольная призма — у нее основания — четырехугольники;
- Пентапризма — пятиугольная призма.
Деление, в общем, продолжается до бесконечности.
Виды призм
Прямая — у такой призмы боковые грани образуют с основаниями прямой угол.
Правильная — ее основанием является какой-либо правильный многоугольник.
Усеченной называется призма, у которой основания не параллельны друг другу.
Формула объема призмы
Объем прямой призмы находится так же, как и объем других многогранников — путем умножения площади основания на высоту.
V=Sосн⋅hV=S_{text{осн}}cdot h
SоснS_{text{осн}} — площадь основания призмы;
hh — высота призмы.
Разберем задачу на нахождение объема прямой призмы.
Найти объем призмы, если ее основанием является равнобедренный треугольник с равными сторонами по 5 см5text{ см} и основанием в 6 см6text{ см}. Высота призмы равна 10 см10text{ см}.
Решение
a=5a=5
b=6b=6
h=10h=10
Вычисляем площадь основания. Нужно провести высоту в данном равнобедренном треугольнике. Тогда, по теореме Пифагора, получаем:
a2=l2+(b2)2a^2=l^2+Big(frac{b}{2}Big)^2,
где ll — высота равнобедренного треугольника.
Отсюда:
l2=a2−(b2)2l^2=a^2-Big(frac{b}{2}Big)^2
l=a2−(b2)2l=sqrt{a^2-Big(frac{b}{2}Big)^2}
l=25−9l=sqrt{25-9}
l=4l=4
Площадь равнобедренного треугольника SS это половина от произведения его основания на высоту:
S=12⋅b⋅l=12⋅6⋅4=12S=frac{1}{2}cdot bcdot l=frac{1}{2}cdot 6cdot 4=12
В нашем случае этот треугольник является основанием призмы, поэтому:
S=SоснS=S_{text{осн}}
Тогда объем призмы найдется по формуле:
V=Sосн⋅h=12⋅10=120 см3V=S_{text{осн}}cdot h=12cdot 10=120text{ см}^3
Ответ
120 см3.120text{ см}^3.
На нашем сайте вы можете оформить решение задач на заказ по самым низким ценам!