Как найти объем правильной восьмиугольной призмы

ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:

Вспомним определение призмы.

ПРИЗМА — многогранник, две грани которого (основания) — равные многоугольники, расположенные в параллельных плоскостях, а другие грани (боковые) — параллелограммы.

Призма называется прямой, когда боковые ребра призмы перпендикулярны основаниям.

Прямая призма называется правильной, если в ее основания лежат правильные многоугольники.

Боковые грани призмы — параллелограммы.

Докажем теорему.

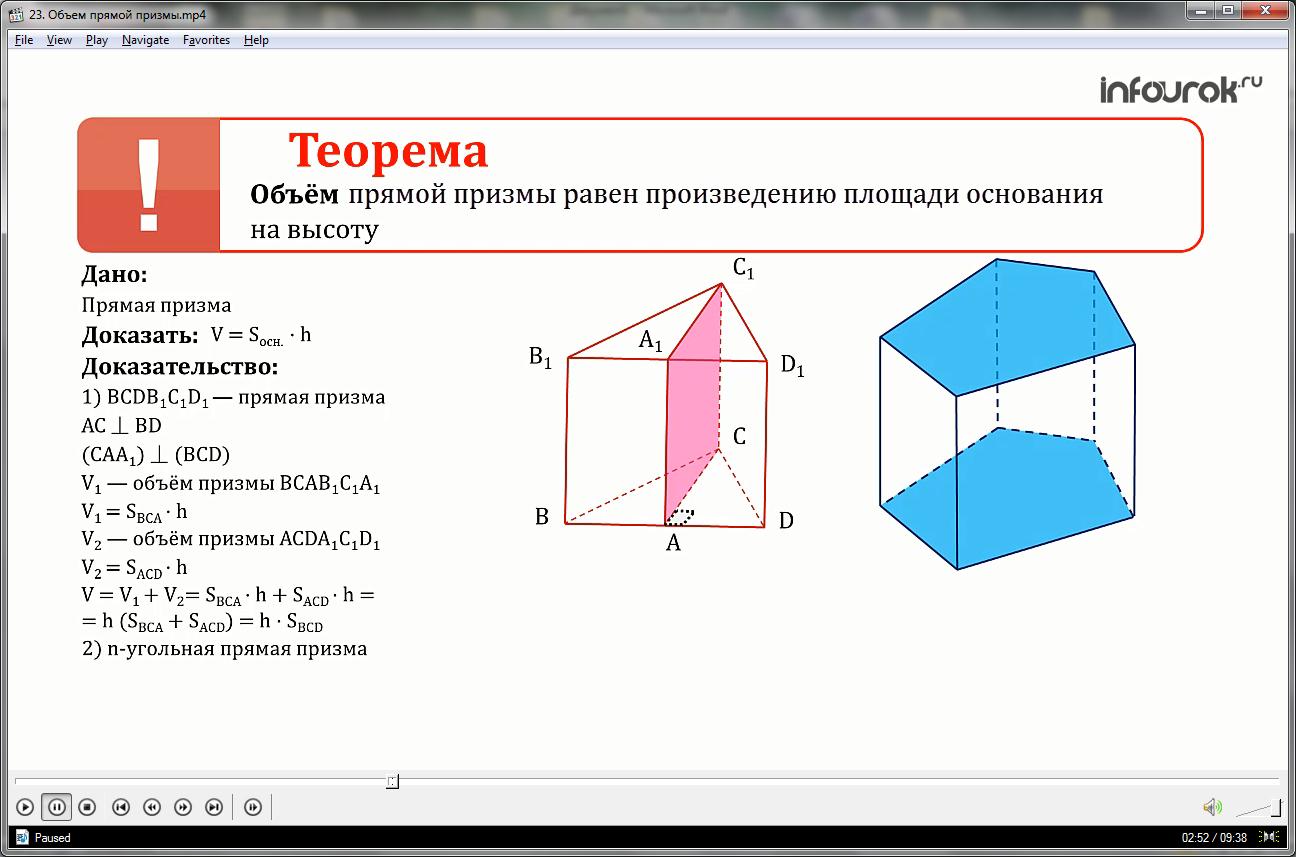
Объём прямой призмы равен произведению площади основания на высоту.

V = • h.

Сначала докажем теорему для треугольной призмы, а затем – для произвольной.

Дано: прямая призма

Доказать: V = Sосн • h.

Доказательство:

1. ВСDB1C1D1— прямая призма. AC BD (выберем высоту, которая делит ΔBCD на два треугольника) проведем плоскость (CAA1) (BCD), получим две призмы, основания которых — прямоугольные треугольники. Тогда V1 – это объем призмы BCAB1C1A1 и равен SBCA•h

V2 – объем призмы ACDA1C1D1 и равен SACD•h

Тогда объем призмы ВСDB1C1D1 будет равен сумме объемов призмы BCAB1C1A1 и ACDA1C1D1, следовательно, V= SBCA•h+ SACD•h вынесем за скобки общий множитель и получим, что объем призмы будет равен h (SBCA + SACD)

А так как сумма площадей треугольников BCA и ACD равна площади треугольника BCD, тогда объем призмы будет равен произведению высоты на площадь основания BCD. Что и требовалось доказать.

2. Рассмотрим n-угольную произвольную призму с площадью основания S, ее можно разбить на прямые треугольные призмы с высотой h.

Следовательно, V1, V2, V3,…,Vn–2 – объемы треугольных призм,

S1, S2, S3,…,Sn–2 – площади оснований треугольных призм.

Значит, объём n-угольной призмы будет равен сумме объёмов всех треугольных призм.

Отсюда следует, что объём будет равен произведению высоты призмы на сумму площадей оснований треугольных призм.

Данную выпуклую пятиугольную призму можно разбить на три прямые треугольные призмы. Найдем объем каждой призмы и сложим эти объемы. Вынесем за скобки общий множитель h, получим, что объем пятиугольной призмы будет равен произведению высоты на сумму площадей оснований треугольных призм. Сумма площадей оснований треугольных призм равна площади основания данной призмы, значит, объем данной призмы равен произведению высоты на основание.

Теорема доказана.

Решение задач

Задача 1

Найдите объем правильной n-угольной призмы, у которой каждое ребро равно a, если а) n=3; б) n=4; в) n=6.г) n=8

Дано:

Правильная n-угольная призма,

а-ребро призмы.

Найти V-?

Решение:

Так как каждое ребро равно а по условию, то и высота призмы h в прямой призме, являющаяся ребром призмы, также равна a

а) n=3

Объем призмы находится по формуле:

V = • h

Основанием правильной n-угольной призмы, при n=3, является правильный треугольник, площадь которого находится по формуле .

Тогда объем равен

б) n=4, то есть в основании лежит четырёхугольник, и так как призма правильная, то он является квадратом, а по условию все ребра призмы равны, значит, правильная четырехугольная призма — это куб, поэтому V=

в) n=6. Объем правильной шестиугольной призмы ищем по формуле:

V = • h

Площадь основания ищем по формуле:

(это и есть формула, так как в основании правильный шестиугольник, то его площадь можно выразить только через сторону а).

г) n=8. Объем правильной восьмиугольной призмы ищем по формуле:

V = • h

Площадь основания ищем по формуле:

(это и есть формула, так как в основании правильный восьмиугольник, то его площадь можно выразить только через сторону а).

Ответ: a) V = ; б) V = ;

в) V = 1,5 • ; г) V = (2+2 ) • .

Задача 2

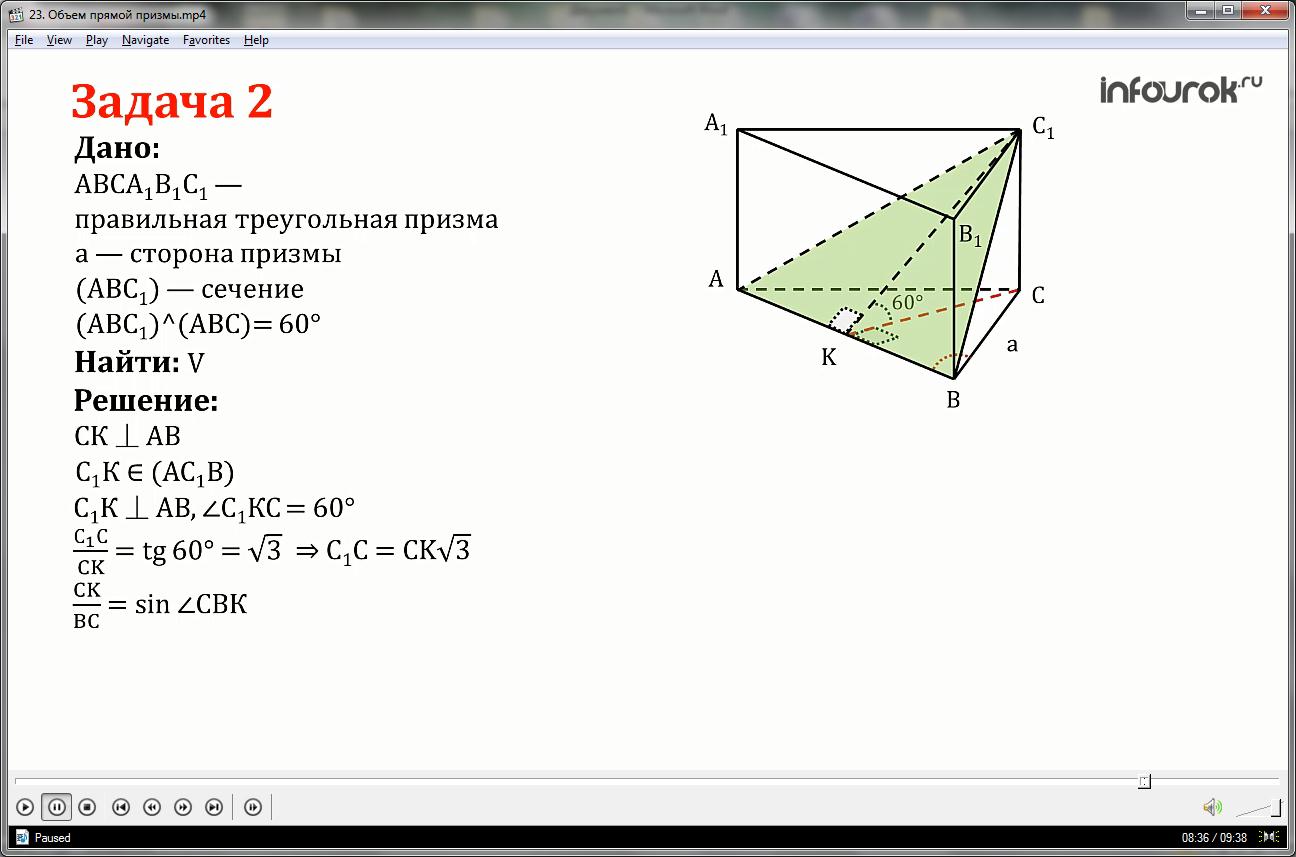
В правильной треугольной призме через сторону нижнего основания и противолежащую ей вершину верхнего основания проведено сечение, составляющее угол 60 с плоскостью основания. Найти объем призмы, если сторона равна а.

Дано:

Правильная треугольная призма со

стороной а.

Проведено сечение АВС1

Найти: V-?

Решение:

Построим СК АВ, отрезок С1К в плоскости сечения АС1В. По теореме о трех перпендикулярах –

С1К АВ; С1КС=60°.

Из ΔС1КС: (отношение сторон треугольника — СС1 к СК равно тангенсу 60 градусов и равно корню квадратному из трех)

Отсюда

Рассмотрим треугольник ΔСКВ, он прямоугольный так как СК высота проведенная в точку К, тогда по определению синуса острого угла прямоугольного треугольника имеем = sin ∠СBК, угол СВК равен 60 градусам, так как треугольник в основании правильный, значит, все его углы равны.

CK=ВС sin60°, так как ВС=а, а синус 60 градусов равен , то ,

Затем подставляем значение СК в формулу СС1, получаем

А площадь равностороннего треугольника вычисляется по формуле:

Находим объем призмы:

V = • h=

Источник

МАТЕМАТИКА

Калькулятор для Объем восьмиугольной призмы

Альтернативное название: Калькулятор объема восьмигранной коробки

Этот калькулятор поможет вам найти объем формы восьмиугольная призма. Формула, используемая в этом калькуляторе, приведена ниже.

Чтобы использовать этот калькулятор, вам нужно знать базовый край и высота.

Чтобы дать вам лучшую мысленную модель восьмиугольная призма, вы можете взглянуть на визуализацию ниже. Вы можете перемещаться по 3D-модели восьмиугольная призма как хотите.

CALCULATOR.RESULTS.HEADER

Объем = 4,828.427

Формула Восьмиугольная Призма Объем

Объяснение переменной формулы:

O представляет объем.
e представляет Базовый край.
h представляет Высота.

Формула LaTeX

Если вы работаете в редакторе на основе TeX, вы можете использовать эту формулу TeX для вычисления восьмиугольная призма объем.

O:=2cdotleft(1+sqrt{2}right)cdot{ e}^{2}cdotmathrm{h}

Как Рассчитать Восьмиугольная Призма Объем Для Себя

Расчет объем довольно просто, если знать приведенную выше формулу. Выполните следующие действия:

Затем измените следующие переменные своими значениями:
1. e следует заменить на Базовый край вашего восьмиугольная призма. Например, e можно изменить на 10.
2. h следует заменить на Высота вашего восьмиугольная призма. Например, h можно изменить на 10.
Теперь вы можете ввести это в калькулятор и получить ответ.