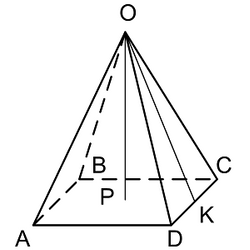
Пирамида – это многогранник, основанием которого является многоугольник, а грани его являются треугольниками.
Онлайн-калькулятор объема пирамиды
У пирамиды есть ребра. Можно сказать, что они тянутся к точке, называемой вершиной данной пирамиды. Ее основанием может быть произвольный многоугольник. Грань — это фигура, которая образуется в результате объединения двух ближайших ребер со стороной основания. Гранью пирамиды является треугольник. Расстояние от вершины пирамиды до середины стороны основания называется апофемой. Высотой пирамиды называется длина перпендикуляра, опущенного из вершины к центру ее основания.
Типы пирамид
Различают следующие типы пирамид.
- Прямоугольная — у нее ребро образует угол в 90 градусов с основанием.
- Правильная — ее основание — какой-либо правильный многоугольник, а вершина проецируется в центр этого основания.
- Тетраэдр — пирамида, у которой в основании лежит треугольник.
Формулы объема пирамиды
Объем пирамиды находится несколькими способами.
По площади основания и высоте пирамиды
Простое умножение одной трети площади основания на высоту пирамиды и является ее объемом.
V=13⋅Sосн⋅hV=frac{1}{3}cdot S_{text{осн}}cdot h
SоснS_{text{осн}} — площадь основания пирамиды;
hh — высота данной пирамиды.
Площадь основания пирамиды равна 100 см2100text{ см}^2, а высота ее равна 30 см30text{ см}. Найдите объем тела.
Решение
Sосн=100S_{text{осн}}=100
h=30h=30
Все величины нам известны, подставляем их численные значения в формулу и находим:
V=13⋅Sосн⋅h=13⋅100⋅30=1000 см3V=frac{1}{3}cdot S_{text{осн}}cdot h=frac{1}{3}cdot 100cdot 30=1000text{ см}^3
Ответ
1000 см3.1000text{ см}^3.
Формула объема правильной треугольной пирамиды
Этот способ подходит, если пирамида правильная и треугольная.
V=h⋅a243V=frac{hcdot a^2}{4sqrt{3}}
hh — высота пирамиды;
aa — сторона основания пирамиды.
Вычислите объем правильной треугольной пирамиды, если в ее основании лежит равносторонний треугольник, в котором сторона равна 5 см5text{ см}, а высота пирамиды равна – 19 см19text{ см}.
Решение
a=5a=5
h=19h=19
Просто подставляем данные величины в формулу для объема:
V=h⋅a243=19⋅5243≈68.6 см3V=frac{hcdot a^2}{4sqrt{3}}=frac{19cdot 5^2}{4sqrt{3}}approx68.6text{ см}^3
Ответ
68.6 см3.68.6text{ см}^3.
Формула объема правильной четырехугольной пирамиды
V=13⋅h⋅a2V=frac{1}{3}cdot hcdot a^2
hh — высота пирамиды;
aa — сторона основания пирамиды.
Дана правильная четырехугольная пирамида. Вычислите ее объем, если ее высота равна 7 см7text{ см}, a сторона основания составляет – 2 см2text{ см}.
Решение
a=2a=2
h=7h=7
По формуле вычисляем:
V=13⋅h⋅a2=13⋅7⋅22≈9.3 см3V=frac{1}{3}cdot hcdot a^2=frac{1}{3}cdot 7cdot 2^2approx9.3text{ см}^3
Ответ
9.3 см3.9.3text{ см}^3.
Формула объема тетраэдра
V=2⋅a312V=frac{sqrt{2}cdot a^3}{12}
aa — длина ребра тетраэдра.
Длина ребра тетраэдра равна 13 см13text{ см}. Найдите его объем.
Решение
a=13a=13
Подставляем aa в формулу для объема тетраэдра:
V=2⋅a312=2⋅13312≈259 см3V=frac{sqrt{2}cdot a^3}{12}=frac{sqrt{2}cdot 13^3}{12}approx259text{ см}^3
Ответ
259 см3.259text{ см}^3.
Формула объема пирамиды как определитель
Наверное, самый экзотический способ вычисления объема данного тела.
Пусть даны векторы, на которых построена пирамида как на сторонах. Тогда ее объем будет равен одной шестой смешанного произведения векторов. Последний в свою очередь равен определителю составленному из координат этих векторов. Итак, если пирамида построена на трех векторах:
a⃗=(ax,ay,az)vec{a}=(a_x, a_y, a_z)
b⃗=(bx,by,bz)vec{b}=(b_x, b_y, b_z)
c⃗=(cx,cy,cz)vec{c}=(c_x, c_y, c_z),
тогда объем соответствующей пирамиды это такой определитель:
V=16⋅∣axayazbxbybzcxcycz∣V=frac{1}{6}cdotbegin{vmatrix}
a_x & a_y & a_z \
b_x & b_y & b_z \
c_x & c_y & c_z \
end{vmatrix}
Найти объем пирамиды через смешанное произведение векторов, координаты которых такие: a⃗=(2,3,5)vec{a}=(2,3,5) , b⃗=(1,4,4)vec{b}=(1,4,4), c⃗=(3,5,7)vec{c}=(3,5,7).
Решение
a⃗=(2,3,5)vec{a}=(2,3,5)
b⃗=(1,4,4)vec{b}=(1,4,4)
c⃗=(3,5,7)vec{c}=(3,5,7)
По формуле:
V=16⋅∣235144357∣=16⋅(2⋅4⋅7+3⋅4⋅3+5⋅1⋅5−5⋅4⋅3−2⋅4⋅5−3⋅1⋅7)=16⋅(56+36+25−60−40−21)=16⋅(−4)=−23≈−0.7V=frac{1}{6}cdotbegin{vmatrix}
2 & 3 & 5 \
1 & 4 & 4 \
3 & 5 & 7 \
end{vmatrix}=frac{1}{6}cdot(2cdot4cdot7 + 3cdot4cdot3 + 5cdot1cdot5 — 5cdot4cdot3 — 2cdot4cdot5 — 3cdot1cdot7) =frac{1}{6}cdot( 56 + 36 + 25 — 60 — 40 — 21)=frac{1}{6}cdot(-4)=-frac{2}{3}approx-0.7
Мы должны взять модуль этого числа, так как объем это неотрицательная величина:
V=0.7 см3V=0.7text{ см}^3
Ответ
0.7 см3.0.7text{ см}^3.
Не знаете, где можно оформить заказ контрольных работ недорого? Наши эксперты помогут вам с решением работ по объемам фигур!
Тест по теме “Объем пирамиды”
Содержание статьи:
- Что это — треугольная пирамида
- Правильная пирамида с треугольным основанием
- Формулы объема треугольной пирамиды
- Усеченная пирамида
- Решение задачи
Главной характеристикой любой геометрической фигуры в пространстве является ее объем. В данной статье рассмотрим, что собой представляет пирамида с треугольником в основании, а также покажем, как находить объем треугольной пирамиды — правильной полной и усеченной.
Что это — треугольная пирамида?
Каждый слышал о древних египетских пирамидах, тем не менее они являются четырехугольными правильными, а не треугольными. Объясним, как получить треугольную пирамиду.
Возьмем произвольный треугольник и соединим все его вершины с некоторой одной точкой, расположенной вне плоскости этого треугольника. Образованная фигура будет называться треугольной пирамидой. Она показана на рисунке ниже.
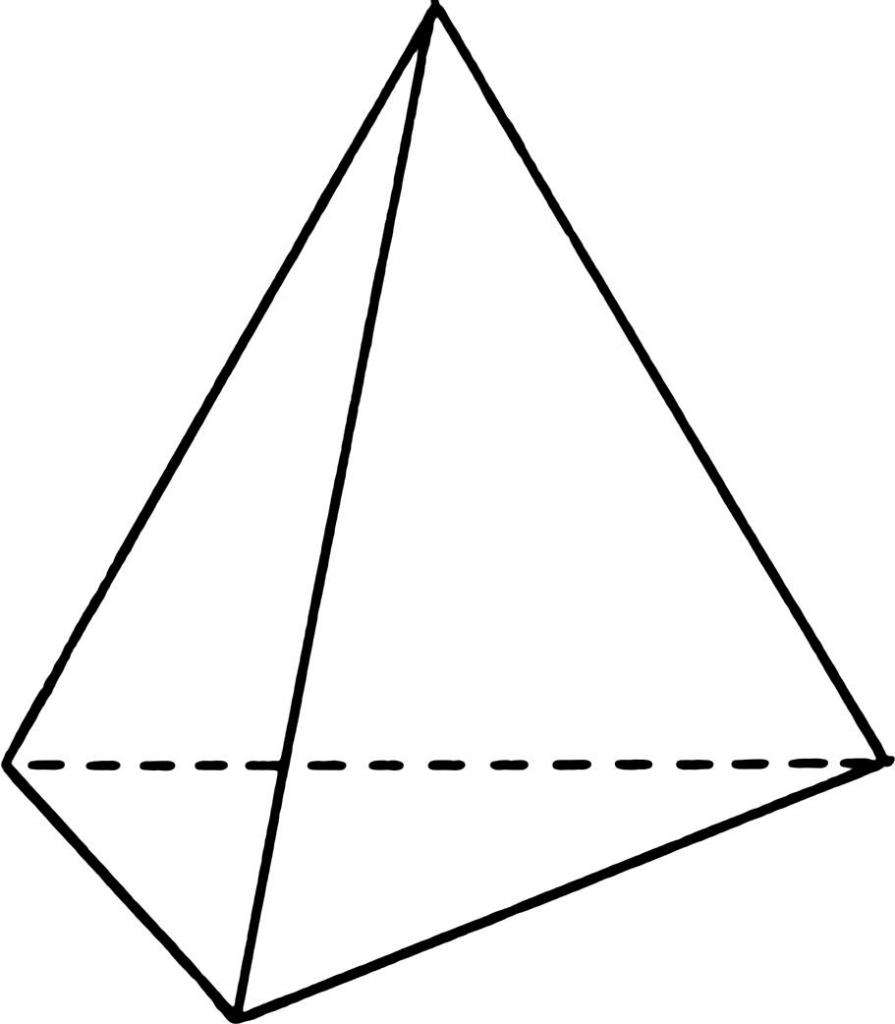
Как видно, рассматриваемая фигура образована четырьмя треугольниками, которые в общем случае являются разными. Каждый треугольник — это стороны пирамиды или ее грань. Эту пирамиду часто называют тетраэдром, то есть четырехгранной объемной фигурой.
Помимо сторон, пирамида также обладает ребрами (их у нее 6) и вершинами (их 4).
Правильная пирамида с треугольным основанием
Фигура, которая получена с использованием произвольного треугольника и точки в пространстве, будет неправильной наклонной пирамидой в общем случае. Теперь представим, что исходный треугольник имеет одинаковые стороны, а точка пространства расположена точно над его геометрическим центром на расстоянии h от плоскости треугольника. Построенная с использованием этих исходных данных пирамида будет правильной.
Очевидно, что число ребер, сторон и вершин у правильной треугольной пирамиды будет таким же, как у пирамиды, построенной из произвольного треугольника.
Однако правильная фигура обладает некоторыми отличительными чертами:
- ее высота, проведенная из вершины, точно пересечет основание в геометрическом центре (точка пересечения медиан);
- боковая поверхность такой пирамиды образована тремя одинаковыми треугольниками, которые являются равнобедренными или равносторонними.
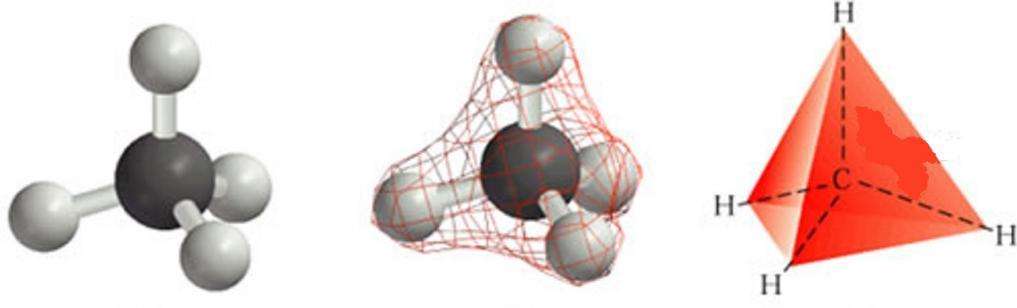
Правильная треугольная пирамида является не только чисто теоретическим геометрическим объектом. Некоторые структуры в природе имеют ее форму, например кристаллическая решетка алмаза, где атом углерода соединен с четырьмя такими же атомами ковалентными связями, или молекула метана, где вершины пирамиды образованы атомами водорода.
Формулы объема треугольной пирамиды
Определить объем совершенно любой пирамиды с произвольным n-угольником в основании можно с помощью следующего выражения:
V = 1/3 × So × h
Здесь символ So обозначает площадь основания, h — это высота фигуры, проведенная к отмеченному основанию из вершины пирамиды.
Поскольку площадь произвольного треугольника равна половине произведения длины его стороны a на апофему ha, опущенную на эту сторону, то формула объема треугольной пирамиды может быть записана в следующем виде:
V = 1/6 × a × ha × h
Для треугольной пирамиды общего типа определение высоты является непростой задачей. Для ее решения проще всего воспользоваться формулой расстояния между точкой (вершиной) и плоскостью (треугольным основанием), представленной уравнением общего вида.

Для правильной пирамиды формула объема имеет конкретный вид. Площадь основания (равностороннего треугольника) для нее равна:
So = √3/4 × a2
Подставляем ее в общее выражение для V, получаем:
V = √3/12 × a2 × h
Частным случаем является ситуация, когда у тетраэдра все стороны оказываются одинаковыми равносторонними треугольниками. В этом случае определить его объем можно, только исходя из знания параметра его ребра a. Соответствующее выражение имеет вид:
V = √2/12 × a3
Усеченная пирамида
Если верхнюю часть, содержащую вершину, отсечь у правильной треугольной пирамиды, то получится усеченная фигура. В отличие от исходной она будет состоять из двух равносторонних треугольных оснований и трех равнобедренных трапеций.
Ниже на фото показано, как выглядит правильная усеченная пирамида треугольная, изготовленная из бумаги.

Для определения объема треугольной пирамиды усеченной необходимо знать три ее линейных характеристики: каждую из сторон оснований и высоту фигуры, равную расстоянию между верхним и нижним основаниями. Соответствующая формула для объема записывается так:
V = √3/12 × h × (A2 + a2 + A × a)
Здесь h — высота фигуры, A и a — длины сторон большого (нижнего) и малого (верхнего) равносторонних треугольников соответственно.
Решение задачи
Чтобы приведенная информация в статье была понятнее для читателя, покажем на наглядном примере, как пользоваться некоторыми из записанных формул.
Пусть объем треугольной пирамиды равен 15 см3. Известно, что фигура является правильной. Следует найти апофему ab бокового ребра, если известно, что высота пирамиды составляет 4 см.
Поскольку известны объем и высота фигуры, то можно воспользоваться соответствующей формулой для вычисления длины стороны ее основания. Имеем:
V = √3/12 × a2 × h =>
a = 12 × V / (√3 × h) = 12 × 15 / (√3 × 4) = 25,98 см
Апофему ab можно рассчитать, если рассмотреть соответствующий прямоугольный треугольник внутри пирамиды. Катетами треугольника являются 1/3 длины высоты основания и высота пирамиды, гипотенузой будет искомая апофема. Тогда:
ab = √(h2 + a2 / 12) = √(16 + 25,982 / 12) = 8,5 см
Рассчитанная длина апофемы фигуры получилась больше ее высоты, что справедливо для пирамиды любого типа.
Загрузить PDF
Загрузить PDF
Квадратная пирамида – объемная фигура с основанием в виде квадрата и треугольными боковыми гранями. Вершина квадратной пирамиды проецируется в центр основания. Если «а» — сторона квадратного основания, «h» — высота пирамиды (перпендикуляр, опущенный из вершины пирамиды к центру ее основания), тогда объем квадратной пирамиды можно вычислить по формуле: a2 × (1/3)h. Эта формула верна для квадратной пирамиды любых размеров (от сувенирных пирамид до египетских пирамид).
-
1
Найдите сторону основания. Так как в основании квадратной пирамиды лежит квадрат, то все стороны основания равны. Поэтому необходимо найти длину любой стороны основания.
- Например, дана пирамида, сторона основания которой равна 5 см.
- Если стороны основания не равны друг другу, то вам дана прямоугольная, а не квадратная пирамида. Тем не менее, формула для вычисления объема прямоугольной пирамиды похожа на формулу для вычисления объема квадратной пирамиды. Если «l» и «w» — две смежные (неравные) стороны прямоугольника в основании пирамиды, то объем пирамиды вычисляется по формуле: (l× w) × (1/3)h
-
2
Вычислите площадь квадратного основания, умножив его сторону саму на себя (или, другими словами, возведя сторону в квадрат).
- В нашем примере: 5 х 5 = 52 = 25 см2.
- Не забудьте, что площадь измеряется в квадратных единицах — квадратных сантиметрах, квадратных метрах, квадратных километрах и так далее.
-
3
Умножьте площадь основания на высоту пирамиды. Высота — перпендикуляр, опущенный из вершины пирамиды на ее основание. Перемножив эти величины, вы получите объем куба с тем же основанием и высотой, как у пирамиды.
- В нашем примере высота равна 9 см: 25 см2 × 9 см = 225 см3
- Не забывайте, что объем измеряется в кубических единицах, в данном случае в кубических сантиметрах.
-
4
Разделите полученный результат на 3 и вы найдете объем квадратной пирамиды.
- В нашем примере: 225 см3 / 3 = 75 см3.
- Объем измеряется в кубических единицах.
Реклама
-
1
Если вам дана либо площадь, либо высота пирамиды и ее апофема, вы можете найти объем пирамиды, используя теорему Пифагора. Апофема – это высота наклонной треугольной грани пирамиды, проведенная из вершины треугольника к его основанию. Для вычисления апофемы используйте сторону основания пирамиды и ее высоту.
- Апофема делит сторону основания пополам и пересекает ее под прямым углом.
- Апофема делит сторону основания пополам и пересекает ее под прямым углом.
-
2
Рассмотрите прямоугольный треугольник, образованный апофемой, высотой и отрезком, соединяющим центр основания и середину его стороны. В таком треугольнике апофема является гипотенузой, которую можно найти по теореме Пифагора. Отрезок, соединяющий центр основания и середину его стороны, равен половине стороны основания (этот отрезок является одним из катетов; вторым катетом является высота пирамиды).
- Напомним, что теорема Пифагора записывается так: a2 + b2 = c2, где «a» и «b» — катеты, «c» — гипотенуза прямоугольного треугольника.
- Например, дана пирамида, у которой сторона основания равна 4 см, а апофема — 6 см. Чтобы найти высоту пирамиды, подставьте эти значения в теорему Пифагора.
- a2 + b2 = c2
- a2 + (4/2)2 = 62
- a2 = 32
- a = √32 = 5,66 см Вы нашли второй катет прямоугольного треугольника, который является высотой пирамиды (аналогично, если была бы дана апофема и высота пирамиды, вы бы могли найти половину стороны основания пирамиды).
-
3
Используйте найденное значение, чтобы найти объем пирамиды по формуле: a2 × (1/3)h.
- В нашем примере вы вычислили, что высота пирамиды равна 5,66 см. Подставьте необходимые значения в формулу для вычисления объема пирамиды:
- a2 × (1/3)h
- 42 × (1/3)(5,66)
- 16 × 1,89 = 30,24 см3.
- В нашем примере вы вычислили, что высота пирамиды равна 5,66 см. Подставьте необходимые значения в формулу для вычисления объема пирамиды:
-
4
Если вам не дана апофема, используйте ребро пирамиды. Ребро – это отрезок, соединяющий вершину пирамиды с вершиной квадрата в основании пирамиды. В этом случае вы получите прямоугольный треугольник, катетами которого являются высота пирамиды и половина диагонали квадрата в основании пирамиды, а гипотенузой – ребро пирамиды. Так как диагональ квадрата равна √2 × сторону квадрата, то вы можете найти сторону квадрата (основания), разделив диагональ на √2. Затем вы сможете найти объем пирамиды по вышеописанной формуле.
- Например, дана квадратная пирамида с высотой 5 см и ребром 11 см. Вычислите половину диагонали следующим образом:
- 52 + b2 = 112
- b2 = 96
- b = 9,80 см.
- Вы нашли половину диагонали, поэтому диагональ равна: 9,80 см × 2 = 19,60 см.
- Сторона квадрата (основания) равна √2 × диагональ, поэтому 19,60 / √2 = 13,90 см. Теперь найдите объем пирамиды по формуле:a2 × (1/3)h
- 13,902 × (1/3)(5)
- 193,23 × 5/3 = 322,05 см3
Реклама
- Например, дана квадратная пирамида с высотой 5 см и ребром 11 см. Вычислите половину диагонали следующим образом:
Советы
- В квадратной пирамиде ее высота, апофема и сторона основания связаны теоремой Пифагора: (сторона ÷ 2)2 + (высота)2 = (апофема)2
- В любой правильной пирамиде апофема, сторона основания и ребро связаны теоремой Пифагора: (сторона ÷ 2)2 + (апофема)2 = (ребро)2
Реклама
Об этой статье
Эту страницу просматривали 11 790 раз.
Была ли эта статья полезной?
Данный сайт находится в режиме тестирования, обо всех выявленных проблемах Вы можете сообщить на почту
Формулы пирамиды
Для расчёта всех основных параметров пирамиды воспользуйтесь калькулятором.
Свойства правильной пирамиды
- Боковые ребра правильной пирамиды равны между собой
- Боковые грани правильной пирамиды равны между собой и являются равнобедренными треугольниками
- Апофемы правильной пирамиды равны
- В любую правильную пирамиду можно вписать и описать около неё сферу
- Все боковые грани образуют с плоскостью основания правильной пирамиды равные углы
Площадь основания правильной пирамиды
$$
S_{осн} = {N * AB^2 over 4 * tan(180/N)}
$$
| Где: | N – количество сторон у основания пирамиды |
Апофема правильной пирамиды
$$
OK = sqrt{OP^2 + ({AB over 2 * tan(180/N)})^2}
$$
| Где: | N – количество сторон у основания пирамиды |
Боковое ребро правильной пирамиды
$$
OD = sqrt{OP^2 + ({AB over 2 * sin(180/N)})^2}
$$
| Где: | N – количество сторон у основания пирамиды |
Объём пирамиды через площадь основы (Sосн) и высоту (OP)
$$
V = {1 over 3} * S_{осн} * OP
$$
Площадь боковой поверхности правильной пирамиды через периметр основания (Pосн) и апофему (OK)
$$
S_Б = {1 over 2} * P_{осн} * OK
$$
При изучении абсолютно любой пространственной фигуры важно знать, как рассчитывать ее объем. В данной статье приводится формула объема правильной четырехугольной пирамиды, а также на примере решения задач показано как этой формулой следует пользоваться.
О какой пирамиде пойдет речь?
Каждому школьнику старших классов известно, что пирамида представляет собой многогранник, состоящий из треугольников и многоугольника. Последний является основанием фигуры. Треугольники имеют одну общую сторону с основанием и пересекаются в единственной точке, являющейся вершиной пирамиды.

Каждая пирамида характеризуется длиной сторон основания, длиной боковых ребер и высотой. Последняя представляет собой перпендикулярный отрезок, опущенный к основанию из вершины фигуры.
Правильная четырехугольная пирамида представляет собой фигуру с квадратным основанием, высота которой пересекает этот квадрат в его центре. Пожалуй, самым известным примером пирамид этого типа являются древние египетские каменные строения. Ниже приведена фотография пирамиды Хеопса.

Изучаемая фигура имеет пять граней, четыре из которых — это одинаковые равнобедренные треугольники. Также она характеризуется пятью вершинами, четыре из которых принадлежат основанию, и восемью ребрами (4 ребра основания и 4 ребра боковых граней).
Формула объема четырехугольной пирамиды правильной
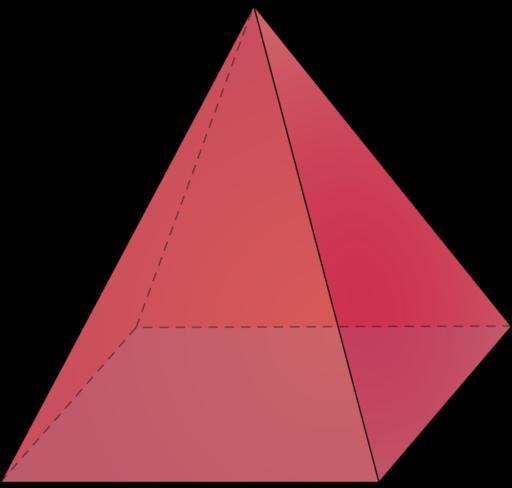
Объем рассматриваемой фигуры представляет собой часть пространства, которое ограничивают пять сторон. Чтобы вычислить этот объем воспользуемся следующей зависимостью площади параллельного основанию пирамиды среза Sz от вертикальной координаты z:
Sz = So * (h — z/h)2
Здесь So — площадь квадратного основания. Если в записанное выражение подставить z = h, то мы получим нулевое значение для Sz. Этой величине z соответствует срез, который будет содержать только вершину пирамиды. Если же z = 0, то мы получаем значение площади основания So.

Объем пирамиды найти несложно, зная функцию Sz(z), для этого достаточно разрезать фигуру на бесконечное число параллельных основанию слоев, а затем провести операцию интегрирования. Следую этой методике, получаем:
V = ∫0h(Sz)*dz = -S0*(h-z)3 / (3*h2)|0h = 1/3*S0*h.
Поскольку S0 — это площадь квадратного основания, то, обозначив сторону квадрата буквой a, получаем формулу объема правильной четырехугольной пирамиды:
V = 1/3*a2*h.
Теперь покажем на примерах решения задач, как следует применять это выражение.
Задача на определение объема пирамиды через ее апофему и боковое ребро
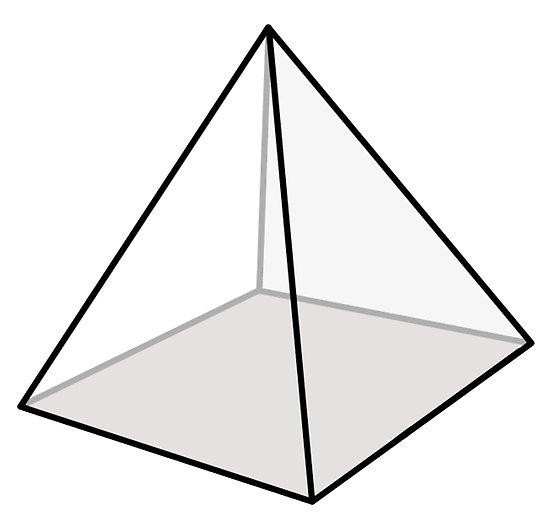
Апофемой пирамиды называют высоту ее бокового треугольника, которая опущена на сторону основания. Поскольку все треугольники равны в правильной пирамиде, то их апофемы также будут одинаковыми. Обозначим ее длину символом hb. Боковое ребро обозначим как b.
Зная, что апофема пирамиды равна 12 см, а ее боковое ребро составляет 15 см, найдите объем правильной пирамиды четырехугольной.
Записанная в предыдущем пункте формула для объема фигуры содержит два параметра: длину стороны a и высоту h. На данный момент нам не известен ни один из них, поэтому займемся их вычислениями.
Длину стороны квадрата a несложно рассчитать, если воспользоваться теоремой Пифагора для треугольника прямоугольного, у которого гипотенузой является ребро b, а катетами будут апофема hb и половина стороны основания a/2. Получаем:
b2 = hb2 + a2/4 =>
a = 2*√(b2 — hb2).
Подставляя известные значения из условия, получим величину a = 18 см.
Чтобы вычислить высоту h пирамиды, можно поступить двумя способами: рассмотреть прямоугольный треугольник с гипотенузой-боковым ребром или с гипотенузой-апофемой. Оба способа равноправны и предполагают выполнение одного и того же количества математических операций. Остановимся на рассмотрении треугольника, где гипотенузой является апофема hb. Катетами в нем будут h и a/2. Тогда получаем:
h = √(hb2-a2/4) = √(122 — 182/4) = 7,937 см.
Теперь можно воспользоваться формулой для объема V:
V = 1/3*a2*h = 1/3*182*7,937 = 857,196 см3.
Таким образом, объем правильной четырехугольной пирамиды равен приблизительно 0,86 литра.
Объем пирамиды Хеопса
Теперь решим интересную и практически важную задачу: найдем, чему равен объем самой большой пирамиды в Гизе. Из литературных данных известно, что исходная высота строения была равна 146,5 метра, а длина его основания составляет 230,363 метра. Эти цифры позволяют применить формулу для вычисления V. Получаем:
V = 1/3*a2*h =1/3*230,3632*146,5 ≈ 2591444 м3.
Полученное значение составляет почти 2,6 млн. м3. Этот объем соответствует объему куба, сторона которого равна 137,4 метра.