Как найти объем правильной четырехугольной пирамиды задачи - AvtoShod.ru

Всего: 41 1–20 | 21–40 | 41–41

Добавить в вариант

Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на Пи .

В правильной четырёхугольной пирамиде SABCD с основанием ABCD боковое ребро SA равно 5, сторона основания равна Найдите объём пирамиды.

Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 6, а боковое ребро равно

Сторона основания правильной четырехугольной пирамиды равна 4, а боковое ребро равно Найдите объем пирамиды.

Сторона основания правильной четырехугольной пирамиды равна 6, а боковое ребро равно Найдите объем пирамиды.

Даны две правильные четырёхугольные пирамиды. Объём первой пирамиды равен 16. У второй пирамиды высота в 2 раза больше, а сторона основания в 1,5 раза больше, чем у первой. Найдите объём второй пирамиды.

Даны две правильные четырёхугольные пирамиды. Объём первой пирамиды равен 9. У второй пирамиды высота в 1,5 раза больше, а сторона основания в 2 раза больше, чем у первой. Найдите объём второй пирамиды.

Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно

Источники:

Демонстрационная версия ЕГЭ  — 2018;

Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 6, а боковое ребро равно

В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 4, а гипотенуза равна Найдите объём призмы, если её высота равна 6.

Найдите объем правильной четырехугольной пирамиды, сторона основания которой равна 6, а боковое ребро равно

Найдите объем правильной четырехугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно

В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 5, а гипотенуза равна Найдите объём призмы, если её высота равна 4.

В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 2, а гипотенуза равна Найдите объём призмы, если её высота равна 3.

Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 6, а боковое ребро равно

Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 2, а боковое ребро равно

Всего: 41 1–20 | 21–40 | 41–41

Источник

В данной публикации мы рассмотрим, как можно найти объем пирамиды и разберем примеры решения задач для закрепления материала.

Формула вычисления объема пирамиды
- 1. Общая формула
- 2. Объем правильной треугольной пирамиды
- 3. Объем правильной четырехугольной пирамиды
- 4. Объем правильной шестиугольной пирамиды
Примеры задач

Формула вычисления объема пирамиды

1. Общая формула

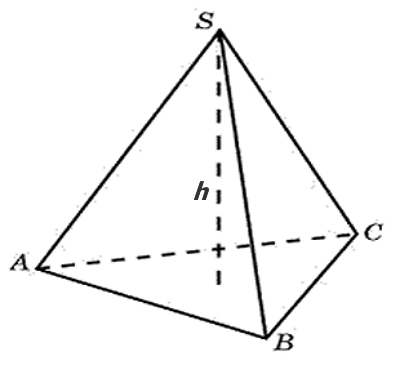
Объем (V) пирамиды равняется одной третьей произведения ее высоты на площадь основания.

ABCD – основание;
E – вершина;
h – высота, перпендикулярная основанию.

2. Объем правильной треугольной пирамиды

Основанием правильной треугольной пирамиды является равносторонний треугольник (ABC), площадь которого вычисляется так (а – сторона треугольника):

Подставляем данное выражение в формулу расчета объема фигуры и получаем:

3. Объем правильной четырехугольной пирамиды

Основанием правильной четырехугольной пирамиды является квадрат, площадь которого считается так: S = a², где а – длина его стороны.

Следовательно, формулу объема можно представить в виде:

4. Объем правильной шестиугольной пирамиды

Основанием правильной шестиугольной пирамиды является правильный шестиугольник, площадь которого вычисляется по формуле (а – сторона основания):

С учетом этого, объем фигуры считается так:

Примеры задач

Задание 1
Найдите объем правильной треугольной пирамиды, если известно, что ее высота составляет 16 см, а длина стороны ее основания – 8 см.

Решение:
Воспользуемся соответствующей формулой, подставив в нее известные значения:

Задание 2
Высота правильной четырехугольной пирамиды равна 12 см, а сторона ее основания – 3 см. Найдите объем фигуры.

Решение:
Площадь квадрата, который является основанием пирамиды, равна 9 см² (3 см ⋅ 3 см). Следовательно, объем равен:

Источник

Видео по теме

Задача 1. В правильной четырехугольной пирамиде точка – центр основания, – вершина, Найдите длину отрезка .

fgk

Решение: + показать

Задача 2. В правильной четырехугольной пирамиде точка – центр основания, – вершина, Найдите боковое ребро

Решение: + показать

Задача 3. Стороны основания правильной четырехугольной пирамиды равны боковые ребра равны Найдите площадь поверхности этой пирамиды.

Решение: + показать

Задача 4. В правильной четырёхугольной пирамиде точка — центр основания, — вершина, Найдите длину отрезка

Решение: + показать

Задача 5. Основанием пирамиды является прямоугольник со сторонами и Ее объем равен Найдите высоту этой пирамиды.

Решение: + показать

Задача 6. В правильной четырёхугольной пирамиде с основанием боковое ребро равно сторона основания равна Найдите объём пирамиды.

Решение: + показать

Задача 7. В правильной четырёхугольной пирамиде все рёбра равны Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых рёбер.

Решение: + показать

Задача 8. Даны две правильные четырёхугольные пирамиды. Объём первой пирамиды равен У второй пирамиды высота в раза больше, а сторона основания в раза больше, чем у первой. Найдите объём второй пирамиды.

Решение: + показать

Задача 9. В правильной четырёхугольной пирамиде боковое ребро равно а тангенс угла между боковой гранью и плоскостью основания равен Найти сторону основания пирамиды.

Решение: + показать

Задача 10. Основанием пирамиды является прямоугольник со сторонами и Ее объем равен Найдите высоту этой пирамиды.

Решение: + показать

Задача 11. Стороны основания правильной четырехугольной пирамиды равны боковые ребра равны Найдите площадь поверхности этой пирамиды.

Решение: + показать

Задача 12. В правильной треугольной пирамиде медианы основания пересекаются в точке . Площадь треугольника равна объем пирамиды равен Найдите длину отрезка .

Решение: + показать

Задача 13. В правильной треугольной пирамиде точка — середина ребра — вершина. Известно, что а . Найдите площадь боковой поверхности пирамиды.

Решение: + показать

Задача 14. Найдите объем правильной треугольной пирамиды, стороны основания которой равны а высота равна

Решение: + показать

Задача 15. Найдите высоту правильной треугольной пирамиды, стороны основания которой равны а объем равен

Решение: + показать

Задача 16. Стороны основания правильной шестиугольной пирамиды равны боковые ребра равны Найдите площадь боковой поверхности этой пирамиды.

Решение: + показать

Задача 17. Объем правильной шестиугольной пирамиды Сторона основания равна Найдите боковое ребро.

Решение: + показать

Задача 18. Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в два раза?

Решение: + показать

Задача 19. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в раз?

Решение: + показать

Задача 20. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в пять раз?

Решение: + показать

Задача 21. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом °. Высота пирамиды равна Найдите объем пирамиды.

Решение: + показать

Задача 22. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно Найдите объем пирамиды.

Решение: + показать

Задача 23. От треугольной призмы, объем которой равен отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.

Решение: + показать

Задача 24. Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен Найдите объем шестиугольной пирамиды. Видео по теме 1 2

Решение: + показать

Задача 25. Сторона основания правильной шестиугольной пирамиды равна 8, боковое ребро равно 16. Найдите объём пирамиды.

Решение: + показать

Задача 26. Сторона основания правильной шестиугольной пирамиды равна а угол между боковой гранью и основанием равен $45^{circ}.$ Найдите объем пирамиды.

Решение: + показать

Задача 27. Найдите объём правильной шестиугольной пирамиды если объём треугольной пирамиды равен

Решение: + показать

Задача 28. Объем параллелепипеда равен Найдите объем треугольной пирамиды

Решение: + показать

Задача 29. Объем куба равен Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Решение: + показать

Задача 30. Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно

Решение: + показать

Задача 31. Объем правильной четырехугольной пирамиды равен Точка — середина ребра . Найдите объем треугольной пирамиды .

Решение: + показать

Задача 32. От треугольной пирамиды, объем которой равен отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

Решение: + показать

Задача 33. Ребра тетраэдра равны Найдите площадь сечения, проходящего через середины четырех его ребер.

Решение: + показать

Вы можете пройти тест

Источник

Формулировка задачи: Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна K, а боковое ребро равно N.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13 (Задачи по стереометрии).

Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения.

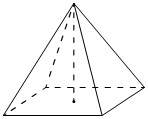
Пример задачи:

Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 8, а боковое ребро равно √41.

Решение:

Объем любой пирамиды равен:

V = 1/3 ⋅ S_осн ⋅ h

В основании правильной четырехугольной пирамиды лежит квадрат со стороной 8. Поэтому площадь основания равна:

S_осн = 8 ⋅ 8 = 64

Теперь нужно вычислить высоту пирамиды, используя сторону основания и боковое ребро. Для этого проведем диагональ в основании правильной четырёхугольной пирамиды. Диагональ квадрата в основании равна:

d = 8√2

Получим прямоугольный треугольник, катетами которого являются половина диагонали и высота пирамиды, а гипотенузой – боковое ребро пирамиды. Поэтому высоту пирамиды можно вычислить по теореме Пифагора:

h = √41 – (4√2)² = √41 – 32 = 3

Осталось найти объем пирамиды, подставив все полученные данные:

V = 1/3 ⋅ 64 ⋅ 3 = 64

Ответ: 64

В общем виде решение данной задачи по стереометрии выглядит следующим образом:

V = 1/3 ⋅ K² ⋅ √N² – (K/2 ⋅ √2)²

где K – сторона основания, N – боковое ребро.

Остается лишь подставить конкретные значения и подсчитать результат.

Источник

Объём правильной пирамиды. Продолжаем рассматривать задачи с пирамидами. На блоге уже рассмотрены задания с правильными пирамидами, в этих статьях шла речь о нахождении элементов и площади поверхности. Здесь разберём примеры связанные с понятием объёма. Для решения подобных заданий обязательно нужно знать формулу объёма пирамиды:

S – площадь основания пирамиды

h – высота пирамиды

Основанием может быть любой многоугольник. Но в большинстве задач на ЕГЭ речь в условии, как правило, идёт о правильных пирамидах. Напомню одно из её свойств:

Вершина правильной пирамиды проецируется в центр её основания

Посмотрите на проекцию правильной треугольной, четырёхугольной и шестиугольной пирамид (ВИД СВЕРХУ):

Можете посмотреть ещё одну статью на блоге, где разбирались задачи связанные с нахождением объёма пирамиды. Рассмотрим задачи:

27087. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна корню из трёх.

Объём пирамиды вычисляется по формуле:

S – площадь основания пирамиды

h – высота пирамиды

Найдём площадь основания пирамиды, это правильный треугольник. Воспользуемся формулой – площадь треугольника равна половине произведения соседних сторон на синус угла между ними, значит:

Таким образом, объём пирамиды равен:

Ответ: 0,25

27088. Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен корню из трёх.

Такие понятия как высота пирамиды и характеристики её основания связаны формулой объёма:

S – площадь основания пирамиды

h – высота пирамиды

Сам объём нам известен, площадь основания можем найти, так как известны стороны треугольника, который является основанием. Зная указанные величины без труда найдём высоту.

Для нахождения площади основания воспользуемся формулой – площадь треугольника равна половине произведения соседних сторон на синус угла между ними, значит:

Таким образом, подставив данные значения в формулу объема можем вычислить высоту пирамиды:

Высота равна трём.

Ответ: 3

27109. В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.

Объём пирамиды вычисляется по формуле:

S – площадь основания пирамиды

h – высота пирамиды

Высота нам известна. Необходимо найти площадь основания. Напомню, что вершина правильной пирамиды проецируется в центр её основания. Основанием правильной четырёхугольной пирамиды является квадрат. Мы можем найти его диагональ. Рассмотрим прямоугольный треугольник (выделен синим):

Отрезок соединяющий центр квадрата с точкой В это катет, который равен половине диагонали квадрата. Этот катет можем вычислить по теореме Пифагора:

Значит BD = 16. Вычислим площадь квадрата воспользовавшись формулой площади четырёхугольника:

Следовательно:

Таким образом, объём пирамиды равен:

Ответ: 256

27178. В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.

Высота пирамиды и её и объём известны, значит можем найти площадь квадрата, который является основанием. Зная площадь квадрата, мы сможем найти его диагональ. Далее рассмотрев прямоугольный треугольник по теореме Пифагора вычислим боковое ребро:

Найдём площадь квадрата (основания пирамиды):

Вычислим диагональ квадрата. Так как его площадь равна 50, то сторона будет равна корню из пятидесяти и по теореме Пифагора:

Точка О делит диагональ BD пополам, значит катет прямоугольного треугольника ОВ = 5.

Таким образом, можем вычислить чему равно боковое ребро пирамиды:

Ответ: 13

245353. Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 3.

Как уже неоднократно было сказано – объём пирамиды вычисляется по формуле:

S – площадь основания пирамиды

h – высота пирамиды

Боковое ребро перпендикулярное основанию равно трём, это означает, что высота пирамиды равна трём. Основания пирамиды – это многоугольник, площадь которого равна:

Таким образом:

Ответ: 27

27086. Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.

Посмотреть решение

27110. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60⁰. Высота пирамиды равна 6. Найдите объем пирамиды.

Посмотреть решение

27111. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.

Посмотреть решение

27113. Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 1. Найдите объем шестиугольной пирамиды.