Масса полой детали
Никогда не устану повторять, что масса тела — это его объем 

Однако, в случае полой или пустотелой детали мы будем иметь дело не с объемом ее тела, а с объемом ее стенок. Объем стенок полой детали проще всего представить как разность объемов двух сплошных тел: с внешними размерами и с внутренними (из полного объема тела вычитается объем внутренней пустоты).
Формулы для объема сплошных тел можно найти в статье «Масса сплошной детали».
Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.
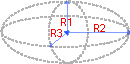
Буквой 
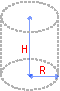
1. Масса трубки (полого цилиндра)





После упрощения получаем формулу для объема:
Тогда масса трубки:
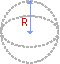
2. Масса полого (пустотелого) шара




Тогда масса:
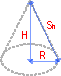
3. Масса полого сегмента шара





После упрощения получаем формулу для объема:
Тогда масса:
4. Масса полого усеченного конуса






После упрощения получаем формулу для объема:
Тогда масса:
5. Масса полой усеченной пирамиды






После упрощения получаем формулу для объема:
Тогда масса:
* в данном случае 


Объем геометрических фигур
Рассчитывает объем геометрических фигур (куб, призма, пирамида, усеченная пирамида, конус, цилиндр, сфера, эллипсоид, тороид).
Данная статья содержит калькуляторы для расчета объема различных геометрических фигур. Основной источник формул: Spiegel, Murray R. Mathematical Handbook of Formulas and Tables. Schaum’s Outline series in Mathematics. McGraw-Hill Book Co., 1968.
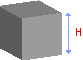
Объем куба
Формула:
Объем куба
Точность вычисления
Знаков после запятой: 5
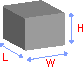
Объем прямоугольной призмы
Формула:
Объем прямоугольной призмы
Точность вычисления
Знаков после запятой: 5
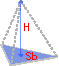
Объем пирамиды
Формула:
Объем пирамиды
Точность вычисления
Знаков после запятой: 5
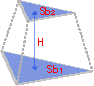
Объем усеченной пирамиды
Формула:
Объем усеченной пирамиды
Площадь первого основания (Sb1)
Площадь второго основания (Sb2)
Точность вычисления
Знаков после запятой: 5
Объем конуса
Формула:
Объем конуса
Точность вычисления
Знаков после запятой: 5
Объем цилиндра
Formula:
Объем цилиндра
Точность вычисления
Знаков после запятой: 5
Объем сферы
Формула:
Объем сферы
Точность вычисления
Знаков после запятой: 5
Объем эллипсоида
Формула:
Объем эллипсоида
Точность вычисления
Знаков после запятой: 5
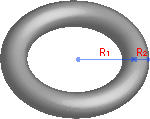
Объем тороида
Формула:
Объем тора
Точность вычисления
Знаков после запятой: 5
Ссылка скопирована в буфер обмена
PLANETCALC, Объем геометрических фигур
Цилиндр – это объемное тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые ее пересекают. Цилиндр (от греческого «kulindros» — ролик, каток) относится к основным геометрическим фигурам. В элементарных математических трактовках, он определяется как трехмерное тело. Объем цилиндра – один из базовых параметров, который необходимо уметь вычислять каждому человеку. Формула применяется во многих сферах промышленности, а также в строительстве, архитектуре, механике, программировании.
Объем цилиндра по высоте и радиусу

Узнать объем полой фигуры можно моментально, воспользовавшись удобной онлайн-программой. Сервис позволяет за секунды вычислить параметры тела и получить результаты в кубических сантиметрах, метрах, литрах. Расчет производится по двум математическим формулам:
- По высоте и радиусу: V = S х h.
- Объём по площади основания и высоте: V = ∏ х R2 х h
Где V — объем, S — площадь, h — высота. Чтобы рассчитать объем необходимо площадь основания тела умножить на h. Следовательно, для этого необходимо знать две переменные.
R – радиус, возведенный в квадрат. От первой формулы, расчет отличается тем, что сначала необходимо найти значение радиуса. Для этого диаметр делится на 2 или применяется формула S/2 х ∏ х H. ∏ — константа 3,14 (отношение длины окружности к диаметру).
Объём цилиндра через площадь основания и высоту

Программа позволяет определить объем тела по обеим формулам. Для этого необходимо только подставить цифры в соответствующие строки и нажать кнопку рассчитать. Пошаговая инструкция вычисления базовых показателей фигуры на калькуляторе по высоте и радиусу:
- в графе «h» ввести длину заданной фигуры, рядом выбрать метрику – в миллиметрах, сантиметрах, метрах;
- в строке «r» ввести радиус тела и выбрать меру длины (мм, см, м);
- в графе «Результат» определить, в чем будет выведен V – кубах, литрах.
Например, длина фигуры составляет 1,6 метра, радиус 25 сантиметров. Объем равен 314.2 литров, 314200 куб. см или 0.314 куб. м. Результат выводится моментально, с точностью до тысячной. Правильность вычисления зависит только от достоверности исходных данных.
Где применяется программа
Сервис разработана для всех пользователей, чья профессиональная деятельность предполагает решение математических задач. Калькулятор будет полезен школьникам 5-9 классов, учащимся 11 классов в подготовительном процессе к ЕГЭ и контрольным срезам, а также родителям для проверки правильности решения задач.
С помощью сервиса можно решить типичные тестовые задания школьной программы, подставляя известные значения и не забывая выставлять метрические параметры (в кубических сантиметрах, кубометрах, миллиметрах, литрах). Например:
- Дан цилиндр, с площадью основания 58,3 см2 и высотой 7 см. Чтобы посчитать V следует воспользоваться расчетом через площадь и высоту.
- Дан цилиндр длиной 11 см и диаметром основания 16 см. Параметры тела следует вычислять в первом калькуляторе «V по высоте и радиусу».
Решение: V = 58,3 см2 х 7 см = 408.1 см³ или 0.408 л.
Вычисление: перед использованием программы следует определить радиус основания – 16см/2 = 8 см. Затем значения подставить в нужные поля. Расчет производится на основании формулы V = 3,14 х 82 х 11 см = 2211.968 см³.
Следует учитывать, что параметры полого горизонтального, наклонного, косого, кругового, равностороннего цилиндров вычисляются с использованием дополнительных формул.
В каждом конкретном случае используют разные методы. Все зависит от того, что нам известно (какие входные данные) и какая точность нам нужна.
Если возможно, то разбивают фигуру на более простые тела, объем которых можно посчитать: параллелепипед, цилиндр, эллипсоид и т.п. Объемы простых фигур складывают.
Если известна функция, которая описывает ограничивающую поверхность, то считают тройной интеграл.
Если аналитические методы не подходят или очень сложные, то можно изготовить такое тело, например, из гипса и бросить в воду. Объем вытесненной воды будет равен объему тела.
Есть и косвенные методы измерения.
Если известна масса тела и материал, из которого оно сделано, то можно вычислить объем по плотности материала.
Это не полный список методов. Наверняка, можно найти другие.
Многие сложные детали (конструкции) можно представить совокупностью различных элементов, объем которых можно вычислить, воспользовавшись набором online-калькуляторов с данной страницы.
Представлены программы для расчета объемов фигур, базисом которых является квадрат или прямоугольник, а также имеющих в основании окружность: цилиндра, конуса и шаровых элементов.
В конструкторской работе при различных расчетах возникает потребность использования значений объема элементарных фигур: параллелепипеда, куба, призмы и пр. В частности это может иметь место при расчете заполнения вагонов и платформ упакованной в транспортную тару готовой продукцией. Такой расчет требует учета многих факторов, в том числе боковой ветровой нагрузки, смещения центра тяжести и пр.
Если неправильно рассчитать объем тары подлежащего отгрузке упакованного товара, можно не вместить в вагон заявленное количество изделий. В результате предприятие потерпит убытки. Онлайн калькуляторы нашего сайта позволят избежать проблемных ситуаций. Расчеты объемов различных фигур выполняются с большой точностью.