Очень часто мы волей-неволей задумываемся над, казалось бы, странными и не имеющими смысла вопросами. Нас очень часто интересуют численные значения каких-нибудь параметров, а также сравнение их с другими, но известными нам величинами. Очень часто такие вопросы приходят в голову детям, и родителям приходится на них отвечать.
Чему равен объем Земли? Ответить на вопрос бывает непросто, потому что мозг очень неохотно запоминает те величины, которые ему редко придется применить в жизни. Если вы услышали ответ на этот вопрос давным-давно, сегодня вы уже вряд ли его вспомните, так как это вам с того времени не пригодилось.
Прежде чем дать точный ответ и привести сравнение объема Земли с известными нам величинами, окунёмся в историю геометрии. Ведь эта наука изначально была создана для измерения различных характеристик нашей планеты.
История
Геометрия зародилась ещё в Древнем Египте. Людям очень часто требовалось (как и сейчас) находить расстояния между городами, измерять те или иные предметы, отмерять площадь земли, принадлежавшую им. Благодаря всему этому появилась специальная наука — геометрия (от слов «гео» — Земля, и «метрос» — измерять). И изначально она сводилась только к прикладному применению. Но для некоторых измерений требовались более сложные вычисления. Тогда и появились на заре развития этой науки такие философы и учёные, как Пифагор и Евклид.
При строительстве даже с первого взгляда простых сооружений необходимо уметь измерять, какое количество материала пойдёт на постройку, вычислить расстояния между точками и величины углов между прямыми плоскостями. Также нужно знать свойства простейших геометрических фигур. Таким образом, египетские пирамиды, сооруженные во 2-3 веке до н. э., поражают точностью своих пространственных соотношений, доказывая, что их строители знали многие геометрические положения и обладали большой базой для точных математических расчётов.
Затем с развитием геометрии она потеряла своё изначальное предназначение и расширила области своего применения. Сегодня невозможно представить какое-либо производство без расчётов с помощью геометрических методов.
В следующем разделе поговорим о методах измерения тех или иных геометрических характеристик для разных тел.
Измерение тел
Для прямоугольных тел измерения объёма и площади наиболее просты. Необходимо всего лишь знать ширину, длину и высоту фигуры, чтобы узнать о ней всё самое необходимое. Объём прямоугольного тела находится произведением трёх пространственных величин. Площадь такой фигуры равна удвоенной сумме попарных произведений сторон. Если представить эти формулы математически, то для объёма будет справедливо такое равенство: V=abc, а для площади: S=2(ab+bc+ac).
Но для шара, например, эти формулы очень неудобны. Чтобы вычислить диаметр шара (а из него радиус), требуется заключить его в куб, с которым бы он соприкасался в шести точках. Длина (ширина или высота) этого куба и будет диаметром шара. Но гораздо проще сразу узнать объём шара, окунув его в наполненный до краёв сосуд. Измерив вылившийся объём воды, мы сможем узнать и объём шара. А так как формула объёма шара V=4/3*π*R3, из неё мы сможем найти радиус, который поможет для нахождения дальнейших характеристик тела.
Есть ещё один интересный способ измерения объёма шара, о котором мы расскажем в следующем разделе.
Как измерить объём Земли?
А если тело слишком большое, например, планета, как измерить точно её объём и площадь поверхности? Приходится прибегать к более интересным и изощрённым методам.
Начнём издалека. Как известно, если представить шар в двумерном пространстве, получится круг. Предположим, что из какой-то точки на шар падают в два разных места недалеко друг от друга два луча. Если посмотреть внимательно, будет видно, что они падают на поверхность под разными углами. Путём нехитрых геометрических построений можно заметить, что из центра шара можно провести линии, соединяющие две эти точки. Между собой эти линии будут образовывать определённый угол, который будет соответствовать измеренному заранее расстоянию между этими точками. Таким образом, мы знаем длину дуги, соответствующую какому-либо углу. Так как всего в круге 360 градусов, мы с лёгкостью можем найти длину окружности круга. А из формулы длины окружности находим радиус, из которого по известной формуле вычисляется объём.
Таким способом и находится объём больших тел, в том числе и небесных. Им ещё в древности пользовались греки, чтобы узнать больше данных о Земле. Так они вычислили и объем Земли. Хотя, конечно, эти данные и приблизительные, потому что есть масса погрешностей, которые оказываются неучтенными при таком способе измерения.
Прежде чем дать ответ на главный вопрос, разберёмся в том, как сегодня измеряют такие сложные величины с наименьшей возможной погрешностью.
Современные методы измерения
Сегодня мы обладаем массой развитых технологий, которые позволяют уточнить вычисления древних учёных насчёт разных характеристик Земли. Для этого в прошлом веке человечество использовало орбитальные спутники. Они могут с наибольшей точностью измерить длину окружности нашей планеты, а на основании этих данных вычислить радиус, зная который, как мы уже выяснили, легко найти объём Земли.
Пришло время узнать точную цифру и сравнить её с известными нам величинами.
Какой объем Земли?
Итак, мы приблизились к главному вопросу этой статьи. Объем Земли равен 1 083 210 000 000 км3. Много ли это? Смотря с чем сравнивать. Из тех объектов, что мы в состоянии сравнить с этой величиной, подходит только другое небесное тело. Таким образом, можно сказать, что объем Луны составляет всего два процента от земного.
Есть также планеты, например, Юпитер, которые имеют огромный объем в силу того, что они имеют небольшую плотность и большую поверхностную площадь. Объем Земли мог бы тоже быть больше, если бы она состояла преимущественно из газов, а не из твёрдых и жидких веществ.
Применение
Такие величины нужны нам скорее для интереса. Но в реальной жизни они применяются очень активно. В астрономии такие величины, как объем Земли, масса Земли, земной радиус, используются для расчётов орбиты спутников, запускаемых с поверхности нашей планеты. Также эти данные могут быть полезны для более фундаментальных исследований. Интересно применение этих данных в географии и геологии, ведь расчет объема Земли представляет интерес для геологоразведочных работ и примерной оценки залежей полезных ископаемых.
Погрешности
Как известно, везде есть свои погрешности. И в расчёте объема Земли их достаточно много. Точнее, только одна погрешность вносит вклад в измерения, но она является самой значимой. Заключается она в том, что Земля не идеально круглая. Она приплюснута в полюсах и к тому же имеет неровности поверхности в виде впадин и гор. Хотя планета покрыта атмосферой, и большинство этих эффектов, влияющих на измерения, сглаживается, измерение плотности оказывается сильно затруднено.
Заключение
Физические характеристики Земли всегда были достаточно значимой темой для каждого. Бывает, что непонятно по какой причине, но хочется знать ответ на вопрос о том, сколько процентов площади планеты занимает мировой океан или каков объем Земли. В этой статье мы попытались не только дать точный ответ, но и рассказать, как и с помощью чего он был вычислен.
На чтение 8 мин Просмотров 13.1к.
Диаметр Земли имеет для ученых важное значение. С его помощью можно вычислить площадь нашей планеты и расстояние до ее центра, также он помогает составлять карты и проводить запуски космических летательных аппаратов. Узнаем, как вычисляются эти параметры и каковы их значения.
Содержание
- Основные параметры Земли
- Форма планеты
- Что такое экватор и для чего он нужен
- Как измерить длину окружности земли
- Как вычислить радиус и диаметр планеты
- Измерение окружности Земли в древние времена
- Сколько времени нужно, чтобы обойти вокруг Земли пешком
- Интересная информация об экваторе Земли
Основные параметры Земли
- Диаметр по экватору – 12756 км, по полюсам – 12713 км.
- Средний радиус – 6371 км. На таком расстоянии от поверхности находится центр ядра. Экваториальный радиус Земли – 6378 км. Расстояние к центру Земли на полюсах – 6356,5 км.
- Окружность Земли по экватору – 40075 км, а по полюсам – 40008 км.
- Удаление от Солнца в километрах – приблизительно 150 миллионов. Оно наиболее подходяще для формирования и поддержания жизни. Если бы орбита Земли была ближе или дальше всего на несколько миллионов километров, условия для эволюции жизни были бы намного хуже.
- Время, за которое Земля совершает один оборот вокруг Солнца – 365 дней 5 часов 48 минут и 46 секунд. В течение 23 часов 46 минут и 4 секунды она совершает оборот вокруг своей оси. Каждые 100 лет эта скорость уменьшается на 0,017 секунд. 140 млн. лет потребуется для того, чтобы длительность суток увеличилась на час.
- Ось вращения планеты наклонена к плоскости орбиты под углом немногим больше 23 градусов. Это обусловливает сезонность климатических условий и четкую смену времен года. Если бы ось вращения была наклонена на несколько градусов меньше или больше – на Земле создались бы менее благоприятные климатические условия, на больше части поверхности образовались бы ледники.
- Средняя температура на Земле – примерно 15 °C.
- Вода занимает примерно 71% всей площади. Ее масса – 1460 миллионов миллиардов тонн. Атмосфера весит в 275 раз меньше. Ее масса – немногим больше 5 квадриллионов тонн.
- В атмосфере 21 % кислорода. Основную массу занимает азот – биологически инертный газ, его в составе атмосферы 78%.
- Масса Земли – примерно 6*1024 килограмма.
- Объем планеты – 1,08*1012 км3.
- Площадь земного шара – 510 млн км2.
- Плотность – 5,5 г/см3.
- Наиболее близкое к нам небесное тело – Луна. Ее среднее расстояние от Земли – примерно 384 тыс. км.
Форма планеты
На вопрос, какая форма у Земли, большинство людей ответит, что шарообразная. И здесь они сделают ошибку. На планету влияют силы гравитации: огромная масса тяготеет к ядру, поэтому происходит постоянное сжатие. Наиболее сильная центробежная сила, появляющаяся из-за движения Земли вокруг собственной оси – на экваторе.
Земля является своего рода «неправильным шаром». Сжатие является причиной того, что экваториальный диаметр планеты немногим больше, чем по полюсам. Ученые определяют форму нашей планеты как близкую к «сплюснутому эллипсоиду».
Интересно, что по причине пренебрежения сжатием Земли по полюсам, эталон метра от 1795 года оказался на 200 микрон короче.
В форме планеты важна также местная топография. Конечно же, она не может в глобальном масштабе влиять на форму планеты. Так, различия между горой Эверест и Марианской впадиной составляет примерно 19 км. В глобальных масштабах эта цифра незначительна. Максимальное расстояние от центра Земли до экватора, учитывая выпуклость земной поверхности – это вершина вулкана Чимборасо, находящегося в Эквадоре.
Что такое экватор и для чего он нужен
Под экватором следует понимать линию, перпендикулярную оси, вдоль поверхности Земли, на одинаковом расстоянии от полюсов.
Вдоль всей этой линии день равняется ночи. Правда, из-за атмосферной рефракции продолжительность дня больше на несколько минут. Два раза в год (в дни равноденствий) Солнце находится в зените, и лучи будут направляться строго перпендикулярно земной поверхности. Широта на экваторе – 0°.
Экватор имеет важнейшее значение для определения широты географического объекта. Все точки, находящиеся к югу от воображаемой линии, имеют южную широту. А объекты, располагающиеся к северу от нее, соответственно, имеют северную широту.
Как измерить длину окружности земли
Размер Земли поддается вычислению. Для измерения длины окружности Земли пользуются высокотехнологичными приборами и спутниками. Однако до появления этих изобретений приходилось пользоваться математическими методами измерений. В 18 веке ученые П. Мешен, А.М. Лежандр, Ц. Кассини использовали способ триангуляции.
Предположим, что нужно измерить дистанцию между некоторыми точками, удаленными на несколько сотен километров. Для этого нам надо построить на местности опорную сеть. Это можно сделать с помощью треугольников. Их вершинами будут места, находящиеся на высоте. На них сооружаются воображаемые пирамиды так, чтобы они направлялись на близко расположенные пункты.
Воображаемые фигуры должны быть удобными для установки угломера и вычисления градусов углов. В одном из треугольников измеряют одну сторону, пролегающую по ровной местности. Это будет базис.
Простейший способ измерения длины экватора – умножить количество километров в одном градусе на 360.
Измерение окружности начинается с треугольника, являющегося базисом. По стороне и по углам вычисляется другие стороны этой фигуры. Одна из них является также стороной смежного треугольника. Она же является исходной для определения сторон иного треугольника. В ходе математических вычислений можно найти параметры последнего треугольника. Так можно получить значение дуги меридиана. Чем длиннее дуги меридианов, тем лучше можно вычислить нужную величину – радиус нашей планеты.
Когда известна протяженность дуги меридиана, несложно посчитать, какая будет длина одного градуса. Такой метод является основой геодезии.
Как вычислить радиус и диаметр планеты
Радиус и диаметр Земли вычислить несложно. Для этого пользуются формулами d=l/π; r=½*π. Буквы означают:
- d – диаметр;
- l – протяженность окружности;
- r – радиус (линия, проложенная от центра и до любой точки на окружности);
- π – число, приблизительно равное 3,14.
Измерение окружности Земли в древние времена
О длине этой величины было известно еще в Древней Греции. Необходимые расчеты были сделаны древнегреческим математиком, астрономом, географом Эратосфеном. Ему было известно о том, что в день солнцестояния 21 июня в Сиене, находящейся за полтысячи миль от Александрии, в полдень освещалось дно колодцев, а от предметов не обнаруживалась тень. Выходит, Солнце в этом участке планеты было в зените. В Александрии ничего подобного не происходило.
В полдень летнего солнцестояния ученый измерил тень от городского обелиска (ему была известна его высота). Так было установлено, что Александрию и Сиену отделяет 7 градусов широты.
Астроном делал вычисления дальше. 7° – это примерно одна пятидесятая часть окружности, равняющейся 360°. Умножив расстояние от Сиены до Александрии на 50, у математика получилось число 25000. Стольким милям равнялась окружность Земли.
Длина окружности Земли, рассчитанная Эратосфеном, немного меньше фактической. Это объясняется не примитивностью расчетов: этот способ узнать окружность Земли достаточно точный. Во времена жизни Эратосфена никто не знал точной дистанции между этими населенными пунктами. Также ученый не принял во внимание то, что оба города расположены на двух разных меридианах.
В средние века упоминания о подобных исследованиях были запрещены церковью. Только в 16 веке кругосветное путешествие Ф. Магеллана позволило убедиться, что планета действительно имеет округлую форму, и что окружность ее действительно равна 40 тыс. км.
Сколько времени нужно, чтобы обойти вокруг Земли пешком
Зная сколько километров составляет длина окружности Земли по экватору, можно вычислить, сколько времени понадобится, чтобы обойти его пешком. Если взять за основу обычную скорость пешехода 6 километров в час, то, воспользовавшись формулой t=S/V, можно получить значение примерно 6700 часов, или 278 суток.
Столько понадобится для того, чтобы пройти пешком вокруг Земли без передышки. Если же допустить, что воображаемый пешеход будет каждый день проходить по 6 часов, то для совершения такого путешествия ему понадобится около 1110 суток, или более 3 лет.
Интересная информация об экваторе Земли
На экваторе круглогодично жаркий и влажный климат. Леса Амазонки и экваториальной Африки, Индонезии отличаются разнообразием растительного и животного мира. Днем температура колеблется между 25 и 30 градусами. Ночью не намного холоднее: настолько сильно прогревается поверхность земли солнечными лучами.
Однако экватор интересен некоторыми географическими особенностями:
- он проходит сквозь более 30 островов;
- пересекает 14 стран;
- Эквадор имеет такое название в честь экватора;
- в большинстве экваториальных государств установлены памятники и памятные знаки в честь нулевой параллели;
- недалеко города Кито располагается вулкан Каямбе высотой около 4,7 км, с белеющей от вечного льда вершиной (и это несмотря на то, что экваториальный климат отличается постоянной жарой);
- река Конго, которая течет в центре африканского материка, проходит через нулевую параллель дважды;
- поскольку в рассматриваемой области Земля обращается очень быстро, здесь легче всего запускать спутники: они быстрее набирают необходимую скорость.
Размеры Земли – одни из главных параметров в астрономии и имеет большое практическое значение. С ее помощью можно узнать диаметр и радиус Земли. Вычислить эти параметры можно, применяя несложные математические вычисления.
Формулы радиуса шара через его объем и площадь поверхности. Объем планеты Земля
Шар является симметричной объемной фигурой, свойства которой рассматривают в школьном курсе геометрии в 8 классе. Данная статья посвящена формулам радиуса шара, позволяющим определить эту величину, зная площадь поверхности фигуры или ее объем.
Что такое шар? Основные формулы
С математической точки зрения шар представляет собой совокупность точек в пространстве, которые лежат на некотором определенном расстоянии от некоторой фиксированной точки, называемой центром. Поверхностью этой фигуры является сфера.
Самый простой способ получить шар заключается в следующем: необходимо взять круг и вращать его вокруг оси, проходящей через диаметр. Поскольку рассматриваемое тело ограничено сферической поверхностью, то формулы для ее площади, а также для объема, который она ограничивает, справедливы и для шара. Запишем их:
- Площадь поверхности шара: S = 4 * pi * R2.
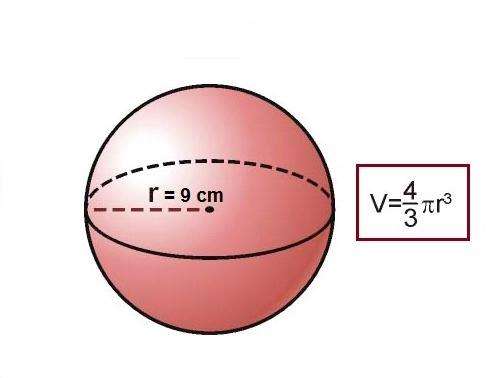
- Объем шара: V = 4/3 * pi * R3.
В приведенных формулах R — это радиус шара, pi — константа, которая называется числом «Пи», она равна приблизительно 3,1416.
Пользуясь этими выражениями, можно получить соответствующие формулы радиуса шара:
- Через площадь S:R = 1/2√(S / pi).
- Через объем V:R = ∛(3V / 4pi).
Приведем еще одно выражение, которое почему-то не рассматривается в школьном курсе, тем не менее оно позволяет вычислить объем шара с точностью 0,03 %, не используя при этом число pi. Оно имеет вид: V = 67 / 16R3. Откуда: R = ∛(16V / 67).
Вычисления объема Земли
Как известно, наша планета не является идеальным шаром. Ее вращение вокруг своей оси за сотни миллионов лет привело к тому, что Земля немного «толще» в экваториальных широтах и немного «тоньше» на полюсах. Соответствующие радиусы равны 6378 и 6357 км. Как видно из этих цифр, они отличаются на небольшую величину (около 0,3 %). Поэтому при рассмотрении Земли в геометрии ее полагают идеальным шаром со средним радиусом 6371 км. Используем это значение и рассчитаем объем нашей голубой планеты.
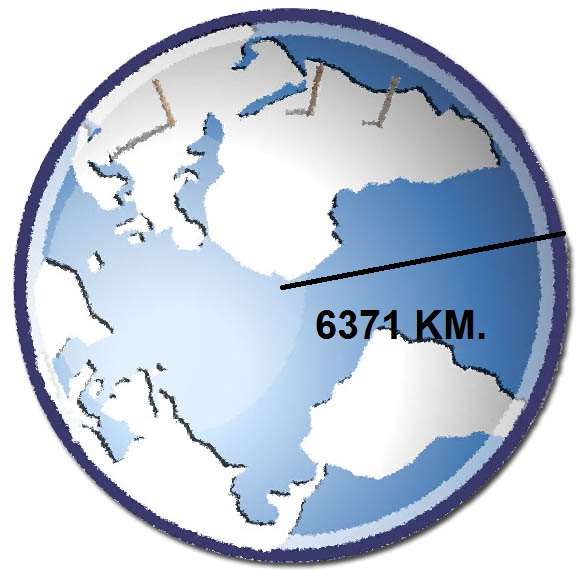
Воспользуемся формулой объема шара по радиусу. Имеем: V = 4/3 * 3,1416 * 63713 ≈ 1,08 * 1012 км3. Теперь рассчитаем V с помощью формулы без pi, получаем: V = 67 / 16 * 63713 ≈ 1,08 * 1012 км3. То есть мы получили точно такое же значение с точностью до 2-х знаков после запятой.
Автор:
25-09-2018 13:48
Жду ваши вопросы и мнения в комментариях
Визуально Земля представляет собой сферический шар, примерные очертания и размеры которого были известны еще в 3 в.до н.э. Изучение контуров Земли продолжается и до наших дней. На сегодняшний день известно, что с точки зрения геометрии, Земля представляет собой трехосный эллипсоидный сфероид, сплюснутый у полюсов. Экваториальный диаметр равен 12 754 км, а полярный – примерно 12 711 км. Общая площадь поверхности сфероида – около 510 млн. кв.км.
Объем Земли равен — около 1121 млрд. кубических километров.
-
- 0
-
-
- 0
-
Те, кто получил результат 26794 км^3, сильно всех обманули, так как при вычислении не воэвели R в 3-тью степень! Радиус «Земли» с таким объемом, был бы равен 18,6 км (ха-ха-ха…)
Если считать , что Земля — шар, радиус которого R = 6400 км, то ее объем будет:
V = 4*П*R^3/3 = 4*3.14*(6400)^3/3 км^3 = 1097509,55*10^6 км^3
= 1.1*10^12 км^3 {П = 3,14}
(10^12 — единица с 12-тью нол
-
Комментариев (0)
-
- 0
-
Путём нехитрых
геометрических построений можно заметить, что из центра шара можно
провести линии, соединяющие две эти точки. Между собой эти линии будут
образовывать определённый угол, который будет соответствовать
измеренному заранее расстоянию между этими точками. Таким образом, мы
знаем длину дуги, соответствующую какому-либо углу. Так как всего в
круге 360 градусов, мы с лёгкостью можем найти длину окружности круга. А
из формулы длины окружности находим радиус, из которого по известной
формуле вычисляется объём.
*Формула длинны окружности: L=2ПР*
-
Комментариев (0)













