Как найти объем отсекаемой части пирамиды - AvtoShod.ru

Видео по теме

Задача 1. В правильной четырехугольной пирамиде точка – центр основания, – вершина, Найдите длину отрезка .

fgk

Решение: + показать

Задача 2. В правильной четырехугольной пирамиде точка – центр основания, – вершина, Найдите боковое ребро

Решение: + показать

Задача 3. Стороны основания правильной четырехугольной пирамиды равны боковые ребра равны Найдите площадь поверхности этой пирамиды.

Решение: + показать

Задача 4. В правильной четырёхугольной пирамиде точка — центр основания, — вершина, Найдите длину отрезка

Решение: + показать

Задача 5. Основанием пирамиды является прямоугольник со сторонами и Ее объем равен Найдите высоту этой пирамиды.

Решение: + показать

Задача 6. В правильной четырёхугольной пирамиде с основанием боковое ребро равно сторона основания равна Найдите объём пирамиды.

Решение: + показать

Задача 7. В правильной четырёхугольной пирамиде все рёбра равны Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых рёбер.

Решение: + показать

Задача 8. Даны две правильные четырёхугольные пирамиды. Объём первой пирамиды равен У второй пирамиды высота в раза больше, а сторона основания в раза больше, чем у первой. Найдите объём второй пирамиды.

Решение: + показать

Задача 9. В правильной четырёхугольной пирамиде боковое ребро равно а тангенс угла между боковой гранью и плоскостью основания равен Найти сторону основания пирамиды.

Решение: + показать

Задача 10. Основанием пирамиды является прямоугольник со сторонами и Ее объем равен Найдите высоту этой пирамиды.

Решение: + показать

Задача 11. Стороны основания правильной четырехугольной пирамиды равны боковые ребра равны Найдите площадь поверхности этой пирамиды.

Решение: + показать

Задача 12. В правильной треугольной пирамиде медианы основания пересекаются в точке . Площадь треугольника равна объем пирамиды равен Найдите длину отрезка .

Решение: + показать

Задача 13. В правильной треугольной пирамиде точка — середина ребра — вершина. Известно, что а . Найдите площадь боковой поверхности пирамиды.

Решение: + показать

Задача 14. Найдите объем правильной треугольной пирамиды, стороны основания которой равны а высота равна

Решение: + показать

Задача 15. Найдите высоту правильной треугольной пирамиды, стороны основания которой равны а объем равен

Решение: + показать

Задача 16. Стороны основания правильной шестиугольной пирамиды равны боковые ребра равны Найдите площадь боковой поверхности этой пирамиды.

Решение: + показать

Задача 17. Объем правильной шестиугольной пирамиды Сторона основания равна Найдите боковое ребро.

Решение: + показать

Задача 18. Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в два раза?

Решение: + показать

Задача 19. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в раз?

Решение: + показать

Задача 20. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в пять раз?

Решение: + показать

Задача 21. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом °. Высота пирамиды равна Найдите объем пирамиды.

Решение: + показать

Задача 22. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно Найдите объем пирамиды.

Решение: + показать

Задача 23. От треугольной призмы, объем которой равен отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.

Решение: + показать

Задача 24. Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен Найдите объем шестиугольной пирамиды. Видео по теме 1 2

Решение: + показать

Задача 25. Сторона основания правильной шестиугольной пирамиды равна 8, боковое ребро равно 16. Найдите объём пирамиды.

Решение: + показать

Задача 26. Сторона основания правильной шестиугольной пирамиды равна а угол между боковой гранью и основанием равен $45^{circ}.$ Найдите объем пирамиды.

Решение: + показать

Задача 27. Найдите объём правильной шестиугольной пирамиды если объём треугольной пирамиды равен

Решение: + показать

Задача 28. Объем параллелепипеда равен Найдите объем треугольной пирамиды

Решение: + показать

Задача 29. Объем куба равен Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Решение: + показать

Задача 30. Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно

Решение: + показать

Задача 31. Объем правильной четырехугольной пирамиды равен Точка — середина ребра . Найдите объем треугольной пирамиды .

Решение: + показать

Задача 32. От треугольной пирамиды, объем которой равен отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

Решение: + показать

Задача 33. Ребра тетраэдра равны Найдите площадь сечения, проходящего через середины четырех его ребер.

Решение: + показать

Вы можете пройти тест

Источник

Задания

Версия для печати и копирования в MS Word

От треугольной пирамиды, объем которой равен 70, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

Спрятать решение

Решение.

Объем пирамиды Площадь основания отсеченной части меньше в 4 раза (так как высота и сторона треугольника в основании меньше исходных в 2 раза), поэтому и объем оставшейся части меньше в 4 раза. Тем самым, он равен 17,5.

Ответ: 17,5.

Источник

Решение:

Объём исходной треугольной пирамиды равен 78 и находится по формуле:

V=frac{1}{3}cdot S_{осн}cdot h=frac{1}{3}cdot S_{Delta }cdot h=78

У отсеченной пирамиды равная высота с исходной пирамидой, а площадь основания в 4 раза меньше, это заметно, если в треугольнике провести ещё две средних линии, получим 4 равных треугольника:

Найдём объём отсечённой пирамиды:

V_{отсеч.}=frac{1}{3}cdotfrac{ S_{Delta }}{4}cdot h=frac{1}{4}cdot frac{1}{3}cdot S_{Delta }cdot h=frac{1}{4}cdot V=frac{1}{4}cdot 78=19,5

Ответ: 19,5.

Источник

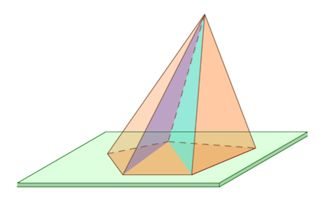
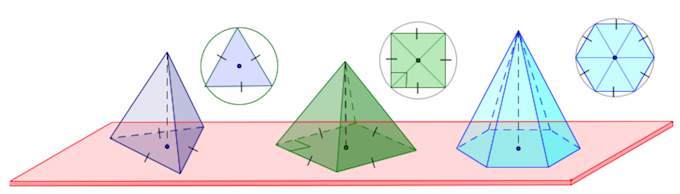
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.

По числу углов основания различают пирамиды треугольные, четырехугольные и т. д.

Вершина пирамиды – точка, соединяющая боковые ребра и не лежащая в плоскости основания.

Основание – многоугольник, которому не принадлежит вершина пирамиды.

Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины. В правильной пирамиде длина апофемы выражается формулой (m = sqrt {{b^2} — largefrac{{{a^2}}}{4}normalsize}).

Высота – отрезок перпендикуляра, проведенного через вершину пирамиды к плоскости ее основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра). В правильной пирамиде высота равна (h = largefrac{{sqrt {4{b^2}{{sin }^2}frac{pi }{n} — {a^2}} }}{{2sin frac{pi }{n}}}normalsize), где (b) − боковое ребро, (a) − сторона основания, (n) − число сторон многоугольника в основании.

Диагональное сечение пирамиды – сечение пирамиды, проходящее через вершину и диагональ основания.

Некоторые свойства пирамиды

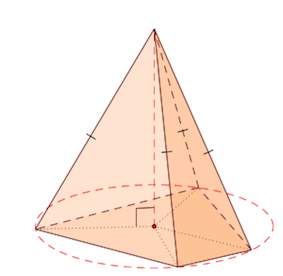
1. Если все боковые ребра равны, то около основания пирамиды можно описать окружность, причем вершина пирамиды проецируется в ее центр.

Боковые ребра образуют с плоскостью основания равные углы.

Верно и обратное.

Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.

Если около основания пирамиды можно описать окружность, причем вершина пирамиды проецируется в ее центр, то все боковые ребра пирамиды равны.

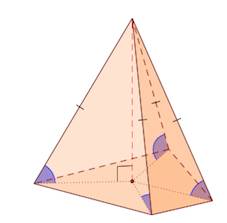
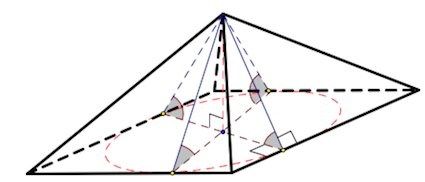
2. Если все грани пирамиды наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, причем вершина пирамиды проецируется в ее центр.

Виды пирамид

Пирамида называется правильной, если основанием ее является правильный многоугольник, а вершина проецируется в центр основания.

Для правильной пирамиды справедливо:

боковые ребра правильной пирамиды равны;
в правильной пирамиде все боковые грани – равные равнобедренные треугольники;
в любую правильную пирамиду можно вписать сферу;
около любой правильной пирамиды можно описать сферу;
площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

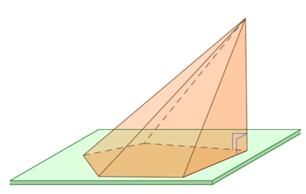
Пирамида называется прямоугольной, если одно из боковых ребер пирамиды перпендикулярно основанию. Тогда это ребро и есть высота пирамиды.

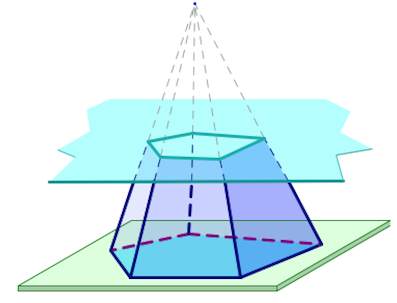
Усеченной пирамидой называется многогранник, заключенный между основанием пирамиды и секущей плоскостью, параллельной ее основанию.

Усеченная пирамида является правильной, если она представляет собой часть правильной пирамиды.

Свойства усеченной пирамиды:

Каждая боковая грань правильной усеченной пирамиды является равнобокими трапециями одной величины.
Основания усеченной пирамиды являются подобными многоугольниками.
Боковые ребра правильной усеченной пирамиды имеют равную величину и один наклонен по отношению к основанию пирамиды.
Боковые грани усеченной пирамиды являются трапециями.
Двугранные углы при боковых ребрах правильной усеченной пирамиды имеют равную величину.

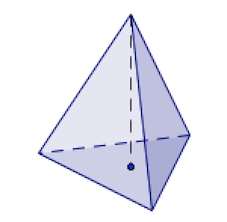
Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.

В правильном тетраэдре все четыре грани являются равносторонними треугольниками.

Соотношение между длиной ребра и высотой в правильном тетраэдре: (h = asqrt {largefrac{2}{3}}normalsize).

Источник

Понятие усеченной пирамиды

Если пересечь обычную пирамиду (с вершиной) плоскостью, которая параллельна ее основанию, то получится две фигуры: первая (верхняя часть) будет меньшей пирамидой, чем исходная, а фигура, которая лежит между секущей плоскостью и основанием исходной пирамиды, получила название усеченной пирамиды.

Онлайн-калькулятор объема усеченной пирамиды

Если пересечь пирамиду, являющуюся правильной, то и усеченная пирамида будет правильной, если неправильную – то неправильной.

Высотой усеченной пирамиды является перпендикуляр, проведенный из ее верхнего основания в нижнее (или наоборот).

Формула объема пирамиды

Для того чтобы вычислить объем пирамиды, нужно проделать следующие действия:

Сложить площади обоих оснований пирамиды.
Возвести произведение этих площадей в степень 1/21/2, то есть извлечь квадратный корень.
Полученные результаты сложить, затем умножить на высоту пирамиды и разделить на 3.

Формулы имеет такой вид:

Объем усеченной пирамиды

V=13⋅h⋅(Sосн 1+Sосн 2+Sосн 1⋅Sосн 2)V=frac{1}{3}cdot hcdot(S_{text{осн 1}}+S_{text{осн 2}}+sqrt{S_{text{осн 1}}cdot S_{text{осн 2}}})

Sосн 1,Sосн 2S_{text{осн 1}}, S_{text{осн 2}} — площади оснований усеченной пирамиды;
hh — высота данной пирамиды.

Разберем решение задач на эту тему.

Задача 1

Найдите объем усеченной пирамиды, если известно, что площадь ее одного основания равна 30 см230text{ см}^2, а площадь второго в 2 раза больше первого. Высота пирамиды равна 7 см7text{ см}.

Решение

Sосн 1=30S_{text{осн 1}}=30
Sосн 2=2⋅Sосн 1S_{text{осн 2}}=2cdot S_{text{осн 1}}
h=7h=7

Первый этап — нахождения площади второго основания:

Sосн 2=2⋅Sосн 1=2⋅30=60S_{text{осн 2}}=2cdot S_{text{осн 1}}=2cdot 30=60

Второй этап — вычисляем объем по формуле:

V=13⋅h⋅(Sосн 1+Sосн 2+Sосн 1⋅Sосн 2)=13⋅7⋅(30+60+30⋅60)≈309 см3V=frac{1}{3}cdot hcdot(S_{text{осн 1}}+S_{text{осн 2}}+sqrt{S_{text{осн 1}}cdot S_{text{осн 2}}})=frac{1}{3}cdot 7cdot(30+60+sqrt{30cdot 60})approx309text{ см}^3

Ответ

309 см3.309text{ см}^3.

Задача 2

В основаниях пирамиды лежат квадраты со сторонами a=8 смa=8text{ см} и b=6 смb=6text{ см}. Высота усеченной пирамиды имеет длину 10 см10text{ см}. Найти ее объем.

Решение

a=8a=8
b=6b=6
h=10h=10

Найдем площадь первого основания. Это просто площадь квадрата, которую мы вычислим по формуле:

Sосн 1=b⋅b=b2=62=36S_{text{осн 1}}=bcdot b=b^2=6^2=36

Аналогично, площадь второго, нижнего основания:

Sосн 2=a⋅a=a2=82=64S_{text{осн 2}}=acdot a=a^2=8^2=64

Наконец, вычисляем объем по формуле:

V=13⋅h⋅(Sосн 1+Sосн 2+Sосн 1⋅Sосн 2)=13⋅10⋅(36+64+36⋅64)≈493.3 см3V=frac{1}{3}cdot hcdot(S_{text{осн 1}}+S_{text{осн 2}}+sqrt{S_{text{осн 1}}cdot S_{text{осн 2}}})=frac{1}{3}cdot 10cdot(36+64+sqrt{36cdot 64})approx493.3text{ см}^3

Ответ

493.3 см3.493.3text{ см}^3.

Профильные эксперты сайта помогут вам выполнить контрольную работу на заказ, скорее оформляйте заказ!

Источник

Онлайн-калькулятор объема усеченной пирамиды

Формула объема пирамиды

Не пропустите также: