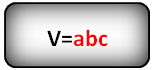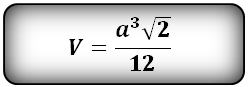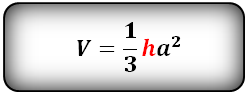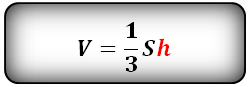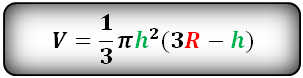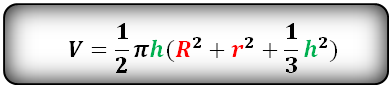Как найти объем нулевой - AvtoShod.ru - решение различных проблем

Если говорить об абстрактной геометрии, то нулевой объем ( V=0 ) вполне может существовать. Теоретически – это будет точка, начало координат на множестве осей, у которой все три величины x, y и z (длина, высота и ширина) будут равняться нулю.

Но в соответствии с современным пониманием физики это очень спорный вопрос — имеет ли нулевой объем какой-либо физический смысл? Например, в физике высоких энергий есть понятие планковской длины — минимальной длины, о которой вообще можно говорить, не теряя ее физических свойств. Логично было бы предположить, что раз есть минимальная длина, то должен быть и минимальный объем — куб со сторонами, имеющими планковскую длину.

Проще говоря, физика не утверждает и не отрицает, что такие объекты могут существовать. «Частица» в классической механике — это тело, описание движения которого можно упростить до движения его центра масс, что является математической абстракцией (а абстрактные объекты, конечно же, могут иметь нулевой объем). Именно это непонимание между абстрактным описанием и реальностью приводит к вопросам о частицах или объектах, не имеющих объема.

Сингулярность черной дыры может иметь нулевой объем

Все мы знаем, что в центре черной дыры располагается гравитационная сингулярность, в которой, цитирую: «величины, описывающие гравитационное поле, становятся бесконечными или неопределёнными. К таким величинам относятся, например, скалярная кривизна или плотность энергии в сопутствующей системе отсчёта».

И что нам говорит теоретическая физика?

Сингулярность — это математическая конструкция, которая описывает точку, в которой какой-либо элемент математической формулы разрушается. Хотя мы не знаем точно, что происходит в центре черной дыры, математика склоняется к предположению, что все сжимается в одну точку. Тогда эта точка должна иметь бесконечный гравитационный градиент, и именно поэтому она соответствует определению математической сингулярности.

Но причина, по которой она имеет нулевой объем, чрезвычайно проста; термин «сингулярность» применим только к одной точке, а точки не имеют размера и, следовательно, по определению, не имеют объема.

Существуют так же споры относительно снижения температуры газа до величины абсолютного нуля. Согласно Газовому закону Чарльза, температура Кельвина (-273,15 градуса по Цельсию) прямо пропорциональна объему газа, в момент, когда масса и давление в нем постоянны. Теоретически, снижая температуру газа до Абсолютного Нуля сохраняя при этом давление и массу постоянными, объем газа также должен уменьшится до Абсолютного Нуля.

Но на самом деле, в экспериментах, когда мы снижаем температуру до нескольких нанокельвинов, но мы никогда не можем достичь абсолютного нуля температуры, поэтому формулировка — «Объем газа будет равен нулю при Абсолютном нуле температуры» — это все еще гипотеза.

Если нам повезет, то в ближайшем будущем мы сможем получить гораздо больше знаний об этом. По мере роста наших исследований и обновления базы знаний ответ может меняться или оставаться неопределенным, подобно принципу неопределенности Гейзенберга.

Источник

The proof will become obvious once you understand what does something has «area/volume/measure» zero means.

For any subset $A$ of $mathbb{R}^2$, we declare it to has «area/volume/measure» zero if and only if you can cover it by countable many rectangles and the sum of «ordinary» area of the rectangles can be make as small as you like.

Consider the example of a single line segment joining $(0,0)$ and $(1,0)$.
For any $epsilon > 0 $, no matter how small $epsilon$ is, one can cover the line
segment by a rectangle $[0, 1] times [ -frac{epsilon}{2}, frac{epsilon}{2} ]$ whose «ordinary» area is $epsilon$. So the «area/volume/measure» of a line segment is $0$.

Let say you have a rectangle $[a,b] times [c,d]$. To prove its boundary has «area/volume/measure» $0$, you just need to show for any $epsilon > 0 $, you can find 4 rectangles covering the four edges of your rectangle and the sum of «ordinary» area of the smaller rectangles is at most $epsilon$. One choices of the smaller rectangles are:
$$[a,b] times [ c-frac{epsilon}{8(b-a)}, c+frac{epsilon}{8(b-a)} ],
[a,b] times [ d-frac{epsilon}{8(b-a)}, d+frac{epsilon}{8(b-a)} ],\
[ a-frac{epsilon}{8(d-c)}, a+frac{epsilon}{8(d-c)} ] times [c,d],
[ b-frac{epsilon}{8(d-c)}, b+frac{epsilon}{8(d-c)} ] times [c,d]$$

Источник

2 / 2 / 0

Регистрация: 03.01.2014

Сообщений: 43

множество нулевого объёма

08.01.2014, 19:18. Показов 2391. Ответов 10

Нужно показать, что если множество $https://www.cyberforum.ru/cgi-bin/latex.cgi?Esubset {R}^{n}$ имеет нулевой объем, то и его замыкание — есть множество нулевого объема.
Подскажите, пожалуйста, как делать)

Модератор

35427 / 19452 / 4071

Регистрация: 12.02.2012

Сообщений: 32,488

Записей в блоге: 13

08.01.2014, 22:18

Сообщение было отмечено как решение

Решение

Если множество имеет нулевой объем, то это означает, что для любого заданного eps, множество можно заключить в систему гиперкубов с суммарным объемом, меньшим eps.

А что такое замыкание? Это множество вместе со своими предельными точками. Предельная точка — это такая точка, любая окрестность которой пересекается с исходным множеством.

Поэтому система гиперкубов с объемом < eps, содержит также и все предельные точки.

Пусть предельная точка (не принадлежащая множеству) не попала в систему кубов. Возьмем расстояние от этой точки, до системы гиперкубов (как inf множества длин отрезков). Пусть это расстояние = d. Тогда окрестность предельной точки радиуса d/2 с системой гиперкубов не пересекается и содержит точки исходного множества (т.к. точка предельная). Получили противоречие с тем, что система гиперкубов содержит все множество.

4163 / 2066 / 424

Регистрация: 19.07.2009

Сообщений: 3,125

Записей в блоге: 24

08.01.2014, 22:54

Ожидал, когда кто-то ответит.

Catstail, Вы используете объем по Борелю, помещая фигуру в систему кубов и переходите к инфинуму объемов всевозможных таких систем.

Я так понимаю, что Ваши рассуждения можно обобщить до теоремы, что замыкание измеримого множества E имеет тот же объём, что и E.

Далее делается следующее утверждение: если фигура E окружена системой кубов C, то все предельные точки находятся внутри этой системы. Тут я кое-чего не понимаю: система кубов полуоткрыта и мы можем заключить максимум то, что инфинум расстояния (по Вашей схеме) равен нулю, а как из этого можно сделать вывод о равенстве объемов E и замыкания E? Интуитивно я понимаю, что эту систему кубов C можно окружить сколь угодно тонкой оболочкой, в которую наверняка попадут все предельные точки, что не попали в C.

Плохо представляю, как это можно формализовать.

Диссидент

27475 / 17161 / 3785

Регистрация: 24.12.2010

Сообщений: 38,668

09.01.2014, 00:05

Catstail, Mysterious Light, Наконец-то я попал в топик, где не понимаю и 20% слов.

Не по теме:

На одну из вечеринок пришел мой приятель, тоже не полный идиот, кандидат каких-то вполне технических наук. Маясь в ожидании накрывания стола, он вынул со стелажа тонкую зеленую книжонку моего шефа, Л.А. Скорнякова, и пытался ее почитать. Потом напружинился, и сказал: «Вот до этого места я дочел. «Хорошо известно, что…». А дальше, простите, ну ничего не понимаю!»:)

Добавлено через 3 минуты

Не по теме:

Вспомнил название книжонки. «Дедекиндовы структуры с дополнением и регулярные кольца»
А Льву Анатольевичу — земля — пухом!

618 / 281 / 10

Регистрация: 22.01.2013

Сообщений: 874

09.01.2014, 01:01

Сообщение было отмечено как решение

Решение

Сообщение от Байт

Catstail, Mysterious Light, Наконец-то я попал в топик, где не понимаю и 20% слов.

Это легко. Ещё чуть-чуть, и они втроём докажут, что (скажем, для n=1) поскольку одномерный объем множества рациональных чисел на [0,1] равен нулю, то и длина его замыкания, т.е. отрезка [0,1], тоже равна нулю. Попутав меру Бореля (Лебега) с мерой Жордана.

4163 / 2066 / 424

Регистрация: 19.07.2009

Сообщений: 3,125

Записей в блоге: 24

09.01.2014, 01:09

Сообщение от Байт

Наконец-то я попал в топик, где не понимаю и 20% слов.

Я понимаю вопрос таким образом.

В n-мерном пространстве объём полуоткрытого куба постулируется равным.
Объём как функция заведомо аддитивная продолжается по аддитивности на фигуры, которые Catstail назвал системами кубов.
Семейство «систем кубов» является замкнутым относительно объединения и пересечения в конечном числе.

$https://www.cyberforum.ru/cgi-bin/latex.cgi?<br /> mathfrak{C} = { (a_1,b_1] times (a_2,b_2] times ldots ;|; a_i,b_iin mathbb{R} }<br />$

Каждое ограниченное множество E имеет семейство систем кубов, которые содержат это множество:

Может так случиться, что среди них есть есть последовательность сходящихся к E систем по объему (неформально). Это означает формально то, что может существовать инфинум объемов:

Это верхняя мера. Двойственно определяется нижняя мера. Если они совпадают, то это множество объявляется измеримым по Жордану, а m(E) называется мерой (объемом) по Жордану.

Вопрос о том, что замыкание множества имеет такую же меру (по крайней мере для нулевого объема), что и само множество.

P.S. низко-низко кланяюсь: попутал названия. Речь идёт только о мере Жордана, о которой написал выше.

Байт

09.01.2014, 01:22

Не по теме:

Сообщение от rahim

меру Бореля (Лебега) с мерой Жордана.

Вот до понимания этих вещей у меня дело не дошло. Мое образование кончилось на попытке нарисовать жорданову кривую. Но когда я слышу эти великие имена, у меня восторженно открывается пасть.:)

75 / 75 / 10

Регистрация: 26.02.2013

Сообщений: 224

09.01.2014, 01:57

Сообщение от rahim

Ещё чуть-чуть, и они втроём докажут, что (скажем, для n=1) поскольку одномерный объем множества рациональных чисел на [0,1] равен нулю, то и длина его замыкания, т.е. отрезка [0,1], тоже равна нулю. Попутав меру Бореля (Лебега) с мерой Жордана.

Не, ну по Жордану вообще неизмеримо …..
А если по Лебегу мерять тут, то наверное таким свойством (мера замыкания равна мере самого множества) будут обладать, в частности, множества (если ограничиться множествами меры 0), у которых для любого существует локально конечная система гиперкубов сумарного обьема меньше … По идее замыкание обьединения локально конечной системы множеств равно обьединению замыканий, и тогда 1) замыкание заданного множества сидит в этом замыкании обьединения системы гиперкубов 2)мера которого должна теоретически совпадать с мерой самого обьединения гиперкубов, т.к. если рассмотреть замыкание гиперкуба, то это его внутренность + конечное кол-во «гиперквадратов», которые есть множества меры 0, следовательно, «мера замыкания обьединения гиперкубов = мера обьединения замыканий гиперкубов = мера обьединения исходных гиперкубов»……

618 / 281 / 10

Регистрация: 22.01.2013

Сообщений: 874

09.01.2014, 06:01

Вы не заметили приведенный мной и процитированный Вами контрпример? Утверждение, которое требуется доказать, не верно для лебеговой меры. А только для меры Жордана.

75 / 75 / 10

Регистрация: 26.02.2013

Сообщений: 224

09.01.2014, 11:24

Сообщение от rahim

Вы не заметили приведенный мной и процитированный Вами контрпример? Утверждение, которое требуется доказать, не верно для лебеговой меры.

Вроде бы в некоторых случаях верно и для лебеговой (т.е. при дополнительном условии…. — о чем и пишу….)

Не по теме:

а ему не удовлетворяет… вроде бы

618 / 281 / 10

Регистрация: 22.01.2013

Сообщений: 874

09.01.2014, 21:33

Ага, посмотрел, что такое «локально конечная система множеств». Тут Вы правы. Конечно, Q нельзя погрузить в «локально конечную» систему гиперкубов длиной меньше произвольного заданного числа.

IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604	09.01.2014, 21:33
11

Источник

Сообщения без ответов | Активные темы | Избранное

	Существуют ли тела, не имеющие объема? 09.07.2011, 13:02
03/07/11 24	Существуют ли тела, не имеющие объема?Именно тела, а не двухмерные фигуры типа круга или квадрата. В старой советской книжке «Преподавание геометрии в 9-10 классах» на с.232 сказано, что такие тела существуют, однако доказательство их существования в ней не приводится. Приведите, пожалуйста, примеры таких тел и математические доказательства.Заранее спасибо!

Kallikanzarid	Re: Существуют ли тела, не имеющие объема? 09.07.2011, 13:10
02/04/11 956	Пересечение шара с объединением двух пересекающихся в его центре плоскостей.

Almazov	Re: Существуют ли тела, не имеющие объема? 09.07.2011, 13:17
03/07/11 24	Пересечение шара с объединением двух пересекающихся в его центре плоскостей. Можно, пожалуйста, более подробно?

мат-ламер

Re: Существуют ли тела, не имеющие объема?

09.07.2011, 13:32

Заслуженный участник

30/01/09
5728

Пересечение шара с объединением двух пересекающихся в его центре плоскостей.

В вопросе топик-стартера подразумевалось тело не имеющее объём (т.е. для которого объём нельзя определить), а не тело, имеющее нулевой объём. Можно доказать существование множества, для которого нельзя определить объём (в смысле Лебега). Доказательство неконструктивное и опирается на аксиому выбора. В литературе обычно рассматривается множество на окружности, но думаю, пример можно обобщить для трёхмерного пространства. Просили привести пример. Сможет ли это доказательство выступать как пример такого множества — я не знаю. Будет ли это множество телом — т.е. иметь размерность три в том смысле, как его определилили Александров с Урысоном — это надо спросить у знатоков.

— Сб июл 09, 2011 14:40:25 —

Но если я усложняю, и имелось в виду тело, имеющее нулевой объём, то можно рассмотреть трёхмерную сферу в четырёхмерном пространстве.

Almazov	Re: Существуют ли тела, не имеющие объема? 09.07.2011, 13:43
03/07/11 24	Пересечение шара с объединением двух пересекающихся в его центре плоскостей. В вопросе топик-стартера подразумевалось тело не имеющее объём (т.е. для которого объём нельзя определить), а не тело, имеющее нулевой объём. Можно доказать существование множества, для которого нельзя определить объём (в смысле Лебега). Доказательство неконструктивное и опирается на аксиому выбора. В литературе обычно рассматривается множество на окружности, но думаю, пример можно обобщить для трёхмерного пространства. Просили привести пример. Сможет ли это доказательство выступать как пример такого множества — я не знаю. Будет ли это множество телом — т.е. иметь размерность три в том смысле, как его определилили Александров с Урысоном — это надо спросить у знатоков. — Сб июл 09, 2011 14:40:25 — Но если я усложняю, и имелось в виду тело, имеющее нулевой объём, то можно рассмотреть трёхмерную сферу в четырёхмерном пространстве. Вы ничего не усложняете.Имелись в виду неизмеримые тела, для которых объём нельзя определить.

мат-ламер

Re: Существуют ли тела, не имеющие объема?

09.07.2011, 15:13

Заслуженный участник

30/01/09
5728

Если речь бы шла об одномерных множествах на окружности, то можно посмотреть http://www.nsu.ru/mmf/tvims/chernova/tv/lec/node7.html. Almazov

Вопрос Ваш не тривиальный.

— Сб июл 09, 2011 16:24:37 —

Нетривиальность в том, что множество, не имеющее объём, построить можно. А вот как насчёт тела?

Munin

Re: Существуют ли тела, не имеющие объема?

09.07.2011, 15:25

Заслуженный участник

30/01/06
72407

Именно на такие части распиливают шар в парадоксе Банаха-Тарского. Поэтому, если существуют два таких тела, сложенные вместе (собственно, шар), то наверное, они существуют и по отдельности. Убедительно? (Парадокс, разумеется, опирается на аксиому выбора.)

мат-ламер

Re: Существуют ли тела, не имеющие объема?

09.07.2011, 15:26

Заслуженный участник

30/01/09
5728

А если объём понимать не в смысле Лебега, а в смысле Римана, то ситуация, вероятно, упрощается.

ewert

Re: Существуют ли тела, не имеющие объема?

09.07.2011, 15:30

Заслуженный участник

11/05/08
32162

А если объём понимать не в смысле Лебега, а в смысле Римана,

Только в смысле Жордана, а не Римана. Тут контрпример очевиден: множество точек с рациональными координатами (ну или, наоборот, иррациональными).

мат-ламер

Re: Существуют ли тела, не имеющие объема?

09.07.2011, 17:42

Заслуженный участник

30/01/09
5728

Это я понимаю. Но тут вопрос был про тела. Будет ли параллелепипед с выброшенными рациональными точками телом? По крайней мере мне тут в одном посте объяснили, что это связное множество.

ewert

Re: Существуют ли тела, не имеющие объема?

09.07.2011, 20:23

Заслуженный участник

11/05/08
32162

Будет ли параллелепипед с выброшенными рациональными точками телом?

«Тело» — это лирика, поэтому вопрос празден.

Almazov	Re: Существуют ли тела, не имеющие объема? 09.07.2011, 20:58
03/07/11 24	Будет ли параллелепипед с выброшенными рациональными точками телом? Подведем предварительные итоги: 1)То, что для превращения измеримой фигуры в неизмеримую необходимо исключить все плоскости с рациональными координатами я понял.Но я не понимаю, как эту фигуру представить графически.Хотелось бы увидеть наглядные примеры. 2)Хотелось бы побольше узнать об упоминавшемся выше парадоксе удвоения шара.Там, вроде, шар как раз разбивается на такие неизмеримые части.Прочел страницу в википедии — ничего не понял.Да и визуально непонятно, как можно из частей одного шара собрать два точно таких же?Разве что клонировать :))

mihailm	Re: Существуют ли тела, не имеющие объема? 09.07.2011, 22:00
19/05/10 ∞ 3940 Россия	… 1)То, что для превращения измеримой фигуры в неизмеримую необходимо исключить все плоскости с рациональными координатами я понял … Ничего вы не поняли, это в пустую плоскость иррациональные точки добавляли))

Sonic86

Re: Существуют ли тела, не имеющие объема?

10.07.2011, 06:30

Заслуженный участник

08/04/08
8549

Да и визуально непонятно, как можно из частей одного шара собрать два точно таких же?Разве что клонировать :))

Так ведь говорится, что доказательство неконструктивно. Т.е. и представить Вы это себе не сможете (ну может кто-то может, я не могу).

Almazov	Re: Существуют ли тела, не имеющие объема? 10.07.2011, 11:57
03/07/11 24	… 1)То, что для превращения измеримой фигуры в неизмеримую необходимо исключить все плоскости с рациональными координатами я понял … Ничего вы не поняли, это в пустую плоскость иррациональные точки добавляли)) А разве нельзя пойти обратным путем и из готовой плоскости исключать рациональные точки?Результат разве не тот же? Ведь , разве не так?

Модераторы: Модераторы Математики, Супермодераторы

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете добавлять вложения

Источник

a — сторона куба

Формула объема куба, (V):

a, b, c — стороны параллелепипеда

Еще иногда сторону параллелепипеда, называют ребром.

Формула объема параллелепипеда, (V):

R — радиус шара

π ≈ 3.14

По формуле, если дан радиус, можно найти объема шара, (V):

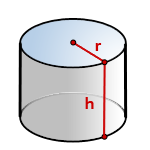
h — высота цилиндра

r — радиус основания

π ≈ 3.14

По формуле найти объема цилиндра, есди известны — его радиус основания и высота, (V):

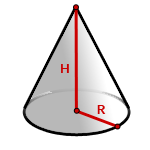
R — радиус основания

H — высота конуса

π ≈ 3.14

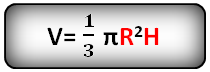
Формула объема конуса, если известны радиус и высота (V):

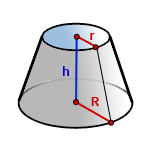
r — радиус верхнего основания

R — радиус нижнего основания

h — высота конуса

π ≈ 3.14

Формула объема усеченного конуса, если известны — радиус нижнего основания, радиус верхнего основания и высота конуса (V ):

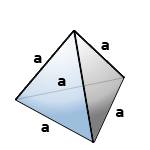
Правильный тетраэдр — пирамида у которой все грани, равносторонние треугольники.

а — ребро тетраэдра

Формула, для расчета объема правильного тетраэдра (V):

Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.

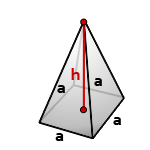
a — сторона основания

h — высота пирамиды

Формула для вычисления объема правильной четырехугольной пирамиды, (V):

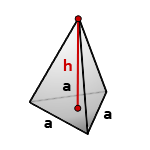
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.

a — сторона основания

h — высота пирамиды

Формула объема правильной треугольной пирамиды, если даны — высота и сторона основания (V):

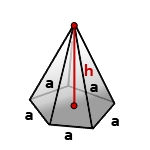
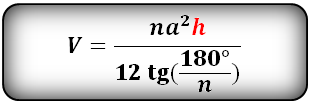
Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.

h — высота пирамиды

a — сторона основания пирамиды

n — количество сторон многоугольника в основании

Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):

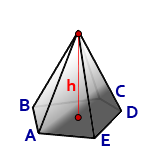
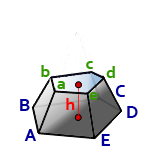
h — высота пирамиды

S — площадь основания ABCDE

Формула для вычисления объема пирамиды, если даны — высота и площадь основания (V):

h — высота пирамиды

S_ниж — площадь нижнего основания, ABCDE

S_верх — площадь верхнего основания, abcde

Формула объема усеченной пирамиды, (V):

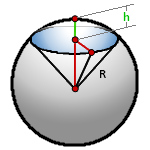
Шаровый сегмент- это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.

R — радиус шара

h — высота сегмента

π ≈ 3.14

Формула для расчета объема шарового сегмента, (V):

R — радиус шара

h — высота сегмента

π ≈ 3.14

Формула объема шарового сектора, (V):

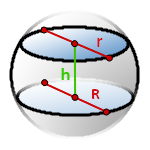
h — высота шарового слоя

R — радиус нижнего основания

r — радиус верхнего основания

π ≈ 3.14

Формула объема шарового слоя, (V):

Источник

Сингулярность черной дыры может иметь нулевой объем

множество нулевого объёма

Решение

Решение

Кто сейчас на конференции

Не пропустите также: