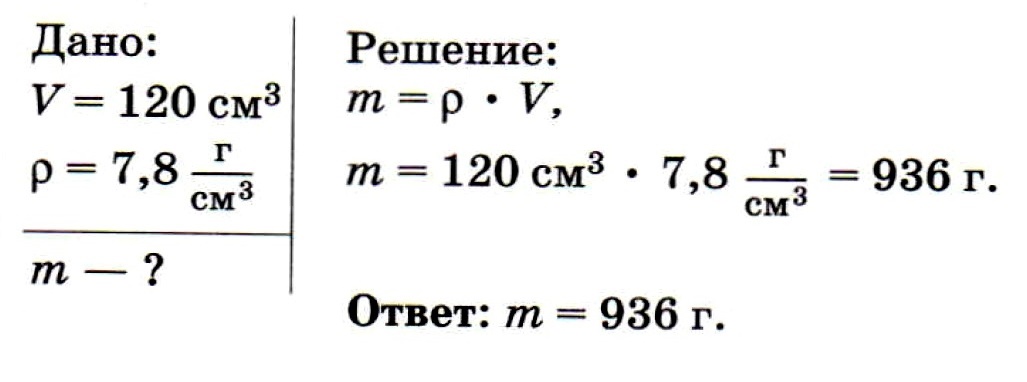Задачи на плотность, массу и объем с решением
Формулы, используемые по теме «Задачи на плотность, массу и объем с решением»
Название величины |
Обозначение |
Единицы измерения |
Формула |
Масса |
m |
кг |
m = ρ * V |
Объем |
V |
м3 |
V = m / ρ |
Плотность |
ρ |
г/см3,
|
ρ = m / V |
Плотность равна отношению массы тела к его объёму. Плотность обозначают греческой буквой ρ (ро).
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Найдите плотность молока, если 206 г молока занимают объем 200 см3?
Задача № 2.
Определите объем кирпича, если его масса 5 кг?
Задача № 3.
Определите массу стальной детали объёмом 120 см3
Задача № 4.
Размеры двух прямоугольных плиток одинаковы. Какая из них имеет большую массу, если одна плитка чугунная, другая — стальная?
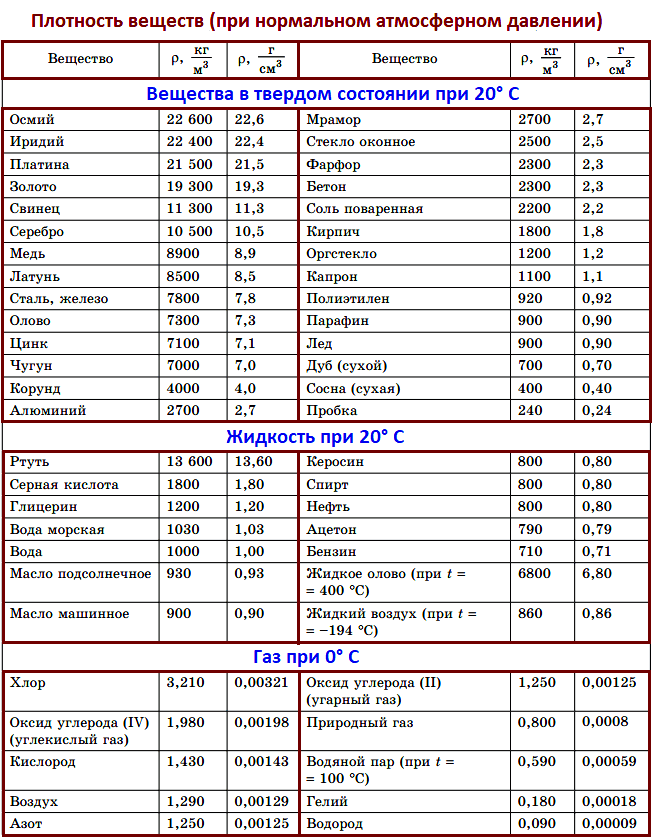
Решение: Из таблицы плотности веществ (см. в конце страницы) определим, что плотность чугуна (ρ2 = 7000 кг/м3) меньше плотности стали (ρ1 = 7800 кг/м3). Следовательно, в единице объема чугуна содержится меньшая масса, чем в единице объема стали, так как чем меньше плотность вещества, тем меньше его масса, если объемы тел одинаковы.
Задача № 5.
Определите плотность мела, если масса его куска объемом 20 см3 равна 48 г. Выразите эту плотность в кг/м3 и в г/см3.
Ответ: Плотность мела 2,4 г/см3, или 2400 кг/м3.
Задача № 6.
Какова масса дубовой балки длиной 5 м и площадью поперечного сечения 0,04 м2 ?
ОТВЕТ: 160 кг.
Указания к решению. Из формулы для плотности получаем m = p • V. С учетом того, что объем балки V = S • l , получаем: m = p • S • l.
Вычисляем: m = 800 кг/м3 • 0,04 м2 • 5 м = 160 кг.
Задача № 7.
Брусок, масса которого 21,6 г, имеет размеры 4 х 2,5 х 0,8 см. Определить, из какого вещества он сделан.
ОТВЕТ: Брусок сделан из алюминия.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Задача № 8 (повышенной сложности).
Полый медный куб с длиной ребра а = 6 см имеет массу m = 810 г. Какова толщина стенок куба?
ОТВЕТ: 5 мм.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Задача № 9 (олимпиадный уровень).
Масса пробирки с водой составляет 50 г. Масса этой же пробирки, заполненной водой, но с куском металла в ней массой 12 г составляет 60,5 г. Определите плотность металла, помещенного в пробирку.
ОТВЕТ: 8000 кг/м3
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Задачи на плотность,
массу и объем с решением
Справочный материал для
«Задачи на плотность, массу и объем«
Таблица плотности веществ.
Как, зная только массу, рассчитать плотность?
- Если объем тела (вещества) неизвестен или не задан явно в условиях задачи, то попытайтесь его измерить, вычислить или узнать, используя косвенные (дополнительные) данные.
- Если вещество сыпучее или жидкое, то оно, как правило, находится в емкости, которая обычно имеет стандартный объем. Так, например, объем бочки обычно равен 200 литров, объем ведра – 10 литров, объем стакана – 200 миллилитров (0,2 литра), объем столовой ложки – 20 мл, объем чайной – 5 мл. Об объеме трехлитровых и литровых банок нетрудно догадаться из их названия.
- Если жидкость занимает не всю емкость или емкость нестандартная, то перелейте ее в другую тару, объем которой известен.Если подходящей емкости нет, перелейте жидкость с помощью мерной кружки (банки, бутылки). В процессе вычерпывания жидкости просто посчитайте количество таких кружек и умножьте на объем мерной тары.
- Если тело имеет простую форму, то вычислите его объем, используя соответствующие геометрические формулы. Так, например, если тело имеет форму прямоугольного параллелепипеда, то его объем будет равен произведению длин его ребер. То есть: Vпар. = a • b • c, где Vпар. – объем прямоугольного параллелепипеда, а a, b, c — значения его длины, ширины и высоты (толщины), соответственно.
- Если тело имеет сложную геометрическую форму, то попробуйте (условно!) разбить его на несколько простых частей, найти объем каждой из них отдельно и затем сложить полученные значения.
- Если тело невозможно разделить на более простые фигуры (например, статуэтку), то воспользуйтесь методикой Архимеда. Опустите тело в воду и измерьте объем вытесненной жидкости. Если тело не тонет, то «утопите» его с помощью тонкой палочки (проволоки).
- Если объем вытесненной телом воды посчитать проблематично, то взвесьте вылившуюся воду, или найдите разность между начальной и оставшейся массой воды. При этом, количество килограммов воды будет равняться количеству литров, количество граммов – количеству миллилитров, а количество тонн – количеству кубометров.
Задачи на плотность,
массу и объем с решением
ВОПРОСЫ ОТ ПОЛЬЗОВАТЕЛЕЙ САЙТА
Публикуем популярные вопросы от наших пользователей, оставленные в поле Комментариев. Прежде чем написать свой вопрос, проверьте: нет ли похожей задачи в начале статьи в разделе «Примеры решения задач» или среди вопросов в данном разделе!
Вопрос № 1. Длина стального листа 120 см, ширина 60 см, толщина 10 мм. Определить массу одного листа.
ОТВЕТ:≈ 56 кг.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Вопрос № 2. Какова масса платинового стержня, объём которого равен 21 дм3 ?
ОТВЕТ: 451,5 кг.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Вопрос № 3. Определить плотность бензина, если бак с бензином ёмкостью 20 литров имеет массу 14,2 кг?
Ответ: 710 кг/м3
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Вопрос № 4. Масса бетонного блока, имеющего форму параллелепипеда, равна 12 кг. Какой станет масса блока, если одну его сторону увеличить в 2 раза, вторую – в 2,5 раза, а третью оставить без изменения?
ОТВЕТ: 60 кг.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Вопрос № 5. Сколько рейсов должен сделать самосвал грузоподъемностью 5 т, чтобы перевезти 100 м3 гранита? Плотность гранита 2600 кг/м3.
ОТВЕТ: 52 рейса.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Вопрос № 6. Плотность некоторого раствора 1300 кг/м3. После того как в этот раствор добавили 10 л воды (деминерализованной) плотность этого раствора стала 1290 кг/м3. Сколько литров раствора было с исходной плотностью?
ОТВЕТ: 290 литров.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Конспект урока по физике в 7 классе «Задачи на плотность, массу и объем с решением». Выберите дальнейшие действия:
- Перейти к теме: «ЗАДАЧИ на силу тяжести и вес тела».
- Вернуться к Списку конспектов по физике для 7-11 классов
- Найти конспект через Кодификатор ОГЭ по физике
- Найти конспект через Кодификатор ЕГЭ по физике
В данной публикации мы рассмотрим, как можно найти объем куба и разберем примеры решения задач для закрепления материала.
- Формула вычисления объема куба
- Примеры задач
Формула вычисления объема куба
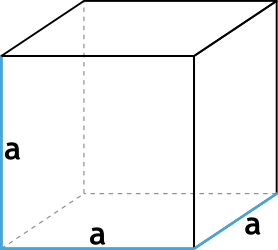
1. Через длину ребра
Объем (V) куба равняется произведению его длины на ширину на высоту. Т.к. данные величины у куба равны, следовательно, его объем равен кубу любого ребра.
V = a ⋅ a ⋅ a = a3
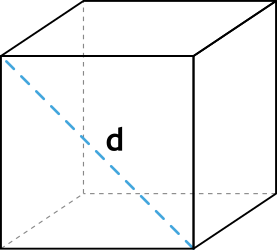
2. Через длину диагонали грани
Как мы знаем, грани куба равны между собой и являются квадратом, сторона которого может быть найдена через длину диагонали по формуле: a=d/√2.
Следовательно, вычислить объем куба можно так:
Примеры задач
Задание 1
Вычислите объем куба, если его ребро равняется 5 см.
Решение:
Подставляем в формулу заданное значение и получаем:
V = 5 см ⋅ 5 см ⋅ 5 см = 125 см3.
Задание 2
Известно, что объем куба равен 512 см3. Найдите длину его ребра.
Решение:
Пусть ребро куба – это a. Выведем его длину из формулы расчета объема:
Задание 3
Длина диагонали грани куба составляет 12 см. Найдите объем фигуры.
Решение:
Применим формулу, в которой используется диагональ грани:
Куб — это трехмерная фигура, представляющая собой правильный многогранник, все грани которого квадраты. Чтобы найти объем куба достаточно знать только длину его стороны (они у куба равны).
Чтобы найти объем куба можно воспользоваться калькулятором, либо одной из подходящих формул, которые мы приводим ниже.
Содержание:
- калькулятор объема куба
- формула объема куба через ребро
- формула объема куба через диагональ грани
- формула объема куба через периметр грани
- формула объема куба через диагональ куба
- формула объема куба через площадь полной поверхности
- примеры задач
Формула объёма куба через ребро
Формула объёма куба через диагональ грани
{V = Big( dfrac{d}{sqrt{2}} Big) ^3}
d — диагональ грани куба
Формула объёма куба через периметр грани
{V= Big( dfrac{P}{4} Big) ^3}
P — периметр грани куба
Формула объёма куба через диагональ куба
{V= dfrac{D^3}{3sqrt{3}}}
D — диагональ куба
Формула объёма куба через площадь полной поверхности
{V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}}}
Sполн — диагональ куба
Примеры задач на нахождение объема куба
Задача 1
Чему равен объём куба с ребром 5 см?
Решение
Для нахождения объема куба, когда известа длина ребра, воспользуемся первой формулой:
V=a ^ 3 = 5 ^ 3 = 125 : см^3
Ответ: 125 см³
Воспользуемся калькулятором для проверки полученного результата.
Задача 2
Найти объем куба, если площадь его поверхности равна 96 см².
Решение
В данном примере нам подойдет эта формула:
V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}} = dfrac{sqrt{{96}^3}}{6sqrt{6}} = dfrac{sqrt{96 cdot 96 cdot 96}}{6sqrt{6}} = dfrac{96 sqrt{96}}{6sqrt{6}} = dfrac{96 sqrt{16 cdot 6}}{6sqrt{6}} = dfrac{96 cdot 4 sqrt{6}}{6sqrt{6}} = dfrac{384 sqrt{6}}{6sqrt{6}} = 64 : см^3
Ответ: 64 см³
Проверить ответ поможет калькулятор .
Также на нашем сайте вы можете найти объем конуса.
Куб (или гексаэдр) — это правильный многогранник, который состоит из многоугольников, являющихся квадратами.
У куба 12 ребер – отрезков, которые являются сторонами квадратов (граней куба).
Также он имеет 8 вершин и 6 граней.
Онлайн-калькулятор объема куба
Формула объема куба
Для нахождения объема куба нужно перемножить его измерения – длину, ширину и высоту. Исходя из того, что куб состоит из квадратов, все его измерения одинаковы и численно равны длине ребра.
Формула для вычисления объема куба такова:
V=a3V=a^3
где aa — длина ребра куба.
Рассмотрим несколько примеров.
Найти объем куба, если периметр PP его грани aa равен 16 cм.16text{ cм.}
Решение
P=16P=16
Периметр PP грани куба связан с длиной его ребра aa по формуле:
P=a+a+a+a=4⋅aP=a+a+a+a=4cdot a
16=4⋅a16=4cdot a
a=164=4a=frac{16}{4}=4
Найдем объем нашего тела:
V=a3=43=64 см3V=a^3=4^3=64text{ см}^3
Ответ: 64 см3.64text{ см}^3.
Одна четвертая часть диагонали квадрата равна 3 см.3text{ см.} Найти объем куба, образованного данным четырехугольником.
Решение
Пусть dd — диагональ фигуры, тогда по условию:
d4=3frac{d}{4}=3
d=4⋅3=12d=4cdot 3=12
Найдем сторону этого квадрата. Обратимся за помощью к теореме Пифагора:
a2+a2=12a^2+a^2=12,
где aa — сторона квадрата.
2⋅a2=122cdot a^2=12
a=6a=sqrt{6}
Приходим к окончательным расчетам для объема:
V=a3=(6)3=66 см3V=a^3=(sqrt{6})^3=6sqrt{6}text{ см}^3
Ответ: 66 см3.6sqrt{6}text{ см}^3.
Чуть более сложный пример.
В куб вписан шар, площадь SS которого равна 64π64pi. Найти объем куба.
Решение
S=64πS=64pi
Первый шагом является нахождение радиуса RR данного шара. Формула его площади такова:
S=4⋅π⋅R2S=4cdotpicdot R^2
64π=4⋅π⋅R264pi=4cdotpicdot R^2
64=4⋅R264=4cdot R^2
644=R2frac{64}{4}=R^2
16=R216=R^2
R=4R=4
Для куба радиус вписанного шара является половиной его стороны aa:
a=2⋅R=2⋅4=8a=2cdot R=2cdot4=8
Объем вычисляется следующим образом:
V=a3=83=512 см3V=a^3=8^3=512text{ см}^3
Ответ: 512 см3.512text{ см}^3.
На Студворке вы можете оформить заказ контрольных работ для студентов по самым низким ценам!
Тест по теме «Объем куба»
Измерение объёма тела по формуле — возможные способы, единицы измерения
Содержание:
- Понятие объема тела
- Свойства объема тела
- Как вычислить объем тела: все формулы
- Примеры решения задач
- Задания для самостоятельной работы
Понятие объема тела
Объем является количественным параметром пространства, занятого телом или веществом.
Термин объема можно рассматривать совместно с понятием вместимости. Это обозначение для объема какого-то внутреннего пространства сосуда, коробки и тому подобного. Объем тела, как и вместимость некой емкости, зависит от таких характеристик, как:
- форма;
- линейные размеры.
Главным свойством объема принято считать аддитивность.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Аддитивность означает равенство объема какого-либо тела сумме объемов частей этого тела, которые не пересекаются между собой.
Согласно СИ, единицей измерения объема является метр кубический (м³). В процессе решения задач можно встретить единицы измерения объемов тел в виде см³, дм³, или литров. В иностранной литературе также используются указания объемов веществ, находящихся в жидком или сыпучем состоянии, в таких единицах измерения, как, например, галлон, баррель и другие.
Величина объема используется при составлении различных уравнений и неравенств. При этом данный параметр обозначают с помощью буквы V. Это сокращение от латинского слова volume, которое в переводе означает объем или наполнение.
Свойства объема тела
В процессе решения разнообразных задач по физике, алгебре и геометрии целесообразно использовать свойства, которыми обладает объем тела. Перечислим основные из них:
- Объем тела не может быть отрицательной величиной.
- В том случае, когда некое геометрическое тело состоит из определенного количества геометрических тел, не обладающих едиными внутренними точками, объем такого тела складывается из объемов составляющих его тел.
- Объем фигуры в виде куба с ребром, значение которого равно единице измерения длины, равен единице.
- Аналогичные друг другу геометрические тела обладают одинаковыми объемами.
- В том случае, когда тело имеет объем V1 и расположено в другом теле с объемом V2, справедливо следующее соотношение: (V1<V2
).
Как вычислить объем тела: все формулы
Существует практический способ определения объема тела, включая тела, обладающие сложной формой и геометрией. Данная методика основана на законе Архимеда и предполагает погружение рассматриваемого тела в некую жидкость. По результатам следует измерить объем вытесненной телом жидкости. Данная величина равна объему измеряемого тела.
Формула расчета объема тела, исходя из известных величин массы и плотности:
(V={frac {m}{rho }})
Здесь m определяется, как масса, а rho является средней плотностью тела.
В том случае, когда тела обладают простыми геометрическими формами, в решении задач допустимо использовать специальные формулы. К примеру, для того чтобы найти объем куба, ребро которого равно а, следует применить такую формулу: (V=a^{3}).
Вычислить объем некого прямоугольного параллелепипеда можно путем умножения длины, ширины и высоты. Запишем другие распространенные формулы для расчета объемов геометрических фигур:
- куб, формула объема: (V=a^{3}):
- прямоугольный параллелепипед, формула объема: (V=abc) (произведение длин трех сторон):
- призма, формула объема: ( V=Bh) (произведение площади основания и высоты):
- пирамида, формула объема: (V={frac {1}{3}}Bh:)
- параллелепипед, формула объема: (V=abc{sqrt {K}}, {begin{aligned}K=1&+2cos(alpha )cos(beta )cos(gamma )\&-cos ^{2}(alpha )-cos ^{2}(beta )-cos ^{2}(gamma )end{aligned}}:
) -
- тетраэдр, формула объема: (V={{sqrt {2}} over 12}a^{3}:)
- шар, формула объема: (V={frac {4}{3}}pi r^{3}):
- эллипсоид, формула объема: (V={frac {4}{3}}pi abc):
- прямой круговой цилиндр, формула объема: (V=pi r^{2}h):
- конус, формула объема: (V={frac {1}{3}}pi r^{2}h):
- тело вращения, формула объема: (V=pi cdot int _{a}^{b}f(x)^{2}mathrm {d} x):
В том случае, когда необходимо определить объем, которым обладает некое тело, имеющее сложную форму, нужно разбить мысленно данное тело на отдельные части. Такие части целого должны иметь простую форму. Далее следует сложить вычисленные объемы простых тел. Результат будет являться значением объема начального тела.
Примеры решения задач
Задача 1
Задача
Имеется пара шаров. Радиус первого шара в 5 раз превышает радиус второго шара.
Требуется определить, во сколько раз площадь поверхности второго шара меньше по сравнению с площадью поверхности первого шара
Решение
Рассчитать площадь поверхности можно по формуле:
(S=4pi R^2)
Тогда запишем отношения площадей пары шаров:
(dfrac{S_1}{S_2}=dfrac{4pi , R_1^2}{4pi , R_2^2})
Сравним радиусы геометрических фигур:
(R_1=5R_2)
В результате:
(dfrac{S_1}{S_2}=dfrac{(5R_2)^2}{R_2^2}=25)
Таким образом, первый шар имеет площадь поверхности, которая в 25 раз больше по сравнению с аналогичной характеристикой второго шара.
Ответ: 25.
Задача 2
На рисунке изображены конусы. Назовем их (K_1) и (K_2).
Полная поверхность (K_1) по площади относится к площади полной поверхности (K_2) как 4:1.
Фигура (K_1) обладает радиусом, который в 4 раза больше образующей (K_1) и в 2 раза больше радиуса (K_2).
Требуется вычислить, как относится образующая (K_2) к образующей (K_1.)
Решение
Представим, что образующая конуса равна 1, а радиус основания обозначим, как R. Тогда можно записать следующее соотношение:
(S=pi R (R+l))
Запишем отношения площадей полной поверхности заданных конусов:
(dfrac41=dfrac{pi ,R_1cdot (R_1+l_1)}{pi , R_2cdot (R_2+l_2)})
Согласно условию задачи, имеем:
(R_1=4l_1, R_2=frac12R_1=2l_1)
В результате:
(dfrac41=dfrac{4l_1cdot (4l_1+l_1)}{2l_1cdot (2l_1+l_2)} quadRightarrowquad dfrac{l_2}{l_1}=dfrac12=0,5)
Ответ: 0,5.
Задача 3
Даны два прямоугольных параллелепипеда. Объем первой фигуры равен 105. Известно, что первый параллелепипед по высоте превышает второй в 7 раз. Ширина второй фигуры в 2 раза больше по сравнению с аналогичным параметром первой фигуры. Первый параллелепипед длиннее в три раза, чем второй. Необходимо вычислить объем, который имеет второй параллелепипед.
Решение
Обозначим высоту, ширину и длину геометрических фигур с помощью букв а, b, с соответственно. Вспомним формулу, по которой можно найти объем прямоугольного параллелепипеда:
V=abc
Применительно к нашей задаче, запишем:
(dfrac{105}{V_2}=dfrac{V_1}{V_2}=dfrac{a_1b_1c_1}{a_2b_2c_2})
Известно, что:
(a_1=7a_2, b_2=2b_1, c_1=3c_2)
В результате:
(dfrac{105}{V_2}=dfrac{7a_2cdot b_1cdot 3c_2}{a_2cdot 2b_1cdot c_2}= dfrac{7cdot 3}2 quadRightarrowquad V_2=dfrac{105cdot 2}{21}=10)
Ответ: 10.
Задача 4
Даны два конуса. Площадь боковой поверхности первой геометрической фигуры относится к площади боковой поверхности второй фигуры как 3:7. Первый конус обладает радиусом, который относится к радиусу второго конуса, как 15:7. Необходимо определить, как относится образующая первого конуса к образующей второго конуса.
Решение
Составим формулу для расчета площади боковой поверхности конуса:
(S=pi Rl)
Запишем отношения площадей боковых поверхностей для первого и второго конусов:
(dfrac 37=dfrac{S_1}{S_2}=dfrac{pi R_1,l_1}{pi R_2,l_2})
Зная, что отношение радиусов двух геометрических фигур равно 15:7, получим:
(frac{R_1}{R_2}=frac{15}7, то dfrac37=dfrac {15}7cdot dfrac{l_1}{l_2} quadRightarrowquad dfrac{l_1}{l_2}=dfrac37cdot dfrac7{15}=dfrac15=0,2)
Ответ: 0,2.
Задача 5
Имеется пара шаров. Объем первой фигуры составляет 54. Радиус второй фигуры в 3 раза меньше по сравнению с радиусом первой. Нужно определить объем второго шара.
Решение
Запишем формулу, согласно которой можно определить объем шара:
(V=dfrac43 pi R^3)
Составим отношение объемов двух фигур:
(dfrac{54}{V_2}=dfrac{V_1}{V_2}= dfrac{frac43 pi ,R_1^3}{frac43 pi ,R_2^3}=left(dfrac{R_1}{R_2}right)^3)
По условиям задачи:
(R_1=3R_2)
В результате:
(dfrac{54}{V_2}=left(dfrac{3R_2}{R_2}right)^3=27 quadRightarrowquad V_2=dfrac{54}{27}=2)
Ответ: 2.
Задача 6
Имеется некая емкость конусообразной формы. Ее заполнили до половины с помощью 75 гр жидкости. Необходимо вычислить вес жидкости, которую нужно добавить в емкость, чтобы заполнить ее до верхнего края.
Решение
Вспомним формулу объема из курса физики:
(V=frac{m}{rho})
Предположим, что O является центром основания большего конуса. Пусть Q — центр основания меньшего конуса, а S обозначает общую вершину данных фигур. В одной плоскости построим радиусы OA и QB:
В таком случае:
(QBparallel OA)
(triangle SQBsim triangle SOA)
В результате:
(dfrac{OA}{QB}=dfrac{OS}{QS}=dfrac21)
Получим, что:
(m_{small{text{ж}}}=V_{small{text{ж}}}cdot rho= dfrac13cdot picdot QScdot QB^2 cdot rho)
Можно сделать вывод, что:
(m=Vrho=dfrac13cdot picdot OScdot OA^2cdot rho= dfrac 13cdot picdot 2QScdot (2QB)^2cdot rho= 8cdot left(dfrac13cdot picdot QScdot QB^2cdot rhoright)=8cdot 75=600 {small{text{грамм}}})
Таким образом, потребуется долить в емкость:
(600-75=525 {small{text{грамм}}})
Ответ: 525.
Задача 7
Изображена четырехугольная пирамида. Ее высота равна h. Отметим точку сбоку на ребре геометрической фигуры так, чтобы она была удалена на frac13h от плоскости основания. Данную точку пересекает плоскость, которая параллельна плоскости основания и отделяет от пирамиды аналогичную фигуру меньшего размера. Объем начальной пирамиды равен 54. Требуется вычислить объем меньшей пирамиды, которая получилась в результате.
Решение
Назовем точку, через которую проведена плоскость, A’ на ребре AS. Параллельность плоскости и основания является причиной пересечения боковых граней по прямым A’B’, B’C’, C’D’, D’A’, параллельным соответственно AB, BC, CD, DA. В этом случае SA’B’C’D’ является правильной четырехугольной пирамидой.
Исследуем плоскость ASO. Построим (A’Hparallel SO), где SO представляет собой высоту начальной фигуры. В таком случае:
(A’Hperp ABC)
В результате получилось расстояние, которое равно (frac13SO:)
(triangle AA’Hsim triangle ASO)
(dfrac{SA}{AA’}=dfrac{SO}{A’H}=3 quadRightarrowquad SA=3AA’ quadRightarrowquad SA’=dfrac23SA)
Таким образом:
(SQ=frac23SO)
(triangle ASBsim triangle A’SB’)
Получим, что:
(dfrac23=dfrac{SA’}{SA}=dfrac{A’B’}{AB} quadRightarrowquad A’B’=dfrac23AB)
Запишем отношения объемов пирамид:
(dfrac{V_{{small{text{м}}}}}{V_{small{text{б}}}}= dfrac{frac13cdot SQcdot A’B’^2}{frac13cdot SOcdot AB^2}=dfrac{SQ}{SO}cdot left(dfrac{A’B’}{AB}right)^2=dfrac23cdot left(dfrac23right)^2=dfrac8{27})
В результате объем малой фигуры составит:
(V_{{small{text{м}}}}=dfrac8{27}cdot 54=16)
Ответ: 16.
Задания для самостоятельной работы
Задание 1
Имеется пара конусов. Вторая фигура обладает радиусом, который в три раза больше по сравнению с радиусом первой фигуры. Второй конус выше первого в шесть раз. Объем второй фигуры равен 18. Требуется вычислить, чему равен объем первого конуса.
Решение
Формула определения объема конуса:
(V=frac13pi R^2h)
Запишем отношения объемов двух фигур:
(dfrac{V_1}{18}=dfrac{V_1}{V_2}= dfrac{frac13pi ,R_1^2,h_1}{frac13 pi ,R_2^2,h_2}=left(dfrac{R_1}{R_2}right)^2cdot dfrac{h_1}{h_2})
Исходя из условий задачи:
(R_2=3R_1)
(h_1=6h_2)
В результате:
(dfrac{V_1}{18}=left(dfrac{R_1}{3R_1}right)^2cdot dfrac{6h_2}{h_2}= dfrac19cdot 6=dfrac23 quadRightarrowquad V_1=dfrac23cdot 18=12)
Ответ: 12
Задание 2
Дано два шара. Объем первого шара в 343 раза больше по сравнению с объемом второго шара. Нужно вычислить, во сколько раз радиус первой фигуры больше, чем радиус второй фигуры.
Решение
Запишем формулу для нахождения объема шара:
(V=dfrac43 pi R^3)
Составим отношения объемов данных шаров:
(dfrac{343}1=dfrac{V_1}{V_2}=dfrac{frac43 pi , R_1^3}{frac43 pi , R_2^3}= left(dfrac{R_1}{R_2}right)^3 quadRightarrowquad dfrac{R_1}{R_2}=sqrt[3]{343}=7)
Сделаем вывод, что радиус первого шара в 7 раз больше по сравнению с радиусом второго шара.
Ответ: 7.
Задание 3
На рисунке изображены два цилиндра. Первый из них обладает площадью боковой поверхности, равной 16. Радиус второй фигуры больше в 4 раза по сравнению с радиусом первой фигуры. Второй цилиндр ниже, чем первый цилиндр, в 5 раз. Требуется вычислить площадь боковой поверхности второго цилиндра.
Решение
Запишем формулу для вычисления площади боковой поверхности цилиндра, которую уже проходили ранее:
(S=2pi RH)
Составим отношение площадей боковых поверхностей двух фигур:
(dfrac{16}{S_2}=dfrac{S_1}{S_2}=dfrac{2pi ,R_1,H_1}{2pi ,R_2,H_2}= dfrac{R_1}{R_2}cdot dfrac{H_1}{H_2})
В результате:
(R_2=4R_1, H_1=5H_2)
Таким образом:
(dfrac{16}{S_2}=dfrac{R_1}{4R_1}cdot dfrac{5H_2}{H_2}= dfrac14cdot 5=dfrac54)
Получим, что:
(S_2=dfrac{16cdot 4}5=12,8)
Ответ: 12,8.
Задание 4
Имеется некая емкость конусообразной формы. Объем этой емкости составляет 2700 мл. Требуется рассчитать количество жидкости, налитой в емкость, если ее уровень в 3 раза меньше по сравнению с высотой емкости.
Решение
Введем обозначения, как на рисунке:
В таком случае:
(QBparallel OA и triangle SQBsim triangle SOA)
Таким образом:
(dfrac{QB}{OA}=dfrac{QS}{OS}=dfrac13)
Соотношение объемов жидкости до определенной линии и емкости:
(dfrac{V_{small{text{ж}}}}{2700}=dfrac{V_{small{text{ж}}}}{V}= dfrac{frac13cdot picdot QB^2cdot QS}{frac13cdot pi cdot OA^2cdot OS}= left(dfrac{QB}{OA}right)^2cdot dfrac{QS}{OS}=dfrac19cdot dfrac13=dfrac1{27})
В результате:
(V_{small{text{ж}}}=dfrac1{27}V=100)
Ответ: 100.
Задача 5
На рисунке изображены фигуры в виде шаров. Первый шар имеет радиус 6. Второй шар имеет радиус 2. Нужно вычислить, во сколько раз объем первой фигуры превышает объем второй фигуры.
Решение
Запишем формулу для расчета объема шара, который не может изменяться:
(V=dfrac43 pi R^3)
Составим отношение объемов двух шаров:
(dfrac{V_1}{V_2}=dfrac{frac43 pi cdot 6^3}{frac43 pi cdot 2^3}= left(dfrac62right)^3=27)
В результате объем первого шара в 27 раз больше по сравнению с объемом второго шара.
Ответ: 27.