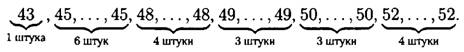Урок 282
Тема урока: Задачи математической статистики.
Цели урока:
Обучающая:
Научить учащихся решать задачи по обработке
статистических данных, используя понятия:
объём измерения, размах измерения, мода
измерения, среднее арифметическое, медиана
измерения, варианта измерения, кратность
варианты, и составлять данные в виде таблиц,
диаграмм, графиков. Ввести понятия: частота
варианты, частота варианты (в процентах).
Развивающая:
Формировать умения
учащихся, решать задачи на
обработку статистических данных, используя
данные в виде таблиц, диаграмм, графиков.
Развивать логическое и математическое мышление.
Воспитывающая:
Воспитывать культуру речи,
построения плана
ответа, сознательной дисциплины, культуры
конструктивного мышления, активность на уроке,
аккуратность при выполнении записи на доске и в
тетради, положительный интерес к изучаемому
предмету.
Тип урока: Комбинированный.
Вид
урока: Урок
решения задач на обработку статистических
данных, используя данные в виде таблиц,
диаграмм, графиков.
Методы
обучения: Репродуктивный.
Материально-техническое
оснащение:
—Математика Учебник Общеобразовательные
дисциплины
Начальное и среднее профессиональное образование
Автор М.И. Башмаков.
Москва Издательский центр «Академия» 201
—Математика Учебник
Общеобразовательные дисциплины
для профессий и специальностей социально-экономического
профиля. Авторы В.А. Гусев, С.Г.Григорьев, С.В.Иволгина
Москва Издательский центр «Академия» 2011
— Математика Задачник Общеобразовательные
дисциплины
Начальное и среднее профессиональное образование
Автор М.И. Башмаков.
Москва
Издательский центр «Академия» 2012
— дидактический
раздаточный материал (карточки для
индивидуальной
работы)
Ход урока
1. Организационный момент урока
— сдача рапорта
2. Целевая ориентация
(
Преподаватель формулирует тему, цели и задачи урока. Мотивирует учащихся к
учебной деятельности. Разъясняет последовательность этапов урока, приводящих к
достижению цели)
3. Проверка
домашнего задания.
4. Вопросы для закрепления изученного
материала.
1). Перечислить
основные этапы простейшей статистической обработки данных.
2). Что называют
объемом измерения?
3). Что такое размах
измерения?
4). Что называют
модой измерения?
5). Что называют
средним арифметическим?
6). Что называют
вариантой измерения?
7). Что называют
медианой измерения?
5.
Формирование
навыков умственного труда
Решение задач у доски
Задача 1
В таблице распределения данных часть информации была утеряна.
Восстановить ее. Если известно, что объем измерения равен 20, размах измерения
равен 6, а мода равна 2.
|
|
Сумма |
|||||
|
— 1 |
0 |
3 |
||||
|
Кратность |
5 |
1 |
7 |
3 |
Решение
По определению. В графе «Сумма» должен стоять объём измерения, т.е. 20.
Этот объём равен сумме всех кратностей, значит, кратность варианты «0», равна
20 – (5+1+7+3) = 4.
Самая большая кратность равна 7. Значит, над ней и расположена мода
измерения, равная 2. Так как размах равен 6, а наибольшая варианта равна 3, то
наименьшая варианта равна 3 — 6 = — 3. эту варианту помещаем в последнюю
свободную графу над кратностью 5.
Ответ:
|
|
Сумма |
|||||
|
— 3 |
— 1 |
0 |
2 |
3 |
||
|
Кратность |
5 |
1 |
4 |
7 |
3 |
20 |
Задача 2
По приведённой гистограмме распределения данных найти: количество
вариант измерения, объем, размах. моду измерения, наиболее удалённую от моды
варианту и ее кратность. Составить таблицу распределения данных.
Решение.
Количество вариант – это количество столбиков в гистограмме, т.е. 7.
Объем измерения равен сумме кратностей всех вариант, т.е. равен сумме высот
всех семи столбиков: 3+2+7+3+5+4+1 = 25. Таблица распределения выглядит так:
|
|
Сумма |
|||||||
|
2 |
4 |
5 |
6 |
7 |
9 |
10 |
||
|
Кратность |
3 |
2 |
7 |
3 |
5 |
4 |
1 |
25 |
1). Наибольшая варианта равна 10, а наименьшая равна 2.
2). Размах равен 8. (10 – 2) =8.
3). Мода измерения равна 5, так как она встречалась чаще других – 7
раз.
4). На наибольшем расстоянии от моды находится варианта 10, её
кратность равна 1.
Определение: Если кратность варианты разделить на объем измерения,
то получится частота варианты. Это число показывает, какую
часть (долю) среди всех данных составляют данные, равные выбранной варианте.
Частоту варианты можно измерить и в процентах.
Частота варианты
(в процентах) =
Задача 3
В десятых классах трёх школ микрорайона провели проверочный диктант по
русскому языку. По их результатам изображена гистограмма распределения
полученных отметок.
а) Найти: общее
количество работ, частоту пятёрок, процентную частоту
двоек.
б) Заполнить сводную таблицу распределения данных.
в) Построить гистограмму распределения частот ( в процентах).
г) Построить круговую диаграмму распределения частот (в процентах).
Решение.
а) На гистограмме указано, что двоек было 40, троек – 50, четвёрок –
75, пятёрок – 35. значит. Всего было 200 работ. Это есть объём измерения.
Частота пятёрок равна , а частота (в процентах) двоек
равна
б) Так как все кратности известны, то можно заполнить всю таблицу
распределения:
|
|
Сумма |
||||
|
2 |
3 |
4 |
5 |
||
|
Кратность |
40 |
50 |
75 |
35 |
200 |
|
Частота |
0,2 |
0.25 |
0.375 |
0,175 |
1 |
|
Частота,% |
20 |
25 |
37,5 |
17,5 |
100 |
в) Для построения гистограммы распределения частот (в процентах)
используем первую и четвёртую строки. Получим четыре вертикальных столбика.
Основания которых соответствуют полученным отметкам, а высоты равны найденным
частотам ( в процентах).
г) разделим круг на четыре сектора. Центральный угол сектора двойки
составляет 20% от 3600. т.е. 720. Центральный угол
сектора тройки составляет 25% от 3600, это прямой угол. Центральные
углы секторов четвёрки и пятёрки равны соответственно 1350 и 630.

5. Вопросы для
закрепления изученного материала.
1). Что называют частотой
варианты?
2). По какой формуле
измеряют частоту варианты в процентах?
6. Итог урока.
Домашнее задание.
Задача.
По приведённой гистограмме распределения данных найти:
а) количество вариант и объем измерения;
б) размах и моду измерения;
в) таблицу распределения данных;
г) среднее результатов измерения.
Решение.
1) Количество вариант – это количество столбиков в гистограмме, т.е. 9.
Объем измерения равен сумме кратностей всех вариант, т.е. равен сумме высот
всех девяти столбиков: 5+6+3+7+4+11+5+4+5 = 50. Таблица распределения выглядит
так:
|
|
Сумма |
|||||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
Кратность |
5 |
6 |
3 |
7 |
4 |
11 |
5 |
4 |
5 |
50 |
2). Наибольшая варианта равна 10, а наименьшая равна 2.
Размах равен 8. (10 – 2) = 8.
Мода измерения равна 7, так как она встречалась чаще других – 11 раз.
3). Таблица распределения выглядит так:
|
|
Сумма |
|||||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
Кратность |
5 |
6 |
3 |
7 |
4 |
11 |
5 |
4 |
5 |
50 |
4). Среднее арифметическое
— это частное от деления суммы всех результатов измерения на объём измерения.
Среднее удобно вычислять после того, как составлена таблица распределения. В
данном случае вычисления выглядят так:
Дата публикации: 09 апреля 2017.
Урок и презентация на тему: «Математическая статистика, элементы статистики»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать:
Математическая статистика, элементы статистики (PPTX)
Статистика, введение
Темой сегодняшнего урока будет математическая статистика.
Этот предмет занимается статистикой, используя различные математические методы. Математическая статистика — это самостоятельно развивающийся раздел математики, в котором существуют и свои уникальные способы решения различных задач.
Так чем же занимается и для чего нужна математическая статистика?
Предположим, что у учеников девятых классов измерили рост. Как представить полученные данные? Можно записать их в строчку друг за другом, можно разделить данные по классам, можно попробовать создать таблицу. Все эти способы довольно громоздки и неудобны. Будет сложно извлечь информацию из такого набора чисел. А теперь представьте, что измерили рост учеников девятых классов всех школ в городе. Количество измерений может перевалить за тысячу.
Математическая статистика занимается обработкой данных и представлением их в виде удобном для восприятия. Это только одна из задач статистики. Построение прогнозов и оценок; применение различных методов исследования; достоверность проведенных испытаний и многое другое — вот чем занимается статистика.
Как же обрабатывает информацию статистика?
- Данные измерений упорядочивают и группируют.
- Составляют таблицы распределений данных.
- По таблицам строят графики распределений.
- В итоге создается паспорт измерений, в котором собраны числовые характеристики полученной информации.
Давайте рассмотрим эти пункты.
Упорядочивание и группировка данных
Первое, что необходимо сделать при анализе данных, определить рамки, в которых находится исследователь. Выбираются наименьшее и наибольшее допустимые значения, которые могут не совпадать с полученными данными. Например, при измерении роста учеников, шансов, что кто-то будет ниже 140 сантиметров и выше 200 сантиметров очень мало. Если найдется такой вариант, то данные статистики можно подкорректировать.
При измерении роста могут получиться числа: 140,150,160,170,180,190,200 – это общий ряд данных, которые принято располагать в порядке возрастания. Общий ряд данных может быть и другим, например: 140,145,150,155,160,…,190,195,200. Как представить общий ряд данных зависит от конкретной задачи.
Пример. Составить общий ряд данных, включающих:
а) месяцы рождения одноклассников,
б) годов рождения родственников и друзей,
в) буквы, с которых начинается слово.
Решение.
а) Всего месяцев 12, если их перечислить по цифрам, то получим общий ряд: 1,2,3,4,5,6,7,8,9,10,11,12.
б) Шанс, что кто-то из родственников старше 100 лет — мал, а что, кто-то родился в этом году — есть. Тогда общий ряд годов рождения можно составить так: 1910,1911,1912,…, 2009,2010,2011,2012,2013,2014.
в) Слово может начинаться с любой буквы алфавита, кроме ь, ы, ъ. Тогда возможны 30 вариантов, если их представить численным рядом, то получим: 1,2,3,4,…,28,29,30.
Понятие «общий ряд» не является строгим, в примере б) мы могли начать ряд с 1900 года, ряд так же назывался «общим».
При проведении эксперимента данные из общего ряда могут не встретиться. Вернемся к нашему примеру б) и рассмотрим конкретный случай.
Вова назвал года рождения родственников: 1935,1937,1960,1965,1980,1981,1997,2005.
Общий ряд представлял собой последовательность: 1910,1911,1912,…,2009,2010,2011,2012,2013,2014.
У Вовы встретились конкретные измерения, которые называются «вариантой измерения».
Варианта измерения – это возможный вариант проведенного измерения.
Если все варианты измерений перечислить по порядку, то получится ряд данных измерения.
Для нашего примера составим таблицу:
Пример. Выписать ряд, состоящий из букв, которые встречаются в словах: мама, папа, брат, сестра, бабушка, дедушка, тетя, дядя.
Решение. Ряд будет выглядеть так: а, б, д, е, к, м, п, р, с, т, у, ш, я. Встретились 13 букв из 33.
Некоторые буквы встречаются несколько раз, например, буква а – девять раз, другие – реже.
Определение. Если среди всех данных конкретного измерения одна из вариант встретилась ровно к раз, то число к называют кратностью измерения.
В этом примере буква а имеет кратность — 9.
Запишем кратности для каждой из букв:
Далее варианты нужно сгруппировать. Создадим сгруппированный ряд данных:
а,а,а,а,а,а,а,а,а,б,б,б,д,д,д,д,е,е,е,к,к,м,м,п,п,р,р,с,с,т,т,т,т,у,у,ш,шя,я,я.
Число повторений каждой варианты равно кратности варианты.
Составление таблицы распределения данных
Если сложить все кратности, получится количество всех данных измерения или объем измерения. Объем измерения равен количеству букв встречающихся в наших словах. Для проверки всегда складывают кратности, сумма должна равняться количеству элементов измерения.
Далее вычисляют частоту варианты.
Частота варианты=Кратность варианты/Объем измерения.
Составим таблицу частот измерений:
Сумма всех частот всегда равна единице, так как это сумма всех дробей с одинаковым знаменателем, а сумма всех числителей как раз и равна знаменателю. Для удобства, часто переводят частоты в проценты от объема измерения. Составим таблицу еще одну таблицу, каждую частоту в новой строке помножим на 100.
Графическое представление данных
Давайте построим графики функций распределения по таблицам. Договоримся, что вместо букв будем использовать цифры 1,2,3,…,13.
Тогда наша таблица примет вид:
По оси абсцисс отложим цифры, соответствующие буквам, а по оси ординат – значения частот появления варианта. Графическое изображение имеющейся информации – график распределения частот.
Таблица значений:
График распределения частот:
График распределения частот также называют полигоном распределения.
Давайте построим график распределения частот процентов. Его тоже называют полигоном распределения процентов.
Таблица значений.
Полигон распределения процентов:
Даже не большая по объему данных задача, представляет собой довольно таки утомительную процедуру подсчета и составления таблиц и графиков распределений.
Числовые характеристики данных измерения
Наши данные обладают уникальными числовыми характеристиками. Давайте определим некоторые из них.
Разность между максимальной и минимальной вариантой называют размахом измерения.
На наших графиках — это область определения (разность крайнего правого значения и крайнего левого значения на оси абсцисс). В нашем примере размах равен $13-1=12$.
Варианта, которая встречается чаще других, называется модой. В нашем примере это буква а или число 1, в зависимости от обозначения.
Если у нас есть таблица распределения частот, то в строчке частот ищем наибольшее число, и смотрим, какому варианту оно соответствует. На графике, это точка в которой достигается максимальное значение.
Наиболее важная характеристика – среднее значение (среднее арифметическое или просто среднее).
Чтобы найти среднее значение нужно:
а) Просуммировать все данные измерения.
б) Полученную сумму разделить на количество вариантов.
Для нашего примера найдем среднее значение:
$frac{1*9+2*3+3*4+4*3+5*2+6*2+7*2+8*2+9*2+10*4+11*2+12*2+13*3}{40}=5,775$.
Среднее значение можно найти другим способом:
а) Каждую варианту умножить на ее частоту.
б) Сложить получившиеся значения.
Подсчитаем этим способом:
1*0,225+2*0,075+3*0,1+4*0,075+5*0,05+6*0,05+7*0,05+8*0,05+9*0,05+10*0,1+11*0,05+12*0,05+13*0,075=5,775.
Давайте рассмотрим еще один пример.
На экзамене по математике 25 учеников 9 класса получили такие оценки:
5,4,3,3,5,4,3,3,4,4,5,5,2,2,5,5,5,3,3,4,5,5,4,3,2.
а) Составить общий ряд данных. Упорядочить и сгруппировать.
б) Составить таблицы распределения и распределения частот.
в) Построить графики распределения и распределения частот.
г) Найти среднее, моду, размах.
Решение.
Возможны такие оценки: 1,2,3,4,5 – общий ряд данных.
В нашем примере встречаются оценки: 2,3,4,5 – ряд данных, все числа в ряде – варианты измерений.
Составим сгруппированный ряд: 2,2,2,3,3,3,3,3,3,3,4,4,4,4,4,4,5,5,5,5,5,5,5,5,5.
б) Объем измерения равен 25, так как 25 оценок выставлено.
Составим таблицу:
в) Нарисуем графики:
Полигон распределения данных:
Полигон распределения частот:
Полигон распределения частот процентов:
Все графики похожи между собой, различия только в масштабе оси ординат.
г)Найдем среднее значение:
$2*0,12+3*0,28+4*0,24+5*0,36=0,24+0,84+0,96+1,8=3,81$.
Мода: чаще всего встречается оценка пять, она и будет модой.
Размах: $5-2=3$.
Задачи статистики для самостоятельного решения
1.На экзамене по математике 50 учеников 9 класса получили такие оценки:
5,3,4,4,5,4,3,2,4,3,5,1,2,3,5,4,5,3,3,4,5,5,4,3,1,3,4,5,4,3,2,2,1,4,4,5,5,4,4,5,3,3,3,2,1,5,4,3,2,5.
а) Составить общий ряд данных. Упорядочить и сгруппировать.
б) Составить таблицы распределения и распределения частот.
в) Построить графики распределения и распределения частот.
г) Найти среднее, моду, размах.
Цель: рассмотреть статистическую
обработку информации, и её основные
характеристики.
ХОД УРОКА
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного
материала
- Ответы на вопросы по домашнему заданию (раздор
не решённых задач). - Контроль усвоения материала (самостоятельная
работа № 27 стр. 64-65) Л. А. Александрова «Алгебра. 9
класс. Самостоятельные работы», Мнемозина, – М.,
2010.
III. Изучение нового материала
Наш XXI в. характеризуют различным образом: век
генной инженерии, век новых технологий ( в
частности, нанотехнологий), век астрофизики
(проверка основополагающих космогонических
теорий, большой андронный коллайдер) и т. д. Если
вдуматься, все определения объединяет прежде
всего, получение принципиально новой информации.
Поэтому правильнее назвать наш век веком
информации. Буквально за несколько последних лет
появились сверхмощные компьютеры, Интернет,
различные поисковые системы, разрабатываются и
совершенствуются методики обработки информации
и т. п.
Многие из нас участвуют в переписи населения,
выборах, опросах и т. д. При этом появляется
определённая информация. Задача статистики –
отражение этой информации и её обработка. Для
этого необходимо ввести некоторые
статистические характеристики. Рассмотрим
следующий пример.
Пример
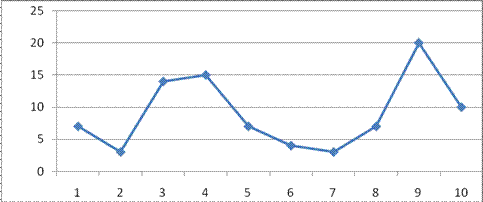
В финал конкурса «Мисс факультета» Вышли 10
студенток, за которых болели и голосовали 90
студентов. В таблице приведены результаты
голосования за участниц с номерами 1-10.
| № участницы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Число голосов | 7 | 3 | 14 | 15 | 7 | 4 | 3 | 7 | 20 | 10 |
Прежде всего, возникает вопрос о наглядном
отражении результатов голосования. Из курса
алгебры вы знаете, что графическая информация
нагляднее табличной. Поэтому применяют три вида
графического отражения информации – диаграммы.
Первый вид диаграммы – линейная
диаграмма (или многоугольник распределения)
строится как обычный график. По оси абцисс
откладываются номера участниц, по оси ординат –
число голосов, отданных за данную участницу, т. е.
точки (1,7), (2,3), (3,14) и т. д. Для наглядности
отмеченные точки соединены отрезками.
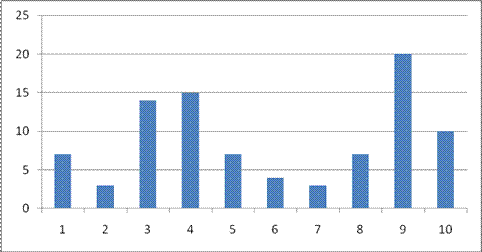
Второй вид диаграммы – столбчатая
диаграмма (или гистограмма распределения)
строится следующим образом. В окрестности каждой
отмеченной точки по оси абцисс строят
прямоугольник, высота которого равна
соответствующей ординате. При этом обычно ширину
прямоугольников делают одинаковой. Достаточно
часто прямоугольники изображаются таким
образом, что два соседних имеют общую сторону.
При этом прямоугольники могут штриховаться (см.
учебник)
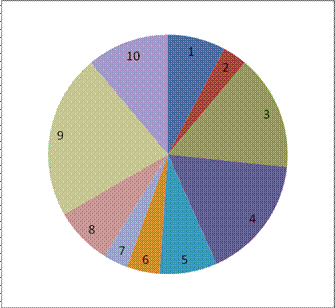
Третья диаграмма – круговая (или
камамбер, по названию французского сыра)
представляет собой круг, разделённый на 10
секторов с различными центральными углами. Так
как всего было подано 90 голосов, то каждому
голосу соответствует 360о : 90 = 4о. Далее
легко пересчитать углы секторов. Например, для
первой участницы строим сектор с углом 4о .
7 = 28о. Каждый сектор маркируется номером
соответствующей участницы.
На практике применяют все три вида диаграмм.
Итак, на конкретном примере были рассмотрены
основные этапы простейшей статистической
обработки данных:
- Систематизация, упорядочивание и
группировка. - Составление таблицы распределения данных.
- Построение диаграммы распределения данных
(любого вида) - Паспорт данных измерения (основные
характеристики информации)
Обсудим некоторые характеристики
рассматриваемого примера.
Объём измерения – количество
источников информации (т.е. число опрошенных
или число голосов) в данном случае 90.
Размах измерения – разница между
наибольшим и наименьшим значениями результатов
измерения. В данном случае 20 – 3 = 17, так как
наибольшее число голосов 20, наименьшее 3.
Мода измерения – наиболее часто
встречающийся результат. В данном случае 9, так
как за участницу №9 было подано 20 голосов
(наибольшее количество).
Среднее (или среднее арифметическое) –
частное от деления суммы всех результатов
измерения на объём измерения. В данном случае
получают:
Обычно результатами измерений являются
некоторые числа. Каждое число, встретившееся
в конкретном измерении, называют вариантой
измерения. В конкретном измерении его
варианты могут быть никак не связаны (например,
билетики с результатами голосования). Однако
обычно результаты обрабатываются. Если записать
все варианты измерения в некотором порядке
(например, по времени поступления голосов в
жюри), то получится ряд данных измерения. Обычно
упорядочивание проходит определённым образом.
Запишем полученные варианты в порядке их
возрастания (точнее, неубывания). Получим
сгруппированный ряд данных:
Среднюю варианту в сгруппированном ряде
данных в случае нечётного количества чисел или
средне арифметическое, двух стоящих
посередине вариант в случае чётного количества
чисел называют медианой измерения.
В нашем случае средних варианты две, это варианты
45 и 46. Каждая из них равна 5, значит, и медиана
равна
В нашем примере ответ 1 встретился 7 раз (за
участницу №1 проголосовали 7 человек). Поэтому
говорят, что абсолютная частота (или кратность)
варианты 1 равна семи. Поэтому ( в другой
терминологии ранее приведённая таблица имеет
вид:
| Варианта | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Сумма |
| Кратность | 7 | 3 | 14 | 15 | 7 | 4 | 3 | 7 | 20 | 10 | 90 |
Таким образом, получаем таблицу распределения
данных измерения. Графа «Сумма» добавляется для
контроля: число в этой графе обязательно
равняется объёму измерения.
Заметим, что при вычислении среднего
арифметического в неявном виде уже
использовалось понятие кратности варианты.
Введём ещё понятие частоты данной варианты
– частное от деления кратности варианты
на объём измерения. Например для варианты 1
находим частоту . Частоту варианты можно выразить в процентах.
Тогда получим:
IV. Задание на уроке (работа в
компьютерном классе)
§19 № 1, 3, 5, 8, 10, 12, 17, 19
V. Задание на дом: §19, №2, 9, 14, 18, 20
VI. Подведение итогов (рефлексия)
- Основные задачи статистики.
- Виды диаграмм распределения и их построение.
- Объём измерения.
- Понятие размаха измерения.
- Мода измерения.
- Среднее арифметическое.
- Понятие медианы измерения.
- Кратность и частота варианты.
Приложение 1
3. Графическое представление информации.Распределение данных измерения рационально задавать в табличном виде. Однако нам известно, что и для функций есть табличный способ их задания. Таблицы являются связующим звеном. С их помощью осуществляется переход от распределения данных к функциям и графикам.
График распределения выборки является графическим представлением информации. Согласно табличным сведениям из примеров выше отметим точки, у которых абсциссы — это номер варианта, а ординаты — кратность. Соединяем отрезками полученные точки:
Пример:
Получили многоугольник или полигон распределения данных. Собственно, polygon и переводится как «многоугольник».
Чтобы представить большой объём информации в графическом виде, можно использовать гистограммы или столбчатые диаграммы.
Пример:

4. Числовые характеристики данных измерения.
У любого из нас имеются не только данные о рождении, но и ряд иных свойств и качеств.
Такие измерения имеют свои числовые характеристики.
Размах измерения — это разность между максимальной и минимальной вариантами.
Мода измерения — вариант, который в измерении встречался чаще других.
Медиана — число, стоящее в середине сгруппированного ряда.
Среднее значение — среднее арифметическое, или просто среднее. Для нахождения среднего значения нужно:
1) вычислить сумму всех данных измерения;
2) полученную сумму разделить на количество данных.
Рядом данных называют результаты измерения, перечисленные в порядке их получения. Каждый из результатов называется вариантой измерения.
Например, результаты написания контрольной работы по математике для класса из 20 человек можно представить в виде следующего ряда данных: 3, 4, 4, 5, 3, 4, 3, 3, 3, 5, 5, 4, 5, 4, 5, 3, 3, 3, 4, 3. Эту же информацию можно представить в
виде таблицы:
Кратность варианты — количество её повторений в ряду данных. В нашем ряду оценка «3» появилась 9 раз, поэтому её кратность равна 9.
Понятно, что таблица распределения отображает данные более наглядно и компактно.
Числовые характеристики данных
Объём измерения — количество всех данных этого измерения. Одна из наиболее важных характеристик варианты — это её частота. Частота варианты показывает долю этой
варианты в ряду распределения. Она вычисляется по формуле:
частота =кратность варианты/объём измерения
В нашем примере частота варианты «4» равна .
Это означает, что оценка 4 составляет 0,3 всех полученных оценок.
Размах измерения — разность между максимальной и минимальной вариантами этого измерения. В нашем примере максимальная варианта равна 5, минимальная — 3, значит, размах равен .
Мода измерения — варианта, которая в измерении встретилась чаще других. В приведённом выше примере чаще всех встретилась оценка 3, значит, она и будет модой этого распределения.
Медиана распределения — это центральное число в упорядоченном ряду данных, если в ряду нечётное количество чисел, или полусумма двух центральных, если в ряду чётное количество чисел.
Например, для ряда распределения 1, 2, 3, 6, 9, объём измерения которого равен 5, медианой распределения будет третье число этого ряда, то есть 3.
Для ряда распределения 7, 3, 2, 1 с объёмом измерения, равным 4, медианой будет полусумма двух центральных чисел данного ряда, то есть число, равное .
Для нахождения медианы распределения необходимо
1. Упорядочить ряд распределения по возрастанию или по убыванию: .
2. Если объём измерения нечётный, то есть , то получим следующую ситуацию:
В этом случае медианой является число .
3. Если объём измерения чётный, то есть , то имеем
В этом случае медианой является число — .
Среднее ряда (среднее арифметическое) — сумма всех чисел ряда, делённая на их количество. Если имеется таблица распределения, то можно
1) умножить каждую варианту на её кратность;
2) просуммировать полученные значения;
3) разделить результат на объём измерения. Например, для ряда распределения 2, 4, б, 8, у которого объём измерения равен 4, среднее значение равно
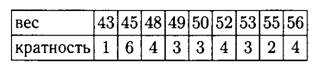
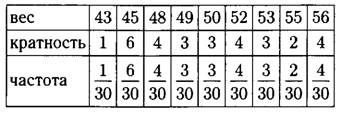
Задача 1. Даны результаты измерения веса школьников 9 класса: 55, 53, 56, 48, 45, 56, 49, 52, 53, 49, 50, 56, 45, 52, 56, 45, 45, 48, 55, 52, 43, 48, 52, 49, 50, 45, 48, 45, 50, 53.
а) Постройте таблицу распределения данных.
б) Найдите объём измерения.
в) Найдите размах ряда.
г) Найдите частоту появления каждого веса в указанном ряду.
д) Найдите медиану, моду и среднее указанного ряда.
Решение.
а) Наименьшее число в ряду — 43, оно встречается в ряду один раз, значит, его кратность равна 1. Следующее по величине — число 45, оно встречается шесть раз, значит, его кратность равна 6. Далее 48, оно встречалось 4 раза, значит, его кратность равна 4.
Продолжая аналогично, заполним таблицу:
б) Найти объём измерения можем несколькими способами.
1- й способ.
Посчитаем количество чисел в ряду, получим 30.
2- й способ.
Сложим кратности всех вариант:
Ответ: 30.
в) Наибольшее значение в ряду 56, наименьшее — 43, значит, размах равен
Ответ: 13.
г) Для каждой варианты делим её кратность на объём измерения (на 30), результаты пишем в таблицу.
д) В данном ряду 30 чисел, значит, медиана равна полусумме 15-го и 16-го чисел в упорядоченном ряду.
Как видно из такой записи чисел, от 43 до 49 — 14 чисел, значит, 15-ое и 16-ое числа равны 50, и значит, медиана равна
Мода — то значение, которое встречается чаще всех, то есть то, у которого больше кратность. Из таблицы распределения находим, что наибольшую кратность имеет число 45, значит, мода равна 45.
Для нахождения среднего необходимо найти сумму всех чисел ряда и разделить ее на количество этих чисел. Сумму можно найти просто складывая подряд все числа ряда. А можно поступить иначе: каждую варианту умножить на её кратность и сложить полученные результаты. Имеем:
.
Осталось разделить полученную сумму на количество всех чисел: .
Ответ: медиана: 50; мода: 45; среднее: 50,1.
Задача 2. Пятерых учеников попросили подсчитать, сколько времени (в минутах) они тратят на дорогу от дома до школы. Получили следующие результаты: 5,15,10,15,20.
1) На сколько среднее значение этого ряда меньше его размаха?
2) На сколько мода этого ряда больше медианы?
3) Найдите процентную частоту значения 10.
Решение.
1) Среднее ряда: , размах:
. Искомое значение равно
.
Ответ: 2.
2) Найдём медиану. Расположим числа в порядке возрастания: 5, 10, 15, 15, 20. Медианой этого набора будет третье число в упорядоченном ряду, то есть 15.
В данном ряду число 15 встретилось 2 раза, остальные — по одному разу. Мода ряда равна 15. Мода и медиана этого ряда равны, значит, ответ 0.
Ответ: 0.
3) Кратность значения 10 равна 1, объём измерения равен 5 (всего 5 чисел). Частота значения 10 равна , процентная частота равна
.
Ответ: 20.
Задача 3. Имеется 4 группы породистых котов. Для некоторого соревнования отбирают котов с длиной шерсти не менее 8 см.
Известно следующее:
1) в первой группе наибольшая длина шерсти равна 10 см;
2) во второй группе средняя длина шерсти равна 8 см;
3) в третьей группе мода длины шерсти равна 8 см;
4) в четвёртой группе медиана длины шерсти равна 9 см.
В какой из групп хотя бы половина котов гарантированно подходит по длине шерсти?
Решение.
1) Из того, что наибольшая длина шерсти равна 10 см, не следует никакой другой информации, то есть ничего не можем сказать про остальных котов этой группы.
2) Рассмотрим для примера группу котов с длиной шерсти 7 см, 7 см и 10 см. Среднее равно , но в этой группе нет половины котов, удовлетворяющих требованиям.
3) Рассмотрим для примера группу котов с шерстью длиной 8 см, 8 см, 7 см, б см, 5 см. Мода равна 8, но опять же нет половины котов, удовлетворяющих требованиям.
4) Если медиана равна 9 см, то есть половина котов с шерстью меньшей или равной длины и половина — с большей или равной длины. Значит, в этой группе найдётся половина котов с шерстью длиной не менее 8 см.
Ответ: 4.
Задача 4. По статистике автозавода из 1000 машин в среднем 20 бракованных. Сколько бракованных машин следует ожидать, если завод собирается выпустить 300 500 машин?
Решение.
Если из 1000 машин 20 бракованных, то частота появления бракованной машины равна . То есть доля бракованных машин будет равна 0,02, тогда из 300 500 машин будет
бракованных.
Ответ: 6010.