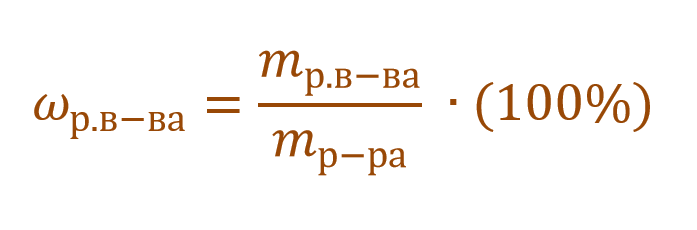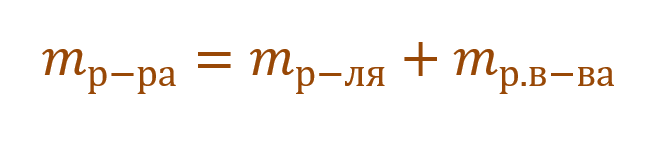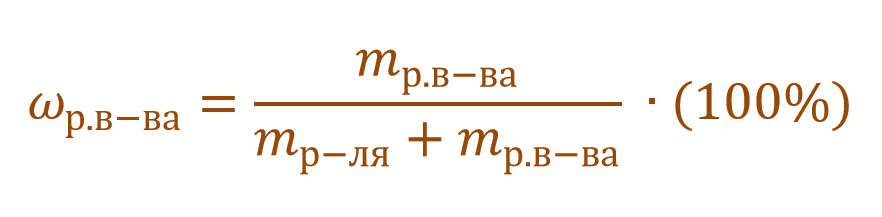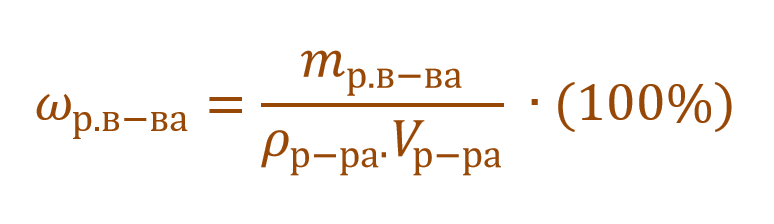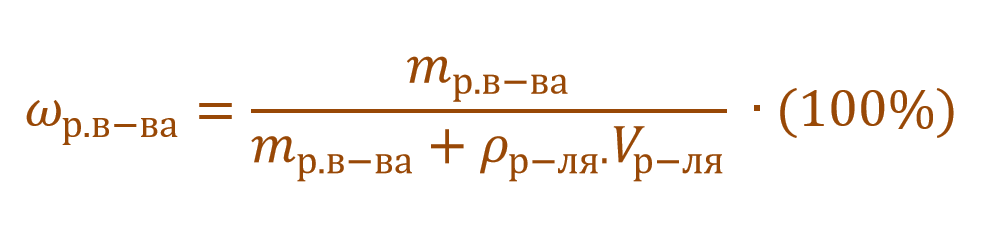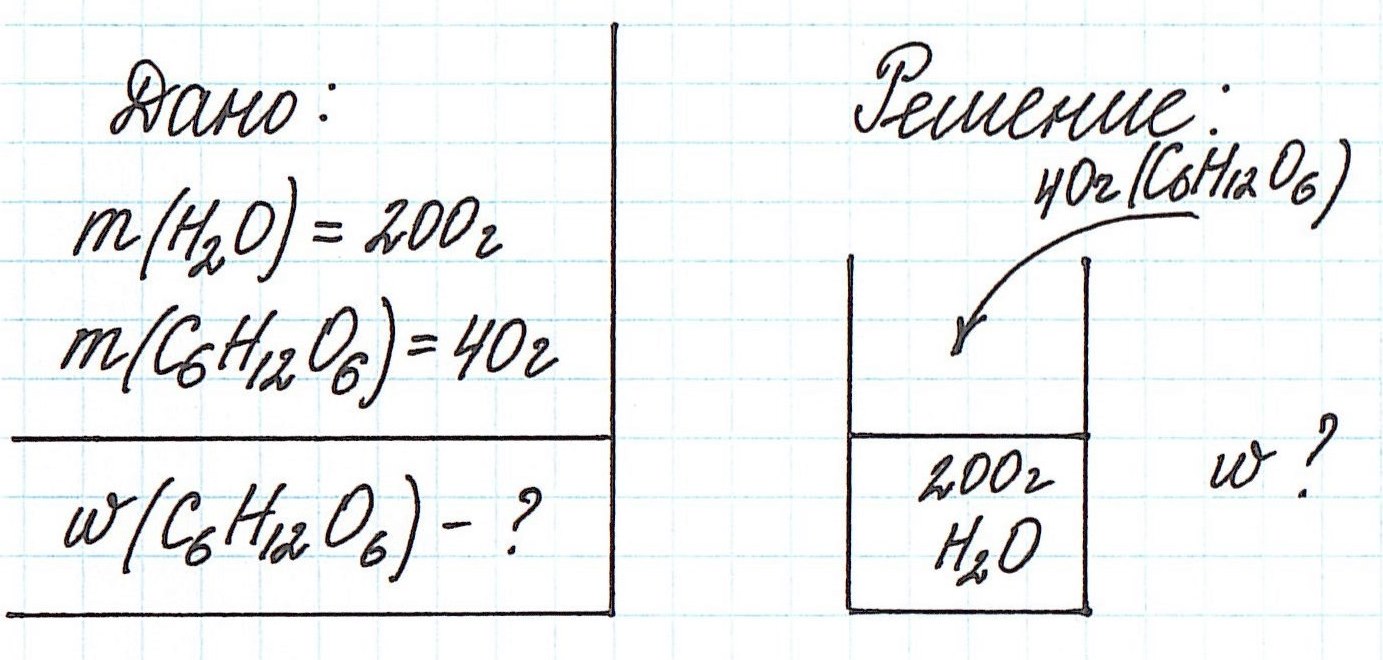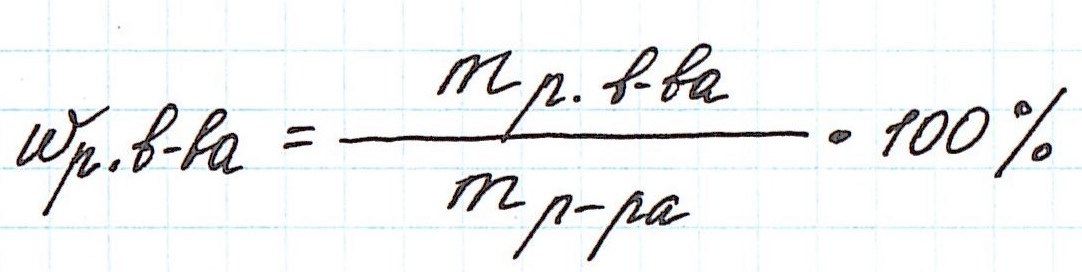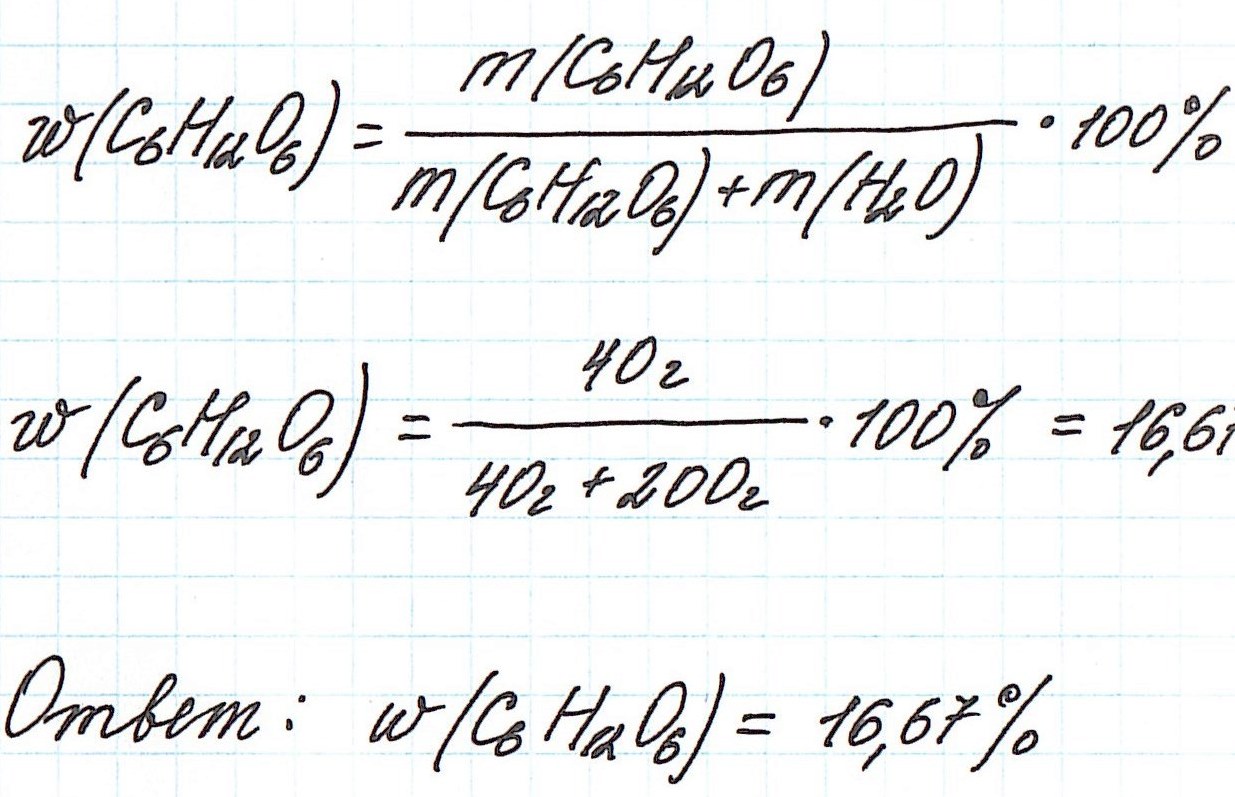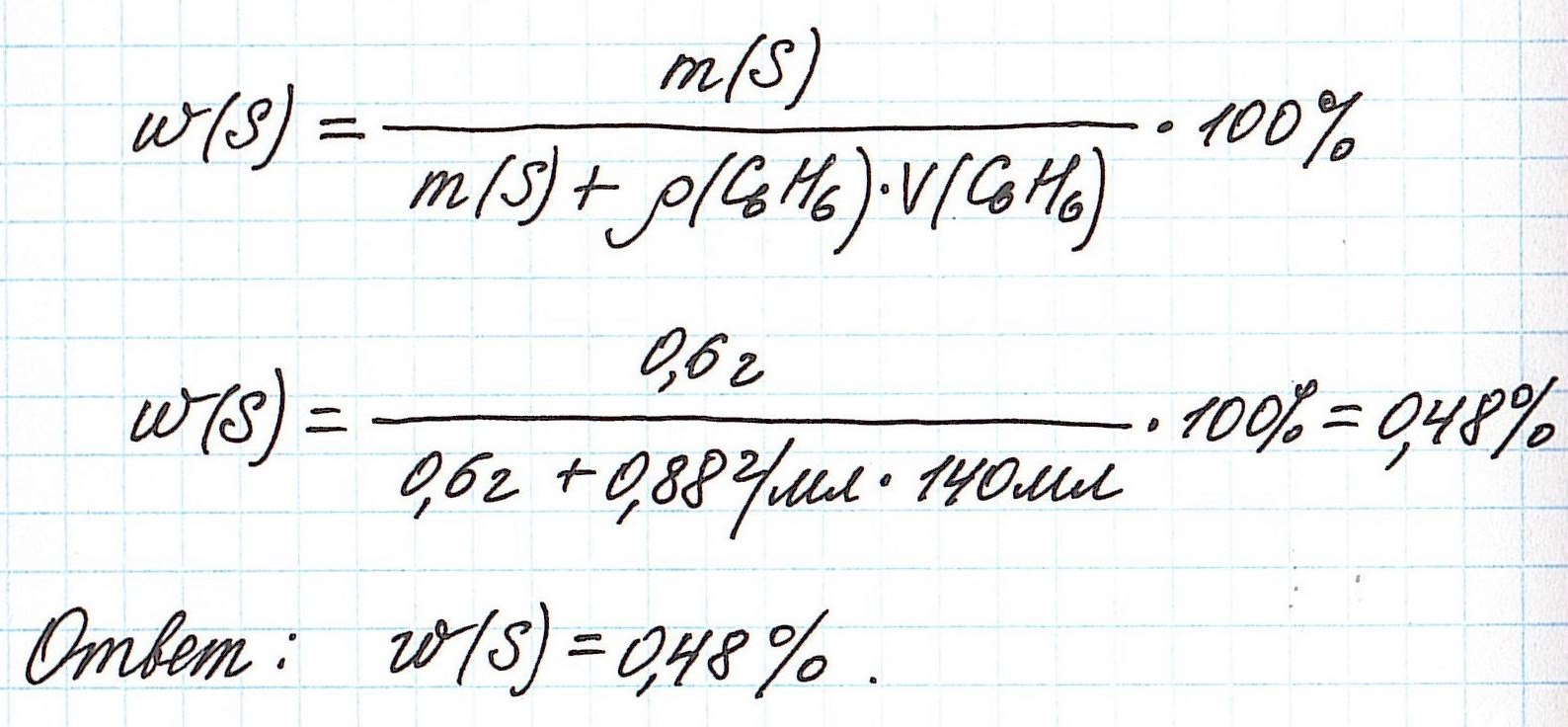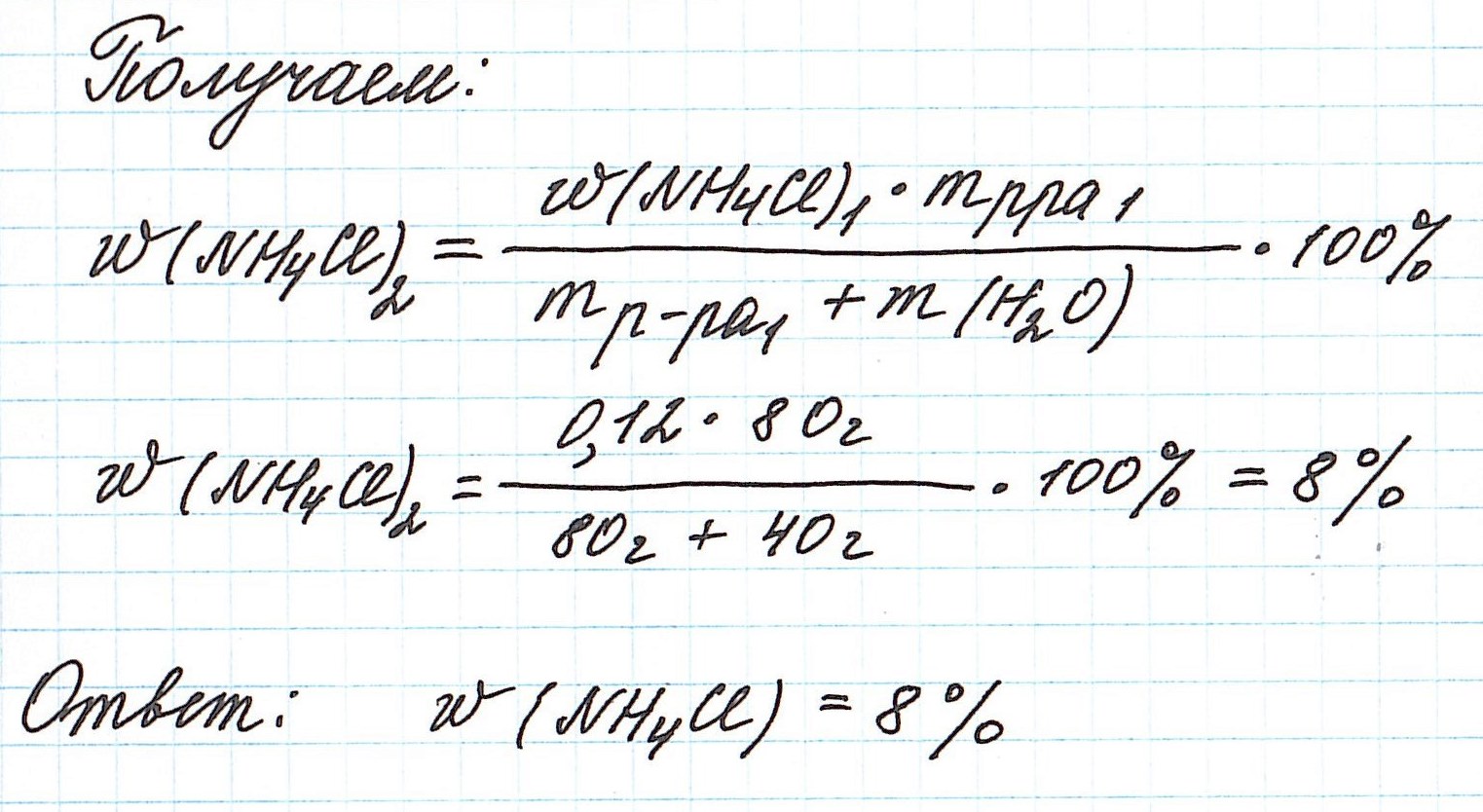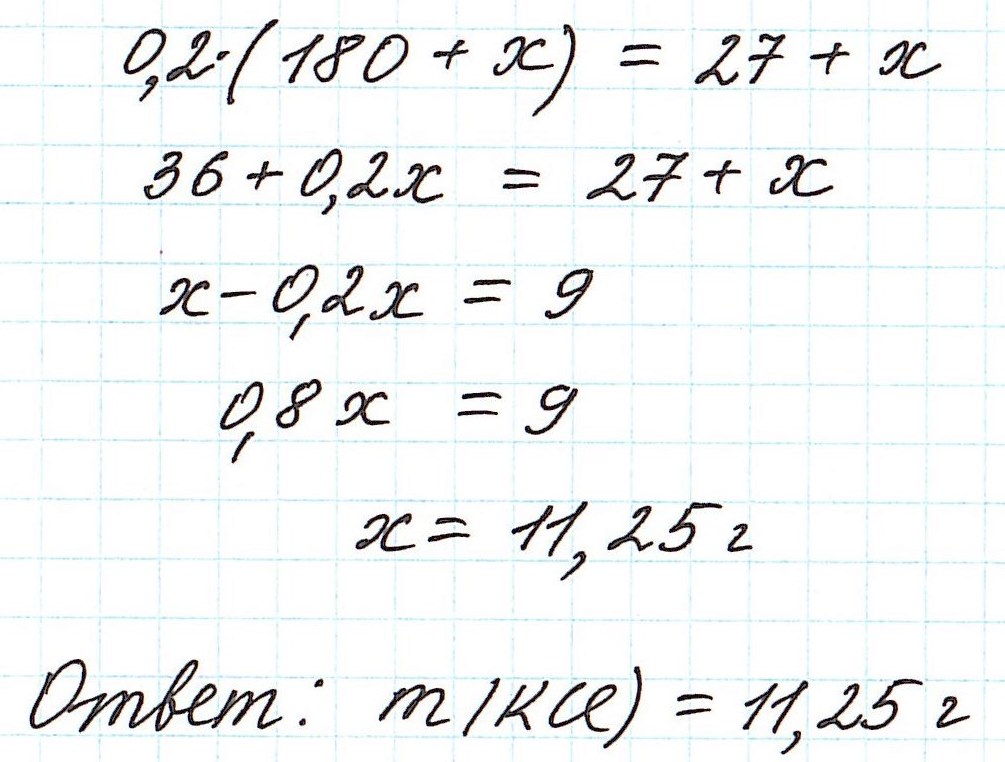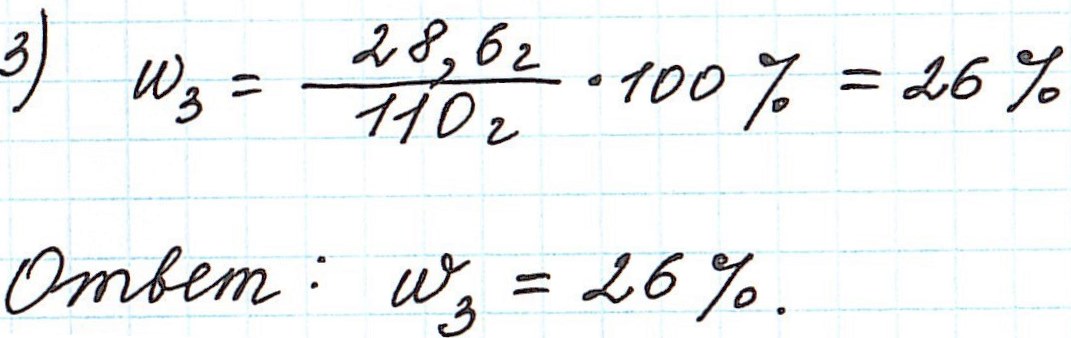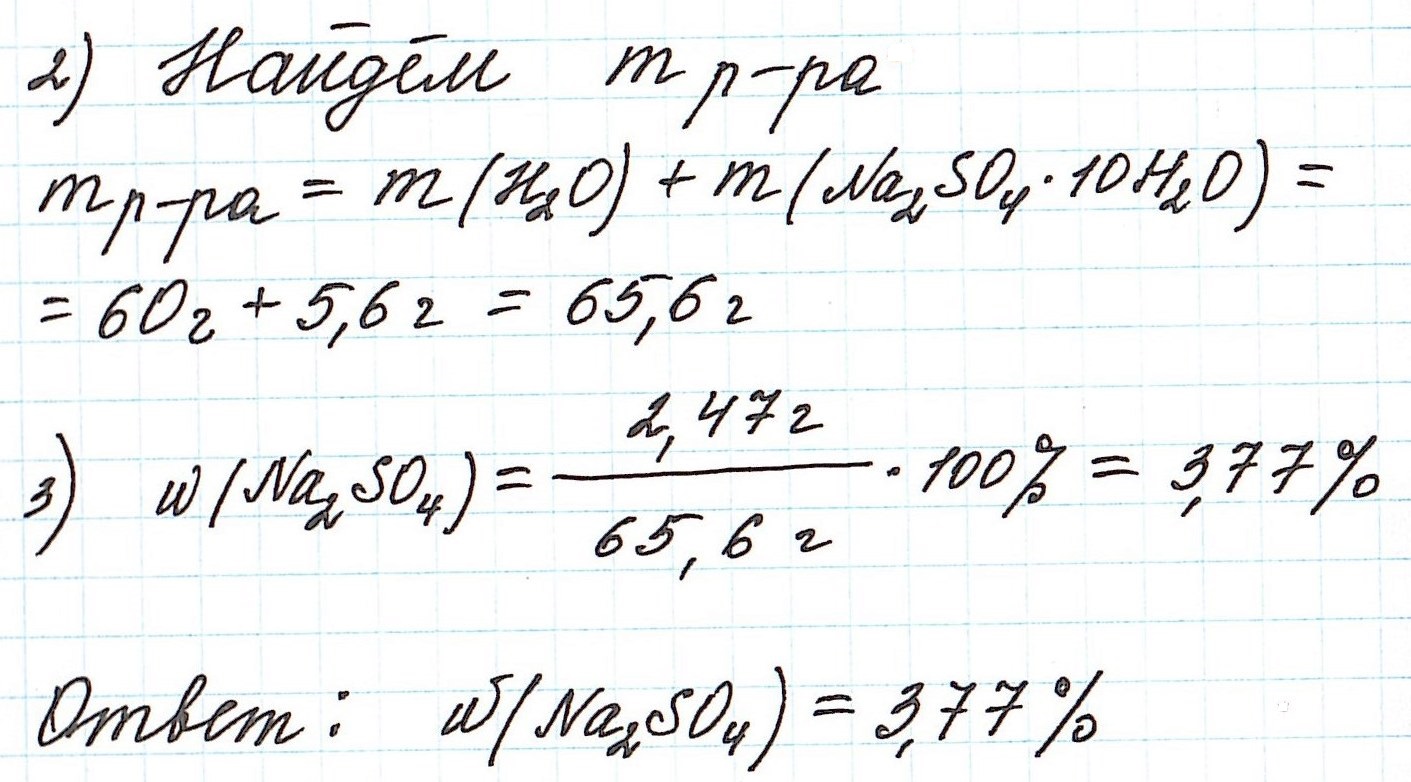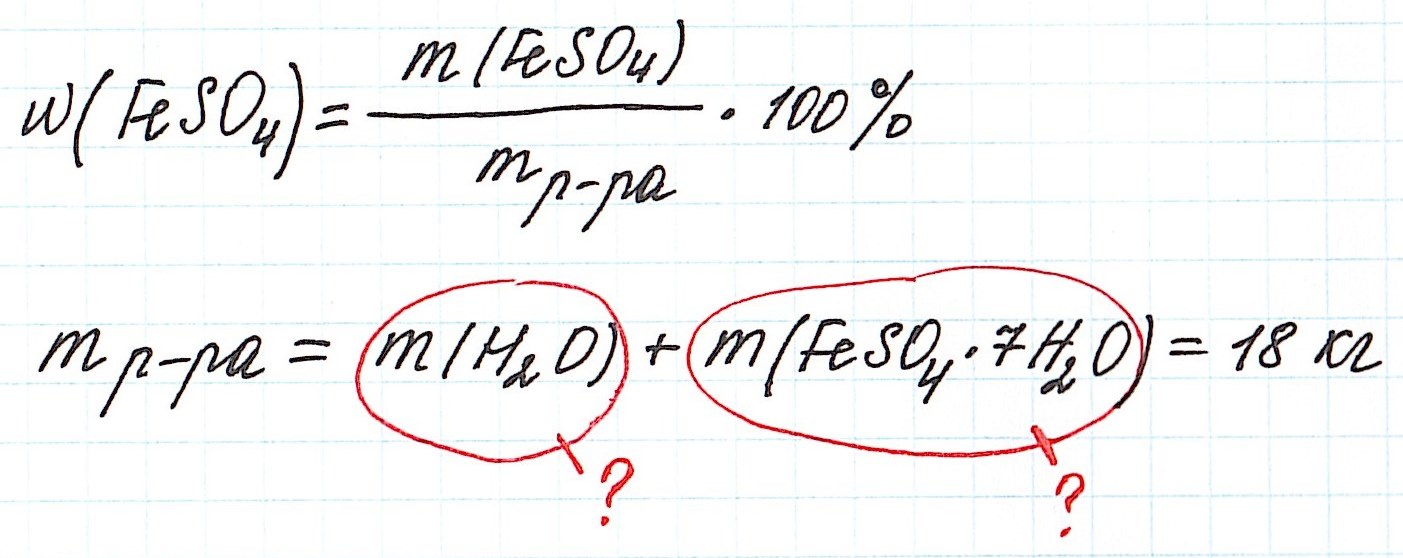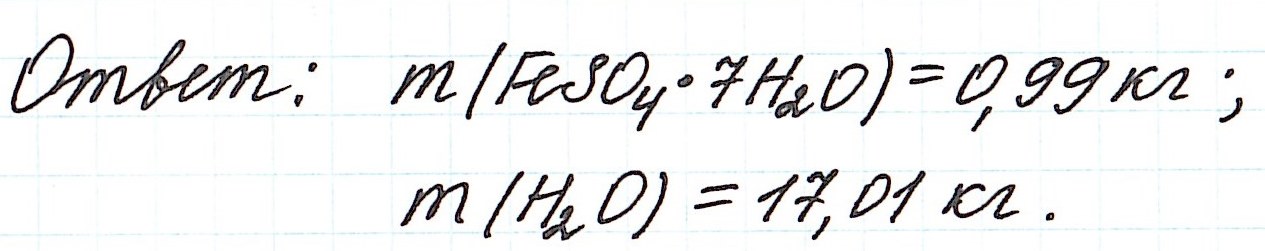Материалы из методички: Сборник задач по теоретическим основам химии для студентов заочно-дистанционного отделения / Барботина Н.Н., К.К. Власенко, Щербаков В.В. – М.: РХТУ им. Д.И. Менделеева, 2007. -155 с.
Растворы. Способы выражения концентрации растворов
Способы выражения концентрации растворов
Существуют различные способы выражения концентрации растворов.
Массовая доля ω компонента раствора определяется как отношение массы данного компонента Х, содержащегося в данной массе раствора к массе всего раствора m. Массовая доля – безразмерная величина, её выражают в долях от единицы:
ωр.в. = mр.в./mр-ра (0 < ωр.в. < 1) (1)
Массовый процент представляет собой массовую долю, умноженную на 100:
ω(Х) = m(Х)/m · 100% (0% < ω(Х) < 100%) (2)
где ω(X) – массовая доля компонента раствора X; m(X) – масса компонента раствора X; m – общая масса раствора.
Мольная доля χ компонента раствора равна отношению количества вещества данного компонента X к суммарному количеству вещества всех компонентов в растворе.
Для бинарного раствора, состоящего из растворённого вещества Х и растворителя (например, Н2О), мольная доля растворённого вещества равна:
χ(X) = n(X)/(n(X) + n(H2O)) (3)
Мольный процент представляет мольную долю, умноженную на 100:
χ(X), % = (χ(X)·100)% (4)
Объёмная доля φ компонента раствора определяется как отношение объёма данного компонента Х к общему объёму раствора V. Объёмная доля – безразмерная величина, её выражают в долях от единицы:
φ(Х) = V(Х)/V (0 < φ(Х) < 1) (5)
Объёмный процент представляет собой объёмную долю, умноженную на 100.
φ(X), % = (φ(X)·100)%
Молярность (молярная концентрация) C или Cм определяется как отношение количества растворённого вещества X, моль к объёму раствора V, л:
Cм(Х) = n(Х)/V (6)
Основной единицей молярности является моль/л или М. Пример записи молярной концентрации: Cм(H2SO4) = 0,8 моль/л или 0,8М.
Нормальность Сн определяется как отношение количества эквивалентов растворённого вещества X к объёму раствора V:
Cн(Х) = nэкв.(Х)/V (7)
Основной единицей нормальности является моль-экв/л. Пример записи нормальной концентрации: Сн(H2SO4) = 0,8 моль-экв/л или 0,8н.
Титр Т показывает, сколько граммов растворённого вещества X содержится в 1 мл или в 1 см3 раствора:
T(Х) = m(Х)/V (8)
где m(X) – масса растворённого вещества X, V – объём раствора в мл.
Моляльность раствора μ показывает количество растворённого вещества X в 1 кг растворителя:
μ(Х) = n(Х)/mр-ля (9)
где n(X) – число моль растворённого вещества X, mр-ля – масса растворителя в кг.
Мольное (массовое и объёмное) отношение – это отношение количеств (масс и объёмов соответственно) компонентов в растворе.
Необходимо иметь ввиду, что нормальность Сн всегда больше или равна молярности См. Связь между ними описывается выражением:
См = Сн · f(Х) (10)
Для получения навыков пересчёта молярности в нормальность и наоборот рассмотрим табл. 1. В этой таблице приведены значения молярности См, которые необходимо пересчитать в нормальность Сн и величины нормальности Сн, которые следует пересчитать в молярность См.
Пересчёт осуществляем по уравнению (10). При этом нормальность раствора находим по уравнению:
Сн = См/f(Х) (11)
Результаты расчётов приведены в табл. 2.
Таблица 1. К определению молярности и нормальности растворов
| Тип химического превращения | См | Сн | Сн | См |
| Реакции обмена | 0,2 M Na2SO4 | ? | 6 н FeCl3 | ? |
| 1,5 M Fe2(SO4)3 | ? | 0,1 н Ва(ОН)2 | ? | |
| Реакции окисления-восстановления | 0,05 М KMnO4
в кислой среде |
? | 0,03 М KMnO4
в нейтральной среде |
? |
Таблица 2
Значения молярности и нормальности растворов
| Тип химического превращения | См | Сн | Сн | См |
| Реакции обмена | 0,2M Ma2SO4 | 0,4н | 6н FeCl3 | 2М |
| 1,5M Fe2(SO4)3 | 9н | 0,1н Ва(ОН)2 | 0,05М | |
| Реакции окисления-восстановления | 0,05М KMnO4 в кислой среде | 0,25н | 0,03М KMnO4
в нейтральной среде |
0,01М |
Между объёмами V и нормальностями Сн реагирующих веществ существует соотношение:
V1 Сн,1 =V2 Сн,2 (12)
Примеры решения задач
Задача 1. Рассчитайте молярность, нормальность, моляльность, титр, мольную долю и мольное отношение для 40 мас.% раствора серной кислоты, если плотность этого раствора равна 1,303 г/см3.
Решение.
Масса 1 литра раствора равна М = 1000·1,303 = 1303,0 г.
Масса серной кислоты в этом растворе: m = 1303·0,4 = 521,2 г.
Молярность раствора См = 521,2/98 = 5,32 М.
Нормальность раствора Сн = 5,32/(1/2) = 10,64 н.
Титр раствора Т = 521,2/1000 = 0,5212 г/см3.
Моляльность μ = 5,32/(1,303 – 0,5212) = 6,8 моль/кг воды.
Обратите внимание на то, что в концентрированных растворах моляльность (μ) всегда больше молярности (См). В разбавленных растворах наоборот.
Масса воды в растворе: m = 1303,0 – 521,2 = 781,8 г.
Количество вещества воды: n = 781,8/18 = 43,43 моль.
Мольная доля серной кислоты: χ = 5,32/(5,32+43,43) = 0,109. Мольная доля воды равна 1– 0,109 = 0,891.
Мольное отношение равно 5,32/43,43 = 0,1225.
Задача 2. Определите объём 70 мас.% раствора серной кислоты (r = 1,611 г/см3), который потребуется для приготовления 2 л 0,1 н раствора этой кислоты.
Решение.
2 л 0,1н раствора серной кислоты содержат 0,2 моль-экв, т.е. 0,1 моль или 9,8 г.
Масса 70%-го раствора кислоты m = 9,8/0,7 = 14 г.
Объём раствора кислоты V = 14/1,611 = 8,69 мл.
Задача 3. В 5 л воды растворили 100 л аммиака (н.у.). Рассчитать массовую долю и молярную концентрацию NH3 в полученном растворе, если его плотность равна 0,992 г/см3.
Решение.
Масса 100 л аммиака (н.у.) m = 17·100/22,4 = 75,9 г.
Масса раствора m = 5000 + 75,9 = 5075,9 г.
Массовая доля NH3 равна 75,9/5075,9 = 0,0149 или 1,49 %.
Количество вещества NH3 равно 100/22,4 = 4,46 моль.
Объём раствора V = 5,0759/0,992 = 5,12 л.
Молярность раствора См = 4,46/5,1168 = 0,872 моль/л.
Задача 4. Сколько мл 0,1М раствора ортофосфорной кислоты потребуется для нейтрализации 10 мл 0,3М раствора гидроксида бария?
Решение.
Переводим молярность в нормальность:
0,1 М Н3РО4 0,3 н; 0,3 М Ва(ОН)2 0,6 н.
Используя выражение (12), получаем: V(H3P04)=10·0,6/0,3 = 20 мл.
Задача 5. Какой объем, мл 2 и 14 мас.% растворов NaCl потребуется для приготовления 150 мл 6,2 мас.% раствора хлорида натрия?
Плотности растворов NaCl:
| С, мас.% | 2 | 6 | 7 | 14 |
| ρ, г/см3 | 2,012 | 1,041 | 1,049 | 1,101 |
Решение.
Методом интерполяции рассчитываем плотность 6,2 мас.% раствора NaCl:
6,2% =6% + 0,2(7% —6% )/(7 – 6) = 1,0410 + 0,0016 = 1,0426 г/см3.
Определяем массу раствора: m = 150·1,0426 = 156,39 г.
Находим массу NaCl в этом растворе: m = 156,39·0,062 = 9,70 г.
Для расчёта объёмов 2 мас.% раствора (V1) и 14 мас.% раствора (V2) составляем два уравнения с двумя неизвестными (баланс по массе раствора и по массе хлорида натрия):
156,39 = V1 1,012 + V2 1,101 ,
9,70 = V1·1,012·0,02 + V2·1,101·0,14 .
Решение системы этих двух уравнений дает V1 =100,45 мл и V2 = 49,71 мл.
Задачи для самостоятельного решения
3.1. Рассчитайте нормальность 2 М раствора сульфата железа (III), взаимодействующего со щёлочью в водном растворе.
12 н.
3.2. Определите молярность 0,2 н раствора сульфата магния, взаимодействующего с ортофосфатом натрия в водном растворе.
0,1 M.
3.3. Рассчитайте нормальность 0,02 М раствора KMnO4, взаимодействующего с восстановителем в нейтральной среде.
0,06 н.
3.4. Определите молярность 0,1 н раствора KMnO4, взаимодействующего с восстановителем в кислой среде.
0,02 M.
3.5. Рассчитать нормальность 0,2 М раствора K2Cr2O7, взаимодействующего с восстановителем в кислой среде.
1,2 M.
3.6. 15 г CuSO4·5H2O растворили в 200 г 6 мас.% раствора CuSO4. Чему равна массовая доля сульфата меди, а также молярность, моляльность и титр полученного раствора, если его плотность составляет 1,107 г/мл?
0,1; 0,695М; 0,698 моль/кг; 0,111 г/мл.
3.7. При выпаривании 400 мл 12 мас.% раствора KNO3 (плотность раствора 1,076 г/мл) получили 2М раствор нитрата калия. Определить объём полученного раствора, его нормальную концентрацию и титр.
255 мл; 2 н; 0,203 г/мл.
3.8. В 3 л воды растворили 67,2 л хлороводорода, измеренного при нормальных условиях. Плотность полученного раствора равна 1,016 г/мл. Вычислить массовую, мольную долю растворённого вещества и мольное отношение растворённого вещества и воды в приготовленном растворе.
0,035; 0,0177; 1:55,6.
3.9. Сколько граммов NaCl надо добавить к 250 г 6 мас.% раствору NaCl, чтобы приготовить 500 мл раствора хлорида натрия, содержащего 16 мас.% NaCl? Плотность полученного раствора составляет 1,116 г/мл. Определить молярную концентрацию и титр полученного раствора.
74,28 г; 3,05 М; 0,179 г/мл.
3.10. Определить массу воды, в которой следует растворить 26 г ВaCl2·2H2O для получения 0,55М раствора ВaCl2 (плотность раствора 1,092 г/мл). Вычислить титр и моляльность полученного раствора.
192,4 г; 0,111 г/мл; 0,56 моль/кг.
В ПОМОЩЬ МОЛОДОМУ
УЧИТЕЛЮ
Расчеты концентрации
растворенных веществ
в растворах
Решение задач на разбавление растворов особой
сложности не представляет, однако требует
внимательности и некоторого напряжения. Тем не
менее можно упростить решение этих задач,
используя закон разбавления, которым пользуются
в аналитической химии при титровании растворов.
Во всех задачниках по химии показаны решения
задач, представленных как образец решения, и во
всех решениях используется закон разбавления,
принцип которого состоит в том, что количество
растворенного вещества и масса m в исходном и разбавленном
растворах остаются неизменными. Когда мы решаем
задачу, то это условие держим в уме, а расчет
записываем по частям и постепенно, шаг за шагом,
приближаемся к конечному результату.
Рассмотрим проблему решения задач на
разбавление, исходя из следующих соображений.
• Количество растворенного вещества :
= c•V,
где c – молярная концентрация
растворенного вещества в моль/л, V – объем
раствора в л.
• Масса растворенного вещества m(р.в.):
m(р. в.) = m(р-ра)•,
где m(р-ра) – масса раствора в г, – массовая доля
растворенного вещества.
Обозначим в исходном (или неразбавленном)
растворе величины c, V, m(р-ра), через с1, V1,
m1(р-ра), 1,
а в разбавленном растворе – через с2, V2,
m2(р-ра), 2.
Составим уравнения разбавления растворов. Левые
части уравнений отведем для исходных
(неразбавленных) растворов, а правые части – для
разбавленных растворов.
Неизменность количества растворенного вещества
при разбавлении будет иметь вид:
Сохранение массы m(р. в.):
Количество растворенного вещества связано с его массой m
(р. в.) cоотношением:
= m(р.
в.)/M(р. в.),
где M(р. в.) – молярная масса растворенного
вещества в г/моль.
Уравнения разбавления (1) и (2) связаны между собой
следующим образом:
с1•V1 = m2(р-ра)•2/M(р. в.),
m1(р-ра)•1 = с2•V2•M(р.
в.).
Если в задаче известен объем растворенного
газа V(газа), то его количество вещества связано с объемом
газа (н.у.) отношением:
= V(газа)/22,4.
Уравнения разбавления примут соответственно
вид:
V(газа)/22,4 = с2•V2,
V(газа)/22,4 = m2(р-ра)•2/M(газа).
Если в задаче известны масса вещества или
количество вещества, взятого для приготовления
раствора, то в левой части уравнения разбавления
ставится m(р. в.) или , в зависимости от условия задачи.
Если по условию задачи требуется объединить
растворы разной концентрации одного и того же
вещества, то в левой части уравнения массы
растворенных веществ суммируются.
Довольно часто в задачах используется плотность
раствора (г/мл). Но
поскольку молярная концентрация с
измеряется в моль/л, то и плотность следует
выражать в г/л, а объем V – в л.
Приведем примеры решения «образцовых» задач.
Задача 1. Какой
объем 1М раствора серной кислоты надо взять,
чтобы получить 0,5 л 0,1М H2SO4?
Дано:
с1 = 1 моль/л,
V2 = 0,5 л,
с2 = 0,1 моль/л.
Найти:
V1 = ?
Решение
V1•с1 = V2•с2,
V1•1 = 0,5•0,1; V1 = 0,05 л,
или 50 мл.
Ответ. V1 = 50 мл.
Задача 2 ([1],
№ 4.23). Определите массу раствора с массовой
долей (СuSО4)
10% и массу воды, которые потребуются для
приготовления раствора массой 500 г с массовой
долей
(СuSО4) 2%.
Дано:
1 = 0,1,
m2(р-ра) = 500 г,
2 = 0,02.
Найти:
m1(р-ра) = ?
m(H2O) = ?
Решение
m1(р-ра)•1 = m2(р-ра)•
2,
m1(р-ра)•0,1 = 500•0,02.
Отсюда m1(р-ра) = 100 г.
Найдем массу добавляемой воды:
m(H2O) = m2(р-ра) – m1(р-ра),
m(H2O) = 500 – 100 = 400 г.
Ответ. m1(р-ра) = 100 г, m(H2O)
= 400 г.
Задача 3 ([1],
№ 4.37). Какой объем раствора с массовой долей
серной кислоты 9,3%
( = 1,05 г/мл)
потребуется для приготовления 0,35М раствора H2SO4
объемом 40 мл?
Дано:
1 = 0,093,
1 = 1050 г/л,
с2 = 0,35 моль/л,
V2 = 0,04 л,
М(H2SO4) = 98 г/моль.
Найти:
V1 = ?
Решение
m1(р-ра)•1 = V2•с2•М(H2SO4),
V1•1•
1
= V2• с2•М(H2SO4).
Подставляем значения известных величин:
V1•1050•0,093 = 0,04•0,35•98.
Отсюда V1 = 0,01405 л, или 14,05 мл.
Ответ. V1 = 14,05 мл.
Задача 4 [2]. Какой
объем хлороводорода (н.у.) и воды потребуется,
чтобы приготовить 1 л раствора ( = 1,05 г/см3), в котором
содержание хлороводорода в массовых долях равно
0,1
(или 10%)?
Дано:
V(р-ра) = 1 л,
(р-ра) = 1050 г/л,
= 0,1,
М(HCl) = 36,5 г/моль.
Найти:
V(HCl) = ?
m(H2O) = ?
Решение
V(HCl)/22,4 = m(р-ра)•/М(HCl),
V(HCl)/22,4 = V(р-ра)•(р-ра)•
/М(HCl),
V(HCl)/22,4 = 1•1050•0,1/36,5.
Отсюда V(HCl) = 64,44 л.
Найдем массу добавляемой воды:
m(H2O) = m(р-ра) – m(HСl),
m(H2O) = V(р-ра)•(р-ра) – V(HCl)/22,4• М(HCl),
m(H2O) = 1•1050 – 64,44/22,4•36,5 = 945 г.
Ответ. 64,44 л HCl и 945 г воды.
Задача 5 ([1],
№ 4.34). Определите молярную концентрацию
раствора с массовой долей гидроксида натрия 0,2 и
плотностью 1,22 г/мл.
Дано:
= 0,2,
= 1220 г/л,
М(NaOH) = 40 г/моль.
Найти:
c = ?
Решение
m(р-ра)• = с•V•М(NaOH),
m(р-ра)• = с•m(р-ра)•М(NaOH)/
.
Разделим обе части уравнения на m(р-ра) и
подставим численные значения величин.
0,2 = c•40/1220.
Отсюда c = 6,1 моль/л.
Ответ. c = 6,1 моль/л.
Задача 6 ([1],
№ 4.30). Определите молярную концентрацию
раствора, полученного при растворении сульфата
натрия массой 42,6 г в воде массой 300 г, если
плотность полученного раствора равна 1,12 г/мл.
Дано:
m(Na2SO4) = 42,6 г,
m(H2O) = 300 г,
= 1120 г/л,
M(Na2SO4) = 142 г/моль.
Найти:
c = ?
Решение
m(Na2SO4) = с•V•М(Na2SO4).
Подставляя численные значения, получим:
42,6 = с•(42,6 + 300)/1120•142.
Отсюда с = 0,98 моль/л.
Ответ. с = 0,98 моль/л.
Задача 7 ([1],
№ 4.19). В лаборатории имеются растворы с
массовой долей хлорида натрия 10% и 20%. Какую массу
каждого раствора надо взять для получения
раствора с массовой долей соли 12% и массой 300 г?
Дано:
1 = 0,1,
2 = 0,2,
3 = 0,12,
m3(р-ра) = 300 г.
Найти:
m1(р-ра) = ?
m2(р-ра) = ?
Решение
m1(р-ра)•1 + m2(р-ра)•
2 = m3(р-ра)•
3,
m1(р-ра)•0,1 + m2(р-ра)•0,2
= 300•0,12.
Поскольку m1(р-ра) + m2(р-ра) = 300
г, то получаем систему из двух уравнений с двумя
неизвестными. Решая совместно два уравнения,
находим:
m1(р-ра) = 240 г, m2(р-ра) =
60 г.
Ответ. m1(р-ра) = 240 г, m2(р-ра)
= 60 г.
Задача 8 ([1],
№ 4.48). В воде массой 100 г при температуре 0 °С
растворяется фторид натрия массой 4,1 г, а при
температуре 40 °С – массой 4,5 г. Какая масса
фторида натрия выпадет в осадок при охлаждении
насыщенного при температуре 40 °С раствора NaF
массой 500 г до температуры 0 °С?
Дано:
m1(NaF) = 4,1 г,
m2(NaF) = 4,5 г,
m2(р-ра) = 500 г,
– массовая доля
NaF,
(1 – ) – массовая
доля воды.
Найти:
m(NaF) = ?
Решение
m(NaF) = m2(р-ра) – m1(р-ра).
Поскольку m2(Н2О) (40 °С) = m1(Н2О)
(0 °С), то можно записать:
m2(р-ра)•(1 – 2) = m1(р-ра)•(1 –
1).
Подставляем значения:
500•(1 – 4,5/(4,5 + 100)) = m1(р-ра)•(1 –
4,1/(4,1 + 100)).
Отсюда m1(р-ра) = 104,1/104,5•500 = 498,09 г,
m(NaF) = 500 – 498,09 = 1,91 г.
Ответ. m(NaF) = 1,91 г.
ЛИТЕРАТУРА
1. Хомченко Г.П., Хомченко И.Г. Задачи по химии
для поступающих в вузы. М.: Новая волна, 2002.
2. Фельдман Ф.Г., Рудзитис Г.Е. Химия-9. М.:
Просвещение, 1990, с. 166.
В.И.МАРТЫНОВ,
учитель химии
(пос. Архипо-Осиповка, Краснодарский край)
Формула концентрации раствора. Их множество. И каждая соответствует тому или иному способу выражения концентрации. А в химии их применяются достаточно: массовая доля растворенного вещества, молярная, нормальная, моляльная, титр и др.
Зачем так много? Ответ на этот вопрос очень прост. Каждый вид концентрации удобен в том или ином случае, когда применение другого вида концентрации неуместно.
Например, при исследовании содержания массы вещества в очень небольшом объеме раствора удобно пользоваться титром. А в каких-то технологиях вообще концентрация заменяется другими количественными характеристиками раствора. Так, в технологии посола рыбы для расчета необходимой концентрации тузлука (раствора поваренной соли) используют не его процентную концентрацию, а плотность.
Содержание:
1. Концентрация – что это такое
2. Формула концентрации раствора: основные виды
3. Массовая доля растворенного вещества и примеры ее вычисления
- разбавление раствора водой
- концентрирование раствора путем упаривания
- концентрирование раствора путем добавления растворенного вещества
- смешивание двух растворов
- применение кристаллогидратов для приготовления раствора (задачи на кристаллогидраты)
4. Правило «креста» в химии растворов как метод решения задач на процентную концентрацию растворов
Концентрация – что это такое
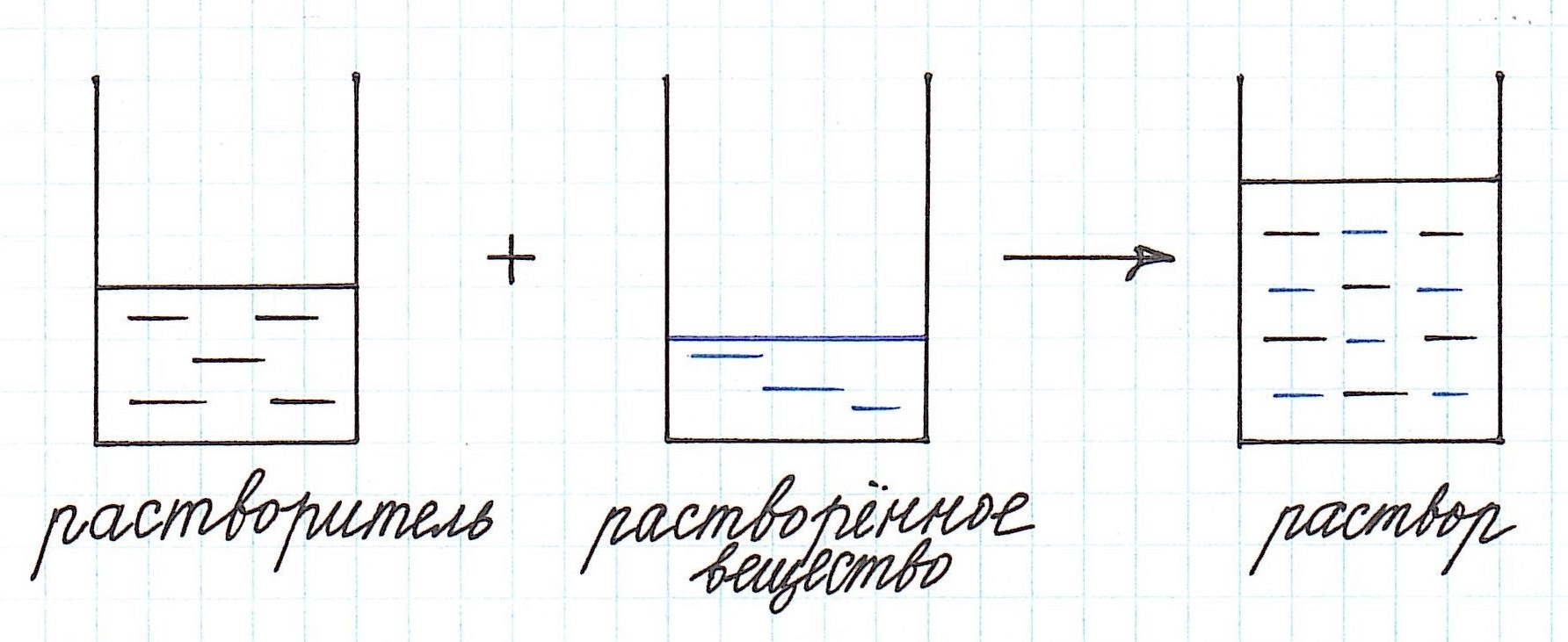
Любой раствор имеет различные характеристики: качественные и количественные. Одной из важнейших количественных характеристик является концентрация раствора.
Концентрация раствора – это количество растворенного вещества, содержащееся в определенном количестве раствора.
Как видно из приведенного определения, основными компонентами раствора являются:
— растворитель;
— растворенное вещество.
Растворенного вещества в растворе всегда меньше, а растворителя больше.
И вот именно с вычислением количественного содержания растворенного вещества чаще всего и связаны все расчеты, основанные на применении формулы концентрации раствора.
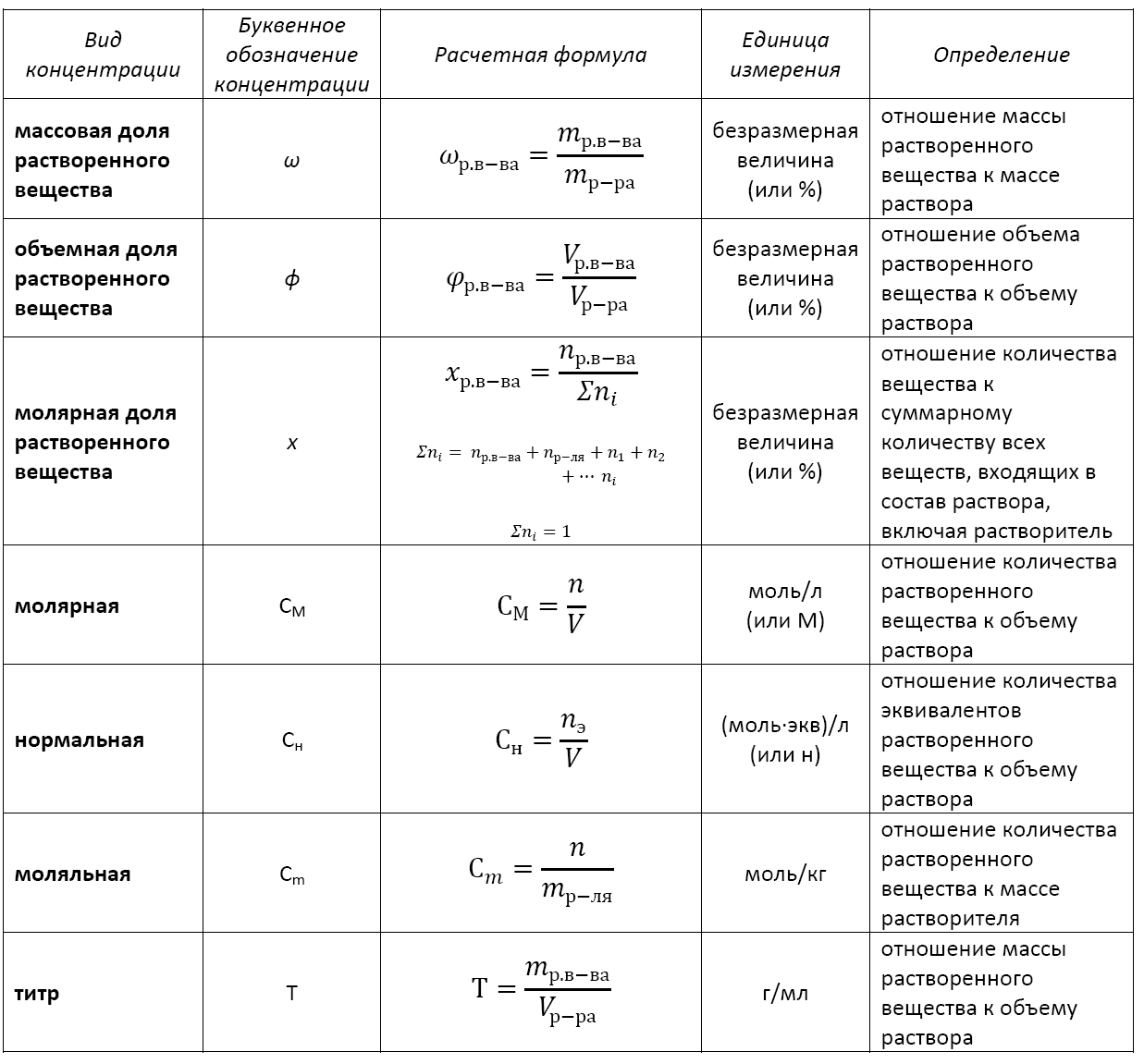
Существует несколько видов концентрации раствора:
— массовая доля растворенного вещества;
— объемная доля растворенного вещества;
— молярная доля растворенного вещества;
— молярная (или молярность);
— моляльная (или моляльность);
— нормальная (или эквивалентная);
— титр.
Формула концентрации раствора: основные виды
Применение того или иного вида концентрации уместно в каждом конкретном случае. Не существует какой-то универсальной концентрации или универсальной формулы концентрации раствора.
Кстати, с помощью математических преобразований можно перейти от одной концентрации к другой или найти взаимосвязь между разными их видами.
Основные расчетные формулы концентрации раствора приведены в таблице:
Массовая доля растворенного вещества и примеры ее вычисления
Массовая доля растворенного вещества – это отношение массы растворенного вещества к массе раствора.
Ее расчетная формула выглядит так:
где ωр.в-ва – массовая доля растворенного вещества, mр.в-ва – масса растворенного вещества, mр-ра – масса раствора.
ωр.в-ва представляет собой долю или от единицы или от 100%. Так, например, имеется двухпроцентный раствор NaCl. Его концентрация будет записана в первом случае ω(NaCl) = 0,02, а во втором – ω(NaCl) = 2%. Форма записи основной сути не меняет. Можно записывать и так, и так.
Что же означает выражение ω(NaCl) = 0,02 или ω(NaCl) = 2%? Буквально следующее: в 100 г водного раствора поваренной соли содержится 2 г этой соли и 98 г воды.
Необходимо помнить, что раствор состоит из растворителя и растворенного вещества. Поэтому масса раствора будет состоять из массы растворителя и массы растворенного вещества:
Тогда основную расчетную формулу для массовой доли растворенного вещества можно преобразовать:
Очень часто в расчетах с процентной концентрацией используются плотность и объем раствора:
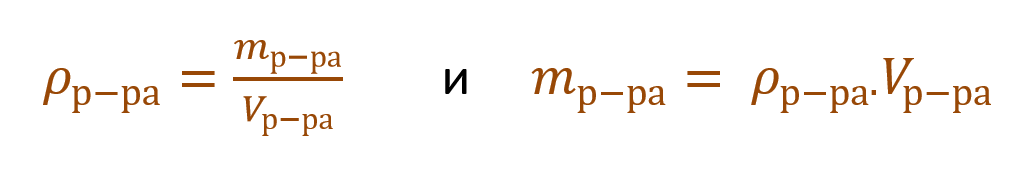
В других ситуациях могут использоваться объем и плотность не раствора, а растворителя. Тогда основная формула для расчета концентрации будет выглядеть так:
На практике бывает необходимо не только приготовить раствор с какой-либо определенной концентрацией, но и увеличить, либо уменьшить ее значение. Это достигается различными приемами:
— упариванием раствора;
— добавлением растворенного вещества;
— добавлением к раствору растворителя (например, воды).
Кроме того, приходится часто смешивать друг с другом растворы разных концентраций.
Разберем все возможные случаи.
Мы рекомендуем задачи, в которых речь идет о растворах, решать с использованием схематических рисунков. Это очень наглядно, особенно, когда речь идет о смешивании растворов.
Начнем с самого простого: вычислим концентрацию раствора.
Пример 1. В 200 г воды растворили 40 г глюкозы. Вычислите массовую долю глюкозы в полученном растворе.
Обратите внимание, что речи о каком-либо химическом взаимодействии не идет! Поэтому записывать уравнения реакций не требуется!
Запишем общую формулу для расчета массовой доли растворенного вещества:
В данной задаче глюкоза (C6H12O6) – растворенное вещество, а вода (H2O) – растворитель. Масса раствора будет складываться из массы глюкозы и массы воды:
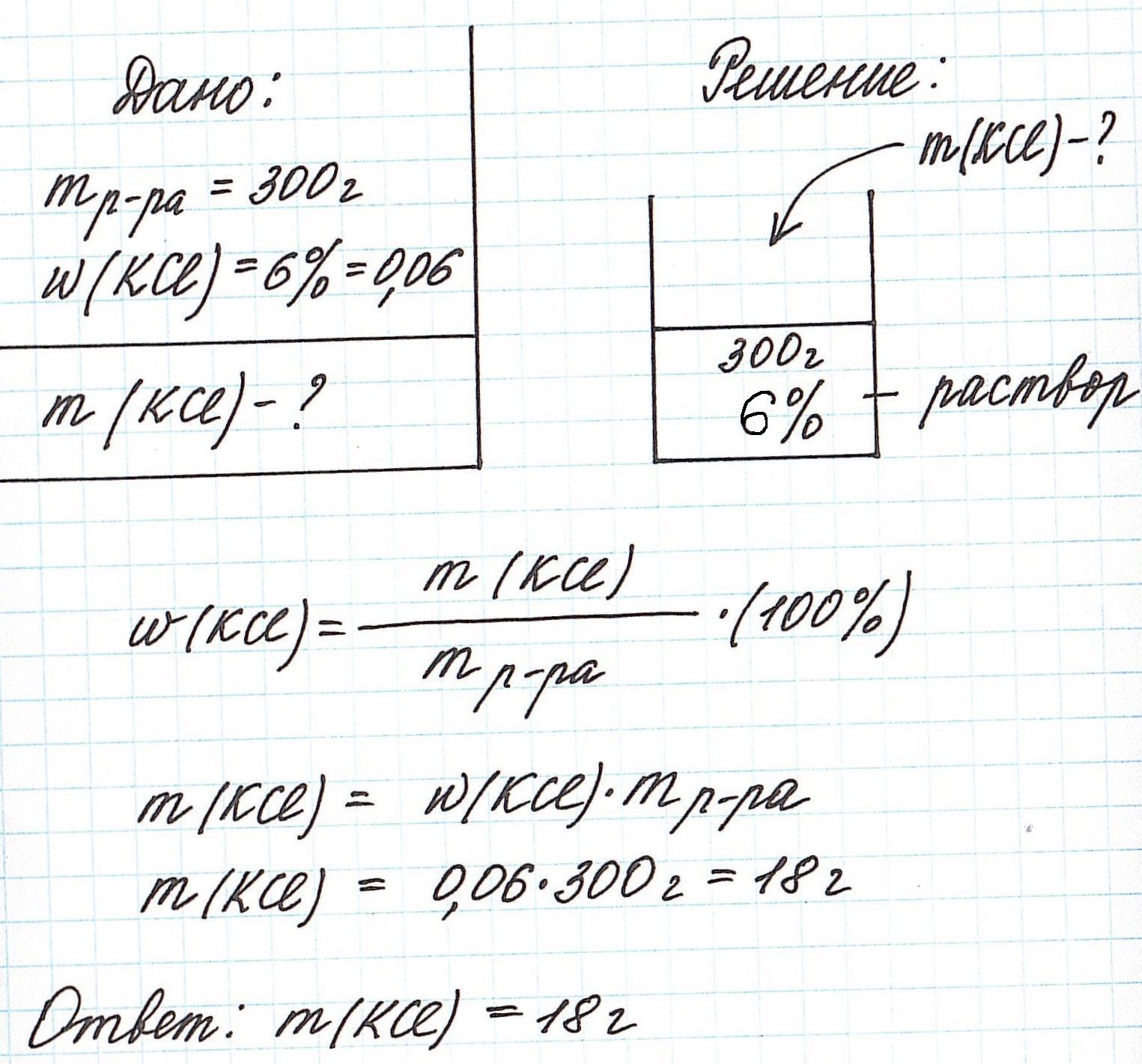
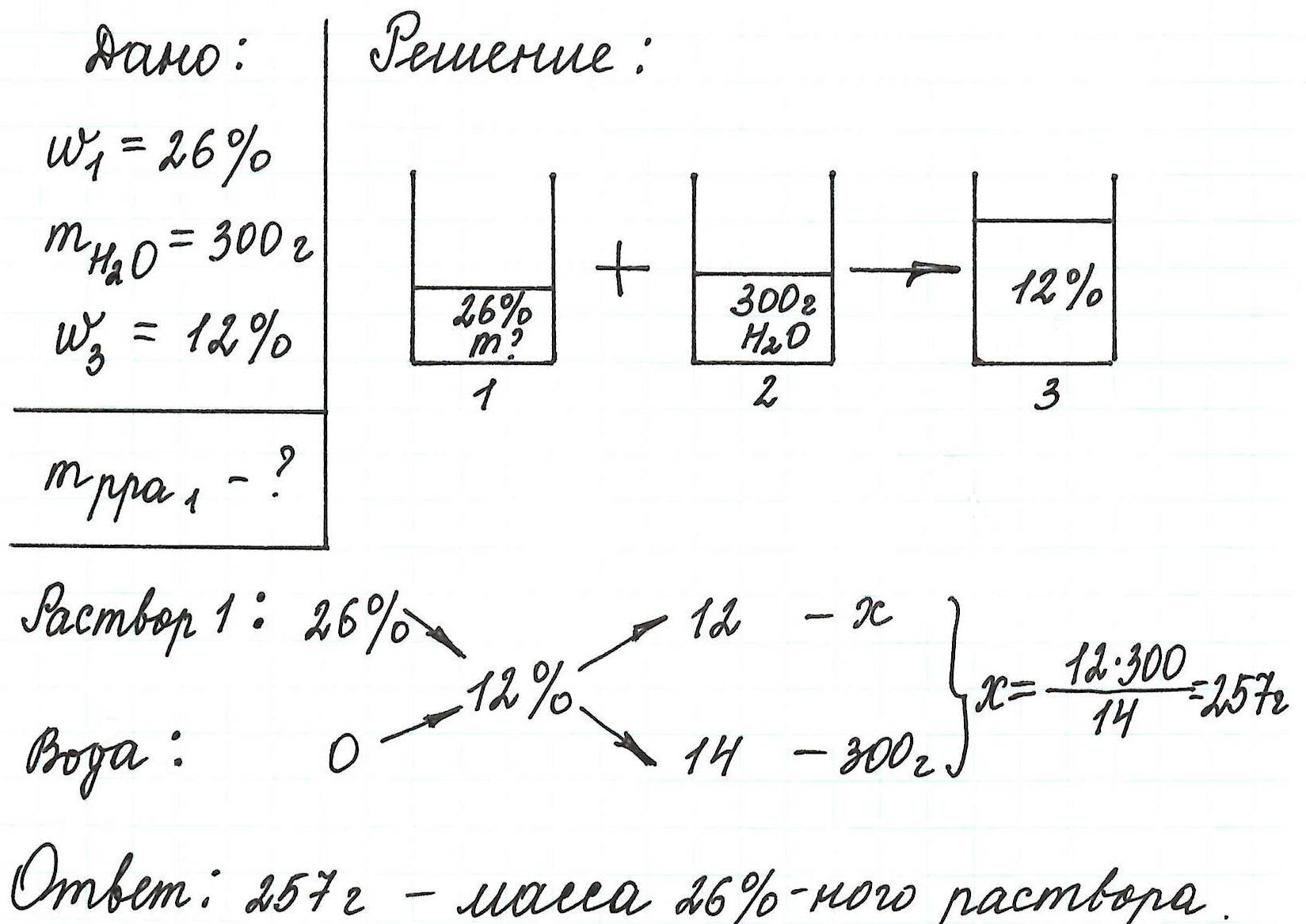
Пример 2. Рассчитайте, сколько потребуется хлорида калия, чтобы приготовить 300 г раствора с массовой долей соли 6%.
Обратите внимание, для того, чтобы расчеты были менее громоздкими, будем использовать выражение концентрации не в %, а в долях от единицы.
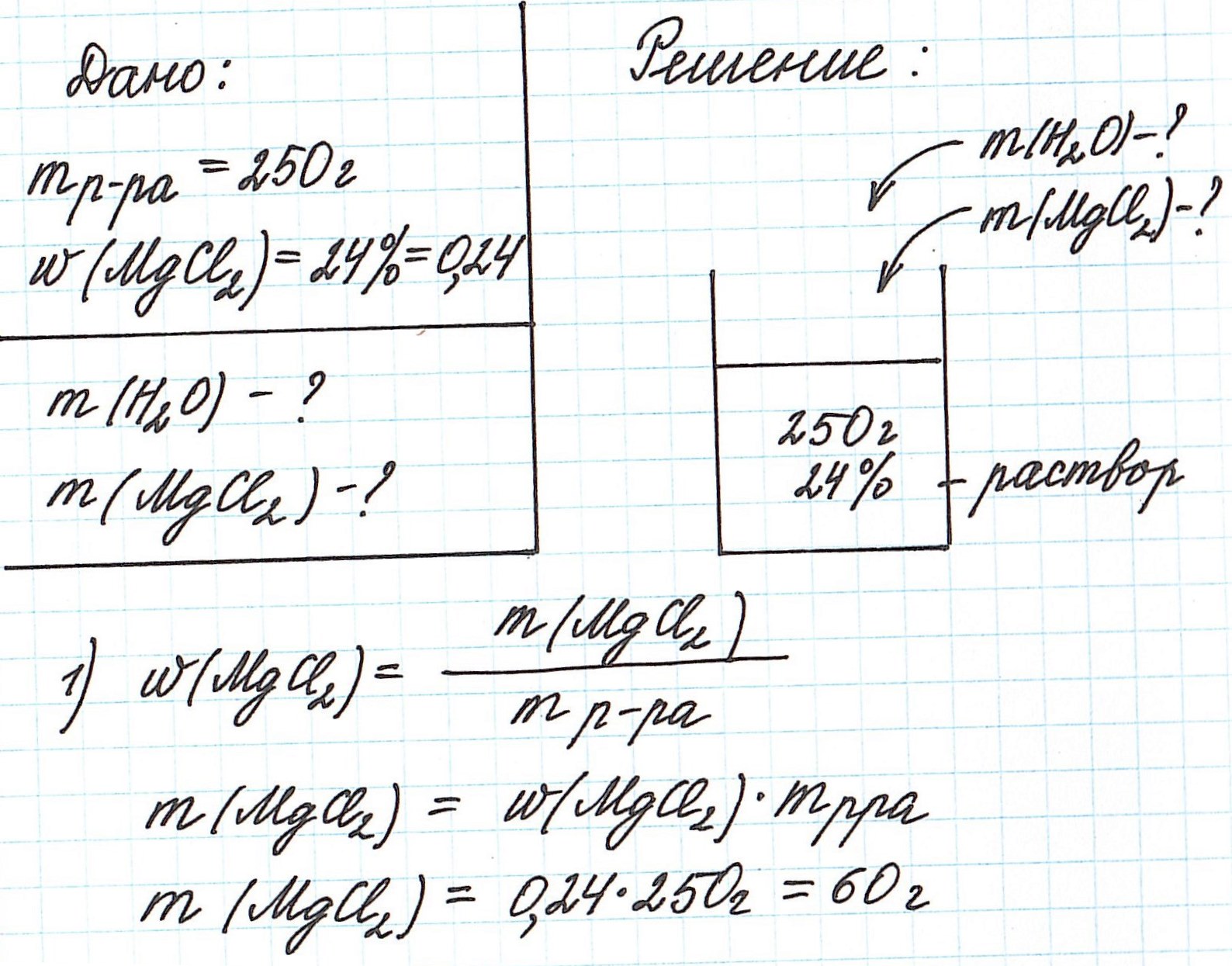
Пример 3. Необходимо приготовить 250 г раствора с массовой долей хлорида магния 24%. Рассчитайте массу требуемых воды и соли.
Так как раствор готовится из хлорида магния и воды, то и масса раствора равна сумме масс хлорида магния и воды:
Рассмотрим задачу, в которой в качестве растворителя выступает не вода, а другое вещество.
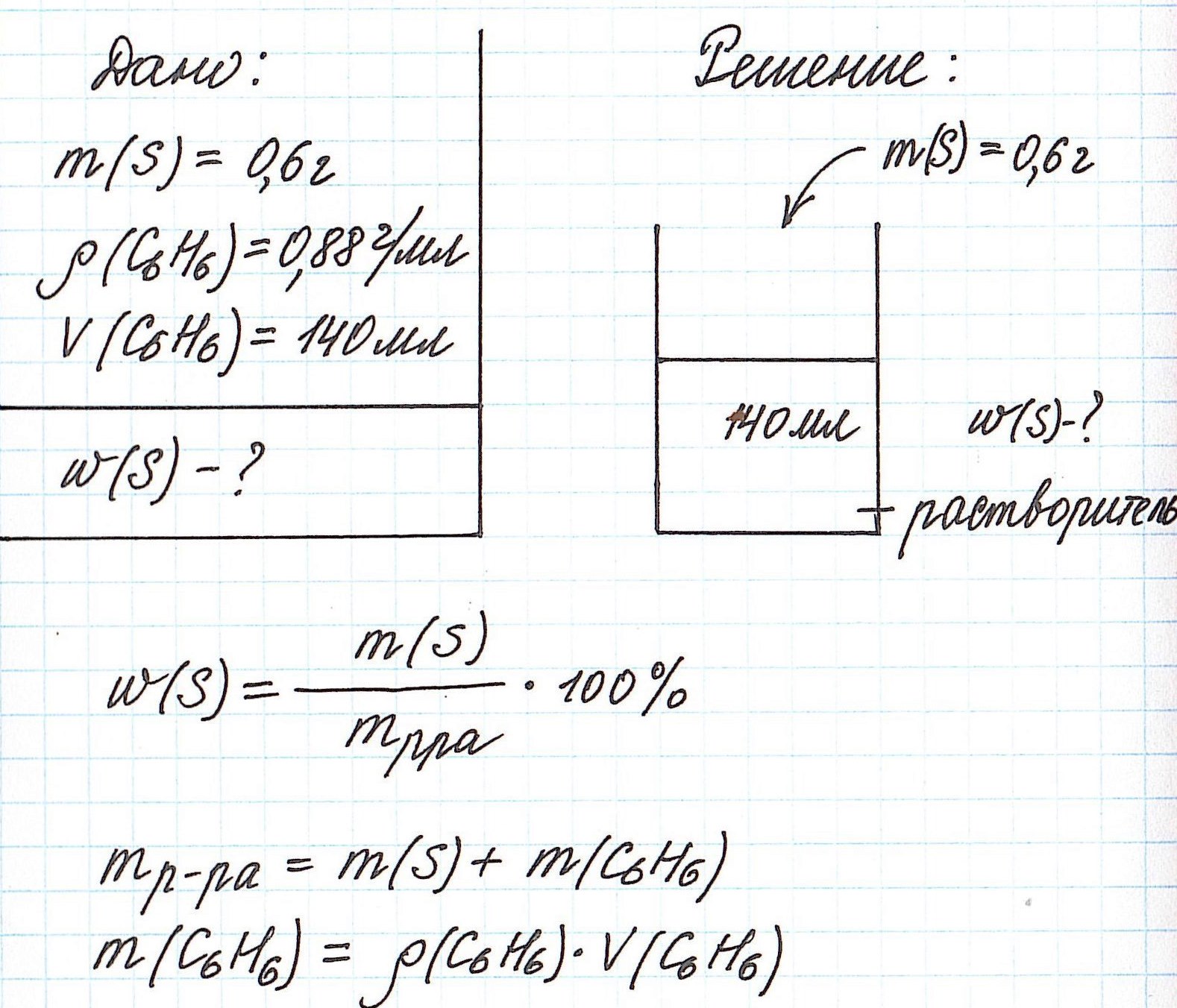
Пример 4. В органическом растворителе бензоле объемом 140 мл растворили серу массой 0,6 г. Вычислите массовую долю серы в полученном растворе, если плотность бензола составляет 0,88 г/мл.
Обратите внимание, что здесь:
— масса раствора не известна;
— масса растворителя (бензола) не известна;
— известны объем и плотность растворителя (бензола), что позволяет нам найти его массу;
— масса раствора состоит из массы растворителя (бензол) и массы растворенного вещества (сера).
Объединим все расчетные формулы в одну и подставим в нее имеющиеся численные значения:
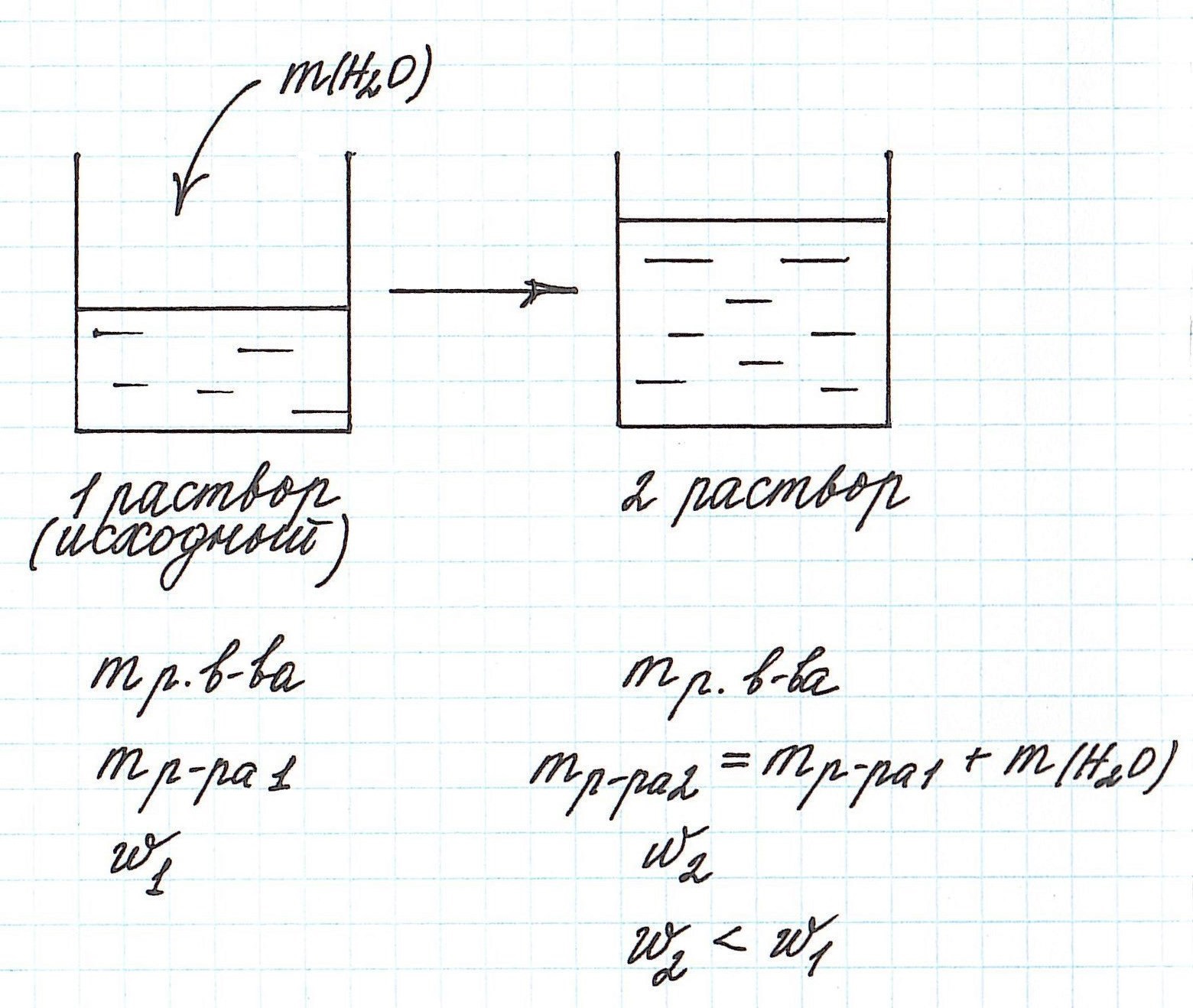
Вычисление массовой доли растворенного вещества при разбавлении раствора водой
Разбавление раствора водой приводит к уменьшению его концентрации.
Запомним, что в таких случаях:
— увеличивается масса раствора;
— увеличивается масса растворителя;
— масса растворенного вещества остается постоянной.
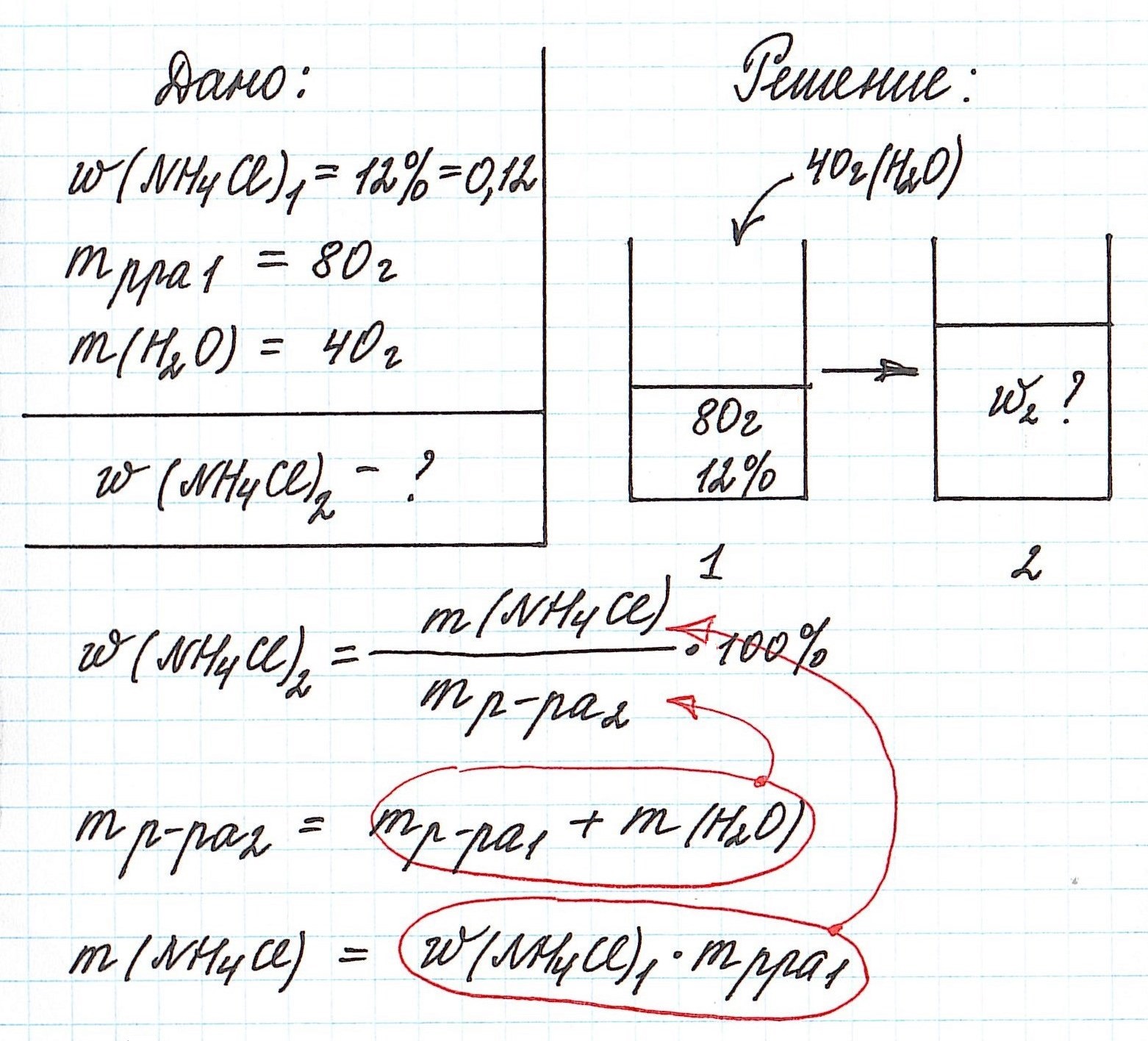
Пример 5. К 80 г раствора с массовой долей NH4Cl 12% добавили 40 г воды. Вычислите массовую долю хлорида аммония в полученном растворе.
Объединим все полученные формулы в одну и подставим имеющиеся данные:
Пример 6. Рассчитайте объем раствора фосфорной кислоты (массовая доля кислоты 12%, плотность 1,065 г/мл), который потребуется для приготовления раствора с массовой долей H3РO4 4% объемом 250 мл (плотность 1,02 г/мл).
В данной задаче речь напрямую о разбавлении раствора не идет. Но судя по тому, что исходный раствор имел концентрацию 12%, а конечный – 4%, становится ясно: последний раствор можно получить путем разбавления первого водой.
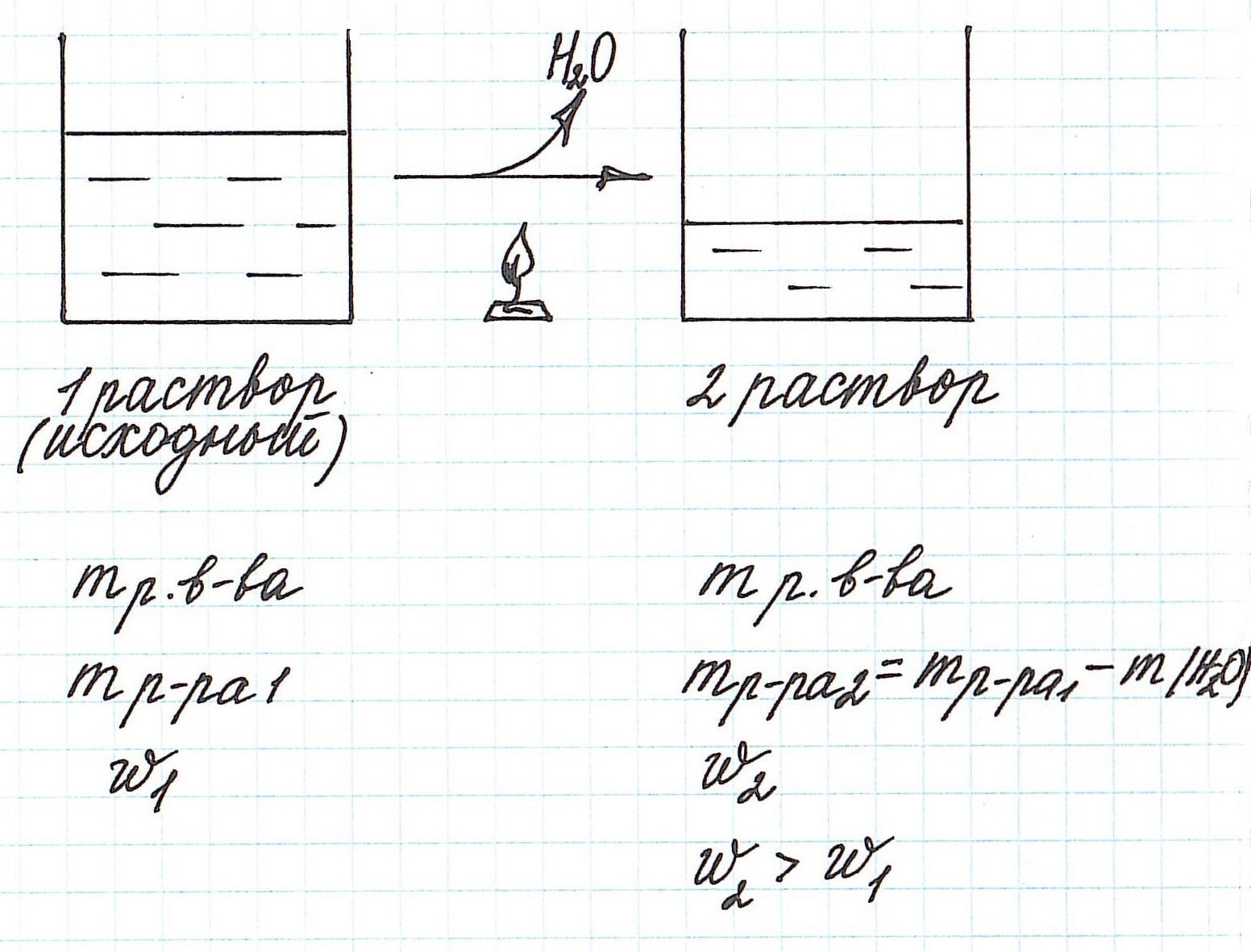
Вычисление массовой доли растворенного вещества при концентрировании раствора путем упаривания
Упаривание раствора, т.е. его нагревание, при котором происходит испарение воды, приводит к увеличению концентрации.
Учтите, что при этом:
— уменьшается масса раствора;
— уменьшается масса растворителя;
— масса растворенного вещества остается постоянной (при условии, что растворенное вещество не разлагается при данной температуре).
Пример 7. Из 200 г 27%-ного раствора глюкозы выпарили 20 г воды. Определите массовую долю глюкозы в полученном растворе.
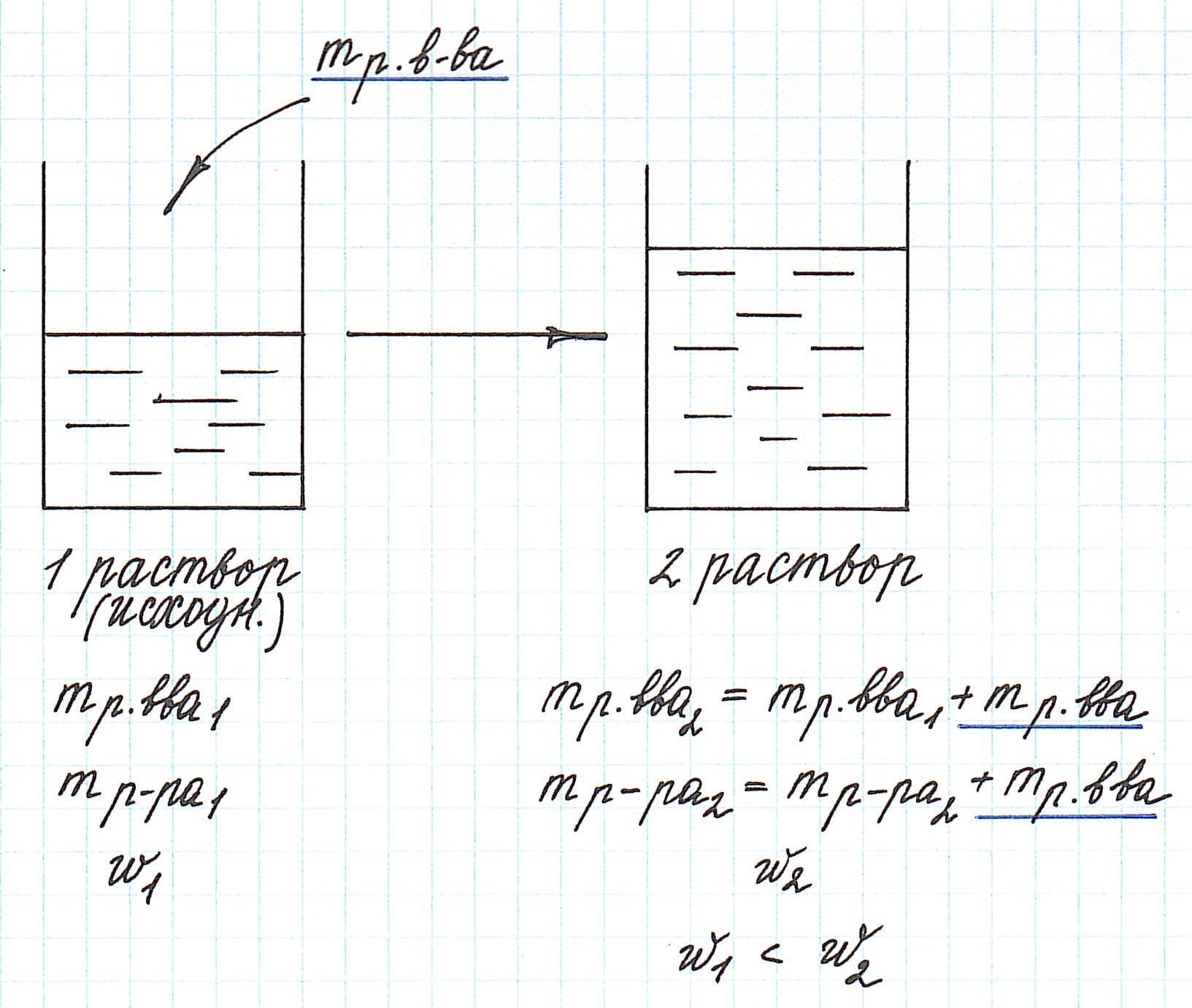
Вычисление массовой доли растворенного вещества при концентрировании раствора путем добавления растворенного вещества
Добавление к уже существующему раствору новой порции растворенного вещества приводит к увеличению концентрации раствора.
Помните, что в таких случаях:
— увеличивается масса раствора;
— увеличивается масса растворенного вещества.
Пример 8. Определите массу хлорида калия, который надо добавить к 180 г 15%-ного раствора этой соли, чтобы получить 20%-ный раствор.
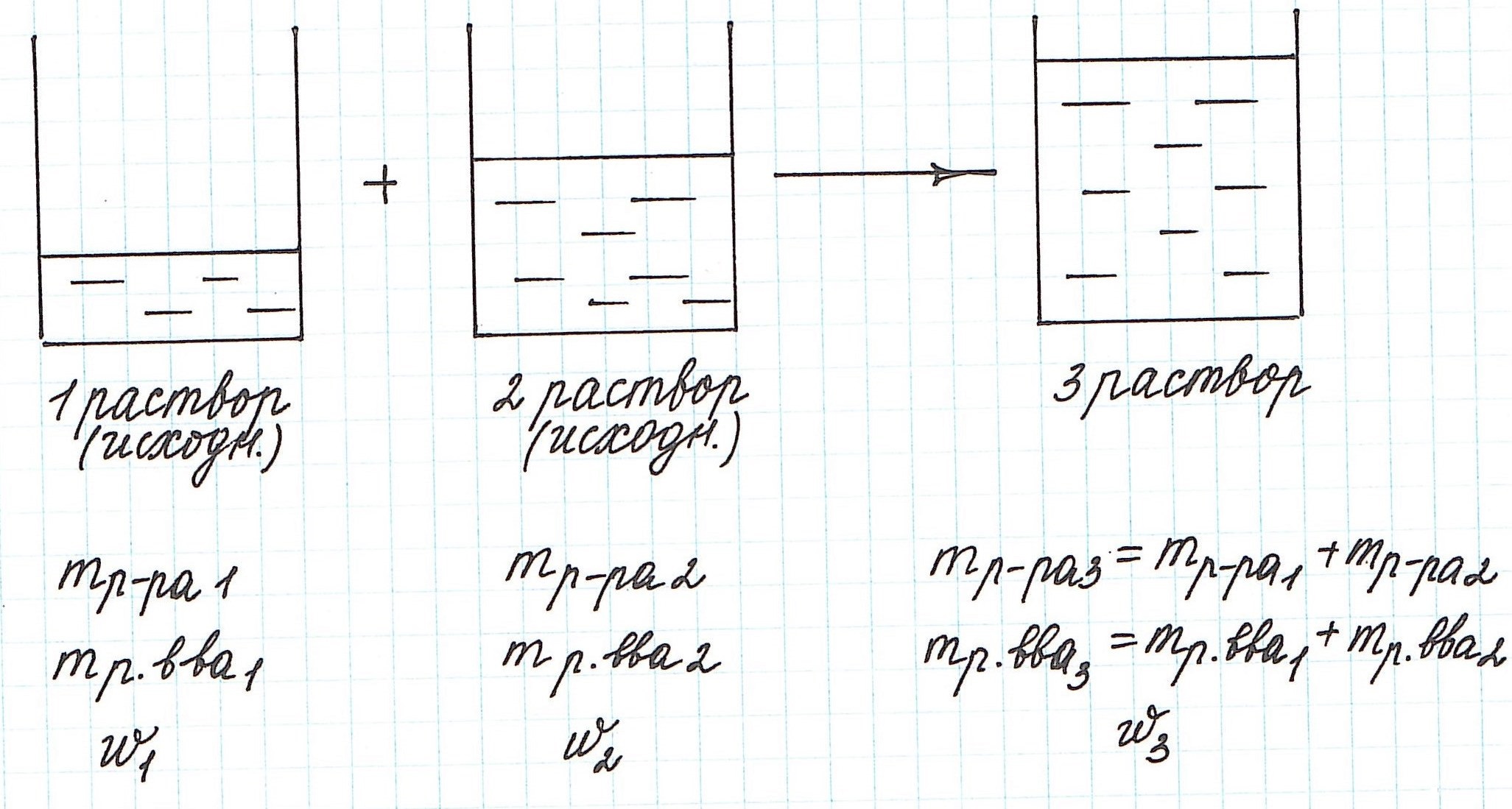
Вычисление массовой доли растворенного вещества при смешивании двух растворов
При смешивании двух растворов (речь о растворах одного и того же вещества конечно же) изменяются все количественные характеристики:
— увеличивается масса раствора;
— увеличивается масса растворенного вещества;
— изменяется массовая доля растворенного вещества.
Пример 9. Смешали 80 г 32%-ного раствора и 30 г 10%-ного раствора нитрата меди (II). Какова концентрация соли в полученном растворе?
Вычисление массовой доли растворенного вещества с применением кристаллогидратов для приготовления раствора
Кристаллогидраты используются для приготовления растворов довольно часто. Кристаллогидраты представляют собой вещества, в состав которых помимо основного вещества входят молекулы воды. Например:
CuSO4·5H2O – кристаллогидрат сульфата меди (II) (или медный купорос);
Na2SO4·10H2O – кристаллогидрат сульфата натрия (или глауберова соль).
Больше примеров здесь.
Вода, входящая в состав кристаллогидрата, называется кристаллизационной.
Кристаллогидраты различаются прочностью связи между основным веществом и кристаллизационной водой. Одни из них теряют воду при комнатной температуре с течением времени и перестают быть кристаллогидратами (например, Na2СO3·10H2O). Другие – обезвоживаются только при сильном нагревании (например, CuSO4·5H2O).
При расчете концентрации с использованием кристаллогидратов для получения растворов часто приходится учитывать и кристаллизационную воду.
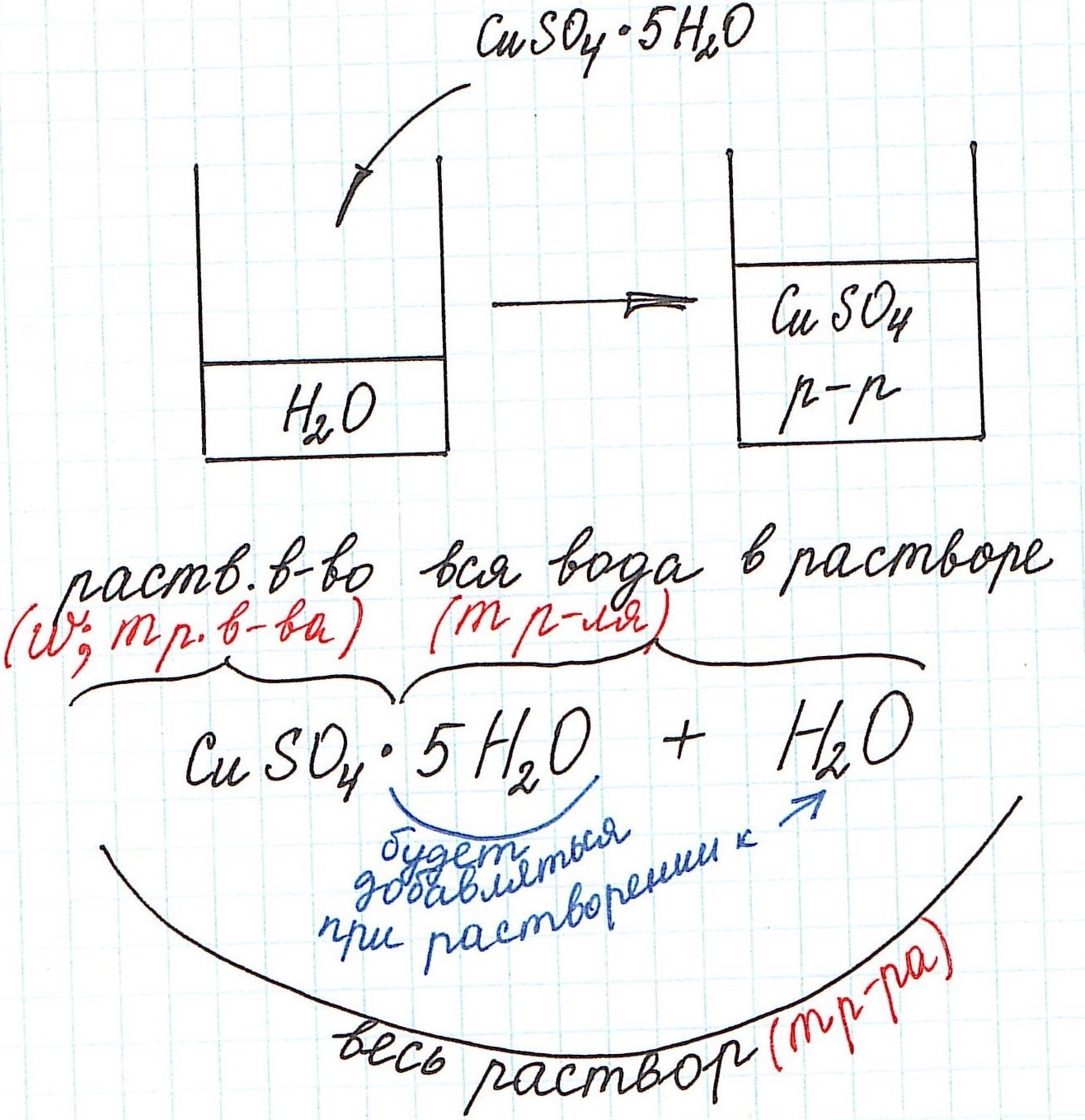
Но сначала поясним некоторые нюансы на конкретном примере:
1) Формула CuSO4·5H2O означает, что 1 моль CuSO4·5H2O содержит 1 моль CuSO4 и 5 моль H2O. Это можно было бы записать так:
n(CuSO4) = n(CuSO4·5H2O); n(H2O) = 5n(CuSO4·5H2O)
2) Относительная молекулярная (и численно молярная) масса будет складываться из относительной молекулярной массы вещества и относительной молекулярной массы воды. Например:
Mr(CuSO4·5H2O) = Mr(CuSO4) + 5·Mr(H2O) = 160 + 5·18 = 250 и, соответственно,
M(CuSO4·5H2O) = M(CuSO4) + 5·M(H2O) = 160 + 5·18 = 250 г/моль.
3) Еще одну особенность поясним с помощью рисунка:
Итак, разберем несколько типичных задач.
Пример 10. В 60 г воды растворили глауберову соль Na2SO4·10H2O массой 5,6 г. Какова массовая доля сульфата натрия в полученном растворе?
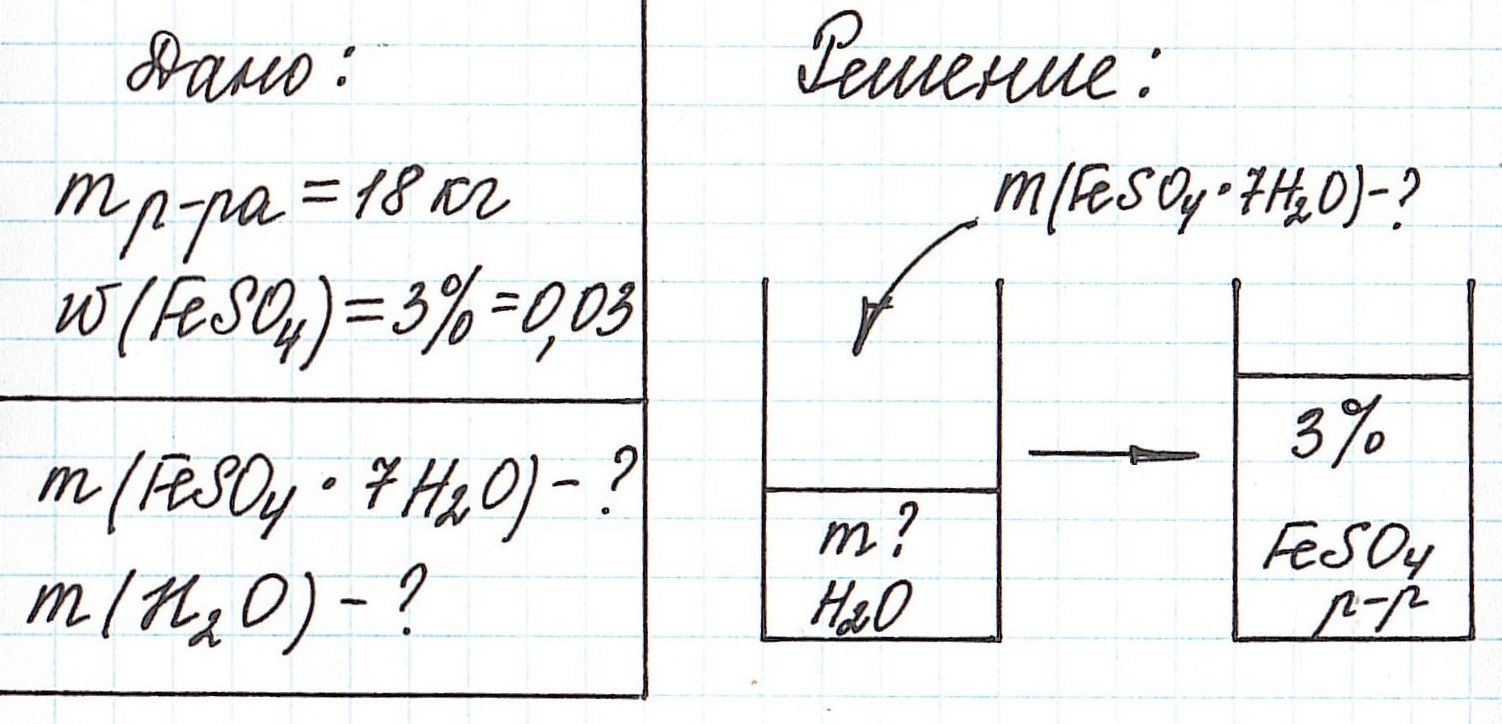
Пример 11. Какая масса железного купороса FeSO4·7H2O и воды потребуется для приготовления 18 кг раствора сульфата железа (II) с массовой долей FeSO4 3%?
Обратите внимание, что масса раствора дана не в граммах (г), а в килограммах (кг). Для того, чтобы привести в ходе расчетов все единицы измерения к единой системе, можно перевести килограммы в граммы и вычислять как обычно.
Но есть более простой способ. Можно считать количество вещества не в моль, а в киломоль (кмоль). Молярную массу вычислять не в г/моль, а в кг/кмоль. В этом случае ответ в задаче мы сразу получим в килограммах.
Пример 12. Вычислите массу кристаллогидрата сульфата никеля NiSO4·7H2O, который надо добавить к 180 г раствора с массовой долей сульфата никеля 1,5%, чтобы получить раствор с массовой долей соли 6%?
Правило «креста» в химии растворов как метод решения задач на процентную концентрацию растворов
Правилом «креста» (или «квадратом Пирсона») очень удобно пользоваться в расчетах, связанных с разбавлением или смешиванием растворов.
Общая схема вычислений выглядит так:
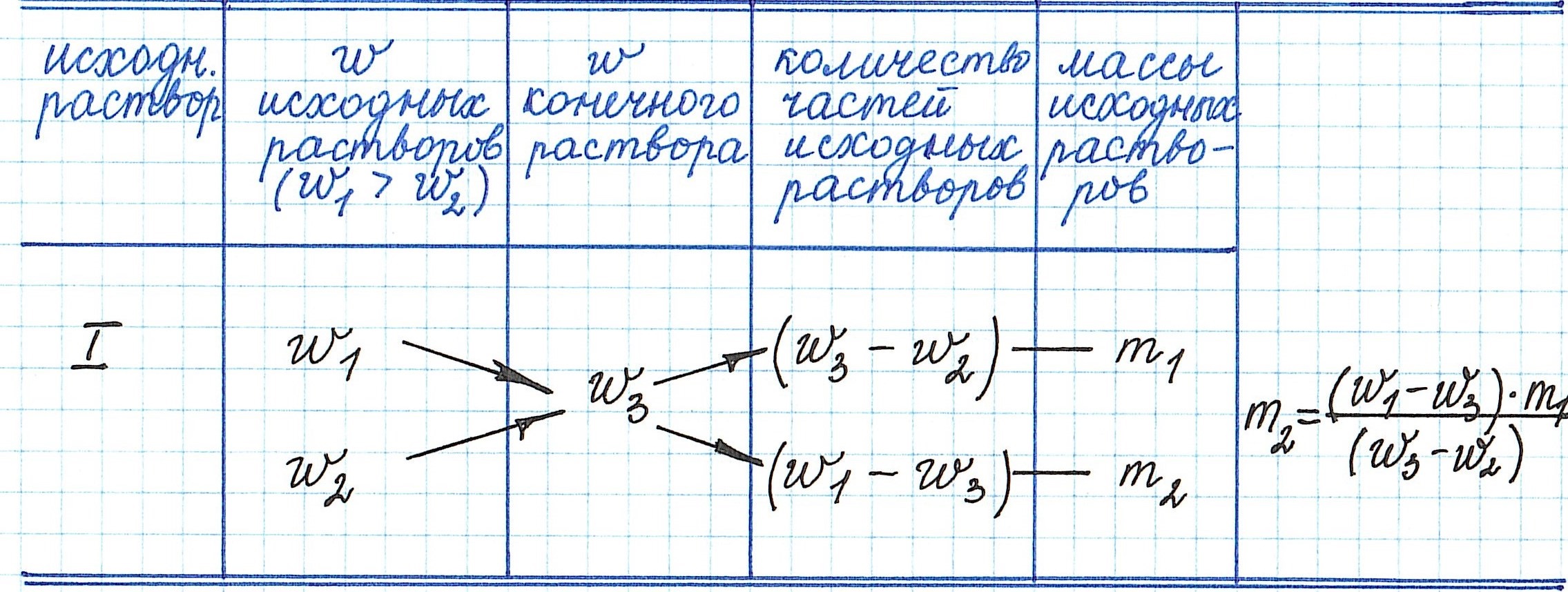
Пример 13. Какую массу 5%-ного раствора глюкозы надо добавить к 70 г 21%-ного раствора этого же вещества, чтобы получить 12%-ный раствор?
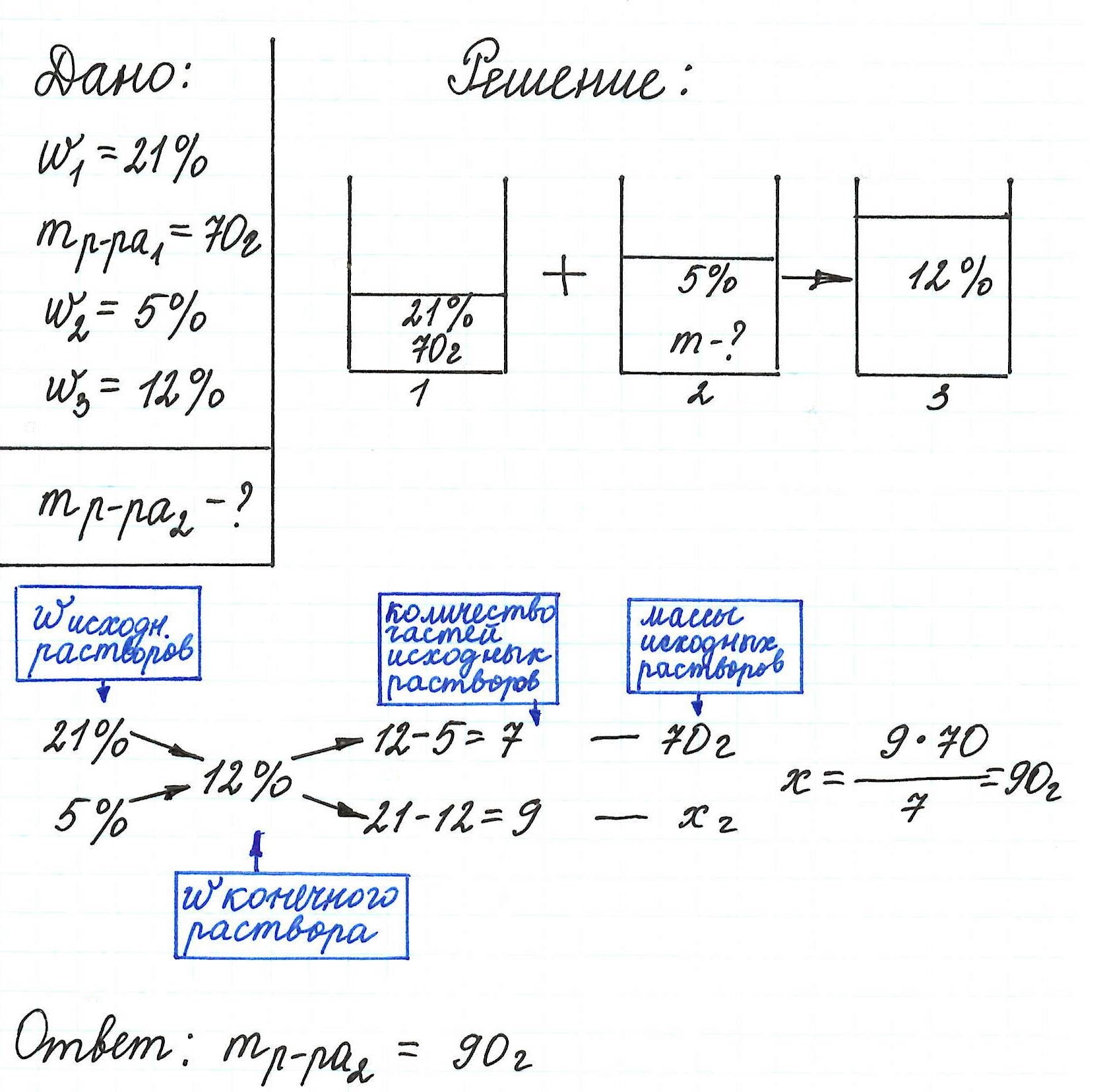
Еще примеры с применением правила «креста» можно посмотреть здесь.
Мы рассмотрели достаточно примеров расчетов, где используется формула такой концентрации раствора как массовая доля растворенного вещества. Как видим, ситуаций, в которых требуется ее применение, множество. Однако, есть достаточно случаев, когда более приемлемыми являются формулы других концентраций (молярной, нормальной, титра и т.д.). Об этом читайте в других статьях.
Чтобы самыми первыми узнавать о новых публикациях на сайте, присоединяйтесь к нашей группе ВКонтакте.
или на Одноклассниках
Пожалуйста, оцените публикацию. Большая просьба, если вы оцениваете публикацию от 1 до 3 звезд, обязательно оставьте свой комментарий с указанием того, что не так с этой публикацией. Мы постараемся устранить недостатки.
Ваше мнение для нас важно!
Расчеты массы (объема, количества вещества) продукта реакции, если одно из веществ дано в виде раствора с определенной массовой долей растворенного вещества
Для расчета массы (объема, количества вещества) продукта реакции, если данные по одному из веществ представлены в виде раствора с определенной массовой долей этого растворенного вещества, следует воспользоваться нижеследующим алгоритмом:
1) Прежде всего следует найти массу растворенного вещества. Возможны две ситуации:
* В условии даны масса раствора и массовая доля растворенного вещества (концентрация). В этом случае масса растворенного вещества рассчитывается по формуле:
* В условии даны объем раствора вещества, плотность этого раствора и массовая доля растворенного вещества в этом растворе. В таком случае следует воспользоваться формулой для расчета массы раствора:
После чего следует рассчитать массу растворенного вещества по формуле 1.
2) Рассчитать количество вещества (моль) участника реакции, масса которого стала известна из расчетов выше. Для этого воспользоваться формулой:
3) Записать уравнение реакции и убедиться в правильности расставленных коэффициентов.
4) Рассчитать количество моль интересующего участника реакции исходя из известного количества другого участника реакции, зная, что количества веществ любых двух участников реакции A и B относятся друг к другу как коэффициенты перед этими же веществами в уравнении реакции, то есть:
Если в условии требовалось рассчитать количество вещества, то действия на этом заканчиваются. Если же требуется найти его массу или объем, следует переходить к следующему пункту.
5) Зная количество вещества, определенное в п.4, мы можем рассчитать его массу по формуле:
Также, если вещество является газообразным и речь идет о нормальных условиях (н.у.), его объем может быть рассчитан по формуле:
Рассмотрим пару примеров расчетных задач по этой теме.
Пример 1
Рассчитайте массу осадка, который образуется при добавлении к 147 г 20%-ного раствора серной кислоты избытка раствора нитрата бария.
Решение:
1) Рассчитаем массу чистой серной кислоты:
m(H2SO4) = w(H2SO4) ∙ m(р-ра H2SO4)/100% = 147 г ∙ 20% /100% = 29,4 г
2) Рассчитаем количество вещества (моль) серной кислоты:
n(H2SO4) = m(H2SO4) / M(H2SO4) = 29,4 г/98 г/моль = 0,3 моль.
3) Запишем уравнение взаимодействия серной кислоты с нитратом бария:
H2SO4 + Ba(NO3)2 = BaSO4↓ + 2HNO3
4) В результате расчетов стало известно количество вещества серной кислоты. Осадок представляет собой сульфат бария. Зная, что:
n(BaSO4)/n(H2SO4) = k(BaSO4)/k(H2SO4), где n — количество вещества, а k — коэффициент в уравнении реакции,
можем записать:
n(BaSO4) = n(H2SO4) ∙ k(H2SO4)/k(BaSO4) = 0,3 моль ∙ 1/1 = 0,3 моль
5) Тогда масса осадка, т.е. сульфата бария, может быть рассчитана следующим образом:
m(BaSO4) = M(BaSO4) ∙ n(BaSO4) = 233 г/моль ∙ 0,3 моль = 69,9 г
Пример 2
Какой объем газа (н.у.) выделится при растворении необходимого количества сульфида железа (II) в 20%-ном растворе соляной кислоты с плотностью 1,1 г/мл и объемом 83 мл.
Решение:
1) Рассчитаем массу раствора соляной кислоты:
m(р-ра HCl) = V(р-ра HCl) ∙ ρ(р-ра HCl) = 83 мл ∙ 1,1 г/мл = 91,3 г
Далее рассчитаем массу чистого хлороводорода, входящего в состав кислоты:
m(HCl) = m(р-ра HCl) ∙ w(HCl)/100% = 91,3 г ∙ 20%/100% = 18,26 г
2) Рассчитаем количество вещества хлороводорода:
n(HCl) = m(HCl)/M(HCl) = 18,26 г/36,5 г/моль = 0,5 моль;
3) Запишем уравнение реакции сульфида железа (II) с соляной кислотой:
FeS + 2HCl = FeCl2 + H2S↑
4) Исходя из уравнения реакции следует, что количество прореагировавшей соляной кислоты с количеством выделившегося сероводорода связано соотношением:
n(HCl)/n(H2S) = 2/1, где 2 и 1 — коэффициенты перед HCl и и H2S соответственно
Следовательно:
n(H2S) = n(HCl)/2 = 0,5/2 = 0,25 моль
5) Объем любого газа, находящегося при нормальных условиях, можно рассчитать по формуле V(газа) = Vm ∙ n(газа), тогда:
V(H2S) = Vm ∙ n(H2S) = 22,4 л/моль ∙ 0,25 моль = 5,6 л
Автор: С.И. Широкопояс https://scienceforyou.ru/