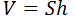Как найти объем через площадь всех граней - AvtoShod.ru

Онлайн калькулятор вычиселения объема параллелепипеда поможет вычислить объем параллелепипеда несколькими методами:

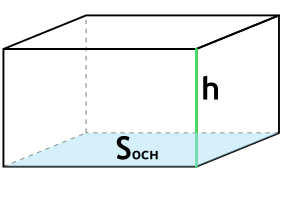
По трем сторонам
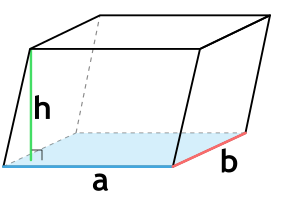
По двум сторонам и высоте
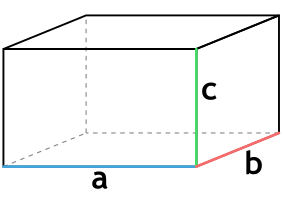
По площади основания и высоте.

Объем параллелепипеда можно вычислить на этом онлайн калькуляторе.Вы получите ответ в развернутом виде шаг за шагом. Тем самым усвоете материал по данной теме.

Параллелепипед – это геометрическая фигура в пространстве, шестигранник, гранями которого являются параллелограммы. Фигура имеет 12 ребер и 6 граней.

Объем любого параллелепипеда равняется произведению площади его основания на высоту.

Эта формула подходит для всех видов геометрической фигуры:

наклонной – боковые грани не перпендикулярны основаниям;
прямой – все боковые грани (4 шт.) являются прямоугольниками;
прямоугольной – все грани (боковые и основания) являются прямоугольниками;
ромбоэдра – все грани являются равными ромбами;
куба – все грани представляют собой равные квадраты.

Источник

Светило науки — 14 ответов — 0 раз оказано помощи

Для того чтобы найти объем параллелепипеда по площадям его граней, необходимо воспользоваться формулой, которая связывает площади граней и объем параллелепипеда.

Пусть S1, S2 и S3 — площади трех попарно перпендикулярных граней параллелепипеда. Тогда его объем V вычисляется по формуле:

V = √(S1 × S2 × S3)

В этой формуле знак «×» означает умножение, а знак «√» — извлечение квадратного корня.

Примечание: Если площадь грани неизвестна, ее можно найти, зная длины ребер параллелепипеда и угол между этими ребрами.

Источник

Площади и объемы многогранников

Что такое многогранник

Простейшей геометрической фигурой является прямая. Ею называется линия, которая имеет свое продолжение вправо и влево. Если эту прямую ограничить с двух сторон, получится отрезок. Для определения его величины достаточно одного измерения — длины. Прямая, ограниченная с одной стороны, имеет свое название. Это отрезок.

луч

Источник: rusinfo.info

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В пределах одной плоскости, кроме прямой, которую можно измерить одной величиной, существуют геометрические фигуры, измеряемые длиной и шириной. Это многоугольники.

много

Источник: sun9-19.userapi.com

Они могут иметь различное количество углов и характеризуются таким понятием как площадь.

Фигура, которая располагается в нескольких плоскостях, характеризуется пространственными величинами или трехмерным измерением. К таким фигурам относят многогранники.

Многогранник — геометрическая фигура, имеющая замкнутую поверхность, которую можно представить совокупностью многоугольников.

Для полной характеристики многогранника необходимо назвать следующие свойства:

стороны обязательно являются смежными с одной соседней стороной;
при необходимости можно, начав движение от одного из многоугольников, достигнуть любого другого, используя принцип смежности;
площадь поверхности многогранника равна сумме площадей многоугольников, ограничивающих фигуру.

При этом каждый многоугольник — это грань, сторона — ребро, а вершина — вершина многогранника.

Многогранник, как геометрическое тело, может быть представлен несколькими параллелепипедами, которые соединены по одной из граней. В таком случае их площадь будет равна сумме площадей свободных сторон и одной стороны, по которой произошло соединение. Объем такого тела будет равен сумме объемов каждого из параллелепипедов.

куб

Источник: examer.ru

Многогранники бывают:

выпуклыми (каждая из точек фигуры находится по одну сторону от плоскости);
невыпуклыми (не все точки располагаются по одну сторону плоскости).

Проще говоря, выпуклый многогранник можно поставить на одну из сторон, и он будет на ней «уверенно стоять». С невыпуклым такого действия совершить нельзя.

Примечание 1

Важно помнить, что многогранник — это не только поверхность, состоящая из нескольких многоугольников. Это еще и тот внутренний объем, который ограничивает данная поверхность. Именно поэтому в стереометрии отделяют два понятия: площадь многогранника и его объем.

Как найти площадь: формулы

В зависимости от того, какой фигурой представлен многогранник, выбирают формулу для расчета площади его поверхности. Рассмотрим примеры.

1. Дана призма (многогранник, у которого в параллельных плоскостях расположены два многоугольника, являющихся гранями. Прочие грани представлены параллелограммами).

призма

Источник: osiktakan.ru

Найти площадь данной фигуры можно следующим образом:

фрмула

Источник: osiktakan.ru

2. Дан параллелепипед (один из вариантов призмы, все шесть граней которой являются параллелограммами).

параллел

Источник: osiktakan.ru

В этом случае S=2(ab+bc+ac)

3.Дана пирамида (вид многогранника с основанием в виде n-угольника и боковыми гранями по форме треугольниками. Обязательное условие: все треугольники имеют одну общую вершину, у которой есть свое название — вершина пирамиды).

пирамида

Источник: osiktakan.ru

Площадь пирамиды можно найти по формуле:

формула2

Источник: osiktakan.ru

Примечание 2

Особый случай, когда у пирамиды нет вершины. Такая фигура носит название усеченной. Ее можно себе представить, если мысленно параллельно основанию провести сечение (см. рисунок).

нет

Источник: osiktakan.ru

S_бок усеченной пирамиды находят по формуле:

формула3

Источник: osiktakan.ru

В стереометрии существует понятие правильного многогранника. Его вводят для фигур, у которых:

все грани представлены правильными многоугольниками;
число граней у всех углов идентично;
ребра являются равными отрезками;
величины плоских углов идентичны.

Перечисленным требованиям отвечают 5 видов многогранников, представленных в таблице:

	Наименование фигуры	Пример
1	Правильный четырехгранник	Правильный тетраэдр
2	Правильный шестигранник	Куб
3	Правильный восьмигранник	Правильный октаэдр
4	Правильный двенадцатигранник	Правильный додекаэдр
5	Правильный двадцатигранник	Правильный икосаэдр

Определить площадь правильных многогранников также несложно, зная следующие формулы (нумерация согласно строке таблицы):

1. S=a²√3

2. S=6a²

3. S=2a²√3

4. формула4

Источник: osiktakan.ru

5. S=5a²√3

Использовать данный формулы нужно в задачах, требующих определить площадь поверхности многогранника, без учета его внутреннего объема.

Объем многогранника: формулы

Объем многогранника, в отличие от площади его поверхности, не может быть определен только касательно поверхности. Ведь он представляет собой все внутреннее пространство, которое ограничивается имеющейся поверхностью. На практике говорят, что объем является величиной, с помощью которой описывают размер трехмерных фигур. Эти фигуры так и называют: объемные (тела). У объемной фигуры имеется не только длина и ширина, но и высота – параметр, измеряемый в третьей плоскости.

Решить задачи по определению объема многогранника также можно с использованием формул.

Рассмотрим следующий рисунок:

рисунок

Источник: interneturok.ru

Объем такого тела определяется по формуле:

V=a*b*c

Поскольку по рисунку видно, что a*b=S, а c является высотой (h), то формулу можно записать в виде: V=S*h

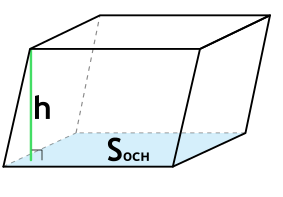
Рассмотренный вариант касается прямоугольного параллелепипеда. Если же произвольный параллелепипед имеет наклонные вертикальные грани, то данная формула также верна, однако проведенная высота отличается от бокового ребра, и, возможно, лежит внутри либо вне самого тела:

Источник: interneturok.ru

Формула определения объема через площадь и высоту подходит и для такого трехмерного тела, как призма (причем как для прямой, так и наклонной):

Источник: interneturok.ru

В быту часто происходит образование новых многогранников в процессе обрезания кусков от старых и приставления их к уже имеющимся. Как же вычислить объем такого геометрического тела? В геометрии используется принцип Кавальери. Суть его в следующем. Площади прямоугольника и параллелограмма равны потому что они в своей структуре имеют отрезки одинакового размера. Проще говоря, если представить рассечение обеих фигур плоскостями, параллельными основанию, величина отрезка слева всегда будет равна величине отрезка справа. Если третья фигура имеет такое же строение, по ее площадь будет такой же.

Источник: interneturok.ru

Объем многогранника, который может быть разделен на два и более многогранников, может определяться суммой их объемов.

найдите

Источник: image2.slideserve.com

Для систематизации формул, применяемых для определения объемов многогранников, рассмотрим таблицу:

	Наименование фигуры	Формула объема
1	Параллелепипед непрямоугольный, призма	V=S*h
	Параллелепипед прямоугольный	V=abc
2	Куб	V=a³
3	Пирамида	S=1/3(Sh)

На практике определить объем трехмерного тела можно и без формулы. Например, найти объем призмы можно, если умножить площадь ее основания на высоту фигуры. При этом вариант, когда в основании призмы лежит треугольник, предполагает, что нужно найти его площадь. Если основание квадрат, на первом этапе — нахождение площади квадрата. Величину высоты определяем, опуская перпендикуляр к основанию.

Примеры решения задач

Задача 1

Треугольник ABC — основание пирамиды DABC. При этом AC=AB=13см, BC=10см. AD=9см, это перпендикуляр к основанию. Найти S боковой поверхности.

задача1

Источник: ege-study.ru

Искомая величина равна сумме площадей боковых граней этой пирамиды.

Из вершин A и D проведем перпендикуляры к стороне BC. Тогда высота треугольника DBC — DK.

Треугольник ABC является равнобедренным, поскольку AB=AC. Тогда высота AK, которую провели по направлению основания BC, совпадает с медианой. Соответственно BK=KC=5см.

решение

Источник: ege-study.ru

Ответ: 192 см³

Задача 2

Имеется выпуклый многогранник. У него 8 граней, в т.ч. 4 пятиугольника и 4 четырехугольника. Определить, сколько у данного тела ребер и вершин. Определим сумму всех граней: 4*4+4*5=36

Поскольку смежные ребра посчитаны дважды, найденное количество необходимо разделить на два: 36/2=18

В+Г-Р=2

В+12-30=2

В+12-2=30

В+10=30

В=20

Ответ: вершин — 20, ребер — 30.

Задача 3

Если переплавить три куба из латуни, у которых ребра равны соответственно 3, 4, 5см, в один куб, какая величина ребра получится у нового куба?

Решение.

решение2

Источник: famiredo.ru

Источник

{V= a cdot b cdot c}

Найти объем параллелепипеда довольно просто. Для этого необходимо знать длины трех его сторон или же две стороны (площадь основания) и высоту. Чтобы облегчить расчет объема параллелепипеда мы создали калькулятор для разных исходных данных. Просто введите известные значения и в режиме онлайн получите результат.

Параллелепипед — многогранник, состоящий из шести граней, причем все они являются параллелограммами.

Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.

Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.

Содержание:

калькулятор объема параллелепипеда
формула объема прямоугольного параллелепипеда через три стороны
формула объема прямоугольного параллелепипеда через площадь основания и высоту
формула объема наклонного параллелепипеда через длины сторон основания и высоту
формула объема наклонного параллелепипеда через площадь основания и высоту
примеры задач

Формула объема прямоугольного параллелепипеда через три стороны

{V= a cdot b cdot c}

a — длина параллелепипеда

b — ширина параллелепипеда

c — высота параллелепипеда

Так как в основании параллелепипеда лежит прямоугольник, то в данной формуле ab — это площадь прямоугольника, который лежит в основании параллелепипеда. И тогда формулу можно сократить до {V= S h}

Формула объема прямоугольного параллелепипеда через площадь основания и высоту

{V= S_{осн} cdot h}

S_осн — площадь основания параллелепипеда

h — высота параллелепипеда

Формула объема наклонного параллелепипеда через длины сторон основания и высоту

{V= a cdot b cdot h}

a — длина основания параллелепипеда

b — ширина основания параллелепипеда

h — высота параллелепипеда

Формула объема наклонного параллелепипеда через площадь основания и высоту

{V= S_{осн} cdot h}

S_осн — площадь основания параллелепипеда

h — высота параллелепипеда

Примеры задач на нахождение объема параллелепипеда

Задача 1

Найдите объём прямоугольного параллелепипеда с измерениями 3см, 4см и 5см.

Решение

Для решения данной задачи нам подходит формула один. Подставим в нее значения длины, ширины и высоты прямоугольного параллелепипеда, произведем расчет и получим ответ.

V= a cdot b cdot c = 3 cdot 4 cdot 5 = 60 : см^3

Ответ: 60 см³

Проверим правильность ответа с помощью калькулятора .

Задача 2

Найдите объём наклонного параллелепипеда с площадью основания 12м² и высотой 3м.

Решение

Используем для решения четвертую формулу. Подставим в нее площадь основания и высоту.

V= S_{осн} cdot h = 12 cdot 3 = 36 : м^3

Ответ: 36 м³

Полученный ответ поможет проверить калькулятор .

Источник

В данной публикации мы рассмотрим, как можно найти объем параллелепипеда и разберем примеры решения задач для закрепления материала.

Формула вычисления объема параллелепипеда
- 1. Общая формула
- 2. Объем прямоугольного параллелепипеда
Примеры задач

Формула вычисления объема параллелепипеда

1. Общая формула

Объем любого параллелепипеда равняется произведению площади его основания на высоту.

V = S_осн ⋅ h

S_осн – площадь основания (ABCD или EFHG, равны между собой);
h – высота.

Данная формула справедлива для всех видов геометрической фигуры:

наклонной – боковые грани не перпендикулярны основаниям;
прямой – все боковые грани (4 шт.) являются прямоугольниками;
прямоугольной – все грани (боковые и основания) являются прямоугольниками;
ромбоэдра – все грани являются равными ромбами;
куба – все грани представляют собой равные квадраты.

2. Объем прямоугольного параллелепипеда

Объем фигуры равен произведению его длины на ширину на высоту.

V = a ⋅ b ⋅ c

Формула следует из следующих утверждений:

Основанием фигуры является прямоугольник, площадь которого считается как произведение его длины (a) на ширину (b).
Высота фигуры – это длина боковой грани (c).

Примеры задач

Задание 1
Найдите объем параллелепипеда, если известно, что площадь его основания равняется 20 см², а высота – 7 см.

Решение:
Используем первую формулу, подставив в нее известные нам значения:
V = 20 см² ⋅ 7 см = 140 см³.

Задание 2
Дан прямоугольный параллелепипед. Длина и ширина его основания равны 9 см и 5 см, соответственно, а высота составляет 6 см. Найдите объем фигуры.

Решение:
Воспользуемся формулой для данного типа фигуры:
V = 9 см ⋅ 5 см ⋅ 6 см = 270 см³.

Источник

Площади и объемы многогранников

Что такое многогранник

Как найти площадь: формулы

Объем многогранника: формулы

Примеры решения задач

Содержание:

Формула объема прямоугольного параллелепипеда через три стороны

Формула объема прямоугольного параллелепипеда через площадь основания и высоту

Формула объема наклонного параллелепипеда через длины сторон основания и высоту

Формула объема наклонного параллелепипеда через площадь основания и высоту

Примеры задач на нахождение объема параллелепипеда

Формула вычисления объема параллелепипеда

1. Общая формула

2. Объем прямоугольного параллелепипеда

Примеры задач

Не пропустите также: