Вы
знаете, ученик третьего класса Максим очень хотел объяснить вам эту тему, но
немного приболел и прийти сегодня не смог. Но, благодаря Интернету, мы можем с
ним связаться.
̶
Здравствуй Максим!
̶
Здравствуйте! Проверьте, чтобы ваши соседи по парте были готовы к уроку. И мы
начинаем.
Прослушайте
название пар множеств и попытайтесь заметить, что повторяется в
каждой паре.
Животные
и герои мультфильмов;
Рыбы
и птицы;
Материки
и части света;
Звёзды
и планеты.
Ну,
что заметили? Конечно, повторялся слово «и».
Если
в названии множества есть союз «И», то каждый его элемент должен находиться
на пересечении двух множеств, т.е. находиться одновременно в двух
множествах. Другими словами мы можем сказать, что пересечение множеств
– это их общая часть.
А
теперь задание.
Необходимо
разместить элементы по своим множествам.
Давайте
посмотрим, что за элементы. Так это имена мальчиков и девочек: Коля, Ваня,
Даша, Игорь, Катя, Саша, Дима, Юля, Ира, Женя. Будем размещать имена мальчиков
в синий прямоугольник, а девочек – в розовый. Ага! Так ведь Сашей и Женей могут
звать как мальчиков, так и девочек. Значит, эти два имени будут находиться
сразу в двух множествах, т.е. на пересечении двух множеств.
Итак,
Коля, Ваня – это мальчики, помещаем эти элементы во множество имён мальчиков.
Даша – имя девочки, помещаем в розовый прямоугольник, где находятся имена
девочек. Игорь – имя мальчика, Катя – имя девочки. Саша, так могут звать и
мальчика, и девочку, значит, этот элемент будет находиться на пересечении
двух множеств. Дима – элемент из множества имён мальчиков. Юля, Ира,
конечно элементы из множества имён девочек. И последнее имя, Женя, это имя
могут иметь как девочки, так и мальчики. Значит, этот элемент будет находиться на
пересечении двух множеств.
Теперь
все имена находятся в своих множествах.
А
сейчас я прочитаю названия ещё нескольких пар множеств, а вы попытайтесь
заметить, что повторяется в этих парах.
Яблоки
или груши;
Полевые
или садовые цветы;
Попугаи
или морские свинки;
Рабочие
или выходные дни.
Заметили,
что повторялось в парах множеств? Конечно, это слово «или».
Посмотрите
ещё раз на названия множеств.
Например,
яблоки или груши. А ведь эти множества можно объединить в одно с общим
названием «фрукты» и все элементы будут располагаться в одном новом
множестве.
Попугаи
или морские свинки. Их можно объединить во множество с названием
«домашние
животные» и все попугаи, и все морские свинки будут находиться в новом
множестве.
Значит,
если в названии множества есть слово «или», то его элемент может
находиться в любом множестве и тогда происходит объединение множеств, т.е. эти множества
объединяются.
Давайте
рассмотрим два множества: домашние животные, дикие животные.
Множество
домашние животные содержат следующие элементы: собака, кошка, морская свинка,
попугай.
Множество
дикие животные состоит из следующих элементов: бегемот, леопард, волк, лев.
Какой
общий признак у элементов этих двух множеств? Элементы
каждого из них относятся с животному миру. Значит, можно, объединив эти
множества, создать новое множество под названием животные. Теперь
все элементы находятся в одном множестве.
А
теперь, конечно, задание.
Распределить
элементы по множествам, объединить их и придумать
название для нового множества.
Итак,
смотрим на элементы. Ага, у нас два множества: множество стульев
и множество столов. Распределяем элементы по множествам. Все элементы
стулья во множество стульев, а все элементы столы во множество столов.
Объединяем
множества. Какое название будет у нашего нового множества?
Множество мебели.
Давайте
ещё раз определим разницу между пересечением и объединением множеств.
Если
в названии множества есть слово «И», то это пересечение,
и каждый элемент должен находиться на пересечении двух множеств.
Если
в названии множества есть слово «или», то его элемент может
находиться в любо области объединённых множеств.
Я
надеюсь, что вы поняли разницу между пересечением и объединением
множеств. А давайте проверим?
Итак,
перед вами рисунок с тремя множествами.
Множество
учеников, которые любят математику, множество учеников, которые любят
информатику и множество всех учеников. Но, среди учеников есть и такие, которые
любят и математику и информатику. Значит, эти два множества пересекаются
и одновременно они являются подмножеством множества всех
учеников. А теперь появляются элементы во множествах.
Используя
полученные знания сегодня на уроке, будем отвечать на вопросы. А все ответы
хранятся на этом рисунке, главное внимательно слушать вопросы и внимательно
смотреть на рисунок.
Первый
вопрос:
Сколько
учеников любят математику? Считаем их во множестве учеников, которые любят
математику, и не забываем посчитать тех учеников, которые находятся на пересечении
двух множеств учеников, которые любят и математику, и информатику. Считаем. Их
шесть.
Сколько
учеников любят информатику? Считаем их во множестве учеников, которые любят
информатику и опять считаем тех учеников, которые находятся на пересечении
двух множеств. Считаем. Их пять.
Сколько
учеников любят и математику, и информатику? Будем считать тех учеников, которые
находятся на пересечении двух множеств. Их три.
Сколько
учеников любят или математику или информатику? Если используется слово «или»,
значит элементы находятся в любом месте множеств за исключением любителей двух
предметов сразу. Значит, считаем учеников и в первом множестве и во втором, но
не включаем тех, кто находится в пересечении. Их пять.
Сколько
учеников любят только математику? Любят математику только те, которые находятся
во множестве учеников, которые любят математику. Ученики, которые находятся на
пересечении двух множеств, сюда относится не будут, т.к. они любят и
математику, и информатику. Итак, считаем и получается, что 3 ученика любят
только математику.
Сколько
учеников любят только информатику? Опять, учеников, которые находятся на пересечении
двух множеств, считать не будем. Любителей информатики двое.
Сколько
учеников не любят математику? Надо посчитать их во множестве учеников, которые
любят информатику, кроме тех, которые находятся на пересечении
множеств, т.к. эти ученики любят информатику и математику. А так же надо
посчитать тех учеников, которые находятся во множестве всех учеников, т.к. они
не любят математику. Их всего 5.
Всем
спасибо за отличную работу. Теперь я точно понял, что хочу быть учителем!
Тебе
спасибо, Максим. Тему объяснил хорошо. До свидания! А мы ещё сделаем выводы.
Итак.
Множество
– это объединение некоторых объектов (элементов) в группу по определённым
признакам.
Множество
может быть подмножеством другого множества. Например: множество
собак является подмножеством множества домашние животные.
Множества
могут пересекаться. Например: множество чисел, которые делятся на
2, и множество чисел, которые делятся на 3, пересекаются, т.к. числа, например,
6 и 12 делится и на 2, и на 3.
Множества
могут и не пересекаться. Например: множество телефонов и
множество цветов.
И
множества могут объединяться. Например: множество рабочих дней
недели и множество выходных можно объединить в одно множество дней недели.
Выводы
сделаны, и я желаю вам успехов при выполнении заданий!
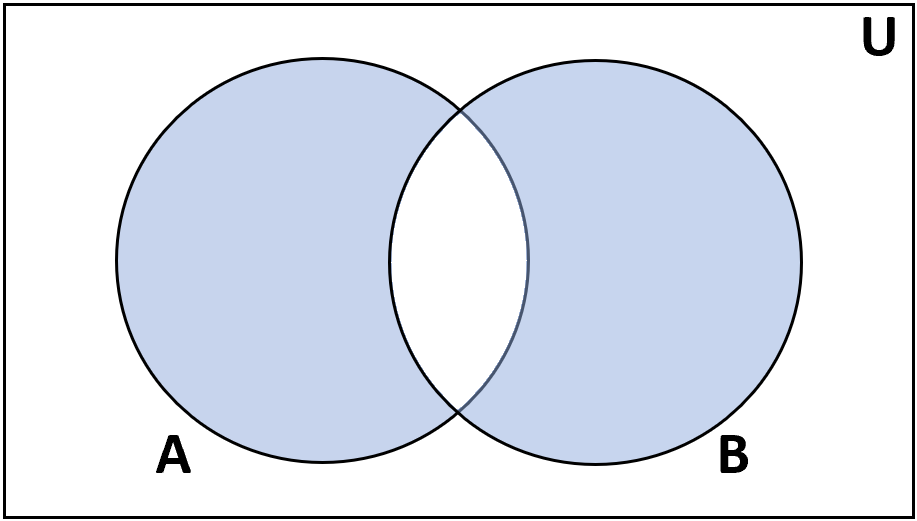
Объединение множеств A и B являет собой такое же, как и исходные, множество, в составе которого наличествуют элементы, принадлежащие одному или прочим из объединяемых множеств. Удостоверяет объединение двух множеств наличие в обозначении между ними специального знака, напоминающего латинскую букву «U».
Понять, как происходит объединение множеств легко на простом примере:
Если A ={1, 3, 5, 7} и B ={2,4,6,8,9}, то A U B = {1,2,3,4,5,6,7,8,9}.
Или: если A ={1, 5, 8} и B ={2,5,7,8,9}, то A U B = {1,2,5,7,8,9}
В отношении объединения множеств действует коммутативный и ассоциативный законы. Задействуются вычисления объединения множеств наравне с разностью и пересечением множеств при решении различных задач алгебры логики и профильной алгебры множеств, при проектировании сложной микропроцессорной и иной электронной техники.
Операции над множествами: объединение, пересечение, дополнение и различие
17 авг. 2022 г.
читать 2 мин
Набор — это набор предметов.
Мы обозначаем набор с помощью заглавной буквы, а элементы в наборе определяем с помощью фигурных скобок. Например, предположим, что у нас есть некоторый набор под названием «A» с элементами 1, 2, 3. Мы запишем это так:
А = {1, 2, 3}
В этом руководстве объясняются наиболее распространенные операции с множествами, используемые в теории вероятностей и статистике.
Союз
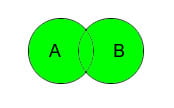
Определение: Объединение множеств A и B — это множество элементов, которые находятся либо в A, либо в B.
Обозначение: А ∪ В
Примеры:
- {1, 2, 3} ∪ {4, 5, 6} = {1, 2, 3, 4, 5, 6}
- {1, 2} ∪ {1, 2} = {1, 2}
- {1, 2, 3} ∪ {3, 4} = {1, 2, 3, 4}
Перекресток
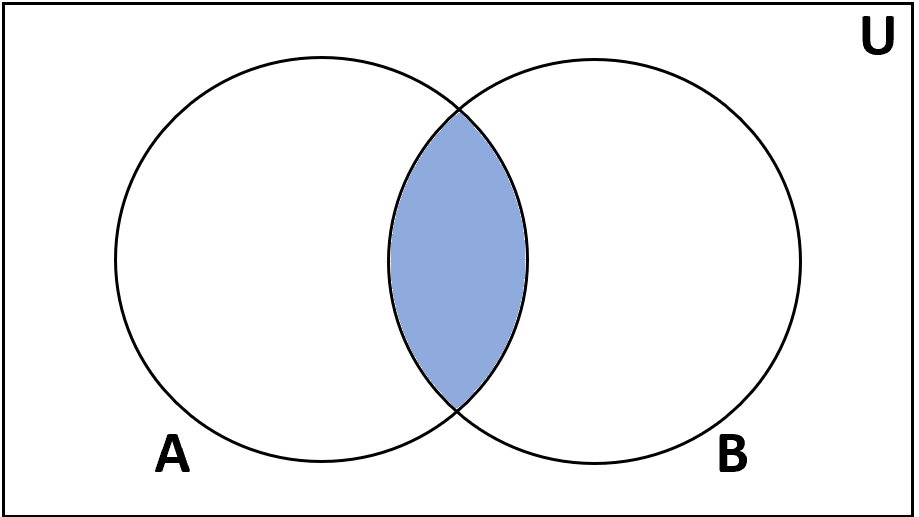
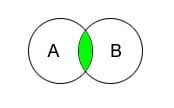
Определение: Пересечение множеств A и B — это множество элементов, которые находятся как в A, так и в B.
Обозначение: А ∩ В
Примеры:
- {1, 2, 3} ∩ {4, 5, 6} = {∅}
- {1, 2} ∩ {1, 2} = {1, 2}
- {1, 2, 3} ∩ {3, 4} = {3}
Дополнение
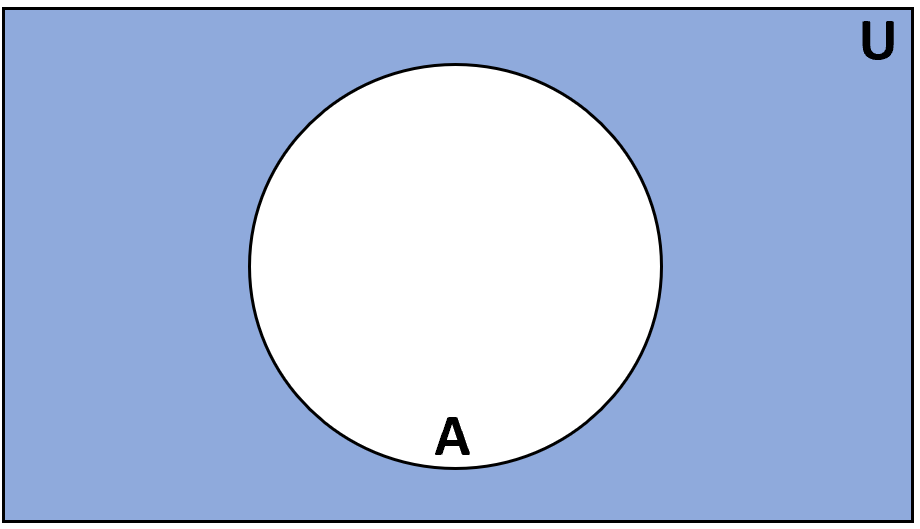
Определение: Дополнением множества A называется множество элементов, которые входят в универсальное множество U, но не входят в A.
Обозначение: A’ или A c
Примеры:
- Если U = {1, 2, 3, 4, 5, 6} и A = {1, 2}, то A c = {3, 4, 5, 6}
- Если U = {1, 2, 3} и A = {1, 2}, то A c = {3}
Разница
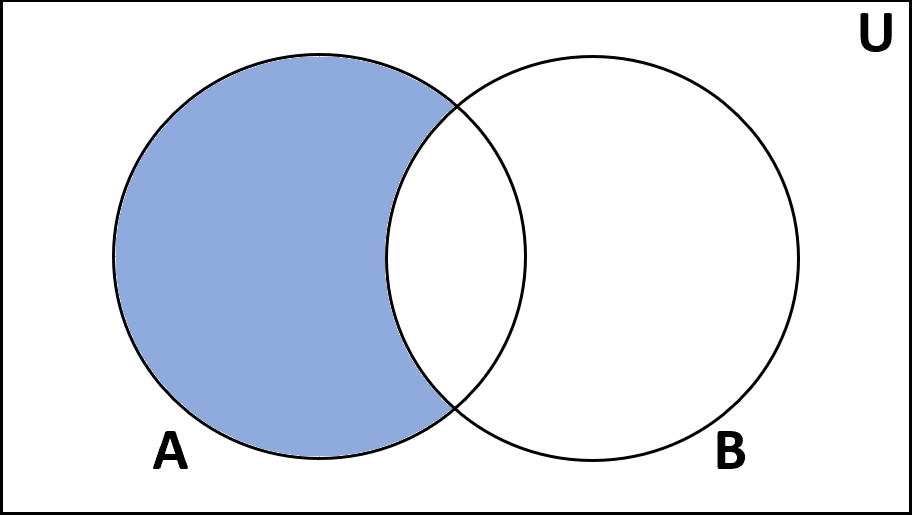
Определение: Разность множеств А и В — это множество элементов, которые есть в А, но отсутствуют в В.
Обозначение: А – Б
Примеры:
- {1, 2, 3} – {2, 3, 4} = {1}
- {1, 2} – {1, 2} = {∅}
- {1, 2, 3} – {4, 5} = {1, 2, 3}
Симметричная разница
Определение: Симметричная разность множеств A и B — это множество элементов, которые находятся либо в A, либо в B, но не в обоих.
Обозначение: А Δ В
Примеры:
- {1, 2, 3} ∆ {2, 3, 4} = {1, 4}
- {1, 2} ∆ {1, 2} = {∅}
- {1, 2, 3} Δ {4, 5} = {1, 2, 3, 4, 5}
Декартово произведение
Определение: Декартово произведение множеств A и B — это множество упорядоченных пар из A и B.
Обозначение: А х В
Примеры:
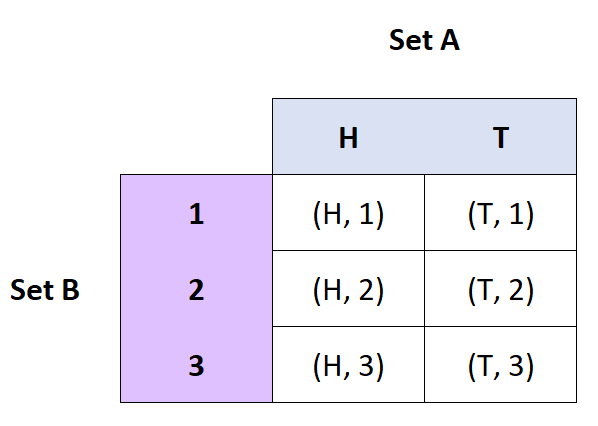
- Если A = {H, T} и B = {1, 2, 3}, то A x B = {(H, 1), (H, 2), (H, 3), (T, 1), ( Т, 2), (Т, 3)}
- Если A = {T, H} и B = {1, 2, 3}, то A x B = {(T, 1), (T, 2), (T, 3), (H, 1), ( Н, 2), (Н, 3)}
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
- Пособие
- — Задачи с множествами
Задачи с множествами
Множество — это совокупность объектов, которая рассматривается как единое целое и обладающих определенным свойством (признаком). Множество может быть ученники класса, фрукты, автомобили на парковке и т.д. В задачах ЕГЭ множествами являются сайты — результаты поисковых запросов в интернете.
Объекты, составляющие множество, называются элементами.
Множества принято обозначать латинскими буквами. Для наглядности множества представляют в виде окружностей, так называемых кругов Эйлера.
Пустым множество называется множество, которое не содержит элементы. Обозначается ∅.
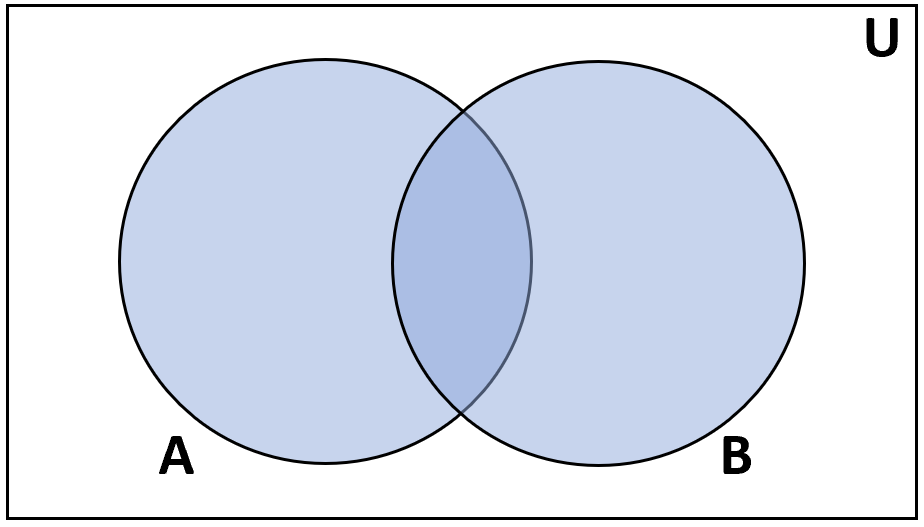
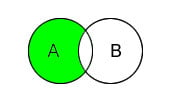
Объединение. Объединение множеств A и B — это множество всех элементов, которые принадлежат хотя бы одному из множеств A или B. Обозначется A ∪ B. В языке запросов поисковых машин объединению соответствует знак | — или.
Пересечение. Пересечение множеств A и B — это множество элементов, которые принадлежат обоим множествам A и B. Обозначается A ∩ B. В языке запросов поисковых машин пересечению соответствует знак & — И.
Разность. Разность множеств A и B — это множество элементов множества A, которые не принадлежат множеству B. Обозначается A B.
Мощностью множества называется число его элементов. Обозначается |A|
Для вычисления мощности объединения множеств имеет место быть формула (принцип включений и исключений):
|A ∪ B| = |A| + |B| — |A ∩ B|
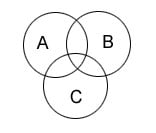
Для вычисления мощности объединения трех множеств:
|A ∪ B ∪ C| = |A| + |B| + |C| — |A ∩ B| — |A ∩ C| — |B ∩ C| + |A ∩ B ∩ C|
Задача: В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество страниц (тыс.) |
| торты | пироги | 12000 |
| торты & пироги | 6500 |
| пироги | 7700 |
Сколько страниц (в тысячах) будет найдено по запросу «торты»?
Решение: Обозначим буквой Т — множество страниц, отвечающих запросу «торты», а буквой П — отвечающих запросу «пироги». Тогда по формуле включений и исключений:
|Т | П| = |Т| + |П| — |Т & П|. Подставляем известные значения: 12000 = |Т| + 7700 — 6500, следовательно |Т| = 10800. Ответ: 10800
Задача: В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
| Запрос | Количество страниц (тыс.) |
| Толстой & Гоголь & Чехов | 110 |
| Гоголь & Чехов | 275 |
| Толстой & Чехов | 215 |
Компьютер печатает количество страниц (в тысячах), которое будет найдено по следующему запросу: (Толстой|Гоголь) & Чехов Укажите целое число, которое напечатает компьютер. Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
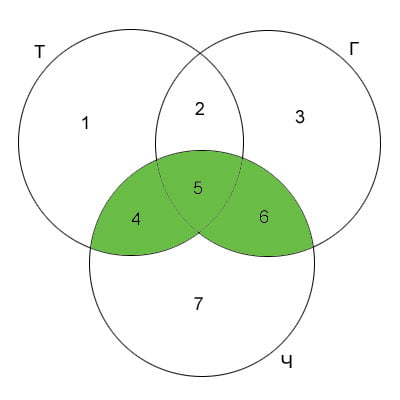
Решение: Представим множества страниц, найденных по запросам в виде кругов Эйлера. Каждую область пронумеруем, а мощность множества соответствующей области будем обозначать как Ni, где i — номер области (множества).
Тогда:
N5 = 110
N5 + N6 = 275
N4 + N5 = 215
Интересующая нас область N4 + N5 + N6.
Сложим второе и третье равентства: N4 + 2N5 + N6 = 490, или N4 + N5 + N6 = 490 — N5 , подставим в правую часть известное нам значение N5, N4 + N5 + N6 = 380. Ответ: 380
Задачи для самостоятельного решения
Бинарные операции над упорядоченными множествами
Время на прочтение
4 мин
Количество просмотров 29K
В предыдущей статье я писал о бинарных операциях над неупорядоченными множествами. В этой статье мы рассмотрим алгоритмы с меньшей сложностью выполнения, для упорядоченных множеств.
Содержание
I. Пересечение упорядоченных множеств
II. Разность упорядоченных множеств
III. Объединение упорядоченных множеств
IV. Симметрическая разность упорядоченных множеств
Заключение
I. Пересечение упорядоченных множеств
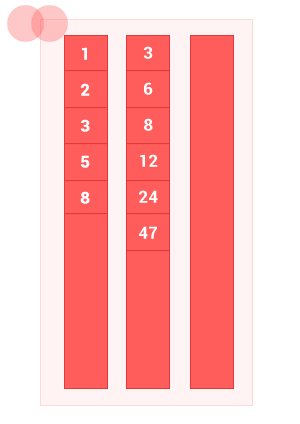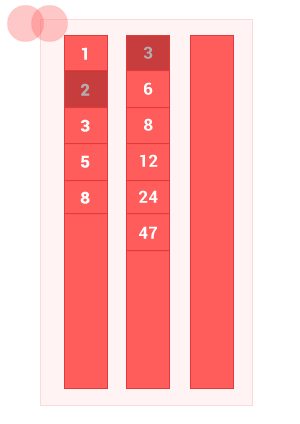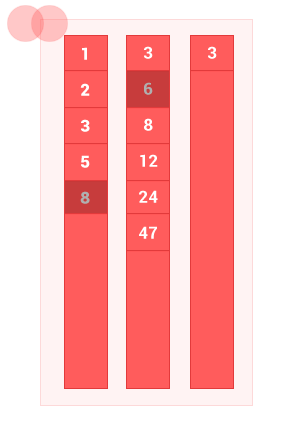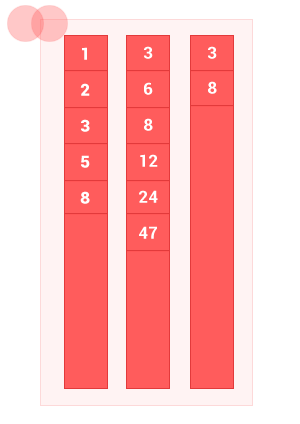
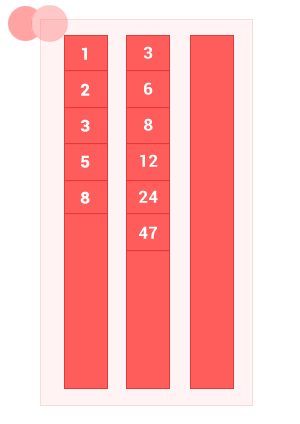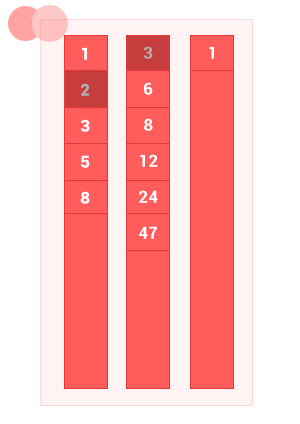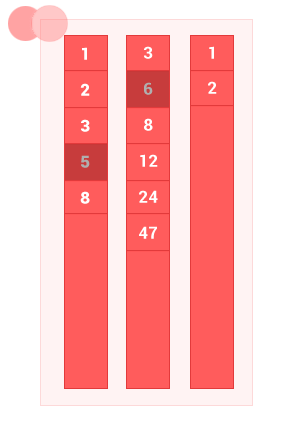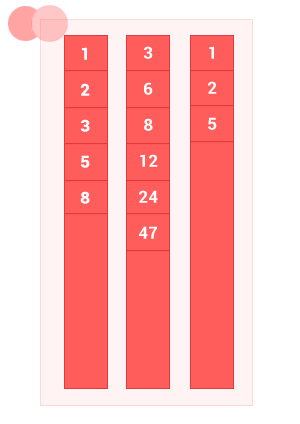
Пересечение двух упорядоченных множеств A и B — это множество только с теми элементами A и B, которые одновременно принадлежат обоим множествам, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных множеств A и B соответственно.
Сделал небольшую анимацию, чтобы показать как работает алгоритм.
Пример реализации на javascript:
function intersec_sort_arr(array_1,array_2)
{
var n = array_1.length, m = array_2.length, i = 0, k = 0, j = 0, array_3 = [];
while ((i < n) && (j < m)) // пока не дошли до конца массива
{
if (array_1[i] == array_2[j])
{
array_3[k] = array_1[i]; // запишем элемент в массив array_3
k++,i++,j++; // и сдвинем позицию во всех 3 массивах
} else {
if (array_1[i] < array_2[j]) {
i++; // сдвинем позицию в первом массиве
} else {
j++; // сдвинем позицию во втором массиве
}
}
}
return array_3;
}
Обращение к функции:
intersec_sort_arr([1, 2, 3, 5, 8], [3, 6, 8, 12, 24, 47]); // на выходе [3, 8]
II. Разность упорядоченных множеств
Разность двух упорядоченных множеств A и B — это множество с элементами A, не совпадающими с элементами B, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных упорядоченных множеств A и B соответственно.
function diff_sort_arr(array_1,array_2)
{
var n = array_1.length, m = array_2.length, i = 0, k = 0, j = 0, array_3 = [];
while ((i < n) && (j < m)) // пока не дошли до конца массива
{
if (array_1[i] == array_2[j])
{
i++,j++;
} else {
if (array_1[i] < array_2[j]) {
array_3[k] = array_1[i];
k++;
i++; // сдвинем позицию в первом массиве
} else {
j++; // сдвинем позицию во втором массиве
}
}
}
while (i < n) {
array_3[k] = array_1[i];
k++, i++;
}
return array_3;
}
diff_sort_arr([1, 2, 3, 5, 8], [3, 6, 8, 12, 24, 47]); // на выходе [1, 2, 5]
III. Объединение упорядоченных множеств
Объединение двух упорядоченных множеств A и B — это множество с элементами A и элементы множества B, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных упорядоченных множеств A и B соответственно.
function sum_sort_arr(array_1,array_2)
{
var n = array_1.length, m = array_2.length, i = 0, k = 0, j = 0, array_3 = [];
while ((i < n) && (j < m)) // пока не дошли до конца массива
{
if (array_1[i] == array_2[j])
{
array_3[k] = array_1[i];
k++,i++,j++;
} else {
if (array_1[i] < array_2[j]) {
array_3[k] = array_1[i];
k++;
i++; // сдвинем позицию в первом массиве
} else {
array_3[k] = array_2[j];
k++;
j++; // сдвинем позицию во втором массиве
}
}
}
while (i < n) {
array_3[k] = array_1[i];
k++, i++;
}
while (j < m) {
array_3[k] = array_2[j];
k++, j++;
}
return array_3;
}
sum_sort_arr([1, 2, 3, 5, 8], [3, 6, 8, 12, 24, 47]); // на выходе [1, 2, 3, 5, 6, 8, 12, 24, 47]
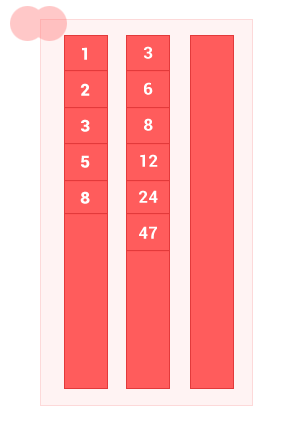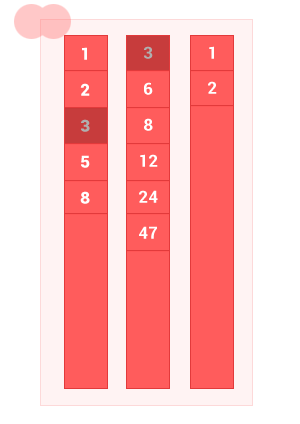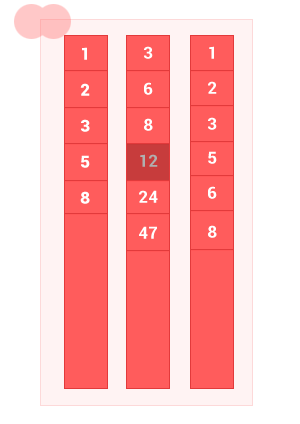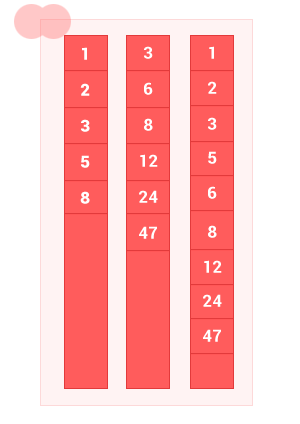
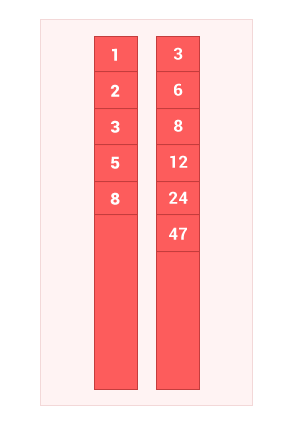
IV. Симметрическая разность упорядоченных множеств
Симметрическая разность двух упорядоченных множеств A и B — это такое множество, куда входят все те элементы первого упорядоченного множества, которые не входят во второе упорядоченное множество, а также те элементы второго упорядоченного множества, которые не входят в первое упорядоченное множество. Сложность алгоритма O(2(m+n)), где m и n — длины входных упорядоченных множеств A и B соответственно.
По сути это вычитание множеств, сначала A из B, затем B из A.
2 прохода
function symmetric_diff_sort_arr(array_1,array_2)
{
var n = array_1.length, m = array_2.length, i = 0, k = 0, j = 0, array_3 = [];
while ((i < n) && (j < m)) // пока не дошли до конца массива
{
if (array_1[i] == array_2[j])
{
i++,j++;
} else {
if (array_1[i] < array_2[j]) {
array_3[k] = array_1[i];
k++;
i++; // сдвинем позицию в первом массиве
} else {
j++; // сдвинем позицию во втором массиве
}
}
}
while (i < n) {
array_3[k] = array_1[i];
k++, i++;
}
n = array_2.length, m = array_1.length, j = 0, i = 0;
while ((i < n) && (j < m)) // пока не дошли до конца массива
{
if (array_2[i] == array_1[j])
{
i++,j++;
} else {
if (array_2[i] < array_1[j]) {
array_3[k] = array_2[i];
k++;
i++; // сдвинем позицию в первом массиве
} else {
j++; // сдвинем позицию во втором массиве
}
}
}
while (i < n) {
array_3[k] = array_2[i];
k++, i++;
}
return array_3;
}
Способ предложенный 0leGG.
1 проход
function symmetric_diff_sort_arr(array_1,array_2)
{
var n = array_1.length, m = array_2.length, i = 0, k = 0, j = 0, array_3 = [];
while ((i < n) && (j < m)) // пока не дошли до конца массива
{
if (array_1[i] < array_2[j]) {
array_3[k] = array_1[i];
k++;
i++; // сдвинем позицию в первом массиве
} else if (array_1[i] > array_2[j]) {
array_3[k] = array_2[j];
k++;
j++; // сдвинем позицию во втором массиве
} else {
i++, j++;
}
}
while (i < n) {
array_3[k] = array_1[i];
k++, i++;
}
while (j < m) {
array_3[k] = array_2[j];
k++, j++;
}
return array_3;
}
symmetric_diff_sort_arr([1, 2, 3, 5, 8], [3, 6, 8, 12, 24, 47]); // на выходе [1, 2, 5, 6, 12, 24, 47]
Заключение
Мне часто приходится работать с отсортированными массивами, поэтому эти алгоритмы очень сильно ускоряют процесс. Пример реализации метода intersec_sort_arr, вы можете посмотреть в моем приложении для vk.com. С помощью данного метода я нахожу общих участников сообществ работая с отсортированными массивами, в миллионы элементов, метод справляется очень быстро. До этого использовал метод описанный в моей предыдущей статье, обработка массивов была очень медленной.