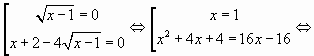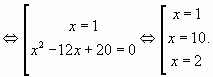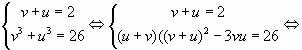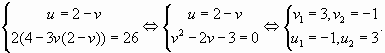Загрузить PDF
Загрузить PDF
Перекрестное умножение — это способ решения уравнения, обе части которого имеют вид дробей и неизвестная величина входит в состав числителя или знаменателя одной из них (или обеих). Перекрестное умножение позволит избавиться от дробей и привести уравнение к простому виду. Этот метод особенно полезен при решении пропорций.
-
1
Умножьте числитель левой дроби на знаменатель правой. Например, нам дано уравнение 2/x = 10/13. Умножьте 2 на 13. 2 * 13 = 26.[1]
-
2
Умножьте числитель правой дроби на знаменатель левой. Теперь умножьте x на 10. x * 10 = 10x. Можете поменять первый шаг и этот местами. Не важно, что вы умножите в первую очередь, а что во вторую; главное — перемножить по диагонали числитель одной дроби со знаменателем другой.[2]
-
3
Приравняйте ответы. Запишите, что 26 равно 10x. 26 = 10x. Последовательность записи ответов не имеет значения. Можете поменять их местами — равенство все равно сохранится. Только записывайте каждый ответ целиком в том виде, в каком его получили (10х — это 10х, а не 10, не х и не 10+х).[3]
- Итак, если вы решаете уравнение 2/x = 10/13, то у вас получится 2 * 13 = x * 10, или 26 = 10x.
-
4
Решите уравнение, чтобы найти неизвестную. Чтобы решить уравнение 26 = 10x, можно начать с поиска наибольшего общего делителя. Найдите число, на которое делятся нацело 26 и 10. Это будет 2; 26/2 = 13 и 10/2 = 5. Остается 13 = 5x. Теперь оставьте в правой части только x, разделив обе части на 5. Получится 13/5 = 5х/5, или х = 13/5. Если вы хотите получить ответ в виде десятичной дроби, можно просто разделить обе части уравнения на 10: 26/10 = 10х/10, или x = 2,6.[4]
Реклама
-
1
Умножьте числитель левой дроби на знаменатель правой. Например, нам дано такое уравнение: (x + 3)/2 = (x + 1)/4. Умножьте (x + 3) на 4, получится 4(x +3). Откройте скобки, получится 4x + 12.[5]
-
2
Умножьте числитель правой дроби на знаменатель левой.[6]
Сделайте все то же, что описано выше. Получится: (x +1) x 2 = 2(x +1). Откройте скобки, получим 2x + 2. -
3
Запишите полученные ответы в виде равенства и перенесите неизвестные в одну часть. У вас получилось уравнение 4x + 12 = 2x + 2. Перенесите все х в одну часть, а известные величины — в другую.
- Перенесем 2x к 4х. Если вычесть из обеих частей уравнения 2x, слева получится «4х — 2х + 12 = 2х + 12», а справа останется только 2.
- Теперь перенесем 12 к 2. Если вычесть из обеих частей 12, то слева останется только 2х, а справа получится 2 — 12 = -10.
- Получилось уравнение 2x = -10.
-
4
Решите уравнение. Для этого осталось только найти неизвестную, разделив обе части на 2. 2х/2 = -10/2; получаем х = -5. Для проверки можно подставить это значение в изначальное уравнение. Получится -1 = -1.
Реклама
Советы
- Результат можно проверить, подставив его в изначальное уравнение. Если получится верное равенство, например 1 = 1, то вы решили уравнение правильно. Если равенстно неверно, например 0 = 1, вы допустили ошибку. Например, в примере из первой части этой статьи подставьте в уравнение 2,6: 2/(2,6) = 10/13. Умножьте левую часть на 5/5 и получится 10/13 = 10/13. Это равенство верно, значит, 2,6 — правильный ответ.
- Если в том же примере вы получили, скажем, 5, то при подсстановке этого значения получится 2/5 = 10/13. Если вы умножите левую часть на 5/5, у вас получится 10/25 = 10/13. Это равенство неверно, значит, при перекрестном умножении вы допустили ошибку.
Реклама
Об этой статье
Эту страницу просматривали 23 768 раз.
Была ли эта статья полезной?
Решение уравнений с дробями
О чем эта статья:
5 класс, 6 класс, 7 класс
Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
- Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.
Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
- Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
- Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Понятие дробного уравнения
Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.
Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:
На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.
Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.
Как решать уравнения с дробями
1. Метод пропорции
Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.
Итак, у нас есть линейное уравнение с дробями:
В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.
2. Метод избавления от дробей
Возьмем то же самое уравнение, но попробуем решить его по-другому.
В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:
- подобрать число, которое можно разделить на каждый из знаменателей без остатка;
- умножить на это число каждый член уравнения.
Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!
Вот так просто мы получили тот же ответ, что и в прошлый раз.
Что еще важно учитывать при решении
- если значение переменной обращает знаменатель в 0, значит это неверное значение;
- делить и умножать уравнение на 0 нельзя.
Универсальный алгоритм решения
Определить область допустимых значений.
Найти общий знаменатель.
Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.
Раскрыть скобки, если нужно и привести подобные слагаемые.
Решить полученное уравнение.
Сравнить полученные корни с областью допустимых значений.
Записать ответ, который прошел проверку.
Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.
Примеры решения дробных уравнений
Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.
Пример 1. Решить дробное уравнение: 1/x + 2 = 5.
- Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Решим обычное уравнение.
Пример 2. Найти корень уравнения
- Область допустимых значений: х ≠ −2.
- Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Переведем новый множитель в числитель..
Сократим левую часть на (х+2), а правую на 2.
Пример 3. Решить дробное уравнение: 
- Найти общий знаменатель:
Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:
Выполним возможные преобразования. Получилось квадратное уравнение:
Решим полученное квадратное уравнение:
Получили два возможных корня:
Если x = −3, то знаменатель равен нулю:
Если x = 3 — знаменатель тоже равен нулю.
Рациональные уравнения с примерами решения
Содержание:
Рациональные уравнения. Равносильные уравнения
два уравнения называют равносильными, если они имеют одни и те же корни. Равносильными считают и те уравнения, которые корней не имеют.
Так, например, равносильными будут уравнения 
Уравнения 
— не равносильны, так как корнем первого уравнения является число 10, а корнем второго — число 9.
Ранее, в 7 классе, вы знакомились со свойствами, которые преобразуют уравнения в равносильные им уравнения.
1) Если в любой части уравнения раскрыть скобки или привести подобные слагаемые, то получим уравнение, равносильное данному;
2) если в уравнении перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получим уравнение, равносильное данному;
3) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, равносильное данному.
Левая и правая части каждого из них являются рациональными выражениями.
Уравнении, левая и правая части которых являются рациональными выражениями, называют рациональными уравнениями.
В первых двух из записанных выше уравнений левая и правая части являются целыми выражениями. Такие уравнения называют целыми рациональными уравнениями. Если хотя бы одна часть уравнения — дробное выражение, то его называют дробным рациональным уравнением. Третье из записанных выше уравнений является дробным рациональным.
Как решать целые рациональные уравнения, мы рассмотрели при изучении математики в предыдущих классах. Рассмотрим теперь, как решать дробные рациональные уравнения, то есть уравнения с переменной в знаменателе.
Применение условия равенства дроби нулю
Напомним, что 
когда 
Пример №202
Решите уравнение 
Решение:
С помощью тождественных преобразований и свойств уравнений приведем уравнение к виду 
где 
и 
— целые рациональные выражения. Имеем:
Окончательно получим уравнение: 
Чтобы дробь 
равнялась нулю, нужно, чтобы числитель 
равнялся нулю, а знаменатель 
не равнялся нулю.
Тогда 
откуда 
При 
знаменатель 
Следовательно, 
— единственный корень уравнения.
Решение последнего, равносильного данному, уравнения, учитывая условие равенства дроби нулю, удобно записывать так:
Значит, решая дробное рациональное уравнение, можно:
1) с помощью тождественных преобразований привести уравнение к виду 
2) приравнять числитель 
к нулю и решить полученное целое уравнение;
3) исключить из его корней те, при которых знаменатель 
равен нулю, и записать ответ.
Использование основного свойства пропорции
Если 
то 
где 
Пример №203
Решите уравнение 
Решение:
Найдем область допустимых значений (ОДЗ) переменной в уравнении. Так как знаменатели дробей не могут равняться нулю, то 
Имеем: 
то есть ОДЗ переменной 
содержит все числа, кроме 1 и 2.
Сложив выражения в правой части уравнения, приведем его к виду: 
получив пропорцию: 
По основному свойству пропорции имеем:
Решим это уравнение:
откуда 
Так как число 4 принадлежит ОДЗ переменной исходного уравнения, то 4 является его корнем.
Запись решения, чтобы не забыть учесть ОДЗ, удобно закончить так:
Таким образом, для решения дробного рационального уравнения можно:
1) найти область допустимых значений (ОДЗ) переменной в уравнении;
2) привести уравнение к виду 
3) записать целое уравнение 
и решить его;
4) исключить из полученных корней те, которые не принадлежат ОДЗ, и записать ответ.
Метод умножения обеих частей уравнения на общий знаменатель дробей
Пример №204
Решите уравнение 
Решение:
Найдем ОДЗ переменной и простейший общий знаменатель всех дробей уравнения, разложив знаменатели на множители:
Областью допустимых значений переменной будут те значения 
при которых 
то есть все значения 
кроме чисел 
А простейшим общим знаменателем будет выражение 
Умножим обе части уравнения на это выражение:
Получим: 
а после упрощения: 
то есть 
откуда 
или 
Число 0 не принадлежит ОДЗ переменной исходного уравнения, поэтому не является его корнем.
Следовательно, число 12 — единственный корень уравнения. Ответ. 12.
Решая дробное рациональное уравнение, можно:
3) умножить обе части уравнения на этот общий знаменатель;
4) решить полученное целое уравнение;
5) исключить из его корней те, которые не принадлежат ОДЗ переменной уравнения, и записать ответ.
Пример №205
Являются ли равносильными уравнения
Решение:
Поскольку уравнения являются равносильными в случае, когда они имеют одни и те же, или не имеют корней, найдем корни данных уравнений.
Первое уравнение имеет единственный корень 
а второе — два корня 
(решите уравнения самостоятельно). Следовательно, уравнения не являются равносильными.
Степень с целым показателем
Напомним, что в 7 классе мы изучали степень с натуральным показателем. По определению:
где 
— натуральное число, 
В математике, а также при решении задач практического содержания, например в физике или химии, встречаются степени, показатель которых равен нулю или является целым отрицательным числом. Степень с отрицательным показателем можно встретить и в научной или справочной литературе. Например, массу атома гелия записывают так: 
кг. Как понимать смысл записи 
Рассмотрим степени числа 3 с показателями 
— это соответственно 
В этой строке каждое следующее число втрое больше предыдущего. Продолжим строку в противоположном направлении, уменьшая каждый раз показатель степени на 1. Получим: 
Число 
должно быть втрое меньше числа 
равного числу 3. Но втрое меньшим числа 3 является число 1, следовательно, 
Равенство 
справедливо для любого основания 
при условии, что 
Нулевая степень отличного от нуля числа а равна единице, то есть 
при 
Вернемся к строке со степенями числа 3, где слева от числа 
записано число 
Это число втрое меньше, чем 1, то есть равно 
Следовательно, 
Рассуждая аналогично получаем: 
и т. д.
Приходим к следующему определению степени с целым отрицательным показателем:
если 
натуральное число, то 
Как домножить обе части уравнения
Два уравнения называют равносильными, если они имеют одно и тоже множество корней.
Свойства уравнений
- Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, равносильное данному.
- Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, равносильное данному.
- Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, равносильное данному
Линейное уравнение
Уравнение вида 
, где 
— переменная, 
и 
некоторые числа, называют линейным уравнением с одной переменной.
| Значения и |
|
|
|
|---|---|---|---|
Корни уравнения  |
|
-любое число |
корней нет |
Одночлены и многочлены
Одночлены
- Выражения, являющиеся произведениями чисел, переменных и их степеней, называют одночленами.
- Одночлен, содержащий только один отличный от нуля числовой множитель, стоящий на первом месте, а все остальные множители которого — степени с разными основаниями, называют одночленом стандартного вида. К одночленам стандартного вида также относят числа, отличные от нуля, переменные и их степени.
- Числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена.
- Одночлены, имеющие одинаковые буквенные части, называют подобными. Степенью одночлена называют сумму показателей степеней всех переменных, входящих в него. Степень одночлена, являющегося числом, отличным от нуля, считают равной нулю.
- Нуль-одночлен степени не имеет.
Многочлены
- Выражение, являющееся суммой нескольких одночленов, называют многочленом.
- Одночлены, из которых состоит многочлен, называют членами многочлена.
- Одночлен является частным случаем многочлена. Считают, что такой многочлен состоит из одного члена.
Умножение одночлена на многочлен
Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый член многочлена и полученные произведения сложить.
Умножение многочлена на многочлен
Чтобы умножить многочлен на многочлен, можно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить.
Формулы сокращенного умножения
Разность квадратов двух выражений
Разность квадратов двух выражений равна произведению разности этих выражений и их суммы:
Произведение разности и суммы двух выражений
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений:
Квадрат суммы и квадрат разности двух выражений
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения:
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений пл юс квадрат второго выражении:
Преобразование многочлена в квадрат суммы или разности двух выражений
позволяют «свернуть» трёхчлен в квадрат двучлена.
Трёхчлен, который можно представить в виде квадрата двучлена, н а зывают полным квадратом.
Сумма и разность кубов двух выражений
Многочлен 
называют неполным квадратом разности.
Сумма кубов двух выражений равна произведению суммы этих выр а жений и неполного квадрата их разности:
Многочлен 
называют неполным квадратом суммы.
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы:
Степень. Свойства степени с целым показателем
Свойства степени с целым показателем
Для любого 
и любых целых 
выполняются равенства:
Для любых , 
и любого целого 
выполняются равенства:
Функция. Область определения и область значений функции
Функция
Правило, с помощью которого по каждому значению независимой переменной можно найти единственное значение зависимой переменной, называют функцией, а соответствующую зависимость одной п e ременной от другой — функциональной.
Обычно независимую переменную обозначают , зависимую обозначают 
, функцию(правило) — 
.
Независимую переменную называют аргументом функции. Значение зависимой переменной называют значением функции.
Тогда функциональную зависимость обозначают 
.
Значения, которые принимает аргумент, образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.
Способы задания функции
Описательный, табличный, с помощью формулы, графический.
График функции
Графиком функции называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
Линейная функция, её график и свойства
Системы линейных уравнений с двумя переменными
Уравнение с двумя переменными
Пару значений переменных, обращающую уравнение с двумя переменными в верное равенство, называют решением уравнения с двумя переменными.
Решить уравнение с двумя переменными — значит найти все его решения или показать, что оно не имеет решений.
Графиком уравнения с двумя переменными называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, координаты которых (пары чисел) являются решениями данного уравнения.
Если некоторая фигура является графиком уравнения, то выполняются два условия:
- все решения уравнения являются координатами точек, принадлежащих графику;
- координаты любой точки, принадлежащей графику, — это пара чисел, являющаяся решением данного уравнения.
Графический метод решения системы двух линейных уравнений с двумя переменными
Графический метод решения системы уравнений заключается в следующем:
- построить в одной координатной плоскости графики уравнений, входящих в систему;
- найти координаты всех точек пересечения построенных графиков;
- полученные пары чисел и будут искомыми решениями.
Если графиками уравнений, входящих в систему линейных уравнении, являются прямые, то количество решений этой системы зависит от взаимного расположения двух прямых на плоскости:
- если прямые пересекаются, то система имеет единственное решение.
- если прямые совпадают, то система имеет бесконечно много решении.
- если прямые параллельны, то система решений не имеет.
Решение системы двух линейных уравнений с двумя переменными методом подстановки
Чтобы решить систему линейных уравнений методом подстановки, следует:
- выразить из любого уравнения системы одну переменную через другую;
- подставить в уравнение системы вместо этой переменной выражение, полученное на первом шаге;
- решить уравнение с одной переменной, полученное на втором шаге;
- подставить найденное значение переменной в выражение, полученное на первом шаге;
- вычислить значение второй переменной;
- записать ответ.
Решение систем линейных уравнений методом сложения
Чтобы решить систему линейных уравнений методом сложения, следует:
- подобрать такие множители для уравнений, чтобы после преобразований коэффициенты при одной из переменной стали противоположными числами
- сложить почленно левые и правые части уравнений, полученных на первом шаге
- решить уравнение с одной переменной, полученной на втором шаге
- подставить найденное на третьем шаге значение переменной в любое из уравнений исходной системы;
- вычислить значение второй переменной;
- записать ответ.
источники:
http://www.evkova.org/ratsionalnyie-uravneniya
http://blackseaweb.ru/7klass-algebra/osnovnye-pravila-matematiki-7-klass-algebra-kratko/
Задачи на неизвестное слагаемое
Задача 1. На столе лежит 9 карандашей: зелёные и 4 синих. Сколько зелёных карандашей лежит на столе?
Решение:
9 — 4 = 5.
Ответ: 5 зелёных карандашей лежит на столе.
Задача 2. За два дня Маша прочитала 15 страниц. За первый день она прочитала 9 страниц. Сколько страниц она прочитала за второй день?
Решение:
15 — 9 = 6.
Ответ: 6 страниц.
Задача 3. В парке рабочие сажали деревья — берёзы и дубы. Они посадили 4 ряда берёз, по 3 дерева в каждом ряду. Всего в парке посадили 25 деревьев. Сколько дубов посадили рабочие?
Решение: Первым действием надо посчитать, сколько берёз посадили рабочие. Для этого нужно 3 берёзы умножить на 4, потому что по 3 берёзы посажены в каждом из 4 рядов:
1) 3 · 4 = 12 (берёз).
Вторым действием нужно из общего количества деревьев вычесть количество берёз:
2) 25 — 12 = 13 (дубов).
В результате вычитания мы узнали, сколько дубов посадили рабочие в парке.
Ответ: 13 дубов.
Правило нахождения неизвестного слагаемого используется для проверки сложения вычитанием.
Видео
Выразить одно через другое
Изучение уравнений по традиции начинается с того, чтобы научиться выражать одно число, входящее в равенство, через ряд других. Давайте не будем нарушать эту традицию и поступим также.
Рассмотрим следующее выражение:
8 + 2
Данное выражение является суммой чисел 8 и 2. Значение данного выражения равно 10
8 + 2 = 10
Получили равенство. Теперь можно выразить любое число из этого равенства через другие числа, входящие в это же равенство. К примеру, выразим число 2.
Чтобы выразить число 2, нужно задать вопрос: «что нужно сделать с числами 10 и 8, чтобы получить число 2». Понятно, что для получения числа 2, нужно из числа 10 вычесть число 8.
Так и делаем. Записываем число 2 и через знак равенства говорим, что для получения этого числа 2 мы из числа 10 вычли число 8:
2 = 10 − 8
Мы выразили число 2 из равенства 8 + 2 = 10. Как видно из примера, ничего сложного в этом нет.
При решении уравнений, в частности при выражении одного числа через другие, знак равенства удобно заменять на слово «есть». Делать это нужно мысленно, а не в самом выражении.
Так, выражая число 2 из равенства 8 + 2 = 10 мы получили равенство 2 = 10 − 8. Данное равенство можно прочесть так:
2 есть 10 − 8
То есть знак = заменен на слово «есть». Более того, равенство 2 = 10 − 8 можно перевести с математического языка на полноценный человеческий язык. Тогда его можно будет прочитать следующим образом:
Число 2 есть разность числа 10 и числа 8
или
Число 2 есть разница между числом 10 и числом 8.
Но мы ограничимся лишь заменой знака равенства на слово «есть», и то будем делать это не всегда. Элементарные выражения можно понимать и без перевода математического языка на язык человеческий.
Вернём получившееся равенство 2 = 10 − 8 в первоначальное состояние:
8 + 2 = 10
Выразим в этот раз число 8. Что нужно сделать с остальными числами, чтобы получить число 8? Верно, нужно из числа 10 вычесть число 2
8 = 10 − 2
Вернем получившееся равенство 8 = 10 − 2 в первоначальное состояние:
8 + 2 = 10
В этот раз выразим число 10. Но оказывается, что десятку выражать не нужно, поскольку она уже выражена. Достаточно поменять местами левую и правую часть, тогда получится то, что нам нужно:
10 = 8 + 2
Пример 2. Рассмотрим равенство 8 − 2 = 6
Выразим из этого равенства число 8. Чтобы выразить число 8 остальные два числа нужно сложить:
8 = 6 + 2
Вернем получившееся равенство 8 = 6 + 2 в первоначальное состояние:
8 − 2 = 6
Выразим из этого равенства число 2. Чтобы выразить число 2, нужно из 8 вычесть 6
2 = 8 − 6
Пример 3. Рассмотрим равенство 3 × 2 = 6
Выразим число 3. Чтобы выразить число 3, нужно 6 разделить 2
Вернем получившееся равенство 
в первоначальное состояние:
3 × 2 = 6
Выразим из этого равенства число 2. Чтобы выразить число 2, нужно 6 разделить 3
Пример 4. Рассмотрим равенство 
Выразим из этого равенства число 15. Чтобы выразить число 15, нужно перемножить числа 3 и 5
15 = 3 × 5
Вернем получившееся равенство 15 = 3 × 5 в первоначальное состояние:
Выразим из этого равенства число 5. Чтобы выразить число 5, нужно 15 разделить 3
Правила нахождения уменьшаемого
При поиске уменьшаемого уравнение может выглядеть следующим образом: x-2=4. Мы имеем разность — результат вычитания и число, которое вычитаем. Необходимо найти уменьшаемое — самое большое число в примере. Формулировка правила: чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое.
Так, если мы вычитаем из неизвестного числа другое число и получаем результат, известный нам, то для поиска уменьшаемого необходимо сложить разность и вычитаемое. Простейший пример: дома были конфеты. Их количество мы не знаем. После того как Дима съел 2 конфеты, их осталось 4. Вопрос: сколько их всего было изначально? Для того чтобы узнать, прибавим 2 к 4 и получим результат — было 6 конфет. Для проверки вычтем 2 из 6. Получим результат 4 — решение верное.
Равносильные уравнения
В предыдущем примере при решении уравнения 3x + 9x + 16x = 56, мы привели подобные слагаемые в левой части уравнения. В результате получили новое уравнение 28x = 56. Старое уравнение 3x + 9x + 16x = 56 и получившееся новое уравнение 28x = 56 называют равносильными уравнениями, поскольку их корни совпадают.
Уравнения называют равносильными, если их корни совпадают.
Проверим это. Для уравнения 3x + 9x + 16x = 56 мы нашли корень равный 2. Подставим этот корень сначала в уравнение 3x + 9x + 16x = 56, а затем в уравнение 28x = 56, которое получилось в результате приведения подобных слагаемых в левой части предыдущего уравнения. Мы должны получить верные числовые равенства
Согласно порядку действий, в первую очередь выполняется умножение:
Подставим корень 2 во второе уравнение 28x = 56
Видим, что у обоих уравнений корни совпадают. Значит уравнения 3x + 9x + 16x = 56 и 28x = 56 действительно являются равносильными.
Для решения уравнения 3x + 9x + 16x = 56 мы воспользовались одним из тождественных преобразований — приведением подобных слагаемых. Правильное тождественное преобразование уравнения позволило нам получить равносильное уравнение 28x = 56, которое проще решать.
Из тождественных преобразований на данный момент мы умеем только сокращать дроби, приводить подобные слагаемые, выносить общий множитель за скобки, а также раскрывать скобки. Существуют и другие преобразования, которые следует знать. Но для общего представления о тождественных преобразованиях уравнений, изученных нами тем вполне хватает.
Рассмотрим некоторые преобразования, которые позволяют получить равносильное уравнение
Если к обеим частям уравнения прибавить одно и то же число, то получится уравнение равносильное данному.
и аналогично:
Если из обеих частей уравнения вычесть одно и то же число, то получится уравнение равносильное данному.
Другими словами, корень уравнения не изменится, если к обеим частям данного уравнения прибавить (или вычесть из обеих частей) одно и то же число.
Пример 1. Решить уравнение 
Вычтем из обеих частей уравнения число 10
Приведем подобные слагаемые в обеих частях:
Получили уравнение 5x = 10. Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x, нужно произведение 10 разделить на известный сомножитель 5.
Отсюда 
.
Вернемся к исходному уравнению 
и подставим вместо x найденное значение 2
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение 
мы вычли из обеих частей уравнения число 10. В результате получили равносильное уравнение 
. Корень этого уравнения, как и уравнения 
так же равен 2
Пример 2. Решить уравнение 4(x + 3) = 16
Раскроем скобки в левой части равенства:
Вычтем из обеих частей уравнения число 12
Приведем подобные слагаемые в обеих частях уравнения:
В левой части останется 4x, а в правой части число 4
Получили уравнение 4x = 4. Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x, нужно произведение 4 разделить на известный сомножитель 4
Отсюда 
Вернемся к исходному уравнению 4(x + 3) = 16 и подставим вместо x найденное значение 1
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение 4(x + 3) = 16 мы вычли из обеих частей уравнения число 12. В результате получили равносильное уравнение 4x = 4. Корень этого уравнения, как и уравнения 4(x + 3) = 16 так же равен 1
Пример 3. Решить уравнение 
Раскроем скобки в левой части равенства:
Прибавим к обеим частям уравнения число 8
Приведем подобные слагаемые в обеих частях уравнения:
В левой части останется 2x, а в правой части число 9
В получившемся уравнении 2x = 9 выразим неизвестное слагаемое x
Отсюда 
Вернемся к исходному уравнению 
и подставим вместо x найденное значение 4,5
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение 
мы прибавили к обеим частям уравнения число 8. В результате получили равносильное уравнение 
. Корень этого уравнения, как и уравнения 
так же равен 4,5
Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом
Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.
То есть корень уравнения не изменится, если мы перенесем слагаемое из одной части уравнения в другую, изменив его знак. Это свойство является одним из важных и одним из часто используемых при решении уравнений.
Рассмотрим следующее уравнение:
Корень данного уравнения равен 2. Подставим вместо x этот корень и проверим получается ли верное числовое равенство
Получается верное равенство. Значит число 2 действительно является корнем уравнения 
.
Теперь попробуем поэкспериментировать со слагаемыми этого уравнения, перенося их из одной части в другую, изменяя знаки.
Например, слагаемое 3x располагается в левой части равенства. Перенесём его в правую часть, изменив знак на противоположный:
Получилось уравнение 12 = 9x − 3x. Приведем подобные слагаемые в правой части данного уравнения:
Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Отсюда x = 2. Как видим, корень уравнения не изменился. Значит уравнения 12 + 3x = 9x и 12 = 9x − 3x являются равносильными.
На самом деле данное преобразование является упрощенным методом предыдущего преобразования, где к обеим частям уравнения прибавлялось (или вычиталось) одно и то же число.
Мы сказали, что в уравнении 12 + 3x = 9x слагаемое 3x было перенесено в правую часть, изменив знак. В реальности же происходило следующее: из обеих частей уравнения вычли слагаемое 3x
Затем в левой части были приведены подобные слагаемые и получено уравнение 12 = 9x − 3x. Затем опять были приведены подобные слагаемые, но уже в правой части, и получено уравнение 12 = 6x.
Но так называемый «перенос» более удобен для подобных уравнений, поэтому он и получил такое широкое распространение. Решая уравнения, мы часто будем пользоваться именно этим преобразованием.
Равносильными также являются уравнения 12 + 3x = 9x и 3x − 9x = −12. В этот раз в уравнении 12 + 3x = 9x слагаемое 12 было перенесено в правую часть, а слагаемое 9x в левую. Не следует забывать, что знаки этих слагаемых были изменены во время переноса
Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом:
Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение равносильное данному.
Другими словами, корни уравнения не изменятся, если обе его части умножить или разделить на одно и то же число. Это действие часто применяется тогда, когда нужно решить уравнение содержащее дробные выражения.
Сначала рассмотрим примеры, в которых обе части уравнения будут умножаться на одно и то же число.
Пример 1. Решить уравнение 
При решении уравнений, содержащих дробные выражения, сначала принято упростить это уравнение.
В данном случае мы имеем дело именно с таким уравнением. В целях упрощения данного уравнения обе его части можно умножить на 8:
Мы помним, что для умножения дроби на число, нужно числитель данной дроби умножить на это число. У нас имеются две дроби и каждая из них умножается на число 8. Наша задача умножить числители дробей на это число 8
Теперь происходит самое интересное. В числителях и знаменателях обеих дробей содержится множитель 8, который можно сократить на 8. Это позволит нам избавиться от дробного выражения:
В результате останется простейшее уравнение
Ну и нетрудно догадаться, что корень этого уравнения равен 4
Вернемся к исходному уравнению 
и подставим вместо x найденное значение 4
Получается верное числовое равенство. Значит уравнение решено правильно.
При решении данного уравнения мы умножили обе его части на 8. В результате получили уравнение 
. Корень этого уравнения, как и уравнения 
равен 4. Значит эти уравнения равносильны.
Множитель на который умножаются обе части уравнения принято записывать перед частью уравнения, а не после неё. Так, решая уравнение 
, мы умножили обе части на множитель 8 и получили следующую запись:
От этого корень уравнения не изменился, но если бы мы сделали это находясь в школе, то нам сделали бы замечание, поскольку в алгебре множитель принято записывать перед тем выражением, с которым он перемножается. Поэтому умножение обеих частей уравнения 
на множитель 8 желательно переписать следующим образом:
Пример 2. Решить уравнение 
Умнóжим обе части уравнения на 15
В левой части множители 15 можно сократить на 15, а в правой части множители 15 и 5 можно сократить на 5
Перепишем то, что у нас осталось:
Раскроем скобки в правой части уравнения:
Перенесем слагаемое x из левой части уравнения в правую часть, изменив знак. А слагаемое 15 из правой части уравнения перенесем в левую часть, опять же изменив знак:
Приведем подобные слагаемые в обеих частях, получим
Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Отсюда 
Вернемся к исходному уравнению 
и подставим вместо x найденное значение 5
Получается верное числовое равенство. Значит уравнение решено правильно. При решении данного уравнения мы умножили обе го части на 15. Далее выполняя тождественные преобразования, мы получили уравнение 10 = 2x. Корень этого уравнения, как и уравнения 
равен 5. Значит эти уравнения равносильны.
Пример 3. Решить уравнение 
Умнóжим обе части уравнения на 3
В левой части можно сократить две тройки, а правая часть будет равна 18
Останется простейшее уравнение 
. Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Отсюда 
Вернемся к исходному уравнению 
и подставим вместо x найденное значение 9
Получается верное числовое равенство. Значит уравнение решено правильно.
Пример 4. Решить уравнение 
Умнóжим обе части уравнения на 6
В левой части уравнения раскроем скобки. В правой части множитель 6 можно поднять в числитель:
Сократим в обеих частях уравнениях то, что можно сократить:
Перепишем то, что у нас осталось:
Раскроем скобки в обеих частях уравнения:
Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное x, сгруппируем в левой части уравнения, а слагаемые свободные от неизвестных — в правой:
Приведем подобные слагаемые в обеих частях:
Теперь найдем значение переменной x. Для этого разделим произведение 28 на известный сомножитель 7
Отсюда x = 4.
Вернемся к исходному уравнению 
и подставим вместо x найденное значение 4
Получилось верное числовое равенство. Значит уравнение решено правильно.
Пример 5. Решить уравнение 
Раскроем скобки в обеих частях уравнения там, где это можно:
Умнóжим обе части уравнения на 15
Раскроем скобки в обеих частях уравнения:
Сократим в обеих частях уравнения, то что можно сократить:
Перепишем то, что у нас осталось:
Раскроем скобки там, где это можно:
Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Не забываем, что во время переноса, слагаемые меняют свои знаки на противоположные:
Приведем подобные слагаемые в обеих частях уравнения:
Найдём значение x
В получившемся ответе можно выделить целую часть:
Вернемся к исходному уравнению и подставим вместо x найденное значение 
Получается довольно громоздкое выражение. Воспользуемся переменными. Левую часть равенства занесем в переменную A, а правую часть равенства в переменную B
Наша задача состоит в том, чтобы убедиться равна ли левая часть правой. Другими словами, доказать равенство A = B
Найдем значение выражения, находящегося в переменной А.
Значение переменной А равно 
. Теперь найдем значение переменной B. То есть значение правой части нашего равенства. Если и оно равно 
, то уравнение будет решено верно
Видим, что значение переменной B, как и значение переменной A равно 
. Это значит, что левая часть равна правой части. Отсюда делаем вывод, что уравнение решено правильно.
Теперь попробуем не умножать обе части уравнения на одно и то же число, а делить.
Рассмотрим уравнение 30x + 14x + 14 = 70x − 40x + 42. Решим его обычным методом: слагаемые, содержащие неизвестные, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Далее выполняя известные тождественные преобразования, найдем значение x
Подставим найденное значение 2 вместо x в исходное уравнение:
Теперь попробуем разделить все слагаемые уравнения 30x + 14x + 14 = 70x − 40x + 42 на какое-нибудь число. Замечаем, что все слагаемые этого уравнения имеют общий множитель 2. На него и разделим каждое слагаемое:
Выполним сокращение в каждом слагаемом:
Перепишем то, что у нас осталось:
Решим это уравнение, пользуясь известными тождественными преобразованиями:
Получили корень 2. Значит уравнения 15x + 7x + 7 = 35x − 20x + 21 и 30x + 14x + 14 = 70x − 40x + 42 равносильны.
Деление обеих частей уравнения на одно и то же число позволяет освобождать неизвестное от коэффициента. В предыдущем примере когда мы получили уравнение 7x = 14, нам потребовалось разделить произведение 14 на известный сомножитель 7. Но если бы мы в левой части освободили неизвестное от коэффициента 7, корень нашелся бы сразу. Для этого достаточно было разделить обе части на 7
Этим методом мы тоже будем пользоваться часто.
Уравнения с умножением и делением
После освоения уравнений на сложение и вычитание можно будет переходить к следующему уровню сложности. Это уравнения с умножением и делением.
Компоненты уравнения с умножением:
- Два множителя.
- Произведение.
Например, 3*x=6. Здесь 3 и x — множители, а 6 — произведение. Так, умножая одно число на другое, в результате получается произведение. То есть, если одно из этих чисел неизвестно, необходимо разделить произведение на известный множитель. В этом случае действует такое же правило, как и при сложении. При перестановке мест множителей произведение не меняется.
Компоненты уравнения с делением:
- Делимое.
- Делитель.
- Частное.
Возьмём простейший пример 8: x=4. Здесь делимое 8, делитель x, а частное — 4. Для поиска неизвестного делителя необходимо разделить делимое на частное. Для упрощения понимания можно представить это уравнение в виде элементарной задачи. В классе 8 учеников, которые разделились на группы по 4 человека. Вопрос: сколько получилось групп?
Есть ещё один вариант — с поиском делимого. Например, уравнение x:2=5. Для поиска делимого необходимо частное умножить на делитель. Пример задачи: 2 мальчика заработали по 5 долларов каждый, какова общая сумма их заработка?
Между делением и умножением похожая взаимосвязь, как между сложением и вычитанием. То есть для того, чтобы лучше решать уравнения с умножением, необходимо также решать их с делением и наоборот. Этот подход в тренировке навыка решения уравнений ускоряет мыслительный процесс.
Поиск неизвестных компонентов уравнения не такой уж и сложный. Главное — начинать с простого и регулярно решать уравнения с одним неизвестным. И тогда для вас будут открыты более сложные задачи — с двумя и более неизвестными.
Теги
Методы решения иррациональных уравнений
Разделы:
Математика
Я бы почувствовал настоящее
удовлетворение лишь в том случае,
если бы смог передать ученику гибкость ума,
которая дала бы ему в дальнейшем
возможность самостоятельно решать задачи.
У.У.Сойер.
Определение. Уравнение с одной
переменной 
называют иррациональным, если хотя бы
одна из функций 
или 
содержит переменную под знаком
радикала.
При решении иррациональных уравнений
необходимо установить область допустимых
значений переменных, исходя из условия, что все
радикалы, входящие в уравнение, должны быть
арифметическими.
1. Метод пристального взгляда
Этот метод основан на следующем теоретическом
положении: “Если функция 
возрастает в области
определения и число 
входит в множество значений, то уравнение 
имеет
единственное решение.”
Для реализации метода, основанного на этом
утверждении требуется:
а) Выделить функцию, которая фигурирует в
уравнении.
b) Записать область определения данной функции.
c) Доказать ее монотонность в области
определения.
d) Угадать корень уравнения.
t) Обосновать, что других корней нет.
f) Записать ответ.
Пример 1. 
.
Наличие радикалов четной степени говорит о том,
что подкоренные выражения должны быть
неотрицательными. Поэтому сначала найдем
область допустимых значение переменной 
.
Очевидно, что левая часть уравнения не
существует ни при одном значении неизвестного . Таким
образом, вопрос о решении уравнения снимается –
ведь нельзя же осуществить операцию сложения в
левой части уравнения, так как не существует сама
сумма. Каков же вывод? Уравнение не может иметь
решений, так как левая часть не существует ни при
одном значении неизвестного .
Пример 2. 
Рассмотрим функцию 
.
Найдем область определения данной функции:
Данная функция является монотонно
возрастающей.
Для 
эта функция будет принимать наименьшее значение
при 
, а
далее только возрастать.
. Число 5 принадлежит
области значения, следовательно, согласно
утверждению 
.
Проверкой убеждаемся, что это действительный
корень уравнения..
2. Метод возведения обеих частей уравнений в
одну и ту же степень.
Теорема.
Если возвести обе части уравнения 
(1) в
натуральную степень 
, то уравнение 
(2)
является следствием уравнения (1).
Доказательство. Если выполняется числовое
равенство 
, то по свойствам степени выполняется
равенство 
, т.е. каждый корень уравнения (1) является
и корнем уравнения (2), это значит, что уравнение (2)
является следствием уравнения (1).
Если 
,
то справедливо и обратная теорема. В этом случае
уравнения (1) и (2) равносильны.
Если 
,
равенство 
справедливо, если выполняется хотя бы
одно из равенств и 
. Значит уравнения (1) и (2) в этом
случае не равносильны. Поэтому, если в ходе
решения иррационального уравнения
приходилось возводить обе его части в степень с
четным показателем, то могли появиться
посторонние корни. Чтобы отделить их, проверки
можно избежать, введя дополнительное требование 
. В этом
случае уравнение 
равносильно системе 
. В
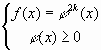
системе отсутствует требование 
,
обеспечивающее существование корня степени 
, т.к. оно
было бы излишним в связи с равенством 
.
Пример 1.
,
,
.
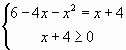
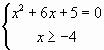
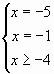
Ответ:
Если в уравнение входят несколько радикалов, то
их можно последовательно исключать с помощью
возведения в квадрат, получая в итоге уравнение
вида 
При этом полезно учитывать область допустимых
значений исходного уравнения.
Пример 2.
Ответ: 
3. Решение уравнений с использованием замены
переменной.
Введение вспомогательной переменной в ряде
случаев приводит к упрощению уравнения. Чаще
всего в качестве новой переменной используют
входящий в уравнение радикал. При этом уравнение
становится рациональным относительно новой
переменной.
Пример1.
Пусть 
тогда исходное уравнение примет вид:
,
корни которого 
и 
Решая уравнение 
, получаем 
и 
Ответ: 
В следующих примерах используется более
сложная замена переменной.
Пример 2
Перенесем в левую часть все члены уравнения и
произведем дополнительные преобразования: 
.
Замена 
приводит уравнение к виду 
корнями
которого являются 
и 
Осталось решить совокупность двух уравнений:
Ответ: 
4. Метод разложения на множители выражений,
входящих в уравнение.
Теорема.
Уравнение 
, определенное на всей числовой оси,
равносильно совокупности уравнений 
Пример1.
При 
уравнение принимает вид:
которое равносильно
совокупности двух уравнений: 
Ответ: 
Выделить общий множитель часто бывает очень
трудно. Иногда это удается сделать после
дополнительных преобразований. В приведенном
ниже примере для этого рассматриваются попарные
разности подкоренных выражений.
Пример 2.
Если внимательно посмотреть на уравнение, то
можно увидеть, что разности подкоренных
выражений первого и третьего , а также второго и
четвертого членов этого уравнения равны одной и
той же величине 
В таком случае далее следует воспользоваться
тождеством:
Уравнение примет вид:
или
Корень уравнения 
т.е. число 
при подстановке в исходное
уравнение дает верное равенство.
Уравнение 
не имеет решений, так как его левая часть
положительна в своей области определения.
Ответ:
5. Метод выделения полных квадратов при решении
иррациональных уравнений.
При решении некоторых иррациональных
уравнений полезна формула 
Пример 1.
Преобразуем уравнение следующим образом:
или
Обозначим 
и решим полученное уравнение
методом интервалов.
Разбирая отдельно случаи 
,
находим,
что решениями последнего уравнения являются 
.
Возвращаясь к переменной 
, получаем неравенства
Ответ:
6. Метод оценки.
Этот способ применим в том случае, когда
подкоренные выражения представляют собой
квадратный трехчлен, не раскладывающийся на
линейные множители. Поэтому целесообразно
оценить левую и правую части уравнения.
Пример 1.
Оценим обе части уравнения:
,
,
Левая часть уравнения существует при всех
значениях переменной , не меньших 5, а правая – при всех
значениях, не больших 5, следовательно, уравнение
будет иметь решение, если обе части уравнения
одновременно равны 5, т. е. справедлива следующая
система:
Корнем второго уравнения системы является
число 
Проверим, является ли это число корнем второго
уравнения:
.
Ответ:
Пример 2.
Для всех 
имеем
Используя неравенство Коши, можем записать:
причем равенство достигается при 
и 
Таким образом, 
-корень исходного уравнения.
Ответ: 
7. Иррациональные уравнения, содержащие
степени выше второй.
Если уравнение имеет вид 
то его можно решить , возводя
обе части этого уравнения в степень . Полученное
уравнение 
при нечетном равносильно данному уравнению, а при
четном является
нго следствием, аналогично рассмотренному выше
случаю при 
Пример 1
Возведем обе части уравнения в куб:
или
которое
равносильно совокупности двух уравнений:
Ответ: 
При решении иррациональных уравнений очень
часто пользуются следующим приемом.
Если 
то 
В последнем равенстве 
заменяют на 
и
получают 
Далее легко избавиться от кубической
иррациональности , возводя обе части в куб.
Пример 2.
Здесь, очевидно, 
Возведем в куб обе части уравнения, получим:
,
или
или
или
или
Проверка подтверждает, что это корень
уравнения.
Ответ: 
Замечание.
Замена в конкретном примере левой части на
правую, вообще говоря , неправомерна –ведь нам
неизвестно ни одно значение , при котором это
уравнение превращается в верное числовое
равенство. Возможно, таких решений нет вообще.
Допуская в практических действиях такую замену,
мы фактически расширяем возможное множество
решений. Поэтому все найденные решения следует
проверять и только те, которые превращают
исходное уравнение в верное равенство, следует
записать в ответ.
От того, что школьник решит лишний десяток
задач, умнее и сообразительнее он не станет,
Результат обучения оценивается не количеством
сообщаемой информации, а качеством ее усвоения.
Это качество будет выше, если на один и тот же
пример посмотреть с разных сторон. Решение задач
разными способами способствует развитию
активного мышления учащихся. Хорошую почву для
этого дает решение примеров разными способами.
Пример 3. Способ 1.
(1)
Возведем обе части уравнения в куб:
Группируя, получаем:
Используя равенство (1) имеем:
или
или
или
корни которого 
Ответ: 
Способ 2.
Иногда полезно ввести не одну вспомогательную
переменную, а несколько, сводя исходное
уравнение к системе уравнений.
Пусть 
Тогда 
Таким образом справедлива следующая система:
Возвращаясь к переменной 
находим
Ответ: 
В следующем примере введение вспомогательной
переменной сводит исходное уравнение к
однородному.
Пример 4.
Положим 
Тогда исходное уравнение примет вид:
Поскольку 
при котором переменная 
обращается в нуль, не является решением
исходного уравнения ( в чем можно убедиться
подстановкой), делим обе части уравнения на 
решая которое , находим: 
Осталось решить уравнения 
и 
Корнями этих уравнений являются числа 
Ответ: 
Пример 5.
Область допустимых значений задается
неравенством
Преобразуем уравнение следующим образом:
Один корень этого уравнения 
Для решения второго уравнения положим 
и решим 
Корни этого уравнения 
Последний корень не принадлежит указанному
промежутку, поэтому, решая уравнение 
, получим 
Ответ : 
8.02.2006
Факт 1.
(bullet) Возьмем некоторое неотрицательное число (a) (то есть (ageqslant 0)). Тогда (арифметическим) квадратным корнем из числа (a) называется такое неотрицательное число (b), при возведении которого в квадрат мы получим число (a): [sqrt a=bquad text{то же самое, что }quad a=b^2] Из определения следует, что (ageqslant 0, bgeqslant 0). Эти ограничения являются важным условием существования квадратного корня и их следует запомнить!
Вспомним, что любое число при возведении в квадрат дает неотрицательный результат. То есть (100^2=10000geqslant 0) и ((-100)^2=10000geqslant 0).
(bullet) Чему равен (sqrt{25})? Мы знаем, что (5^2=25) и ((-5)^2=25). Так как по определению мы должны найти неотрицательное число, то (-5) не подходит, следовательно, (sqrt{25}=5) (так как (25=5^2)).
Нахождение значения (sqrt a) называется извлечением квадратного корня из числа (a), а число (a) называется подкоренным выражением.
(bullet) Исходя из определения, выражения (sqrt{-25}), (sqrt{-4}) и т.п. не имеют смысла.
Факт 2.
Для быстрых вычислений полезно будет выучить таблицу квадратов натуральных чисел от (1) до (20): [begin{array}{|ll|}
hline
1^2=1 & quad11^2=121 \
2^2=4 & quad12^2=144\
3^2=9 & quad13^2=169\
4^2=16 & quad14^2=196\
5^2=25 & quad15^2=225\
6^2=36 & quad16^2=256\
7^2=49 & quad17^2=289\
8^2=64 & quad18^2=324\
9^2=81 & quad19^2=361\
10^2=100& quad20^2=400\
hline end{array}]
Факт 3.
Какие действия можно выполнять с квадратными корнями?
(bullet) Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть [sqrt apmsqrt bne sqrt{apm b}] Таким образом, если вам нужно вычислить, например, (sqrt{25}+sqrt{49}), то первоначально вы должны найти значения (sqrt{25}) и (sqrt{49}), а затем их сложить. Следовательно, [sqrt{25}+sqrt{49}=5+7=12] Если значения (sqrt a) или (sqrt b) при сложении (sqrt
a+sqrt b) найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме (sqrt
2+ sqrt {49}) мы можем найти (sqrt{49}) – это (7), а вот (sqrt
2) никак преобразовать нельзя, поэтому (sqrt 2+sqrt{49}=sqrt
2+7). Дальше это выражение, к сожалению, упростить никак нельзя
(bullet) Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть [sqrt acdot sqrt b=sqrt{ab}quad text{и}quad
sqrt a:sqrt b=sqrt{a:b}] (при условии, что обе части равенств имеют смысл)
Пример: (sqrt{32}cdot sqrt 2=sqrt{32cdot
2}=sqrt{64}=8);
(sqrt{768}:sqrt3=sqrt{768:3}=sqrt{256}=16);
(sqrt{(-25)cdot (-64)}=sqrt{25cdot 64}=sqrt{25}cdot sqrt{64}=
5cdot 8=40).
(bullet) Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
Рассмотрим пример. Найдем (sqrt{44100}). Так как (44100:100=441), то (44100=100cdot 441). По признаку делимости число (441) делится на (9) (так как сумма его цифр равна 9 и делится на 9), следовательно, (441:9=49), то есть (441=9cdot 49).
Таким образом, мы получили: [sqrt{44100}=sqrt{9cdot 49cdot 100}=
sqrt9cdot sqrt{49}cdot sqrt{100}=3cdot 7cdot 10=210] Рассмотрим еще один пример: [sqrt{dfrac{32cdot 294}{27}}=
sqrt{dfrac{16cdot 2cdot 3cdot 49cdot 2}{9cdot 3}}= sqrt{
dfrac{16cdot4cdot49}{9}}=dfrac{sqrt{16}cdot sqrt4 cdot
sqrt{49}}{sqrt9}=dfrac{4cdot 2cdot 7}3=dfrac{56}3]
(bullet) Покажем, как вносить числа под знак квадратного корня на примере выражения (5sqrt2) (сокращенная запись от выражения (5cdot
sqrt2)). Так как (5=sqrt{25}), то [5sqrt2=sqrt{25}cdot sqrt2=sqrt{25cdot 2}=sqrt{50}] Заметим также, что, например,
1) (sqrt2+3sqrt2=4sqrt2),
2) (5sqrt3-sqrt3=4sqrt3)
3) (sqrt a+sqrt a=2sqrt a).
Почему так? Объясним на примере 1). Как вы уже поняли, как-то преобразовать число (sqrt2) мы не можем. Представим, что (sqrt2) – это некоторое число (a). Соответственно, выражение (sqrt2+3sqrt2) есть не что иное, как (a+3a) (одно число (a) плюс еще три таких же числа (a)). А мы знаем, что это равно четырем таким числам (a), то есть (4sqrt2).
Факт 4.
(bullet) Часто говорят “нельзя извлечь корень”, когда не удается избавиться от знака (sqrt {} ) корня (радикала) при нахождении значения какого-то числа. Например, извлечь корень из числа (16) можно, потому что (16=4^2), поэтому (sqrt{16}=4). А вот извлечь корень из числа (3), то есть найти (sqrt3), нельзя, потому что нет такого числа, которое в квадрате даст (3).
Такие числа (или выражения с такими числами) являются иррациональными. Например, числа (sqrt3, 1+sqrt2, sqrt{15}) и т.п. являются иррациональными.
Также иррациональными являются числа (pi) (число “пи”, приблизительно равное (3,14)), (e) (это число называют числом Эйлера, приблизительно оно равно (2,7)) и т.д.
(bullet) Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой (mathbb{R}).
Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.
Факт 5.
(bullet) Модуль вещественного числа (a) – это неотрицательное число (|a|), равное расстоянию от точки (a) до (0) на вещественной прямой. Например, (|3|) и (|-3|) равны 3, так как расстояния от точек (3) и (-3) до (0) одинаковы и равны (3). 
(bullet) Если (a) – неотрицательное число, то (|a|=a).
Пример: (|5|=5); (qquad |sqrt2|=sqrt2).
(bullet) Если (a) – отрицательное число, то (|a|=-a).
Пример: (|-5|=-(-5)=5); (qquad |-sqrt3|=-(-sqrt3)=sqrt3).
Говорят, что у отрицательных чисел модуль “съедает” минус, а положительные числа, а также число (0), модуль оставляет без изменений.
НО такое правило годится только для чисел. Если у вас под знаком модуля находится неизвестная (x) (или какая-то другая неизвестная), например, (|x|), про которую мы не знаем, положительная она, равна нулю или отрицательная, то избавиться от модуля мы не можем. В этом случае это выражение таким и остается: (|x|).
(bullet) Имеют место следующие формулы: [{large{sqrt{a^2}=|a|}}] [{large{(sqrt{a})^2=a}},
text{ при условии } ageqslant 0] Очень часто допускается такая ошибка: говорят, что (sqrt{a^2}) и ((sqrt a)^2) – одно и то же. Это верно только в том случае, когда (a) – положительное число или ноль. А вот если (a) – отрицательное число, то это неверно. Достаточно рассмотреть такой пример. Возьмем вместо (a) число (-1). Тогда (sqrt{(-1)^2}=sqrt{1}=1), а вот выражение ((sqrt {-1})^2) вообще не существует (ведь нельзя под знак корня помещать отрицательные числа!).
Поэтому обращаем ваше внимание на то, что (sqrt{a^2}) не равен ((sqrt a)^2)!
Пример: 1) (sqrt{left(-sqrt2right)^2}=|-sqrt2|=sqrt2), т.к. (-sqrt2<0);
(phantom{00000}) 2) ((sqrt{2})^2=2).
(bullet) Так как (sqrt{a^2}=|a|), то [sqrt{a^{2n}}=|a^n|] (выражение (2n) обозначает четное число)
То есть при извлечении корня из числа, находящегося в какой-то степени, эта степень уменьшается в два раза.
Пример:
1) (sqrt{4^6}=|4^3|=4^3=64)
2) (sqrt{(-25)^2}=|-25|=25) (заметим, что если модуль не поставить, то получится, что корень из числа равен (-25); но мы помним, что по определению корня такого быть не может: у нас всегда при извлечении корня должно получаться положительное число или ноль)
3) (sqrt{x^{16}}=|x^8|=x^8) (так как любое число в четной степени неотрицательно)
Факт 6.
Как сравнить два квадратных корня?
(bullet) Для квадратных корней верно: если (sqrt a<sqrt b), то (a<b); если (sqrt a=sqrt b), то (a=b).
Пример:
1) сравним (sqrt{50}) и (6sqrt2). Для начала преобразуем второе выражение в (sqrt{36}cdot sqrt2=sqrt{36cdot 2}=sqrt{72}). Таким образом, так как (50<72), то и (sqrt{50}<sqrt{72}). Следовательно, (sqrt{50}<6sqrt2).
2) Между какими целыми числами находится (sqrt{50})?
Так как (sqrt{49}=7), (sqrt{64}=8), а (49<50<64), то (7<sqrt{50}<8), то есть число (sqrt{50}) находится между числами (7) и (8).
3) Сравним (sqrt 2-1) и (0,5). Предположим, что (sqrt2-1>0,5): [begin{aligned}
&sqrt 2-1>0,5 big| +1quad text{(прибавим единицу к обеим
частям)}\[1ex]
&sqrt2>0,5+1 big| ^2 quadtext{(возведем обе части в
квадрат)}\[1ex]
&2>1,5^2\
&2>2,25 end{aligned}] Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и (sqrt 2-1<0,5).
Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
Возводить обе части уравнения/неравенства в квадрат можно ТОЛЬКО ТОГДА, когда обе части неотрицательные. Например, в неравенстве из предыдущего примера возводить обе части в квадрат можно, в неравенстве (-3<sqrt2) нельзя (убедитесь в этом сами)!
(bullet) Следует запомнить, что [begin{aligned}
&sqrt 2approx 1,4\[1ex]
&sqrt 3approx 1,7 end{aligned}] Знание приблизительного значения данных чисел поможет вам при сравнении чисел!
(bullet) Для того, чтобы извлечь корень (если он извлекается) из какого-то большого числа, которого нет в таблице квадратов, нужно сначала определить, между какими “сотнями” оно находится, затем – между какими “десятками”, а потом уже определить последнюю цифру этого числа. Покажем, как это работает, на примере.
Возьмем (sqrt{28224}). Мы знаем, что (100^2=10,000), (200^2=40,000) и т.д. Заметим, что (28224) находится между (10,000) и (40,000). Следовательно, (sqrt{28224}) находится между (100) и (200).
Теперь определим, между какими “десятками” находится наше число (то есть, например, между (120) и (130)). Также из таблицы квадратов знаем, что (11^2=121), (12^2=144) и т.д., тогда (110^2=12100), (120^2=14400), (130^2=16900), (140^2=19600), (150^2=22500), (160^2=25600), (170^2=28900). Таким образом, мы видим, что (28224) находится между (160^2) и (170^2). Следовательно, число (sqrt{28224}) находится между (160) и (170).
Попробуем определить последнюю цифру. Давайте вспомним, какие однозначные числа при возведении в квадрат дают на конце (4)? Это (2^2) и (8^2). Следовательно, (sqrt{28224}) будет заканчиваться либо на 2, либо на 8. Проверим это. Найдем (162^2) и (168^2):
(162^2=162cdot 162=26224)
(168^2=168cdot 168=28224).
Следовательно, (sqrt{28224}=168). Вуаля!