Прежде чем перейти к изучению темы «Нули функции»
внимательно изучите уроки
«Что такое функция в математике»
и
«Как решать задачи на функцию».
Запомните!
Нули функции — это
значения « x »
(аргумента функции),
при которых « y = 0 ».
В заданиях «Найдите нули функции» чаще всего сама функция задана через формулу
(аналитически). Разберем алгоритм решения
подобных задач.
Как найти нули функции, заданной формулой
Важно!
Чтобы найти нули функции, нужно:
- в формулу функции вместо
« у » (или « f(x) »,
« g(x) » и т.п.)
подставить «0»; - решить полученное уравнение
относительно « x »; - записать полученные решения уравнения для « x » в ответ.
По традиции разберемся на примере.
Разбор примера
Найдите нули функции:
Подставим вместо значения функции « f(x) » ноль.
0 = 0,2x + 3
Решаем полученное линейное уравнение
и записываем полученный ответ
для « x ».
Перенесем неизвестное « 0,2x » из правой части уравнения в левую с
противоположным
знаком.
−0,2x = 3 | · (−1)
0,2x = −3
Переведем десятичную дробь «0,2» в
обыкновненную для упрощения дальнейших расчетов.
0,2x = −3
· x = −3 | · 10
· x · 10 = −3 · 10
· x = −30
2x = −30
x =
x = −15
Ответ: x = −15 является нулем
функции f(x) = 0,2x + 3
Разбор примера
Найдите нули функции:
Вместо « f(x) » подставим ноль.
0 = x 3 − 4x
−x 3 + 4x = 0 | · (−1)
(−1) · (−x 3 + 4x) = 0 · (−1)
x 3 − 4x = 0
Вынесем общий множитель
« x » за скобки.
В левой части полученного уравнения у нас два множителя:
« x »
и «(x 2 − 4)». Результат их умножения равен нулю.
Это возможно, когда любой
из множителей равен нулю. Поэтому рассмотрим оба варианта: когда множитель
« x » равен нулю и когда множитель «(x 2 − 4)»
равен нулю.
Решаем квадратное уравнение
«x 2 − 4 = 0».
Используем формулу
для решения квадратного уравнения с дискриминантом.
a · x 2 + b · x + c = 0
x1;2 =
x 2 − 4 = 0
x1;2 =
| 0 ± √02 − 4 · 1 · (−4) |
| 2 · 1 |
x1;2 =
x1;2 =
Запишем все полученные корни уравнений в ответ в порядке возрастания. Они будут являться нулями функции.
Ответ: x = −2; x = 0; x = 2 являются нулями функции
f(x) = x 3 − 4x
Разбор примера
Найдите нули функции:
Подставим вместо « h(x) » ноль.
Перенесем правую часть
в левую, изменив ее знак на минус.
Единственный вариант, когда дробь будет равна нулю, только если
ее числитель
«x 2 − x − 6» будет равен нулю. Знаменатель
«x + 3» не может быть равен нулю, так как на ноль делить нельзя.
Решим полученное квадратное уравнение через формулу с дискриминантом.
a · x 2 + b · x + c = 0
x1;2 =
x 2 − x − 6 = 0
x1;2 =
| −(−1) ± √(−1)2 − 4 · 1 · (−6) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
| x1 = | x2 = |
| x1 = | x2 = |
| x1 = 3 | x2 = −2 |
Ответ: x = −2; x = 3 являются нулями функции
h(x) =
Разбор примера
Найдите нули функции:
Заменим «f(x)» на ноль.
Единственное число, квадратный корень которого равен нулю — это сам ноль.
Поэтому, квадратный корень
«√ x 2 − 4 = 0 »
будет равен нулю, когда его подкоренное выражение
« x 2 − 4 »
будет равно нулю.
Осталось решить полученное квадратное уравнение, чтобы найти нули функции
«f(x) = √x 2 − 4».
x1;2 =
x 2 − 4 = 0
x1;2 =
| −(−0) ± √(−0)2 − 4 · 1 · (−4) |
| 2 · 1 |
x1;2 =
x1;2 =
Ответ: x = −2; x = 2 являются нулями
функции f(x) = √x 2 − 4
Как найти нули функции на графике функции
Важно!
Графически нули функции — это точки пересечения графика функции
с осью «Ox»
(осью абсцисс).
По определению
нули функции — это значения « x »,
при которых
« y = 0 ». Другими словами, у точек
графика функции, которые являются нулями функции,
координата « x » равна нулю.
Чтобы найти нули функции на графике
нам остается, только найти, какая у них
координата
по оси « Ox ».
Рассмотрим на примере.
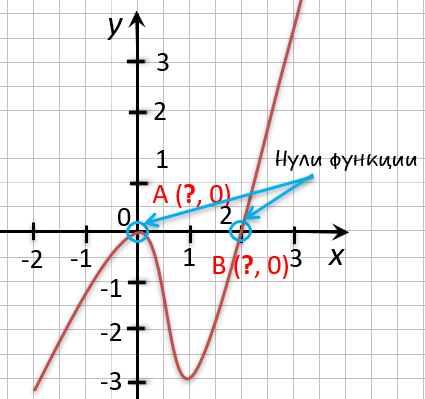
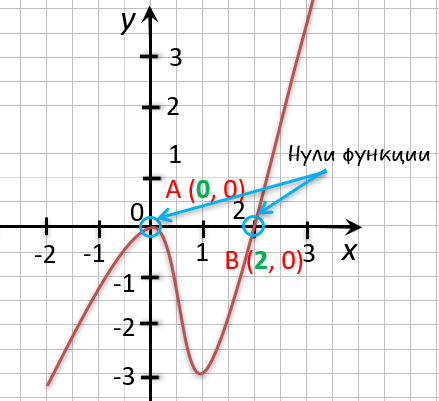
Разбор примера
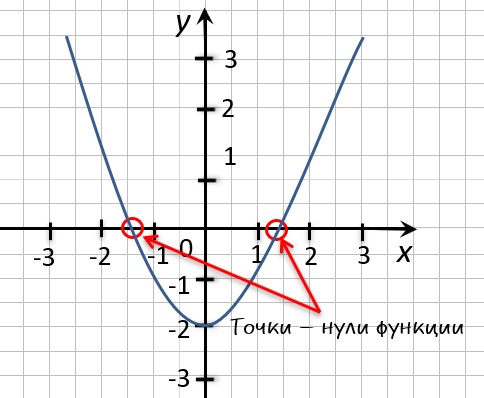
На рисунке ниже изображен график функции « y = f(x) », определенной на множестве действительных чисел. Используя график,
найдите нули функции.
Отметим на графике функции его точки пересечения с осью « Ox ».
Назовем полученные точки «(·)А» и «(·)B».
В точках «(·)А» и «(·)B» график функции пересекает
ось
« Ox » , то есть координаты точки «(·)А» и «(·)B»
по оси « Oy »
равны нулю.
Точки «(·)А» и «(·)B»
— нули функции. Теперь определим, чему равны их координаты по оси « Ox ».
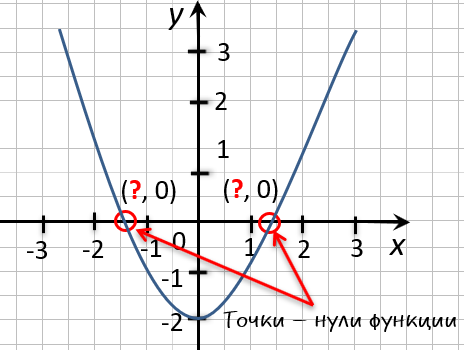
На графике видно, что у точки «(·)А» координата « x » равна
« 0 », а у точки «(·)B» координата « x » равна
« 2 ».
Запишем полученные значения координат « x » в ответ.
Ответ: x = 0; x = 2 являются нулями функции.
Как найти нули функции, заданной таблицей
В некоторых заданиях, где требуется найти нули функции, сама функция задана не вполне привычно с помощью формулы,
а с помощью таблицы. Поиск нулей в таких примерах является легкой задачей.
Разбор примера
Найдите нули функции, заданной таблицей.
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −3 | −1,5 | 0 | 2 | 1 | 0 |
Вспомним определение нулей функции.
Запомните!
Нули функции — это
значения « x » в функции,
при которых « y = 0 ».
Согласно определению нулей функции нам достаточно найти значения « x » в таблице,
где
« y = 0 ». Выделим их цветом.
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −3 | −1,5 | 0 | 2 | 1 | 0 |
Остаётся только записать в ответ значения « x » из таблицы.
Ответ: x = 0; x = 3 являются нулями функции, заданной таблицей.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
На этой странице вы узнаете
- Как мы ежедневно расставляем знаки неравенства в жизни?
- Как быстро определить верное обозначение точки на прямой?
- Как правильно чередовать знаки на числовой прямой?
Решая уравнение, мы стремимся к тому, чтобы обе части были равны. Но существуют такие примеры, где мы заведомо знаем, что два выражения не могут быть равны между собой. Они называются неравенствами.
Метод интервалов
Неравенство — это алгебраическое выражение, в котором одна сторона имеет отличное от другой значение. В неравенствах обычно одна сторона больше другой.
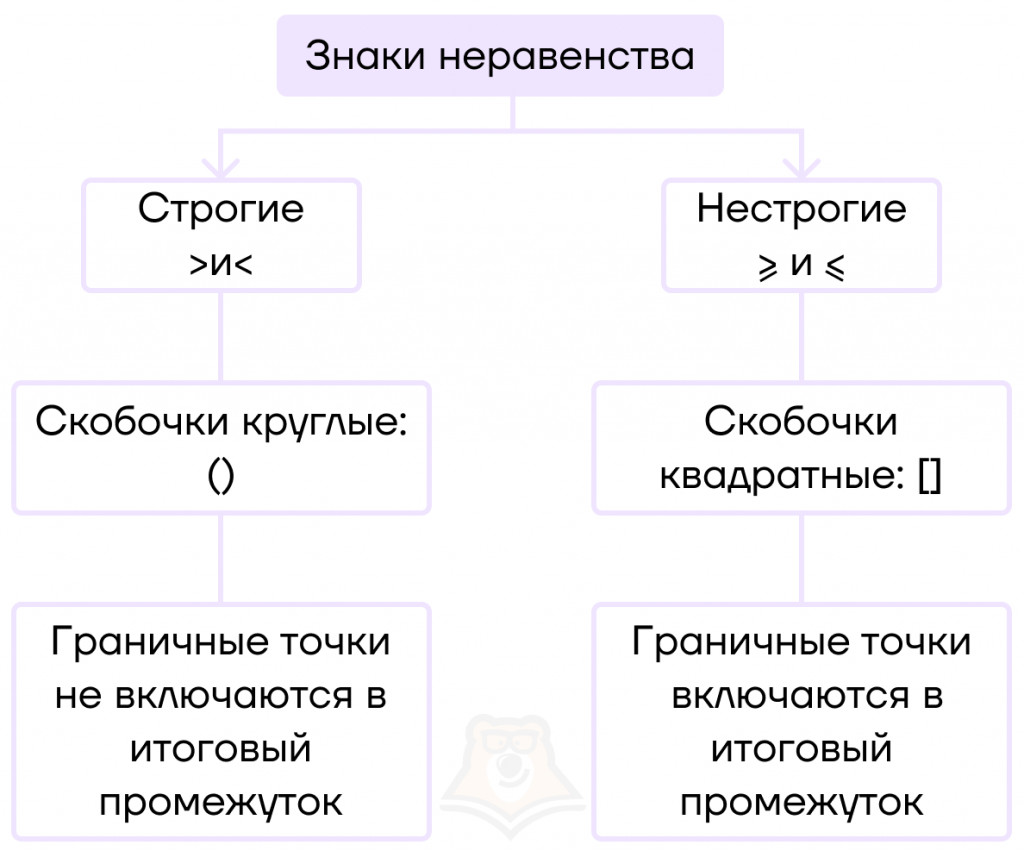
Для записи неравенств используют знаки > , < , ≥ , ≤ .
При этом “>” и “<” — это строгие знаки неравенства, а “≥” и “≤” — нестрогие знаки неравенства.
Их отличие в том, что нестрогие знаки неравенства включают граничные точки в итоговый промежуток, а строгие — нет.
Посмотрим на привычные ситуации с точки зрения строгости знаков неравенства.
Например, возьмем известную игру “Камень, ножницы, бумага”.
Правила игры говорят нам, что камень всегда побеждает ножницы, а бумага побеждает камень. Если перенести это на язык неравенства, то получится:
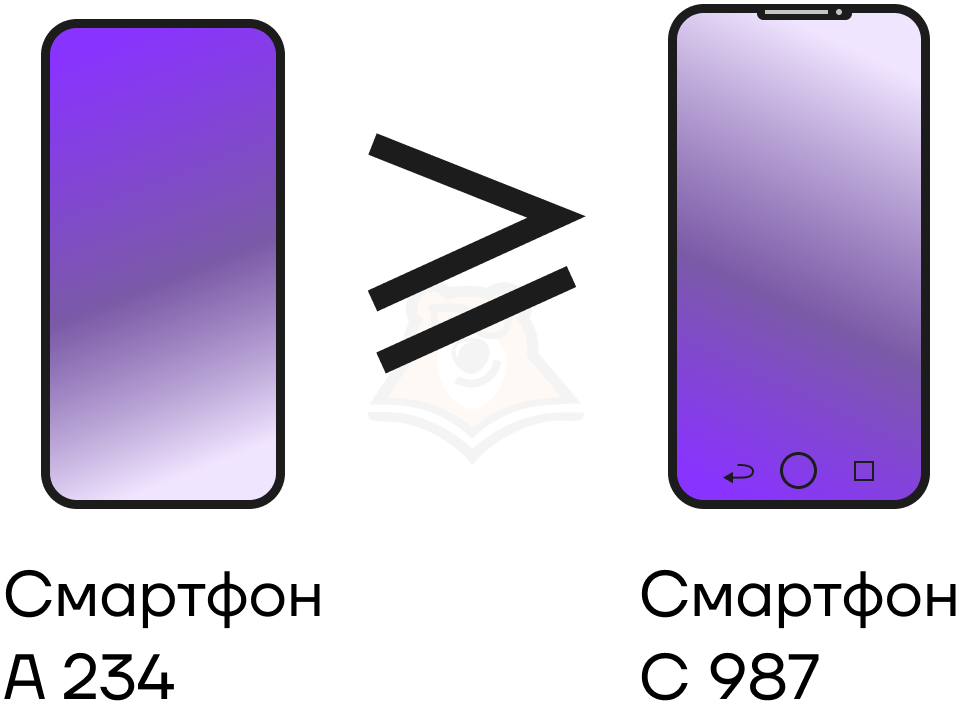
Теперь зайдем в магазин цифровой техники и попробуем выбрать себе новый мобильный телефон. Задачка непростая, не так ли? Две разные модели могут настолько незначительно отличаться друг от друга своими характеристиками, что будут казаться почти одинаковыми. Тогда мы можем сказать, что они практически равны между собой, то есть неравенство нестрогое. Но один из них всё-таки понравился нам больше.
И каждый наш выбор, каждый шаг – это расстановка знака неравенства в настоящей жизни. Просто по бокам от него не цифры и переменные, а существующие ситуации и вещи.
Рассмотрим пример неравенства (х — 10)(х + 21) > 0.

Его можно решить несколькими способами. Например, вспомним, что положительным будет произведение двух положительных или двух отрицательных множителей, тогда получается совокупность из двух систем.
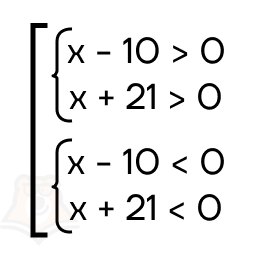
Однако этот способ решения очень трудоемкий и требует много времени. А если множителей будет больше, например, три или четыре, то время на решение в разы увеличивается.
Небольшой секрет тайм-менеджмента: как сократить время при решении неравенств? В таких случаях на помощь приходит метод интервалов.
Метод интервалов — специальный алгоритм решения для сложных неравенств вида f(x) > 0. При этом знак неравенства может быть любым.
Интервал — это промежуток на числовой прямой, ограниченный двумя различными числами.
Алгоритм решения неравенств методом интервалов
1 шаг. Перенести все части неравенства в одну сторону так, чтобы с другой остался только 0.
2 шаг. Найти нули функции, для этого необходимо решить уравнение f(x) = 0.
3 шаг. Начертить числовую прямую и отметить на ней все полученные корни. Таким образом, числовая прямая разобьется на интервалы.
4 шаг. Определить знаки на каждом интервале. Для этого необходимо подставить любое удобное значение в f(x) и определить, какой знак будет иметь функция на данном интервале.
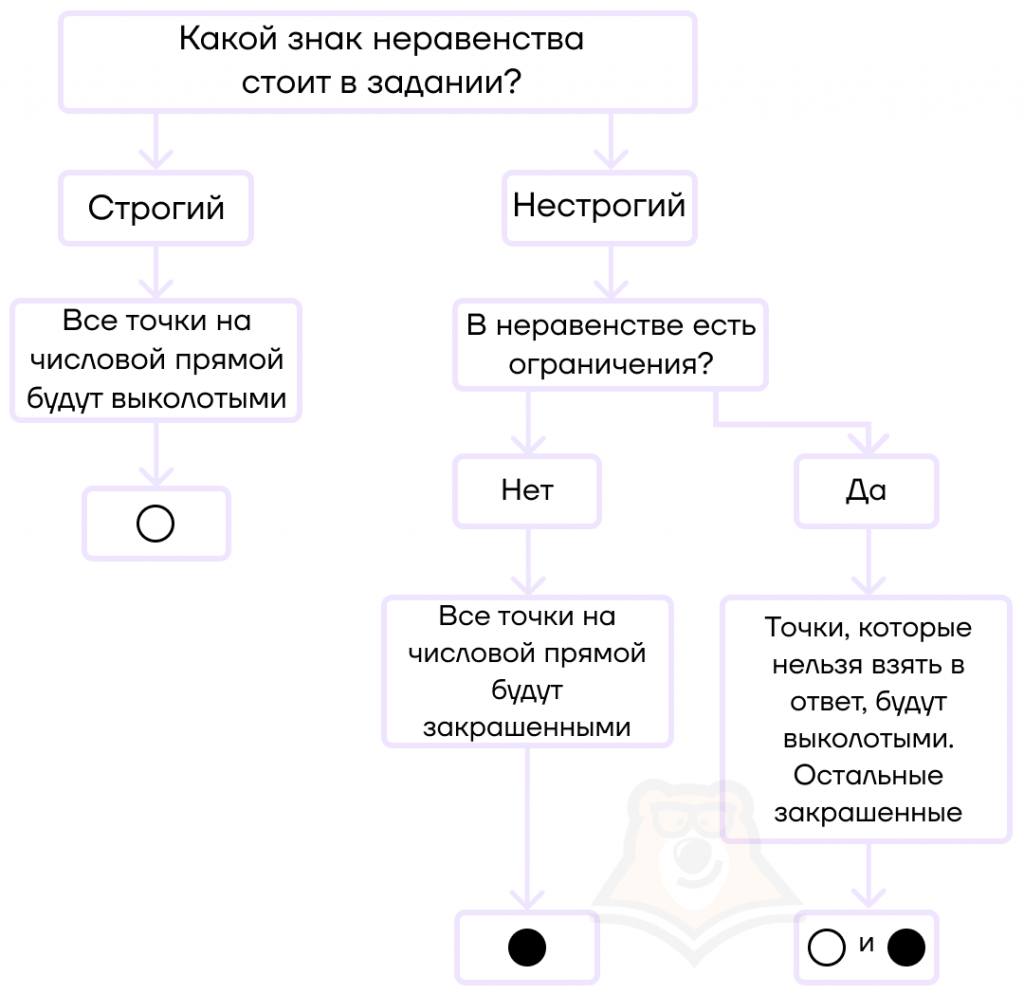
Расставляя полученные корни на прямой, необходимо отмечать их точками. При этом от того, какая отмечена точка (выколотая или закрашенная), будет зависеть ответ.
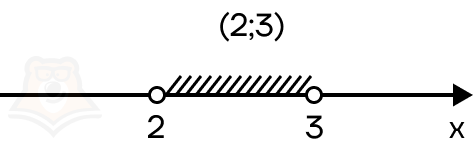
- Если в неравенстве стоит строгий знак неравенства, то все точки на прямой должны быть выколотыми.
Таким образом, граничные точки не будут включены в итоговый промежуток. Для записи таких точек используют круглые скобочки. Например, в промежуток (2;3) включаются все значения от 2 до 3, но не включаются граничные точки.
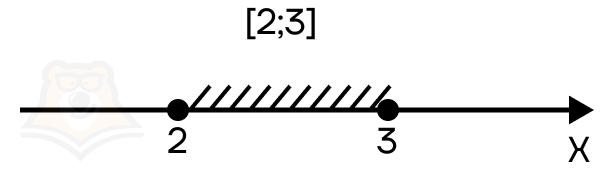
- Если в неравенстве стоит нестрогий знак неравенства, то найденные корни должны быть отмечены закрашенными точками.
Это означает, что мы включаем их в итоговый промежуток. Для записи таких точек используют квадратные скобочки. Например, в промежуток [2;3] включаются все значения от 2 до 3, в том числе и граничные точки.
- Если в неравенстве появляются ограничения и некоторые точки нельзя взять в ответ, то такие точки должны быть выколотыми на числовой прямой, при этом знак самого неравенства может быть как строгим, так и нестрогим.
Например, если необходимо решить неравенство с дробью, то нули знаменателя на числовой прямой обязательно должны быть обозначены выколотыми точками.
В случае сомнений мы всегда можем проверить себя по простой схеме.
Вывод:
— если знак неравенства строгий, то все точки будут выколотыми;
— если знак неравенства нестрогий, то точки будут закрашенными, кроме тех точек, которые нельзя взять в ответ (например, они не удовлетворяют ОДЗ).
Стоит отметить, что непрерывная функция будет менять знак только в точках, в которых она равна 0. Подробнее узнать про смену знака функции можно в статье «Определение и график функции». Именно поэтому в методе интервалов мы ищем и отмечаем нули функции на прямой — только при переходе через них будет меняться знак функции.
При этом существует способ, с помощью которого можно быстро расставить знаки на прямой. Достаточно определить знак на одном из интервалов, а дальше чередовать знаки при переходе через каждую точку на прямой.
Правила чередования знаков:
- Если корень повторяется нечетное количество раз (то есть его степень нечетная), то знак при переходе на следующий интервал меняется.
- Если корень повторяется четное количество раз (его степень четная), то знак при переходе на следующий интервал не меняется.
Всегда будет нелишним перепроверить знак на каждом интервале, подставив значения в функцию, и убедиться в правильности расстановки знаков на прямой.
Но при расстановке можно пользоваться следующим алгоритмом, что значительно сократит время расстановки знаков.
Методом интервалов можно решить практически любое неравенство в задании 14 из ЕГЭ по профильной математике, также он может понадобиться в заданиях 8, 11 и 17 «профиля» или в задании 17 ЕГЭ по базовой математике.
На ОГЭ данным методом можно воспользоваться при решении неравенств из первой и второй частей — №13 и №20.
Так что осваивайте метод и 2 балла ЕГЭ или 3 балла ОГЭ будут у вас в кармане. Обязательно следуйте алгоритму решения неравенств методом интервалов, тогда вы точно решите неравенство верно.
Практика
Рассмотрим несколько примеров, чтобы на практике разобрать применение метода интервалов для решения неравенств.
Пример 1. Решить неравенство x2 + 8x — 33 > 0.
Шаг 1. Первым шагом необходимо найти нули функции, для этого приравниваем выражение слева к 0: x2 + 8x — 33 = 0.
Шаг 2. Находим корни уравнения, получаем х = 3 и х = -11.
Шаг 3. Расставляем полученные корни на числовой прямой. Поскольку знак неравенства строгий, то точки должны быть выколотыми:

Шаг 4. Дальше необходимо определить знаки на каждом интервале. Для этого подставим х = -12 в x2 + 8x — 33. Получаем:
(-12)2 + 8*(-12) — 33 = 144 — 96 — 33 = 15.
Получается положительное число, следовательно, интервал от минус бесконечности до -11 положительный. Поскольку все корни в неравенстве повторяются нечетное количество раз (по одному разу), то знаки чередуются.
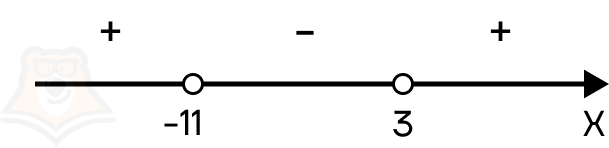
В ответ необходимо записать промежутки с положительным знаком, следовательно, ответом будет х ∈ (-∞; -11) U (3; +∞).
Пример 2. Решить неравенство (frac{2х^2 + 22х — 204}{(х-3)(х+5)} ≤ 0).
1. Находим нули функции.
Нули числителя: 2х2 + 22х — 204 = 0. Решая уравнение, получаем х = 6 и х = -17.
Нули знаменателя: (х — 3)(х + 5) = 0, следовательно, х = 3 и х = -5.
2. Расставляем полученные корни на числовой прямой. Нули числителя будут обозначены закрашенными точками, поскольку знак неравенства нестрогий. А вот нули знаменателя — выколотыми, поскольку знаменатель не может равняться 0, следовательно, и нули знаменателя не должны входить в итоговый промежуток.

3. Определяем знак на крайнем левом промежутке, подставляя х=-20 в дробь:
(frac{2(-20)^2 + 22(-20) — 204}{(-20 -3)(-20 +5)} = frac{2 * 400 — 440 — 204}{(-23) * (-15)} = 156345. )
Следовательно, промежуток положительный.
4. Поскольку каждый корень встречается один раз, то есть нечетное количество раз, то знаки будут чередоваться.

В ответ необходимо включить отрицательные промежутки. Следовательно, ответом будет х ∈ [-17; -5) U (3; 6].
Пример 3. Решить неравенство (frac{1}{х^2} ≥ frac{1}{х+2})
1. Первым делом следует отметить, что знаменатели не могут быть равны 0, следовательно, х2 ≠ 0 и х + 2 ≠ 0, отсюда получаем х ≠ 0 и х ≠ -2.
2. Теперь перенесем все части неравенства влево:
(frac{1}{х^2} — frac{1}{х+2} ≥ 0).
Приведем к общему знаменателю:
(frac{х + 2 — х^2}{х^2 (х + 2)} ≥ 0).
Для решения неравенства будет удобнее, если перед х2 в числителе будет стоять положительный знак, для этого умножим неравенство на -1.
При умножении неравенства на отрицательное число знак неравенства меняется на противоположный.
Получаем:
(frac{х^2 — х — 2}{х^2 (х + 2)} ≤ 0).
Теперь найдем нули функции.
Нули числителя: х2 — х — 2 = 0. Тогда х = -1 и х = 2.
Нули знаменателя: х = 0 и х = -2.
2. Расставим корни на числовой прямой, при этом нули числителя будут обозначены закрашенными точками, а нули знаменателя — выколотыми.

3. Определим знак на крайнем левом промежутке, подставив для этого х = -3 в дробь:
(frac{(-3)^2 — (-3) — 2}{(-3)^2 ((-3) + 2)} = frac{9 + 3 — 2}{9 * (-1)} = frac{10}{-9})
Промежуток отрицательный.
4. Дальше расставляем знаки, чередуя их. При этом следует заметить, что х = 0 — корень, повторяющийся четное количество раз (поскольку у х2 четная степень). Следовательно, при переходе через эту точку знак функции меняться не будет.

В ответ необходимо включить отрицательные промежутки, следовательно: х ∈ (-∞; -2) U [-1; 0) U (0; 2].
Давайте подведем итог. Для чего мы это изучили?
Конечно же, эти знания пригодятся на экзаменах, а также в решении школьных примеров с 8 класса по 11 класс.
Советуем после прочтения этой статьи попрактиковаться в рубрике «Проверь себя», чтобы закрепить полученные знания. После чего можете приступить к решению заданий посложнее, чтобы на экзамене у вас точно получилось решить подобные задания и набрать за них максимум баллов.
Фактчек
- Метод интервалов позволяет упростить решение любого неравенства, а также экономит время, которое ограничено на экзамене.
- Чтобы решить неравенство с помощью метода интервалов необходимо найти нули функции, расставить их на числовой прямой, а после определить знак каждого полученного интервала.
- Нули функции на прямой обозначаются точками, при этом закрашенные точки включают граничные значения в итоговый промежуток, а незакрашенные, напротив, исключают их из промежутка.
- Для определения знака на каждом интервале необходимо подставить любое значение из этого интервала в функцию.
- Для упрощения расстановки знаков можно пользоваться правилами чередования, определив знак только на одном интервале, а дальше менять знаки на каждом следующем. При этом если корень встречается в функции нечетное количество раз, то знак при переходе через эту точку на следующий интервал меняется, а если корень встречается четное количество раз, то знак на следующем интервале не меняется.
Проверь себя
Задание 1.
Какие знаки неравенства существуют?
- Строгие
- Нестрогие
- Строгие и нестрогие
- Больше и меньше
Задание 2.
Какой знак неравенства может встретиться в методе интервалов?
- Только больше или меньше.
- Только “больше или равно” или “меньше или равно”.
- Только “больше” и “больше или равно” или только “меньше” и “меньше или равно”.
- Любой.
Задание 3.
Какое утверждение верное?
- Если в неравенстве строгий знак неравенства, то точки на числовой прямой закрашены.
- Если в неравенстве строгий знак неравенства, то точки на числовой прямой выколоты.
- Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой закрашены, даже если в неравенстве есть ограничения.
- Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой выколоты.
Задание 4.
Какое утверждение верное?
- При переходе на числовой прямой на следующий интервал, знак на интервале всегда будет меняться.
- Если корень встречается в неравенстве четное количество раз, то при переходе через него на следующий интервал знак не меняется.
- Если корень встречается в неравенстве нечетное количество раз, то при переходе через него на следующий интервал знак не меняется.
- Невозможно определить правильное чередование знаков на прямой, не подставляя значение из каждого интервала в функцию.
Задание 5.
Если в неравенстве строгий знак неравенства, то какие скобочки могут встретиться в ответе?
- Круглые
- Квадратные
- И круглые, и квадратные
- Ни один из перечисленных вариантов
Ответы: 1. — 3 2. — 4 3. — 2 4. — 2 5. — 1
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства
Остановимся подробнее на свойствах функций.
Нули функции
Определение
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.
График функции у=k/x выглядит следующим образом: 
- Для того чтобы найти нули функции, которая задана формулой, надо подставить вместо у число нуль и решить полученное уравнение.
- Если график функции дан на рисунке, то ищем точки пересечения графика с осью х.
Рассмотрим примеры нахождения нулей функции. Пример №1. Найти нули функции (если они существуют):
- а) у= –11х +22
- б) у= (х + 76)(х – 95)
- в) у= – 46/х
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
- Находим х, разделив 22 на 11: х=22:11
- Получим х=2.
- Таким образом, мы нашли нуль функции: х=2
б) Аналогично во втором случае. Подставляем вместо у число 0 и решаем уравнение вида 0=(х + 76)(х – 95). Вспомним, что произведение двух множителей равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0.
Таким образом, так как у нас два множителя, составляем два уравнения: х + 76 = 0 и х – 95 = 0. Решаем каждое, перенося числа 76 и -95 в правую часть, меняя знаки на противоположные. Получаем х = – 76 и х = 95.
Значит, нули функции это числа (-76) и 95.
в) в третьем случае: если вместо у подставить 0, то получится 0 = – 46/х, где для нахождения значения х нужно будет -46 разделить на нуль, что сделать невозможно. Значит, нулей функции в этом случае нет.
Пример №2. Найти нули функции у=f(x) по заданному графику.
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Определение
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
Рассмотрим по нашему рисунку, на какие промежутки разбивается область определения данной функции [-3; 7] ее нулями. По графику видно, что это 4 промежутка: [-3; -1), (-1;4), (4; 6) и (6; 7]. Помним, что значения из области определения смотрим по оси х.
На рисунке синим цветом выделены части графика в промежутках [-3; -1) и (4; 6), которые расположены ниже оси х. Зеленым цветом выделены части графика в промежутках (-1;4) и (6; 7], которые расположены выше оси х.
Значит, что в промежутках [-3; -1) и (4; 6) функция принимает отрицательные значения, а в промежутках (-1;4) и (6; 7] она принимает положительные значения. Это и есть промежутки знакопостоянства.
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает положительные значения в промежутках [-2; -1) и (3; 8). Обратите внимание, что эти части на рисунке выделены зеленым цветом.
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
На графике видно, что с увеличением значения х от -3 до 2 значения у тоже увеличиваются. Также с увеличением значения х от 5 до 7 значения у опять увеличиваются. Проще говоря, слева направо график идет вверх (синие линии). То есть в промежутках [-3; 2] и [5; 7] функция у=f(x) является возрастающей.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Определение
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Метод интервалов: примеры, решения
Метод интервалов принято считать универсальным для решения неравенств. Иногда этот метод также называют методом промежутков. Применим он как для решения рациональных неравенств с одной переменной, так и для неравенств других видов. В нашем материале мы постарались уделить внимание всем аспектам вопроса.
Что ждет вас в данном разделе? Мы разберем метод промежутков и рассмотрим алгоритмы решения неравенств с его помощью. Затронем теоретические аспекты, на которых основано применение метода.
Особое внимание мы уделяем нюансам темы, которые обычно не затрагиваются в рамках школьной программы. Например, рассмотрим правила расстановки знаков на интервалах и сам метод интервалов в общем виде без его привязки к рациональным неравенствам.
Алгоритм
Кто помнит, как происходит знакомство с методом промежутков в школьном курсе алгебры? Обычно все начинается с решения неравенств вида f(x) или ≥). Здесь f(x) может быть многочленом или отношением многочленов. Многочлен, в свою очередь, может быть представлен как:
произведение линейных двучленов с коэффициентом 1 при переменной х;
произведение квадратных трехчленов со старшим коэффициентом 1 и с отрицательным дискриминантом их корней.
Приведем несколько примеров таких неравенств:
- (x+3)·(x2−x+1)·(x+2)3≥0,
- (x-2)·(x+5)x+3>0 ,
- (x−5)·(x+5)≤0,
- (x2+2·x+7)·(x-1)2(x2-7)5·(x-1)·(x-3)7≤0 .
Запишем алгоритм решения неравенств такого вида, как мы привели в примерах, методом промежутков:
- находим нули числителя и знаменателя, для этого числитель и знаменатель выражения в левой части неравенства приравниваем к нулю и решаем полученные уравнения;
- определяем точки, которые соответствуют найденным нулям и отмечаем их черточками на оси координат;
- определяем знаки выражения f(x) из левой части решаемого неравенства на каждом промежутке и проставляем их на графике;
- наносим штриховку над нужными участками графика, руководствуясь следующим правилом: в случае, если неравенство имеет знаки или ≥, то выделяем штриховкой участки, отмеченные знаком «+».
Четреж, с которым мы будем работать, может иметь схематический вид. Излишние подробности могут перегружать рисунок и затруднять решение. Нас будет мало интересовать маштаб. Достаточно будет придерживаться правильного расположения точек по мере роста значений их координат.
При работе со строгими неравенствами мы будем использовать обозначение точки в виде круга с незакрашенным (пустым) центром. В случае нестрогих неравенств точки, которые соответствуют нулям знаменателя, мы будем изображать пустыми, а все остальные обычными черными.
Отмеченные точки разбивают координатную прямую на несколько числовых промежутков. Это позволяет нам получить геометрическое представление числового множества, которое фактически является решением данного неравенства.
Научные основы метода промежутков
Основан подход, положенный в основу метода промежутков, основан на следующем свойстве непрерывной функции: функция сохраняет постоянный знак на интервале (a, b), на котором эта функция непрерывна и не обращается в нуль. Это же свойство характерно для числовых лучей (−∞, a) и (a, +∞).
Приведенное свойство функции подтверждается теоремой Больцано-Коши, которая приведена во многих пособиях для подготовки к вступительным испытаниям.
Обосновать постоянство знака на промежутках также можно на основе свойств числовых неравенств. Например, возьмем неравенство x-5x+1>0 . Если мы найдем нули числителя и знаменателя и нанесем их на числовую прямую, то получим ряд промежутков: (−∞, −1), (−1, 5) и (5, +∞).
Возьмем любой из промежутков и покажем на нем, что на всем промежутке выражение из левой части неравенства будет иметь постоянный знак. Пусть это будет промежуток (−∞, −1). Возьмем любое число t из этого промежутка. Оно будет удовлетворять условиям t
Нули функции
Что такое нули функции? Как определить нули функции аналитически и по графику?
Нули функции — это значения аргумента, при которых функция равна нулю.
Чтобы найти нули функции, заданной формулой y=f(x), надо решить уравнение f(x)=0.
Если уравнение не имеет корней, нулей у функции нет.
Примеры.
1) Найти нули линейной функции y=3x+15.
Решение:
Чтобы найти нули функции, решим уравнение 3x+15=0.
3x=-15; x= -5.
Таким образом, нуль функции y=3x+15 — x= -5.
Ответ:x= -5.
2) Найти нули квадратичной функции f(x)=x²-7x+12.
Решение:
Для нахождения нулей функции решим квадратное уравнение
x²-7x+12=0.
Его корни x1=3 и x2=4 являются нулями данной функции.
Ответ: x=3; x=4.
3)Найти нули функции
Решение:
Дробь имеет смысл, если знаменатель отличен от нуля. Следовательно, x²-1≠0,x²≠1,x≠±1. То есть область определения данной функции (ОДЗ)
x ∈ (-∞; -1)U(-1; 1)U(1;∞).
Решаем уравнение
Из корней уравнения x²+5x+4=0 x1=-1 x2=-4 в область определения входит только x=-4.
Ответ: x=-4.
Чтобы найти нули функции, заданной графически, надо найти точки пересечения графика функции с осью абсцисс.
Если график не пересекает ось Ox, функция не имеет нулей.
Например,
функция, график которой изображен на рисунке,имеет четыре нуля —
В алгебре задача нахождения нулей функции встречается как в виде самостоятельного задания, так и при решения других задач, например, при исследовании функции, решении неравенств и т.д.
Нули функции
Что такое нули функции? Как определить нули функции аналитически и по графику?
Нули функции — это значения аргумента, при которых функция равна нулю.
Чтобы найти нули функции, заданной формулой y=f(x), надо решить уравнение f(x)=0.
Если уравнение не имеет корней, нулей у функции нет.
1) Найти нули линейной функции y=3x+15.
Чтобы найти нули функции, решим уравнение 3x+15 =0.
Таким образом, нуль функции y=3x+15 — x= -5 .
2) Найти нули квадратичной функции f(x)=x²-7x+12.
Для нахождения нулей функции решим квадратное уравнение
Его корни x1=3 и x2=4 являются нулями данной функции.
3)Найти нули функции
Дробь имеет смысл, если знаменатель отличен от нуля. Следовательно, x²-1≠0, x² ≠ 1,x ≠±1. То есть область определения данной функции (ОДЗ)
Из корней уравнения x²+5x+4=0 x1=-1 x2=-4 в область определения входит только x=-4.
Чтобы найти нули функции, заданной графически, надо найти точки пересечения графика функции с осью абсцисс.
Если график не пересекает ось Ox, функция не имеет нулей.
функция, график которой изображен на рисунке,имеет четыре нуля —
В алгебре задача нахождения нулей функции встречается как в виде самостоятельного задания, так и при решения других задач, например, при исследовании функции, решении неравенств и т.д.
Нули функции онлайн
Одной из задач, возникающих при исследовании функции, является нахождение её нулей — т.е. точек пересения с осью абсцисс. Рассмотрим график некоторой функции :
Нулями функции являются точки в которых, как было сказано выше, график функции пересекает ось абсцисс. Чтобы найти нули функции необходимо и достаточно решить уравнение:
Нулями функции будут корни этого уравнения. Таким образом, нули функции находятся в точках .
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha способен найти нули практически любой, даже очень сложной функции.
Что такое нули функции и как их определить

Что такое нули функции? Ответит довольно прост — это математический термин, под которым подразумевают область определения заданной функции, на котором ее значение нулевое. Нули функции также называют корнями уравнения. Проще всего пояснить, что такое нули функции, на нескольких простых примерах.
Примеры
Рассмотрим несложное уравнение у=х+3. Поскольку нуль функции — это значение аргумента, при котором у приобрел нулевое значение, подставим 0 в левую часть уравнения:
В данном случае -3 и есть искомый нуль. Для данной функции существует только один корень уравнения, но так бывает далеко не всегда.
Рассмотрим другой пример:
Подставим 0 в левую часть уравнения, как и в предыдущем примере:
Очевидно, что в данном случае нулей функции будет два: х=3 и х=-3. Если бы в уравнении был аргумент третьей степени, нулей было бы три. Можно сделать простой вывод, что количество корней многочлена соответствует максимальной степени агрумента в уравнении. Однако многие функции, например у=х 3 , на первый взгляд противоречат этому утверждению. Логика и здравый смысл подсказывают, что у этой функции только один нуль — в точке х=0. Но на самом деле корней три, просто все они совпадают. Если решать уравнение в комплексной форме, это становится очевидным. х=0 в данном случае, корень, кратность которого 3. В предыдущем примере нули не совпадали, потому имели кратность 1.
Алгоритм определения
Из представленных примеров видно, как определить нули функции. Алгоритм всегда один и тот же:
- Записать функцию.
- Подставить у или f(x)=0.
- Решить получившееся уравнение.
Сложность последнего пункта зависит от степени аргумента уравнения. При решении уравнений высоких степеней особенно важно помнить, что количество корней уравнения равно максимальной степени аргумента. Особенно это актуально для тригонометрических уравнений, где деление обоих частей на синус или косинус приводит к потере корней.
Уравнения произвольной степени проще всего решать методом Горнера, который был разработан специально для нахождения нулей произвольного многочлена.
Значение нулей функций может быть как отрицательным, так и положительным, действительным или лежащим в комплексной плоскости, единичным или множественным. Или же корней уравнения может и не быть. Например, функция у=8 не приобретет нулевого значения ни при каком х, потому что она не зависит от этой переменной.
Уравнение у=х 2 -16 имеет два корня, и оба лежат в комплексной плоскости: х1=4і, х2=-4і.
Типичные ошибки
Частая ошибка, которую допускают школьники, еще не разобравшиеся толком в том, что такое нули функции, — это замена на ноль аргумента (х), а не значения (у) функции. Они уверенно подставляют в уравнение х=0 и, исходя из этого, находят у. Но это неправильный подход.
Другая ошибка, как уже упоминалось, сокращение на синус или косинус в тригонометрическом уравнении, из-за чего и теряется один или несколько нулей функции. Это не означает, что в таких уравнениях нельзя ничего сокращать, просто при дальнейших подсчетах необходимо учитывать эти «потерянные» сомножители.
Графическое представление
Понять, что такое нули функции, можно с помощью математических программ, таких как Maple. В ней можно построить график, указав желаемое количество точек и нужный масштаб. Те точки, в которых график пересечет ось ОХ, и есть искомые нули. Это один из самых быстрых способов нахождения корней многочлена, особенно если его порядок выше третьего. Так что если есть необходимость регулярно выполнять математические расчеты, находить корни многочленов произвольных степеней, строить графики, Maple или аналогичная программа будет просто незаменима для осуществления и проверки расчетов.
http://mathforyou.net/online/calculus/zeros/
http://fb.ru/article/271350/chto-takoe-nuli-funktsii-i-kak-ih-opredelit