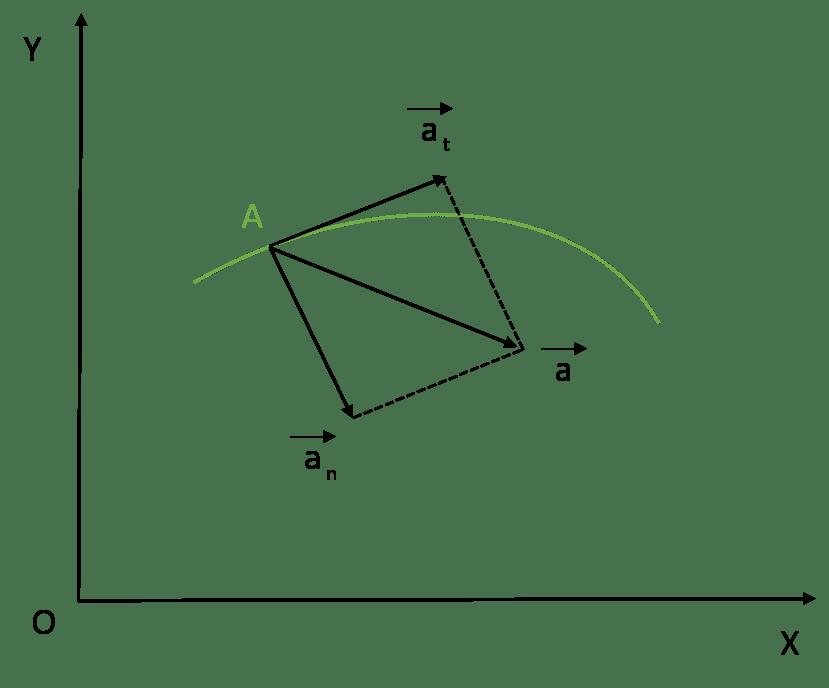
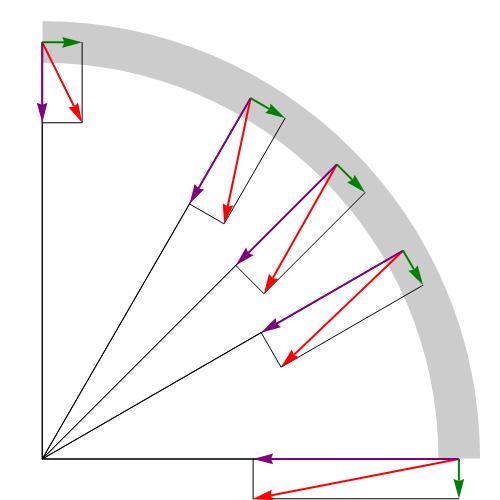
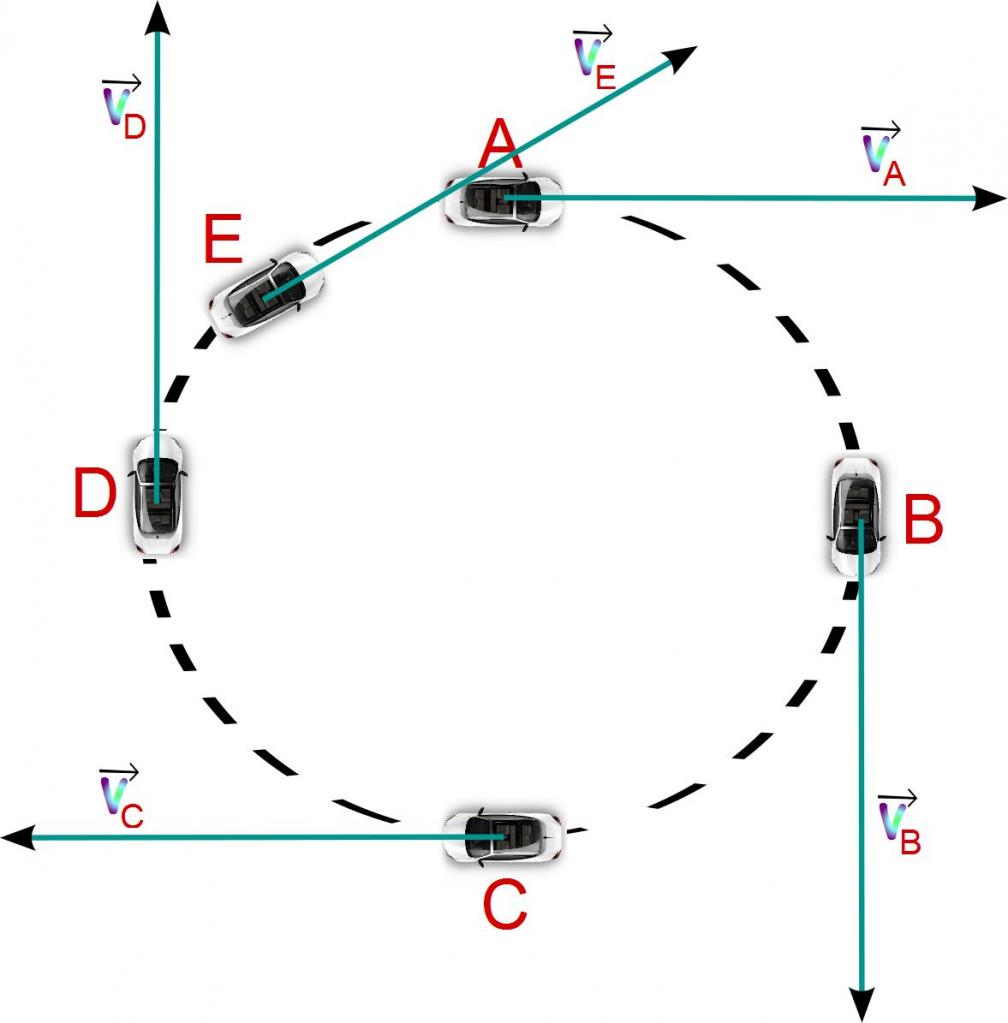
Рассмотрим определение скорости и ускорения точек при естественном способе задания движения:
Из определения скорости точки
где
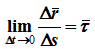
— единичный вектор касательной, тогда
Алгебраическая скорость – это проекция вектора скорости на касательную, равная производной от дуговой координаты по времени.
Если производная положительна, то точка движется в положительном направлении отсчета дуговой координаты.
Из определения ускорения точки
поскольку τ — переменный по направлению вектор, то:
Производная
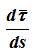
определяется только свойствами траектории в окрестности данной точки, при этом
n — единичный вектор главной нормали,
ρ — радиус кривизны траектории в данной точке.
Таким образом,
т.е. вектор ускорения раскладывается на две составляющие — касательное и нормальное ускорения:
Здесь:
- алгебраическое значение касательного ускорения (проекция вектора ускорения на касательную) характеризует изменение скорости по величине;
- нормальное ускорение (проекция вектора ускорения на главную нормаль) характеризует изменение скорости по направлению. Вектор ускорения всегда лежит в соприкасающейся плоскости и проекция ускорения на бинормаль равна нулю (ab=0).
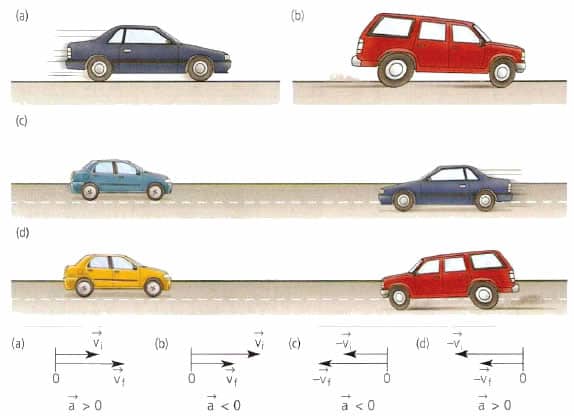
Движение точки ускоренное, если знаки проекций векторов скорости и ускорения на касательную совпадают.
Примеры решения задач >
Задачи кинематики твердого тела >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Содержание:
Основы кинематики сплошной среды:
Сплошной средой считают деформируемые тела, различные жидкости, не очень разреженные газы. Понятия скорости и ускорения точки сплошной среды такие же, как и в кинематике одной точки. В кинематике сплошной среды роль точки отводится малой частице этой среды. Рассмотрим задания движения сплошной среды и получим формулы, по которым вычисляются скорости и ускорения точек сплошной среды.
Движение сплошной среды может быть изучено двумя методами, один из которых — метод Лагранжа — является обобщением метода, применявшегося в кинематике одной точки. Движение в методе Лагранжа задается в переменных Лагранжа. Другой метод — метод Эйлера — широко использует концепцию теории поля. При этом движение задается и изучается в переменных Эйлера. При рассмотрении движения сплошной среды преимущественно используется полевой подход, базирующийся на методе Эйлера и соответственно использующий переменные Эйлера.
Переменные Лагранжа
В выделенном объеме сплошной среды каждая его точка (малая частица) в фиксированный момент времени, например
допускающими вторые производные по всем переменным. Параметры 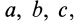
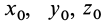
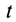
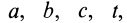
Для задания движения сплошной среды в переменных Лагранжа, как и в случае одной точки, достаточно задать декартовы координаты 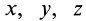
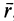
или
В кинематике одной точки, которая рассматривалась ранее, использовались переменные Лагранжа для этой точки. Параметры 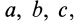
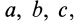
Если движение сплошной среды задано в переменных Лагранжа, то скорости и ускорения в этих переменных определяются по обычным формулам кинематики точки:
или
или
Производные по времени 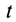
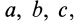
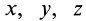
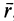
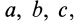
В методе Лагранжа объектом изучения являются сами точки движущейся сплошной среды.
Переменные Эйлера
В механике сплошной среды, особенно для жидкостей и газов, а также в теории поля преимущественно используются метод Эйлера и соответственно переменные Эйлера. В методе Эйлера рассматриваются не фиксированные точки сплошной среды, а точки пространства, занятые движущейся сплошной средой. За независимые переменные принимают время 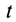
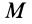
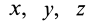
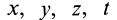
Различные векторные и скалярные величины, характеризующие сплошную среду, такие, как, например, скорость, ускорение, плотность и т. п., рассматривают как функции этих переменных. В случае сплошной среды изучаются поля скалярных и векторных величин, характеризующих движущуюся сплошную среду и ее свойства. Изучаются распределение этих величин по точкам пространства, занятого сплошной средой, и их изменение с течением времени.
По известному векторному полю скоростей сплошной среды, заданному в переменных Эйлера 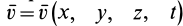
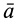
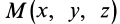
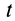
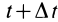
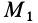
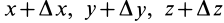
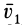
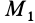
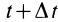
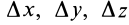
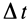
Разложим скорость 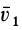
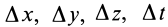
Индексы 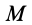
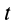
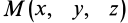
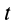
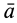
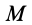
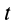
Остальные слагаемые ряда в пределе обращаются в ноль. Подставляя (1) в (2) и опуская для краткости индексы 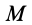
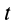
В проекциях на координатные оси имеем
По векторной формуле (3) вычисляют поле ускорений в переменных Эйлера, если известно поле скоростей. В эту формулу входят 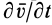
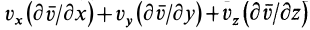
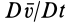
Локальная производная 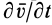
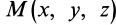
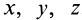
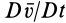
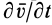
Группа слагаемых, представляющая конвективную производную, учитывает изменение вектора скорости, вызванное переносом рассматриваемой точки сплошной среды самой движущейся средой.
Рассмотрим частные случаи
1. Если 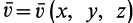
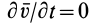
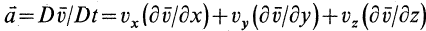
2. При 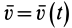
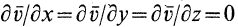
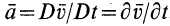
3. Если 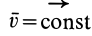
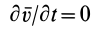
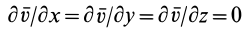
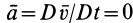
По формуле (3) вычисляют полные, или субстанциальные, производные по времени в переменных Эйлера от любых векторных или скалярных величин, характеризующих сплошную среду. Пусть, например, известно скалярное поле плотностей 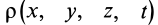
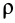
Если сплошная среда неподвижна, т. е. 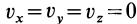
Преобразованием конвективной производной из (3) можно получить другое выражение для ускорения (формула Лэмба — Громеко):
где 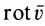

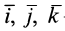
В дальнейшем используется также вектор 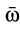
В проекциях на оси координат
Для выяснения физического смысла 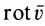
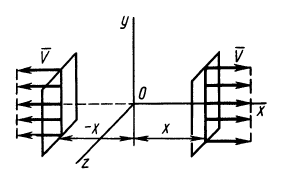
Пример 1.
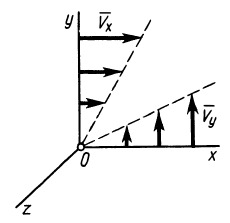
Сплошная среда совершает плоское движение, параллельное оси 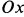
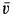
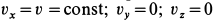
По формуле (5) для вектора вихря 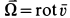
Рис. 104
Рис. 105
Рис. 106
Рис. 107
Следовательно, 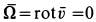
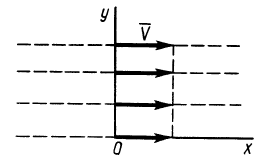
Пример 2.
Сплошная среда совершает плоское движение, параллельное оси 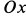
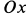
где 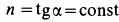
Таким образом, во всех точках потока сплошной среды
где 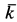
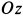
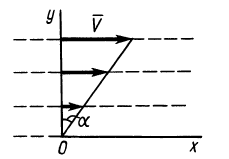
Пример 3.
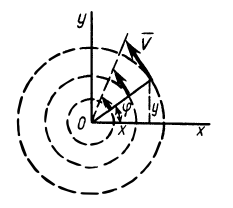
Точки сплошной среды движутся по круговым траекториям с центрами на оси 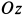
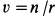
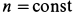
так как
где 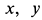
так как 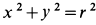
Следовательно, 
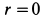
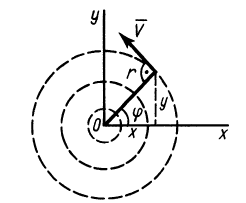
Пример 4.
Сплошная среда вращается как твердое тело вокруг неподвижной оси 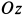
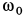
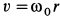
По формулам для вихря скорости имеем
Следовательно,
де 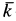
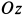

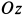

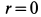
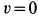
Угловая скорость
т. е. равна половине вихря вектора скорости. Таким образом, половина вихря вектора скорости является вектором угловой скорости вращения твердого тела вокруг неподвижной оси.
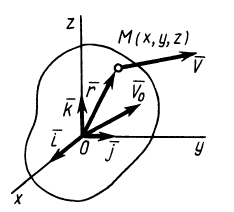
Распределение скоростей в малой окрестности точки пространства
Пусть известны скорость в точке 
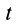
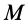

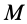


Точки 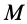

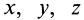
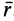
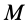
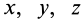
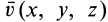
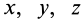
где 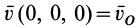



Рис. 108
Введем компоненты тензора скоростей деформации 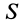

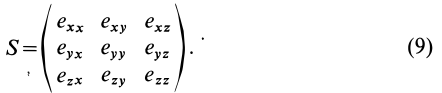
Тензор скоростей деформаций удобно представить в форме таблицы или матрицы:
Компоненты тензора скоростей деформаций, характеризующие движение сплошной среды, зависят от точки пространства и направления осей координат. Тензор 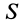
Для таких симметричных тензоров в линейной алгебре доказывается, что в каждой точке существуют такие прямоугольные оси координат, называемые главными осями, для которых тензор принимает диагональную форму:
где 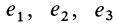
Скалярная величина
называется дивергенцией (расхождением) вектора скорости и обозначается 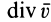
Величины 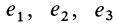
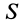
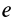
Известно, что числу соответствует геометрический образ, которым является точка на числовой оси. Вектору соответствует прямолинейный отрезок. Тензору 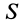
Применим для производных по координатам от проекций вектора скорости на оси координат тождественные преобразования Коши, прибавляя и вычитая одинаковые величины и используя (6′) и (8). Имеем
Из (7′) с учетом этих преобразований получаем
В векторной форме (11) примет вид
где 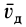
По формуле (11′) вычисляется скорость в момент времени 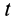
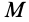
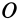
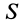
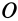
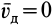
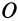
Рассмотрим скорость деформации 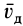
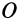
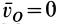
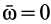
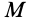
или в проекциях на оси координат
Если в точке 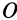
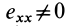
Из (14) следует, что точки сплошной среды из малой окрестности точки 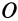
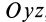
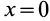
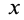
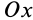
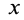
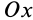
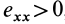
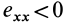
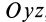
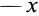
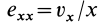
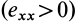
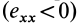
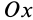
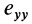
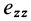
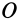
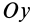
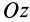
Допустим, что 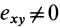
Рис. 109
Рис. 110
Это показывает, что точки сплошной среды из малой окрестности точки 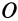
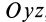
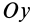
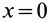
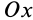
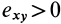
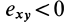
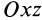
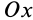
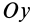
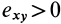
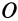
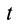
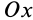
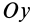
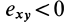
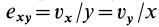
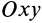
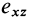
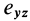
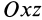
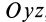
В общем случае, если все компоненты тензора скоростей деформации отличны от нуля, рассмотренные эффекты в окрестности точки 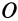
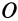
- Заказать решение задач по теоретической механике
Линии и трубки тока
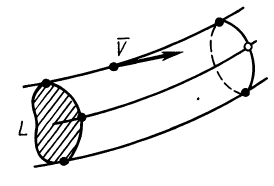
При рассмотрении движения сплошной среды и применении переменных Эйлера используется понятие линий тока, т. е. линий, в каждой точке которых в рассматриваемый момент времени векторы скоростей параллельны касательным этих линий. Если вектор в какой-либо точке линии тока направлен по касательной к этой линии, то, по определению линии тока, он должен быть параллельным вектору скорости 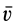
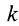
Рис. 111
Если проекции вектора 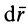
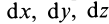
Отбрасывая произвольный множитель 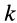
Два уравнения (15′) относительно координат 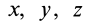
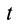
Линии тока являются векторными линиями для векторного поля скоростей точек сплошной среды. Аналогичные векторные линии можно получить для любого другого векторного поля, например векторного поля вихря вектора скорости и т. п.
Если выбрать в пространстве, в котором движется сплошная среда, какой-либо замкнутый контур 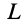
Поток и циркуляция вектора скорости
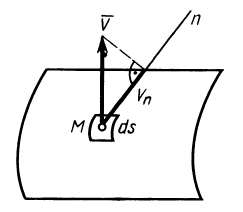
Поток вектора скорости: Выберем в пространстве, в котором движется сплошная среда, неподвижную поверхность относительно рассматриваемой системы отсчета. Разобьем ее на малые элементарные площадки с площадью 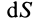
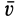
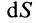
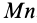
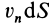
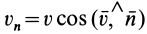
Рис. 112
Для замкнутой поверхности внешней нормалью в каждой ее точке называют нормаль, которая направлена во внешнюю часть объема, ограниченного поверхностью. Для незамкнутых поверхностей дополнительно уславливаются, какое направление нормали считать внешним.
Потоком 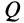
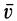
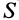
Для вычисления потока можно получить другие выражения, если учесть, что
где 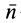
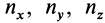
Кроме того,
После этого для потока получаем
Наиболее часто используемое выражение для потока получают применением формулы Гаусса—Остроградского для преобразования интеграла по замкнутой поверхности 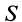
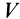
где 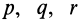
Если принять 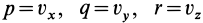
Ho
поэтому
Для вектора вихря скорости поток через замкнутую поверхность равен нулю, так как с учетом формул для проекций вектора вихря на координатные оси имеем
Из (18) для потока 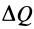
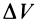
Отсюда получаем для дивергенции вектора скорости
т. е. дивергенцию вектора скорости в какой-либо точке можно рассматривать как предел потока вектора скорости через замкнутую поверхность, приходящуюся на единицу объема, ограниченного поверхностью, при стягивании объема в эту точку.
Рис. 113
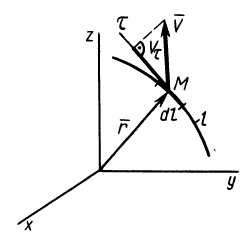
Циркуляция вектора скорости: Для введения понятия циркуляции вектора скорости по какому-либо контуру следует выбрать контур 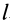
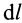
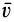
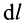
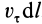
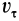
Циркуляция вектора скорости по всему контуру
Для вычисления циркуляции можно получить другие формулы, если учесть, что
где 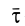
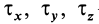
получим
Ho
где 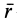
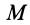
Таким образом,
Для замкнутого контура можно применить формулу Стокса, преобразующую интеграл по контуру в интеграл по поверхности, натянутой на этот контур:
Если принять 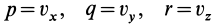
Учитывая, что
являются проекциями вихря скорости, для циркуляции по замкнутому контуру получим
Если 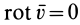
Для вектора силы 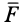
- Аксиомы классической механики
- Дифференциальные уравнения движения материальной точки
- Две основные задачи динамики точки
- Прямолинейное движение точки
- Мгновенный центр вращения
- Вращение твердого тела вокруг неподвижной точки
- Сложное движение точки
- Сложение движение твердого тела
Поток вектора скорости



Поток вектора скорости
- В пространстве, где движется сплошная среда, выберите поверхность, которая зафиксирована относительно рассматриваемой системы отсчета. Разделите на основные регионы с небольшой площадью dS (рис. 112). Течение вектора скорости r через базовый узел dS, определяемое внешней нормалью Mn, называется скаляром. Кажущееся значение равно v „dS, где« n = t> cos (t5, l) — проекция скорости на внешнюю нормаль сайта.
Поскольку цилиндрический шарнир имеет две неизвестные величины, например, составляющую силы реакции вдоль координатных осей, то число неизвестных может быть четыре, независимых условий равновесия — три. Людмила Фирмаль
Для замкнутых поверхностей внешняя нормаль в каждой точке называется нормалью и направлена на внешнюю часть объема, окруженную поверхностью. Для открытых поверхностей дополнительно определяется Направление нормали считается внешним. Рисунок 112 Поток Q вектора скорости v через виртуальную поверхность S называется скалярной величиной. e-ff «.ds-jf [» IooS (S. ) + 1-, CoS (e. ) + y, ”s (ii. -)] ds- -ff | r, drd; + r, d: dy + l. Дд-ды). (16) См.
- Применение формулы Гаусса-Остроградского для преобразования интеграла на замкнутой поверхности S в интеграл на объеме K, окруженном этой поверхностью. ff [p cos (u, x) + qco & (n, j) + rcos (n, z)] dS = (S), O ‘) Где p, q и r — функции переменных Эйлера с частичным дифференцированием. Закрытая поверхность должна быть достаточно гладкой.
Осевой момент инерции d, момент инерции для любой оси, перпендикулярной оси симметрии B: равный соответственно инерции шпинделя относительно оси, проведенной через неподвижную точку O. Людмила Фирмаль
Если p = vx, q = vy, r = vz, то применяя (17) к потоку через замкнутую поверхность, Q = WÅгex cos (© — * *) + vycos («> Lu) + t’z cos (u, z z)] dS = -DI), если 2, проходит через основную замкнутую поверхность, окружающую объем DI. Отсюда находим расхождение вектора скорости divw = lim-, доктор-оди То есть расхождение вектора скорости в любой точке можно рассматривать как предел потока вектора скорости через закрытую поверхность на единицу объема, ограниченного поверхностью, когда объем сокращается до этой точки. ,
Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.





















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Поток векторного поля: теория и примеры
Понятие потока векторного поля и его вычисление как поверхностного интеграла
Своим названием поток векторного поля обязан задачам гидродинамики о потоке жидкости. Поток векторного поля может быть вычислен в виде поверхностного интеграла, который выражает общее количество жидкости, протекающей в единицу времени через некоторую поверхность в направлении вектора скорости течения жидкости в данной точке. Понятие потока векторного поля обобщается также на магнетический поток, поток электричества, поток тепла через заданную поверхность и другие. Поток векторного поля может быть вычислен в виде поверхностного интеграла как первого, так и второго рода и далее мы дадим его вывод через эти интегралы.
Пусть в некоторой области пространства задано векторное поле
и поверхность σ, в каждой точке M которой определён единичный вектор нормали . Пусть также направляющие косинусы этого вектора — непрерывные функции координат x, y, z точки M.
Определение потока векторного поля. Потоком W поля вектора через поверхность σ называется поверхностный интеграл
.
Обозначим как a n проекцию вектора на на единичный вектор . Тогда поток можем записать как поверхностный интеграл первого рода
.
.
поток векторного поля можно вычислить и как поверхностный интеграл второго рода
.
Направление и интенсивность потока векторного поля
Поток векторного поля зависит от местоположения поверхности σ. Если поверхность размещена так, что во всех её точках вектор поля образует с вектором нормали поверхности острый угол, то проекции вектора a n положительны и, таким образом поток W также положителен (рисунок ниже). Если же поверхность размещена так, что во всех её точках вектор образует с вектором нормали поверхности тупой угол, то поток W отрицателен.
Через каждую точку поверхности проходит одна векторная линия, поэтому поверхность σ пересекает бесконечное множество векторных линий. Однако условно можно принять, что поверхность σ пересекает некоторое конечное число векторных линий. Поэтому можно считать, что поток векторного поля — это число векторных линий, пересекающих поверхность σ. Чем интенсивнее поток векторного поля, тем более плотно расположены векторные линии и в результате получается бОльший поток жидкости.
Если поток векторного поля — поле скорости частиц текущей жидкости через поверхность σ, то поверхностный интеграл равен количеству жидкости, протекающей в единицу времени через поверхность σ. Если рассматривать магнетическое поле, которое характеризуется вектором магнетической индукции , то поверхностный интеграл называется магнетическим потоком через поверхность σ и равен общему количеству линий магнетической индукции, пересекающих поверхность σ. В случае электростатического поля интеграл выражает число линий электрической силы, пересекающих поверхность σ. Этот интеграл называется потоком вектора интенсивности электростатического поля через поверхнсть σ. В теории теплопроводности рассматривается стационарный поток тепла через поверхность σ. Если k — коэффициент теплопроводности, а u(M) — температура в данной области, то поток тепла, протекающего через поверхность σ в единицу времени, определяет интеграл .
Вычисление потока векторного поля: примеры
Пример 1. Вычислить поток векторного поля через верхнюю сторону треугольника, образованного пересечением плоскости с координатными плоскостями. Решить задачу двумя способами: 1) через поверхностный интеграл первого рода; 2) через поверхностный интеграл второго рода.
1) Поверхностью σ является треугольник ABC , а её проекцией на ось xOy — треугольник AOB .
Координатами вектора нормали данной поверхности являются коэффициенты при переменных в уравнении плоскости:
.
Длина вектора нормали:
.
Единичный вектор нормали:
.
Из выражения единичного вектора нормали следует, что направляющий косинус . Тогда .
Теперь можем выразить поток векторного поля в виде поверхностного интеграла первого рода и начать решать его:
Выразим переменную «зет»:
Продолжаем вычислять интеграл и, таким образом, поток векторного поля:
Получили ответ: поток векторного поля равен 64.
2) Выражая поток векторного поля через поверхностный интеграл второго рода, получаем
.
Представим этот интеграл в виде суммы трёх интегралов и каждый вычислим отдельно. Учитывая, что проекция поверхности на ось yOz является треугольник OCB , который ограничивают прямые y = 0 , z = 0 , y + 3z = 6 или y = 6 − 3z и в точках поверхности 2x = 6 − y − 3 , получаем первый интеграл и вычисляем его:
Проекцией поверхности на ось xOz является треугольник OAC , который ограничен прямыми x = 0 , z = 0 , 2x + 3z = 6 или . По этим данным получаем второй интеграл, который сразу решаем:
Проекцией поверхности на ось xOy является треугольник OAB , который ограничен прямыми x = 0 , y = 0 , 2x + y = 6 . Получаем третий интеграл и решаем его:
Осталось только сложить все три интеграла:
.
Получили ответ: поток векторного поля равен 64. Как видим, он совпадает с ответом, полученным в первом случае.
Пример 2. Вычислить поток векторного поля через верхнюю сторону треугольника, образованного пересечением плоскости с координатными плоскостями. Решить задачу двумя способами: 1) через поверхностный интеграл первого рода; 2) через поверхностный интеграл второго рода.
Решение. Данная поверхность представляет собой треугольник ABC , изображённый на рисунке ниже.
1) Коэффициенты при x , y и z из уравнения плоскости являются координатами вектора нормали плоскости, которые нужно взять с противоположным знаком (так как вектор нормали верхней стороны треугольника образует с осью Oz острый угол, так что третья координата вектора нормали плоскости должна быть положительной). Таким образом, вектор нормали запишется в координатах так:
.
Длина этого вектора:
,
единичный вектор нормали (орт):
.
Скалярное произведение векторного поля и единичного нормального вектора:
Поток векторного поля, таким образом, представим в виде поверхностного интеграла первого рода
.
Выразим «зет» и продифференцируем то, что уже можно продифференцировать:
2) Представим поток векторного поля в виде поверхностного интеграла второго рода:
.
Первый и второй интегралы берём со знаком «минус», так как вектор нормали поверхности образует с осями Ox и Oy тупой угол.
Вычисляем первый интеграл:
Вычисляем второй интеграл:
Вычисляем третий интеграл:
Складываем три интеграла и получаем тот же самый результат:
.
Пример 3. Вычислить поток векторного поля через внешнюю сторону параболоида в первом октанте, отсечённую плоскостью z = 9 .
Поток векторного поля представим в виде поверхностного интеграла второго рода:
Второй интеграл берём со знаком минус, так как нормальный вектор поверхности образует с осью Oz тупой угол. Вычисляем первый интеграл:
Вычисляем второй интеграл:
В сумме получаем искомый поток векторного поля:
.
Скорость, Вектор скорости и траектория, Сложение скоростей
Скорость
Средняя скорость частицы характеризует быстроту ее движения за конечный промежуток времени. Неограниченно уменьшая этот промежуток, мы придем к физической величине, характеризующей быстроту движения в данный момент времени. Такая величина называется мгновенной скоростью или просто скоростью:
обозначает математическую операцию перехода к пределу. Под этим символом записывается условие, при котором выполняется данный предельный переход; в рассматриваемом случае это стремление к нулю промежутка времени. При вычислении скорости по этому правилу мы убедимся, что уменьшение промежутка времени приводит к тому, что на некотором этапе получаемые очередные значения средней скорости будут все меньше и меньше отличаться друг от друга. Поэтому на практике при нахождении скорости можно остановиться на конечном значении, достаточно малом для получения требуемой точности значения скорости.
Вектор скорости и траектория.
Рассматриваемый предельный переход имеет ясный геометрический смысл. Поскольку вектор перемещения направлен по хорде, соединяющей две точки траектории, то при сближении этих точек, происходящем при, он принимает положение, соответствующее касательной к траектории в данной точке. Это значит, что вектор скорости направлен по касательной к траектории. Так будет в любой точке траектории (рис. 14). При прямолинейной траектории движения вектор скорости направлен вдоль этой прямой.
Скорость прохождения пути.
Аналогичным переходом определяется мгновенная скорость прохождения пути:
Для плавной кривой, каковой является траектория любого непрерывного механического движения, длина дуги тем меньше отличается от длины стягивающей ее хорды, чем короче эта дуга. В пределе эти длины совпадают. Поэтому при можно считать, что . Это означает, что скорость прохождения пути равна модулю мгновенной скорости . Движение, при котором модуль скорости остается неизменным, называется равномерным. В случае прямолинейной траектории при равномерном движении вектор скорости постоянен, а в случае криволинейной траектории изменяется только его направление.
Сложение скоростей.
Если тело одновременно участвует в нескольких движениях, то его скорость равна векторной сумме скоростей каждого из этих движений. Это непосредственно следует из правила сложения перемещений: так как , то после деления на получаем
Иногда бывает удобно представить некоторое сложное движение как суперпозицию, т. е. наложение двух простых движений. В этом случае равенство (3) можно трактовать как правило разложения вектора скорости на составляющие.
По этой ссылке вы найдёте полный курс лекций по математике:
Задачи.
1.
Переправа через реку. Скорость течения в реке с параллельными берегами всюду одинакова и равна. Ширина реки (рис. 15). Катер может плыть со скоростью относительно воды. На какое расстояние s снесет катер вниз по течению реки, если при переправе нос катера направить строго поперек берегов?
Катер участвует одновременно в двух движениях: со скоростью , направленной поперек течения, и вместе с водой со скоростью которая направлена параллельно берегу. В соответствии с правилом сложения скоростей полная скорость катера относительно берегов равна векторной сумме (рис. 16). Очевидно, что движение катера происходит по прямой, направленной вдоль вектора. Искомое расстояние s, на которое снесет катер при переправе, можно найти из подобия треугольника, образованному векторами скоростей:
Эту задачу легко решить и не прибегая к сложению векторов скоростей.
Очевидно, что расстояние s равно произведению скорости течения на время в течение которого катер пересекает реку. Это время можно найти, разделив ширину реки на скорость движения катера поперек реки. Таким образом, находим Рис. 16. Сложение скоростей при переправе через .В этой простой задаче второй способ решения предпочтительнее, так как он проще. Однако уже при небольшом усложнении условия задачи становятся отчетливо видны преимущества первого способа, основанного на сложении векторов скоростей.
2. Переправа поперек реки. Предположим, что теперь нам нужно переправиться на катере через ту же реку точно поперек, т. е. попасть в точку В, лежащую напротив начальной точки А (рис. 17). Как нужно направить нос катера при переправе? Сколько времени займет такая переправа?Решение. В рассматриваемом случае полная скорость v катера относительно берегов, равная векторной сумме скоростей должна быть направлена поперек реки.
Из рис. 17 сразу видно, что вектор, вдоль которого и смотрит нос катера, должен отклоняться на некоторый угол а вверх по течению реки от направления . Синус этого угла равен отношению модулей скоростей течения и катера относительно воды. Переправа поперек реки без сноса возможна только в том случае, когда скорость катера относительно воды больше скорости течения. Это сразу видно либо из треугольника скоростей на рис. 17 (гипотенуза всегда больше катета), либо из формулы (синус угла а должен быть меньше единицы).Время переправы найдем, разделив ширину реки на полную скорость катера по теореме Пифагора.
Возможно вам будут полезны данные страницы:
3. Снос при быстром течении.
Предположим теперь, что скорость катера относительно воды меньше скорости течения: В таком случае переправа без сноса невозможна. Как следует направить нос катера при переправе, чтобы снос получился минимальным? На какое расстояние этом снесет катер? Решение. Полная скорость относительно берегов во всех рассматриваемых случаях дается формулой. Однако теперь нагляднее выполнить сложение векторов и по правилу треугольника (рис. 18) первым изображаем век гор для которого мы знаем модуль направление, а затем к его концу пристраиваем начало вектора известен только модуль, направление еще предстоит выбрать. Этот выбор нужно сделать так, вектор результирующей скорости как можно меньше отклонялся от направления поперек реки.
Рис. 19. Определение курса (направление вектора) переправы минимальным сносом 18. Сложение скоростей переправе Конец любом направлении должен лежать на окружности радиуса центр которой совпадает концом вектора. Эта окружность показана Так условию задачи то точка соответствующая началу лежит вне этой окружности.
Из рисунка видно, что образует прямой
наименьший угол тогда, когда он направлен касательной Следовательно, перпендикулярен вектору треугольник прямоугольный. Таким образом, направлять вверх течению под углом линии Синус этого угла дастся выражением Траектория направлена вдоль вектора, т.е. она перпендикулярна направлению, в котором смотрит катера. Это значит, своей траектории катер движется боком. другом берегу реки причалит точке, до найти из подобия треугольников. Модуль находится теореме Пифагора. результате получаем
4. Лодка тросе. Лодку подтягивают за привязанный носу трос, наматывая равномерно вращающийся барабан Барабан установлен высоком берегу. какой скоростью лодка тот момент, трос горизонтом? Трос выбирается барабаном скоростью.
Решение.
Точка троса, где он привязан к лодке, движется с той же скоростью, что и лодка. Эта скорость v направлена горизонтально. Чтобы связать ее со скоростью выбирания троса, нужно сообразить, что движение троса сводится к повороту вокруг точки В, где он касается барабана, и скольжению вдоль собственного направления, т. е. прямой . Поэтому естественно разложить скорость точки на две составляющие , направленные вдоль и поперек троса (рис. 21). Скорость , направленная поперек, связана с поворотом троса. Модуль скорости направленной вдоль троса, — это и есть данное в условии задачи значение скорости.
По мере приближения лодки к берегу угол а становится больше. Это значит, что cos а убывает и искомая скорость возрастает. Задача для самостоятельного решения Человек находится в поле на расстоянии от прямолинейного участка шоссе. Слева от себя он замечает движущийся по шоссе автомобиль. В каком направлении следует бежать к шоссе, чтобы выбежать на дорогу впереди автомобиля и как можно дальше от него? Скорость автомобиля и, скорость человека.
• Объясните, почему вектор скорости всегда направлен по касательной к траектории.
• В некоторых случаях траектория движения частицы может иметь изломы. Приведите примеры таких движений. Что можно сказать о направлении скорости в точках, где траектория имеет излом?
• В случае непрерывного механического движения вектор скорости не испытывает скачков ни по модулю, ни по направлению. Появление скачков скорости всегда связано с некоторой идеализацией реального процесса. Какие идеализации присутствовали в приведенных вами примерах траекторий с изломами?
• Найдите ошибку в приводимом ниже решении задачи 4. Разложим скорость , точки троса на вертикальную и горизонтальную составляющие (рис. 22). Горизонтальная составляющая это и есть искомая скорость лодки. Поэтому и (неверно!).
Скорость как производная.
Вернемся к выражению (1) для мгновенной скорости. При движении частицы ее радиус-вектор г изменяется, т. е. является некоторой функцией времени:. Перемещение Дг за промежуток времени At представляет собой разность радиусов-векторов в моменты времени. Поэтому формулу (1) можно переписать в виде В математике такую величину называют производной от функции по времени Для нее используют следующие обозначения. Последнее обозначение (точка над буквой) характерно именно для производной по времени. Отметим, что в данном случае производная представляет собой вектор, так как получается в результате дифференцирования векторной функции по скалярному аргументу. Для модуля мгновенной скорости в соответствии справедливо выражение в начале статьи.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
http://function-x.ru/fields_stream.html
http://natalibrilenova.ru/skorost-vektor-skorosti-i-traektoriya-slozhenie-skorostej/
Определение скорости при координатном способе
задания
движения
Воспользуемся
уравнением (4)
и возьмем от него производную по времени
.
(8)
В
(8)
при единичных векторах стоят проекции
вектора скорости на координатные оси
.
(9)
Проекции
скорости на координатные оси определяются
как первые производные по времени от
соответствующих координат.
Зная
проекции, можно найти модуль вектора и
его направление
,
(10)
.
(11)
Определение
скорости при естественном способе
задания
движения
Пусть
дана траектория материальной точки и
закон изменения криволинейной координаты.
Предположим, при t1
точка имел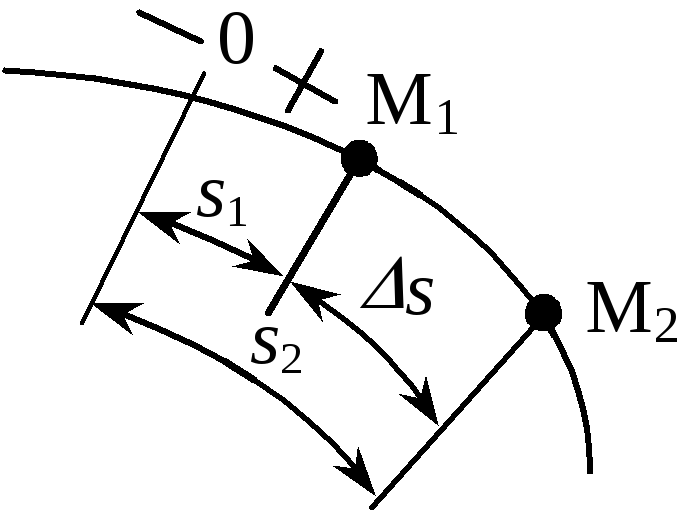
координатуs1,
а при t2
– координату s2.
За время
координата
получила приращение
,
тогда средняя скорость точки
.
Для
нахождения скорости в заданный момент
времени перейдем к пределу
,
.
(12)
Вектор
скорости точки при естественном способе
задания движения определяется как
первая производная по времени от
криволинейной координаты.
Ускорение точки
Под
ускорением материальной точки понимают
векторную величину, характеризующую
быстроту изменения вектора скорости
точки по величине и направлению с
течением времени.
Ускорение точки при векторном способе
задания движения
Рассмотрим
точку в два момента времени t1
()
иt2
(),
тогда— приращение времени,
— приращение скорости.
Вектор
всегда
лежит в плоскости движения и направлен
в сторону вогнутости траектории.
П
ускорением точки
за время t
понимают
величину
.
(13)
Для
нахождения ускорения в заданный момент
времени перейдем к пределу
,
.
(14)
Ускорение
точки в данный момент времени определяется
как вторая производная по времени от
радиус-вектора точки или первая
производная от вектора скорости по
времени.
Вектор
ускорения расположен в соприкасающейся
плоскости и направлен в сторону вогнутости
траектории.
Ускорение точки при координатном способе задания движения
Воспользуемся
уравнением связи векторного и координатного
способов задания движения
.
И возьмем от него
вторую производную
,
.
(15)
В
уравнении (15)
при единичных векторах стоят проекции
вектора ускорения на координатные оси

(16)
Проекции
ускорения на координатные оси определяются
как первые производные по времени от
проекций скорости или как вторые
производные от соответствующих координат
по времени.
Модуль и направление
вектора ускорения можно найти по
следующим выражениям
,
(17)
,
,
.
(18)
Ускорение точки при естественном способе задания движения
П
точка движется по криволинейной
траектории. Рассмотрим два ее положения
в моменты времениt
(s,
M,
v)
и t1
(s1,
M1,
v1).
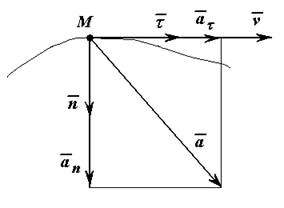
Ускорение
при этом определяется через его проекции
на оси естественной системы координат,
движущейся вместе с точкой M.
Оси при этом направлены следующим
образом:
M
— касательная, направлена вдоль касательной
к траектории, в сторону положительного
отсчета расстояния,
Mn
– главная нормаль, направлена по нормали,
лежащей в соприкасающейся плоскости,
и направлена в сторону вогнутости
траектории,
Mb
– бинормаль, перпендикулярна плоскости
Mn
и образует с первыми осями правую тройку.
Так
как вектор ускорения лежит в соприкасающейся
плоскости, то ab=0.
Найдем проекции ускорения на другие
оси.
.
(19)
Спроектируем
(19)
на координатные оси
,
(20)
.
(21)
Проведем
через точку M1
оси параллельные осям в точке M
и найдем проекции скорости:
M:
,
Mn:
,
(22)
где — так называемый угол смежности.
Подставляем
(22)
в (20)
.
При
t0
0,
cos1,
тогда
.
(23)
Касательное
ускорение точки определяется первой
производной по времени от скорости или
второй производной по времени от
криволинейной координаты.
Касательное
ускорение характеризует изменение
вектора скорости по величине.
Подставим
(22)
в (21)
.
Умножим
числитель и знаменатель на s
чтобы получить известные пределы
,
(24)
где(первый
замечательный предел),
,
,
,
где
— радиус кривизны траектории.
Подставляя
вычисленные пределы в (24),
получим
.
(25)
Нормальное
ускорение точки определяется отношением
квадрата скорости к радиусу кривизны
траектории в данной точке.
Нормальное
ускорение характеризует изменение
вектора скорости по направлению и всегда
направлено в сторону вогнутости
траектории.
Окончательно
получим проекции ускорения материальной
точки на оси естественной системы
координат и модуль вектора

(26)
.
(27)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
02.04.2015390.66 Кб2316.doc
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти нормальное ускорение зная тангенциальное
Содержание
- Этот видеоурок доступен по абонементу
- На этом уроке мы вспомним, что такое ускорение. Рассмотрим две его составляющие, тангенциальную и нормальную, и пример нахождения этих составляющих. А также решим две задачи из сборника для подготовки к Единому государственному экзамену на нахождение радиуса траектории в наивысшей точке.
- Ускорение. Нормальная и тангенциальная составляющие ускорения
- Пример нахождения тангенциальной и нормальной составляющей ускорения
- Задача 1
- Задача 2
- Нахождение закона изменения скорости от времени
- В физике
- Траектория движения и компоненты полного ускорения
- Ускорение тангенциальное
- Ускорение нормальное
- Ускорение полное, нормальное и тангенциальное
- Решение задачи
Тангенциальным (касательным) ускорением называют ту составляющую вектора ускорения, которая направлена по касательной к траектории в данной точке траектории движения. Тангенциальное ускорение описывает степень изменения скорости по модулю при совершении криволинейного движения.
Если тело движется по криволинейной траектории, то его скорость направлена по касательной к этой траектории.
Так как направление скорости все время меняется, значит, в таком случае криволинейное движение всегда происходит с ускорением, также, если модуль скорости не меняется.
В большинстве случаев ускорение направлено под некоторым углом к скорости. Составляющую ускорения, которая направлена вдоль скорости, называют тангенциальным ускорением 
Нормальное ускорение 
Здесь R – это радиус кривизны траектории в заданной точке.
Тангенциальное и нормальное ускорение всегда имеют перпендикулярное направление, откуда получаем модуль полного ускорения:

Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти

Ускорение. Нормальная и тангенциальная составляющие ускорения
Механическое движение по характеру подразделяется на поступательное, вращательное и колебательное; по виду траектории – прямолинейное и криволинейное. Также механическое движение можно подразделять по характеру изменения скорости.
Физическая величина, которая определяет быстроту изменения скорости, называется ускорением. Математически ускорение определяется отношением изменения скорости к промежутку времени, за которое оно произошло (производная от скорости по времени):  и нормальную (перпендикулярную вектору скорости).</p>
<p style=)
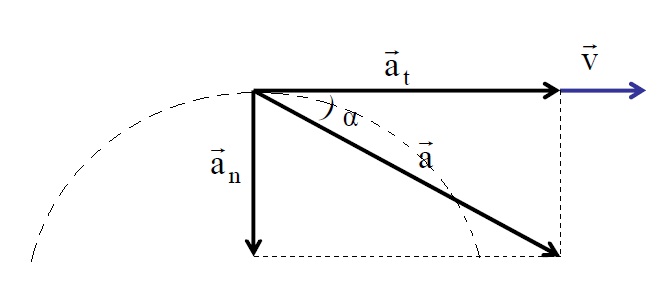
Рис. 1. Тангенциальная и нормальная составляющие полного ускорения
Тангенциальная составляющая ускорения характеризует быстроту изменения величины (модуля) скорости. Тангенциальное ускорение всегда коллинеарно скорости.
1) Если тангенциальная составляющая ускорения сонаправлена со скоростью, то движение будет ускоренное (см. рис. 2).
Рис. 2. Тангенциальная составляющая ускорения сонаправлена со скоростью
2) Если тангенциальная составляющая ускорения противонаправлена скорости, то движение будет замедленным (см. рис. 3).
Рис. 3. Тангенциальная составляющая ускорения противонаправлена скорости
Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению. Нормальное ускорение всегда перпендикулярно скорости и направлено к центру по радиусу траектории, по которой движется тело (см. рис. 4).
Рис. 4. Направление нормального ускорения
Величина нормального ускорения связана с радиусом траектории и со скоростью движения следующим соотношением:
При прямолинейном движении тело имеет только тангенциальное ускорение. Нормальное ускорение отсутствует, так как скорость тела по направлению остаётся неизменной (см. рис. 5).
Рис. 5. Прямолинейное движение
При криволинейном движении, как правило, тело имеет тангенциальную и нормальную составляющую ускорения (см. рис. 6).
Рис. 6. Криволинейное движение
Пример нахождения тангенциальной и нормальной составляющей ускорения
Рассмотрим движение тела, брошенного под углом к горизонту (см. рис. 7). Найдём составляющие ускорения в тот момент, когда скорость тела направлена под углом 
Рис. 7. Траектория движения тела
Касательная к траектории в точке A – это направление скорости
Рис. 8. Проекции ускорения
На рисунке видно, что тангенциальная составляющая ускорения направлена против скорости, то есть скорость тела в данный момент уменьшается (см. рис. 8). Нормальная составляющая ускорения направлена перпендикулярно скорости, следовательно, скорость в следующий момент наклонится в сторону 
Величины составляющих ускорения находим геометрически.
Рис. 9. Геометрическое определение величины составляющих ускорения
Угол A в треугольнике разложения на составляющие (треугольник выделен жёлтым на рисунке) имеет взаимно перпендикулярные стороны с углом 

Нормальная составляющая ускорения равна: 
Задача 1
Обод радиусом 1 метр катится по горизонтальной поверхности со скоростью 10 м/с. Найти радиус траектории точки поверхности обода при прохождении наивысшего положения.
Дано: 

Решение
Рис. 10. Иллюстрация к задаче
На рисунке изображён обод, который катится по горизонтальной поверхности со скоростью 


С центром обода у всех точек, лежащих на её поверхности, связано нормальное ускорение, так как оно направлено перпендикулярно скорости движения точки по окружности в любой момент времени.
Ускорение остаётся неизменным для всех точек поверхности обода, так как при переходе к системе отсчёта, связанной с Землёй, центр обода движется равномерно: 
Тогда для точки
В этой задаче заданное значение начальной скорости было лишним. Избыточные данные часто включают в задания ЕГЭ по физике.
Ответ: 
Задача 2
После удара футбольный мяч за 2 с пролетел 40 м и упал на землю. Чему равен радиус траектории мяча в верхней точке траектории?
Дано: 

Решение
Рис. 11. Иллюстрация к задаче
На рисунке изображена траектория полёта мяча (см. рис. 11). Точка A – верхняя точка траектории, скорость мяча в которой 

Следовательно, радиус траектории в верхней точке равен: 
Ответ: 
Нахождение закона изменения скорости от времени
Сведения об ускорении необходимы для того, чтобы найти закон изменения скорости от времени. Например, зависимость скорости от времени находится как неопределённый интеграл от ускорения по времени: 
При равноускоренном движении 

- Вопросы в конце параграфа 13 (стр. 46); — Касьянов В.А. Физика. 10 кл. (см. список рекомендованной литературы) (Источник)
- Камень брошен со скоростью 20 м/c под углом
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.
В кинематике для однозначного определения характеристик движения тела в любой точке траектории необходимо знать его скорость и ускорение. Зависимость от времени этих величин предоставляет всю необходимую информацию для вычисления пройденного телом пути. Рассмотрим подробнее в статье, что такое ускорение тангенциальное и нормальное ускорение.
В физике
Прежде чем рассматривать для механического движения ускорение нормальное и тангенциальное ускорение, познакомимся с самим физическим понятием. Определение ускорения является достаточно простым. В физике под ним понимают характеристику изменения скорости. Последняя является векторной величиной, определяющей быстроту изменения координат движущегося объекта в пространстве. Скорость измеряется в метрах в секунду (расстояние, пройденное за единицу времени). Если ее обозначить символом v¯, тогда математическое определение ускорения a¯ будет выглядеть так:
Это равенство определяет так называемое полное мгновенное ускорение. Мгновенным оно называется потому, что характеризует изменение скорости лишь в данный момент времени.
Если движение является равноускоренным, то есть в течение длительного времени ускорение не меняет своего модуля и направления, тогда можно записать следующую формулу для его определения:
Где Δt>>dt. Величина a¯ здесь называется средним ускорением, которое в общем случае отличается от мгновенного.
Ускорение измеряется в системе СИ в метрах в квадратную секунду (м/с 2 ).
Траектория движения и компоненты полного ускорения
Чаще всего тела в природе движутся по кривым траекториям. Примерами такого перемещения являются: вращение по своим орбитам планет, параболическое падение камня на землю, поворот автомобиля. В случае криволинейной траектории в любой момент времени скорость направлена по касательной к рассматриваемой точке траектории. Как при этом направлено ускорение?
Чтобы ответить на поставленный выше вопрос, запишем скорость тела в следующей форме:
Здесь ut¯ — вектор скорости единичный, индекс t означает, что он направлен по касательной к траектории (тангенциальная компонента). Символом v обозначен модуль скорости v¯.
Теперь, следуя определению ускорения, можно провести дифференцирование скорости по времени, имеем:
Таким образом, полное ускорение a¯ представляет собой векторную сумму двух компонент. Первое и второе слагаемое называются нормальным и тангенциальным ускорением точки. Подробнее рассмотрим каждую из этих компонент.
Ускорение тангенциальное
Запишем еще раз формулу для этой компоненты полного ускорения:
Это выражение позволяет описать свойства величины at¯:
- Она направлена точно так же, как и сама скорость или противоположно ей, то есть по касательной к траектории. Об этом свидетельствует элементарный вектор ut¯.
- Она характеризует изменение скорости по абсолютной величине, что отражает множитель dv/dt.
Эти свойства позволяют сделать важный вывод: для прямолинейного движения полное и тангенциальное ускорения — это одна и та же величина. В случае криволинейного перемещения полное ускорение всегда больше по модулю, чем тангенциальное. Когда рассматривают физические задачи на прямолинейное равноускоренное движение, то ведут речь именно об этой компоненте ускорения.
Ускорение нормальное
Рассматривая тему скорости, ускорения тангенциального и ускорения нормального, дадим характеристику последней величине. Запишем формулу для нее:
Чтобы записать явно правую часть равенства, воспользуемся следующими соотношениями:
Здесь dL — это пройденный телом путь за промежуток времени dt, r — радиус кривизны траектории. Первое выражение соответствует определению скорости, второе равенство следует из геометрических соображений. Пользуясь этими формулами, получаем конечное выражение для нормального ускорения:
То есть величина an¯ не зависит от изменения скорости, как тангенциальная компонента, а определяется исключительно ее модулем. Нормальное ускорение вдоль нормали к данному участку траектории направлено, то есть к центру кривизны. Например, во время движения по окружности вектор an¯ направлен к ее центру, поэтому нормальное ускорение называют часто центростремительным.
Если за изменение абсолютной величины скорости ответственно ускорение тангенциальное, то нормальная компонента ответственна за изменение вектора скорости, то есть она определяет траекторию перемещения тела.
Ускорение полное, нормальное и тангенциальное
Разобравшись с понятием ускорения и с его компонентами, приведем теперь формулу, которая позволяет определить полное ускорение. Поскольку рассмотренные компоненты направлены под углом 90 o друг к другу, то для определения абсолютной величины их векторной суммы можно использовать теорему Пифагора. Формула для полного ускорения имеет вид:
Направление величины a¯ можно определить по отношению к вектору любой из компонент. Например, угол между a¯ и an¯ вычисляется так:
Учитывая приведенную выше формулу для модуля a¯, можно сделать вывод: при равномерном движении по окружности полное ускорение совпадает с центростремительным.
Решение задачи
Пусть тело движется по окружности радиусом 1 метр. Известно, что его скорость изменяется по следующему закону:
Необходимо определить ускорение тангенциальное и нормальное ускорение в момент t = 4 секунды.
Для тангенциального имеем:
Для того чтобы найти модуль ускорения нормального, сначала следует вычислить значение скорости в заданный момент времени. Имеем:
Теперь можно воспользоваться формулой для an:
Таким образом, мы определили все величины, которые требовалось найти для решения задачи.


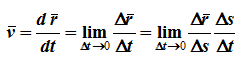
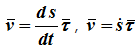
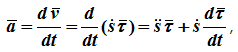
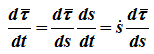
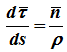
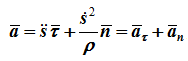
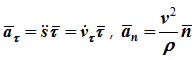
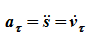
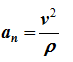
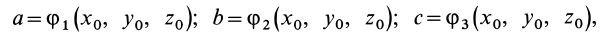
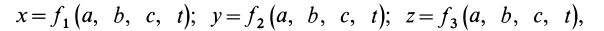
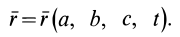
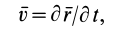
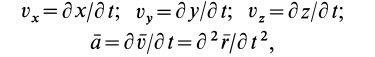
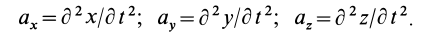
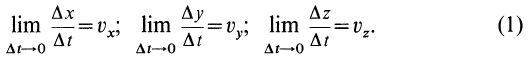
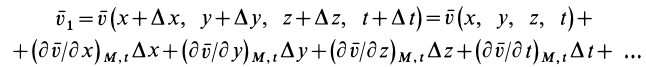
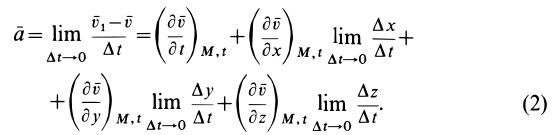
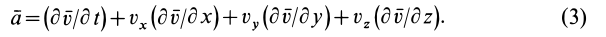
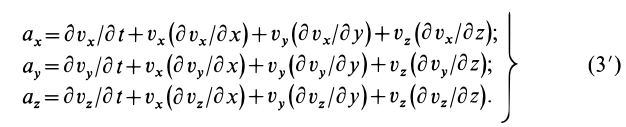
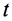
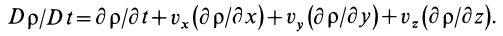
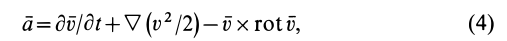
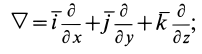
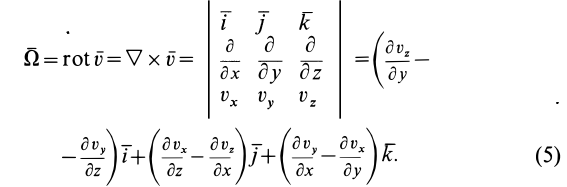

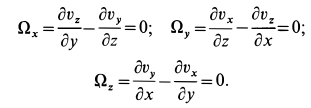
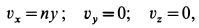
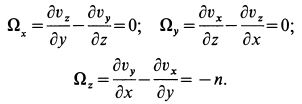
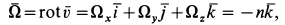
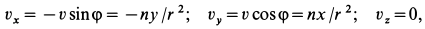
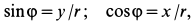
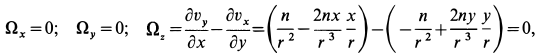
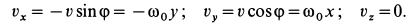
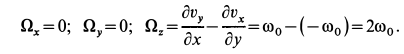
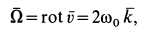
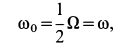
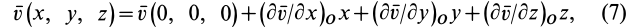
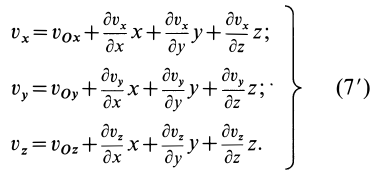
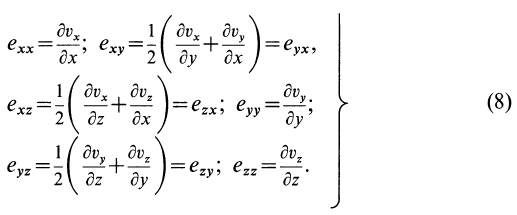
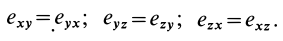
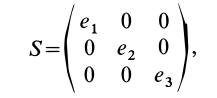
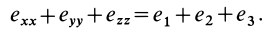
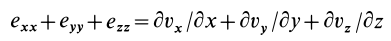
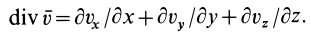
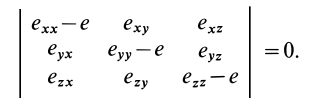

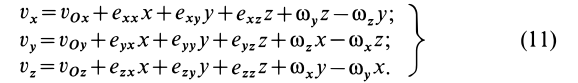

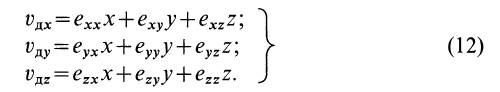

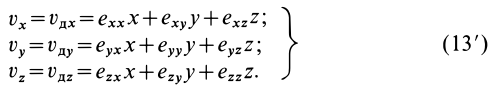
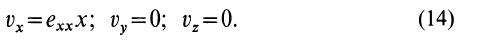
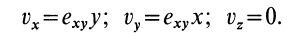

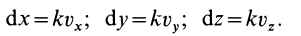
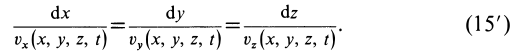

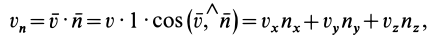
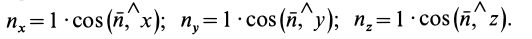
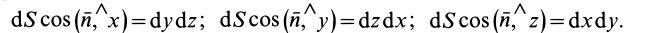
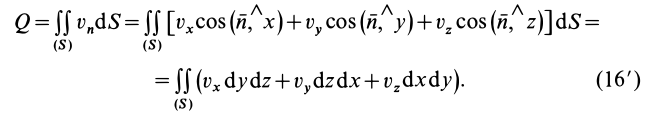
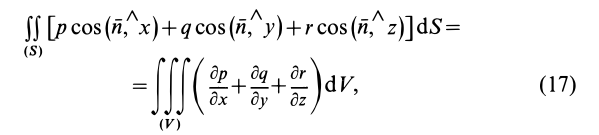
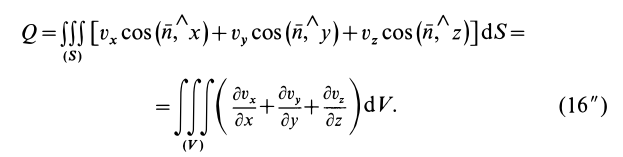
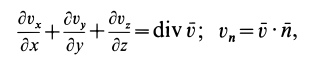
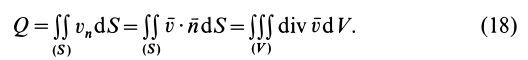
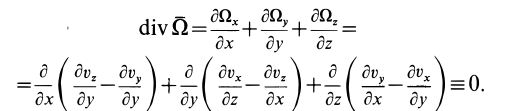
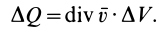
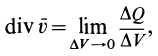

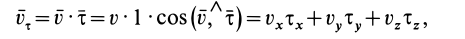
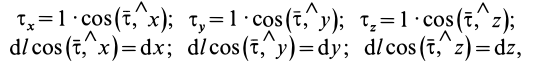
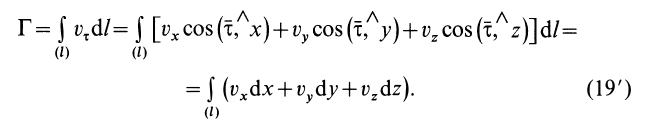
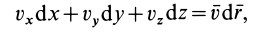
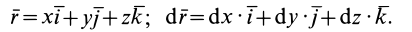
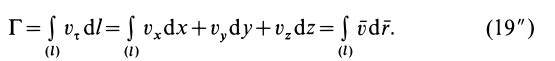
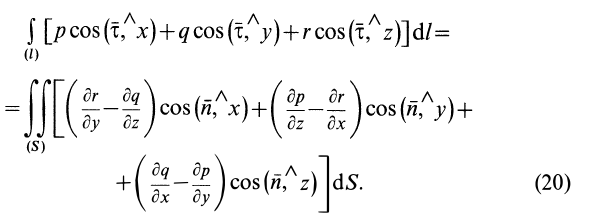
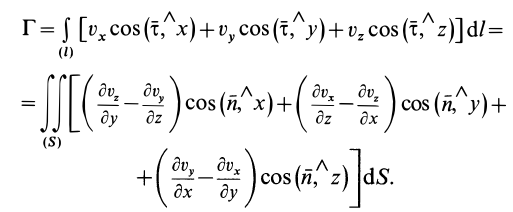
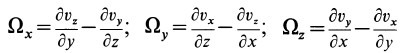
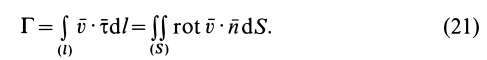





.</p>
<p style=)




















.</li>
<li>Интернет-портал Gym1belovo.smartlearn.ru (Источник).</li>
<li>Интернет-портал Studopedia.info (Источник).</li>
</ol>
<p style=) Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.