Чтобы найти наименьшее общее кратное (НОК) нескольких чисел надо:
1) представить каждое число как произведение его простых множителей, например:
504 = 2 · 2 · 2 · 3 · 3 · 7 ,
2) записать степени всех простых множителей:
504 = 2 · 2 · 2 · 3 · 3 · 7 = 23 · 32 · 71,
3) выписать все простые делители (множители) каждого из этих чисел;
4) выбрать наибольшую степень каждого из них, встретившуюся во всех разложениях этих чисел;
5) перемножить эти степени.
П р и м е р . Найти НОК чисел: 168, 180 и 3024.
Р е ш е н и е . 168 = 2 · 2 · 2 · 3 · 7 = 23 · 31 · 71 ,
180 = 2 · 2 · 3 · 3 · 5 = 22 · 32 · 51 ,
3024 = 2 · 2 · 2 · 2 · 3 · 3 · 3 · 7 = 24 · 33 · 71 .
Выписываем наибольшие степени всех простых делителей
и перемножаем их:
НОК = 24 · 33 · 51 · 71 = 15120 .
Как найти НОК (наименьшее общее кратное)
Общее кратное для двух целых чисел — это такое целое число, которое делится нацело без остатка на оба заданных числа.
Наименьшее общее кратное для двух целых чисел — это наименьшее из всех целых чисел, которое делится нацело и без остатка на оба заданных числа.
Способ 1. Найти НОК можно, по очереди, для каждого из заданных чисел, выписывая в порядке возрастания все числа, которые получаются путем их умножения на 1, 2, 3, 4 и так далее.
Пример для чисел 6 и 9.
Умножаем число 6, последовательно, на 1, 2, 3, 4, 5.
Получаем: 6, 12, 18, 24, 30
Умножаем число 9, последовательно, на 1, 2, 3, 4, 5.
Получаем: 9, 18, 27, 36, 45
Как видно, НОК для чисел 6 и 9 будет равно 18.
Данный способ удобен, когда оба числа небольшие и их несложно умножать на последовательность целых чисел. Однако, бывают случаи, когда нужно найти НОК для двузначных или трехзначных чисел, а также, когда исходных чисел три или даже больше.
Способ 2. Найти НОК можно, разложив исходные числа на простые множители.
После разложения необходимо вычеркнуть из получившихся рядов простых множителей одинаковые числа. Оставшиеся числа первого числа будут множителем для второго, а оставшиеся числа второго — множителем для первого.
Пример для числе 75 и 60.
Наименьшее общее кратное чисел 75 и 60 можно найти и не выписывая подряд кратные этих чисел. Для этого разложим 75 и 60 на простые множители:
75 = 3 * 5 * 5, а
60 = 2 * 2 * 3 * 5.
Как видно, множители 3 и 5 встречаются в обоих строках. Мысленно их «зачеркиваем».
Выпишем оставшиеся множители, входящие в разложение каждого из этих чисел. При разложении числа 75 у нас осталось число 5, а при разложении числа 60 — остались 2 * 2
Значит, чтобы определить НОК для чисел 75 и 60, нам нужно оставшиеся числа от разложения 75 (это 5) умножить на 60, а числа, оставшиеся от разложения числа 60 (это 2 * 2 ) умножить на 75. То есть, для простоты понимания, мы говорим, что умножаем «накрест».
75 * 2 * 2 = 300
60 * 5 = 300
Таким образом мы и нашли НОК для чисел 60 и 75. Это — число 300.
Пример. Определить НОК для чисел 12, 16, 24
В данном случае, наши действия будут несколько сложнее. Но, сначала, как всегда, разложим все числа на простые множители
12 = 2 * 2 * 3
16 = 2 * 2 * 2 * 2
24 = 2 * 2 * 2 * 3
Чтобы правильно определить НОК, выбираем наименьшее из всех чисел (это число 12) и последовательно проходим по его множителям, вычеркивая их, если хотя бы в одном из других рядов чисел встретился такой же, еще не зачеркнутый множитель.
Шаг 1 . Мы видим, что 2 * 2 встречаются во всех рядах чисел. Зачеркиваем их.
12 = 2 * 2 * 3
16 = 2 * 2 * 2 * 2
24 = 2 * 2 * 2 * 3
Шаг 2. В простых множителях числа 12 осталось только число 3. Но оно присутствует в простых множителях числа 24. Вычеркиваем число 3 из обоих рядов, при этом для числа 16 никаких действий не предполагается.
12 = 2 * 2 * 3
16 = 2 * 2 * 2 * 2
24 = 2 * 2 * 2 * 3
Как видим, при разложении числа 12 мы «вычеркнули» все числа. Значит нахождение НОК завершено. Осталось только вычислить его значение.
Для числа 12 берем оставшиеся множители у числа 16 (ближайшего по возрастанию)
12 * 2 * 2 = 48
Это и есть НОК
Как видим, в данном случае, нахождение НОК было несколько сложнее, но когда нужно его найти для трех и более чисел, данный способ позволяет сделать это быстрее. Впрочем, оба способа нахождения НОК являются правильными.
2080.1947
Дроби, задачи на нахождение частей от целого |
Описание курса
| Привести дробь к наименьшему общему знаменателю
Как найти нок трехзначных чисел. Как найти наименьшее общее кратное двух чисел
Наибольший общий делитель
Определение 2
Если натуральное число a делится на натуральное число $b$, то $b$ называют делителем числа $a$, а число $a$ называют кратным числа $b$.
Пусть $a$ и $b$-натуральные числа. Число $c$ называют общим делителем и для $a$ и для $b$.
Множество общих делителей чисел $a$ и $b$ конечно, так как ни один из этих делителей не может быть больше, чем $a$. Значит,среди этих делителей есть наибольший, который называют наибольшим общим делителем чисел $a$ и $b$ и для его обозначения используют записи:
$НОД (a;b) или D (a;b)$
Чтобы найти наибольший общий делитель двух, чисел необходимо:
- Найти произведение чисел, найденных на шаге 2. Полученное число и будет искомым наибольшим общим делителем.
Пример 1
Найти НОД чисел $121$ и $132.$
$242=2cdot 11cdot 11$
$132=2cdot 2cdot 3cdot 11$
Выбрать числа, которые входят в разложение этих чисел
$242=2cdot 11cdot 11$
$132=2cdot 2cdot 3cdot 11$
Найти произведение чисел, найденных на шаге 2.Полученное число и будет искомым наибольшим общим делителем.
$НОД=2cdot 11=22$
Пример 2
Найти НОД одночленов $63$ и $81$.
Будем находить согласно представленному алгоритму. Для этого:
Разложим числа на простые множители
$63=3cdot 3cdot 7$
$81=3cdot 3cdot 3cdot 3$
Выбираем числа, которые входят в разложение этих чисел
$63=3cdot 3cdot 7$
$81=3cdot 3cdot 3cdot 3$
Найдем произведение чисел, найденных на шаге 2.Полученное число и будет искомым наибольшим общим делителем.
$НОД=3cdot 3=9$
Найти НОД двух чисел можно и по-другому, используя множество делителей чисел.
Пример 3
Найти НОД чисел $48$ и $60$.
Решение:
Найдем множество делителей числа $48$: $left{{rm 1,2,3.4.6,8,12,16,24,48}right}$
Теперь найдем множество делителей числа $60$:$ left{{rm 1,2,3,4,5,6,10,12,15,20,30,60}right}$
Найдем пересечение этих множеств: $left{{rm 1,2,3,4,6,12}right}$- данное множество будет определять множество общих делителей чисел $48$ и $60$. Наибольший элемент в данном множестве будет число $12$. Значит наибольший общий делитель чисел $48$ и $60$ будет $12$.
Определение НОК
Определение 3
Общим кратным натуральных чисел
$a$ и $b$ называется натуральное число, которое кратно и $a$ и $b$.
Общими кратными чисел называются числа которые делятся на исходные без остатка.Например для чисел $25$ и $50$ общими кратными будут числа $50,100,150,200$ и т.д
Наименьшее из общих кратных будет называться наименьшим общим кратным и обозначается НОК$(a;b)$ или K$(a;b).$
Чтобы найти НОК двух чисел, необходимо:
- Разложить числа на простые множители
- Выписать множители, входящие в состав первого числа и добавить к ним множители, которые входят в состав второго и не ходят в состав первого
Пример 4
Найти НОК чисел $99$ и $77$.
Будем находить согласно представленному алгоритму. Для этого
Разложить числа на простые множители
$99=3cdot 3cdot 11$
Выписать множители, входящие в состав первого
добавить к ним множители, которые входят в состав второго и не ходят в состав первого
Найти произведение чисел, найденных на шаге 2.Полученное число и будет искомым наименьшим общим кратным
$НОК=3cdot 3cdot 11cdot 7=693$
Составление списков делителей чисел часто очень трудоемкое занятие. Существует способ нахождение НОД, называемый алгоритмом Евклида.
Утверждения, на которых основан алгоритм Евклида:
Если $a$ и $b$ —натуральные числа, причем $avdots b$, то $D(a;b)=b$
Если $a$ и $b$ —натуральные числа, такие что $b
Пользуясь $D(a;b)= D(a-b;b)$, можно последовательно уменьшать рассматриваемые числа до тех пор, пока не дойдем до такой пары чисел, что одно из них делится на другое. Тогда меньшее из этих чисел и будет искомым наибольшим общим делителем для чисел $a$ и $b$.
Свойства НОД и НОК
- Любое общее кратное чисел $a$ и $b$ делится на K$(a;b)$
- Если $avdots b$ , то К$(a;b)=a$
Если К$(a;b)=k$ и $m$-натуральное число, то К$(am;bm)=km$
Если $d$-общий делитель для $a$ и $b$,то К($frac{a}{d};frac{b}{d}$)=$ frac{k}{d}$
Если $avdots c$ и $bvdots c$ ,то $frac{ab}{c}$ — общее кратное чисел $a$ и $b$
Для любых натуральных чисел $a$ и $b$ выполняется равенство
$D(a;b)cdot К(a;b)=ab$
Любой общийй делитель чисел $a$ и $b$ является делителем числа $D(a;b)$
Онлайн калькулятор позволяет быстро находить наибольший общий делитель и наименьшее общее кратное как для двух, так и для любого другого количества чисел.
Калькулятор для нахождения НОД и НОК
Найти НОД и НОК
Найдено НОД и НОК: 5806
Как пользоваться калькулятором
- Введите числа в поле для ввода
- В случае ввода некорректных символов поле для ввода будет подсвечено красным
- нажмите кнопку «Найти НОД и НОК»
Как вводить числа
- Числа вводятся через пробел, точку или запятую
- Длина вводимых чисел не ограничена
, так что найти НОД и НОК длинных чисел не составит никакого труда
Что такое НОД и НОК?
Наибольший общий делитель
нескольких чисел – это наибольшее натуральное целое число, на которое все исходные числа делятся без остатка. Наибольший общий делитель сокращённо записывается как НОД
.
Наименьшее общее кратное
нескольких чисел – это наименьшее число, которое делится на каждое из исходных чисел без остатка. Наименьшее общее кратное сокращённо записывается как НОК
.
Как проверить, что число делится на другое число без остатка?
Чтобы узнать, делится ли одно число на другое без остатка, можно воспользоваться некоторыми свойствами делимости чисел. Тогда, комбинируя их, можно проверять делимость на некоторые их них и их комбинации.
Некоторые признаки делимости чисел
1. Признак делимости числа на 2
Чтобы определить, делится ли число на два (является ли оно чётным), достаточно посмотреть на последнююю цифру этого числа: если она равна 0, 2, 4, 6 или 8, то число чётно, а значит делится на 2.
Пример:
определить, делится ли на 2 число 34938 .
Решение:
смотрим на последнюю цифру: 8 — значит число делится на два.
2. Признак делимости числа на 3
Число делится на 3 тогда, когда сумма его цифр делится на три. Таким образом, чтобы определить, делится ли число на 3, нужно посчитать сумму цифр и проверить, делится ли она на 3. Даже если сумма цифр получилась очень большой, можно повторить этот же процесс вновь.
Пример:
определить, делится ли число 34938 на 3.
Решение:
считаем сумму цифр: 3+4+9+3+8 = 27. 27 делится на 3, а значит и число делится на три.
3. Признак делимости числа на 5
Число делится на 5 тогда, когда его последняя цифра равна нулю или пяти.
Пример:
определить, делится ли число 34938 на 5.
Решение:
смотрим на последнюю цифру: 8 — значит число НЕ делится на пять.
4. Признак делимости числа на 9
Этот признак очень похож на признак делимости на тройку: число делится на 9 тогда, когда сумма его цифр делится на 9.
Пример:
определить, делится ли число 34938 на 9.
Решение:
считаем сумму цифр: 3+4+9+3+8 = 27. 27 делится на 9, а значит и число делится на девять.
Как найти НОД и НОК двух чисел
Как найти НОД двух чисел
Наиболее простым способом вычисления наибольшего общего делителя двух чисел является поиск всех возможных делителей этих чисел и выбор наибольшего из них.
Рассмотрим этот способ на примере нахождения НОД(28, 36) :
- Раскладываем оба числа на множители: 28 = 1·2·2·7 , 36 = 1·2·2·3·3
- Находим общие множители, то есть те, которые есть у обоих чисел: 1, 2 и 2.
- Вычисляем произведение этих множителей: 1·2·2 = 4 — это и есть наибольший общий делитель чисел 28 и 36.
Как найти НОК двух чисел
Наиболее распространены два способа нахождения наименьшего кратного двух чисел. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди них такое число, которое будет общим для обоих чисел и при этом наименьшем. А второй заключается в нахождении НОД этих чисел. Рассмотрим только его.
Для вычисления НОК нужно вычислить произведение исходных чисел и затем разделить его на предварительно найденный НОД. Найдём НОК для тех же чисел 28 и 36:
- Находим произведение чисел 28 и 36: 28·36 = 1008
- НОД(28, 36), как уже известно, равен 4
- НОК(28, 36) = 1008 / 4 = 252 .
Нахождение НОД и НОК для нескольких чисел
Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел. Также для нахождение НОД нескольких чисел можно воспользоваться следующим соотношением: НОД(a, b, c) = НОД(НОД(a, b), c)
.
Аналогичное соотношение действует и для наименьшего общего кратного чисел: НОК(a, b, c) = НОК(НОК(a, b), c)
Пример:
найти НОД и НОК для чисел 12, 32 и 36.
- Cперва разложим числа на множители: 12 = 1·2·2·3 , 32 = 1·2·2·2·2·2 , 36 = 1·2·2·3·3 .
- Найдём обшие множители: 1, 2 и 2 .
- Их произведение даст НОД: 1·2·2 = 4
- Найдём теперь НОК: для этого найдём сначала НОК(12, 32): 12·32 / 4 = 96 .
- Чтобы найти НОК всех трёх чисел, нужно найти НОД(96, 36): 96 = 1·2·2·2·2·2·3 , 36 = 1·2·2·3·3 , НОД = 1·2·2·3 = 12 .
- НОК(12, 32, 36) = 96·36 / 12 = 288 .
Но многие натуральные числа делятся нацело ещё и на другие натуральные числа.
Например
:
Число 12 делится на 1, на 2, на 3, на 4, на 6, на 12;
Число 36 делится на 1, на 2, на 3, на 4, на 6, на 12, на 18, на 36.
Числа, на которые число делится нацело (для 12 это 1, 2, 3, 4, 6 и 12) называются делителями числа
. Делитель натурального числа a
— это такое натуральное число, которое делит данное число a
без остатка. Натуральное число, которое имеет более двух делителей, называется составным
.
Обратите внимание, что числа 12 и 36 имеют общие делители. Это числа: 1, 2, 3, 4, 6, 12. Наибольший из делителей этих чисел — 12. Общий делитель двух данных чисел a
и b
— это число, на которое делятся без остатка оба данных числа a
и b
.
Общим кратным
нескольких чисел называется число, которое делится на каждое из этих чисел. Например
, числа 9, 18 и 45 имеют общее кратное 180. Но 90 и 360 — тоже их общие кратные. Среди всех jбщих кратных всегда есть наименьшее, в данном случае это 90. Это число называется наименьшим
общим кратным (НОК)
.
НОК всегда натуральное число, которое должно быть больше самого большого из чисел, для которых оно определяется.
Наименьшее общее кратное (НОК). Свойства.
Коммутативность:
Ассоциативность:
В частности, если и — взаимно-простые числа , то:
Наименьшее общее кратное двух целых чисел m
и n
является делителем всех других общих кратных m
и n
. Более того, множество общих кратных m, n
совпадает с множеством кратных для НОК(m, n
).
Асимптотики для могут быть выражены через некоторые теоретико-числовые функции.
Так, функция Чебышёва
. А также:
Это следует из определения и свойств функции Ландау g(n)
.
Что следует из закона распределения простых чисел.
Нахождение наименьшего общего кратного (НОК).
НОК(a, b
) можно вычислить несколькими способами:
1. Если известен наибольший общий делитель , можно использовать его связь с НОК:
2. Пусть известно каноническое разложение обоих чисел на простые множители:
где p 1 ,…,p k
— различные простые числа, а d 1 ,…,d k
и e 1 ,…,e k
— неотрицательные целые числа (они могут быть нулями, если соответствующее простое отсутствует в разложении).
Тогда НОК (a
,b
) вычисляется по формуле:
Другими словами, разложение НОК содержит все простые множители , входящие хотя бы в одно из разложений чисел a, b
, причём из двух показателей степени этого множителя берётся наибольший.
Пример
:
Вычисление наименьшего общего кратного нескольких чисел может быть сведено к нескольким последовательным вычислениям НОК от двух чисел:
Правило.
Чтобы найти НОК ряда чисел, нужно:
— разложить числа на простые множители;
— перенести во множители искомого произведения самое большое разложение (произведение множителей самого большого числа из заданных), а потом добавить множители из разложения других чисел, которые не встречаются в первом числе или стоят в нем меньшее число раз;
— полученное произведение простых множителей будет НОК заданных чисел.
Любые два и более натуральных чисел имеют свое НОК. Если числа не кратны друг другу или не имеют одинаковых множителей в разложении, то их НОК равно произведению этих чисел.
Простые множители числа 28 (2, 2, 7) дополнили множителем 3 (числа 21), полученное произведение (84) будет наименьшим числом, которое делится на 21 и 28 .
Простые множители наибольшего числа 30 дополнили множителем 5 числа 25, полученное произведение 150 больше самого большого числа 30 и делится на все заданные числа без остатка. Это наименьшее произведение из возможных (150, 250, 300…), которому кратны все заданные числа.
Числа 2,3,11,37 — простые, поэтому их НОК равно произведению заданных чисел.
Правило
. Чтобы вычислить НОК простых чисел, нужно все эти числа перемножить между собой.
Еще один вариант:
Чтобы найти наименьшее общее кратное (НОК) нескольких чисел нужно:
1) представить каждое число как произведение его простых множителей, например:
504 = 2 · 2 · 2 · 3 · 3 · 7 ,
2) записать степени всех простых множителей:
504 = 2 · 2 · 2 · 3 · 3 · 7 = 2 3 · 3 2 · 7 1 ,
3) выписать все простые делители (множители) каждого из этих чисел;
4) выбрать наибольшую степень каждого из них, встретившуюся во всех разложениях этих чисел;
5) перемножить эти степени.
Пример
. Найти НОК чисел: 168, 180 и 3024.
Решение
. 168 = 2 · 2 · 2 · 3 · 7 = 2 3 · 3 1 · 7 1 ,
180 = 2 · 2 · 3 · 3 · 5 = 2 2 · 3 2 · 5 1 ,
3024 = 2 · 2 · 2 · 2 · 3 · 3 · 3 · 7 = 2 4 · 3 3 · 7 1 .
Выписываем наибольшие степени всех простых делителей и перемножаем их:
НОК = 2 4 · 3 3 · 5 1 · 7 1 = 15120.
Второе число:
b=
Разделитель разрядов
Без разделителя пробел » ´
Результат:
Наибольший общий делитель НОД(a
,b
)=6
Наименьшее общее кратное НОК(a
,b
)=468
Наибольшее натуральное число, на которое делятся без остатка числа a и b, называется наибольшим общим делителем
(НОД) этих чисел. Обозначается НОД(a,b), (a,b), gcd(a,b) или hcf(a,b).
Наименьшее общее кратное
(НОК) двух целых чисел a и b есть наименьшее натуральное число, которое делится на a и b без остатка. Обозначается НОК(a,b), или lcm(a,b).
Целые числа a и b называются взаимно простыми
, если они не имеют никаких общих делителей кроме +1 и −1.
Наибольший общий делитель
Пусть даны два положительных числа a
1 и a
2 1). Требуется найти общий делитель этих чисел, т.е. найти такое число λ
, которое делит числа a
1 и a
2 одновременно. Опишем алгоритм.
1) В данной статье под словом число будем понимать целое число.
Пусть a
1 ≥ a
2 , и пусть
где m
1 , a
3 некоторые целые числа, a
3 <a
2 (остаток от деления a
1 на a
2 должен быть меньше a
2).
Предположим, что λ
делит a
1 и a
2 , тогда λ
делит m
1 a
2 и λ
делит a
1 −m
1 a
2 =a
3 (Утверждение 2 статьи «Делимость чисел. Признак делимости»). Отсюда следует, что всякий общий делитель a
1 и a
2 является общим делителем a
2 и a
3 . Справедливо и обратное, если λ
общий делитель a
2 и a
3 , то m
1 a
2 и a
1 =m
1 a
2 +a
3 также делятся на λ
. Следовательно общий делитель a
2 и a
3 есть также общий делитель a
1 и a
2 . Так как a
3 <a
2 ≤a
1 , то можно сказать, что решение задачи по нахождению общего делителя чисел a
1 и a
2 сведено к более простой задаче нахождения общего делителя чисел a
2 и a
3 .
Если a
3 ≠0, то можно разделить a
2 на a
3 . Тогда
,
где m
1 и a
4 некоторые целые числа, (a
4 остаток от деления a
2 на a
3 (a
4 <a
3)). Аналогичными рассуждениями мы приходим к выводу, что общие делители чисел a
3 и a
4 совпадают с общими делителями чисел a
2 и a
3 , и также с общими делителями a
1 и a
2 . Так как a
1 , a
2 , a
3 , a
4 , … числа, постоянно убывающие, и так как существует конечное число целых чисел между a
2 и 0, то на каком то шаге n
, остаток от деления a
n на a
n+1 будет равен нулю (a
n+2 =0).

Каждый общий делитель λ
чисел a
1 и a
2 также делитель чисел a
2 и a
3 , a
3 и a
4 , …. a
n и a
n+1 . Справедливо и обратное, общие делители чисел a
n и a
n+1 являются также делителями чисел a
n−1 и a
n , …. , a
2 и a
3 , a
1 и a
2 . Но общий делитель чисел a
n и a
n+1 является число a
n+1 , т.к. a
n и a
n+1 без остатка делятся на a
n+1 (вспомним, что a
n+2 =0). Следовательно a
n+1 является и делителем чисел a
1 и a
2 .
Отметим, что число a
n+1 является наибольшим из делителей чисел a
n и a
n+1 , так как наибольший делитель a
n+1 является сам a
n+1 . Если a
n+1 можно представить в виде произведения целых чисел, то эти числа также являются общими делителями чисел a
1 и a
2 . Число a
n+1 называют наибольшим общим делителем
чисел a
1 и a
2 .
Числа a
1 и a
2 могут быть как положительными, так и отрицательными числами. Если один из чисел равен нулю, то наибольший общий делитель этих чисел будет равен абсолютной величине другого числа. Наибольший общий делитель нулевых чисел не определен.
Вышеизложенный алгоритм называется алгоритмом Евклида
для нахождения наибольшего общего делителя двух целых чисел.
Пример нахождения наибольшего общего делителя двух чисел
Найти наибольший общий делитель двух чисел 630 и 434.
- Шаг 1. Делим число 630 на 434. Остаток 196.
- Шаг 2. Делим число 434 на 196. Остаток 42.
- Шаг 3. Делим число 196 на 42. Остаток 28.
- Шаг 4. Делим число 42 на 28. Остаток 14.
- Шаг 5. Делим число 28 на 14. Остаток 0.
На шаге 5 остаток от деления равен 0. Следовательно наибольший общий делитель чисел 630 и 434 равен 14. Заметим, что числа 2 и 7 также являются делителями чисел 630 и 434.
Взаимно простые числа
Определение
1.
Пусть наибольший общий делитель чисел a
1 и a
2 равен единице. Тогда эти числа называются взаимно простыми числами
, не имеющими общего делителя.
Теорема
1.
Если a
1 и a
2 взаимно простые числа, а λ
какое то число, то любой общий делитель чисел λa
1 и a
2 является также общим делителем чисел λ
и a
2 .
Доказательство. Рассмотрим алгоритм Евклида для нахождения наибольшего общего делителя чисел a
1 и a
2 (см. выше).

Из условия теоремы следует, что наибольшим общим делителем чисел a
1 и a
2 , и следовательно a
n и a
n+1 является 1. Т.е. a
n+1 =1.
Умножим все эти равенства на λ
, тогда

Пусть общий делитель a
1 λ
и a
2 есть δ
. Тогда δ
входит множителем в a
1 λ
, m
1 a
2 λ
и в a
1 λ
—m
1 a
2 λ
=a
3 λ
(см. «Делимость чисел»,Утверждение 2). Далее δ
входит множителем в a
2 λ
и m
2 a
3 λ
, и, следовательно, входит множителем в a
2 λ
—m
2 a
3 λ
=a
4 λ
.
Рассуждая так мы убеждаемся, что δ
входит множителем в a
n−1 λ
и m
n−1 a
n λ
, и, следовательно, в a
n−1 λ
−m
n−1 a
n λ
=a
n+1 λ
. Так как a
n+1 =1, то δ
входит множителем в λ
. Следовательно число δ
является общим делителем чисел λ
и a
2 .
Рассмотрим частные случаи теоремы 1.
Следствие
1.
Пусть a
и c
простые числа относительно b
. Тогда их произведение ac
является простым числом относительно b
.
Действительно. Из теоремы 1 ac
и b
имеют тех же общих делителей, что и c
и b
. Но числа c
и b
взаимно простые, т.е. имеют единственный общий делитель 1. Тогда ac
и b
также имеют единственный общий делитель 1. Следовательно ac
и b
взаимно простые.
Следствие
2.
Пусть a
и b
взаимно простые числа и пусть b
делит ak
. Тогда b
делит и k
.
Действительно. Из условия утверждения ak
и b
имеют общий делитель b
. В силу теоремы 1, b
должен быть общим делителем b
и k
. Следовательно b
делит k
.
Следствие 1 можно обобщить.
Следствие
3.
1. Пусть числа a
1 , a
2 , a
3 , …, a
m простые относительно числа b
. Тогда a
1 a
2 , a
1 a
2 ·a
3 , …, a
1 a
2 a
3 ···a
m , произведение этих чисел простое относительно числа b
.
2. Пусть имеем два ряда чисел
таких, что каждое число первого ряда простое по отношению каждого числа второго ряда. Тогда произведение
Требуется найти такие числа, которые делятся на каждое из этих чисел.
Если число делится на a
1 , то оно имеет вид sa
1 , где s
какое-нибудь число. Если q
есть наибольший общий делитель чисел a
1 и a
2 , то
где s
1 — некоторое целое число. Тогда
является наименьшим общим кратным чисел
a
1 и a
2 .
a
1 и a
2 взаимно простые, то наименьшее общее кратное чисел a
1 и a
2:
Нужно найти наименьшее общее кратное этих чисел.
Из вышеизложенного следует, что любое кратное чисел a
1 , a
2 , a
3 должно быть кратным чисел ε
и a
3 , и обратно. Пусть наименьшее общее кратное чисел ε
и a
3 есть ε
1 . Далее, кратное чисел a
1 , a
2 , a
3 , a
4 должно быть кратным чисел ε
1 и a
4 . Пусть наименьшее общее кратное чисел ε
1 и a
4 есть ε
2 . Таким образом выяснили, что все кратные чисел a
1 , a
2 , a
3 ,…,a
m совпадают с кратными некоторого определенного числа ε
n , которое называют наименьшим общим кратным данных чисел.
В частном случае, когда числа a
1 , a
2 , a
3 ,…,a
m взаимно простые, то наименьшее общее кратное чисел a
1 , a
2 как было показано выше имеет вид (3). Далее, так как a
3 простое по отношению к числам a
1 , a
2 , тогда a
3 простое по отношению числа a
1 ·a
2 (Следствие 1). Значит наименьшее общее кратное чисел a
1 ,a
2 ,a
3 является число a
1 · a
2 ·a
3 . Рассуждая аналогичным образом мы приходим к следующим утверждениям.
Утверждение
1.
Наименьшее общее кратное взаимно простых чисел a
1 , a
2 , a
3 ,…,a
m равен их произведению a
1 ·a
2 ·a
3 ···a
m .
Утверждение
2.
Любое число, которое делится на каждое из взаимно простых чисел a
1 , a
2 , a
3 ,…,a
m делится также на их произведение a
1 ·a
2 ·a
3 ···a
m .
Перейти к содержанию
На чтение 2 мин. Просмотров 6k.
- Наименьшим общим кратным данных натуральных чисел называют наименьшее натуральное число, кратное каждому из данных чисел. Пример. НОК(24, 42)=168. Это самое маленькое число, которое делится и на 24 и на 42.
- Для нахождения НОК нескольких данных натуральных чисел надо: 1) разложить каждое из данных чисел на простые множители; 2) выписать разложение большего из чисел и умножить его на недостающие множители из разложений других чисел.
- Наименьшее кратное двух взаимно простых чисел равно произведению этих чисел.
Пример 1
Найти НОК(35; 40).
Разложим числа 35 и 40 на простые множители.

Берем разложение большего числа 40 и дополняем его недостающими множителями. НОК(35; 40)=23∙5∙7=40∙7=280.
Ответ: НОК(35; 40)=280.
Пример 2
Найти НОК(45; 54).
Раскладываем числа 45 и 54 на простые множители.

Берем разложение числа 54 и умножаем на недостающие множители из разложения числа 45, т. е. на число 5.
НОК(45; 54)=2∙33∙5=54∙5=270.
Ответ: НОК(45; 54)=270.
Пример 3
Найти НОК(75; 120; 150).
Разложим числа 75, 120 и 150 на простые множители.
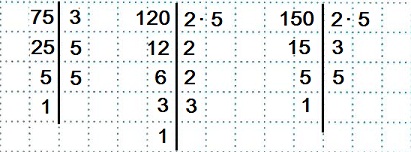
Возьмем разложение большего числа 150 и дополним его двумя «двойками», так как в разложении числа 120 имеется три «двойки», а в разложении числа 150 – только одна.
НОК(75; 120; 150)=2∙3∙52∙2∙2=150∙4=600.
Ответ: НОК(75; 120; 150)=600.
Вывод: при нахождении НОК выписывают произведение всех простых (различных) множителей, имеющихся в разложениях этих чисел, причем, каждый из множителей берется с наибольшим из имеющихся показателей степеней.
( 5 оценок, среднее 4 из 5 )
Елена Борисовна Калюжная
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Поиск наименьшего общего кратного — задача, с которой все мы сталкиваемся при необходимости найти общий знаменатель для дроби. Ниже для удобства обозначения мы будем использовать не только термин «наименьшее общее кратное», но и его сокращение — НОК.
Давайте рассмотрим подробнее, что значит НОК.
Определение 1
Наименьшее общее кратное нескольких чисел $a, b, c, d$ — это наименьшее натуральное число, которое делится без остатка на все эти числа.
Нахождение НОК
Существует несколько различных приёмов для определения НОК:
- Через связь наименьшего общего кратного и наибольшего общего делителя;
- Через разложение чисел, для которых ищется НОК, на простые множители.
Как искать НОК через наибольший общий делитель
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Для начала вспомним, что такое наибольший общий делитель.
Замечание 1
Наибольшим общим делителем называют наибольшее число, в результате деления на которое двух или более чисел не остаётся остатка.
Для любых натуральных чисел $a$ и $b$ справедливо следующее тождество:
$НОД(a, b) cdot НОК(a, b)=a cdot b$.
Способы нахождения НОД для определения НОК:
- Бинарный метод.
- Алгоритм Евклида.
Алгоритм Евклида для поиска НОК рассмотрен подробнее в другой статье на нашем сайте.
Также НОД можно вычислить через каноническое разложение чисел на простые множители. Для этого числа, для которых ищется НОД, сначала раскладывают на простые множители.
После этого отдельной строкой выписывают все простые множители, входящие в каждое разложение хотя бы один раз.
После к простым множителям подписывают их наименьшую степень и перемножают. Полученное произведение будет являться наибольшим общим делителем данных чисел.
«Как найти наименьшее общее кратное» 👇
Если же НОД уже известен, то для определения НОК через этот метод можно воспользоваться следующей формулой:
$НОК(a,b)=frac{|a cdot b|}{НОД(a, b)}$
Здесь $НОД$ — наибольший общий делитель для чисел $a$ и $b$.
Как найти НОК через разложение чисел
Определение 2
Представление числа через произведение простых чисел, возведённых в разные степени, называется разложением числа на простые множители.
Из этого определения можно сделать следующий вывод: любое натуральное число кроме единицы либо является простым, либо его можно разложить до простых множителей, причём единственным способом. Числа, которые можно разложить на простые множители, называются составными.
Для осуществления разложения числа на множители используют признаки делимости чисел.
Существуют пары чисел, наибольший общий делитель которых равен единице. Такие числа называются взаимно простыми.
При поиске НОК для взаимно простых чисел их разложения не содержат одних и тех же простых множителей.
Существует ещё одна закономерность для взаимно простых чисел: если число делится на каждое из взаимно простых чисел, то оно делится и на их произведение.
Наиболее частым является каноническое разложение, при его использовании числа раскладываются на множители в порядке возрастания.
Теперь, узнав основные используемые понятия, можно перейти к алгоритму определения НОК данным методом.
Алгоритм определения НОК
- Разложить числа, для которых нужно найти наименьшее общее кратное на простые множители.
- В отдельную строчку выписать все простые числа, которые входят в каждое из разложений.
- Для каждого из простых чисел выписать максимальную степень, с которой оно встречается в разложении.
- Записать произведение всех выписанных простых чисел в максимальных встреченных степенях.
Как найти НОК трех чисел и более
Для того чтобы найти НОК более чем для двух чисел, сначала необходимо выбрать 2 любых числа из необходимых и найти НОК для них, после этого нужно взять следующее число и найти НОК для него и уже посчитанного ранее наименьшего общего кратного.
Эту процедуру необходимо выполнять до тех пор, пока не закончатся числа, для которых необходимо найти наименьшее общее кратное.
Другим способом найти НОК сразу для нескольких чисел является выписывание в строку всех простых множителей, содержащихся в разложениях, с их наибольшей степенью и затем их последующее перемножение.
Пример 1
Приведите дроби к общему знаменателю:
- $frac{25}{104}$ и $frac{37}{520}$.
- $frac{7}{132}$ и $frac{9}{154}$
- $frac{3}{4};frac{13}{20};frac{41}{60}; frac{17}{75};frac{11}{25}$.
Решение:
-
Чтобы привести дроби $frac{25}{104}$ и $frac{37}{520}$ к общему знаменателю, для начала необходимо найти общее кратное для чисел $104$ и $520$, стоящих под чертой дроби. Для этого разложим их на множители:
$104=1 cdot 2^3 cdot 13$;
$520=1 cdot 2^3 cdot 5 cdot 13$.
Теперь вычислим наименьшее общее кратное. Чтобы это сделать, выпишем каждый простой множитель, встречающийся в разложениях обоих чисел хотя бы раз с его наибольшей степенью, имеем:
$НОК= cdot 2^3 cdot 5 cdot 13=520$.
Теперь найдём множители для каждой из дробей, на которые их необходимо для множить. Для дроби $frac{25}{104}$ этот множитель равен $520:104=5$, для второй дроби $frac{37}{520}$ он равен $520:520=1$. Следовательно, первую дробь нужно домножить на $frac{5}{5}$, а вторую на $frac{1}{1}$:
$frac{25 cdot 5}{104 cdot 5}$ и $frac{37 cdot 1}{520 cdot 1}$;
$frac{125}{520}$ и $frac{37}{520}$.
-
Найдём наименьшее кратное для дробей $frac{7}{132}$ и $frac{9}{154}$. Для этого вновь разложим знаменатели используя каноническое разложение:
$132=1 cdot 2^2 cdot 3^1 cdot 11^1$;
$154= 1 cdot 2 cdot 7^1 cdot 11^1$.
Найдём НОК:
$НОК=2^2 cdot 3 cdot 7 cdot 11 = 924$.
Множитель, на который нужно умножить числитель и знаменатель первой дроби для приведения к общему знаменателю — $7$, а вторую нужно домножить на $6$.
Получаем:
$frac{7 cdot 7}{132 cdot 7}$ и $frac{9 cdot 6}{154 cdot 6}$;
$frac{49}{924}$ и $frac{36}{924}$.
-
Сначала разложим на простые множители знаменатели дробей
$frac{3}{4};frac{13}{20};frac{41}{60}; frac{17}{75};frac{11}{25}$:
$4=1 cdot 2^2$;
$20=1 cdot 2^2 5$;
$60=1 cdot 2^2 cdot 3 cdot 5$;
$75= 1 cdot 3 cdot 5^2$;
$25=1 cdot 5^2$.
Выпишем все множители при старших степенях для вычисления НОК:
$НОК=2^2 cdot 3 cdot 5^2=300$.
Множители для каждой дроби соответственно $75;15;5;4;12$.
В результате приведения к общему знаменателю получим:
$frac{225}{300}; frac{195}{300}; frac{195}{300}; frac{205}{300}; frac{68}{300}; frac{132}{300}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме





