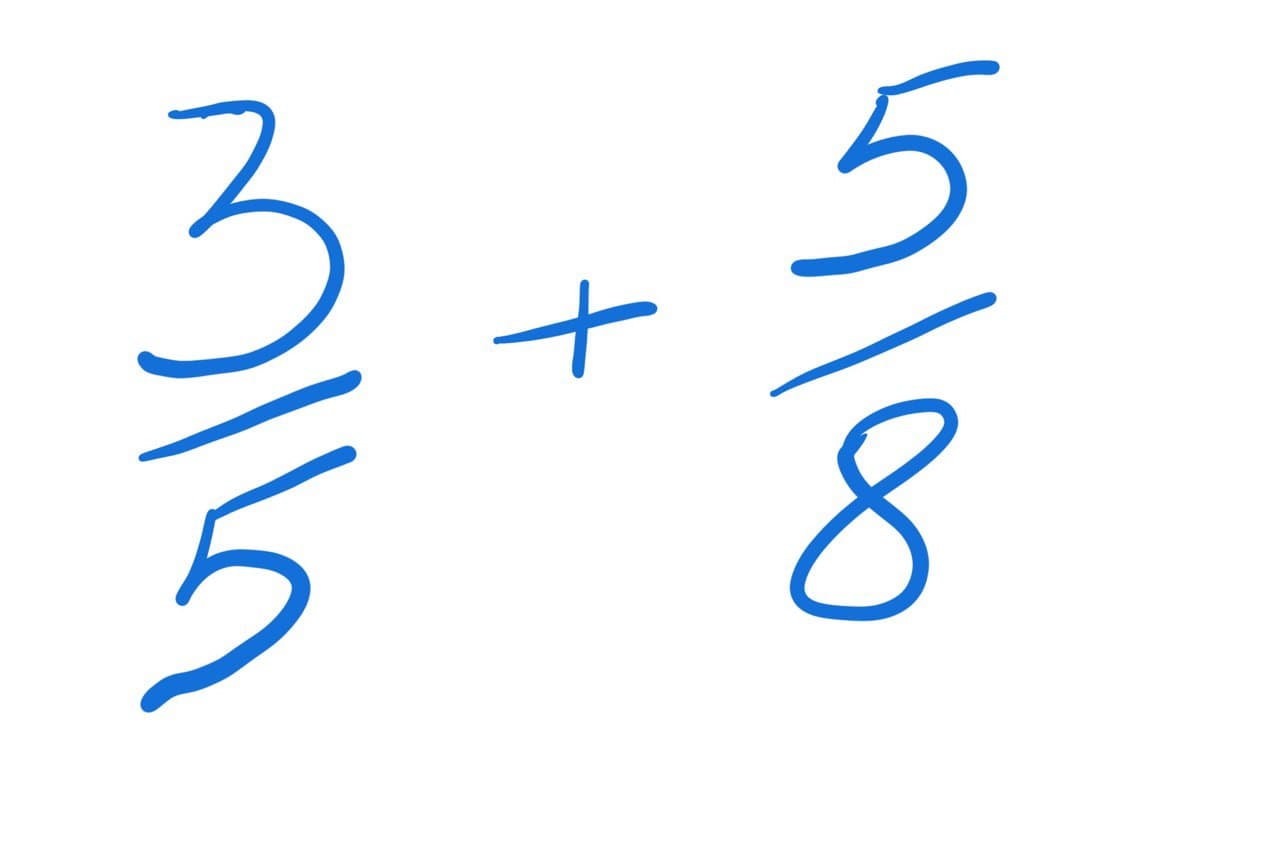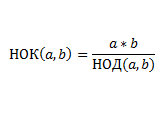Мы уже не раз складывали два простых числа, две десятичные дроби или даже простое число с десятичной дробью. Однако мир состоит не только из примитивных данных, порой нам приходится работать и с дробями, с обыкновенными дробями.
Обыкновенные дроби
#
сложение дробей
Обыкновенная дробь, как мы знаем из школы, состоит из двух частей: верхней и нижней. Это если не считать чёрточку посередине за часть дроби. Верхнюю часть дроби в математике принято называть числитель, а нижнюю часть знаменатель. В английском соответственно numerator и denominator.
Для того, что бы мы могли проводить математические операции с дробями мы должны привести их к общему знаменателю и научиться сокращать их. Для этого нам нужно вспомнить про НОД и НОК.
НОД — наибольший общий делитель
#
Greatest common divisor — GCD.
НОД´ом для чисел 25 и 15 является 5. Это наибольший общий делитель двух этих чисел.
Для чисел 9 и 15 НОД´ом является 3. Оба числа делятся на 3 без остатка. И три является наибольшим общим делителем.
Математика древняя наука и впервые НОД был описан Евклидом в третьем веке до нашей эры. Алгоритм нахождения назван в его честь — Алгори́тм Евкли́да.
В Java Алгоритм Евклида будет реализован вот так:
public static int euclideanAlgorithm(int a, int b) {
while (a != b) {
if (a > b) {
a = a - b;
} else {
b = b - a;
}
}
return a;
}
Этот алгоритм в цикле занимается вычитанием от одной переменной другой и в итоге находит нод. если задуматься, то “бесконечное” вычитание пока A не сравняется с B это деление с нахождением остатка деления. Сегодня у нас есть оператор модуло и мы можем “усовершенствовать” алгоритм:
public static int gcdAlgorithmModulo(int a, int b) {
while (b != 0) {
int temp = b;
b = a % b;
a = temp;
}
return a;
}
Этот же алгоритм мы можем решить с применением рекурсии, мы должны прописать условие выхода и само решение:
public static int gcdRecursionAlgorithm(int a, int b) {
if (b == 0) {
return a;
}
return gcdRecursionAlgorithm(b, a % b);
}
Это не единственные способы решения. Всегда ещё можно решить бинарным поиском. Но думаю на этом мы пока уже можем остановиться и сказать, что НОД мы находить научились и можем попробовать найти НОК.
НОК — Наименьшее общее кратное
#
Least common multiple — LCM
НОК — это произведение наших двух чисел и делении его на НОД. Реализуется это вот так:
public static int leastCommonMultiple(int a, int b) {
return a / gcdRecursionAlgorithm(a, b) * b;
}
Теперь мы попробуем реализовать правильное “поведение” дробей.
public class Fraction {
private int numerator;
private int denominator;
Fraction(int numerator) {
this.numerator = numerator;
this.denominator = 1;
}
public Fraction(int numerator, int denominator) {
this.numerator = numerator;
this.denominator = denominator;
}
public int getNumerator() {
return numerator;
}
public int getDenominator() {
return denominator;
}
public Fraction sum(Fraction fraction) {
Fraction result = sum(fraction, this);
return result;
}
public static Fraction sum(Fraction a, Fraction b) {
// описать сложение;
// выполнить сокращение дробей, если это возможно
// находим нок знаменателей дробей
// подставить полученное значение в знаменатель РЕЗУЛЬТАТА
// Разделить нок на знаменатели данных дробей.
// умножить числитель и знаменатель каждой дроби на дополнительный множитель
int cDenominator = Math.nok(a.denominator, b.denominator);
int cNumerator =
a.numerator * (cDenominator / a.denominator) +
b.numerator * (cDenominator / b.denominator);
Fraction c = new Fraction(cNumerator, cDenominator);
return c;
}
@Override
public String toString() {
return "Fraction(дробь){" +
"numerator(числитель)=" + numerator +
", denominator(знаменатель)=" + denominator +
'}';
}
}
class Math {
static int nok(int a, int b) {
return a * b / nod(a, b);
}
static int nod(int a, int b) {
if (b == 0) {
return a;
}
return nod(b, a % b);
}
}
Дополнительные ссылки
#
- https://docs.oracle.com/javase/8/docs/api/java/lang/Number.html
- https://habr.com/ru/post/205106/
- https://www.baeldung.com/java-least-common-multiple
Алгоритм Евклида
Для начала разберемся, что это и как это работает. Алгоритм Евклида позволяет найти нам наибольший общий делитель чисел. Как это работает:
Пусть a = 18, b = 30.
Цикл: a!=0 and b!=0
Если a > b, то a = a % b, если меньше, то b = b % a, таким образом мы сначала находим остаток деления, а потом повторяем действия. У нас a < b, значит, ищем остаток деления b % a (30 % 18) = 12, присваиваем b = 12, повторяем цикл но теперь у нас уже a > b(b = 12)
значит выполняем a % b (18 % 12) = 6? снова переходим к циклу, теперь снова b > a, значит выполняем b % a (30 % 6), остаток от деления 0, на этом мы прекращаем наш цикл и узнаем, что наибольший общий делитель 18 и 30 = 6. и выводим a + b (b = 0, a = 6).
Python
#!/usr/bin/env python
a = 18
b = 30
while a!=0 and b!=0:
if a > b:
a = a % b
else:
b = b % a
print (a+b)
Perl:
sub nod
{
return $_[0] != 0 ? nod ( ( $_[1] % $_[0] ), $_[0] ) : $_[1];
}
C:
int gcd(int a, int b) {
int c;
while (b) {
c = a % b;
a = b;
b = c;
}
return abs(a);
}
Pascal:
function nod( a, b: longint): longint;
begin
while (a <> 0) and (b <> 0) do
if a >= b then
a:= a mod b
else
b:= b mod a;
nod:= a + b;
end;
Java:
public class GCD {
public static int gcd(int a,int b) {
while (b !=0) {
int tmp = a%b;
a = b;
b = tmp;
}
return a;
}
}
C#:
int gcd(int a, int b)
{
while (b != 0)
b = a % (a = b);
return a;
}
Не понимаю, что может быть не так?
Наибольший общий делитель (НОД).
Ввести с клавиатуры 2 целых положительных числа.
Вывести в консоль наибольший общий делитель.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStream;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;
public class NOD {
public static void main(String[] args) throws IOException {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
String X = reader.readLine();
String Y = reader.readLine();
reader.close();
if (X.indexOf("-",0) == -1 || Y.indexOf("-",0) == -1) {
try {
int x = Integer.parseInt(X);
int y = Integer.parseInt(Y);
System.out.println(MostCommonЬultiple(x, y));
} catch (Exception e) {}
} else {}
}
public static int MostCommonЬultiple(int x, int y){
List<Integer> arrayX = del(x);
List<Integer> arrayY = del(y);
List<Integer> XandY = CompareArray(arrayX,arrayY);
return MaxOfCom(XandY);
}
public static List<Integer> del(int a){
List<Integer> divider = new ArrayList<>();
for (int i = 1; i <= a; i++) {
if (a % i == 0) {
divider.add(i);
}
}
return divider;
}
public static List<Integer> CompareArray(List<Integer> a, List<Integer> b){
List<Integer> compare = new ArrayList<>();
for (int i = 0; i < a.size(); i++){
for (int j = 0; j < b.size(); j++){
if (a.get(i).equals(b.get(j))) compare.add(a.get(i));
}
}
return compare;
}
public static int MaxOfCom(List<Integer> a){
int max = a.get(0);
for (int i = 0; i<a.size();i++){
if(max<a.get(i)) max = a.get(i);
}
return max;
}
}
задан 9 фев 2020 в 17:01
3
Для такой простой задачи это слишком сложный код. Всегда помните про KISS.
import java.util.Scanner;
public class NOD {
public static void main(String[] args) {
try {
Scanner sc = new Scanner(System.in);
int nod = mostCommonMultiple(Integer.valueOf(sc.nextLine()),Integer.valueOf(sc.nextLine()));
System.out.println("NOD: " + nod);
} catch (NumberFormatException | UnsupportedOperationException e) {
System.out.println(e.getMessage());
}
}
private static int mostCommonMultiple(int x, int y) {
if (x<=0 || y<=0) throw new UnsupportedOperationException("Incorrect input");
while(x!=0 && y!=0){
if (x>y) x=x%y;
else y=y%x;
}
return x+y;
}
}
ответ дан 9 фев 2020 в 17:44
ДмитрийДмитрий
10.2k2 золотых знака10 серебряных знаков26 бронзовых знаков
Tак проще:
public static void main(String[] args) throws Exception {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
int count;
int x = 0;
int y = 0;
try {
x = Integer.parseInt(reader.readLine());
y = Integer.parseInt(reader.readLine());
} catch (Exception e){
System.out.println("Введи с клавиатуры 2 целых положительных числа.");
} finally {
reader.close();
}
count = Math.min(x, y);
for (int n = count; n >= 1; n--){
if (x % n == 0 && y % n == 0){
count = n;
break;
}
}
System.out.println(count);
}
0xdb
51.4k194 золотых знака56 серебряных знаков232 бронзовых знака
ответ дан 10 мар 2022 в 7:09
10 марта, 2014 | Автор:
| Категория:
Java, Алгоритмы |
Нет комментариев »
НОД (Наибольший общий делитель) или gcd (Greatest Common Divisor)
НОД — наибольшее число, которое является делителем одновременно для чисел a и b.
Реализация (Алгоритм Евклида):
long gcd(long a,long b){
return b == 0 ? a : gcd(b,a % b);
}
Применение:
System.out.println(gcd(10,24));//результат: 2 System.out.println(gcd(12,24));//результат: 12 System.out.println(gcd(11,24));//результат: 1
НОК (Наименьшее общее кратное) или lcm (Least Common Multiple)
НОК — наименьшее число, которое делится на a и b без остатка.
НОК можно найти через НОД по следующей формуле:
Реализация:
long lcm(long a,long b){
return a / gcd(a,b) * b;
}
Примечание: a / gcd(a,b) * b более предпочтительно, чем a * b / gcd(a,b), т.к. во втором случае при больших числах переполнение случиться намного раньше.
Применение:
System.out.println(lcm(3, 4));//результат: 12 System.out.println(lcm(3, 9));//результат: 9 System.out.println(lcm(5,12));//результат: 60
| Поделиться данной статьей через: |
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| package com.javarush.test.level14.lesson08.bonus02; | |
| /* НОД | |
| Наибольший общий делитель (НОД). | |
| Ввести с клавиатуры 2 целых положительных числа. | |
| Вывести в консоль наибольший общий делитель. | |
| */ | |
| import java.io.BufferedReader; | |
| import java.io.InputStreamReader; | |
| public class Solution | |
| { | |
| public static void main(String[] args) throws Exception | |
| { | |
| BufferedReader reader = new BufferedReader(new InputStreamReader(System.in)); | |
| int a = Integer.parseInt(reader.readLine()); | |
| int b = Integer.parseInt(reader.readLine()); | |
| System.out.println(gcd_3(a, b)); | |
| } | |
| public static int gcd_3(int a, int b) { | |
| while (a != b) { | |
| if (a > b) { | |
| a = a — b; | |
| } else { | |
| b = b — a; | |
| } | |
| } | |
| return a; | |
| } | |
| } |