Определение значения синуса, косинуса, тангенса и котангенса
Определение
Тригонометрия — это техническая часть математики, в которой представлены особенности взаимосвязи между сторонами и углами треугольников.
Тригонометрические функции, является очень важной составляющей не только математики, но других технических наук.
Применяя основные формулы и законы тригонометрии при вычислении задач. Огромное значение имеют таблицы значений данных функций. Они существенно упрощают решение задач различной сложности.
Процесс работы и расчета функций данного вида, очень непростой. Решение задач и уравнение, очень часто вызывают сложности. Поэтому, со временем, были созданы и разработаны несколько видов решений, чтобы облегчить жизнь математика и всем представителям технических наук. Преобразовывая тригонометрические формулы, необходимо руководствоваться следующими правилами:
- Нельзя продумывать весь процесс решения от начала до самого конца сразу. Нужно определиться с основными задачами и данными.
- Весь пример, подвергать упрощению или преобразования постепенно;
- Разрешается применять все преобразования и действия, связанные с алгеброй, а именно: вынести значение за пределы скобок. сократить значение и многое другое:
[ sin x=frac{a}{c} ; cos x=frac{b}{c} ; operatorname{tg} x=frac{sin x}{cos x} ; operatorname{ctg}=frac{1}{operatorname{tg} x}=frac{sin x}{cos x} ]
Зная основные определения тригонометрических функций, можно определить их угловые значения. Для углов от нуля до трехсот шестидесяти градусов, вычислим данные и запишем их в виде таблицы.
Значения вышеупомянутых математических функций, в частности в разделе геометрия, вычисляются как соотношения длин прямоугольного треугольника.
Углы геометрической фигуры имеют соответствующие значения в градусах. Используя основные определения математики, а именно тригонометрии можно определить нужные нам данные.
Определим основные значения
1.синуса (sin):
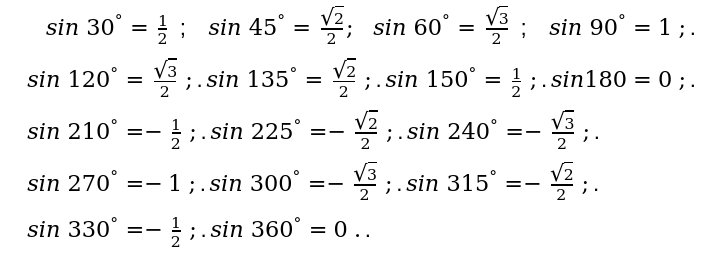
2. косинуса (cos):
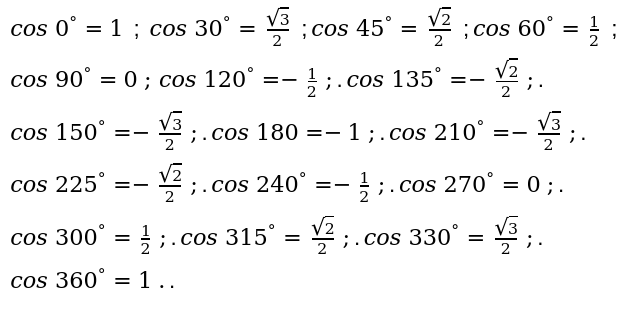
3. тангенса(tg):
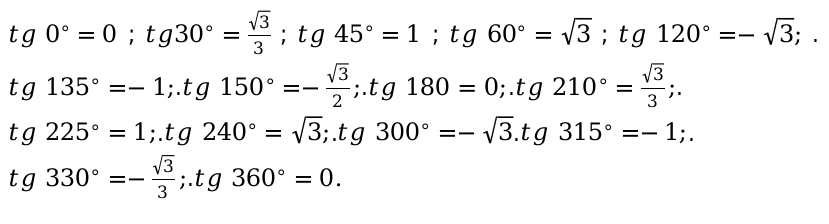
[ operatorname{tg} 90^{circ}, 270^{circ} ]
Данные выше угловые значения, не определяются, согласно основным законам геометрии и математики.
4. котангенса (ctg)
[ operatorname{ctg} 0^{circ}, 180^{circ}, 360^{circ} ]
Для перечисленных выше угловых значений по законам математики и всех технических наук в целом, значения не определяются
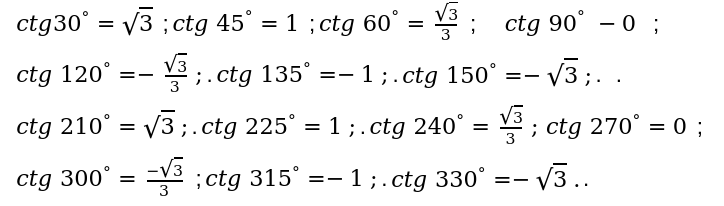
Мы произвели основные расчеты. Определили результаты угловых значений.
Мы определились с основными угловыми значениями функций. Следующим шагом будет их сведение в таблицу.
Таблица1. Основные значения функций косинус, синус, тангенс и котангенс, для угловых значений и радиан
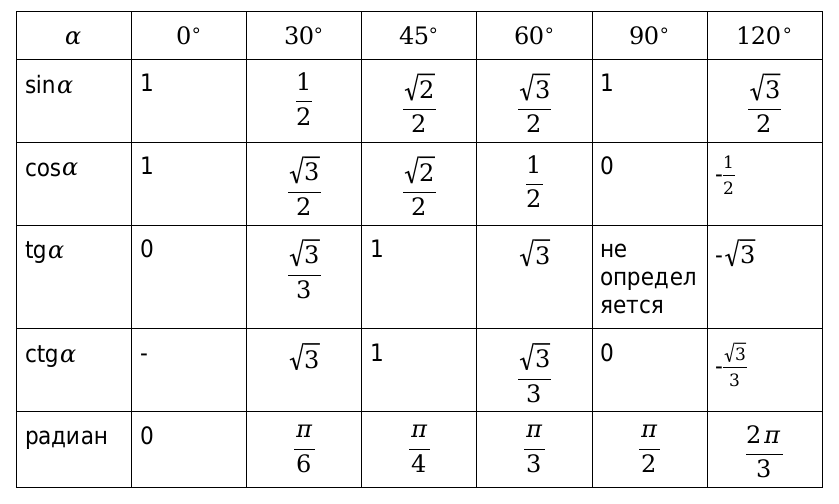
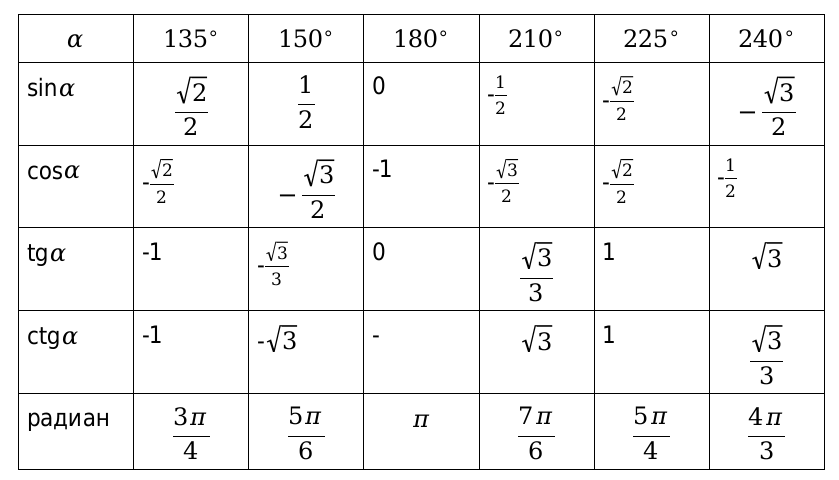
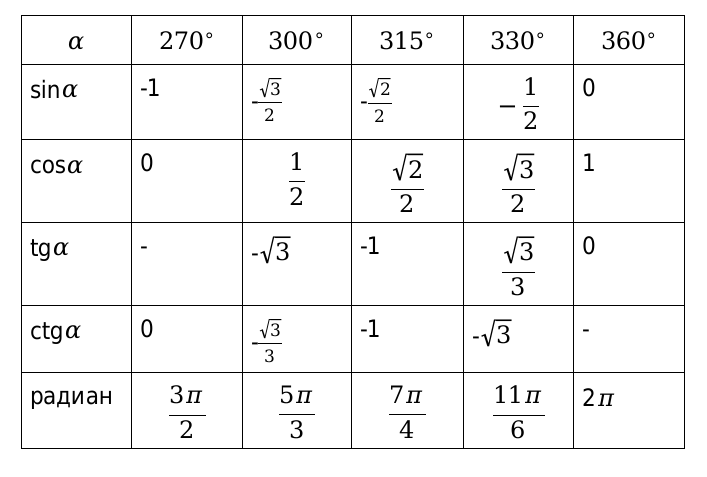
Вычисленные значения принято сводить в таблицу, показанную выше. Особенно рекомендуются, ее заучивать наизусть, для более лучшего восприятия. Рассмотрим, также значения для нестандартных угловых значений и сведем их в таблицу.
Таблица 2. Нестандартные углы функций косинус, синус, тангенс и котангенс в тригонометрии

В данной таблице приведены значения углов, которые считаются нестандартными, также таблица необходима, чтобы облегчить жизнь, в первую очередь, школьной программе.
Например:
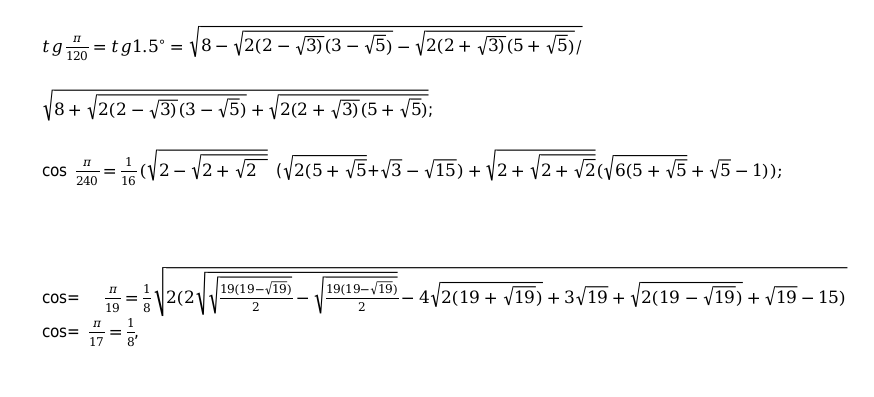
Значение заданной функции берется из таблицы. Оно равняется данному, которое попадает на пересечение столбца и строки.
Пример №1. Необходимо определить чему равен [operatorname{tg} 300]
Берем левый столбец с наименованием функции, находим в верхней строке нужный градус, и на пересечении определяем нужный ответ.
Следовательно:[operatorname{tg} 300^{circ}=-sqrt{3}].
Пример №2. Необходимо определить чему равен [cos frac{5 pi}{3}].
Берем левый столбец с наименованием функции, находим в нижней строке значение радиан, поднимается на верх таблицы и определяем градусы.
[text { Следовательно: } operatorname{tg} 300^{circ}=frac{1}{2} .]
Пример №3. Необходимо определить чему равен [cos frac{11 pi}{6}].
Проводим аналогичные действия, как в предыдущих двух примерах и определяем угловое значение.
[text { Следовательно } cos =frac{sqrt{3}}{2}=330^{circ}.]
Таблица Брадиса для решения основных задач по тригонометрии
Первое упоминание о таблице, датируется 20-ми годами прошлого века. Основоположником, является советский ученый математик, и талантливый педагог Владимир Брадис. Созданная Брадисом таблица, позволяет определить значения тригонометрических функций, с большой точностью, а именно до четырех знаков. На практике решений, обычно требуется точность в три-четыре знака, после запятой, но не более. Для расчета, с такой точностью, значение синуса, в формуле достаточно трех известных слагаемых, а иногда и двух. Произвести простых четыре перемножения. Дважды разделить, умножить и отнять.
Если производить действия инженерным калькулятором, становится понятно, что все вышеперечисленные действия, уже запрограммированы в его микросхеме. В таблице представлены следующие данные:
- число в квадратной и кубической степени;
- числа квадратных корней;
- логарифмические функции и значение;
- функции тригонометрии, представленный в градусах и радианах;
- обратные функции.
Можно определить точность углового значения до минуты. Существуют также таблицы, где есть семизначные значения.
Для того чтобы составить таблицы следует пользовался методом разложения функций (либо метод разложения на степень в ряд)
Примеры решения задач
Пример 1:
Необходимо определить синус угла 18 ° 44 ‘.
По таблице значений определяем данные синуса 18 ° 42 ‘. Далее используем поправку, равную две минуты. Плюсуем ее и заданные минуты: 18 ° 44 ‘ − 18 ° 42 ‘ = 2 ‘
Нужное значение равняется — 0,0006.
Узнав все необходимые значения, находим окончательное решение:
sin 18 ° 44 ‘ = 0. 3208 + 0. 0006 = 0. 3214
Пример 2:
Условие задачи, заключается в необходимости вычислить угол функции синус 76 ° 12. В таблице находим столбец с название угол и ищем 76 градусов и строку со значением 12. Далее, исходя из найденных ячеек, находим значение угла — 0,2284.
Ответ: синус 76 ° 12 =0,2284.
Пример 3:
Нужно найти значение синус 16 градусов 32 минут. Для того чтобы посчитать значение 16 ° 32 минуты. В таблице находим значение нужного угла, которое ближе всего по значению подходит к заданному. Это sin16 30 =0.2840. Так как 16 32=16 30+2, то в столбце, выбираем нужную поправку, которая находится на пересечении со строкой, со значением 16 градусов стоит 0,0006, то есть
sin 16 ° 32 ‘ = 0. 3208 + 0. 0006 = 0. 3214
Пример 4:
Нужно найти значение синус 22 градусов 10 минут. Чтобы посчитать значение 22 ° 12, в таблице найдем значение необходимого угла, наиболее подходящее заданному. Это sin16 30 =0.3778. Так как 22 ° 10= 22 ° 12+2, то тогда выбираем поправку равную двум и видим, что нужный нам градус равный 22 ° имеет значение 0,0005. Далее записываем:
sin 22 ° 10 ‘ = (22 12-2) =0. 3778 + 0. 0005 = 0. 3773
Пример 5:
Нужно найти значение косинус 50 градусов 33 минут. Для того, чтобы посчитать значение 53 31 в таблице найдем значение нужного угла, наиболее близкого к искомому со знаком минус. Это косинус 50 33 =0.6361 Так как 50 33=50 30+3, то в нужном столбце выбираем значение 3. Далее находим значение 0,0007, и записываем следующее уравнение:
косинус 50 ° 33 ‘ = (50 30-3) =0. 6361 +(- 0. 0007) = 0. 6454
Пример 6:
Нужно найти tg 35 градусов 6 минут. В таблице значений функции, в столбце найдем значение 35 градусов, а в строке 6 минут. Определяем нужное значение по таблице равное 0,7028.
Пример 7:
Нужно найти значение котангенс 13 градусов 42 минут. Снова применим таблицу значения функций и найдем значение 13 градусов, а в строке 40 минут и поправку равную 2. Находим искомое значение 4,102.
Пример 8:
Нужно найти значение косинус для 49° 33 минут.
Для того чтобы вычислить значение 49° 31. В таблице найдем значение угла, наиболее близкого по значению к заданному, но только с отрицательным знаком минус. Это косинус 49° 31/ =0.6361 Так как 49° 31/=50 30+3, из этого следует, что поправка равняется трем. Значение 49 градусов равно 0,0007, поэтому: косинус 49° 33 ‘ = ( 49° 31-3) =0 . 6361 +(- 0 . 0007) = 0,6454
Нет времени решать самому?
Наши эксперты помогут!
Основные способы, которые помогут заполнить таблицу функций
1 Действие: Необходимо изобразить простую таблицу, где будет несколько столбцов и строк, необходимых для заполнения данных. Следующая задача, состоит в том, что нужно пустые графы заполнить. Записываем в первом столбике значение математических функций, ранее нами изученных.
В начальной строке, должны отображаться самые часто используемые значения углов: от нуля до девяноста градусов и так далее.
Оставшиеся ячейки нужно оставить незаполненными, для следующих действий. Чтобы понять тригонометрию, нужно изучать не только основные функции. Стоит уделить внимание и таким функциях как: косеканс (cosec) и секанс (sec).
2. Действие: Заполняем пустые ячейки со значение синус. Берем выражение [frac{sqrt{x}}{2}] и подставляем числовые значения, то есть величины углов. они записаны в первом столбике. Далее применяя [frac{sqrt{x}}{2}] можно вычислить данные для углов, которые нам необходимы. Вычисленные значения, записываются в таблицу.
Для наглядности все прописанные действия, можно разобрать на конкретном примере.
Например, мы заполняем ячейку sin 0 градусов. На месте неизвестного значения в выражении [frac{sqrt{x}}{2}] записываем значение угла.
Получаем следующую запись: [frac{sqrt{x}}{2}=frac{0}{2}=0]. Затем, проводим те же операции для заполнения оставшихся пустых строк.
[ frac{sqrt{1}}{2}=frac{1}{2} ; frac{sqrt{2}}{2}=frac{(sqrt{2 cdot 2})}{(2 cdot sqrt{2})}=frac{2}{2 cdot sqrt{2}}=frac{1}{sqrt{2}} ; frac{sqrt{3}}{2} frac{sqrt{4}}{2}=frac{2}{2}=1 ]
Необходимо первым делом заполнять неизвестные ячейки, для функции синус. Это значительно в будущем облегчит заполнение всей таблицы. Так как именно за данной функции и ее данных и завязана вся работы таблицы.
3. Действие: Продолжаем считать таблицу. для этого значения синуса, которые подсчитаны были ранее, переписываем для функции косинус. Только делаем это в порядке обратном значению синусу. Данная теория действительна, потому что sin x° = cos (90-x). Если в самой крайней ячейке синус, имеется 1(sin90°=1). То в первую строку значения косинус, перепишется это числовое значение, cos 0° = 1. Таким образом заканчиваем заполнение до конца.
4. Действие: Для определения тангенса. Необходимо произвести деление данных синуса на косинус. Так как тангенс равен данной функции. [operatorname{tg}=frac{sin }{cos }]. Выходим что искомое значение равно данному выражению. Если [operatorname{tg} 45^{circ}=frac{sin }{cos }=frac{sqrt{1}}{2} / frac{sqrt{3}}{2}=frac{1}{sqrt{3}} .]
Аналогично поступаем и далее.
5. Действие: Для заполнения граф косеканс и секанс нужно 1/sin и 1/cos.
[text { Так как, } operatorname{cosec}=frac{1}{sin } . text { Например, } sin 40^{circ}=frac{1}{2}, text { поэтому } operatorname{cosec} 40^{circ}=frac{1}{frac{1}{2}}=2]
Действие 6: Оставшиеся функции тангенс и котангенс. также записываются обратно значениям. Если tg90 равняется ctg0, значение tg60 будет соответственно равен значению ctg 30 градусов.
[text { Таким же методом заполняются оставшиеся строки таблицы. Так } text { как } operatorname{ctg}=frac{1}{t g}, text { в свою очередь } operatorname{ctg}=frac{cos }{sin }]
Вычисление данных при помощи фигуры — прямоугольный треугольник
Для этого строится нужный треугольник заданным углом, который необходимо определить. Строится угол, точка и луч, которые выходят из данной точки под определенным углом. Соединяем лучи, прямой линией перпендикулярной, одному из лучей. В конечном итоге получаем фигуру, угол которой равняется заданному в задаче углу. В процессе вычисления, также задаются длины сторон. Поэтому трудней с построением не должно возникнуть.
Вычисление при помощи длин сторон треугольника происходит следующим образом:
- обозначается катет;
- сторона возле угла;
- сторона напротив угла с прямым значением.
Функции могут выражаться по-разному в отношении сторон. Например, нам нужно определим значение sin 45°. Поделим имеющуюся длину значения противолежащего катета на значение длины гипотенузы. Если заданные значения длины равны 4 и 6 соответственно. Тогда, составим следующее выражение и получим sin[45^{circ}=frac{4}{6}=0,67]
Для определения значений основных функций в математике, необходимо заучить наизусть определение основных понятий, связанный с данной темой.
В процессе решения задачи, это придется применять постоянно.
Значения косеканса и секанса определяются в обратном порядке. Для этого необходимо знать какие стороны нужно делить для определения вышеперечисленных функций.
Косеканс находится [operatorname{cosec}=frac{1}{sin }] следовательно, нужно разделить гипотенузу на противолежащий катет. Секанс, наоборот к прилежащему катету [mathrm{sec}=frac{1}{cos }].
Например, для определения cosec 40°, если катет равен 5, а гипотенуза соответственно равна 8. Нужно разделить 5/8 и получим ответ cosec 40° = 0,63.
При вычислениях всегда рекомендуется исключать значение под корнем в знаменателе, это наиболее облегчает процесс расчета.
Рассмотренная тема преобразования и расчета функций, является довольно громоздкой, на первый взгляд. Применяя для решения огромные формулы и функции можно растеряться и не сразу сообразить, как производить их расчет. Однако досконально рассмотрев и изучив каждый раздел, становится понятно, что все достаточно просто и громоздкие таблицы освоить можно быстро и легко.
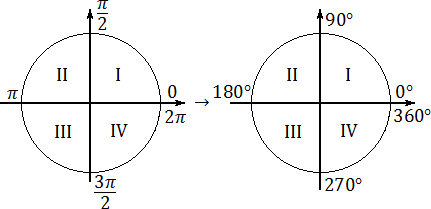
Вычисление значений углов по окружности
Самый простой и понятный способ для вычисления углов и радиан.
Для этого вычерчиваем окружность с радиусом R. Он в свою очередь, равен единичному значению. Центр окружности равен центру системы координат. От положительной оси считаем углы, по часовой стрелке, выполняющей движении против хода. Точка, имеющая координаты 1;0 равняется угловому значению ноль. если координаты -1;0, тогда угол равен 90 градусов. Точка, находящаяся на окружности, соответствует углу от нуля до 360 градусов. Так как окружность является единичной, значения углов для синуса и косинуса находятся в пределах от -1 до 1:
Определяются знаки функций, также по окружности. если угловое значение более 360 градусов, делается два оборота по часовой стрелке и плюсуется еще дополнительно 12 минут.
[ cos (alpha+360 cdot n)=sin alpha ;] [ sin (alpha+360 cdot n)=sin alpha / ]
Значения тангенсов и котангенсов, можно вычислить аналогично, по окружности. Однако легче посчитать по формулам, уже известных данных.
[ operatorname{tg} alpha=frac{sin alpha}{cos alpha} ; operatorname{ctg} alpha=frac{cos alpha}{sin alpha} ]
|
|
Как найти нестандартные углы синуса
|
|
14/12/09 |
Помогите, пожалуйста, найти нестандартные углы синуса (решение необязательно , нужен точный ответ в радианах):
Вообще, надо найти значение:
|
|
|
|
|
G_Ray |
Re: Как найти нестандартные углы синуса
|
|
21/12/08 |
|
|
|
|
|
Koftochka |
Re: Как найти нестандартные углы синуса
|
|
14/12/09 |
В том и дело, что нужен точный ответ.
|
|
|
|
|
ShMaxG |
Re: Как найти нестандартные углы синуса
|
||
11/04/08 |
Выражение, очевидно, равно нужен точный ответ в радианах Точный — это как? Можно ведь и в ряд Тейлора для арксинуса подставить — чем не точное значение?
|
||
|
|
|||
|
ewert |
Re: Как найти нестандартные углы синуса
|
||
11/05/08 |
ну, наверное, надо взять косинус от этой суммы, и наверное, после раскрытия всех скобок там получится что-то стандартное, а иначе никак. Тупо, удручающе и математически откровенно бессмысленно. И кому только такие задачки в голову приходят?…
|
||
|
|
|||
|
ShMaxG |
Re: Как найти нестандартные углы синуса
|
||
11/04/08 |
ewert Я уже попробовал так сделать. Ничего хорошего там не нашел…
|
||
|
|
|||
|
Sasha2 |
Re: Как найти нестандартные углы синуса
|
|
21/06/06 |
Первый арксинус равен
|
|
|
|
|
jetyb |
Re: Как найти нестандартные углы синуса
|
||
19/06/09 |
|
||
|
|
|||
|
Padawan |
Re: Как найти нестандартные углы синуса
|
||
13/12/05 |
— Сб янв 23, 2010 22:56:54 — Так что у меня тоже возникает вопрос Точный — это как?
|
||
|
|
|||
|
Sonic86 |
Re: Как найти нестандартные углы синуса
|
||
08/04/08 |
|||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы
Радианная мера угла
3 ноября 2011
В школьном курсе математики есть два определения основных тригонометрических функций — синуса, косинуса, тангенса и котангенса:
- Геометрический подход — основан на сторонах прямоугольного треугольника и их соотношениях. В этом случае все синусы и косинусы положительны, поскольку длина отрезка всегда задается положительным числом;
- Алгебраический подход — работа ведется на тригонометрической окружности. Такой подход возникает на стыке 9—10 классов, и с этого момента синусы и косинусы вполне могут быть отрицательными. А «старые» геометрические определения становятся лишь частным случаем.
Для решения задачи B11 нужен именно алгебраический подход. Чуть позже мы убедимся, что такие задачи решаются элементарно — буквально с помощью одной формулы. Но для начала научимся быстро (буквально на лету) определять координатную четверть, в которой расположен искомый угол. В этом нам помогут следующие правила.
Переход от радианной меры к градусной
Вспомните: в 8—9 классах мы работали лишь с несколькими стандартными углами. А именно: 30°, 45° и 60°. В особо продвинутых случаях учителя рассказывали еще об углах 90° и 0°. Любые другие значения назывались «сложными», и возникновение таких углов, скорее всего, указывало на ошибку в решении.
С введением тригонометрической окружности все ограничения на углы отпадают. Здесь я не буду рассказывать, как устроена тригонометрическая окружность — все это подробно описано в любом учебнике по математике. Вместо этого предлагаю обсудить другой вопрос — более важный, но которому почему-то не уделяется достаточно внимания. Речь идет о переходе от радианной меры угла к градусной.
Исторически так сложилось (и небезосновательно), что углы на тригонометрической окружности измеряют в радианах. Например, полный оборот — 360° — обозначается как 2π радиан. А всеми любимый (или ненавидимый) угол 45° равен π/4 радиан.
У многих возникает вопрос: при чем здесь число π? Ведь π ≈ 3,14. Так вот, чтобы избежать путаницы, запомните простое, но очень важное правило:
Во всех тригонометрических функциях — синусе, косинусе, тангенсе и котангенсе — можно без ущерба для здоровья заменять число π на 180°. Пишется это так: π → 180°.
Обратите внимание: данное правило работает только для тригонометрических функций! Например, мы спокойно можем записать sin π = sin 180°. Но если мы хотим найти примерную длину отрезка l = 5π, придется считать: l = 5 · π ≈ 5 · 3,14 = 15,7.
Разумеется, существует и обратное правило — переход от градусной меры угла к радианной. Однако нас это сейчас не интересует, поскольку в задачах B11 такой переход не встречается.
Теперь взгляните на конкретные примеры:
Задача. Перейдите от радианной меры угла к градусной (значение тригонометрических функций вычислять не надо):
- sin π/3;
- cos 7π/6;
- tg π;
- sin π/4;
- tg 2π/3;
- ctg π/2;
- sin 3π/2;
- cos 5π/4.
Итак, перед нами восемь тригонометрических функций, аргументы которых заданы в радианах. Мы можем перейти от радианной меры аргументов к градусной по правилу: π → 180°. Имеем:
- sin π/3 = sin 180/3 = sin 60°;
- cos 7π/6 = cos (7 · 180/6) = cos 210°;
- tg π = tg 180°;
- sin π/4 = sin 180/4 = sin 45°;
- tg 2π/3 = tg (2 · 180/3) = tg 120°;
- ctg π/2 = ctg 180/2 = ctg 90°;
- sin 3π/2 = sin (3 · 180/2) = sin 270°;
- cos 5π/4 = cos (5 · 180/4) = cos 225°.
- α ∈ (0°; 90°) ⇒ это угол I координатной четверти;
- α ∈ (90°; 180°) ⇒ II координатная четверть;
- α ∈ (180°; 270°) ⇒ III координатная четверть;
- α ∈ (270°; 360°) ⇒ IV координатная четверть.
- sin 8π/9;
- tg 12π/15;
- cos 9π/10;
- cos 7π/18;
- sin 3π/5;
- ctg 5π/3;
- tg 4π/9;
- cos 9π/20.
- sin 8π/9 = sin (8 · 180/9) = sin 160°; т.к. 160° ∈ [90°; 180°], это II четверть;
- tg 12π/15 = tg (12 · 180/15) = tg 144°; т.к. 144° ∈ [90°; 180°], это II четверть;
- cos 9π/10 = cos (9 · 180/10) = cos 162°; т.к. 162° ∈ [90°; 180°], это II четверть;
- cos 7π/18 = cos (7 · 180/18) = cos 70°; т.к. 70° ∈ [0°; 90°], это I четверть;
- sin 3π/5 = sin (3 · 180/5) = sin 108°; т.к. 108° ∈ [90°; 180°], это II четверть;
- ctg 5π/3 = ctg (5 · 180/3) = ctg 300°; т.к. 300° ∈ [270°; 360°], это IV четверть;
- tg 4π/9 = tg (4 · 180/9) = tg 80°; т.к. 80° ∈ [0°; 90°], это I четверть;
- cos 9π/20 = cos (9 · 180/20) = cos 81°; т.к. 81° ∈ [0°; 90°], это I четверть.
- Перейти от радианной меры угла к градусной. Для этого достаточно сделать замену: π → 180°;
- Если полученный угол оказался больше 360°, отнимаем от него по 360° до тех пор, пока новый угол не окажется на отрезке [0°; 360°];
- Аналогично, если угол будет отрицательным, увеличиваем его на 360° до тех пор, пока он не попадет в отрезок [0°; 360°];
- Выясняем, в какой координатной четверти находится полученный угол, ориентируясь на стандартные границы: 90°, 180°, 270° и 360°.
- sin 21π/6;
- cos 19π/3;
- sin (−25π/9);
- tg (−11π/4).
- sin 21π/6 = sin (23 · 180/6) = sin 690°. Очевидно, что 690° > 360°, поэтому выполняем преобразование: sin 690° → sin (690° − 360°) = sin 330°. Но 330° ∈ [270°; 360°], это IV четверть;
- cos 19π/3 = cos (19 · 180/3) = cos 1140°. Поскольку 1140° > 360°, имеем: cos 1140° → cos (1140° − 360°) = cos 780° → cos (780° − 360°) = cos 420° → cos (420° − 360°) = cos 60°. Т.к. 60° ∈ [0°; 90°], это I четверть;
- sin (−7π/9) = sin (−7 · 180/9) = sin (−140°). Но −140° < 0°, поэтому увеличиваем угол: sin (−140°) → sin (−140° + 360°) = sin 220°. Поскольку 220° ∈ [180°; 270°], это III четверть;
- tg (−11π/4) = tg (−11 · 180/4) = tg (−495°). Т.к. −495° < 0°, начинаем увеличивать угол: tg (−495°) → tg (−495° + 360°) = tg (−135°) → tg (−135° + 360°) = tg 225°. Это уже нормальный угол. Т.к. 225° ∈ [180°; 270°], это III четверть.
>
Итак, вместо непонятного множителя π мы получаем вполне вменяемое число, которое можно умножать и делить по стандартным правилам.
Границы координатных четвертей
Теперь, когда мы умеем заменять радианную меру углов градусной, попробуем переписать всю тригонометрическую окружность. Это будет ключом к решению задачи B11. Основные правила останутся прежними: «нулевой градус» совпадает с положительным направлением оси ОХ, а углы откладываются в направлении против часовой стрелки. Но числа, стоящие на границах координатных четвертей, станут другими. Взгляните:
Отныне вместо непонятных «пи» и «пи-пополам» используйте простую и понятную шкалу:
Хорошая новость состоит в том, что эти правила очень быстро откладываются в голове — стоит лишь немного потренироваться. И вы точно не забудете эти числа на ЕГЭ по математике, чего нельзя сказать про радианную меру.
Если же память на числа плохая, могу посоветовать одну хитрость. Взгляните еще раз на границы координатных четвертей: 90°, 180°, 270° и 360°. Первая из них — 90° — это прямой угол, знакомый еще из курса средней школы. Его вы точно не забудете. Остальные углы отличаются друг от друга на эти же самые 90°. Взгляните: 90° + 90° = 180°; 180° + 90° = 270°; 270° + 90° = 360°. Таким образом, даже если вы забудете эти числа, их всегда можно восстановить, если просто запомнить, что прямой угол — это 90°.
А теперь разберем конкретные примеры. Будем учиться искать координатные четверти быстро, поскольку от этого умения напрямую зависит решение задачи B11.
Задача. Определите, в какой координатной четверти находится аргумент тригонометрической функции:
Для начала переведем все углы из радиан в градусы по правилу: π → 180°. А затем найдем координатную четверть, ориентируясь по границам: 90°, 180°, 270°, 360°. Имеем:
Как видите, далеко не всегда можно найти значение самой тригонометрической функции. Например, попробуйте вычислить cos 162° или sin 108°. Зато мы всегда можем определить, в какой координатной четверти находится данный угол.
Нестандартные углы и периодичность
До сих пор мы рассматривали углы α ∈ [0°; 360°]. Но что произойдет, если, например, угол α = 420°? А как насчет отрицательных углов? Такие углы редко встречаются на ЕГЭ по математике (по крайней мере, в части B), но лучше застраховать себя от подобных «неожиданностей», поэтому предлагаю разобрать и такие задачи. Тем более, схема решения практически ничем не отличается от «стандартных» углов.
Итак, что если угол α > 360°? Судя по тригонометрической окружности, точка сделает полный оборот — а затем пройдет еще чуть-чуть. Это самое «чуть-чуть» вычисляется очень просто. Достаточно отнять от исходного угла величину 360° (иногда это приходится делать несколько раз).
С отрицательными углами работаем аналогично. Если добавлять к отрицательному углу величину 360°, мы очень скоро получим новый угол α ∈ [0°; 360°]. Таким образом, вся схема решения выглядит следующим образом:
Задача. Определите, в какой координатной четверти находится аргумент тригонометрической функции:
Снова переводим все углы из радиан в градусы по правилу: π → 180°. Дальше уменьшаем или увеличиваем аргумент на 360° до тех пор, пока он не окажется на отрезке [0°; 360°]. И только затем выясняем координатную четверть. Получим:
Вот и все! Обратите внимание: во втором пункте пришлось вычитать 360° три раза — и только затем получился нормальный угол. Аналогично, в четвертом пункте пришлось прибавлять два раза по 360°, чтобы выйти на положительный угол. Таким образом, добавлять и вычитать углы иногда приходится много раз — это не должно настораживать.
В заключение хочу добавить, что если вы хорошо знаете математику и быстро ориентируетесь в радианных углах, то совсем необязательно переводить их в градусы. Однако большинство людей (и не только школьники) предпочитают именно градусную меру — знакомую еще со средней школы и, как следствие, более понятную.
Смотрите также:
- Тест к уроку «Знаки тригонометрических функций» (1 вариант)
- Знаки тригонометрических функций
- Что такое логарифм
- Комбинированные задачи B12
- Задача B2: лекарство и таблетки
- ЕГЭ 2022, задание 6. Касательная и уравнение с параметром
Сообщения без ответов | Активные темы
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Заголовок сообщения: Значения тригонометрических функций нестандартных углов
|
||||
|
Вопрос навеян одной из предыдущих тем, где был вычислен один из интересненьких углов. А еще какие нестандартные углы могут быть вычислены и каким способом? К примеру, можно ли вычислить [math]sin 10^{circ}[/math], [math]sin 13^{circ}[/math], [math]sin frac{pi}{7}[/math], [math]sin frac{pi}{11}[/math] и т.п. Очень стал интересен этот вопрос. Может, где-то об этом почитать можно? (Ведь их же выводят как-то…)
|
|||
| Вернуться к началу |
|
|||
| За это сообщение пользователю Sviatoslav «Спасибо» сказали: valentina |
||||
|
Talanov |
Заголовок сообщения: Re: Значения тригонометрических функций нестандартных углов
|
|
Sviatoslav писал(а): можно ли вычислить [math]sin {10^0}[/math] [math]sin {30^0}=3 sin {10^0} — 4 sin^3 {10^0}=1|2[/math] [math]x^3-frac{3}{4} x +frac{1}{8}=0[/math]
|
|
| Вернуться к началу |
|
| За это сообщение пользователю Talanov «Спасибо» сказали: Sviatoslav |
|
|
Talanov |
Заголовок сообщения: Re: Значения тригонометрических функций нестандартных углов
|
|
Avgust писал(а): [math]sin(frac{pi}{7})=x[/math] [math]64x^6-112x^4+56x^2-7=0[/math] [math]sin(frac{pi}{7})approx 0.4338839…[/math] Вы, не въехали в тему? Нужно определять точно, в радикалах.
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Коэффициенты МНК для нестандартных функций
в форуме Математическая статистика и Эконометрика |
Cthline |
8 |
726 |
10 июл 2013, 22:00 |
|
Значение нестандартных обратных тринометрических функций
в форуме Тригонометрия |
guest66 |
3 |
366 |
01 фев 2015, 09:17 |
|
Найти значения углов в 4-хугольнике
в форуме Геометрия |
NikolajSladkov |
9 |
723 |
13 дек 2014, 14:00 |
|
Тригонометрических функций
в форуме Интегральное исчисление |
Nelo |
26 |
1131 |
02 мар 2014, 17:56 |
|
Интегрирование тригонометрических функций
в форуме Интегральное исчисление |
overkill21 |
1 |
352 |
23 апр 2014, 13:16 |
|
Производная тригонометрических функций
в форуме Пределы числовых последовательностей и функций, Исследования функций |
Olga1975 |
2 |
298 |
17 апр 2016, 20:01 |
|
Интеграл от тригонометрических функций
в форуме Интегральное исчисление |
jagdish |
0 |
231 |
23 сен 2016, 13:02 |
|
Исследование тригонометрических функций
в форуме Тригонометрия |
Uchenica |
3 |
767 |
17 окт 2013, 11:58 |
|
Синтаксис тригонометрических функций
в форуме Тригонометрия |
fingolfin |
2 |
366 |
26 окт 2015, 01:51 |
|
Пределы тригонометрических функций
в форуме Пределы числовых последовательностей и функций, Исследования функций |
DarKRs |
3 |
527 |
17 дек 2014, 18:11 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 2 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
В статье, мы полностью разберемся, как выглядит таблица тригонометрических значений, синуса, косинуса, тангенса и котангенса . Рассмотрим основное значение тригонометрических функций, от угла в 0,30,45,60,90,…,360 градусов.
И посмотрим как пользоваться данными таблицами в вычислении значения тригонометрических функций.
Первой рассмотрим таблицу косинуса, синуса, тангенса и котангенса от угла в 0, 30, 45, 60, 90,.. градусов.
Определение данных величин дают определить значение функций углов в 0 и 90 градусов:
Так же исходя из свойств периодичности таблицу можно увеличить, если заменим углы на 00+3600*z …. 3300+3600*z, в котором z является целым числом. В данной таблице возможно вычислить значение всех углов, соответствующими точками в единой окружности.
Разберем наглядно как использовать таблицу в решении.
Все очень прост. Так как нужное нам значение лежит в точке пересечения нужных нам ячеек. К примеру возьмем cos угла 60 градусов, в таблице это будет выглядеть как:
В итоговой таблице основных значений тригонометрических функций, действуем так же. Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 10200 = 3000+3600*2. Найдем по таблице.
Для более поиска тригонометрических значений углов с точностью до минут используются таблицы Брадиса. Подробная инструкция как ими пользоваться на странице по ссылке.
Таблица Брадиса. Для синуса, косинуса, тангенса и котангенса.
Разберемся как пользоваться таблицами Брадиса в решении задач.
Найдем обозначение sin (обозначение в столбце с левого края) 42 минут (обозначение находится на верхней строчке). Путем пересечения ищем обозначение, оно = 0,3040.
Величины минут указаны с промежутком в шесть минут, как быть если нужное нам значение попадет именно в этот промежуток. Возьмем 44 минуты, а в таблице есть только 42. Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.
При sin 47 мин, берем за основу 48 мин и отнимаем от нее 1 поправку, т.е 0,3057 — 0,0003 = 0,3054
При вычислении cos работаем аналогично sin только за основу берем нижнюю строку таблицы. К примеру cos 200 = 0.9397
Значения tg угла до 900 и cot малого угла, верны и поправок в них нет. К примеру, найти tg 780 37мин = 4,967
Ну вот мы и рассмотрели основные тригонометрические таблицы. Надеемся это информация была для вас крайне полезной. Свои вопросы по таблицам, если они появились, обязательно пишите в х!
Заметка: Стеновые отбойники — отбойная доска для защиты стен (http://www.spi-polymer.ru/otboyniki/)
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Когда прямые пересекаются, то получается четыре разные области по отношению к точке пересечения.
Эти новые области называют углами.
Мы говорили о том, что когда объект делает полный круг вокруг точки, то он проходит 360°, однако, когда объект делает более одного круга, то он делает угол более 360 градусов. Это обычное явление в повседневной жизни. Колесо проходит многие круги, когда автомобиль движется, то есть оно образует угол больше 360°.
Для того, чтобы узнать количество циклов (пройденных кругов) при вращении объекта, мы считаем количество раз, которое нужно прибавить 360 к самому себе, чтобы получить число равное или меньшее, чем данный угол. Точно так же мы находим число, которое мы умножаем на 360, чтобы получить число меньшее, но наиболее близкое к данному углу.
a) 380 = (1 × 360) + 20
Объект описал один круг и 20°
Так как $20^{circ} = frac{20}{360} = frac{1}{18}$ круга
Объект описал $1frac{1}{18}$ кругов. b) 2 × 360 = 720
770 = (2 × 360) + 50
Объект описал два круга и 50°
$50^{circ} = frac{50}{360} = frac{5}{36}$ круга
Объект описал $2frac{5}{36}$ круга
c)2 × 360 = 720
1000 = (2 × 360) + 280
$280^{circ} = frac{260}{360} = frac{7}{9}$ кругов
Объект описал $2frac{7}{9}$ кругов
Когда объект вращается по часовой стрелки, то он образует отрицательный угол вращения, а когда вращается против часовой стрелке — положительный угол. До этого момента мы рассматривали только положительные углы.
Это означает, что при наличии отрицательного угла, мы можем получить соответствующий ему положительный угол.
Например, нижняя часть вертикальной прямой это 270°. Когда измеряется в негативную сторону, то получим -90°. Мы просто вычитаем 270 из 360.
Имея отрицательный угол, мы прибавляем 360, для того чтобы получить соотвествующий положительный угол.
2. Найти соответствующий отрицательный угол 80°, 167°, 330°и 1300°.
Решение
1. Для того, чтобы найти соответствующий положительный угол мы прибавляем 360 к значению угла.
a) -35°= 360 + (-35) = 360 — 35 = 325°
b) -60°= 360 + (-60) = 360 — 60 = 300°
c) -180°= 360 + (-180) = 360 — 180 = 180°
d) -670°= 360 + (-670) = -310
Это означает один круг по часовой стрелке (360)
360 + (-310) = 50°
2. Для того, чтобы получить соответсвующий отрицательный угол мы вычитаем 360 от значения угла.
80° = 80 — 360 = — 280°
167° = 167 — 360 = -193°
330° = 330 — 360 = -30°
1300° = 1300 — 360 = 940 (пройден один круг)
940 — 360 = 580 (пройден второй круг)
580 — 360 = 220 (пройден третий круг)
220 — 360 = -140°
Угол равен -360 — 360 — 360 — 140 = -1220°
Радиан — это угол из центра круга, в который заключена дуга, длина которой равна радиусу данного круга.
Это единица измерения угловой величины. Такой угол примерно равен 57,3°.
В большинстве случаев, это обозначается как рад.
Таким образом $1 рад approx 57,3^{circ}$
Радианы обычно выражаются через $pi$ во избежание десятичных частей в вычислениях. В большинстве книг, аббревиатура рад (rad)
не встречается, но читатель должен знать, что, когда речь идет об угле, то он задан через $pi$, а
единицами измерения автоматически становятся радианы.
Пример 4
1. Преобразовать 240°, 45°, 270°, 750° и 390° в радианы через $pi$.
Умножим углы на $frac{pi}{180}$.
2. Преобразовать следующие углы в градусы.
a) $frac{5}{4}pi$ b) $3,12pi$
c) 2,4 радиан
$180^{circ} = pi$
a) $frac{5}{4} pi = frac{5}{4} imes 180 = 225^{circ}$
b) $3,12pi = 3,12 imes 180 = 561,6^{circ}$ c) 1 рад = 57,3°
Для того чтобы преобразовать отрицательный угол в положительный, мы складываем его с $2pi$.
Для того чтобы преобразовать положительный угол в отрицательный, мы вычитаем из него $2pi$.
Пример 5
1. Преобразовать $-frac{3}{4}pi$ и $-frac{5}{7}pi$ в позитивные углы в радианах.
Когда объект вращается на угол больший, чем $2pi$;, то он делает больше одного круга.
Для того, чтобы определить количество оборотов (кругов или циклов) в таком угле, мы находим такое число, умножая которое на $2pi$, результат равен или меньше, но как можно ближе к данному числу.
Источник: https://www.math10.com/ru/geometria/ugli/izmerenie-uglov/izmerenie-uglov.html
Здесь рассматриваем задачи Proc32 — Proc33 из задачника Абрамяна: описание функций преобразования углов из градусов в радианы и наоборот.
Так что такое радианная мера угла? Рассмотрим некоторую окружность радиуса R с центром в точке О. Поскольку окружность делится на 360 градусов, а длина окружности равна 2πR, то на 1 градус приходится длина дуги равная 2πR/360 = πR/180. Тогда углу α градусов соответствует длина дуги L = πRα/180.
В этом смысле очень интересна ситуация, когда длина дуги L равна радиусу окружности R. Каков при этом угол дуги? Вспоминая предыдущую формулу для вычисления длины дуги, имеем: πRα/180 = R, откуда πα/180 = 1, а отсюда получаем α = 180/π.
Например, если длина дуги равна 1.5R, то радианная мера угла этой дуги равна 1.5; если длина дуги равна 0.25R, то радианная мера равна 0.25; для дуги длиной 2πR (вся окружность) радианная мера равна 2π и т.д. Вообще, для дуги длиной L угол в радианах равен L/R, где R – радиус.
Радиан – это очень удобный способ измерения углов, поскольку вместо самих углов мы можем оперировать коэффициентами отношений длин дуг и их радиусов. В высшей математике во всех тригонометрических функциях используется только радианная мера.
Proc32. Описать функцию DegToRad(D) вещественного типа, находящую величину угла в радианах, если дана его величина D в градусах (D — вещественное число, 0 ≤ D < 360). Воспользоваться следующим соотношением: 180° = π радианов. В качестве значения π использовать 3.14. С помощью функции DegToRad перевести из градусов в радианы пять данных углов.
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 | { Функция возвращает величину угла в радианах, если дана его величина D в градусах (D — вещественное число, 0 ≤ D < 360) } function DegToRad(D: real): real; const pi = 3.14; { |
Источник: https://progmatem.ru/proc/proc-32-33.html
Радианная и градусная мера угла
3 ноября 2011
В школьном курсе математики есть два определения основных тригонометрических функций — синуса, косинуса, тангенса и котангенса:
- Геометрический подход — основан на сторонах прямоугольного треугольника и их соотношениях. В этом случае все синусы и косинусы положительны, поскольку длина отрезка всегда задается положительным числом;
- Алгебраический подход — работа ведется на тригонометрической окружности. Такой подход возникает на стыке 9—10 классов, и с этого момента синусы и косинусы вполне могут быть отрицательными. А «старые» геометрические определения становятся лишь частным случаем.
Для решения задачи B11 нужен именно алгебраический подход. Чуть позже мы убедимся, что такие задачи решаются элементарно — буквально с помощью одной формулы. Но для начала научимся быстро (буквально на лету) определять координатную четверть, в которой расположен искомый угол. В этом нам помогут следующие правила.
Переход от радианной меры к градусной
Вспомните: в 8—9 классах мы работали лишь с несколькими стандартными углами. А именно: 30°, 45° и 60°. В особо продвинутых случаях учителя рассказывали еще об углах 90° и 0°. Любые другие значения назывались «сложными», и возникновение таких углов, скорее всего, указывало на ошибку в решении.
С введением тригонометрической окружности все ограничения на углы отпадают. Здесь я не буду рассказывать, как устроена тригонометрическая окружность — все это подробно описано в любом учебнике по математике. Вместо этого предлагаю обсудить другой вопрос — более важный, но которому почему-то не уделяется достаточно внимания. Речь идет о переходе от радианной меры угла к градусной.
Исторически так сложилось (и небезосновательно), что углы на тригонометрической окружности измеряют в радианах. Например, полный оборот — 360° — обозначается как 2π радиан. А всеми любимый (или ненавидимый) угол 45° равен π/4 радиан.
У многих возникает вопрос: при чем здесь число π? Ведь π ≈ 3,14. Так вот, чтобы избежать путаницы, запомните простое, но очень важное правило:
Во всех тригонометрических функциях — синусе, косинусе, тангенсе и котангенсе — можно без ущерба для здоровья заменять число π на 180°. Пишется это так: π → 180°.
Обратите внимание: данное правило работает только для тригонометрических функций! Например, мы спокойно можем записать sin π = sin 180°. Но если мы хотим найти примерную длину отрезка l = 5π, придется считать: l = 5 · π ≈ 5 · 3,14 = 15,7.
Разумеется, существует и обратное правило — переход от градусной меры угла к радианной. Однако нас это сейчас не интересует, поскольку в задачах B11 такой переход не встречается.
Теперь взгляните на конкретные примеры:
Задача. Перейдите от радианной меры угла к градусной (значение тригонометрических функций вычислять не надо):
- sin π/3;
- cos 7π/6;
- tg π;
- sin π/4;
- tg 2π/3;
- ctg π/2;
- sin 3π/2;
- cos 5π/4.
Итак, перед нами восемь тригонометрических функций, аргументы которых заданы в радианах. Мы можем перейти от радианной меры аргументов к градусной по правилу: π → 180°. Имеем:
- sin π/3 = sin 180/3 = sin 60°;
- cos 7π/6 = cos (7 · 180/6) = cos 210°;
- tg π = tg 180°;
- sin π/4 = sin 180/4 = sin 45°;
- tg 2π/3 = tg (2 · 180/3) = tg 120°;
- ctg π/2 = ctg 180/2 = ctg 90°;
- sin 3π/2 = sin (3 · 180/2) = sin 270°;
- cos 5π/4 = cos (5 · 180/4) = cos 225°.
Итак, вместо непонятного множителя π мы получаем вполне вменяемое число, которое можно умножать и делить по стандартным правилам.
Границы координатных четвертей
Теперь, когда мы умеем заменять радианную меру углов градусной, попробуем переписать всю тригонометрическую окружность. Это будет ключом к решению задачи B11.
Основные правила останутся прежними: «нулевой градус» совпадает с положительным направлением оси ОХ, а углы откладываются в направлении против часовой стрелки.
Но числа, стоящие на границах координатных четвертей, станут другими. Взгляните:

Отныне вместо непонятных «пи» и «пи-пополам» используйте простую и понятную шкалу:
- α ∈ (0°; 90°) ⇒ это угол I координатной четверти;
- α ∈ (90°; 180°) ⇒ II координатная четверть;
- α ∈ (180°; 270°) ⇒ III координатная четверть;
- α ∈ (270°; 360°) ⇒ IV координатная четверть.
Хорошая новость состоит в том, что эти правила очень быстро откладываются в голове — стоит лишь немного потренироваться. И вы точно не забудете эти числа на ЕГЭ по математике, чего нельзя сказать про радианную меру.
Если же память на числа плохая, могу посоветовать одну хитрость. Взгляните еще раз на границы координатных четвертей: 90°, 180°, 270° и 360°. Первая из них — 90° — это прямой угол, знакомый еще из курса средней школы. Его вы точно не забудете.
Остальные углы отличаются друг от друга на эти же самые 90°. Взгляните: 90° + 90° = 180°; 180° + 90° = 270°; 270° + 90° = 360°.
Таким образом, даже если вы забудете эти числа, их всегда можно восстановить, если просто запомнить, что прямой угол — это 90°.
А теперь разберем конкретные примеры. Будем учиться искать координатные четверти быстро, поскольку от этого умения напрямую зависит решение задачи B11.
Задача. Определите, в какой координатной четверти находится аргумент тригонометрической функции:
- sin 8π/9;
- tg 12π/15;
- cos 9π/10;
- cos 7π/18;
- sin 3π/5;
- ctg 5π/3;
- tg 4π/9;
- cos 9π/20.
Для начала переведем все углы из радиан в градусы по правилу: π → 180°. А затем найдем координатную четверть, ориентируясь по границам: 90°, 180°, 270°, 360°. Имеем:
- sin 8π/9 = sin (8 · 180/9) = sin 160°; т.к. 160° ∈ [90°; 180°], это II четверть;
- tg 12π/15 = tg (12 · 180/15) = tg 144°; т.к. 144° ∈ [90°; 180°], это II четверть;
- cos 9π/10 = cos (9 · 180/10) = cos 162°; т.к. 162° ∈ [90°; 180°], это II четверть;
- cos 7π/18 = cos (7 · 180/18) = cos 70°; т.к. 70° ∈ [0°; 90°], это I четверть;
- sin 3π/5 = sin (3 · 180/5) = sin 108°; т.к. 108° ∈ [90°; 180°], это II четверть;
- ctg 5π/3 = ctg (5 · 180/3) = ctg 300°; т.к. 300° ∈ [270°; 360°], это IV четверть;
- tg 4π/9 = tg (4 · 180/9) = tg 80°; т.к. 80° ∈ [0°; 90°], это I четверть;
- cos 9π/20 = cos (9 · 180/20) = cos 81°; т.к. 81° ∈ [0°; 90°], это I четверть.
Как видите, далеко не всегда можно найти значение самой тригонометрической функции. Например, попробуйте вычислить cos 162° или sin 108°. Зато мы всегда можем определить, в какой координатной четверти находится данный угол.
Нестандартные углы и периодичность
До сих пор мы рассматривали углы α ∈ [0°; 360°].
Но что произойдет, если, например, угол α = 420°? А как насчет отрицательных углов? Такие углы редко встречаются на ЕГЭ по математике (по крайней мере, в части B), но лучше застраховать себя от подобных «неожиданностей», поэтому предлагаю разобрать и такие задачи. Тем более, схема решения практически ничем не отличается от «стандартных» углов.
Итак, что если угол α > 360°? Судя по тригонометрической окружности, точка сделает полный оборот — а затем пройдет еще чуть-чуть. Это самое «чуть-чуть» вычисляется очень просто. Достаточно отнять от исходного угла величину 360° (иногда это приходится делать несколько раз).
С отрицательными углами работаем аналогично. Если добавлять к отрицательному углу величину 360°, мы очень скоро получим новый угол α ∈ [0°; 360°]. Таким образом, вся схема решения выглядит следующим образом:
- Перейти от радианной меры угла к градусной. Для этого достаточно сделать замену: π → 180°;
- Если полученный угол оказался больше 360°, отнимаем от него по 360° до тех пор, пока новый угол не окажется на отрезке [0°; 360°];
- Аналогично, если угол будет отрицательным, увеличиваем его на 360° до тех пор, пока он не попадет в отрезок [0°; 360°];
- Выясняем, в какой координатной четверти находится полученный угол, ориентируясь на стандартные границы: 90°, 180°, 270° и 360°.
Задача. Определите, в какой координатной четверти находится аргумент тригонометрической функции:
- sin 21π/6;
- cos 19π/3;
- sin (−25π/9);
- tg (−11π/4).
Снова переводим все углы из радиан в градусы по правилу: π → 180°. Дальше уменьшаем или увеличиваем аргумент на 360° до тех пор, пока он не окажется на отрезке [0°; 360°]. И только затем выясняем координатную четверть. Получим:
- sin 21π/6 = sin (23 · 180/6) = sin 690°. Очевидно, что 690° > 360°, поэтому выполняем преобразование: sin 690° → sin (690° − 360°) = sin 330°. Но 330° ∈ [270°; 360°], это IV четверть;
- cos 19π/3 = cos (19 · 180/3) = cos 1140°. Поскольку 1140° > 360°, имеем: cos 1140° → cos (1140° − 360°) = cos 780° → cos (780° − 360°) = cos 420° → cos (420° − 360°) = cos 60°. Т.к. 60° ∈ [0°; 90°], это I четверть;
- sin (−7π/9) = sin (−7 · 180/9) = sin (−140°). Но −140° < 0°, поэтому увеличиваем угол: sin (−140°) → sin (−140° + 360°) = sin 220°. Поскольку 220° ∈ [180°; 270°], это III четверть;
- tg (−11π/4) = tg (−11 · 180/4) = tg (−495°). Т.к. −495° < 0°, начинаем увеличивать угол: tg (−495°) → tg (−495° + 360°) = tg (−135°) → tg (−135° + 360°) = tg 225°. Это уже нормальный угол. Т.к. 225° ∈ [180°; 270°], это III четверть.
Вот и все! Обратите внимание: во втором пункте пришлось вычитать 360° три раза — и только затем получился нормальный угол. Аналогично, в четвертом пункте пришлось прибавлять два раза по 360°, чтобы выйти на положительный угол. Таким образом, добавлять и вычитать углы иногда приходится много раз — это не должно настораживать.
В заключение хочу добавить, что если вы хорошо знаете математику и быстро ориентируетесь в радианных углах, то совсем необязательно переводить их в градусы. Однако большинство людей (и не только школьники) предпочитают именно градусную меру — знакомую еще со средней школы и, как следствие, более понятную.
Источник: https://www.berdov.com/ege/trigonometry/radian_degree_measure/
Определение и численные соотношения между единицами измерения углов в РФ. Тысячные, угловые градусы, минуты, секунды, радианы, обороты
Таблица . Единицы измерения углов (плоских) вводятся как:
Единицы измерения углов
| тысячная (артиллерийская РФ) | 1/6000 полного оборота |
| угловая секунда = 1» | 1/60 угловой минуты |
| угловая минута = 1′ | 1/60 углового градуса |
| угловой градус = 1° | 1/360 полного оборота |
| радиан = 1 рад | Угловая величина дуги длины=1 взятой на окружности радиуса=1 . Таким образом, величина полного угла равна 2 π радиан. |
| полный оборот = полный угол = оборот = 1 об. | Очевидно |
Таблица 1. Перевод угловых градусов, минут, секунд, радиан, оборотов в тысячные.
Перевод угловых градусов, минут, секунд, радиан, оборотов в тысячные.
| Точно в тысячных | Численное значение | |
| 1 угловая секунда = 1» | 6000/360*60*60=1/216 | 0,00462963 … тысячных |
| 1 угловая минута = 1′ | 6000/360*60=5/18 | 0,27777778 … тысячных |
| 1 угловой градус = 1° | 6000/360=50/3 | 16,66666667 …. тысячных |
| 1 радиан = 1 рад | 6000/2π | 954,92965855 … тысячных |
| 1 полный оборот = полный угол = оборот = об. | 6000 | 6000 тысячных |
Таблица 2. Перевод тысячных, угловых градусов, минут, радиан, оборотов в угловые секунды.
Перевод тысячных, угловых градусов, минут, радиан, оборотов в угловые секунды.
| Точно в угловых секундах | Численное значение | |
| 1 тысячная (артиллерийская РФ) | 360*60*60/6000=216 | 216 угловых секунд |
| 1 угловая минута = 1′ | 60 | 60 угловых секунд |
| 1 угловой градус = 1° | 360*60=21600 | 21600 угловых секунд |
| 1 радиан = 1 рад | 360*60*60/2π | 206264,80624710…угловых секунд |
| 1 полный оборот = полный угол = оборот = 1 об. | 360*60*60=1296000 | 1296000 угловых секунд |
Таблица 3. Перевод тысячных, угловых градусов, секунд, радиан, оборотов в угловые минуты.
Перевод тысячных, угловых градусов, секунд, радиан, оборотов в угловые минуты.
| Точно угловых минут | Численное значение | |
| 1 тысячная (артиллерийская РФ) | 360*60/6000=18/5=3,6 | 3,6 угловых минут |
| 1 угловая секунда = 1» | 1/60 | 0,01666667…угловых минут |
| 1 угловой градус = 1° | 60 | 60 угловых минут |
| 1 радиан = 1 рад | 360*60/2π | 3437,74677078 … угловых минут |
| 1 полный оборот = полный угол = оборот = 1 об. | 360*60=21600 | 21600 угловых минут |
Таблица 4. Перевод тысячных, угловых минут, секунд, радиан, оборотов в угловые градусы.
Перевод тысячных, угловых минут, секунд, радиан, оборотов в угловые градусы.
| Точно в угловых градусах | Численное значение | |
| 1 тысячная (артиллерийская РФ) | 360/6000=3/50=0,06 | 0,06 угловых градусов |
| 1 угловая секунда = 1» | 1/60/60=1/3600 | 0,000277778… угловых градусов |
| 1 угловая минута = 1′ | 1/60 | 0,016666667 …. угловых градусов |
| 1 радиан = 1 рад | 360/2π | 57,295779513 … угловых градусов |
| 1 полный оборот = полный угол = оборот = 1 об. | 360 | 360 угловых градусов |
Таблица 5. Перевод тысячных, угловых градусов, минут, секунд, оборотов в радианы.
Перевод тысячных, угловых градусов, минут, секунд, оборотов в радианы.
| Точно в радианах | Численное значение | |
| 1 тысячная (артиллерийская РФ) | 2π/6000 | 0,0010471976… радиан |
| 1 угловая секунда = 1» | 2π/360/60/60 | 0,0000048481…радиан |
| 1 угловая минута = 1′ | 2π/360/60 | 0,0002908882… радиан |
| 1 угловой градус = 1° | 2π/360 | 0,0174532925…радиан |
| 1 полный оборот = полный угол = оборот = 1 об. | 2π | 6,2831853072 … радиан |
Таблица 6. Перевод тысячных, угловых градусов, минут, секунд, радиан в обороты.
Перевод тысячных, угловых градусов, минут, секунд, радиан в обороты.
| Точно в оборотах | Численное значение | |
| 1 тысячная (артиллерийская РФ) | 1/6000 | 0,00016666667…оборотов |
| 1 угловая секунда = 1» |
Источник: https://dpva.ru/Guide/GuideMathematics/GuideMathematicsFiguresTables/FlatAngleDegrees/
Таблица СИНУСОВ для углов от 0° до 360° градусов
- Таблица СИНУСОВ…
- Таблица косинусов…
- Таблица тангенсов…
- Таблица котангенсов…
СИНУС (SIN α) — это одна из прямых тригонометрических функций для углов, в прямоугольном треугольнике синус острого угла равен отношению противолежащего катета к его единственной гипотенузе.
Малая таблица значений тригонометрических функций (в радианах и градусах)
√
| 1/2 | √2/2 | √3/2 | 1 | -1 |
α (радианы)
π/6
π/4
π/3
π/2
π3π/2
2π
α (градусы)
0°
30°
45°
60°
90°
180°
270°
360°
SIN α (СИНУС)
…
Полная таблица синусов для углов от 0° до 360° с шагом всего в 1°
| 0° | |
| 1° | 0.0175 |
| 2° | 0.0349 |
| 3° | 0.0523 |
| 4° | 0.0698 |
| 5° | 0.0872 |
| 6° | 0.1045 |
| 7° | 0.1219 |
| 8° | 0.1392 |
| 9° | 0.1564 |
| 10° | 0.1736 |
| 11° | 0.1908 |
| 12° | 0.2079 |
| 13° | 0.225 |
| 14° | 0.2419 |
| 15° | 0.2588 |
| 16° | 0.2756 |
| 17° | 0.2924 |
| 18° | 0.309 |
| 19° | 0.3256 |
| 20° | 0.342 |
| 21° | 0.3584 |
| 22° | 0.3746 |
| 23° | 0.3907 |
| 24° | 0.4067 |
| 25° | 0.4226 |
| 26° | 0.4384 |
| 27° | 0.454 |
| 28° | 0.4695 |
| 29° | 0.4848 |
| 30° | 0.5 |
| 31° | 0.515 |
| 32° | 0.5299 |
| 33° | 0.5446 |
| 34° | 0.5592 |
| 35° | 0.5736 |
| 36° | 0.5878 |
| 37° | 0.6018 |
| 38° | 0.6157 |
| 39° | 0.6293 |
| 40° | 0.6428 |
| 41° | 0.6561 |
| 42° | 0.6691 |
| 43° | 0.682 |
| 44° | 0.6947 |
| 45° | 0.7071 |
| 46° | 0.7193 |
| 47° | 0.7314 |
| 48° | 0.7431 |
| 49° | 0.7547 |
| 50° | 0.766 |
| 51° | 0.7771 |
| 52° | 0.788 |
| 53° | 0.7986 |
| 54° | 0.809 |
| 55° | 0.8192 |
| 56° | 0.829 |
| 57° | 0.8387 |
| 58° | 0.848 |
| 59° | 0.8572 |
| 60° | 0.866 |
| 61° | 0.8746 |
| 62° | 0.8829 |
| 63° | 0.891 |
| 64° | 0.8988 |
| 65° | 0.9063 |
| 66° | 0.9135 |
| 67° | 0.9205 |
| 68° | 0.9272 |
| 69° | 0.9336 |
| 70° | 0.9397 |
| 71° | 0.9455 |
| 72° | 0.9511 |
| 73° | 0.9563 |
| 74° | 0.9613 |
| 75° | 0.9659 |
| 76° | 0.9703 |
| 77° | 0.9744 |
| 78° | 0.9781 |
| 79° | 0.9816 |
| 80° | 0.9848 |
| 81° | 0.9877 |
| 82° | 0.9903 |
| 83° | 0.9925 |
| 84° | 0.9945 |
| 85° | 0.9962 |
| 86° | 0.9976 |
| 87° | 0.9986 |
| 88° | 0.9994 |
| 89° | 0.9998 |
| 90° | 1 |
Угол в градусах
Sin (Синус)
…
Полная таблица синусов для углов от 91° до 180°
| 91° | 0.9998 |
| 92° | 0.9994 |
| 93° | 0.9986 |
| 94° | 0.9976 |
| 95° | 0.9962 |
| 96° | 0.9945 |
| 97° | 0.9925 |
| 98° | 0.9903 |
| 99° | 0.9877 |
| 100° | 0.9848 |
| 101° | 0.9816 |
| 102° | 0.9781 |
| 103° | 0.9744 |
| 104° | 0.9703 |
| 105° | 0.9659 |
| 106° | 0.9613 |
| 107° | 0.9563 |
| 108° | 0.9511 |
| 109° | 0.9455 |
| 110° | 0.9397 |
| 111° | 0.9336 |
| 112° | 0.9272 |
| 113° | 0.9205 |
| 114° | 0.9135 |
| 115° | 0.9063 |
| 116° | 0.8988 |
| 117° | 0.891 |
| 118° | 0.8829 |
| 119° | 0.8746 |
| 120° | 0.866 |
| 121° | 0.8572 |
| 122° | 0.848 |
| 123° | 0.8387 |
| 124° | 0.829 |
| 125° | 0.8192 |
| 126° | 0.809 |
| 127° | 0.7986 |
| 128° | 0.788 |
| 129° | 0.7771 |
| 130° | 0.766 |
| 131° | 0.7547 |
| 132° | 0.7431 |
| 133° | 0.7314 |
| 134° | 0.7193 |
| 135° | 0.7071 |
| 136° | 0.6947 |
| 137° | 0.682 |
| 138° | 0.6691 |
| 139° | 0.6561 |
| 140° | 0.6428 |
| 141° | 0.6293 |
| 142° | 0.6157 |
| 143° | 0.6018 |
| 144° | 0.5878 |
| 145° | 0.5736 |
| 146° | 0.5592 |
| 147° | 0.5446 |
| 148° | 0.5299 |
| 149° | 0.515 |
| 150° | 0.5 |
| 151° | 0.4848 |
| 152° | 0.4695 |
| 153° | 0.454 |
| 154° | 0.4384 |
| 155° | 0.4226 |
| 156° | 0.4067 |
| 157° | 0.3907 |
| 158° | 0.3746 |
| 159° | 0.3584 |
| 160° | 0.342 |
| 161° | 0.3256 |
| 162° | 0.309 |
| 163° | 0.2924 |
| 164° | 0.2756 |
| 165° | 0.2588 |
| 166° | 0.2419 |
| 167° | 0.225 |
| 168° | 0.2079 |
| 169° | 0.1908 |
| 170° | 0.1736 |
| 171° | 0.1564 |
| 172° | 0.1392 |
| 173° | 0.1219 |
| 174° | 0.1045 |
| 175° | 0.0872 |
| 176° | 0.0698 |
| 177° | 0.0523 |
| 178° | 0.0349 |
| 179° | 0.0175 |
| 180° |
Угол в градусах
Sin (Синус)
…
Таблица синусов для углов 181° — 270°
| 181° | -0.0175 |
| 182° | -0.0349 |
| 183° | -0.0523 |
| 184° | -0.0698 |
| 185° | -0.0872 |
| 186° | -0.1045 |
| 187° | -0.1219 |
| 188° | -0.1392 |
| 189° | -0.1564 |
| 190° | -0.1736 |
| 191° | -0.1908 |
| 192° | -0.2079 |
| 193° | -0.225 |
| 194° | -0.2419 |
| 195° | -0.2588 |
| 196° | -0.2756 |
| 197° | -0.2924 |
| 198° | -0.309 |
| 199° | -0.3256 |
| 200° | -0.342 |
| 201° | -0.3584 |
| 202° | -0.3746 |
| 203° | -0.3907 |
| 204° | -0.4067 |
| 205° | -0.4226 |
| 206° | -0.4384 |
| 207° | -0.454 |
| 208° | -0.4695 |
| 209° | -0.4848 |
| 210° | -0.5 |
| 211° | -0.515 |
| 212° | -0.5299 |
| 213° | -0.5446 |
| 214° | -0.5592 |
| 215° | -0.5736 |
| 216° | -0.5878 |
| 217° | -0.6018 |
| 218° | -0.6157 |
| 219° | -0.6293 |
| 220° | -0.6428 |
| 221° | -0.6561 |
| 222° | -0.6691 |
| 223° | -0.682 |
| 224° | -0.6947 |
| 225° | -0.7071 |
| 226° | -0.7193 |
| 227° | -0.7314 |
| 228° | -0.7431 |
| 229° | -0.7547 |
| 230° | -0.766 |
| 231° | -0.7771 |
| 232° | -0.788 |
| 233° | -0.7986 |
| 234° | -0.809 |
| 235° | -0.8192 |
| 236° | -0.829 |
| 237° | -0.8387 |
| 238° | -0.848 |
| 239° | -0.8572 |
| 240° | -0.866 |
| 241° | -0.8746 |
| 242° | -0.8829 |
| 243° | -0.891 |
| 244° | -0.8988 |
| 245° | -0.9063 |
| 246° | -0.9135 |
| 247° | -0.9205 |
| 248° | -0.9272 |
| 249° | -0.9336 |
| 250° | -0.9397 |
| 251° | -0.9455 |
| 252° | -0.9511 |
| 253° | -0.9563 |
| 254° | -0.9613 |
| 255° | -0.9659 |
| 256° | -0.9703 |
| 257° | -0.9744 |
| 258° | -0.9781 |
| 259° | -0.9816 |
| 260° | -0.9848 |
| 261° | -0.9877 |
| 262° | -0.9903 |
| 263° | -0.9925 |
| 264° | -0.9945 |
| 265° | -0.9962 |
| 266° | -0.9976 |
| 267° | -0.9986 |
| 268° | -0.9994 |
| 269° | -0.9998 |
| 270° | -1 |
Угол
Sin (Синус)
…
Таблица синусов для углов от 271° до 360°
| 271° | -0.9998 |
| 272° | -0.9994 |
| 273° | -0.9986 |
| 274° | -0.9976 |
| 275° | -0.9962 |
| 276° | -0.9945 |
| 277° | -0.9925 |
| 278° | -0.9903 |
| 279° | -0.9877 |
| 280° | -0.9848 |
| 281° | -0.9816 |
| 282° | -0.9781 |
| 283° | -0.9744 |
| 284° | -0.9703 |
| 285° | -0.9659 |
| 286° | -0.9613 |
| 287° | -0.9563 |
| 288° | -0.9511 |
| 289° | -0.9455 |
| 290° | -0.9397 |
| 291° | -0.9336 |
| 292° | -0.9272 |
| 293° | -0.9205 |
| 294° | -0.9135 |
| 295° | -0.9063 |
| 296° | -0.8988 |
| 297° | -0.891 |
| 298° | -0.8829 |
| 299° | -0.8746 |
| 300° | -0.866 |
| 301° | -0.8572 |
| 302° | -0.848 |
| 303° | -0.8387 |
| 304° | -0.829 |
| 305° | -0.8192 |
| 306° | -0.809 |
| 307° | -0.7986 |
| 308° | -0.788 |
| 309° | -0.7771 |
| 310° | -0.766 |
| 311° | -0.7547 |
| 312° | -0.7431 |
| 313° | -0.7314 |
| 314° | -0.7193 |
| 315° | -0.7071 |
| 316° | -0.6947 |
| 317° | -0.682 |
| 318° | -0.6691 |
| 319° | -0.6561 |
| 320° | -0.6428 |
| 321° | -0.6293 |
| 322° | -0.6157 |
| 323° | -0.6018 |
| 324° | -0.5878 |
| 325° | -0.5736 |
| 326° | -0.5592 |
| 327° | -0.5446 |
| 328° | -0.5299 |
| 329° | -0.515 |
| 330° | -0.5 |
| 331° | -0.4848 |
| 332° | -0.4695 |
| 333° | -0.454 |
| 334° | -0.4384 |
| 335° | -0.4226 |
| 336° | -0.4067 |
| 337° | -0.3907 |
| 338° | -0.3746 |
| 339° | -0.3584 |
| 340° | -0.342 |
| 341° | -0.3256 |
| 342° | -0.309 |
| 343° | -0.2924 |
| 344° | -0.2756 |
| 345° | -0.2588 |
| 346° | -0.2419 |
| 347° | -0.225 |
| 348° | -0.2079 |
| 349° | -0.1908 |
| 350° | -0.1736 |
| 351° | -0.1564 |
| 352° | -0.1392 |
| 353° | -0.1219 |
| 354° | -0.1045 |
| 355° | -0.0872 |
| 356° | -0.0698 |
| 357° | -0.0523 |
| 358° | -0.0349 |
| 359° | -0.0175 |
| 360° |
Угол
Sin (Синус)
…
Таблица синусов особенно нужна, когда у вас под рукой нет супер навороченного инженерного калькулятора с маленькой спасительной кнопкой с надписью «sin». В таком случае, чтобы узнать, чему же равняется синус определенного заданного угла, просто найдите информацию о интересующем градусе.
Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите полностью всё таблицу, на выделенном фоне нажмите уже правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Как пользоваться таблицей? Всё гораздо проще, чем Вы думаете, ищем в левой вертикальной колонке, соответствующий градус, и напротив него и будет указано нужное значение синуса для данного нужного нам угла.
Пример
Чему равен синус 45? …
— А вот собственно и сам ответ на поставленную задачку.sin 45 = 0.7071
Bill4iam
Источник: https://kvn201.com.ua/table-of-sines.htm
Перевод градусов в радианы, перевод радианов в градусы на algebra24
- Гостям разрезали круглый торт на 12 равных кусков.
Скольким радианам будет равен угол при вершине каждого из кусков? Посмотреть решение Решение:
- Поскольку круг описывает угол 360 градусов, то каждый из кусков будет отсекать угол 360/12=30 градусов.
- Чтобы найти радианную меру угла 30 градусов, воспользуемся формулой
- $$ alpha = 30^0 cdot frac{ pi }{ 180^0 } = 30^0 cdot frac{3,14}{180^0} approx 0,524 rad $$
Ответ:
$$ alpha approx 0,524 rad$$
- Спутник Земли за некоторое время пролетел расстояние, равное 2 ее радиусам. Какой угол он при этом описал? Ответ подайте в радианах и градусах. Посмотреть решение Решение:
Согласно определению, 1 радиан отсекает на окружности сектор с длиной дуги, равной радиусу. Таким образом, если дуга равна 2 радиусам, то отсеченный угол равен 2 радиана. Переведем 2 радиана в градусы, воспользовавшись формулой:
$$ alpha = 2 cdot frac{ 180^0 }{ pi } = 2 cdot frac{180^0}{3,14}=114,592^0 $$
Ответ:
$$ alpha approx 114,592^0$$
- Двигаясь на север, капитан корабля решил повернуть на северо-восток. На сколько радиан ему нужно изменить курс судна? Посмотреть решение Решение:
Угол между направлениями север и северо-восток составляет 45 градусов. Для его перевода в радианную меру применим формулу:
$$ alpha = 45^0 cdot frac{pi}{180^0} = 45^0 cdot frac{3,14}{180^0} approx 0,785 $$ радиан.
Ответ:
$$ alpha approx 0,785 rad$$
- Определите центральный угол в градусах, если он отсекает дугу 16 см, не прибегая к измерениям. Радиус окружности 12 см. Посмотреть решение Решение:
- Для определения радианной меры центрального угла воспользуемся формулой θ=L/R, где L – длина дуги, R – радиус окружности. Чтобы перевести его в градусную меру, воспользуемся формулой:
- $$ heta^0 = heta cdot frac{180^0}{ pi} $$
- Преобразуем формулу и получим решение в виде:
- $$ heta^0 = L cdot frac{180^0}{(pi cdot R)} = 16 cdot frac{180^0}{3,14 cdot 12} = 76,433^0 $$
Ответ:
$$ heta approx 76,433^0$$
- Известно, что точка, двигаясь по окружности, произвела угловое перемещение на 15 радиан. На какой угол в градусах она отклонилась от первоначального положения после остановки? Посмотреть решение Решение:(способ 1)
Для перевода 15 радиан в градусы воспользуемся формулой:
$$ alpha^0 = alpha cdot frac{180^0}{pi} = 15 cdot frac{180^0}{3,14} = 859,87^0 $$
С учетом того, что каждые $$360^0$$ — это полный оборот, найдем остаток от деления $$859,87^0$$ на $$360^0$$. Получим $$139,87^0$$.
Ответ:
$$ alpha = 139,87^0$$
Решение:(способ 2)
Учитываем, что полный оборот соответствует углу с радианной мерой $$2pi$$. Находим остаток от деления $$15$$ радиан на $$2pi approx 6,28 $$, получим $$2,44 $$радиана.
Затем воспользуемся формулой для перевода в градусы:
$$ alpha^0 = alpha cdot frac{180^0}{pi} = 2,44 cdot frac{180^0}{3,14} = 139,87^0 $$
Ответ:
$$ alpha = 139,87^0$$
Источник: https://algebra24.ru/gradus-radian
- Главная
- Прочее
Оценка статьи:

Загрузка…
Adblock
detector

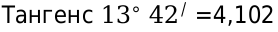

 и
и  .
. .
. . И требуется найти этот арксинус…
. И требуется найти этот арксинус…  .
.
 скорее всего иррациональное число. По крайней мере разложение в непрерывную дробь не обрывается до 30 членов.
скорее всего иррациональное число. По крайней мере разложение в непрерывную дробь не обрывается до 30 членов.