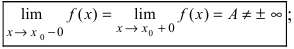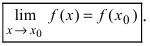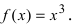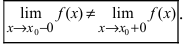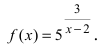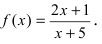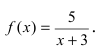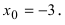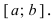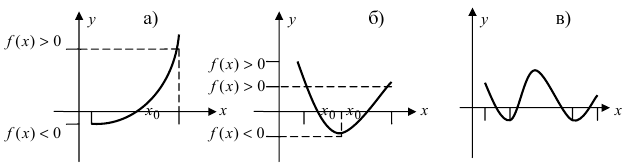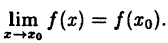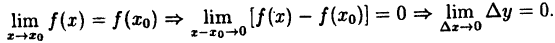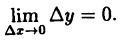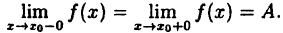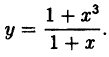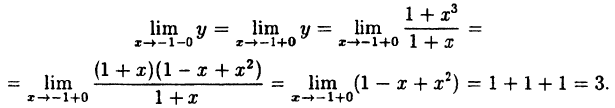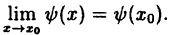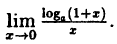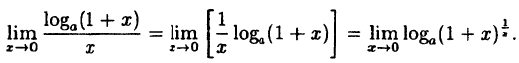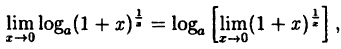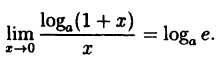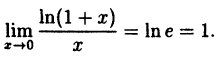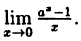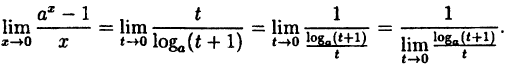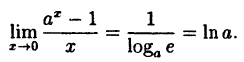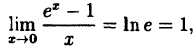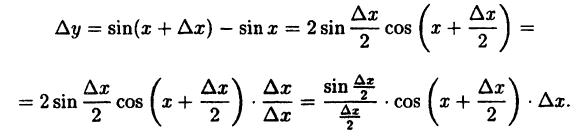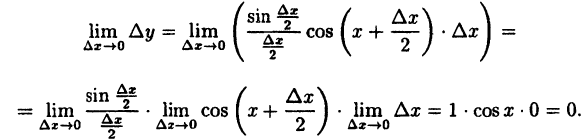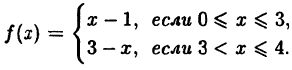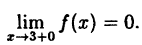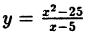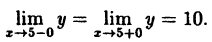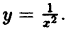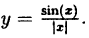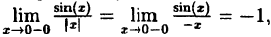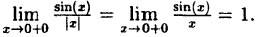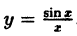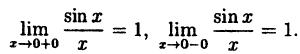Содержание:
Непрерывность функций и точки разрыва
Непрерывность функции
Определение: Функция
- — она определена в этой точке и ее некоторой
-окрестности;
- — существуют конечные лево- и правосторонние пределы от функции в этой точке и они равны между собой, т.е.
— предел функции в точке 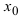
Пример:
Найти область непрерывности функции
Решение:
Данная функция непрерывна 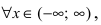
Замечание: Всякая элементарная функция непрерывна в области своего определения.
Точки разрыва
Определение: Точки, в которых не выполняется хотя бы одно из условий непрерывности функции, называются точками разрыва. Различают точки разрыва первого и второго родов.
Определение: Точкой разрыва I рода называется точка, в которой нарушается условие равенства лево- и правостороннего пределов, т.е.
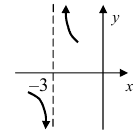
Пример:
Доказать, что функция 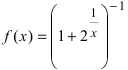
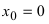
Решение:
Нарисуем график функции в окрестности нуля (Рис. 64): 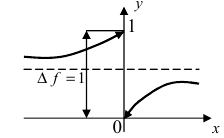
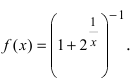
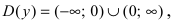
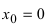
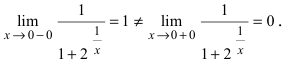
Замечание: По поводу точки разрыва I рода иначе говорят, что в этой точке функция испытывает конечный скачок (на Рис. 64 скачок равен 1).
Определение: Точка, подозрительная на разрыв, называется точкой устранимого разрыва, если в этой точке левосторонний предел равен правостороннему.
Пример:
Доказать, что функция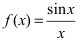
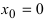
Решение:
В точке 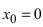
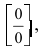
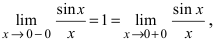
Определение: Все остальные точки разрыва называются точками разрыва II рода.
Замечание: Для точек разрыва второго рода характерен тот факт, что хотя бы
один из односторонних пределов равен 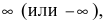
Пример:
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: 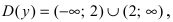
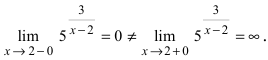
Пример:
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: 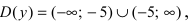
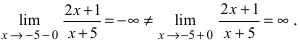
Операции над непрерывными функциями
Теорема: Сумма (разность) непрерывных функций есть непрерывная функция.
Доказательство: Докажем приведенную теорему для суммы двух функций 
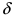
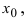
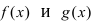
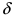
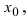
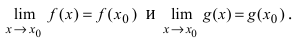
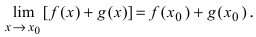
Теорема: Произведение непрерывных функций есть непрерывная функция.
Теорема: Частное двух непрерывных функций 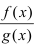
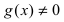
Теорема: Сложная функция от непрерывных функций есть непрерывная функция.
- Заказать решение задач по высшей математике
Схема исследования функции на непрерывность
Исследование функции на непрерывность проводят по следующей схеме:
Пример:
Исследовать на непрерывность функцию
Решение:
Согласно схеме исследования функции на непрерывность имеем:
Рис. 65. Поведение графика функции 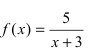
Из рисунка видно, что график функции 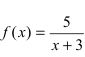
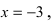
Свойства непрерывных функций на отрезке (a; b)
Свойства непрерывных функций на отрезке 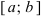
Определение: Замкнутый интервал 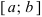
Приведем без доказательства свойства непрерывных функций на сегменте 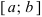
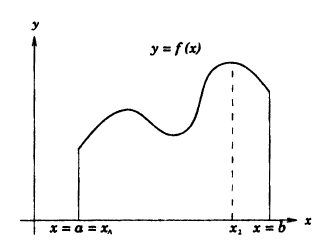
Теорема: Если функция 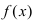
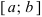
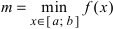
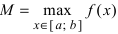
Пример:
Привести примеры графиков функций, удовлетворяющих условиям теорем(см. Рис. 66).
Рис. 66. Графики функций, удовлетворяющих условиям теоремы.
Решение:
На графике а) функция достигает своего наименьшего 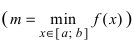
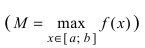
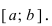
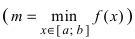
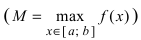
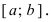
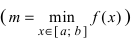
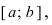
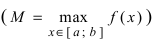
Тб. Если функция 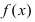
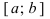
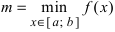
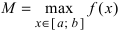
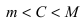
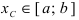
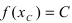
Пример:
Изобразить графики функций, удовлетворяющих условиям Тб (см. Рис. 67).
Рис. 67. Графики функций, удовлетворяющих условиям Тб.
Теорема: Если функция 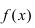
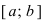
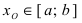
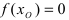
Пример:
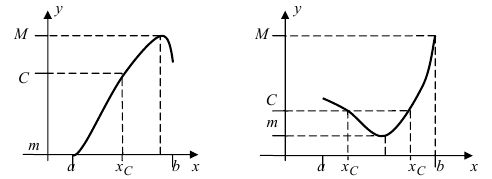
Изобразить графики функций, удовлетворяющих условиям теоремы(см. Рис. 68).
Рис. 68. Графики функций, удовлетворяющих условиям теоремы.
На графике а) существует единственная точка, в которой выполняются условия теоремы. На графиках б) и в) таких точек две и четыре, соответственно. Однако в случаях б) и в) для удовлетворения условий теоремы надо разбивать сегмент на отдельные отрезки.
- Точки разрыва и их классификация
- Дифференциальное исчисление
- Исследование функций с помощью производных
- Формула Тейлора и ее применение
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Замечательные пределы
Непрерывность функции в точке
30 декабря 2021
В этом уроке мы выясним, что такое непрерывность функции в точке, непрерывность на множестве; познакомимся с основными свойствами таких функций; научимся искать точки разрыва и решим множество интересных задач.
Содержание:
- Интуитивное определение непрерывности
- Непрерывность функции в точке
- Непрерывность функции на множестве
- Точки разрыва
Поначалу теория будет совсем простой, но затем выкладки и задачи начнут быстро усложняться. И чем глубже вы хотите разобраться в математике, тем больше пользы получите от этого урока.
1. Интуитивное определение непрерывности
Большинство студентов, когда слышат термин «непрерывная функция», представляют себе линию, которую можно начертить, не отрывая карандаша от бумаги. Например, обычную параболу:
Или просто какую-нибудь плавную кривую:
Главное, чтобы у этих линий не было никаких особенностей. Они не «разваливаются» на куски, не «улетают» в бесконечность рядом с какой-то точкой, и вообще для любого $x$ мы прямо по графику можем определить, чему будет равен $y$.
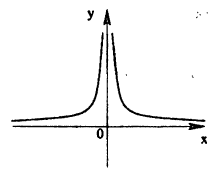
Другое дело — функции с нарушением непрерывности. Или, как говорят, с точками разрыва. Обычно студенты сразу называют функцию $y={1}/{{{x}^{2}}};$ — классическую гиперболу, которая не определена в точке $x=0$, а график «улетает» в бесконечность в окрестности этой точки:
Впрочем, для возникновения разрыва функции вовсе не обязательно уходить куда-то в бесконечность. Достаточно просто иметь выколотую точку. Взгляните:
Перед нами всё та же парабола $y={{x}^{2}}$, но с выколотой точкой $x=-2$. Как такое возможно? Очень просто. Например, именно так выглядит график функции
[y=frac{{{x}^{2}}left( x+2 right)}{x+2}]
Значение этой функции не определено при $x=-2$, поскольку знаменатель дроби обращается в ноль. Но во всех остальных точках знаменатель $x+2ne 0$, и можно выполнить сокращение:
[y=frac{{{x}^{2}}left( x+2 right)}{x+2}={{x}^{2}}quad left( xne -2 right)]
И это не какая-то «искусственная» задача — такие функции регулярно встречаются на ОГЭ и ЕГЭ по математике, особенно в задачах с параметром.
Но и это ещё не всё. Функция может быть определена на всей числовой прямой — и всё равно иметь точку разрыва:
Это график кусочно-заданной функции
[fleft( x right)=left{ begin{align} & 1, & x gt 0 \ & 0, & x=0 \ & -1, & x lt 0 \ end{align} right.]
Она определена для всех $xin mathbb{R}$, в т.ч. при $x=0$. Однако именно в точке $x=0$ происходит скачкообразное изменение: $fleft( 0 right)=0$, но малейший шаг влево — и вот уже $fleft( x right)=-1$. А малейший шаг вправо — и $fleft( x right)=1$.
Итого проблемы возникают там, где функция «улетает» в бесконечность, либо меняется скачкообразно, либо вообще не определена. И тут мы переходим к строгому определению непрерывности.
2. Непрерывность функции в точке
Определение 1. Функция $fleft( x right)$ называется непрерывной в точке ${{x}_{0}}$, если она определена в этой точке и имеет предел, равный значению функции в этой точке:
[limlimits_{xto {{x}_{0}}} fleft( x right)=fleft( {{x}_{0}} right)]
На практике удобно считать, что функция непрерывна в точке ${{x}_{0}}$, если выполнены сразу три условия:
- Функция определена в этой точке, т.е. существует $fleft( {{x}_{0}} right)$;
- Существует конечный предел функции $limlimits_{xto {{x}_{0}}} fleft( x right)$;
- Этот предел равен значению функции в точке: $limlimits_{xto {{x}_{0}}} fleft( x right)=fleft( {{x}_{0}} right)$.
Если хотя бы одно из этих условий не выполнено, функция перестаёт быть непрерывной. Так, в приведённых выше примерах гипербола $y={1}/{x};$ не определена и не имеет предела в точке $x=0$. Парабола с выколотой точкой просто не определена при $x=-2$. А кусочно-заданная функция определена в точке $x=0$, но имеет разные левые и правые пределы, отличные от $fleft( 0 right)$.
2.1. Непрерывность по Коши и по Гейне
Среди трёх условий непрерывности особый интерес представляет второй пункт — существование предела $limlimits_{xto {{x}_{0}}} fleft( x right)$. Именно на вычислении предела функции в точке спотыкается большинство учеников.
Если вы чувствуете себя неуверенно в вычислении таких пределов, рекомендую повторить тему «Что такое предел функции в точке». А сейчас мы адаптируем два ключевых определения из того урока — предел функции по Коши (в нотации «$varepsilon $—$delta $») и по Гейне (через последовательности) — для проверки непрерывности.
Определение 2. (непрерывность по Коши) Функция $fleft( x right)$ непрерывна в точке ${{x}_{0}}$, если
[begin{align} & forall left( varepsilon gt 0 right)quad exists left( delta =delta left( varepsilon right) gt 0 right): \ & xin {{overset{circ }{mathop{U}},}_{delta }}left( {{x}_{0}} right)Rightarrow left| fleft( x right)-fleft( {{x}_{0}} right) right| lt varepsilon\ end{align}]
Когда «посвящённый» человек слышит фразу «предел функции в точке», он чаще всего вспоминает именно такое определение (по Коши, т.е. в нотации «$varepsilon $—$delta $»). Но есть ещё одно определение:
Определение 3. (непрерывность по Гейне) Функция $fleft( x right)$ непрерывна в точке ${{x}_{0}}$, если для любой числовой последовательности $left{ {{x}_{n}} right}$ такой, что
[limlimits_{nto infty } {{x}_{n}}={{x}_{0}}]
выполняется условие
[limlimits_{nto infty } fleft( {{x}_{n}} right)=fleft( {{x}_{0}} right)]
Все три определения непрерывности эквивалентны. Это следует из эквивалентности определения предела по Коши и по Гейне (доказательство такой эквивалентности — в уроке про пределы функции в точке).
Нас сейчас интересует другое: а как вообще проверить, что все эти пределы существуют? Тут нам на помощь приходят односторонние пределы.
2.2. Критерий существования предела в точке
Теорема 1. Предел функции в точке $limlimits_{xto a} fleft( x right)$ существует и равен числу $Ain mathbb{R}$ тогда и только тогда, когда существуют конечные односторонние пределы $limlimits_{xto a+} fleft( x right)$ и $limlimits_{xto a-} fleft( x right)$, причём эти пределы должны быть равны числу $A$:
[limlimits_{xto a} fleft( x right)=limlimits_{xto a+} fleft( x right)=limlimits_{xto a-} fleft( x right)=A]
Эта теорема прекрасно подходит и для проверки непрерывности, и для классификации точек разрыва (об этом позже). Давайте рассмотрим пару примеров, а затем сформулируем общий алгоритм.
Пример 1. Непрерывная функция.
Рассмотрим график функции $y={{x}^{2}}$ и найдём односторонние пределы в точке ${{x}_{0}}=2$.
Вот график с интересующей нас точкой:
Если встать в начало координат, а затем приближаться к точке ${{x}_{0}}=2$ слева, значения функции будут постепенно расти, становясь всё ближе к $y=4$:
А если двигаться из бесконечности влево, приближаясь к ${{x}_{0}}=2$, значения функции будут убывать, становясь всё ближе к тому же $y=4$:
Получается, что односторонние пределы существуют и равны одному и тому же числу:
[limlimits_{xto 2-} {{x}^{2}}=limlimits_{xto 2+} {{x}^{2}}=4]
Это значит, что и стандартный предел функции в точке ${{x}_{0}}=2$ тоже существует и равен
[limlimits_{xto 2} {{x}^{2}}=4]
Значение функции $y={{x}^{2}}$ в точке ${{x}_{0}}=2$ тем более определено и равно тому же самому числу:
[fleft( 2 right)={{2}^{2}}=4]
Вот и получается, что (1) функция равна 4, (2) предел существует (мы доказали это через односторонние пределы) и равен 4, (3) значения функции и предела в точке совпадают. Следовательно, функция $y={{x}^{2}}$ непрерывна в точке ${{x}_{0}}=2$.
Возможно, прочитав всё это, вы скажете: «Спасибо, кэп. А разве бывает иначе?» Ещё как бывает! Взгляните на следующий пример.
Пример 2. Функция с разрывом в точке ${{x}_{0}}=0$.
Рассмотрим график функции $y={left| x right|}/{x};$ и найдём односторонние пределы в точке ${{x}_{0}}=0$.
Этот график весьма схож с тем, что мы рассматривали в самом начале урока. Для удобства обозначим точки $left( 0;1 right)$ и $left( 0;-1 right)$, не принадлежащие графику, выколотыми точками (а не стрелками, как было раньше):
Функция не определена в нуле — одно из условий непрерывности уже не выполняется, и на этом можно было бы закончить. Но нас сейчас интересуют односторонние пределы.
Начнём движение по левой ветке графика — из минус бесконечности влево к $x=0$:
При этом значение функции будет оставаться неизменным: $y=-1$. Следовательно,
[limlimits_{xto 0-} frac{left| x right|}{x}=-1]
Теперь пройдёмся по правой ветке — из плюс бесконечности к $x=0$:
Как бы близко к нулю мы ни приближались, значения функции всё равно равны $y=1$. Поэтому
[limlimits_{xto 0+} frac{left| x right|}{x}=1]
Получается, что односторонние пределы существуют, но не равны:
[limlimits_{xto 0-} frac{left| x right|}{x}ne limlimits_{xto 0+} frac{left| x right|}{x}]
Следовательно, общего предела функции в точке $x=0$ не существует.
2.3. Алгоритм исследования функции на непрерывность
Сформулируем универсальный алгоритм, по которому доказывается непрерывность функции $fleft( x right)$ в точке ${{x}_{0}}$. Или наоборот — опровергается. Алгоритм состоит из трёх шагов:
- Проверить, определена ли функция $fleft( x right)$ в точке $x={{x}_{0}}$. Другими словами, можно ли найти значение $fleft( {{x}_{0}} right)$. Если посчитать $fleft( {{x}_{0}} right)$ нельзя — функция не является непрерывной, исследование закончено. Если можно, переходим к пункту 2;
- Найти односторонние пределы и проверить: выполняется ли критерий существования предела функции в точке. Если односторонние пределы существуют и равны — переходим к пункту 3. Если хотя бы один односторонний предел не существует, либо они не равны — функция не является непрерывной, исследование закончено.
- Сравнить значения $fleft( {{x}_{0}} right)$ и $limlimits_{xto {{x}_{0}}} fleft( x right)$. Если они равны, функция непрерывна. Если нет — значит, функция не является непрерывной.
Может показаться, что действий слишком много. И что проверка слишком сложная. На самом деле это не так. Взгляните:
Пример 3. Доопределите функцию $fleft( x right)$ в точке ${{x}_{0}}$ так, чтобы она стала непрерывной:
[fleft( x right)=frac{sin x}{x},quad {{x}_{0}}=0]
Это одна из любимейших задач всех преподавателей по матанализу. Очевидно, функция не проходит уже первый пункт проверки: $fleft( 0 right)$ не существует, поскольку деление на ноль не определено.
Однако нам предлагают доопределить функцию, т.е. найти такое $Ain mathbb{R}$, чтобы полученная функция
[fleft( x right)=left{ begin{align} & frac{sin x}{x}, & xne 0 \ & A, & x=0 \ end{align} right.]
была непрерывна в точке ${{x}_{0}}=0$.
Поэтому проверим пункт 2. Посчитаем левосторонний и правосторонний пределы:
[begin{align} & limlimits_{xto 0+} frac{sin x}{x}=1; \ & limlimits_{xto 0-} frac{sin x}{x}=limlimits_{xto 0-} frac{sin left( -x right)}{-x}=limlimits_{tto 0+} frac{sin t}{t}=1 \ end{align}]
[begin{align} limlimits_{xto 0+} frac{sin x}{x}&=1; \ limlimits_{xto 0-} frac{sin x}{x}&=limlimits_{xto 0-} frac{sin left( -x right)}{-x} \ &=limlimits_{tto 0+} frac{sin t}{t}=1 \ end{align}]
Односторонние пределы легко сводятся к первому замечательному пределу и равны $A=1$. Следовательно, если мы доопределим $fleft( x right)$ так, чтобы $fleft( 0 right)=1$, мы получим функцию, непрерывную в ${{x}_{0}}=0$:
[fleft( x right)=left{ begin{align} & frac{sin x}{x}, & xne 0 \ & 1, & x=0 \ end{align} right.]
Вот и всё. Задача решена.
Обратите внимание на график функции $y=fleft( x right)$. Вот так он выглядит изначально (очевидно нарушение непрерывности в ${{x}_{0}}=0$):
А вот так — после того, как мы доопределим $fleft( 0 right)=1$:
Получили функцию, которая непрерывна в любой точке. И это видно на графике. Из чего сразу сделаем два замечания:
Замечание 1. Если в задании требуется исследовать функцию на непрерывность, обязательно постройте хотя бы примерный график этой функции. Так вы сразу поймёте: где могут быть проблемы, как ведёт себя функция в окрестности «проблемных» точек и что с этим можно сделать.
Замечание 2. Исследование на непрерывность всегда проводится в конкретных точках. Но график функции — это чаще всего бесконечное множество точек, большинство из которых ничем не примечательны. Поэтому нужно научиться определять непрерывность на бесконечных множествах.
Вот вторым пунктом — непрерывностью на бесконечных множествах — мы сейчас и займёмся.
3. Непрерывность функции на множестве
До сих пор мы говорили о непрерывности лишь в одной конкретной точке — некой ${{x}_{0}}in mathbb{R}$. Но большинство функций определено на огромных множествах — вплоть до всей числовой прямой. Как быть в этом случае? Здесь нам помогут следующие определения.
3.1. Непрерывность на интервале
Определение 4. Функция $fleft( x right)$ непрерывна на интервале $left( a;b right)$, если она непрерывна в каждой точке ${{x}_{0}}in left( a;b right)$.
Пример. Функция $y={1}/{x};$ непрерывна на интервале $left( -infty ;0 right)$ и на интервале $left( 0;+infty right)$.
Почему именно интервал? Почему не отрезок? Потому что интервал — это открытое множество, т.е. каждая точка ${{x}_{0}}in left( a;b right)$ входит в этот интервал с некоторой своей $delta $-окрестностью. На языке кванторов записывается это так:
[begin{align} {{x}_{0}}in left( a;b right) & Rightarrow exists left( delta gt 0 right): \ xin {{U}_{delta }}left( {{x}_{0}} right) & Rightarrow xin left( a;b right) \ end{align}]
А на числовой прямой всё это безобразие выглядит так:
На интервале мы никогда достигаем границ — точек $a$ и $b$. Поэтому не имеет значения, как близко к этим границам располагается точка ${{x}_{0}}$. Всегда можно взять расстояние до ближайшей границы (например, $left| {{x}_{0}}-a right|$), поделить пополам — вот вам и отступ $delta gt 0$.
3.2. Непрерывность на отрезке
Отрезок $left[ a;b right]$ принципиально отличается от интервала $left( a;b right)$ тем, что мы можем зайти, например, в левый конец отрезка — точку $a$ — и ничего левее этой точки принадлежать отрезку уже не будет.
Никакие отступы, никакие $delta $-окрестности тут не помогут. Поэтому нам нужны два новых определения.
Определение 5. Функция $fleft( x right)$ называется непрерывной справа в точке ${{x}_{0}}$, если
[limlimits_{xto {{x}_{0}}+} fleft( x right)=fleft( {{x}_{0}} right)]
непрерывной слева в точке ${{x}_{0}}$, если
[limlimits_{xto {{x}_{0}}-} fleft( x right)=fleft( {{x}_{0}} right)]
Теперь мы можем рассматривать непрерывность на любых привычных нам множествах — интервалах и отрезках. Чуть позже в этом уроке мы сформулируем замечательную теорему о непрерывности элементарных функций, но пока давайте рассмотрим пару примеров.
Пример 4. Функция $fleft( x right)=sqrt{4-{{x}^{2}}}$ непрерывна на всей своей области определения.
Проверить это и построить график.
Для начала найдём область определения $fleft( x right)$. Поскольку арифметический квадратный корень определён только из неотрицательного числа, имеем:
[begin{align} 4-{{x}^{2}} & ge 0 \ {{x}^{2}} & le 4 \ left| x right| & le 2 \ x& in left[ -2;2 right] \ end{align}]
Для лучшего понимания ситуации начертим график $y=sqrt{4-{{x}^{2}}}$. Заметим, что
[begin{align} {{y}^{2}} & =4-{{x}^{2}} \ {{x}^{2}}+{{y}^{2}} & ={{2}^{2}} \ end{align}]
это уравнение окружности с центром в начале координат и радиусом $r=2$. Графиком функции будет лишь та часть этой окружности, для которой $yge 0$:
Очевидно, что функция непрерывна для всех $xin left[ -2;2 right]$, причём в $x=-2$ непрерывна справа, в $x=2$ непрерывна слева.
Пример 5. Функция $fleft( x right)=sqrt{x}$ непрерывна на всей своей области определения.
Проверить это и построить график.
Область определения функции $fleft( x right)=sqrt{x}$:
[xin left[ 0;+infty right)]
График — стандартная «уложенная набок» ветвь параболы:
Видим, что функция $fleft( x right)$непрерывна во всех точках $xin left[ 0;+infty right)$, причём в $x=0$ непрерывна справа. Задача решена.
Возможно, вы уже заметили, что все функции, которые мы сегодня изучали, были непрерывны на всей своей области определения. Проблемы возникали лишь во всяких конструкциях вида ${1}/{x};$, где возможно деление на ноль. Но даже гипербола $y={1}/{x};$ не определена лишь в точке $x=0$, а во всех остальных точках она определена и непрерывна.
И это не случайно. Существует целый класс функций, которые непрерывны на всей своей области определения. Настала пора познакомиться с ними.
3.3. Непрерывность элементарных функций
В математическом анализе существует особый класс функций, которые называются элементарными.
Определение 6. Элементарные функции — это любые функции из списка:
- Любой многочлен $Pleft( x right)={{a}_{n}}{{x}^{n}}+…+{{a}_{1}}x+{{a}_{0}}$;
- Рациональная функция $fleft( x right)={Pleft( x right)}/{Qleft( x right)};$, где $Pleft( x right)$ и $Qleft( x right)$ — многочлены;
- Степенная функция $fleft( x right)={{x}^{a}}$, где $ain mathbb{R}$;
- Логарифмическая функция $fleft( x right)={{log }_{a}}x$, где $a gt 0$, $ane 1$;
- Показательная функция $fleft( x right)={{a}^{x}}$, где $a gt 0$, $ane 1$;
- Все тригонометрические функции: $sin x$, $cos x$, $operatorname{tg}x$, $operatorname{ctg}x$;
- Все обратные тригонометрические функции: $arcsin x$, $arccos x$, $operatorname{arctg}x$, $operatorname{arcctg}x$;
- Любые функции, которые можно составить из предыдущих с помощью конечного числа арифметических операций и композиций.
Кстати, модуль тоже является элементарной функцией:
[left| x right|=sqrt{{{x}^{2}}}]
Для всех таких функций выполняется замечательная теорема:
Теорема 2. Все элементарные функции непрерывны на всей своей области определения.
Если область определения представляет собой отрезок или иное замкнутое множество, то на концах таких отрезков выполняется односторонняя непрерывность.
Универсального доказательства этой теоремы сразу для всех элементарных функций не существует. Сначала доказывают непрерывность степенной и показательной функции. Затем показывают непрерывность арифметических операций (тот ещё квест, особенно для многочленов).
Кроме того, есть целая группа теорем, которые верны для всех непрерывных функций:
- 1.Теорема о нуле непрерывной функции и о промежуточном значении на отрезке.
- 2.Теоремы Вейерштрасса об ограниченности непрерывной функции на отрезке и о достижении точной верхней и нижней грани.
- 3.Теоремы о непрерывности обратной функции и композиции функций.
Каждой из этих теорем посвящён отдельный урок — с точной формулировкой, доказательством и примерами (см. содержание раздела). Сейчас нас интересуют более приземлённые вопросы.
Например, может возникнуть вопрос: а что, разве есть какие-то другие функции, помимо элементарных? Конечно есть.
Пример 6. Функция Дирихле:
[Dleft( x right)=left{ begin{align} & 1, & xin mathbb{Q} \ & 0, & xnotin mathbb{Q} \ end{align} right.]
Функция Дирихле определена для всех $xin mathbb{R}$. Она равна единице в том случае, если $x={p}/{q};$ — рациональное число, и равна нулю во всех остальных случаях.
Очевидно, что в любой $delta $-окрестности точки ${{x}_{0}}in mathbb{Q}$ и слева, и справа найдутся иррациональные числа. И наоборот: в любой $delta $-окрестности иррационального числа $ain mathbb{R}backslash mathbb{Q}$ найдутся его рациональные приближения с избытком и недостатком. Следовательно, односторонние пределы
[limlimits_{xto {{x}_{0}}-} Dleft( x right)quad limlimits_{xto {{x}_{0}}+} Dleft( x right)]
не существуют ни в одной точке графика. И функция Дирихле терпит разрыв в каждой точке числовой прямой.:)
Кстати, сам график выглядит примерно так:
Линия $y=1$ проведена пунктиром из тех соображений, что множество рациональных чисел счётно, а множество всех действительных чисел — нет. Но это всё условности.:)
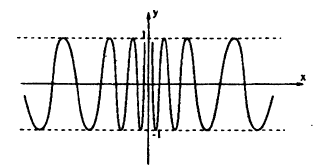
Пример 7. Исследовать на непрерывность функцию
[fleft( x right)=sin left( {1}/{x}; right)]
Эта функция представляет собой композицию двух элементарных функций: $sin x$ и ${1}/{x};$. Следовательно, перед нами элементарная функция, которая определена и непрерывна везде, кроме $x=0$.
Посчитаем левосторонний и правосторонний предел в точке $x=0$. Для этого заметим, что при $xto 0$ величина ${1}/{x};to infty $. Следовательно, в любой $delta $-окрестности точки $x=0$ найдутся и точки вида $t=pi n$, $nin mathbb{Z}$, в которых $sin t=0$; и точки вида $t={pi }/{2};+pi n$, в которых $sin t=pm 1$.
Следовательно, ни левосторонний, ни правосторонний пределы не определены:
[limlimits_{xto 0+} sin frac{1}{x}quad limlimits_{xto 0-} sin frac{1}{x}]
А это значит, что общий предел в точке $x=0$ тоже не определён. Следовательно, $x=0$ — не просто точка разрыва (это и так понятно, поскольку в нуле функция не определена). Принципиально невозможно доопределить $fleft( x right)$ в нуле так, чтобы получилась непрерывная функция.
График $y=sin left( {1}/{x}; right)$ выглядит так (единичный отрезок — две клетки):
Чем ближе $xto 0$, тем быстрее график «бегает» между $y=-1$ и $y=1$. В какой-то момент из-за конечной толщины линий на чертеже строить график становится невозможно. Даже если мы возьмём за единичный отрезок тысячу клеток. Даже если будем чертить на огромных листах. Никакие листы и отрезки не могут сравниться с бесконечностью.:)
Ну и перед тем как переходить к практике, давайте разберёмся, что же произойдёт, если хотя бы одно условие непрерывности не выполняется.
4. Точки разрыва
Урок о непрерывности функции в точке будет неполным, если мы не поговорим про точки разрыва.
Напомню, что функция $fleft( x right)$ является непрерывной в точке ${{x}_{0}}$, когда выполнены три условия:
- Функция $fleft( x right)$ определена в этой точке, т.е. мы можем посчитать $fleft( {{x}_{0}} right)$.
- Существует конечный предел $limlimits_{xto {{x}_{0}}} fleft( x right)$.
- Должно выполняться равенство $limlimits_{xto {{x}_{0}}} fleft( x right)=fleft( {{x}_{0}} right)$.
А что, если хотя бы одно условие не выполнено? Перед нами точка разрыва.
Определение 7. Если функция $fleft( x right)$ не является непрерывной в точке ${{x}_{0}}$, то она называется разрывной в точке ${{x}_{0}}$. Сама точка ${{x}_{0}}$ при этом называется точкой разрыва функции $fleft( x right)$.
Определение 8. Точка разрыва ${{x}_{0}}$ называется точкой разрыва первого рода функции $fleft( x right)$, если существуют конечные односторонние пределы $limlimits_{xto {{x}_{0}}+} fleft( x right)$ и $limlimits_{xto {{x}_{0}}-} fleft( x right)$.
В противном случае ${{x}_{0}}$ называется точкой разрыва второго рода.
Классический пример точки разрыва второго рода:
[y=frac{1}{x},quad {{x}_{0}}=0]
Ветви гиперболы «улетают» в бесконечность рядом с точкой ${{x}_{0}}=0$.
Ещё один пример:
[y=sin frac{1}{x},quad {{x}_{0}}=0]
Мы уже рассматривали график этой функции и знаем, что односторонних пределов в ${{x}_{0}}=0$ не существует. Поэтому функция терпит разрыв второго рода.
Да даже обычный $y=operatorname{tg}x$ терпит разрыв второго рода в точках вида ${{x}_{n}}={pi }/{2};+pi n$, $nin mathbb{Z}$.
Определение 9. Разрыв первого рода в точке ${{x}_{0}}$ называется устранимым, если существует конечный предел $limlimits_{xto {{x}_{0}}} fleft( x right)=A$, но $Ane fleft( {{x}_{0}} right)$.
То же самое, если существует конечный предел $limlimits_{xto {{x}_{0}}} fleft( x right)=A$, но $fleft( {{x}_{0}} right)$ не определена.
Из определения очевидно, что устранимыми могут быть только разрывы первого рода. Вот несколько примеров:
- $y=frac{sin x}{x}$, ${{x}_{0}}=0$ (устранимый: $yleft( 0 right)=1$)
- $y=frac{left| x-1 right|}{x-1}$, ${{x}_{0}}=1$ (неустранимый)
- $y=frac{{{x}^{2}}left( x+2 right)}{x+2}$, ${{x}_{0}}=-2$ (устранимый: $yleft( -2 right)=4$)
Рассмотрим более сложный пример
Пример 8. Исследуйте точки разрыва функции
[y=xcdot {{e}^{{1}/{x};}}]
Это элементарная функция, поэтому единственная точка разрыва: $x=0$ — в ней не определена дробь ${1}/{x};$.
Выясним, какого рода этот разрыв. Посчитаем предел слева:
[begin{align} limlimits_{xto 0-} xcdot {{text{e}}^{{1}/{x};}} & =limlimits_{xto 0-} frac{x}{{{text{e}}^{-{1}/{x};}}}=frac{limlimits_{xto 0-} x}{limlimits_{xto 0-} {{text{e}}^{-{1}/{x};}}}= \ & =frac{0}{limlimits_{xto 0+} {{text{e}}^{{1}/{x};}}}=left[ frac{0}{infty } right]=0 end{align}]
[begin{align}limlimits_{xto 0-}xcdot {{text{e}}^{{1}/{x};}}&=limlimits_{xto 0-}frac{x}{{{text{e}}^{-{1}/{x};}}}= \ &=frac{limlimits_{xto 0-}x}{underset{xto 0-}{{text{e}}^{-{1}/{x};}}}= \ &=frac{0}{limlimits_{xto 0+}{{text{e}}^{{1}/{x};}}}= \ &=left[ frac{0}{infty } right]=0 end{align}]
И предел справа:
[begin{align} limlimits_{xto 0+} xcdot {{text{e}}^{{1}/{x};}} & =limlimits_{xto 0+} frac{{{text{e}}^{{1}/{x};}}}{{1}/{x};}=left[ {x=1}/{t}; right]= \ & =limlimits_{tto +infty } frac{{{text{e}}^{t}}}{t}=+infty\ end{align}]
[begin{align}limlimits_{xto 0+}xcdot {{text{e}}^{{1}/{x};}}&=limlimits_{xto 0+}frac{{{text{e}}^{{1}/{x};}}}{{1}/{x};}= \ &=left[ {x=1}/{t}; right]= \ &=limlimits_{tto +infty }frac{{{text{e}}^{t}}}{t}=+infty end{align}]
Понятно, что показательная функция $y={{text{e}}^{t}}$ растёт быстрее линейной $y=t$ при $tto +infty $. Поэтому конечного предела нет.
Итого функция терпит разрыв второго рода в точке $x=0$. Этот разрыв хорошо виден на графике:
Обратите внимание: точка $x=1$ является точкой локального минимума, а прямая $y=x+1$ — наклонная асимптота нашего графика. Чтобы находить такие точки, нужно разобраться с производными.
О производных и дифференциалах мы поговорим в отдельных уроках. А пока лишь одна заключительная рекомендация:
При исследовании функции на непрерывность обязательно чертите её график. Хотя бы в виде эскиза. Даже если задание кажется вам «очевидным».
Так вы защитите себя от глупых ошибок. И намного быстрее поймёте, как ведёт себя функция в окрестностях точек разрыва.
На этом всё. Приступайте к практике.:)
Смотрите также:
- Теоремы Вейерштрасса о непрерывной функции
- Критерий Коши сходимости последовательности
- Тест к уроку «Что такое логарифм» (средний)
- Не пишите единицы измерения в задаче B12
- Однородные тригонометрические уравнения: общая схема решения
- Задача B4: тарифы на сотовую связь
Непрерывность функции и точки разрыва
- Приращение аргумента и приращение функции
- Непрерывность функции в точке
- Непрерывность функции на промежутке
- Односторонние пределы
- Классификация точек разрыва
- Точки разрыва первого рода
- Точки разрыва второго рода
- Алгоритм исследования функции на непрерывность
- Примеры
п.1. Приращение аргумента и приращение функции
Приращением аргумента называют разность $$ triangle x= x-x_0 $$ где x — произвольное число, которое мало отличается от начальной точки (x_0). Приращение аргумента может быть как положительным, так и отрицательным.
Приращением функции называют соответствующую разность $$ triangle y=f(x)-f(x_0) $$ Приращение функции может быть как положительным, так и отрицательным.
Например:
 |
Пусть (y=3x-1) (x_0=1, x=1,1 ) Тогда begin{gather*} triangle x=x-x_0=0,1\ triangle y=(3x-1)-(3x_0-1)=\ =3(x-x_0 )=3triangle x=0,3 end{gather*} В данном случае приращение функции всегда в 3 три раза больше приращения аргумента. |
п.2. Непрерывность функции в точке и на промежутке
Функция (y=f(x)) непрерывна в точке (x_0), если в этой точке малому приращению аргумента (triangle x=x-x_0) соответствует малое приращение функции (triangle y=f(x)-f(x_0)): $$ lim_{triangle xrightarrow 0}triangle y=lim_{xrightarrow x_0}triangle y=0 $$
На «языке ε-δ» определение непрерывности будет следующим:
Функция (y=f(x)) непрерывна в точке (x_0), если для любого (varepsilongt 0) существует такое (delta(varepsilon)gt 0), что для любого (x, |x-x_0|ltdelta) выполняется (|f(x)-f(x_0)|ltvarepsilon:) $$ forall varepsilongt 0 existsdelta=delta(varepsilon)gt 0: forall x, |x-x_0|ltdeltaRightarrow |f(x)-a|ltvarepsilon $$
ε-δ определение непрерывности похоже на ε-δ определение предела функции, с той разницей, что модуль (|x-x_0|) может быть равен 0 для непрерывной функции, т.е. сама точка (x_0) входит в δ-окрестность.
Проанализируем предел приращения функции: begin{gather*} lim_{triangle xrightarrow 0}triangle y= lim_{triangle xrightarrow 0}left(f(x)-f(x_0)right)= lim_{triangle xrightarrow 0}f(x)-lim_{triangle xrightarrow 0}f(x_0)=\ =lim_{triangle xrightarrow 0}f(x)-f(x_0) end{gather*} т.к. (f(x_0)) — величина постоянная и от (triangle x) не зависит.
Для непрерывной функции: $$ lim_{triangle xrightarrow 0}triangle y =0 Leftrightarrow lim_{triangle xrightarrow 0}f(x)-f(x_0)=0Leftrightarrow lim_{triangle xrightarrow 0}f(x)=f(x_0) $$ Учитывая, что (triangle xrightarrow 0Leftrightarrow x-x_0rightarrow 0Leftrightarrow xrightarrow x_0)
получаем (lim{xrightarrow x_0}f(x)=f(x_0).)
Функция (y=f(x)) непрерывна в точке (x_0), если существует предел функции в этой точке и он равен значению функции в точке: $$ lim{xrightarrow x_0}f(x)=f(x_0) $$
Все три представленных определения непрерывности функции в точке эквивалентны.
Существуют и другие эквивалентные определения. Мы дадим ещё одно из них дальше, в этом же параграфе.
п.3. Непрерывность функции на промежутке
Промежуток – это интервал, отрезок, луч и т.п. (см. §16 справочника для 8 класса).
Функция (y=f(x)) непрерывна на промежутке, если она непрерывна в каждой точке этого промежутка.
График непрерывной функции – это непрерывная линия.
Кроме непрерывности, эта линия еще и «плавная», без «заломов».
При наличии заломов функция называется кусочно-непрерывной.
п.4. Односторонние пределы
Односторонний предел – это предел числовой функции при приближении к предельной точке с определенной стороны (слева или справа).
Обозначение односторонних пределов: begin{gather*} lim_{xrightarrow x_0 -0}f(x)=a — text{левый предел}\ lim_{xrightarrow x_0 +0}f(x)=b — text{правый предел} end{gather*}
Рассмотрим гиперболу (y=frac{1}{x-2}).
 |
У этой гиперболы две асимптоты (y=0) и (x=2). Точка (x_0=2) не входит в область определения. Если мы будем приближаться к (x_0=2) слева, начав, например с 1,5, мы будем постепенно опускаться по ветке гиперболы на минус бесконечность. Т.е., левый предел: $$ lim_{xrightarrow 2-0}frac{1}{x-2}=-infty $$ |
Если же мы будем приближаться к (x_0=2) справа, начав, например с 2,5, мы будем постепенно подниматься по ветке гиперболы на плюс бесконечность. Т.е., правый предел: $$ lim_{xrightarrow 2+0}frac{1}{x-2}=+infty $$ Левый и правый пределы в точке (x_0=2) для данной гиперболы не равны: $$ lim_{xrightarrow 2-0}frac{1}{x-2} ne lim_{xrightarrow 2+0}frac{1}{x-2} $$
Теперь рассмотрим параболу (y=x^2-2)
Областью определения параболы является вся числовая прямая (xinmathbb{R})
 |
В этом случае, если приближаться к (x_0=2) слева, мы получаем: $$ lim_{xrightarrow 2-0}(x^2-2)=2 $$ И если приближаться (x_0=2) справа, мы тоже получаем: $$ lim_{xrightarrow 2+0}(x^2-2)=2 $$ Левый и правый пределы равны: $$ lim_{xrightarrow 2-0}(x^2-2) =lim_{xrightarrow 2+0}(x^2-2) $$ |
Функция (y=f(x)) непрерывна в точке (x_0), если одновременно выполняются следующие три условия:
1) точка (x_0) принадлежит области определения функции (xin D);
2) левый и правый пределы в точке (x_0) равны и конечны: $$ lim_{xrightarrow x_0 -0}f(x) =lim_{xrightarrow x_0 +0}f(x)=lim_{xrightarrow x_0}f(x)=aneinfty $$ 3) предел функции в точке (x_0) равен значению функции в этой точке: $$ lim_{xrightarrow x_0}f(x)=f(x_0) $$
Это еще одно определение непрерывности, которым удобно пользоваться на практике.
п.5. Классификация точек разрыва
Точка (x_0) будет точкой разрыва для функции (y=f(x)), если выполняется хотя бы одно из условий:
1) точка (x_0) не принадлежит области определения функции (xnotin D);
2) левый и правый пределы в точке (x_0) не равны или бесконечны: $$ lim_{xrightarrow x_0 -0}f(x) nelim_{xrightarrow x_0 +0}f(x) text{или} lim_{xrightarrow x_0 -0}f(x) =lim_{xrightarrow x_0 +0}f(x)=pminfty $$ 3) предел функции в точке (x_0) не совпадает со значением функции в этой точке: $$ lim_{xrightarrow x_0}f(x)ne f(x_0) $$
| Точки разрыва | 1-го рода Односторонние пределы существуют и конечны |
Устранимые Односторонние пределы равны между собой, но не равны (f(x_0)) |
| Неустранимые (скачок) Односторонние пределы не равны между собой |
||
| 2-го рода Хотя бы один из односторонних пределов бесконечен или не существует |
п.6. Точки разрыва первого рода
Устранимые точки разрыва 1-го рода
Левый и правый пределы в точке (x_0) равны и конечны: $$ lim_{xrightarrow x_0 -0}f(x)=lim_{xrightarrow x_0 +0}f(x)=lim_{xrightarrow x_0}f(x)=aneinfty $$ НО:
либо точка (x_0) НЕ принадлежит области определения функции (xnotin D);
либо предел НЕ равен значению функции в точке (x_0): (lim_{xrightarrow x_0}f(x)ne f(x_0))
Например:
 |
(y=frac{x^2-4}{x-2}, x_0=2) Эта функция эквивалентна системе $$ y=frac{x^2-4}{x-2} Leftrightarrow begin{cases} y=x+2\ xne 2 end{cases} $$ При этом (lim_{xrightarrow 2-0}(x+2)=lim_{xrightarrow 2+0}(x+2)=4) В точке (x_0=2notin D) функция имеет устранимый разрыв. |
Разрыв можно устранить (функцию можно «склеить»), отдельно задав «гладкое» значение в особой точке: $$ y= begin{cases} frac{x^2-4}{x-2}, xne 2\ 4, x=2 end{cases} $$ В таком случае система станет эквивалентна всей прямой, т.е. станет непрерывной функцией: $$ y= begin{cases} frac{x^2-4}{x-2}, xne 2\ 4, x=2 end{cases} Leftrightarrow y=x+2 $$
Неустранимые точки разрыва 2-го рода (скачок)
Левый и правый пределы в точке (x_0) конечны, но не равны: $$ begin{cases} lim_{xrightarrow x_0 -0}f(x)=aneinfty\ lim_{xrightarrow x_0 +0}f(x)=bneinfty\ ane b end{cases} $$ Такой разрыв также называют скачком.
Величина скачка рассчитывается по формуле: $$ triangle y=lim_{xrightarrow x_0 +0}f(x)- lim_{xrightarrow x_0 -0}f(x)=b-a $$
Например:
 |
(y= begin{cases} x+1, xlt 2\ 3-x^2, xgeq 2 end{cases} , x_0=2) Односторонние пределы: begin{gather*} lim_{xrightarrow 2-0}f(x)= lim_{xrightarrow 2-0}(x+1)=3\ lim_{xrightarrow 2+0}f(x)= lim_{xrightarrow 2+0}(3-x^2)=-1 end{gather*} Пределы не равны, но конечны. Функция в точке (x_0=2) делает скачок вниз. Величина скачка: $$ triangle y=-1-3=-4 $$ |
п.7. Точки разрыва второго рода
В точках разрыва 2-го рода хотя бы один из односторонних пределов бесконечен или не существует.
Например:
 |
(y=e^frac1x, x_0=0)
(x_0=0ne D) — точка не входит в ОДЗ Точка (x_0=0) – точка разрыва второго рода. |
На практике, при моделировании реальных процессов, разрывы 2-го рода в функциональных зависимостях встречаются довольно часто. Их положено заботливо анализировать и тщательно обходить, выбирая рабочие участки характеристических кривых, – чтобы «система не пошла в разнос».
п.8. Алгоритм исследования функции на непрерывность
На входе: функция (y=f(x))
Шаг 1. Найти ОДЗ функции, определить точки и промежутки, не принадлежащие ОДЗ.
Шаг 2. Составить множество точек, в которое входят точки и границы промежутков, не принадлежащие ОДЗ, а также – для кусочно-непрерывных функций – точки сшивания. Полученное множество состоит из точек, подозрительных на разрыв.
Шаг 3. Исследовать каждую из точек, подозрительных на разрыв, с помощью односторонних пределов. Если разрыв обнаружен, определить тип разрыва.
На выходе: список точек разрыва и тип разрыва для каждой точки.
п.9. Примеры
Пример 1. Исследуйте функцию на непрерывность:
a) ( y=frac{x+3}{x-1} )
ОДЗ: (x-1ne 0Rightarrow xne 1)
(x_0=1notin D) — точка не входит в ОДЗ, подозрительная на разрыв.
Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 1-0}frac{x+3}{x-1}=frac{1-0+3}{1-0-1}=frac{4}{-0}=-infty\ lim_{xrightarrow 1+0}frac{x+3}{x-1}=frac{1+0+3}{1+0-1}=frac{4}{+0}=+infty end{gather*} Односторонние пределы не равны и бесконечны.
Точка (x_0=1) — точка разрыва 2-го рода.
б) ( y=frac{x}{sqrt{x+2}-2} )
ОДЗ: ( begin{cases} x+2geq 0\ sqrt{x+2}-2ne 0 end{cases} Rightarrow begin{cases} xgeq -2\ sqrt{x+2}ne 2 end{cases} Rightarrow begin{cases} xgeq -2\ xne 2 end{cases} )
(x_0=-2) — левая граница ОДЗ
(x_1=2notin D)- точка не входит в ОДЗ
Точки (x_0) и (x_1) — подозрительные на разрыв
Исследуем (x_0=-2). Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 2-0}frac{x}{sqrt{x+2}-2} — text{предел не существует}\ lim_{xrightarrow 2+0}frac{x}{sqrt{x+2}-2}=frac{-2+0}{sqrt{-2+0+2}-2}=frac{-2}{-2}=1 end{gather*} Один из односторонних пределов не существует.
Точка (x_0=-2) — точка разрыва 2-го рода.
Исследуем (x_1=2). Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 2-0}frac{x}{sqrt{x+2}-2} =frac{2-0}{sqrt{2-0+2}-2}=frac{2}{-0}=-infty\ lim_{xrightarrow 2+0}frac{x}{sqrt{x+2}-2}=frac{2+0}{sqrt{2+0+2}-2}=frac{2}{+0}=+infty end{gather*} Односторонние пределы не равны и бесконечны.
Точка (x_1=2) — точка разрыва 2-го рода.
в) ( y=frac{tgx}{3x} )
ОДЗ: (xne 0)
(x_0=0notin D)- точка не входит в ОДЗ, подозрительная на разрыв
Найдем односторонние пределы: begin{gather*} lim_{xrightarrow -0}frac{tgx}{3x}=frac13lim_{xrightarrow -0}frac{tgx}{x}=frac13cdot 1=frac13\ lim_{xrightarrow +0}frac{tgx}{3x}=frac13lim_{xrightarrow +0}frac{tgx}{x}=frac13cdot 1=frac13 end{gather*} Односторонние пределы конечны и равны.
Точка (x_0=0) — точка разрыва 1-го рода, устранимый разрыв.
г) ( y= begin{cases} x+1, xlt 3\ x^2+3, xgeq 3 end{cases} )
ОДЗ: (xinmathbb{R})
(x_0=3)- точка сшивания, подозрительная на разрыв.
Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 3-0}y=lim_{xrightarrow 3-0}(x+1)=3+1=4\ lim_{xrightarrow 3+0}y=lim_{xrightarrow 3+0}(x^2+3)=3^2+3=12 end{gather*} Односторонние пределы конечны, но неравны.
Точка (x_0=3) — точка разрыва 1-го рода, неустранимый разрыв (скачок).
Величина скачка: (lim_{xrightarrow 3+0}y-lim_{xrightarrow 3-0}y=12-4=8)
Пример 2. Доопределите функцию в точке разрыва так, чтобы она стала непрерывной в этой точке:
a) ( y=frac{2x^3-x^2}{7x} )
ОДЗ: (xne 0)
(x_0=0notin D)- точка не входит в ОДЗ, подозрительная на разрыв.
Упростим выражение: (frac{2x^3-x^2}{7x}=frac{x^2(2x-1)}{7x}=frac{x(2x-1)}{7}) $$ y=frac{2x^3-x^2}{7x}Leftrightarrow y= begin{cases} frac{x(2x-1)}{7}\ xne 0 end{cases} $$ Найдем односторонние пределы: begin{gather*} lim_{xrightarrow -0}frac{x(2x-1)}{7}=0, lim_{xrightarrow +0}frac{x(2x-1)}{7}=0 end{gather*} Односторонние пределы конечны и равны.
Точка (x_0=0) — точка разрыва 1-го рода, устранимый разрыв.
Доопределить функцию нужно значением предела в точке разрыва: (y(0)=0).
Доопределенная непрерывная функция: $$ y= begin{cases} frac{2x^3-x^2}{7x}, xne 0\ 0, x=0 end{cases} $$ б) ( y=frac{1-cos4x}{x^2} )
ОДЗ: (xne 0)
(x_0=0notin D)- точка не входит в ОДЗ, подозрительная на разрыв.
Упростим выражение: (frac{1-cos4x}{x^2}=frac{2sin^2 2x}{x^2}=frac{2sin^2 2x}{frac{(2x)^2}{4}}=8left(frac{sin2x}{2x}right)^2) $$ y=frac{1-cos4x}{x^2}Leftrightarrow y= begin{cases} 8left(frac{sin2x}{2x}right)^2\ xne 0 end{cases} $$ Найдем односторонние пределы: begin{gather*} lim_{xrightarrow -0}8left(frac{sin2x}{2x}right)^2=8cdot 1=8, lim_{xrightarrow +0}8left(frac{sin2x}{2x}right)^2=8cdot 1=8 end{gather*} Односторонние пределы конечны и равны.
Точка (x_0=0) — точка разрыва 1-го рода, устранимый разрыв.
Доопределить функцию нужно значением предела в точке разрыва: (y(0)=8).
Доопределенная непрерывная функция: $$ y= begin{cases} frac{1-cos4x}{x^2}, xne 0\ 8, x=0 end{cases} $$
Содержание:
- Непрерывность функции
- Непрерывность функции в точке
- Непрерывность функции в точке
- Задача пример №57
- Непрерывность функции на интервале
- Непрерывность функции на отрезке
- Задача пример №58
- Задача пример №59
- Задача пример №60
Непрерывность функции
Непрерывность функции часто можно легко объяснить следующим образом. Если график какой-либо функции можно построить не отрывая карандаш от бумаги, то эта функция непрерывна. В противном случае, у графика есть точки разрыва (скачка) и данная функция является разрывной функцией. График разрывной функции невозможно изобразить, не отрывая карандаш от листа.
Непрерывность функции в точке
Для того, чтобы функция была непрерывной в точке, ее график не должен прерываться, т.е. график не должен иметь «скачков». График функций на рисунках прерывается или имеет «скачок» в точке 



1. Функция не определена в точке 
2. В точке 

3. Предел функции 


Точка 
Если функция не удовлетворяет ни одному из указанных выше условий, то ее можно назвать непрерывной в точке 
Непрерывность функции в точке
Для того, чтобы функция 

1. Функция должна быть определена в точке 
2. Должен существовать предел 
3. Должно выполняться равенство 
Задача пример №57
Исследуйте непрерывность следующих функций.
Решение:
а) из графика функции 




Отметим, что во всех точках кроме 
b)
Как видно из графика, при стремлении значений 

Предел функции:
Значение функции: 




Непрерывность функции на интервале
Определение. Функция называется непрерывной на интервале 
Непрерывность функции на отрезке
Определение. Функция 




Любая функция — многочлен непрерывна на всей числовой оси. Рациональная функция непрерывна во всех точках, кроме тех, которые обращают знаменатель в 0. Функции 

Для функции, непрерывной на отрезке, справедлива следующая теорема.
Теорема Вейерштрасса. Функция, непрерывная на отрезке, принимает в нем наименьшее и наибольшее значения.
Теорема Коши. Если функция 


Следствие. Функция, непрерывная на отрезке, принимает все значения от наименьшего до наибольшего.
Применяя эту теорему, можно решить следующий тип задач.
Задача пример №58
Существует ли такое действительное число, куб которого больше самого числа на 1?
Решение:
искомое число 










Если какая-либо функция непрерывна на интервале 

Задача пример №59
Исследуйте непрерывность функции
Решение:
как видно из графика, при стремлении 
Т.е. в точке 



Задача пример №60
Определите точки разрыва функции
Решение: Линейная функция 





Сначала исследуем непрерывность функции в точке 
1. Значение функции. Функция определена в точке 

2. Существование предела. Для определения предела 






3. Значение и предел функции в точке. Так как 


Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:
Другие темы которые вам помогут понять математику:
|
|
|
|
Лекции:
- Теорема о разложении на множители
- Экстремум функции многих переменных
- Пределы в математике
- Дифференциал функции
- Объемы подобных фигур
- Непрерывность функции
- Интервал сходимости степенного ряда
- Уравнение прямой через две точки
- Круги Эйлера фигуры, условно изображающие множества
- Тригонометрические комплексные числа
Непрерывность функции:
Непрерывные функции, точки разрыва и их классификация, действия над непрерывными функциями, свойства функций, непрерывных на сегменте.
Определение:
Функция у = f(x) называется непрерывной в точке х₀, если:
- функция определена в точке x₀ и в некоторой ее окрестности, содержащей эту точку;
- функция имеет предел при х → x₀;
- предел функции при х → x₀ равен значению функции в точке x₀:
(10.1)
Если в точке x₀ функция непрерывна, то точка x₀ называется точкой непрерывности функции.
Пример:
Исследовать на непрерывность функцию 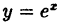
Решение:
Чтобы доказать, что функция 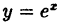
Таким образом, доказано, что функция 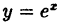
Замечание:
Формулу (10.1) можно записать в виде
(10.2)
так как 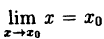
Введем понятие непрерывности функции в точке х₀ справа и слева.
Если, существует 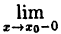
Так как ∆x = x-x₀, a ∆y = f(x)-(x₀), то условие (10.1) равносильно следующему:
Определение:
Функция у = f(x) называется непрерывной в точке х₀, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции
(10.3)
Пример:
Показать, что функция у = х³ непрерывна для любого значения аргумента х.
Решение:
Найдем приращение функции ∆y.
∆y= (x+∆x)³-x³ = x³+3x²∆x+3x∆x²+∆x³-x³ = 3x²∆x+3x∆x²+∆x³.
Используя теоремы о пределе суммы и произведения функции, получим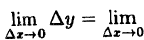
Следовательно, функция у = х³ непрерывна при — ∞< х < ∞.
Точки разрыва функции и их классификация
Определение:
Точка х₀ называется точкой разрыва функции у = f(x), если она принадлежит области определения функции или ее границе и не является точкой непрерывности.
Так, например, функция 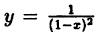
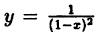
Определение:
Точка разрыва x₀ функции у = f(x) называется точкой устранимого разрыва, если существуют оба односторонних предела в точке x₀ и они равны, т. е.
Пример:
Исследовать на непрерывность функцию
Решение:
В точке x=-1 функция не определена, так как, выполнив подстановку, получаем неопределенность 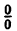
Таким образом, при x = -1 данная функция имеет устранимый разрыв.
Он будет устранен, если положить, что при x = -1 ⇒ у =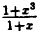
Определение:
Если в точке x₀ односторонние пределы слева и справа существуют, но не равны, точка x₀ называется точкой разрыва I рода.
Пример:
Исследовать на непрерывность функцию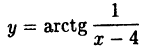
Решение: Вычислим односторонние пределы функции в точке ее разрыва х = 4.
Предел слева —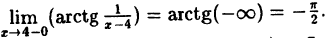
Предел справа — 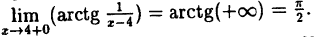
Пределы слева и справа существуют, но не равны, следовательно, точка x = 4 для данной функции — точка разрыва I рода (точка скачка).
Определение:
Точки разрыва, не являющиеся точками разрыва I рода, называются точками разрыва II рода.
В точках разрыва II рода не существует хотя бы один из односторонних пределов. Функция 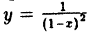
Действия над непрерывными функциями
Теорема:
Непрерывность суммы, произведения и частного непрерывных функций. Если функции ϕ(x) и ψ(x) непрерывны в точке Хо, то их сумма и произведение также непрерывны в точке x₀. Если, кроме того, знаменатель в рассматриваемой точке не равен нулю, то частное непрерывных функций есть функция непрерывная.
Докажем непрерывность произведения.
Дано: непрерывность функций в точке x₀: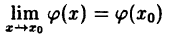
Доказать, что f(x) — ϕ(x) ∙ ψ(x) есть функция непрерывная в точке x₀, т. е. 
Доказательство:



Можно строго доказать, что все основные элементарные функции непрерывны при всех значениях х, для которых они определены.
Например, степенная у = xⁿ, показательная у = 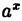
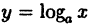
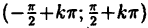
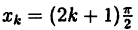
Теорема:
Непрерывность сложной функции. Если функция и = ϕ(x) непрерывна в точке x₀, а функция у = f(u) непрерывна в точке и₀ = ϕ(x₀), то сложная функция у = f [ϕ(x)] непрерывна в точке x₀.
Без доказательства.
В заключение этого раздела рассмотрим два предела, которые нам понадобятся в дальнейшем.
Пример:
Вычислить
Решение:
Заметим, что при х → 0 числитель и знаменатель одновременно стремятся к нулю, т.е. имеет место неопределенность вида 
Так как данная логарифмическая функция непрерывна в окрестности точки х = 0, то можно перейти к пределу под знаком функции (

но 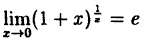
Следовательно,
(10.4)
В частности, при а = е
(10.5)
Таким образом, у = ln( 1 + х) и у = х — эквивалентные бесконечно малые функции при х → 0.
Пример:
Вычислить
Решение:
Здесь мы имеем дело с неопределенностью вида 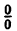
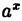
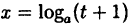
Так как на основании результата, полученного в предыдущем примере, 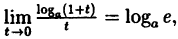
(10.6)
В частности, если а = е, имеем
т.е. у = 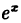
Свойства функций, непрерывных на сегменте
Определение:
Функция у = f(x) непрерывна на сегменте [а, b], если она непрерывна во всех внутренних точках Этого сегмента, а на концах сегмента (в точках a и b) непрерывна соответственно справа и слева.
Теорема:
Если функция у = f(x) непрерывна на сегменте [а, b], то она достигает на этом сегменте своего наибольшего и(или) наименьшего значения.
Простым доказательством этой теоремы, является геометрическая иллюстрация функции у = f(x) на рисунке 91. Непрерывная на сегменте [α, b] функция достигает наименьшего своего значения в точке х = x₁= а, а наибольшего значения в точке х₂.
Следствие:
Если функция у = f(x) непрерывна на сегменте [a, b], то она ограничена на этом сегменте.
Действительно, если по теореме 10.3 функция достигает на сегменте наибольшего M и наименьшего т значений, то имеет место неравенство m ≤ f(x) ≤ M для всех значений функции на рассматриваемом сегменте. Т. е. |f(x)| ≤ M и, следовательно, функция у = f(x) ограничена на сегменте [а, b].
Теорема:
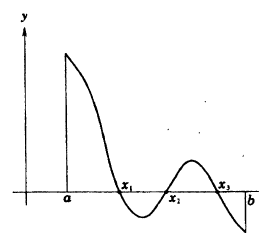
Теорема Больцано-Коши. Если функция у = f(x) непрерывна на сегменте [а, b] и на ее концах принимает значения разных знаков, то внутри этого сегмента найдется, по крайней мере, одна тонка С, в которой функция равна нулю.
Геометрический смысл теоремы заключается в следующем: если точки графика функции у = f(x), соответствующие концам сегмента [a, b], лежат по разные стороны от оси ОХ, то этот график хотя бы в одной точке сегмента пересекает ось OX. На данном рисунке 92 это три точки x₁, x₂, x₃.
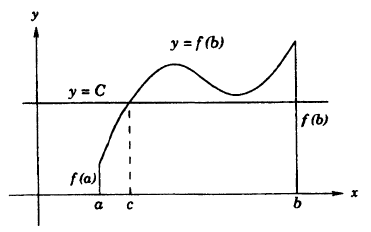
Теорема:
О промежуточных значениях функции. Если функция у = f(x) непрерывна на сегменте [α, b] и f(α) = A и f(b) = В, то для любого числа С, заключенного между A и B, найдется внутри этого сегмента такая точка с, что f(c) = С.
Из графика на рисунке 93 видно, что непрерывная функция, переходя от одного значения к другому, обязательно проходит через все промежуточные значения.
Теорема:
О непрерывности обратной функции.) Если функция у = f(x) непрерывна на сегменте [а, b] в возрастает (убывает) на этом сегменте, то обратная функция х = f⁻¹(y) на соответствующем сегменте оси OY существует и является также непрерывной возрастающей (убывающей) функцией.
Эту теорему мы принимаем без доказательства.
Решение на тему: Непрерывная функция
Пример:
Показать, что функция у = 4x² непрерывна в точке х = 2.
Решение:
Для этого необходимо показать, что в точке х = 2 выполняется все три условия непрерывности функции:
1) функция у = 4х² определена в точке х = 2 ⇒ f(2) = 16;
2) существует 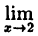
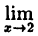
3) этот предел равен значению функции в точке х = 2
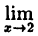
Пример:
Показать, что функция у = sin x непрерывна для любого значения аргумента х.
Решение:
Найдем приращение функции ∆y, используя формулы тригонометрических тождеств
Так как 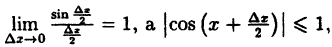
Следовательно, функция у = sin x непрерывна при -∞ < х < ∞.
Пример:
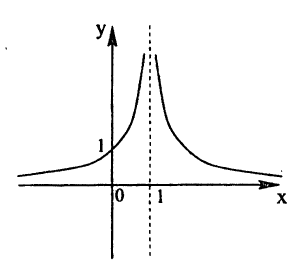
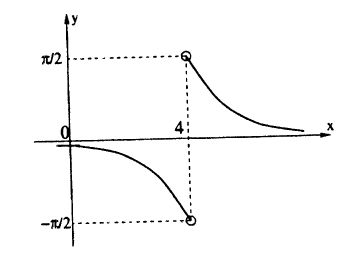
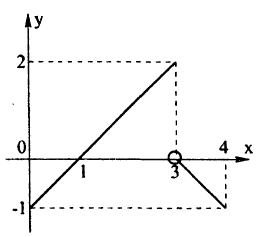
Исследовать на непрерывность функцию
Решение:
Эта функция (рис. 94) определена во всех точках сегмента [0,4] и ее значение при х = 3 ⇒ у = 2. Функция терпит разрыв, так как она не имеет предела при х → 3 :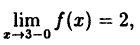
Следовательно, точка х = 3, точка разрыва первого рода. При этом в граничных точках исследуемого сегмента [0,4], функция f(x) непрерывна справа (х = 0) и непрерывна слева (х = 4).
Пример:
Исследовать на непрерывность функцию
Решение:
В точке х = 5 функция не определена, т.к., выполнив подстановку, получаем неопределенность вида 0/0. Легко доказать, что
Следовательно, точка х = 5 точка устранимого разрыва.
Пример:
Исследовать на непрерывность функцию
Решение:
В точке х = 0 функция (рис. 95) терпит разрыв, так как она не определена в этой точке. Пределы функции слева и справа от точки х = 0 равны ∞. Следовательно, точка х = 0 для данной функции является точкой разрыва второго
Пример:
Исследовать на непрерывность функцию
Решение:
В точке х = 0 функция терпит разрыв 1-го рода, так как односторонние пределы существуют в этой точке, но не равны:
предел слева
предел справа
Пример:
Исследовать на непрерывность функцию 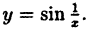
Решение:
Функция 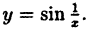
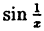
Пример:
Исследовать на непрерывность функцию
Решение:
Функция 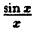
Если доопределить функцию 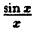
f(х) =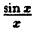
Доопределив функцию в точке х = 0, мы устранили разрыв.
Непрерывность функций
Смотрите также:
Предмет математический анализ
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

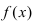
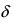 -окрестности;
-окрестности;