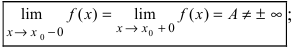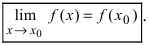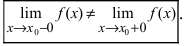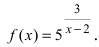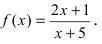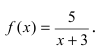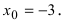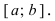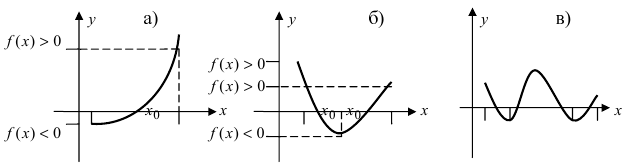Определение
6.4.
Функция f(x) называется непрерывной на
интервале (a,b), если
она непрерывна в каждой точке этого
интервала. Обозначают f(x)∈C(a,b).
Определение
6.5.
Функция f(x) называется непрерывной
на полуинтервале [a,b), (или (a,b]), если
она непрерывна на интервале (a,b) и
непрерывна справа в точке a (или
непрерывна слева в
точке b). Пишутf(x)∈C[a,b) (или f(x)∈C(a,b]).
Определение
6.6.
Функция f(x) называется непрерывной
на отрезке [a,b], если
она непрерывна на интервале (a,b),непрерывна
справа в точке a и
непрерывна слева в точке b. Обозначают f(x)∈C[a,b].
Теорема
6.7.
Каждая
основная элементарная функция непрерывна
в области определения.
Д
о к а з а т е л ь с т в о.
Доказательство
следует из теоремы
6.4 и определений
6.4-6.6.
■
6.4. Свойства
функций, непрерывных на отрезке
Свойство
6.1.
Функция,
непрерывная на отрезке, ограничена на
нём.
Свойство
6.2.
Функция f(x), непрерывная
на отрезке [a,b], принимает
на нем наибольшее и наименьшее значения,
т.е. существуют такие
точки ξ η отрезка [a,b], что f(ξ)=m, f(η)=M, и
для всех точек x этого
отрезка выполняются неравенства m≤f(x)≤M.
Свойство
6.3.
Если
функция f(x) непрерывна
на отрезке [a,b] и f(a)=A, f(b)=B, причем A≠B, то
для любогоC такого,
что A<C<B, найдется
точка ξ∈(a,b) такая,
что f(ξ)=C.
Как
следствие из свойства
6.3 получаем:
если функция f(x) непрерывна
на отрезке [a,b] и
принимает на его концах значения разных
знаков, то найдётся такая
точка ξ∈(a,b), что f(ξ)=0, Точка ξ в
которойf(ξ)=0, называется нулём
функции f(x).
Теорема
6.8.
Пусть
функция y=f(x) строго
монотонна (возрастает или убывает) и
непрерывна на отрезке [a,b].Тогда
обратная функция x=f−1(y) определена,
строго монотонна (возрастает или убывает)
и непрерывна на соответствующем отрезке
оси Oy.
6.5.
Точки разрыва функций и их классификация
Согласно определению
6.1 для
функции f(x), непрерывной
в точке x0, должны
выполняться три условия непрерывности:
1)
функция определена в точке x0 (∃f(x0));
2)
функция имеет конечный предел
при x→x0 (∃ конечный предел limx→x0f(x));
3)
предел функции при x→x0 равен
значению функции в самой
точке x0 (limx→x0f(x)=f(x0)).
Определение
6.7.
Точка x0 называется точкой
разрыва функции f(x), а
сама функция разрывной в
точке x0, если
она не является непрерывной в этой
точке, т.е. нарушено хотя бы одно из
указанных выше условий: либоx0∉Df, либо
не существует конечного
предела limx→x0f(x), либо limx→x0f(x)≠f(x0).
Рассмотрим
функции, заданные графически на рис.
6.5.
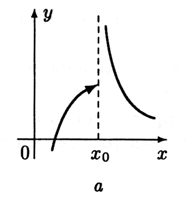
Для всех этих функций x0 —
точка разрыва.
Таблица
|
Рис. |
Рис. |
Рис. |
В
первом случае (рис.
6.5, а)
не выполнено условие 1, так как в
точке x0 функция
не определена.
Во
втором случае (рис.
6.5, б)
нарушено ксловие 2, так как
предел limx→x0f(x) не
существует.
В
третьем случае (рис.
6.5, в)
не выполнено условие 3, так
как limx→∞f(x)=A≠f(x0).
Определение
6.8.
Пусть x0 —
точка разрыва функции f(x). Точка x0 называется точкой
разрыва первого рода, если функция имеет
в этой точке пределы справа и слева,
т.е.
limx→x+0f(x)=f(x+0)≠∞ и limx→x−0f(x)=f(x−0)≠∞.
В
этом случае
либо f(x+0)≠f(x−0), либо f(x+0)=f(x−0)≠f(x0), причем f(x) может
быть и не определена в точке x0.
Разность f(x+0)−f(x−0) называют скачком функции f(x) в
точке x0.
Определение
6.9.
Точка
разрыва первого рода x0, в
которой f(x+0)=f(x−0), называется точкой
устранимого разрыва.
Рассмотрим
функцию f(x)=xsin1x, для
которой x=0 есть
точка разрыва, так как функция не
определена в этой точке. Односторонние
пределы функции в этой точке конечны и
равны,
посколькуf(+0)=limx→+0xsin1x=0, f(−0)=limx→−0xsin1x=0. Следовательно, x=0 —
точка устранимого разрыва.
Полагая f(0)=f(+0)=f(−0)=0, получим
функцию, непрерывную в точке x=0:
ϕ(x)=⎧⎩⎨xsin1x, 0,x≠0;x=0.
Тем
самым мы доопределили по непрерывности
данную функцию f(x).
Определение
6.10.
Точка
разрыва x0, не
являющаяся точкой разрыва первого рода,
называется точкой
разрыва второго рода. В этом случае хотя
бы один из односторонних пределов
функции в точке x0 не
существует или равен бесконечности.
Замечание
6.2.
Принимая
во внимание замечание
6.1 и определение
6.7,
подчеркнем еще раз: для того, чтобы
функция f(x) балы
непрерывной в точке x0 необходимо
и достаточно вполнение условий:
1)
функция f(x) определена
в точке x0 (∃ f(x0));
2)
cуществуют конечные односторонние
пределы функции в этой
точке(∃f(x+0)≠∞, ∃f(x−0)≠∞);
3)
односторонние пределы функции в
точке x0 равны
значению функции в этой
точке(f(x+0)=f(x−0)=f(x0)).
Поэтому
при исследовании функции на непрерывность
и определении точек разрыва функции
рекомендуется придерживаться следующей
схемы.
1
Найти область определения функции.
2
Указать промежутки области определения
функции, на которых функция непрерывна.
3
Выявить точки, в которых может быть
нарушена непрерывность функции.
4
Найти односторонние пределы функции в
каждой из указанных точек. Если функция
определена в них, то найти значения
функции в этих точках.
5
Сравнить в каждой такой точке односторонние
пределы и значение функции, если она
определена в этой точке, и установить
либо непрерывность, либо разрыв функции
в каждой из полученных точек.
6
В случае разрыва функции определить
тип точки разрыва.
6.6. Типовые
примеры
Задача
1.
Найти
односторонние пределы в точке x0=1 функции
f(x)={ x+1,3x+2,0≤x<1;1<x<3.
Р
е ш е н и е.
Найдем
правый предел f(1+0) функции f(x) в
точке x0=1, т.е.
при x→1 и x>1. Имеем
f(1+0)=limx→1+0f(x)=limx→1+0(3x+2)=5.
Для
левого предела f(1−0) в
точке x0=1 (x→1,x<1) получим
f(1−0)=limx→1−0f(x)=limx→1−0(x+1)=2.
■
Задача
2.
Найти
точки разрыва функции f(x)=∣∣x∣∣x и
определить тип каждой точки разрыва.
Р
е ш е н и е.
Точка x0=0 является
точкой разрыва функции, так как в ней
функция не определена. Найдем правый и
левый пределы функции в этой точке:
f(+0)=limx→+0|x|x=limx→+0xx=1;
f(−0)=limx→−0|x|x=limx→−0−xx=−1.
Односторонние
пределы конечны и различны, точка x0=0 —
точка разрыва первого рода. На графике
(рис. 6.6) виден конечный скачок функции
в точке x0=0, равный f(+0)−f(−0)=2.
■

Рис.
6.6

Рис.
6.7
Задача
3.
Найти
точки разрыва функции f(x)=sinxx и
определить тип каждой точки разрыва.
Р
е ш е н и е.
В
точке x0=0 функция
не определена, т.е. x0 —
точка разрыва функции. Найдем правый и
левый пределы функции в этой точке:
f(+0)=limx→+0sinxx=1;
f(−0)=limx→−0sinxx=1.
Так
как односторонние пределы конечны и
равны, т.е. f(+0)=f(−0), то x0=0 —
точка устранимого разрыва данной функции
(рис. 6.7). Если
положить f(0)=1, то
разрыв можно устранить. Тем самым
первоначальную функцию доопределим по
непрерывности в точкеx0=0. Аналитически
новую функцию ϕ(x), непрерывную
на всей числовой оси, запишем в виде
ϕ(x)=⎧⎩⎨ sinxx, 1,x≠0;x=0.
■
Задача
4.
Исследовать
на непрерывность функцию
f(x)=⎧⎩⎨⎪⎪ x3+2,2,1,x>0;x<0;x=0.
Р
е ш е н и е.
Функции y1=x3+2 и y2=2 непрерывны
при любом x. Единственной
точкой, в которой функция f(x) может
иметь разрыв, является точка x=0. Вычислим
односторонние пределы функции f(x) в
этой точке:
f(+0)=limx→+0f(x)=limx→+0(x3+2)=2;
f(−0)=limx→−0f(x)=limx→−02=2.
Так
как f(0)=1≠f(+0)=f(−0)=2, то x=0 —
точка разрыва первого рода данной
функции (рис. 6.8).
■
Задача
5.
Исследовать
на непрерывность функцию f(x)=sin1x.
Р
е ш е н и е.
Данная
функция непрерывна всюду, кроме
точки x0=0. Рассмотрим f(+0)=limx→+0sin1x. Так
как 1x→+∞ при x→+0 и
значения функции f(x) колеблются
между −1 и +1, не
приближаясь к какому-либо определенному
значению, то f(+0) не
существует. Аналогично, не существует
и f(−0). Следовательно, x=0 —
точка разрыва второго рода (рис. 3.11).
■
Задача
6.
Исследовать
на непрерывность функцию f(x)=xx2−4.
Р
е ш е н и е.
Данная
рациональная функция непрерывна всюду,
кроме точек, где знаменатель обращается
в ноль. Следовательно, функция терпит
разрыв в точках x1=2 и x2=−2. Найдем
односторонние пределы данной функции
в этих точках:
f(2+0)=limx→2+0xx2−4=+∞;
f(2−0)=limx→2−0xx2−4=−∞;
f(−2+0)=limx→−2+0xx2−4=+∞,
f(−2−0)=limx→−2−0xx2−4=−∞.
Точки x1=2 и x2=−2 —
точки разрыва второго рода (рис. 6.9).
■

Рис.
6.8

Рис.
6.9

Рис.
6.10
Задача
7.
Исследовать
на непрерывность в
точке x0=0 функцию f(x)=∣∣sinx∣∣2x.
Р
е ш е н и е.
В
точке x0=0 функция
не определена. Следовательно, x0=0 —
точка разрыва функции. Найдем односторонние
пределы функции в этой точке.
Если x→0 и x>0, то ∣∣sinx∣∣2x>0 иf(+0)=limx→+0∣∣sinx∣∣2x=12. Если x→0 и x<0, то ∣∣sinx∣∣2x<0 и f(−0)=limx→−0∣∣sinx∣∣2x=−12. Так
как односторонние пределы f(+0) и f(−0) конечны
и различны, то x0=0 —
точка разрыва первого рода, причем
скачок функции в этой точке
равен f(+0)−f(−0)=12−(−12)=1(рис.
6.10).
■
Задача
8.
Исследовать
на непрерывность функцию
f(x)={x2,2x−1,−1≤x<2;2≤x≤3.
Р
е ш е н и е.
Функция f(x) определена
всюду на [−1,3], непрерывна
на полуинтервале [−1,2) и
на отрезке[2,3]. Единственной
точкой, в которой возможен разрыв
функции f(x) является
точка x0=2.Вычислим
односторонние пределы функции f(x) в
этой точке
f(2−0)=limx→2−0x2=4,
f(2+0)=limx→2+0(2x−1)=3.
Односторонние
пределы f(2−0) и f(2+0) конечны
и различны. Следовательно, x0=2 —
точка разрыва первого рода. Скачок
функции в точке x0=2 равенf(2+0)−f(2−0)=3−4=−1 (рис.
6.11).
■

Рис.
6.11

Рис.
6.12
Задача
9.
Найти
и исследовать точки разрыва
функции f(x)=sinxx2+2x.
Р
е ш е н и е.
Точками
разрыва функции f(x) будут
точки x1=0 и x2=−2 в
которых функция f(x) не
определена (x2+2x=0). Исследуем
точку x1=0. При x→0 и x>0 функция sinx>0,sinxx(x+2)>0, f(+0)=limx→+0sinxx2+2x=limx→+0sinxx(x+2)=12. При x→0 и x<0 функция sinx<0,sinxx(x+2)>0, f(−0)=limx→−0sinxx2+2x=limx→−0sinxx(x+2)=12. Односторонние
пределы f(+0) иf(−0) в
точке x1=0 конечны
и равны. Следовательно, x1=0 —
точка устранимого разрыва. Разрыв
устраняется, если положить f(0)=12. Рассмотрим
точку x2=−2. Еслиx→−2 и x>−2, то sinx<0, x<0, x+2>0, sinxx(x+2)>0 иf(−2+0)=limx→−2+0sinxx(x+2)=+∞. Если x→−2 и x<−2, то sinx<0, x<0, x+2<0,sinxx(x+2)<0 и f(−2−0)=limx→−2−0sinxx(x+2)=−∞. Следовательно, x2=−2 —
точка разрыва второго рода (рис. 6.12).
■
Задача
10.
Исследовать
на непрерывность функцию f(x)=e1x+3.
Р
е ш е н и е.
Данная
функция непрерывна всюде, кроме
точки x0=−3. Найдем
односторонние
пределыf(−3+0) и f(−3−0) Если x→−3 и x>−3, то x+3>0, 1x+3→+∞ иf(−3+0)=limx→−3+0e1x+3=+∞ Если x→−3 и x<−3, то x+3<0, 1x+3→−∞ иf(−3−0)=limx→−3−0e1x+3=0. Следовательно,
точка x0=−3 —
точка разрыва второго рода (рис. 6.13).
■

Рис.
6.13

Рис.
6.14
Задача
11.
Исследовать
на непрерывность функцию f(x)=12−21/x.
Р
е ш е н и е.
Данная
функция непрерывна всюду, кроме
точек x1=0 и x2=1, так
как в точке x1=0 не
определена дробь 1x в
точке x2=1 знаменатель 2−21/x исходной
дроби равен нулю. Найдем односторонние
пределы данной функции в
точках x1 и x2 При x→0 и x>0 дробь 1x→+∞,21/x→+∞ и f(+0)=limx→+012−21/x=0. При x→0 и x<0 дробь 1x→−∞, 21/x→0 иf(−0)=limx→−012−21/x=12. Так
как в точке x1=0 односторонние
пределы f(+0)=0 иf(−0)=12 конечны
и различны, то x1 —
точка разрыва первого рода.
Найдем f(1+0) иf(1−0). При x→1 и x>1 дробь 1x<1, 21/x<2, разность 2−21/x→0, оставаясь
положительной.
Поэтому f(1+0)=limx→1+012−21/x=+∞. При x→1 и x<1 дробь 1x>1,21/x>2, разность 2−21/x→0, оставаясь
отрицательной,
иf(1−0)=limx→1−012−21/x=−∞. Следовательно, x2=1 —
точка разрыва второго рода (рис. 6.14).
■
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Непрерывность функций и точки разрыва
Непрерывность функции
Определение: Функция
- — она определена в этой точке и ее некоторой
-окрестности;
- — существуют конечные лево- и правосторонние пределы от функции в этой точке и они равны между собой, т.е.
— предел функции в точке 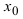
Пример:
Найти область непрерывности функции
Решение:
Данная функция непрерывна 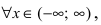
Замечание: Всякая элементарная функция непрерывна в области своего определения.
Точки разрыва
Определение: Точки, в которых не выполняется хотя бы одно из условий непрерывности функции, называются точками разрыва. Различают точки разрыва первого и второго родов.
Определение: Точкой разрыва I рода называется точка, в которой нарушается условие равенства лево- и правостороннего пределов, т.е.
Пример:
Доказать, что функция 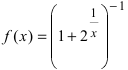
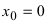
Решение:
Нарисуем график функции в окрестности нуля (Рис. 64): 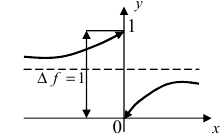
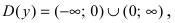
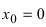
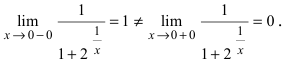
Замечание: По поводу точки разрыва I рода иначе говорят, что в этой точке функция испытывает конечный скачок (на Рис. 64 скачок равен 1).
Определение: Точка, подозрительная на разрыв, называется точкой устранимого разрыва, если в этой точке левосторонний предел равен правостороннему.
Пример:
Доказать, что функция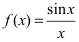
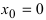
Решение:
В точке 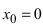
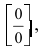
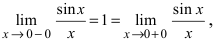
Определение: Все остальные точки разрыва называются точками разрыва II рода.
Замечание: Для точек разрыва второго рода характерен тот факт, что хотя бы
один из односторонних пределов равен 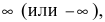
Пример:
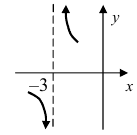
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: 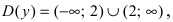
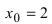
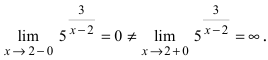
Пример:
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: 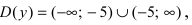
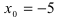
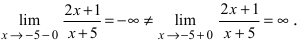
Операции над непрерывными функциями
Теорема: Сумма (разность) непрерывных функций есть непрерывная функция.
Доказательство: Докажем приведенную теорему для суммы двух функций 
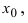
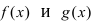
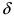
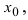
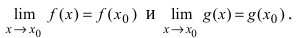
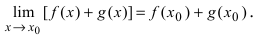
Теорема: Произведение непрерывных функций есть непрерывная функция.
Теорема: Частное двух непрерывных функций 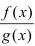
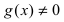
Теорема: Сложная функция от непрерывных функций есть непрерывная функция.
- Заказать решение задач по высшей математике
Схема исследования функции на непрерывность
Исследование функции на непрерывность проводят по следующей схеме:
Пример:
Исследовать на непрерывность функцию
Решение:
Согласно схеме исследования функции на непрерывность имеем:
Рис. 65. Поведение графика функции 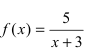
Из рисунка видно, что график функции 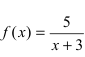
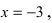
Свойства непрерывных функций на отрезке (a; b)
Свойства непрерывных функций на отрезке 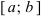
Определение: Замкнутый интервал 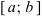
Приведем без доказательства свойства непрерывных функций на сегменте 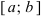
Теорема: Если функция 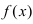
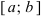
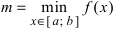
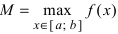
Пример:
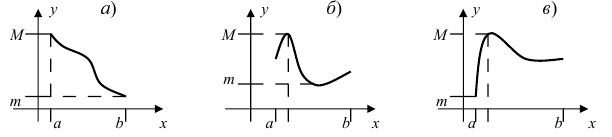
Привести примеры графиков функций, удовлетворяющих условиям теорем(см. Рис. 66).
Рис. 66. Графики функций, удовлетворяющих условиям теоремы.
Решение:
На графике а) функция достигает своего наименьшего 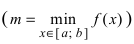
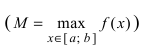
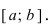
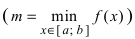
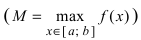
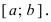
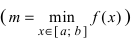
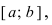
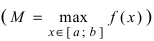
Тб. Если функция 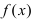
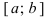
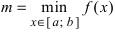
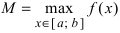
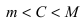
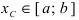
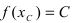
Пример:
Изобразить графики функций, удовлетворяющих условиям Тб (см. Рис. 67).
Рис. 67. Графики функций, удовлетворяющих условиям Тб.
Теорема: Если функция 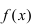
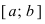
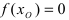
Пример:
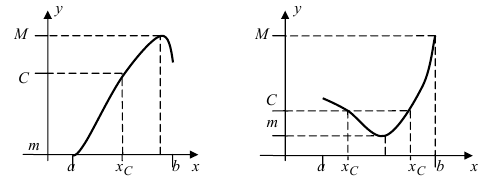
Изобразить графики функций, удовлетворяющих условиям теоремы(см. Рис. 68).
Рис. 68. Графики функций, удовлетворяющих условиям теоремы.
На графике а) существует единственная точка, в которой выполняются условия теоремы. На графиках б) и в) таких точек две и четыре, соответственно. Однако в случаях б) и в) для удовлетворения условий теоремы надо разбивать сегмент на отдельные отрезки.
- Точки разрыва и их классификация
- Дифференциальное исчисление
- Исследование функций с помощью производных
- Формула Тейлора и ее применение
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Замечательные пределы
Теорема Вейерштрасса о непрерывной функции на отрезке
30 декабря 2021
Теорема Вейерштрасса — фундаментальная теорема матанализа, которая состоит из двух частей:
- Теорема об ограниченности;
- Теорема о достижении максимума и минимума.
Сейчас мы сформулируем и докажем обе эти теоремы. Прежде всего дадим определения, на которые будем опираться:
Определение 1. Функция $fleft( x right)$ непрерывна в точке $x=a$, если $limlimits_{xto a}fleft( x right)=fleft( a right)$.
Определение 2. Функция $fleft( x right)$ непрерывна на интервале $left[ a;b right]$, если она непрерывна в каждой точке этого отрезка. При этом на концах отрезка речь идёт об односторонней непрерывности.
Всё это подробно разобрано в уроке про непрерывность функции в точке. Перейдём к теоремам.
1. Теорема Вейерштрасса об ограниченности функции
Теорема 1. (об ограниченности непрерывной функции) Функция, непрерывная на отрезке $left[ a;b right]$, ограничена на этом отрезке.
Другими словами, найдётся $Min mathbb{R}$ такое, что
[forall left( xin left[ a;b right] right)quad left| fleft( x right) right| lt M]
Приведу два доказательства — выбирайте то, которое больше нравится именно вам (или вашему преподу).
1.1. Доказательство методом Больцано
Предположим противное: пусть $fleft( x right)$ не ограничена на $left[ a;b right]$. Обозначим середину этого отрезка ${{c}_{1}}={left( a+b right)}/{2};$ и рассмотрим два новых отрезка:
[left[ a;{{c}_{1}} right]quad left[ {{c}_{1}};b right]]
Вместе эти отрезки покрывают отрезок $left[ a;b right]$. Следовательно, функция $fleft( x right)$ не ограничена как минимум на одном из них. Иначе если $fleft( x right)$ ограничена на обоих отрезках, то она будет ограничена и на из объединении, что противоречит нашему предположению.
Обозначим тот отрезок, на котором $fleft( x right)$ не ограничена, как ${{I}_{1}}=left[ {{a}_{1}};{{b}_{1}} right]$. Найдём середину этого отрезка ${{c}_{2}}={left( {{a}_{1}}+{{b}_{1}} right)}/{2};$. Вновь рассмотрим пару отрезков $left[ {{a}_{1}};{{c}_{1}} right]$ и $left[ {{c}_{1}};{{b}_{1}} right]$. Как минимум на одном из них функция $fleft( x right)$ будет не ограничена. Обозначим этот отрезок как ${{I}_{2}}=left[ {{a}_{2}};{{b}_{2}} right]$.
Проделаем эту операцию много раз. Получим последовательность стягивающихся отрезков:
[{{I}_{1}}supset {{I}_{2}}supset ldots supset {{I}_{n}}supset ldots ]
Длина отрезка ${{I}_{n}}$ равна $left| {{I}_{n}} right|=left| b-a right|cdot {{2}^{-n}}$ и стремится к нулю при $nto +infty $. По лемме о стягивающихся отрезках существует точка ${{x}_{0}}in mathbb{R}$ такая, что ${{x}_{0}}in {{I}_{n}}$ для любого $nin mathbb{N}$.
Кроме того, ${{x}_{0}}in left[ a;b right]$, поэтому функция $fleft( x right)$ непрерывна в т.ч. и в точке $x={{x}_{0}}$:
[limlimits_{xto {{x}_{0}}}fleft( x right)=fleft( {{x}_{0}} right)]
Вспомним определение предела функции в точке:
[begin{align} & limlimits_{xto {{x}_{0}}} fleft( x right)=fleft( {{x}_{0}} right)Rightarrow\ & forall left( varepsilon gt 0 right)quad exists left( delta =delta left( varepsilon right) gt 0 right): \ & xin {{overset{circ }{mathop{U}},}_{delta }}left( {{x}_{0}} right)Rightarrow left| fleft( x right)-fleft( {{x}_{0}} right) right| lt varepsilon\ end{align}]
Возьмём $varepsilon =1$. Следовательно, найдётся $delta =delta left( 1 right) gt 0$ такое, что в проколотой $delta $-окрестности точки ${{x}_{0}}$ выполняется условие $left| fleft( x right)-fleft( {{x}_{0}} right) right| lt 1$. Но тогда
[begin{align} left| fleft( x right) right|&=left| fleft( x right)-fleft( {{x}_{0}} right)+fleft( {{x}_{0}} right) right|le\ & le left| fleft( x right)-fleft( {{x}_{0}} right) right|+left| fleft( {{x}_{0}} right) right| lt \ & lt 1+left| fleft( {{x}_{0}} right) right| \ end{align}]
Получается, что внутри $delta $-окрестности функция ограничена числом $M=1+left| fleft( {{x}_{0}} right) right|$. Но поскольку $delta gt 0$ — фиксированное положительное число, а длины отрезков $left| {{I}_{n}} right|=left| b-a right|cdot {{2}^{-n}}$ стремятся к нулю, начиная с какого-то момента эти отрезки будут полностью лежать внутри этой $delta $-окрестности:
Мы даже можем приблизительно вычислить этот момент — достаточно потребовать, чтобы величина $delta $ оказалась больше длины $left| {{I}_{n}} right|$:
[begin{align} delta& gt left| b-a right|cdot {{2}^{-n}} \ {{2}^{n}} & gt {left| b-a right|}/{delta }; \ n& ge left[ {{log }_{2}}{left| b-a right|}/{delta }; right]+1 \ end{align}]
Здесь $left[ l right]$ следует понимать как «целая часть числа $l$» (подробнее об этом — в уроке «Что такое предел последовательности»).
Но тогда для всякого такого отрезка, полностью лежащего в $delta $-окрестности точки ${{x}_{0}}$, одновременно выполняется два условия:
- Функция $fleft( x right)$ ограничена на этом отрезке, потому что $left| fleft( x right) right| lt left| fleft( {{x}_{0}} right) right|+1$;
- Функция $fleft( x right)$ не ограничена на этом отрезке, потому что мы так выбрали ${{I}_{n}}$.
Получили противоречие. Следовательно, исходное предположение не верно. Теорема доказана.
1.2. Доказательство по Гейне
Рассмотрим более хитрое доказательство, которое опирается на теорема Больцано-Вейерштрасса о сходящейся подпоследовательности.
Итак, нужно доказать, что функция, непрерывная на отрезке $left[ a;b right]$, будет ограничена на этом отрезке. Вновь предположим, что это не так: пусть функция $fleft( x right)$ не ограничена, т.е.
[begin{align} & forall left( cin mathbb{R} right)quad exists left( xin left[ a;b right] right): \ & left| fleft( x right) right| gt c \ end{align}]
Рассмотрим натуральные значения $c$.
Пусть $c=1$. Тогда найдётся ${{x}_{1}}in left[ a;b right]$ такое, что $left| fleft( {{x}_{1}} right) right| gt 1$.
Пусть $c=2$. Тогда найдётся ${{x}_{2}}in left[ a;b right]$ такое, что $left| fleft( {{x}_{2}} right) right| gt 2$.
Продолжаем так много раз. Пусть $c=n$. Тогда найдётся ${{x}_{n}}in left[ a;b right]$ такое, что $left| fleft( {{x}_{n}} right) right| gt n$.
Получили последовательность $left{ {{x}_{n}} right}$, которая бесконечна и ограничена: $ale {{x}_{n}}le b$. По теореме Больцано-Вейерштрасса из неё можно выбрать сходящуюся подпоследовательность $left{ {{x}_{{{n}_{k}}}} right}$:
[limlimits_{kto +infty } {{x}_{{{n}_{k}}}}=xi ]
Но поскольку члены последовательности $ale {{x}_{{{n}_{k}}}}le b$, её предел $xi in left[ a;b right]$ (почему это так — смотрите свойства предела последовательности), и функция $fleft( x right)$, непрерывная на $left[ a;b right]$, будет непрерывна и в точке $x=xi $.
Согласно определению непрерывности функции по Гейне имеем
[limlimits_{kto +infty } fleft( {{x}_{{{n}_{k}}}} right)=fleft( xi right)]
С другой стороны, последовательность [left{ {{x}_{{{n}_{k}}}} right}] сконструирована таким образом, что
[left| fleft( {{x}_{{{n}_{k}}}} right) right| gt {{n}_{k}}ge k]
Но тогда предел
[limlimits_{kto +infty } fleft( {{x}_{{{n}_{k}}}} right)=infty ]
Получаем, что один и тот же предел одновременно равен и $fleft( xi right)in mathbb{R}$, и $infty notin mathbb{R}$. Чего не может быть, поскольку если предел существует, то он единственный.
Вновь получили противоречие. Следовательно, исходное предположение не верно. Теорема Вейерштрасса об ограниченности функции доказана.
1.3. Важное замечание
Эту теорему можно обобщить, рассмотрев вместо отрезка произвольный компакт.
С другой стороны, если вместо отрезка рассмотреть интервал (или любое другое открытое множество), то теорема будет не верна!
Пример 1. Функция $y= operatorname{tg}x$, где $xin left( -frac{pi }{2};frac{pi }{2} right)$.
Тангенс непрерывен в каждой точке указанного интервала, однако неограниченно возрастает при $xto {pi }/{2};$ и неограниченно убывает при $xto -{pi }/{2};$.
Принципиально важно, чтобы функция была определена на концах отрезка $left[ a;b right]$, т.е. принимала бы конкретные значения $fleft( a right)$ и $fleft( b right)$. И следовательно, была бы ограниченна в некоторой $delta $-окрестности этих концов.
2. Теорема Вейерштрасса о достижении максимума и минимума
В матанализе есть понятие локального максимума и минимума (смотрите раздел про производные), поэтому при формулировке теоремы Вейерштрасса лучше говорить о точной верхней грани и точной нижней грани значений функции на отрезке:
[suplimits_{xin left[ a;b right]}fleft( x right)quad inflimits_{xin left[ a;b right]}fleft( x right)]
Теорема 2. (о достижении точной верхней и нижней грани) Функция, непрерывная на отрезке $left[ a;b right]$, достигает своей точной верхней грани и точной нижней грани:
[begin{align} & exists left( {{x}_{1}}in left[ a;b right] right): & fleft( {{x}_{1}} right)=underset{xin left[ a;b right]}{mathop{sup }},fleft( x right) \ & exists left( {{x}_{2}}in left[ a;b right] right): & fleft( {{x}_{2}} right)=underset{xin left[ a;b right]}{mathop{inf }},fleft( x right) \ end{align}]
Докажем эту теорему только для точной верхней грани. Затем достаточно рассмотреть функцию $gleft( x right)=-fleft( x right)$ и заметить, что
[inflimits_{xin left[ a;b right]} fleft( x right)=-suplimits_{xin left[ a;b right]} gleft( x right)]
2.1. Доказательство для точной верхней грани
Пусть функция $fleft( x right)$ непрерывна на $left[ a;b right]$. Тогда по теореме Вейерштрасса об ограниченности, которую мы доказали выше, найдётся такое $Min mathbb{R}$, что
[forall left( xin left[ a;b right] right)quad left| fleft( x right) right| lt M]
Но тогда существует точная верхняя грань
[A=suplimits_{xin left[ a;b right]} fleft( x right)]
Докажем теорему от противного. Пусть $Ane fleft( x right)$ для любого $xin left[ a;b right]$. Тогда очевидно, что $A gt fleft( x right)$ при каждом $xin left[ a;b right]$.
Рассмотрим функцию $gleft( x right)=A-fleft( x right)$. Она непрерывна на отрезке $left[ a;b right]$. Кроме того для всякого $xin left[ a;b right]$
[gleft( x right)=A-fleft( x right) gt 0]
Следовательно, функция
[{{g}_{1}}left( x right)=frac{1}{gleft( x right)}=frac{1}{A-fleft( x right)} gt 0]
тоже непрерывна на отрезке $left[ a;b right]$ и принимает лишь положительные значения. Но тогда ${{g}_{1}}left( x right)$ ограничена на $left[ a;b right]$. Следовательно, найдётся число $B gt 0$ такое, что
[begin{align} left| {{g}_{1}}left( x right) right| & lt B \ 0 lt frac{1}{A-fleft( x right)}& lt B \ end{align}]
Но тогда
[begin{align} A-fleft( x right) & gt frac{1}{B} gt 0 \ fleft( x right) & lt A-frac{1}{B} \ end{align}]
Получается, что мы нашли верхнюю грань $A-{1}/{B};$, которая меньше точной верхней грани $A=suplimits_{xin left[ a;b right]} fleft( x right)$.
Но это противоречит определению точной меньшей грани. Следовательно, исходное предположение неверно. Теорема доказана.
Смотрите также:
- Теорема о промежуточном значении функции
- Непрерывность функции в точке
- Тест к уроку «Что такое логарифм» (средний)
- Тест к уроку «Площади многоугольников без координатной сетки» (средний)
- Как решать биквадратное уравнение
- Задача B4: экономика
Содержание:
- Непрерывность функции
- Непрерывность функции в точке
- Непрерывность функции в точке
- Задача пример №57
- Непрерывность функции на интервале
- Непрерывность функции на отрезке
- Задача пример №58
- Задача пример №59
- Задача пример №60
Непрерывность функции
Непрерывность функции часто можно легко объяснить следующим образом. Если график какой-либо функции можно построить не отрывая карандаш от бумаги, то эта функция непрерывна. В противном случае, у графика есть точки разрыва (скачка) и данная функция является разрывной функцией. График разрывной функции невозможно изобразить, не отрывая карандаш от листа.
Непрерывность функции в точке
Для того, чтобы функция была непрерывной в точке, ее график не должен прерываться, т.е. график не должен иметь «скачков». График функций на рисунках прерывается или имеет «скачок» в точке 



1. Функция не определена в точке 
2. В точке 

3. Предел функции 


Точка 
Если функция не удовлетворяет ни одному из указанных выше условий, то ее можно назвать непрерывной в точке 
Непрерывность функции в точке
Для того, чтобы функция 

1. Функция должна быть определена в точке 
2. Должен существовать предел 
3. Должно выполняться равенство 
Задача пример №57
Исследуйте непрерывность следующих функций.
Решение:
а) из графика функции 




Отметим, что во всех точках кроме 
b)
Как видно из графика, при стремлении значений 

Предел функции:
Значение функции: 




Непрерывность функции на интервале
Определение. Функция называется непрерывной на интервале 
Непрерывность функции на отрезке
Определение. Функция 




Любая функция — многочлен непрерывна на всей числовой оси. Рациональная функция непрерывна во всех точках, кроме тех, которые обращают знаменатель в 0. Функции 

Для функции, непрерывной на отрезке, справедлива следующая теорема.
Теорема Вейерштрасса. Функция, непрерывная на отрезке, принимает в нем наименьшее и наибольшее значения.
Теорема Коши. Если функция 


Следствие. Функция, непрерывная на отрезке, принимает все значения от наименьшего до наибольшего.
Применяя эту теорему, можно решить следующий тип задач.
Задача пример №58
Существует ли такое действительное число, куб которого больше самого числа на 1?
Решение:
искомое число 










Если какая-либо функция непрерывна на интервале 

Задача пример №59
Исследуйте непрерывность функции
Решение:
как видно из графика, при стремлении 
Т.е. в точке 



Задача пример №60
Определите точки разрыва функции
Решение: Линейная функция 





Сначала исследуем непрерывность функции в точке 
1. Значение функции. Функция определена в точке 

2. Существование предела. Для определения предела 






3. Значение и предел функции в точке. Так как 


Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:
Другие темы которые вам помогут понять математику:
|
|
|
|
Лекции:
- Теорема о разложении на множители
- Экстремум функции многих переменных
- Пределы в математике
- Дифференциал функции
- Объемы подобных фигур
- Непрерывность функции
- Интервал сходимости степенного ряда
- Уравнение прямой через две точки
- Круги Эйлера фигуры, условно изображающие множества
- Тригонометрические комплексные числа
Функция, непрерывная во всех точках некоторой области,
называется непрерывной в этой области.
Функция $f(x)$ называется непрерывной справа в
точке $alpha$, если
$f(a+0)=lim _{x rightarrow a+0} f(x)=f(a)$ .
Функция $f(x)$ называется непрерывной слева в
точке $alpha$, если
$f(a+0)=lim _{x rightarrow a-0} f(x)=f(a)$ .
Функция $y=f(x)$ называется непрерывной в
интервале $(a;b)$, если она непрерывна в каждой
точке этого интервала.
Функция $y=f(x)$ называется непрерывной на отрезке
$[a;b]$, если она является непрерывной в интервале
$(a;b)$, непрерывной справа в точке
$alpha$, то есть
$f(a+0)=f(a)$ и непрерывной слева в точке
$b$, то есть
$f(b-0)=f(b)$ .



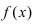
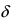 -окрестности;
-окрестности;