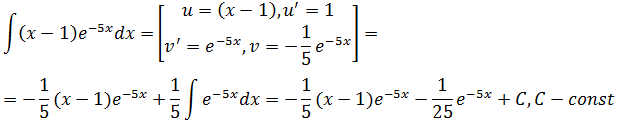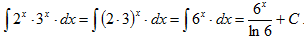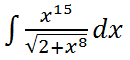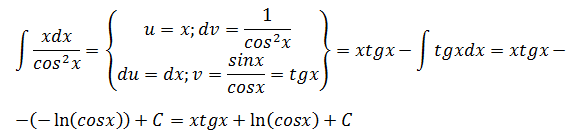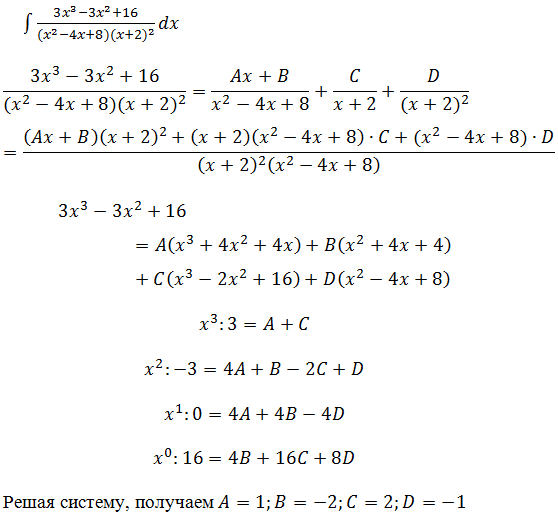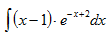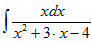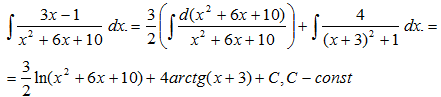Как найти неопределенный интеграл xdx - AvtoShod.ru

Первообразная (неопределенный интеграл)

Ранее мы по заданной функции, руководствуясь различными формулами и правилами, находили ее производную. Производная имеет
многочисленные применения: это скорость движения (или, обобщая, скорость протекания любого процесса); угловой коэффициент касательной
к графику функции; с помощью производной можно исследовать функцию на монотонность и экстремумы; она помогает решать задачи на
оптимизацию.

Но наряду с задачей о нахождении скорости по известному закону движения встречается и обратная задача — задача о восстановлении
закона движения по известной скорости. Рассмотрим одну из таких задач.

Пример 1. По прямой движется материальная точка, скорость ее движения в момент времени t задается формулой v=gt. Найти
закон движения.
Решение. Пусть s = s(t) — искомый закон движения. Известно, что s'(t) = v(t). Значит, для решения задачи нужно подобрать функцию
s = s(t), производная которой равна gt. Нетрудно догадаться, что ( s(t) = frac{gt^2}{2} ). В самом деле
( s'(t) = left( frac{gt^2}{2} right)’ = frac{g}{2}(t^2)’ = frac{g}{2} cdot 2t = gt )
Ответ: ( s(t) = frac{gt^2}{2} )

Сразу заметим, что пример решен верно, но неполно. Мы получили ( s(t) = frac{gt^2}{2} ). На самом деле задача имеет бесконечно
много решений: любая функция вида ( s(t) = frac{gt^2}{2} + C ), где C — произвольная константа, может служить законом движения,
поскольку ( left( frac{gt^2}{2} +C right)’ = gt )

Чтобы задача стала более определенной, нам надо было зафиксировать исходную ситуацию: указать координату движущейся точки в
какой-либо момент времени, например при t = 0. Если, скажем, s(0) = s₀, то из равенства s(t) = (gt²)/2 + C
получаем: s(0) = 0 + С, т. е. C = s₀. Теперь закон движения определен однозначно: s(t) = (gt²)/2 + s₀.

В математике взаимно обратным операциям присваивают разные названия, придумывают специальные обозначения, например:
возведение в квадрат (х²) и извлечение квадратного корня ( ( sqrt{x} ) ), синус (sin x) и арксинус (arcsin x) и т. д.
Процесс нахождения производной по заданной функции называют дифференцированием, а обратную операцию, т. е. процесс нахождения
функции по заданной производной, — интегрированием.

Сам термин «производная» можно обосновать «по-житейски»: функция у = f(x) «производит на свет» новую функцию у’ = f'(x).
Функция у = f(x) выступает как бы в качестве «родителя», но математики, естественно, не называют ее «родителем» или «производителем»,
они говорят, что это, по отношению к функции у’ = f'(x), первичный образ, или первообразная.

Определение. Функцию y = F(x) называют первообразной для функции y = f(x) на промежутке X, если для ( x in X )
выполняется равенство F'(x) = f(x)

На практике промежуток X обычно не указывают, но подразумевают (в качестве естественной области определения функции).

Приведем примеры.
1) Функция у = х² является первообразной для функции у = 2х, поскольку для любого х справедливо равенство
(x²)’ = 2х
2) Функция у = х³ является первообразной для функции у = 3х², поскольку для любого х справедливо равенство
(x³)’ = 3х²
3) Функция у = sin(x) является первообразной для функции y = cos(x), поскольку для любого x справедливо равенство
(sin(x))’ = cos(x)

При нахождении первообразных, как и производных, используются не только формулы, но и некоторые правила. Они непосредственно
связаны с соответствующими правилами вычисления производных.

Мы знаем, что производная суммы равна сумме производных. Это правило порождает соответствующее правило нахождения первообразных.

Правило 1. Первообразная суммы равна сумме первообразных.

Мы знаем, что постоянный множитель можно вынести за знак производной. Это правило порождает соответствующее правило нахождения первообразных.

Правило 2. Если F(x) — первообразная для f(x), то kF(x) — первообразная для kf(x).

Теорема 1. Если y = F(x) — первообразная для функции y = f(x), то первообразной для функции у = f(kx + m) служит функция
( y=frac{1}{k}F(kx+m) )

Теорема 2. Если y = F(x) — первообразная для функции y = f(x) на промежутке X, то у функции у = f(x) бесконечно много
первообразных, и все они имеют вид y = F(x) + C.

Методы интегрирования

Метод замены переменной (метод подстановки)

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом
заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора
подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть требуется вычислить интеграл ( textstyle int F(x)dx ). Сделаем подстановку ( x= varphi(t) ) где
( varphi(t) ) — функция, имеющая непрерывную производную.
Тогда ( dx = varphi ‘ (t) cdot dt ) и на основании свойства инвариантности формулы интегрирования неопределенного интеграла
получаем формулу интегрирования подстановкой:
( int F(x) dx = int F(varphi(t)) cdot varphi ‘ (t) dt )

Интегрирование выражений вида ( textstyle int sin^n x cos^m x dx )

Если m нечётное, m > 0, то удобнее сделать подстановку sin x = t.
Если n нечётное, n > 0, то удобнее сделать подстановку cos x = t.
Если n и m чётные, то удобнее сделать подстановку tg x = t.

Интегрирование по частям

Интегрирование по частям — применение следующей формулы для интегрирования:
( textstyle int u cdot dv = u cdot v — int v cdot du )
или:
( textstyle int u cdot v’ cdot dx = u cdot v — int v cdot u’ cdot dx )

Таблица неопределённых интегралов (первообразных) некоторых функций

$$ int 0 cdot dx = C $$

$$ int 1 cdot dx = x+C $$

$$ int x^n dx = frac{x^{n+1}}{n+1} +C ;; (n neq -1) $$

$$ int frac{1}{x} dx = ln |x| +C $$

$$ int e^x dx = e^x +C $$

$$ int a^x dx = frac{a^x}{ln a} +C ;; (a>0, ;; a neq 1) $$

$$ int cos x dx = sin x +C $$

$$ int sin x dx = -cos x +C $$

$$ int frac{dx}{cos^2 x} = text{tg} x +C $$

$$ int frac{dx}{sin^2 x} = -text{ctg} x +C $$

$$ int frac{dx}{sqrt{1-x^2}} = text{arcsin} x +C $$

$$ int frac{dx}{1+x^2} = text{arctg} x +C $$

$$ int text{ch} x dx = text{sh} x +C $$

$$ int text{sh} x dx = text{ch} x +C $$

Источник

Пример 1:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 2:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 3:

Найти неопределенный интеграл:

Решение от преподавателя:

Пример 4:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 5:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 6:

Вычислить интеграл:

Решение от преподавателя:

Пример 7:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 8:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 9:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Для вычисления был использован табличный интеграл

Пример 10:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 11:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 12:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 13:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 14:

Вычислить интеграл:

Решение от преподавателя:

Пример 15:

Вычислить неопределенный интреграл:

Решение от преподавателя:

Пример 16:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 17:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Интегралы вида

где m, n, p — рациональные числа (целые или дробные), называются интегралами от дифференциального бинома. В примерах мы увидим, что в подынтегральных выражениях переменная икс присутствует не только под корнем: она под корнем, но ещё и в степени. В этом главное отличие рассматриваемых интегралов от тех, которые были рассмотрены в первом параграфе.

Чтобы найти такие интегралы, используются подстановки Чебышева.

1. Если p — целое число, то используется подстановка

где k — наименьшее общее кратное знаменателей m и n.

2. Если — целое число, то используется подстановка

где s — знаменатель дроби p.

3. Если — целое число, то используется подстановка

где s — знаменатель дроби p.

Определим для нашей функции.

m = -2; p = ; n = 2

p = – не целое
– не целое
– не целое.

Вывод: использовать подстановки нельзя

Это четвертый случай. Такой интеграл является не берущимся.

Пример 18:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 19:

Вычислить неопределенный интерграл:

Решение от преподавателя:

Приравняем числители и учтем, что коэффициенты при одинаковых степенях x, стоящие слева и справа должны совпадать:

Пример 20:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 21:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 22:

Вычислить интеграл:

Решение от преподавателя:

Пример 23:

Найти неопределенный интеграл

Решение от преподавателя:

Пример 24:

Вычислить неопределенный интеграл:

Решение от преподавателя:

$https://chart.googleapis.com/chart?cht=tx&chl=intlimits_%7b%7d%5e%7b%7d%7b(frac%7b6cdot%20x%2B1%7d%7bsqrt%7bx%5e%7b2%7d%2B2cdot%20x%2B10%7d%7d)%7d%20dx$
Представим подынтегральное выражение в виде:
$https://chart.googleapis.com/chart?cht=tx&chl=intlimits_%7b%7d%5e%7b%7d%7bfrac%7b6*x%2B1%7d%7bsqrt%7bx%5e%7b2%7d%2B2*x%2B10%7d%7d%7d%20dx$ = $https://chart.googleapis.com/chart?cht=tx&chl=%5e%7b%7d%7bfrac%7bd(x%5e%7b2%7d%2B2*x%2B10)%7d%7bsqrt%7bx%5e%7b2%7d%2B2*x%2B10%7d%7d%7d$ + $https://chart.googleapis.com/chart?cht=tx&chl=%5e%7b%7d%7bfrac%7b-5%7d%7bsqrt%7bx%5e%7b2%7d%2B2*x%2B10%7d%7d%7d$ dx
Представляя выражение x^2+2*x+10 как переменную t, получаем:

Выделим полные квадраты:

Вычисляем табличный интеграл вида:
$https://chart.googleapis.com/chart?cht=tx&chl=intlimits_%7b%7d%5e%7b%7d%7bfrac%7bdx%7d%7bsqrt%7bx%5e%7b2%7d%20%20pm%20%20a%5e%7b2%7d%7d%7d%7d%20=%20ln(x%2Bsqrt%7bx%5e%7b2%7d%20%20pm%20%20a%5e%7b2%7d%7d)%2BC$
$https://chart.googleapis.com/chart?cht=tx&chl=-5%20intlimits_%7b%7d%5e%7b%7d%7bfrac%7b1%7d%7bsqrt%7b(x%2B1)%5e%7b2%7d%2B3%5e%7b2%7d%7d%7d%7d%20dx%20=%20-5ln(x%2B1%2Bsqrt%7b(x%2B1)%5e%7b2%7d%2B9%7d)$
$https://chart.googleapis.com/chart?cht=tx&chl=intlimits_%7b%7d%5e%7b%7d%7b(frac%7b6cdot%20x%2B1%7d%7bsqrt%7bx%5e%7b2%7d%2B2cdot%20x%2B10%7d%7d)%7d%20dx$ =

Пример 25:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 26:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 27:

Найти неопределённый интеграл:

Решение от преподавателя:

Пример 28:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 29:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 30:

Найти неопределенный интеграл:

Решение от преподавателя:

Пример 31:

Найти неопределённый интеграл:

Решение от преподавателя:

Пример 32:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 33:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 34:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 35:

Найти неопределенный интеграл:

Решение от преподавателя:

Пример 36:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 37:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 38:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 39:

Найти неопределенный интеграл:

Решение от преподавателя:

Пример 40:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 41:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 42:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 43:

Найти неопределенный интеграл:

Решение от преподавателя:

Пример 44:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 45:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 46:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 47:

Найти неопределенный интеграл:

Решение от преподавателя:

Используем метод разложения на простейшие. Разложим функцию на простейшие слагаемые:
$https://chart.googleapis.com/chart?cht=tx&chl=frac%7b-2x%2B4%7d%7bx(x%2B4)%7d%20=%20frac%7bA%7d%7bx%7d%20%2B%20frac%7bB%7d%7bx%2B4%7d%20=%20frac%7bA(x%2B4)%20%2B%20Bx%7d%7bx(x%2B4)%7d$
Приравняем числители и учтем, что коэффициенты при одинаковых степенях x, стоящие слева и справа должны совпадать:
-2x+4 = A(x+4) + Bx
x: A + B = -2
1: 4A = 4
Решая ее, находим:
A = 1;B = -3;
$https://chart.googleapis.com/chart?cht=tx&chl=frac%7b-2x%2B4%7d%7bx(x%2B4)%7d%20=%20frac%7b1%7d%7bx%7d%20%2B%20frac%7b-3%7d%7bx%2B4%7d$
Вычисляем табличный интеграл:
$https://chart.googleapis.com/chart?cht=tx&chl=%20intlimits_%7b%7d%5e%7b%7d%7bfrac%7b1%7d%7bx%7d%20dx%7d%20=%20ln(x)$
Вычисляем табличный интеграл:
$https://chart.googleapis.com/chart?cht=tx&chl=-3%20intlimits_%7b%7d%5e%7b%7d%7bfrac%7b1%7d%7bx%2B4%7d%20dx%7d%20=%20-3cdot%20ln(x%2B4)$
Ответ:
$https://chart.googleapis.com/chart?cht=tx&chl=intlimits_%7b%7d%5e%7b%7d%7bfrac%7b-2cdot%20x%2B4%7d%7bx%5e%7b2%7d%2B4cdot%20x%7d%7d%20dx$ =ln(x)-3ln(x+4) + C

Пример 48:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 49:

Найти неопределенный интеграл:

Решение от преподавателя:

Пример 50:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 51:

Найти неопределенный интеграл:

Решение от преподавателя:

Пример 52:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 53:

Найти неопределенный интеграл:

Решение от преподавателя:

Пример 54:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 55:

Найдите неопределенный интеграл:

Решение от преподавателя:

Пример 56:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 57:

Найти неопределенный интеграл:

Решение от преподавателя:

Пример 58:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 59:

Найдите неопределенный интеграл:

Решение от преподавателя:

Пример 60:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 61:

Найти неопределенный интеграл:

Решение от преподавателя:

Пример 62:

Найти неопределенные интегралы методом подстановки:

Решение от преподавателя:

Пример 63:

Найдите неопределенный интеграл:

Решение от преподавателя:

Пример 64:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 65:

Найти неопределенный интеграл:

Решение от преподавателя:

Пример 66:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 67:

Найдите неопределенный интеграл:

Решение от преподавателя:

Пример 68:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 69:

Найти неопределенный интеграл:

Решение от преподавателя:

Пример 70:

Найти интегралы методом интегрирования по частям:

Решение от преподавателя:

Пример 71:

Найти неопределенный интеграл:

Решение от преподавателя:

Пример 72:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 73:

Найти неопределенный интеграл:

Решение от преподавателя:

Пример 74:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 75:

Вычислить:

Решение от преподавателя:

Пример 76:

Найти неопределенные интегралы:

Решение от преподавателя:

Пример 77:

Вычислить:

Решение от преподавателя:

Пример 78:

Найти интегралы от рациональных функций:

Решение от преподавателя:

Пример 79:

Вычислить следующий интеграл:

Решение от преподавателя:

Пример 80:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 81:

Вычислить следующий интеграл:

Решение от преподавателя:

Пример 82:

Вычислить интеграл:

Решение от преподавателя:

Пример 83:

Вычислить следующий интеграл:

Решение от преподавателя:

Пример 84:

Найти неопределенные интегралы:

Решение от преподавателя:

Пример 85:

Вычислить следующий интеграл:

Решение от преподавателя:

Пример 86:

Найти интеграл от рациональной функций:

Решение от преподавателя:

Пример 87:

Вычислить следующий интеграл:

Решение от преподавателя:

Пример 88:

Вычислить интеграл:

Решение от преподавателя:

Пример 89:

Вычислить следующий интеграл:

Решение от преподавателя:

Пример 90:

Вычислить интеграл:

Решение от преподавателя:

Пример 91:

Вычислить следующий интеграл:

Решение от преподавателя:

Пример 92:

Вычислить неопределенные интегралы:

Решение от преподавателя:

Пример 93:

Вычислить:

Решение от преподавателя:

Пример 94:

Вычислить неопределённый интеграл.

Решение от преподавателя:

Пример 95:

Вычислить:

Решение от преподавателя:

Пример 96:

Вычислить интеграл:

Решение от преподавателя:

Пример 97:

Вычислить:

Решение от преподавателя:

Пример 98:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 99:

Вычислить:

Решение от преподавателя:

Пример 100:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 101:

Вычислить:

Решение от преподавателя:

Пример 102:

Вычислить неопределённый интеграл.

Решение от преподавателя:

Пример 103:

Вычислить интеграл:

Решение от преподавателя:

Пример 104:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 105:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 106:

Вычислить неопределённый интеграл.

Решение от преподавателя:

Пример 107:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 108:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 109:

Вычислить неопределённый интеграл.

Решение от преподавателя:

Пример 110:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 111:

Вычислить неопределенный интеграл:

Решение от преподавателя:

Пример 112:

Вычислить неопределенные интегралы:

Решение от преподавателя:

Пример 113:

Вычислить неопределенные интегралы:

Решение от преподавателя:

Пример 114:

Вычислить неопределенные интегралы:

Решение от преподавателя:

Пример 115:

Вычислить неопределенные интегралы:

Решение от преподавателя:

Пример 116:

Вычислить неопределенные интегралы:

Решение от преподавателя:

Пример 117:

Найти неопределенный интеграл.

Решение от преподавателя:

Пример 118:

Найти неопределённый интеграл.

Решение от преподавателя:

Пример 119:

Найти неопределённый интеграл.

Решение от преподавателя:

Пример 120:

Найти неопределённый интеграл.

Решение от преподавателя:

Пример 121:

Найти неопределённый интеграл.

Решение от преподавателя:

Пример 122:

Найти неопределённый интеграл.

Решение от преподавателя:

Пример 123:

Найти неопределённый интеграл.

Решение от преподавателя:

Пример 124:

Найти неопределённый интеграл.

Решение от преподавателя:

Пример 125:

Найти неопределённый интеграл.

Решение от преподавателя:

Пример 126:

Найти неопределённый интеграл.

Решение от преподавателя:

Пример 127:

Найти неопределённый интеграл:

Решение от преподавателя:

Источник

Элементарно.

f’*dX=X*dX=X*X/2+C, Если решать графически, то еще проще, рисуешь Y=X и получаешь как бы треугольник, гипотенуза это f’=Y, а значения по ординате и абсцисс — X, но так как X=Y, то получается значения ординаты и абсцисс равны, по определению интеграл это площадь под графиком кривой, т.е. под f’, значит осталось ток и найти площадь треугольника, который прямоугольный, т.к. Y перпендикулярна X. Площадь прямоугольного треугольника по определению равна A*B/2=A*A/2, т.к. у нас катеты равны, но не забываем добавляем C, потому что не в частном случаи имело быть место сдвигу вдоль оси Y, ибо треугольник необязательно проходит через точку (x=0,y=0) и (x=A,y=A) (данное свойство связано с системой координат, мы как бы знаем характер кривой, но не знаем к какому — началу координат она привязана и что бы площадь была верно найдена, переписываем уравнение A*A/2+С1*X или иначе A*A/2+C1*X=X*X/2+C1*X=X*(X/2+C1)=X*X/2+C. Если все же считать, что f’=y=x и проходит через (x=0,y=0) на интервале вдоль оси X (0…X=A), то получаем X*dX=X*X/2, однако это возможно только при условии определенности границ интегрирования, если же не известно ни начала ни конца, то это не верно!

Источник