Как найти нейтральный элемент примеры - AvtoShod.ru

Тема: Найдите нейтральный элемент (Прочитано 3219 раз)

0 Пользователей и 1 Гость просматривают эту тему.

Как найти нейтральный элемент для следующей операции *
х*у = ху+7х+7у+42

Знаю, что нейтральный элемент — это элемент Е удовлетворяющий условию А*Е=Е*А=А
Ну и как же найти этот нейтральный элемент?

« Последнее редактирование: 24 Мая 2011, 23:35:43 от NELL »

Не знаком с нейтральными элементами, но хорошо знаю алгебру. Чтобы выполнялось тождество, должно быть: 7х+7у+42=0 и, следовательно,
y=-x-6

За жизнью надо тщательно следить, все время избегая с ней разлуки.

xy сокращаются и остается 7х+7у+42=0. Отсюда y=-x-6

За жизнью надо тщательно следить, все время избегая с ней разлуки.

нееет! Вы не поняли.

В условии дается такая бинарная операция » * » (умножения), которая определяется выражением
х*у = ху+7х+7у+42

т.е. х * у — это не такое обычное умножение, а это операция, которая определяется этим вот большим выражением

« Последнее редактирование: 25 Мая 2011, 02:03:00 от NELL »

Тишина…

ex=e*x+7x+7e+42=x
e(x+7)=-42-6x
e = -(42+6x)/(x+7)
e = -6(x+7)/(x+7)
e = -6

Ого! Спасибо большое!

Источник

Нейтра́льный элеме́нт бинарной операции — это элемент, который оставляет любой другой элемент неизменным при применении к ним этой бинарной операции.

Содержание

1 Определение
2 Замечания
3 Примеры
4 См. также

Определение

Пусть — множество с определённой на нём бинарной операцией . Элемент называется нейтральным относительно , если

{displaystyle xcdot e=ecdot x=x,quad forall xin M.}

Иногда различают нейтральный слева элемент ${displaystyle e_{mathrm {l} }}$ , для которого

${displaystyle e_{mathrm {l} }cdot x=x,quad forall xin M,}$

и нейтральный справа элемент ${displaystyle e_{mathrm {r} }}$ , для которого

${displaystyle xcdot e_{mathrm {r} }=x,quad forall xin M.}$

Замечания

Если существует только левый или только правый нейтральный элемент, то в общем случае их может быть больше одного. Если одновременно существуют левый и правый нейтральный элементы, то они совпадают.

В приведённой выше мультипликативной нотации нейтральный элемент принято называть «единицей». Если для обозначения операции используется аддитивная нотация , то нейтральный элемент называют «нулём».

Примеры

Множество	Бинарная операция	Нейтральный элемент
Вещественные числа	(сложение)	0
Вещественные числа		1
Вещественные числа	${displaystyle a^{b}}$ (возведение в степень)	1 (нейтральный справа)
Матрицы размера	(матричное сложение)	нулевая матрица
Матрицы размера	(матричное произведение)	единичная матрица
Функции вида	(композиция функций)	Тождественное отображение
Функции вида	* (свёртка)	(дельта-функция)
Символьные строки	конкатенация	пустая строка
Расширенная числовая прямая	или
Расширенная числовая прямая	или
Подмножества множества	(пересечение множеств)
Множества	(объединение множеств)	(пустое множество)
Булева логика	(логическое и)	(истина)
Булева логика	(логическое или)	(ложь)

См. также

Обратный элемент;
Моноид;
Группа.

ar:عنصر حيادي
bg:Неутрален елемент
ca:Element neutre
cs:Neutrální prvek
et:Ühikelement
he:איבר יחידה
hu:Neutrális elem
lmo:Elemeent néutar
nl:Neutraal element
pl:Element neutralny
simple:Identity element
sk:Neutrálny prvok
sl:Nevtralni element
sr:Неутрал
sv:Neutralt element
uk:Нейтральний елемент
vi:Phần tử đơn vị
yi:נאטוראלע עלעמענט

Источник

Нейтральный элемент

Материал из Большого Справочника

Нейтра́льный элеме́нт бинарной операции — элемент, который оставляет любой другой элемент неизменным при применении этой бинарной операции к этим двум элементам.

Содержание

1 Определение
2 Примеры
3 Терминология
- 3.1 В алгебре
- 3.2 В теории решёток
4 См. также
5 Ссылки

Определение

Пусть — множество с определённой на нём бинарной операцией « cdot ». Элемент ein M называется нейтральным относительно cdot (умножения), если

В случаях некоммутативных операций, вводят левый нейтральный элемент ${displaystyle e_{mathrm {l} }}$ , для которого

${displaystyle e_{mathrm {l} }cdot x=x,quad forall xin M}$

и правый нейтральный элемент ${displaystyle e_{mathrm {r} }}$ , для которого

${displaystyle xcdot e_{mathrm {r} }=x,quad forall xin M}$

В общем случае может существовать произвольное количество элементов, нейтральных слева или справа. Если одновременно существуют и нейтральный слева элемент $e_{{{mathrm l}}}$ , и нейтральный справа элемент $e_{{{mathrm r}}}$ , то они обязаны совпадать (так как $e_{{{mathrm r}}}=e_{{{mathrm l}}}cdot e_{{{mathrm r}}}=e_{{{mathrm l}}}$ ).

Примеры

Множество	Бинарная операция	Нейтральный элемент
Вещественные числа	(сложение)	число 0
Вещественные числа	(умножение)	число 1
Вещественные числа	(вычитание)	число 0 (нейтральный справа)
Вещественные числа	$a^{b}$ (возведение в степень)	число 1 (нейтральный справа)
Расширенная числовая прямая	(деление)	число 1 (нейтральный справа)
Векторное пространство	(сложение векторов)	(нуль-вектор)
Матрицы размера	(матричное сложение)	нулевая матрица
Матрицы размера	(матричное произведение)	единичная матрица
Функции вида	(композиция функций)	тождественное отображение
Символьные строки	конкатенация	пустая строка
Расширенная числовая прямая	(минимум) или (инфимум)
Расширенная числовая прямая	(максимум) или (супремум)
Подмножества множества	(пересечение множеств)
Множества	(объединение множеств)	(пустое множество)
Исчисление высказываний	(конъюнкция)	(истина)
Исчисление высказываний	(дизъюнкция)	(ложь)

Терминология

В алгебре

В приведённой в определении мультипликативной нотации нейтральный элемент принято называть единичным элементом или просто единицей по аналогии с одноимённым числом. См. статью «единица (алгебра)» о двусторонних нейтральных элементах умножения в кольцах, полях, и алгебрах над ними.

Если речь идёт о нейтральном элементе операции, обозначаемой (и называемой) сложением, то нейтральный элемент называют нулём, опять-таки по аналогии с одноимённым числом. Сложением называют не только операцию в теории колец и линейной алгебре, но и (иногда) групповую операцию в абелевых группах.

В теории решёток

В теории решёток нейтральный элемент операции «∨» обозначается «0», а нейтральный элемент операции «∧» обозначается «1».

См. также

Обратный элемент
Моноид
Группа

Ссылки

Куликов Л.Я. Алгебра и теория чисел: Учеб. пособие для педагогических институтов. — М.: Высш. школа, 1979. — 559 с. стр 77 «Нейтральные элементы»
http://www.algebraical.info/doku.php?id=glossary:element:groupoid:identity (рус.)
http://mathforum.org/library/drmath/view/56032.html (рус.)
https://brilliant.org/identity-element/ (англ.)
Weisstein, Eric W. «Identity Element.» From MathWorld—A Wolfram Web Resource (англ.)

Источник

Нейтральные элементы

Пусть

— бинарная операция на непустом множестве
А.

def.
Элемент е
из А
называется левым
нейтральным относительно
операции

,
если для любого а
из А
выполняется равенство е

а
= а.

def.
Элемент е
из А
называется правым
нейтральным относительно
операции

,
если для любого а
из А
имеем а

е
= а.

def.
Элемент е
из А
называется нейтральным
относительно
операции

,
если для любого элемента а
из А
верны равенства e

a
= a
= a

Теорема 1.
Если нейтральный элемент относительно
операции

существует, то он единственен.

Доказательство.

Следствие.
Если нейтральный элемент относительно
операции

существует, то все левые и правые
нейтральные элементы относительно

с ним совпадают.

Примеры.

1) Число 0 есть
нейтральный элемент относительно
сложения целых чисел. Число 1 есть
нейтральный элемент относительно
умножения целых чисел.

2) На множестве
Р(М)
относительно

нейтральный ;
относительно

нейтральный P(M).

Симметричные элементы

Пусть

– бинарная операция на множестве А,
обладающая нейтральным элементом е.

def.
Элемент v
из А
называется левым
симметричным
к элементу а

А
относительно операции

,
если v

a
= e.

def.
Элемент v
из А
называется правым
симметричным
к а
относительно операции

,
если а

v
= е.

def.
Элемент а’

А
называется симметричным
к элементу а

А относительно
операции

,
если а

a’
= е
= a’
a.
В этом случае элемент а
называется симметризуемым,
а элементы а
и а’
– взаимно
симметричными.

Примеры.

1) Относительно
сложения целых чисел симметричным к
данному целому числу является то же
число, взятое со знаком «минус».

2) Относительно
умножения рациональных чисел симметричным
к нулевому числу а
является

;
число нуль не имеет симметричного
относительного умножения.

Теорема 2.
Если операция

ассоциативна и элемент a
симметризуем, то существует единственный
элемент, симметричный к а.

Доказательство.

Следствие.
Если элемент a
имеет симметричный элемент а’
относительно ассоциативной операции

,
то все левые и все правые симметричные
к а
элементы совпадают с элементом а’.

Аддитивная и мультипликативная форма записи

Наиболее часто
используется аддитивная и мультипликативная
формы записи бинарной операции. При
аддитивной форме записи бинарную
операцию

называют сложением
и пишут а
+ b
вместо a

b,
называя элемент a
+ b
суммой
a
и b.
Элемент, симметричный элементу а,
обозначают (-а)
и называют противоположным
элементу а.
Нейтральный элемент относительно
сложения обозначают символом 0 и называют
нулевым
элементом
относительно сложения. При аддитивной
записи свойства ассоциативности и
коммутативности записывается в виде

a
+ (b
+ c)
= (a
+ b)
+ c,
a
+ b
= b
+ a.

При мультипликативной
форме записи бинарную операцию называют
умножением
и пишут a

b
(вместо а

b),
называется элемент a

b
произведением
а
и b.
Элемент, симметричный а,
обозначают а^-1
и называют обратным
элементу а.
Нейтральный элемент относительно
умножения обозначают через e
и 1 и называют единичным
элементом
или единицей
относительно умножения.
При мультипликативной записи свойства
ассоциативности и коммутативности
записываются в виде a

c)=(a

c,
a

b
= b

Свойство
дистрибутивности умножения относительно
сложения записываются в виде (a
+ b)

c
= a

c
+ b

c,
c

(a
+ b)
= c

a
+ c

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

то элемент называется
нейтральным относительно данной операции (другое название – единичный
элемент).

Примеры.

1. Число 1 является
нейтральным элементом множества относительно
операции умножения.

2. Матрица 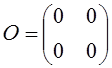— нейтральный элемент множества всех
матриц второго порядка относительно операции сложения матриц.

3. Множество натуральных
чисел не имеет нейтрального элемента относительно операции, задаваемой формулой
, т.к. иначе для некоторого числа и любого выполнялись
бы равенства: и , что
невозможно.

Эти примеры показывают, что может существовать один
нейтральный элемент и что нейтрального элемента может не быть вовсе.
Оказывается, других возможностей нет, т.е. не может быть более одного
нейтрального элемента.

Доказательство:

Пусть и — два нейтральных элемента относительно
операции *. Тогда (т.к —
нейтральный элемент), и (т.к — нейтральный элемент), откуда .

Пусть теперь множество содержит
нейтральный элемент относительно некоторой бинарной
операции *. Элемент называется правым обратным
для элемента , если ,
элемент называется левым обратным для , если . Если
операция ассоциативна, то левый и правый обратные элементы совпадают.

Доказательство:

(2)

(3)

Умножим равенство (2) слева на :

По ассоциативности: ,

из (3) следует: , но , а , значит
.

Таким образом, в случае ассоциативной операции можно
говорить просто об обратном элементе.

Обозначение: . Ясно, что .

Примеры.

1. Рассмотрим операцию умножения на множестве действительных чисел. Нейтральный элемент
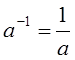
– число 1. Если , то обратный элемент существует. Для числа 0 обратного нет.
Если рассматривать операцию умножения только на множестве положительных действительных чисел, то все
элементы будут иметь обратные.

2. Множество с
операцией сложения. Каждый элемент имеет обратный, равный .

3. Множество квадратных матриц второго порядка с
операцией матричного умножения. Каждая невырожденная матрица обладает обратной,
а для вырожденной матрицы обратной не существует.

Рассмотренные примеры показывают, что некоторые элементы
обладают обратными, но могут существовать и элементы, не имеющие обратных.
Естественно возникает вопрос: может ли какой-нибудь элемент обладать
несколькими обратными? В рассмотренных примерах все элементы имели не более
одного обратного, и это не случайно, т.к справедливо утверждение:

Если операция ассоциативна, то никакой элемент не может
иметь более одного обратного.

Доказательство:

Пусть и — обратные элементы для элемента . Тогда и (совпадение левого и правого обратных уже
доказано).

Теперь получаем:

Подгруппы

Пусть множество является
группой относительно некоторой бинарной операции. Подмножество множества , являющееся группой относительно той же
операции, называется подгруппой группы .

Непосредственно из определения следует, что всякая группа
является своей подгруппой, и что множество, состоящее из одного элемента –
единицы группы, также будет ее подгруппой. У группы могут быть и другие
подгруппы. Подгруппа называется собственной,
если и .

Примеры.

1. Множество положительных рациональных чисел является группой относительно операции
умножения и поэтому подгруппой мультипликативной группы положительных
действительных чисел.

2. Множество целых чисел , будучи
группой относительно сложения, составляет подгруппу аддитивной группы
действительных чисел.

Чтобы установить, что непустое множество группы есть
подгруппа этой группы, достаточно проверить два условия:

1) Для любых двух элементов , их композиция принадлежит
.

2) Для любого элемента обратный
ему элемент также принадлежит .

Докажем это. Условие (1) означает, что операция на множестве
будет операцией и на множестве . Ассоциативность операции на следует из ее ассоциативности на . Из условий (1) и (2) следует, что : взяв какой-либо элемент , по условию (2) найдем в обратный ему элемент , а по условию (1) получим, что содержится в .