- Учебники
- 2 класс
- Математика 👍
- Петерсон
- №5
авторы: Петерсон.
издательство: Ювента
Раздел:
- ЧАСТЬ 2
- Урок 37. Таблица умножения на 3
ГДЗ учебник по математике 2 класс Петерсон. Урок 37. Таблица умножения на 3. Номер №5
- Предыдущее
- Следующее
Найди неизвестную площадь или сторону прямоугольника:
reshalka.com
ГДЗ учебник по математике 2 класс Петерсон. Урок 37. Таблица умножения на 3. Номер №5
Решение а
9 * 3 = 27
(
с
м
2
)
− площадь прямоугольника.
Ответ: 27
с
м
2
Решение б
15 : 5 = 3 (м) − ширина прямоугольника.
Ответ: 3 м
Решение в
24 : 3 = 8 (дм) − длина прямоугольника.
Ответ: 8 дм
- Предыдущее
- Следующее
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
- Объясни по рисункам смысл равенств. Что ты замечаешь?
Решение
Если взять по два три раза или по три два раза, то получим одно и то же произведение 6. Если произведение разделим на один из множителей, то получим другой множитель.
2. Объясни по рисунку смысл равенств.
Что означают первые два равенства? Третье и четвертое равенства? Что тебе напоминают эти 4 равенства?
Решение
Первые два равенства означают, если нужно вычислить произведение чисел 3 и 4, то от перемены их местами все равно получится 12. Если произведение 12 разделить на один из множителей 3 или 4, то получим другой множитель 4 или 3. Эти равенства напоминают таблицу умножения и деления.
3. Пользуясь таблицей умножения, составь 4 равенства из чисел:
а) 3, 6 и 18; б) 8, 3 и 24; в) 3, 7 и 21.
Решение
4. Объясни по рисунку смысл равенств, где а и b — длина и ширина прямоугольника, а S — его площадь.
Что ты замечаешь? Сделай вывод.
Решение
Первые
два равенства показывают, как найти площадь прямоугольника, которая равна
произведению его сторон а и b или b и а.
Если площадь разделить на одну из сторон прямоугольника, то получится его другая сторона.
Зная площадь прямоугольника и длину одной из сторон, можно найти длину другой стороны.
5. Найди длину неизвестной стороны прямоугольника:
Решение
а)
Чтобы найти неизвестную сторону прямоугольника, надо площадь разделить на
известную сторону.
8
: 2 = 4 (см)
б)
Чтобы найти неизвестную сторону прямоугольника, надо площадь разделить на
известную сторону.
10
: 5 = 2 (дм)
в)
Чтобы найти неизвестную сторону прямоугольника, надо площадь разделить на
известную сторону.
18 : 2 = 9 (м)
6. Площадь прямоугольника 14 см², а длина — 7 см. Найди ширину и периметр прямоугольника.
Решение
1)
14 : 7 = 2 (см) – ширина прямоугольника.
2)
(7 + 2) ∙ 2 = 18 (см) — периметр прямоугольника.
Ответ: 2 см, 18 см.
7. а) Длина прямоугольника 6 см. Это на 4 см больше, чем ширина. Построй этот прямоугольник, найди его периметр и площадь.
б) Составь все возможные равенства из чисел, выражающих длины сторон и площадь построенного прямоугольника.
Решение
а) 1) 6 – 4 = 2 (см)
– ширина прямоугольника.
2) (6 + 2) ∙ 2 = 16 (см) — периметр
прямоугольника.
3) 6 ∙ 2 = 12 (см²) – площадь прямоугольника.
8. Какие уравнения не имеют решений, а в каких решением является любое число?
х ∙ 1 = х 0 ∙ х = 2 х : 1 = х х : 0 = 0
Решение
х ∙ 1 = х
Решением уравнения является любое число, так как при умножении любого
числа на 1 получается то же самое число.
0
∙ х = 2 У этого уравнения нет решений, так как при умножении
нуля на любое число получается нуль
х
: 1 = х Решением уравнения является
любое число, так как при делении любого числа на 1 получается то же самое
число.
х : 0 = 0 У этого
уравнения нет решений, так как нуль делить нельзя.
9. Составь программу действий и вычисли:
Решение
10. Составь слова и исключи лишнее слово:
УДБ НЁКЛ АНИБЯР ФАШК АИСОН
Решение
ДУБ КЛЁН
РЯБИНА ШКАФ ОСИНА
Лишнее слово – ШКАФ, так как это мебель, а все остальные слова – названия деревьев.
Назад к содержанию
Зная в прямоугольнике площадь и сторону можно найти вторую сторону, и затем все остальные параметры по порядку. Вторая сторона прямоугольника будет равна отношению площади к известной стороне.
b=S/a
Для того чтобы найти периметр прямоугольника через площадь и сторону, необходимо подставить в формулу вместо второй стороны полученное отношение
P=2(a+b)=2(a+S/a)
Диагональ прямоугольника можно найти через теорему Пифагора в прямоугольном треугольнике, который она образует. Обе диагонали прямоугольника принимают одно и то же значение. Выразив b через площадь и известную сторону, получим следующее выражение. (рис. 56.1)
d_1=d_2=√(a^2+b^2 )=√(a^2+(S/a)^2 )=√(a^2+S^2/a^2 )
Используя тригонометрические отношения в полученном треугольнике можно найти углы при пересечении диагоналей со сторонами. Для этого проще всего будет использовать тангенс, как отношение катетов друг к другу. Точно также, как и в предыдущих формулах, заменяем неизвестную сторону на равное ей выражение.
α=arc tan〖b/a〗=arc tan〖S/a^2 〗
β=arc tan〖a/b=arc tan〖a^2/S〗 〗
Угол, образованный при пересечении диагоналей, и дополнительный ему до 180° зависят только от углов при диагонали и стороне, и равны удвоенному их значению. (рис. 56.2)
γ=2α
δ=2β
Радиус описанной вокруг прямоугольника окружности равен половине диагонали, так как лежит на ней и исходит из точки пересечения диагоналей. (рис. 56.3)
R=d/2=√(a^2+S^2/a^2 )/2
Площадь прямоугольника онлайн
С помощю этого онлайн калькулятора можно найти площадь прямоугольника. Для нахождения площади прямоугольника введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Площадь прямоугольника. Определение
Определение 1. Площадь прямоугольника − это величина той части плоскости, которую занимает прямоугольник.
Площадь прямоугольника. Доказательство
Теорема 1. Площадь S прямоугольника со смежными сторонами a и b равна произведению этих сторон :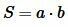
Доказательство. Рассмотрим прямоугольник со сторонами a, b и площадью S (Рис.1). Докажем, что 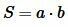
Достроим прямоугольник до квадрата со стороной a+b (Рис.2). Площадь этого квадрата равна (a+b)·(a+b) (см. статью Площадь квадрата онлайн).
С другой стороны, данный квадрат состоит из двух квадратов со сторонами со сторонами a и b и площадями a2 и b2, соответственно и из двух прямоугольников с площадями S. Поэтому сумма площадей этих двух квадратов и двух прямоугольников равна площади квадрата со стороной a+b:
Упрощая полученное равенство, получим: 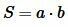
Площадь прямоугольника через стороны
Из вышеизложенной теоремы следует, что площадь прямоугольника через его смежные стороны вычисляется из формулы:
Пример 1. Стороны прямоугольника равны 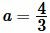
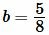
Решение. Для нахождения площади прямоугольника воспользуемся формулой (1). Подставим 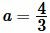
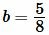
Ответ:
Площадь прямоугольника через сторону и диагональ
Пример 2. Известна сторона прямоугольника 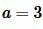
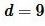
Решение. Найдем сначала неизвестную сторону прямоугольника. Для этого воспользуемся теоремой Пифагора:
Площадь прямоугольника вычисляется из формулы (1). Подставляя (2) в (1), получим формулу вычисления площади прямоугольника через диагональ и сторону:
Подставим 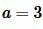
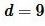
Ответ:
Площадь прямоугольника через периметр и сторону
Пример 3. Известны сторона прямоугольника 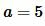
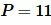
Решение. Найдем сначала неизвестную сторону прямоугольника. Для этого воспользуемся теоремой Пифагора:
Площадь прямоугольника вычисляется из формулы (1). Подставляя (4) в (1), получим формулу вычисления площади прямоугольника через периметр и сторону:
Подставим 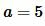
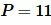
Ответ:
Площадь прямоугольника через диагональ и периметр
Пример 4. Известны диагональ прямоугольника 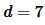
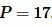
Решение. Найдем сначала стороны прямоугольника. Запишем формулу Пифагора и формулу периметра прямоугольника:
Из формулы (7) найдем ( small b ) и подставим в (6):
Упростив (9), получим квадратное уравнение относительно неизвестной ( a ):
Вычислим дискриминант квадратного уравнения (10):
Подставляя значения 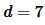
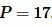
Поскольку дискриминант неотрицательное число, то такой прямоугольник существует.
Стороны прямоугольника вычисляются из формул:
Почему ( small b ), как и ( small a ) получается неотрицательным, посмотрите «примечание» на странице Прямоугольник. Онлайн калькулятор.
Площадь прямоугольника по двум сторонам равна:
Подставляя (12) в (13), получим:
Далее, из (11) и (14) следует:
Подставляя 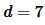
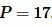
Ответ:
Смотрите также:
- Прямоугольник. Онлайн калькулятор
Где d — диагональ,b — сторона.
Где d — диагональ,α — угол между диагональю и искомой стороной.
Где d — диагональ,α — угол между диагональю и другой стороной.
Где S — площадь, b— известная сторона.
Где P — периметр, b — известная сторона.
Где d — диагональ, α — угол между диагоналями.
- Прямоугольник — это четырехугольник у которого противоположные стороны равны и параллельны AB = CD и BC = DA.
- Стороны прямоугольника являются его высотами.
- Между прилегающими сторонами угол всегда 90°.
Как найти длину стороны прямоугольника?
Сторона прямоугольника может быть легко найдена с помощью нашего онлайн калькулятора. Так же Вы можете воспользоваться формулами ниже для самостоятельного расчета.
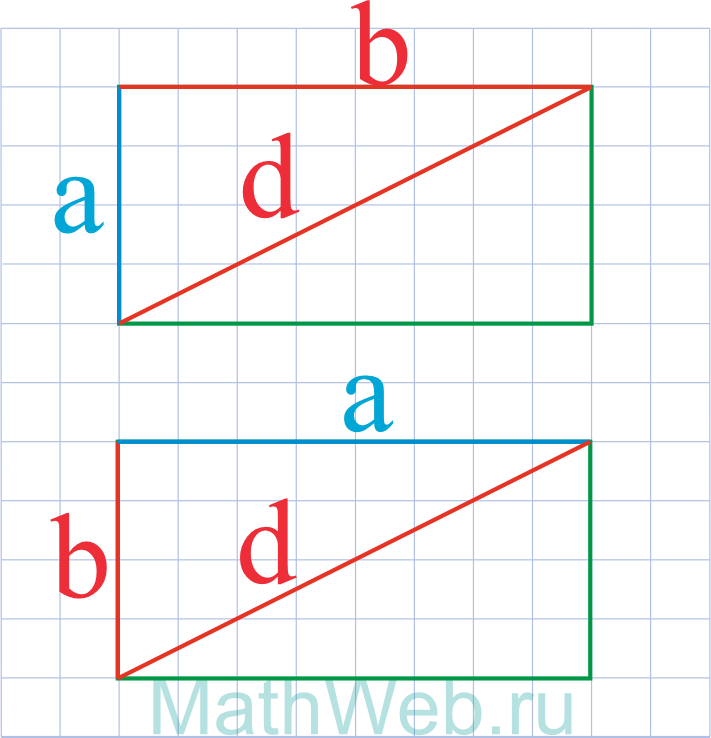 |
a = √d2 ― b2 |
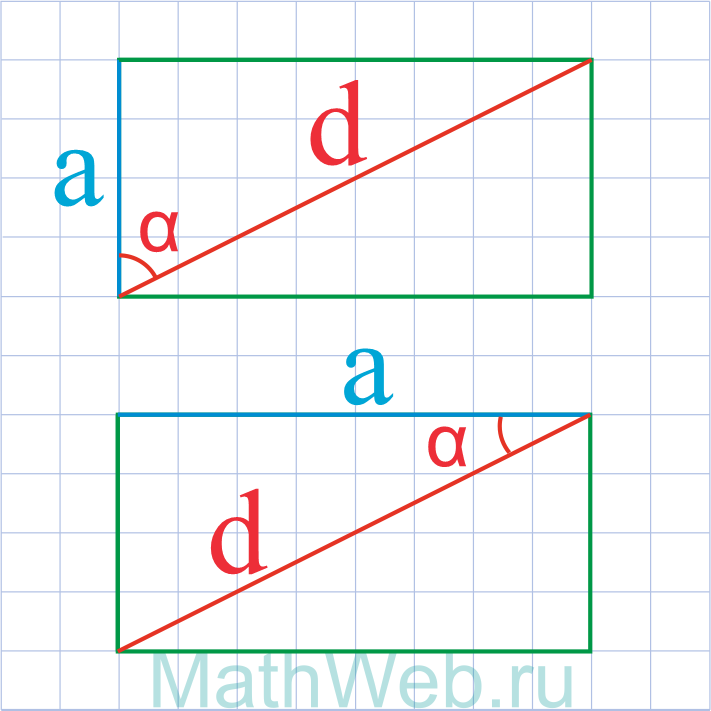 |
a = d·cos(α) |
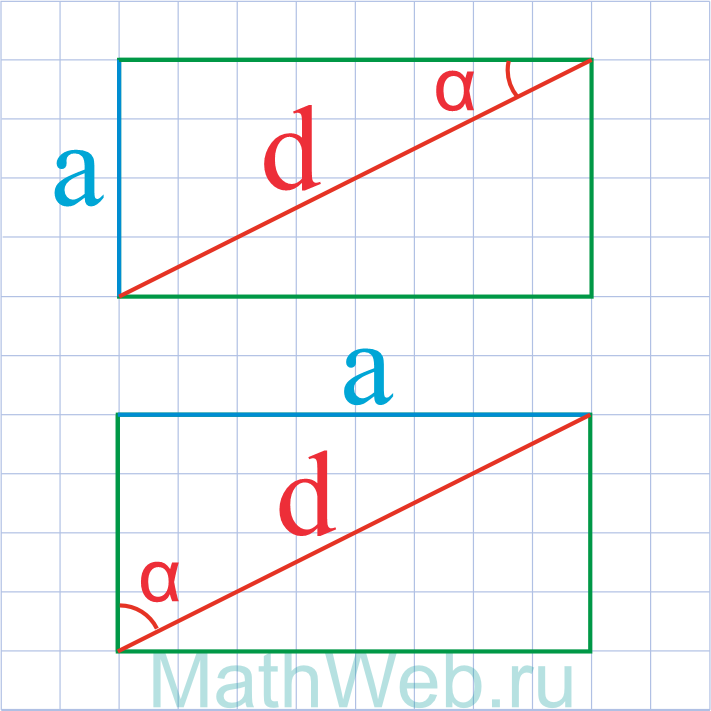 |
a = d·sin(α) |
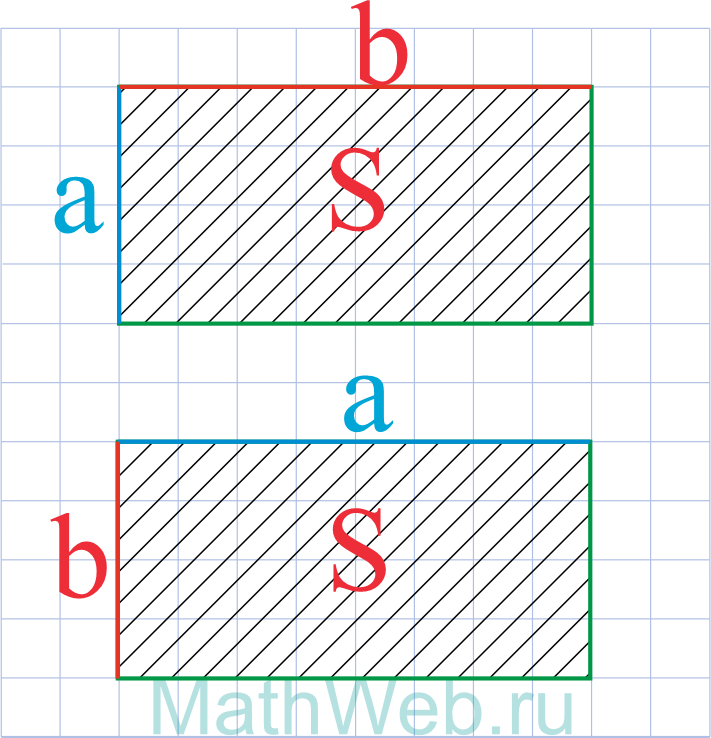 |
a = S b |
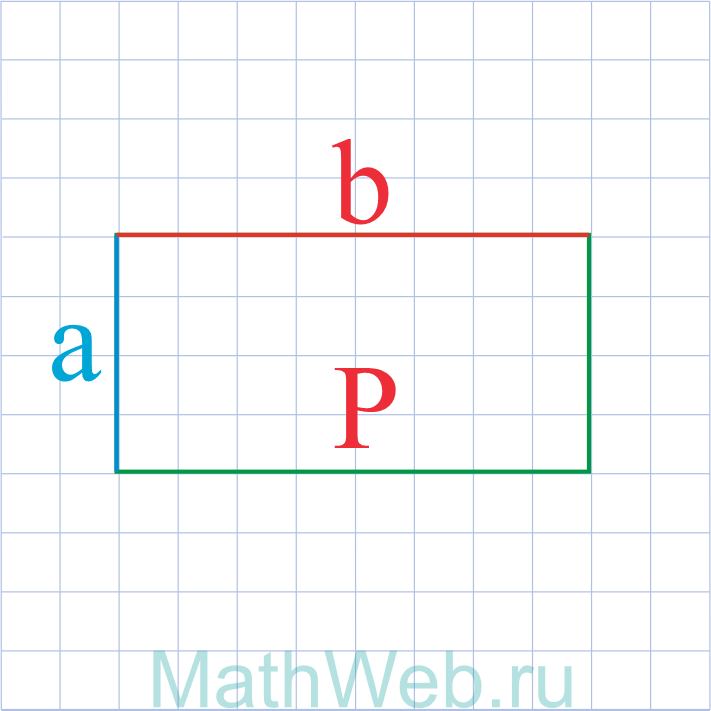 |
a = P — 2b 2 |
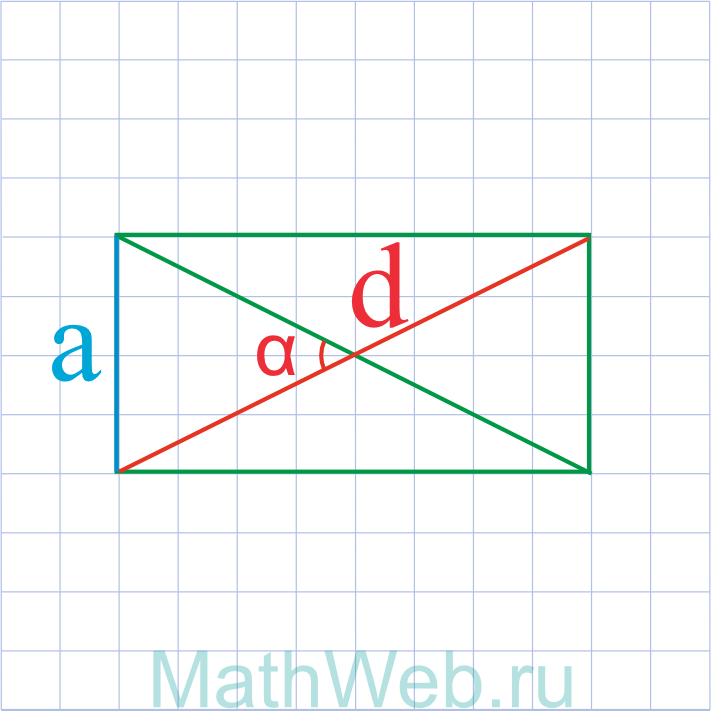 |
a = d·sin(0.5·α) |