Узнай цену своей работы
Формулировка задачи:
Короче у меня есть пример 14=2X+4
Как мне это надо ввести в паскаль? Чтобы вот такой форме была записано. Как мне это сделать?
напишите мне решение пожалуйста.
Код к задаче: «Как найти неизвестную?»
textual
Листинг программы
var x:integer;
begin
writeln('Решаем пример 14=2х+4');
x:=(14-4) div 2;
write('x=',x);
end.
Полезно ли:
8 голосов , оценка 4.125 из 5
Похожие ответы
- Как записать формулу
- Функции. Найти периметр
- Объясните, пожалуйста, как составить матрицу.
- Ввести a>=1. Найти значение какого из выражений больше: 1/а или sin (а)
- Найти периметры и площади трех прямоугольников с противоположными вершинами
- Как присвоить к ответу название детали?
- Найти минимальное значение среди корней этих уравнений.
- Найти сумму целых положительных чисел из промежутка от А до B, кратных 4.
- Как переделать программу, чтобы внешний цикл был repeat.until, а цикл for вложенным? Паскаль
- Найти сумму положительных целых чисел, меньших 100
- Найти номер первого столбца, не содержащего ни одного элемента кратного 2.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
const errMsgPos: String[21] = '*** Ошибка в позиции '; digits=['0'..'9']; function ReadSign(const s: String; var i, n: Integer; Opt: Boolean): Boolean; var j: Integer; begin j:=i; n:=1; if i<=Length(s) then if s[i]='+' then Inc(i) else if s[i]='-' then begin n:=-1; Inc(i); end; ReadSign:=Opt or (i>j); end; function ReadNum(const s: String; var i, n: Integer): Boolean; var j: Integer; begin j:=i; n:=0; while (i<=Length(s)) and (s[i] in digits) do begin n:=n*10+Ord(s[i])-Ord('0'); Inc(i); end; ReadNum:=i>j; end; var s: String; i, sg, sx, a, b, x: Integer; begin Write('Введите выражение вида a+x=b: '); ReadLn(s); i:=1; ReadSign(s,i,sg,True); if s[i]='x' then sx:=sg else if ReadNum(s,i,a) then a:=a*sg else begin WriteLn(errMsgPos,i); Exit; end; if not ReadSign(s,i,sg,False) then begin WriteLn(errMsgPos,i); Exit; end; if s[i]='x' then if sx=0 then begin sx:=sg; Inc(i); end else begin WriteLn(errMsgPos,i); Exit; end else if ReadNum(s,i,a) then a:=a*sg else begin WriteLn(errMsgPos,i); Exit; end; if s[i]='=' then Inc(i) else begin WriteLn(errMsgPos,i); Exit; end; ReadSign(s,i,sg,True); if ReadNum(s,i,b) then b:=b*sg else begin WriteLn(errMsgPos,i); Exit; end; x:=(b-a)*sx; WriteLn('x=',x); end. |
Цели урока:
- Повторить с учащимися правила решения
квадратных уравнений - Вспомнить алгоритмическую конструкцию IF-THEN-ELSE
- Составить блок-схему программы и саму программу
на языке Pascal - Проверить работоспособность программы на
конкретных примерах - Расширить представления учащихся о применении
языка Pascal - Воспитать у учащихся чувство аккуратности,
внимательности, ответственности - Научить учащихся самостоятельно находить свои
ошибки в программах
Оборудование:
- Таблички с формулами
- Плакат с блок-схемой алгоритма КВУР
- Листочки с индивидуальными заданиями
- Система программирования «Turbo Pascal 7.0»
ХОД УРОКА
1. Введение.
До сих пор мы с вами говорили о каких-то
отвлечённых задачах из области математики.
Сегодня мы поговорим о конкретной задаче,
которая встречается у вас почти на каждом уроке.
Это решение квадратного уравнения. Я хочу, чтобы
вы на примере этой задачи поняли, что
программирование — это не просто прихоть
учителя, это действительно раздел информатики,
который может нам помочь, например, в решении
конкретных математических задач. Нужно только
уметь разбираться в этом.
2. Математическое решение
Давайте вспомним, что понимают под квадратным
уравнением?
Вопросы:
Что из себя представляют числа a,b,c и как их
называют?
С чего начинают решение квадратного уравнения?
Найдите вокруг себя формулу дискриминанта. (D=b2-4ac)
(Приложение 3)
Как мы решаем далее квадратное уравнение?
(сравнение D с нулём)
Какие выводы мы из этого делаем?
(если D <0, то нет корней, если D=0, то один корень,
если D>0, то два корня)
Как найти корни квадратного уравнения? Найдите
формулы корней среди тех, что развешены повсюду.
Если я случай наличия корней квадратного
уравнения сведу к условию D0, то что я получу в случае D=0?
(Два одинаковых корня)
Давайте ещё раз подробно разберём нашу задачу:
Итак, у нас есть квадратное уравнение ax2+bx+c=0.
Мы должны решить его, т.е. найти такие значения
х, при которых правая часть уравнения =0. Мы знаем,
что для этого нам надо:
Найти дискриминант D=b2 — 4ac.
Сравнить его с нулём
Если D<0 , то «корней нет» иначе два корня х1 и
х2.
Х1 = , Х2=
Пример: (вызываем ученика)
3х2-10х+3=0
D=b2-4ac=102-4*3*3=100 — 36 =64
D>0, два корня
Х1=,
X2 =
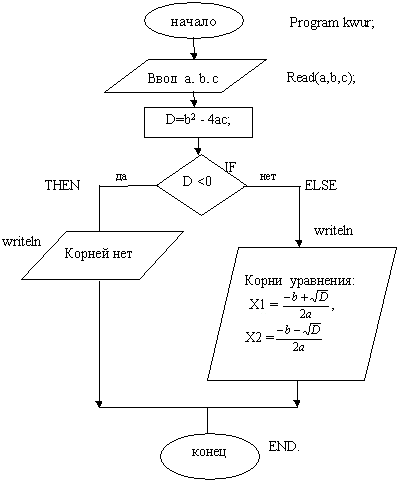
3. Составление блок-схемы алгоритма.
По заданному решению попробуем составить
блок-схему алгоритма в тетради. Кто справится
первым, прошу к доске.
Подпишем основные элементы блок — схемы
применительно к языку программирования.
4. Составление программы по блок — схеме.
Теперь, пользуясь нашими записями, составим
программу и покажем её учителю. Тот, кто до конца
урока составит только программу, не проверив её
на компьютере, получит три, тот, кто наберёт
программу на компьютере, но не проверит её на
примерах, получит три. Тот, кто выполнит всё
задание, получит пять.
А я раздам вам домашнее задание.
Ответ:
Program kwur;
Uses CRT;
Var a,b,c,d,x1,x1: real;
Begin
Clrscr;
Write(‘введите коэффициенты уравнения a,b,c’);
readln(a,b,c);
D:=b*b-4*a*c;
If d>=0 then
Begin
X1:=(-b+sqrt(d))/(2*a); x2:=(-b-sqrt(d))/(2*a);
Writeln(‘x1=’,x1′ x2=’,x2)
END;
Else writeln(‘действительных корней нет’)
End.
5. Практическая работа (Приложение
1).
1. Составить и набрать программу КВУР на
компьютере.
Подсказка:
Загрузка среды Pascal- 2ЩЛКМ по значку Pascal, нажать
ALT+ENTER.
Запуск программы — ЩЛКМ по кнопке RUN выбрать RUN.
2. Решить следующие квадратные уравнения и
показать учителю их решения (если нет такой
возможности, то занести их в маршрутный лист (Приложение 4)
3х2 -10х +1=0
0,5х2+2х — 4=0
4х2 + х — 6=0
2х2 + 3х +8=0
х2 +4 =0
5х2 -8х = 0
1,5х2-0,6х — 4,8 = 0
-2х2+4х — 8 = 0
9х2+4х -7 = 0
0,1х2— 9 = 0
3. Переделайте программу КВУР таким образом,
чтобы в ней учитывался случай, когда D=0 и
уравнение имеет один корень.
4. Закрыть программу.
Подсказка: Меню File — Exit или ALT+X.
Оценивание:
1. За простое воспроизведение (набор программы)
без проверки оценка «3»
2. За проверку работы программы на примерах,
представленных учителем оценка «4»
3. За решение всех заданий и дополнительное
изменение программы для случая D=0, оценка «5»
4. Закрыть программу.
Подсказка: Меню File — Exit или ALT+X.
Ответы:
| № | Х1 | Х2 |
| 1 | 3,230139 | 0,1031947 |
| 2 | 1,464102 | -5,464102 |
| 3 | 1,106107 | -1,356107 |
| 4 | Корней нет | |
| 5 | Корней нет | |
| 6 | 1,6 | 0 |
| 7 | 2 | -1,6 |
| 8 | Корней нет | |
| 9 | 0,6872614 | -1,131706 |
| 10 | 9,486833 | -9,486833 |
Можно дать дополнительное задание:
Изменить программу так, чтобы ответ был с
точностью до 2-х знаков после запятой.
6. Домашнее задание: (Приложение 2)
1) Напишите программу проверки пароля. Пусть
пароль — некоторое число, зафиксированное в
программе. Программа печатает приглашение
«введите пароль» и вводит число. Если введённое
число совпадает с фиксированным паролем, то
программа выводит приветствие, если нет —
сообщает о том, что пароль не угадан.
7. Подведение итогов урока.
Итак, ребята, сегодня мы с вами решали
конкретные задачи из математики, применяя свои
умения по программированию. Вы получили
следующие оценки за свои знания. (Перечисление
оценок) На следующем уроке нам предстоит
познакомиться с новыми алгоритмами —
Циклическими.
На сегодня наш урок закончен. До свидания.
Литература:
- И. Семакин, Л. Залогова «Информатика. Базовый
курс. 9 класс», М., БИНОМ, 2005г. - А.А. Чернов «Конспекты уроков информатики в 9-11
классах», Волгоград: Учитель, 2006г. - Л.И. Белоусова, С.А. Веприк «Сборник задач по
курсу информатики», М., «Экзамен», 2007.
Приветствуем читателей нашего сайта! С сегодняшнего дня две недели подряд мы решаем задачи из сборника Абрамяна. Сегодня мы наконец-то добьем if16-30. А вообще мы решим все задачи из While и For и, может быть, Series.
If16. Даны три переменные вещественного типа: A, B, C. Если их значения упорядочены по возрастанию, то удвоить их; в противном случае заменить значение каждой переменной на противоположное. Вывести новые значения переменных A, B, C.
Program If_16;
var a, b, c: integer;
begin
write('Введите A, B и C: ');
readln(a, b, c);
if (b<c) and (a<b) then
begin
a := 2 * a;
b := 2 * b;
c := 2 * c;
end
else begin
a := -a;
b := -b;
c := -c;
end;
writeln (a,' ', b,' ', c);
end.
If17. Даны три переменные вещественного типа: A, B, C. Если их значения упорядочены по возрастанию или убыванию, то удвоить их; в противном случае заменить значение каждой переменной на противоположное. Вывести новые значения переменных A, B, C.
Program If_17;
var
a, b, c: integer;
begin
write('Введите A, B и C: ');
readln(a, b, c);
if (b < a) and (c < b) or (b < c) and (a < b) then
begin
a := 2 * a;
b := 2 * b;
c := 2 * c;
end
else
begin
a := -a;
b := -b;
c := -c;
end;
writeln(a, ' ', b, ' ', c);
end.
If18. Даны три целых числа, одно из которых отлично от двух других, равных между собой. Определить порядковый номер числа, отличного от остальных.
Program If_18; var a, b, c: integer; begin readln(a, b, c); if a = b then write(3); if b = c then write(1); if a = c then write(2); end.
If19. Даны четыре целых числа, одно из которых отлично от трех других, равных между собой. Определить порядковый номер числа, отличного от остальных.
Используем метод полностью противоположный предыдущему. Проверяем числа на неравенство, а не на равенство.
program if19;
var
a, b, c, d: integer;
begin
read(a, b, c, d);
if (a <> b) and (a <> c) then write(1) {проверяем неравенство два раза. вдруг это b другое число.}
else
if (a <> b) and (b <> c) then write(2)
else
if (c <> a) and (c <> b) then write(3)
else write(4); {если все варианты совпадают, следовательно 4 другой}
end.
If20. На числовой оси расположены три точки: A, B, C. Определить, какая из двух последних точек (B или C) расположена ближе к A, и вывести эту точку и ее расстояние от точки A.
Для того чтобы решить эту задачу, используем модуль, ведь модуль — это расстояние. В Паскаль есть специальная функция для превращения любого числа в положительное число — abs.
program if20;
var
A, B, C, ras1, ras2: integer;
begin
write('Введите A: ');
read(A);
write('Введите B и C: ');
read(B, C);
ras1 := Abs(A - B);
ras2 := Abs(A - C);
if ras1 < ras2 then Write('Ближайшая к точке А точка B и растояние между ними - ', ras1)
else write('Ближайшая к точке А точка C и растояние между ними - ', ras2);
end.
If21. Даны целочисленные координаты точки на плоскости. Если точка совпадает с началом координат, то вывести 0. Если точка не совпадает с началом координат, но лежит на оси OX или OY, то вывести соответственно 1 или 2. Если точка не лежит на координатных осях, то вывести 3.
program if21; var x, y: integer; begin read(x, y); if (x = 0) and (y = 0) then write(0) else if x = 0 then write(2) else if y = 0 then write(1) else write(3); end.
If22°. Даны координаты точки, не лежащей на координатных осях OX и OY. Определить номер координатной четверти, в которой находится данная точка.
Если кто-то не помнит как располагаются координатные четверти, вот небольшая картинка.
program if22;
var
X, Y: integer;
begin
write('Введите X: ');
read(X);
write('Введите Y: ');
read(Y);
if (X > 0) and (Y > 0) then write(1);
if (X < 0) and (Y > 0) then write(2);
if (X < 0) and (Y < 0) then write(3);
if (X > 0) and (Y < 0) then write(4);
end.
If23. .аны целочисленные координаты трех вершин прямоугольника, стороны которого параллельны координатным осям. Найти координаты его четвертой вершины.
Очень много if. Суть метода в том, что сравнивая введенные x и y друг с другом, мы находим, какие точки лежат на одной прямой, какие нет, а затем в зависимости от их положения находим неизвестный x и y.
program if23;
var
x1, y1, x2, y2, x3, y3, x4, y4: integer;
begin
write('Введите x1. y1: ');
readln(x1, y1);
write('Введите x2, y2: ');
readln(x2, y2);
write('Введите x3, y3: ');
readln(x3, y3);
if x1 = x2 then x4 := x3;
if x1 = x3 then x4 := x2;
if x2 = x3 then x4 := x1;
if y1 = y2 then y4 := y3;
if y1 = y3 then y4 := y2;
if y2 = y3 then y4 := y1;
writeln('Координаты четвертой вершины: (', x4, ';', y4,')' );
end.
If24. Для данного вещественного x найти значение следующей функции f, принимающей вещественные значения: f(x) =
2·sin(x), если x > 0,
6 – x, если x ≤ 0.
program if24;
var
x, f: real;
begin
write('Введите X: ');
readln(x);
if x > 0 then f := 2 * Sin(x)
else f := 6 - x;
writeln('f(x) = ', f:1:2);
end.
If25. Для данного целого x найти значение следующей функции f, принимающей значения целого типа: f(x) =
2·x, если x < –2 или x > 2,
–3·x, в противном случае.
program if25;
var
x, f: integer;
begin
write('Введите X: ');
readln(x);
if (x < -2) or (x > 2) then f := 2 * x
else f := -3 * x;
writeln('f(x) = ', f);
end.
If26°. Для данного вещественного x найти значение следующей функции f, принимающей вещественные значения: f(x) =
–x, если x ≤ 0,
x2, если 0 < x < 2,
4, если x ≥ 2.
program if26;
var
x, f: real;
begin
write('Введите X: ');
readln(x);
if (x <= 0) then f := -x else if (x >= 2) then f := 4
else f := Sqr(x);
writeln('f(x) = ', f:1:2);
end.
If27. Для данного вещественного x найти значение следующей функции f, принимающей значения целого типа: f(x) =
0, если x < 0,
1, если x принадлежит [0, 1), [2, 3), …,
–1, если x принадлежит [1, 2), [3, 4), ….
Как решать эту задачу? Давайте поразмышляем. Посмотрите на второе условие, нижняя граница полуинтервала — четное число. Любое число в этом интервале задается формулой — четное число. набор цифр. Тогда наша цель — достать целую часть из вещественного числа. Для этого используем функцию trunc. Осталось только узнать четность числа, в этом нам помогут div и mod.
program if27;
var
f, x: real;
begin
write('Введите X = '); {предположим вы ввели 1.5}
readln(X);
if (x < 0) then f := 0
else
if (Trunc(x) mod 2 = 0) then f := 1 { trunk(1.5) = 1, 1 mod 2 <> 0}
else f := -1;
writeln('f(x) = ', f); { вывод: -1}
end.
If28. Дан номер года (положительное целое число). Определить количество дней в этом году, учитывая, что обычный год насчитывает 365 дней, а високосный — 366 дней. Високосным считается год, делящийся на 4, за исключением тех годов, которые делятся на 100 и не делятся на 400 (например, годы 300, 1300 и 1900 не являются високосными, а 1200 и 2000 — являются).
program if28;
var
year: integer;
begin
write('Введите год: ');
readln(year);
if year mod 4 = 0 then
if year mod 100 = 0 then
if year mod 400 <> 0 then write('365 дней')
else write('366 дней')
else write('366 дней')
else write('365 дней');
end.
If29. Дано целое число. Вывести его строку-описание вида «отрицательное четное число», «нулевое число», «положительное нечетное число» и т. д.
program if29;
var
number: integer;
begin
write('Введите число: ');
readln(number);
if number = 0 then
begin
write('нулевое число');
exit // обрывает работу программы
end
else
if number > 0 then write('Положительное ') else write('Отрицательное ');
if number mod 2 = 0 then write('четное ') else write('нечетное ');
end.
If30. Дано целое число, лежащее в диапазоне 1–999. Вывести его строку-описание вида «четное двузначное число», «нечетное трехзначное число» и т. д.
program if30;
var
a: integer;
begin
write('Введите число: ');
read(a);
if Odd(a) then write('Нечетное ') else write('Четное ');
if a >= 100 then write('трехзначное число') else
if a < 10 then write('однозначное число') else write('двухзначное число');
end.
На сегодня все! Не забудьте подписаться на наш сайт и покликать по кнопочкам. Если у вас возникли вопросы, задавайте их в комментариях.

Наиболее распространенные прямые методы основаны на приведении СЛАУ к «треугольному» виду (см. матрицу Т). Это достигается последовательным исключением неизвестных из уравнений исходной системы. Сначала с помощью первого уравнения исключается X1 из всех последующих уравнений системы, затем, используя второе уравнение, исключается X2 из третьего и всех последующих уравнений. Этот процесс, называемый прямым ходом метода Гаусса, продолжается до тех пор, пока в левой части последнего (n-го) уравнения не останется лишь один член с неизвестным Xn, т. е. матрица системы будет приведена к треугольному виду. (Замечание: к такому виду приводится только невырожденная матрица, иначе данный метод неприменим).
Пусть методом исключения Гаусса требуется решить СЛАУ
x1 + x2 + x3 – x4 = 2 ; x1 – x2 – x3 + x4 = 0 ; 2x1 + x2 – x3 + 2x4 = 9 ; 3x1 + x2 + 2x3 – x4 = 7 .
Для удобства обозначим уравнения буквами и будем выписывать только коэффициенты при неизвестных и свободные члены уравнений. Тогда исходная СЛАУ примет вид
|
A1 |
1 1 1 -1 |
2 |
|
A2 |
1 -1 -1 1 |
0 |
|
A3 |
2 1 -1 2 |
9 |
|
A4 |
3 1 2 -1 |
7 |
Исключая члены, содержащие x1, получим
|
B1 = A1/1 |
1 1 1 -1 |
2 |
|
B2 = A2 – B1 |
0 -2 -2 2 |
-2 |
|
B3 = A3 – 2B1 |
0 -1 -3 4 |
5 |
|
B4 = A4 – 3B1 |
0 -2 -1 2 |
1 |
После исключения членов с x2 имеем
|
B1 |
1 1 1 |
-1 |
2 |
|
C2 = B2/(-2) |
0 1 1 -1 |
1 |
|
|
C3 = B3 + C2 |
0 0 -2 3 |
6 |
|
|
C4 = B4 + 2C2 |
0 0 1 0 |
3 |
|
|
Исключения членов с x3 дает |
|||
|
В1 |
1 1 1 |
-1 |
2 |
|
С2 |
0 1 1 |
-1 |
1 |
|
D3 = C3 /(-2) |
0 0 1 |
-3/2 |
-3 |
|
D4 = C4 – D3 |
0 0 0 |
3/2 |
6 |
Продолжая аналогичные действия с последним рядом, получим
64
|
B1 |
1 1 1 |
-1 |
2 |
|
C2 |
0 1 1 |
-1 |
1 |
|
D3 |
0 0 1 |
-3/2 |
-3 |
|
E4 = 2D4 /3 |
0 0 0 1 |
4 |
Возвращаясь к общепринятой форме уравнений, запишем
|
x1 + x2 + x3 – |
x4 |
= 2 ; |
|
x2 + x3 – |
x4 |
= 1 ; |
x3 – 1.5 x4 = -3 ; x4 = 4 .
Обратный ход метода Гаусса состоит в последовательном вычислении исходных неизвестных. Из последнего уравнения находим единственное неизвестное x4, подставляя значение x4 в третье уравнение, x3 – во второе и т. д., находим решение заданной СЛАУ:
x1 = 1, x2 = 2, x3 = 3, x4 = 4.
Аналогично строится алгоритм для СЛАУ с произвольным числом уравнений. Необходимо помнить, что при решении СЛАУ может потребоваться операция перестановок уравнений (т. е. перестановки соответствующих коэффициентов), служащая для предотвращения деления на нулевой элемент.
Данный метод целесообразно использовать для решения систем с плотно заполненной матрицей. Все элементы матрицы и правые части системы уравнений (все вместе есть расширенная матрица) находятся в оперативной памяти ЭВМ. Объем вычислений определяется порядком системы n: число арифметических операций примерно равно (2/3)n3.
Вычисленное по методу Гаусса решение X* для СЛАУ, записанной в матричном виде A X = B, отличается от точного решения X из-за погрешностей округления, связанных с ограниченностью разрядной сетки ЭВМ. Существуют две величины, характеризующие степень отклонения полученного решения X* от точного X. Одна из них – погрешность Е, равная разности этих значений: E = X – X*.
Другая – невязка r, равная разности между правой и левой частями уравнений при подстановке в них решения: r = B – A X*.
Реализация метода на языке Паскаль
Потребуется описание используемых типов для расширенной матрицы коэффициентов и для вектора значений переменных:
type mat=array[1..20,1..21] of real; vec=array[1..20] of real;
var n:integer; {Реальное число уравнений} a:mat; x:vec;
65
Ввод матрицы наиболее эффективно реализовать из файла данных. Для этого потребуется файловый тип и файловая переменная
var f:text;
В основной части программы ввод можно организовать следующим образом:
Write(‘Введите число уравнений N = ‘); readln(n); assign(f,’alex.dat’); {имя файла данных на диске} reset(f);
for i:=1 to n do begin
for j:=1 to n+1 do read(f,a[i,j]); readln(f);
end;
close(f);
Прямой ход метода Гаусса (формирование треугольной матрицы коэффициентов) может выглядеть так:
for k:=1 to n do begin s:=a[k,k];j:=k;
for i:=k+1 to n do begin r:=a[i,k];
if abs(r)>abs(s) then begin
s:=r; j:=i; end;
end; if s=0 then
begin
writeln(‘Переставьте уравнения чтобы на главной диагонали не было нулевых коэффициентов !’);
halt;
end;
if j<>k then
for i:=k to n+1 do begin
r:=a[k,i]; a[k,i]:=a[j,i];a[j,i]:=r; end;
for j:=k to n+1 do a[k,j]:=a[k,j]/s; for i:=k+1 to n do
begin
66
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #