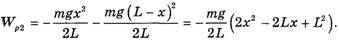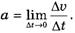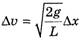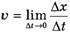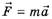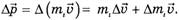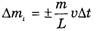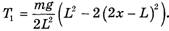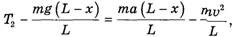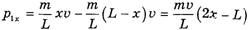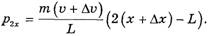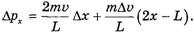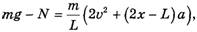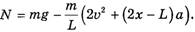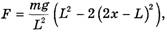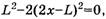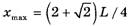Как найти натяжение нити перекинутой через блок

Блоки, нити, грузы и перегрузки

Задача 1.  К телу массой кг подвешено на веревке тело массой кг. Масса веревки кг. Вся система движется ускоренно вверх под действием силы Н, приложенной к верхнему телу (рис.1). Найти натяжение веревки в ее центре и в точках крепления тел и .

Представим всю систему единым телом массой . Будем действовать на эту систему с силой . Тогда по второму закону Ньютона

Откуда найдем ускорение системы:

Теперь вернемся к первому рисунку и запишем уравнения по второму закону Ньютона для верхнего  и нижнего грузов:

Откуда

Очевидно, что посередине веревки сила ее натяжения будет средним арифметическим найденных двух сил:

Ответ: Н, Н, Н.

Задача 2. Маляр массой кг работает в подвесном кресле. Ему понадобилось срочно подняться вверх. Он начинает тянуть веревку с такой силой, что сила давления на кресло уменьшается до Н. Масса кресла кг. Чему равно ускорение маляра? Чему равна нагрузка на блок?

Расставим силы. Отметим все силы, действующие не маляра, и силы, действующие на люльку:

Теперь можно написать уравнения:

Вычитаем уравнения:

Ответ: м/с.

Задача 3.

Через легкий неподвижный блок перекинута невесомая нерастяжимая нить с двумя грузами на концах, массы которых и , . Система приходит в движение, причем нить не проскальзывает относительно блока. Определить ускорение грузов, силу натяжения нити и силу давления на ось блока.

Понятно, что больший груз перетянет и начнет двигаться вниз, а меньший – подниматься. Запишем для них уравнение по второму закону:

Сложим уравнения:

Откуда

Теперь можно найти и силу натяжения нити:

Сила давления на блок равна :

Ответ: , ,
.

Задача 4.

Через блок перекинута нить, на концах которой висят два груза с одинаковыми массами . Одновременно на каждый из грузов кладут по перегрузку: справа  массой , слева (рис. 2). Определить ускорение системы, силу натяжения нити и силу давления перегрузков на основные грузы.

Запишем уравнение по второму закону Ньютона для обоих грузов с учетом массы перегрузков:

Сложение уравнений даст нам

Сила натяжения нити найдется подстановкой найденного ускорения в любое уравнение системы:

Определим силу давления меньшего перегрузка массой на груз :

Для большего перегрузка

Ответ: , , , .

Задача 5.

Через неподвижный блок перекинута нить, к которой подвешены три одинаковых груза массой кг каждый (рис. 3). Найти ускорение системы и силу натяжения нити между грузами 1 и 2. Какой путь пройдут грузы за первые с движения? Трением пренебречь.

Сначала мысленно объединим два груза слева в один и запишем уравнение по второму закону:

Для правого грузика

Складываем уравнения:

Определим силу натяжения нити между грузиками. Обозначим ее . Тогда для самого нижнего грузика слева:

Определяем путь грузиков за 4 с:

Ответ: м/с, Н, м.

Задача 6.

Определить ускорение грузов и силы натяжения всех нитей в системе, изображенной на рисунке. Масса каждого груза , массой блока пренебречь.

Сначала определяем ускорение. Для этого записываем уравнение по второму закону для грузиков справа и слева, пока не вспоминая о том, что их там несколько. Для нас сейчас это  груз массой  справа и слева. Силу натяжения основной нити обозначим :

Складываем уравнения:

Тогда

Рассмотрим теперь грузы, висящие справа. Обозначим натяжение нити между ними . Для нижнего груза справа

Осталось определить и . Для верхнего грузика слева

Откуда

А для нижнего грузика слева

Ответ: , , , , .

Задача 7.

Два груза массами г и г соединены нерастяжимой нитью, перекинутой через невесомый блок (рис.). Грузы прижимаются друг к другу с постоянными силами Н. Коэффициент трения между ними . Найти ускорение, с которым движутся грузы.

Записываем уравнение по второму закону:

Тогда

Ответ: .

Задача 8.

Невесомая нить, перекинутая через неподвижный блок, пропущена через щель (рис.). При движении нити на нее действует постоянная сила трения . На концах нити подвешены грузы, массы которых и . Определить ускорение грузов.

Давайте предположим, что . Тогда левый груз начинает движение вверх, правый – вниз. Записываем для них уравнение  по второму закону с учетом наличия силы трения:

Складывая уравнения, имеем:

Откуда

Но, если бы , тогда

Тогда, чтобы учесть обе возможности, запишем ответ так:

Ответ: .

Задача 9.

Через невесомый блок перекинута легкая нерастяжимая нить, к одному концу которой привязан груз массой г, а по другому
скользит кольцо массой г (рис.). С каким ускорением движется кольцо, если груз  неподвижен?

Сила трения кольца в данном случае и порождает силу натяжения нити, то есть это одна и та же сила. Поэтому для неподвижного груза

А для кольца

Ответ: 6 м/с.

4 комментария

Рассмотрим широко известную задачу (см. [1]-[5]), условие которой сформулируем следующим образом.

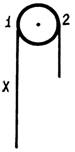
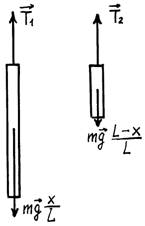
Однородная гладкая веревка массой m и длиной L переброшена через блок. В начальный момент веревка висит симметрично и покоится, а затем в результате незначительного толчка начинает двигаться по блоку. Какова скорость υ конца веревки в тот момент, когда с одной стороны блока свешивается большая часть веревки длиной x? Чему равно ускорение a конца веревки в этот момент? С какой силой F веревка давит на блок в этот момент? Чему равны силы натяжения веревки T_t и T₂ в точках 1 и 2 (рис. 1)? Массой блока пренебречь, радиус блока считать малым, веревка нерастяжима.

Рис. 1

Приступая к решению задачи, допустим, что веревка натянута в каждом своем сечении, что важно для дальнейших рассуждений. В частности, в этом случае модули линейных скоростей всех элементов веревки равны, что позволяет легко вычислять кинетическую энергию веревки. Выберем нулевой уровень потенциальной энергии на уровне оси блока. Тогда в начальный момент потенциальная энергия веревки

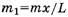
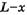
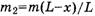
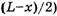
так как центр масс ниже нулевого уровня на L/4. В момент, когда с одной стороны свешивается часть веревки длиной xи массой  (ее центр масс ниже оси блока на x/2), а с другой — часть веревки длиной  и массой  (ее центр масс ниже оси блока на , потенциальная энергия всей веревки

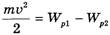
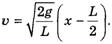
Тогда из закона сохранения механической энергии  легко найти скорость конца веревки υ:

                                             (1)

Перейдем к нахождению ускорения конца веревки. Поскольку зависимость для скорости известна, оптимальным способом будет нахождение ускорения в соответствии с определением

Из соотношения (1) найдем

и, учитывая, что по определению

окончательно имеем:

                                              (2)

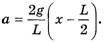
Для определения сил натяжения веревки в точках 1 и 2 в литературе [4] (задача 8.20), [6] для левого и правого концов веревки составляется система уравнений, аналогичная стандартной системе уравнений для движения грузов массами m₁и m₂,связанных невесомой нерастяжимой нитью, перекинутой через блок (рис. 2):

                                               (*)

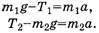
Рис. 2

Из этой системы следует, что

                                        (3)

                                           (4)

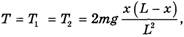
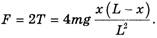
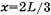
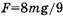
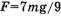
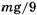
Кстати, формула ускорения, получаемая из системы (*), имеет вид (2).) Однако, если по формуле (4) найти ответ к задаче 2.4.13 из [5] (при ), то получим , хотя в книге ответ другой: . В чем же дело? И какой ответ правильный? Оказывается, второй, а значит, формулы (3) и (4) неверны. В [6] сделана попытка объяснить это различие тем, что «небольшой блок может сыграть дурную шутку: ведь часть веревки, которая находится на блоке, обладает центростремительным ускорением и таким образом «съедает» часть силы давления». Далее находится эта часть . Такой подход представляется формальным и недостаточно обоснованным, ибо не позволяет выявить истинную причину правильности второго ответа. К тому же формула (3) остается даже при таком подходе, а она неверна, что мы и покажем ниже.

Попробуем корректно найти силы, о которых идет речь в задаче. Главный источник ошибки при выводе формул (3) и (4) — игнорирование того факта, что второй закон Ньютона в форме

применим только к простейшей модели — материальной точке (или поступательно движущемуся абсолютно твердому телу). Веревка же в описанной ситуации ею не является, она даже поступательно не движется. Более того, в отличие от аналогичной ситуации с грузами на невесомой веревке, массы левого и правого концов веревки все время изменяются. В этой ситуации необходимо применять закон изменения импульса системы точек в форме

                                               (5)

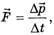
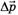
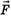
где  — изменение суммарного импульса системы точек за время Δt, а  — векторная сумма внешних сил, действующих на тела системы.

Рассмотрим два возможных варианта дальнейшего решения задачи. Поскольку блок мал, массой части веревки, прилегающей к блоку, пренебрегаем.

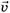
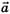
Решение 1. Формулу (5) будем применять для правого и левого концов веревки отдельно, что очень удобно с точки зрения равенства скоростей  и ускорений  всех точек данного конца веревки. Так как изменяется и масса m₁ свисающего конца веревки, и его скорость, то

Учитывая определение ускорения и то, что

(знак «+» — при увеличении массы, знак «–» — приуменьшении массы), перепишем (5) в виде

                                               (6)

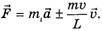
Тогда для левого конца веревки (сила T₁ являетсядля него внешней) (см. рис. 2)

                                    (7)

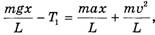
откуда с учетом (1) и (2)

Аналогично для правого конца веревки

откуда с учетом (1) и (2)

                                                  (8)

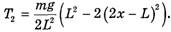
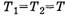
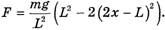
Таким образом, . (Сравните формулы (3) и (8).) Значит, веревка давит на блок с силой

                                  (9)

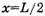
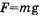
При  получаем ,

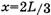
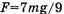
при  —  (см. выше).

Решение 2. Формулу (5) применяем для всей веревки (рис. 3):

                                       (10)

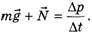
Рис. 3

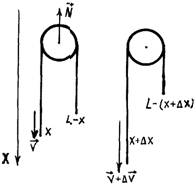
Пусть за время Δt левый конец веревки сместился на Δx, а скорость его увеличилась на Δυ. Тогда с учетом направления движения концов веревки запишем проекции начального импульса

и конечного импульса всей веревки

Пренебрегая слагаемым второго порядка малости, содержащим произведение 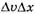, для проекции изменения импульса имеем:

Учитывая определения скорости и ускорения и формулу (10), получим

откуда

Так как по третьему закону Ньютона 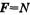, то, учитывая (1) и (2), окончательно имеем:

что совпадает с (9).

Проанализируем формулы (8) и (9). Решив квадратное уравнение

получим, что при длине левого конца веревки

веревка перестанет действовать на блок. Очевидно, что

Таким образом, формулы (1), (2), (7)-(9) перестают быть справедливыми при 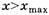. Значит, веревка перестанет действовать на блок раньше, чем вся она соскользнет с блока и станет невесомой. При длине веревки 1 м длина короткого конца веревки в этот момент составит весьма заметную величину порядка 14 см. В этот момент модель, принятая нами, перестанет действовать. Натяжение веревки в точках 1 и 2 исчезает. Точно описать поведение всей веревки в дальнейшем мы не можем. Для этого необходимо знать силы натяжения веревки в ее различных сечениях. (Можно провести наблюдение за скольжением металлической цепочки с мелкими звеньями по стеклянной палочке и направлением падения ее верхнего конца.) Правомерно ли в таком случае требовать нахождения скорости веревки (как единого целого) в тот момент, когда она сойдет с блока (подразумевается прохождение конца вертикально расположенной веревки через точку 1),если мы не уверены в том, что все точки веревки двигаются с одинаковой линейной скоростью? А ведь именно так стоит вопрос к этой задаче в большинстве сборников задач ([1]-[3]).

И последнее. Почему выражение, получаемое для ускорения из заведомо ложной системы уравнений (*), получается правильным? Очевидно, это происходит потому, что при сложении выражений, предшествующих (7) и (8), слагаемые 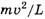компенсируют друг друга (поскольку они имеют противоположные знаки). При этом получается точно такое же уравнение, как и при сложении уравнений системы (*).

1. Фейнмановские лекции по физике. Задачи и упражнения. — М.: Мир, 1967.

2. Гольдфарб Н.И. Сборник вопросов и задач по физике. — М.: Высш. шк., 1975.

3. Сборник задач по физике / Под ред. С.М.Козела. — М.: Наука, 1990.

4. Гельфгат И.М., Генденштейн Л.Э., Кирик Л.А. 1001 задача по физике с ответами, указаниями, решениями. — М.: Илекса, 2001.

5. Задачи по физике / Под ред. О.Я.Савченко. — М.: Наука, 1988.

6. Корсунский Б. Внимание: ловушка! // Квант. — 1992. — № 7.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?